Estimating Growing Stock Volume at Tree and Stand Levels for Chinese Fir (Cunninghamia lanceolata) in Southern China Using UAV Laser Scanning
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Field-Measured Data
2.3. UAV-LS Data
2.4. Base Models and Variable Selection
2.5. Dummy Variable Models
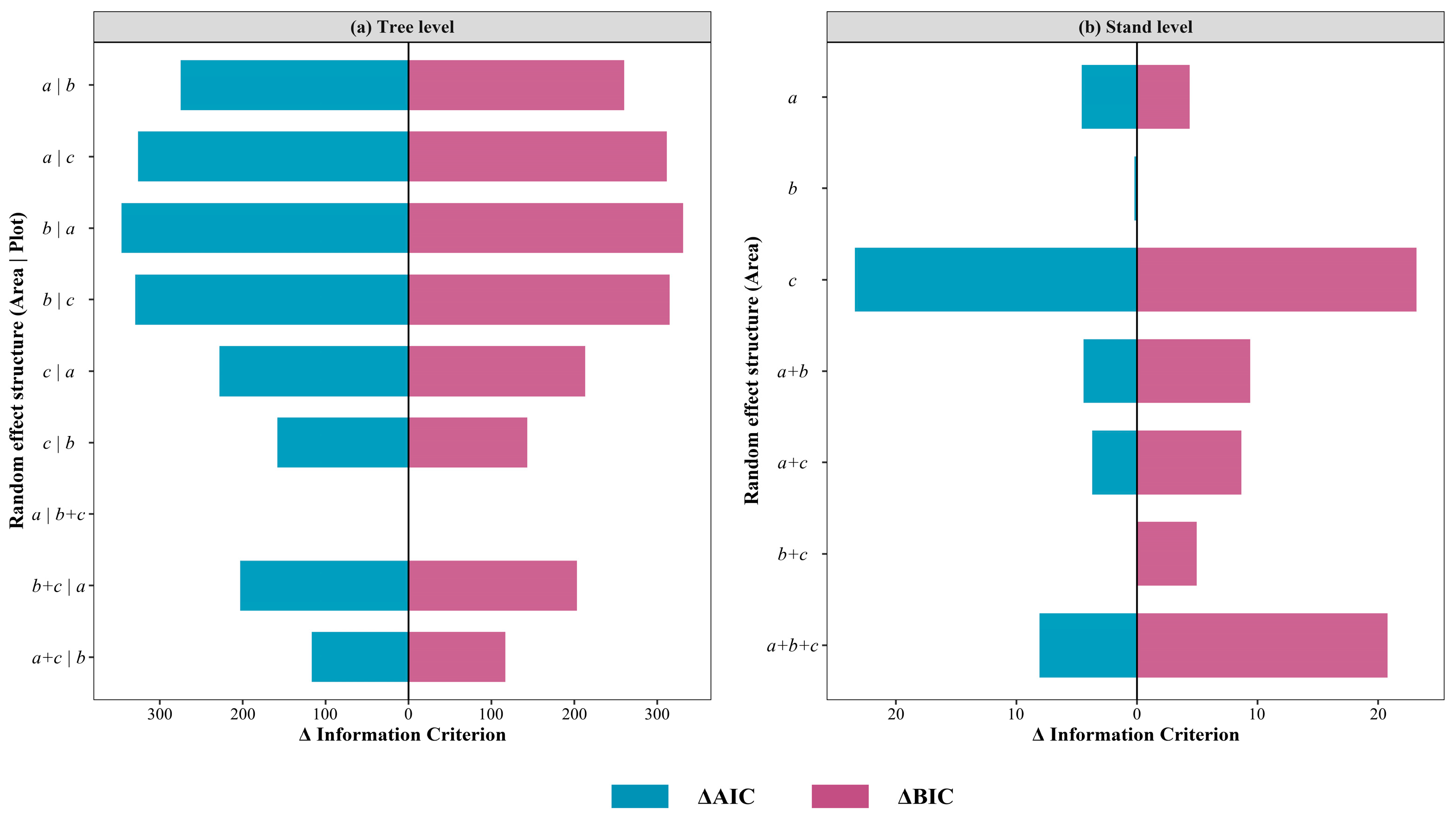
2.6. Nonlinear Mixed-Effects Models
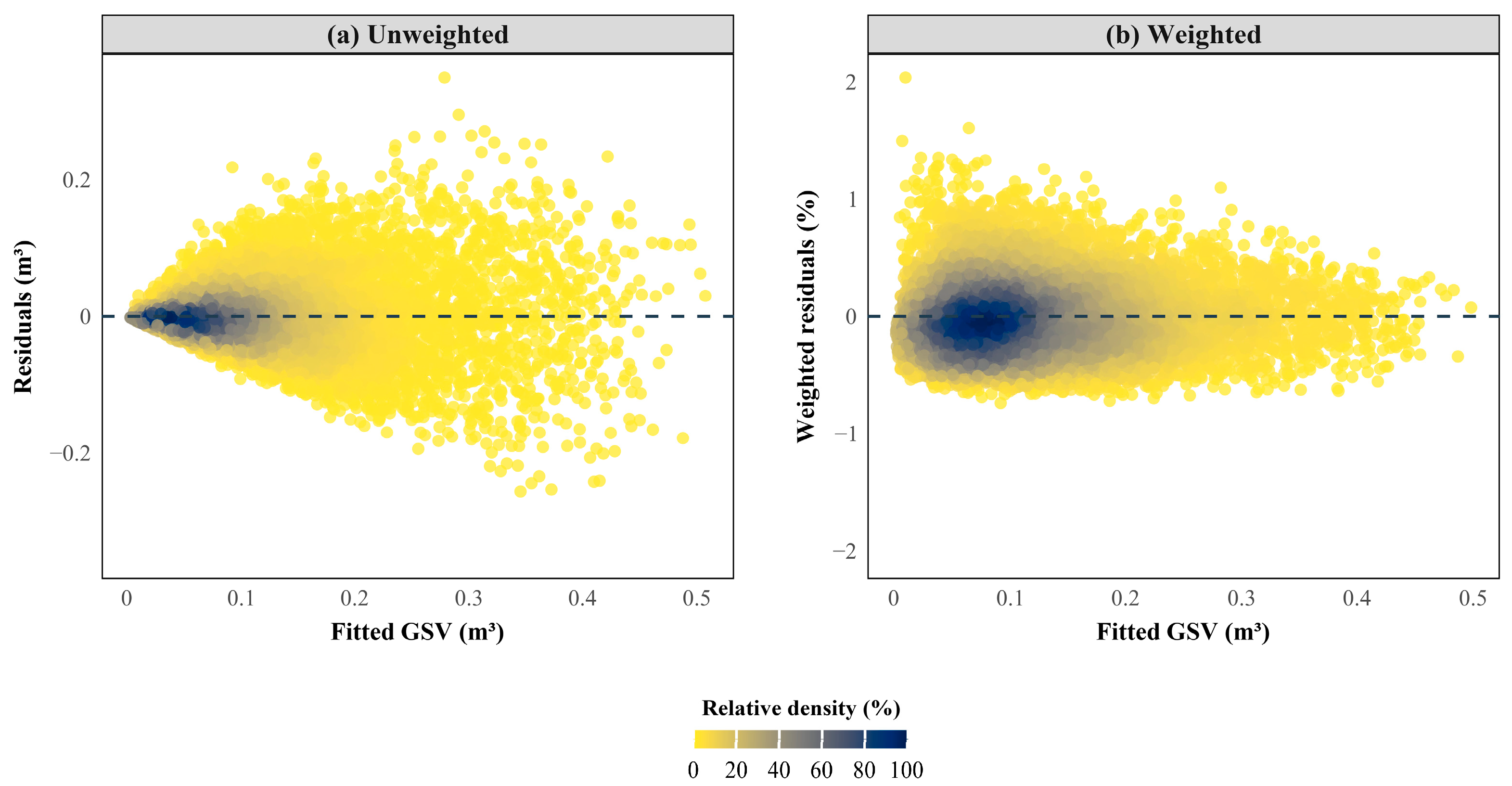
2.7. Heteroscedasticity Correction and Model Evaluation
3. Results
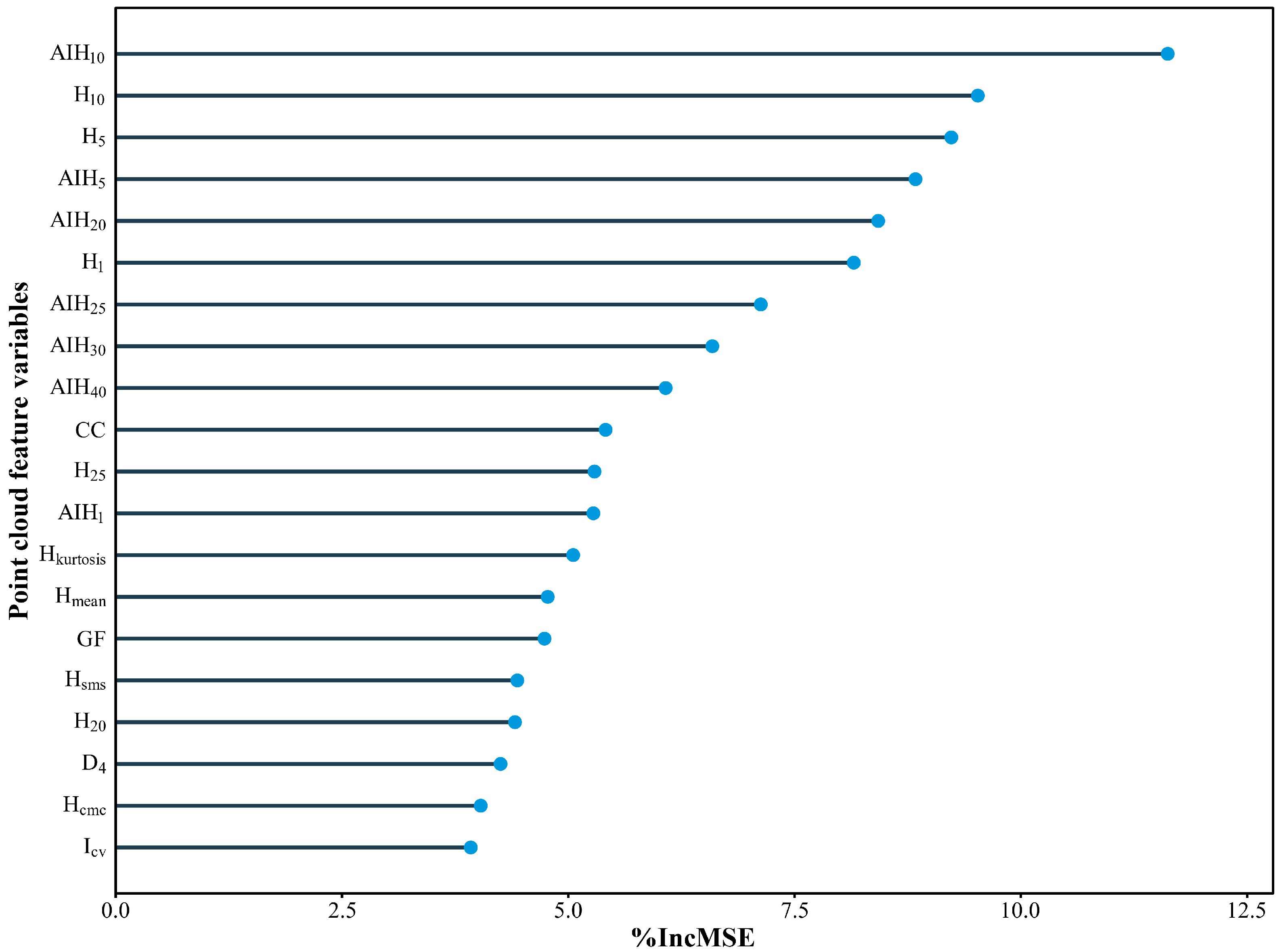
3.1. Variable Importance Assessment
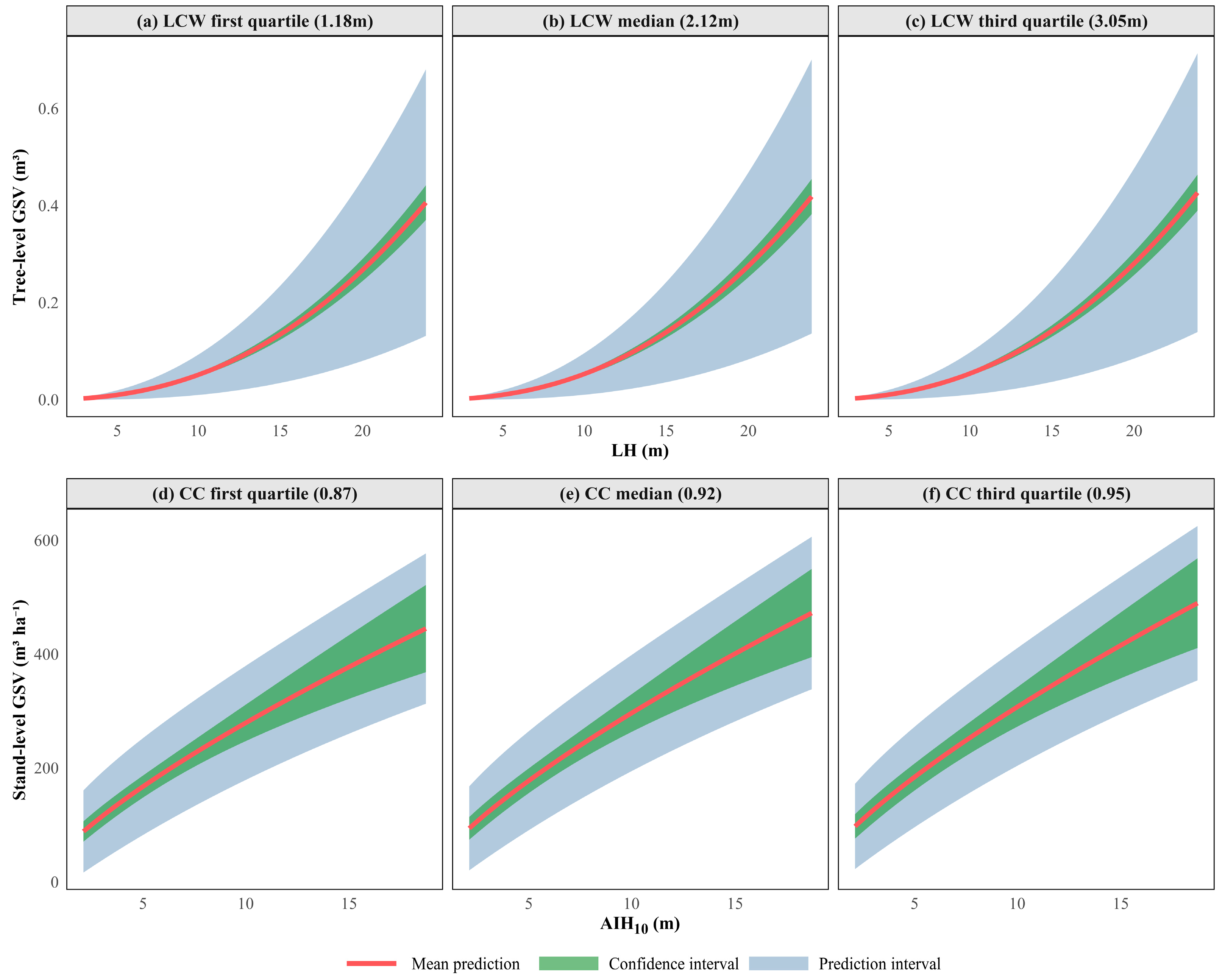
3.2. Model Development and Training Performance
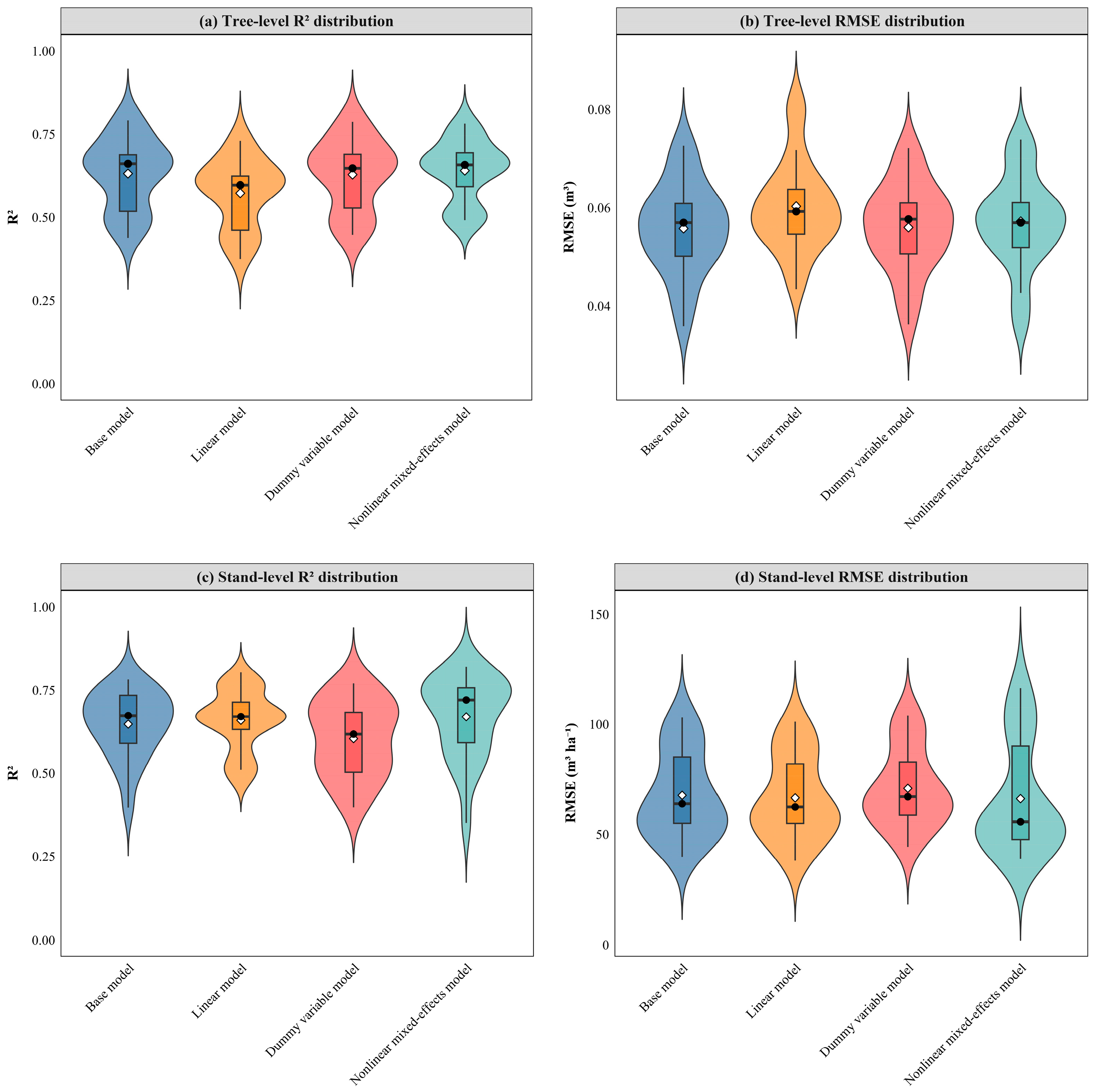
3.3. Randomized Testing and Spatial Cross-Validation
4. Discussion
5. Conclusions
- (1)
- At the stand level, height metrics were the most critical for accurate GSV prediction. The optimal predictor combination was the 10th cumulative height percentile (AIH10) and canopy cover (CC), exhibiting a nearly linear relationship with GSV. At the tree level, the preferred predictors were LiDAR-derived tree height (LH) and crown width (LCW), with LH accounting for the majority of the variation in GSV.
- (2)
- Regardless of scale (tree or stand level), the base models demonstrated superior fit and prediction accuracy compared to the linear models. The dummy variable models provided only a marginal improvement over the base models. The nonlinear mixed-effects models significantly outperformed the base models. While tree-level models exhibited larger errors for individual tree estimates, they yielded smaller errors for population-level estimates. Stand-level model prediction errors remained within acceptable limits. Consequently, both approaches are suitable for areal forest resource monitoring.
- (3)
- For tree-level models, the area-level random effect primarily governed the baseline GSV, while the plot-level random effect mainly affected the allometric relationship between GSV and predictors LH and LCW. At the stand level, the area-level random effect predominantly influenced the allometric relationship between GSV and AIH10.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| LH | LCW | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 | 2.2 | |
| 2 | 0.00106 | 0.00109 | 0.00112 | 0.00113 | 0.00115 | 0.00116 | 0.00117 | 0.00118 | 0.00118 | 0.00119 | 0.00120 |
| 3 | 0.00275 | 0.00285 | 0.00291 | 0.00296 | 0.00299 | 0.00302 | 0.00304 | 0.00307 | 0.00308 | 0.00310 | 0.00312 |
| 4 | 0.00543 | 0.00563 | 0.00575 | 0.00584 | 0.00590 | 0.00596 | 0.00601 | 0.00605 | 0.00609 | 0.00612 | 0.00615 |
| 5 | 0.00920 | 0.00954 | 0.00974 | 0.00989 | 0.01001 | 0.01010 | 0.01018 | 0.01025 | 0.01032 | 0.01037 | 0.01042 |
| 6 | 0.01416 | 0.01468 | 0.01499 | 0.01522 | 0.01539 | 0.01554 | 0.01567 | 0.01578 | 0.01587 | 0.01596 | 0.01604 |
| 7 | 0.02038 | 0.02113 | 0.02158 | 0.02190 | 0.02216 | 0.02237 | 0.02255 | 0.02271 | 0.02285 | 0.02297 | 0.02309 |
| 8 | 0.02794 | 0.02897 | 0.02959 | 0.03003 | 0.03038 | 0.03067 | 0.03092 | 0.03113 | 0.03133 | 0.03150 | 0.03165 |
| 9 | 0.03691 | 0.03827 | 0.03908 | 0.03967 | 0.04013 | 0.04052 | 0.04084 | 0.04113 | 0.04138 | 0.04161 | 0.04181 |
| 10 | 0.04735 | 0.04909 | 0.05013 | 0.05089 | 0.05148 | 0.05197 | 0.05239 | 0.05276 | 0.05308 | 0.05337 | 0.05364 |
| 11 | 0.05931 | 0.06149 | 0.06280 | 0.06375 | 0.06449 | 0.06510 | 0.06563 | 0.06609 | 0.06649 | 0.06686 | 0.06719 |
| 12 | 0.07285 | 0.07553 | 0.07714 | 0.07830 | 0.07921 | 0.07997 | 0.08061 | 0.08117 | 0.08167 | 0.08212 | 0.08253 |
| 13 | 0.08802 | 0.09125 | 0.09320 | 0.09460 | 0.09571 | 0.09662 | 0.09740 | 0.09808 | 0.09868 | 0.09922 | 0.09972 |
| 14 | 0.10487 | 0.10872 | 0.11104 | 0.11271 | 0.11403 | 0.11512 | 0.11604 | 0.11685 | 0.11757 | 0.11822 | 0.11880 |
| 15 | 0.12345 | 0.12798 | 0.13070 | 0.13267 | 0.13422 | 0.13550 | 0.13659 | 0.13755 | 0.13839 | 0.13915 | 0.13984 |
| 16 | 0.14379 | 0.14906 | 0.15224 | 0.15454 | 0.15634 | 0.15783 | 0.15910 | 0.16021 | 0.16119 | 0.16208 | 0.16289 |
| 17 | 0.16594 | 0.17203 | 0.17569 | 0.17834 | 0.18042 | 0.18214 | 0.18361 | 0.18489 | 0.18603 | 0.18705 | 0.18798 |
| 18 | 0.18994 | 0.19691 | 0.20111 | 0.20414 | 0.20652 | 0.20849 | 0.21017 | 0.21163 | 0.21293 | 0.21410 | 0.21517 |
| 19 | 0.21583 | 0.22375 | 0.22852 | 0.23196 | 0.23467 | 0.23691 | 0.23881 | 0.24048 | 0.24196 | 0.24328 | 0.24449 |
| 20 | 0.24364 | 0.25258 | 0.25797 | 0.26186 | 0.26491 | 0.26744 | 0.26959 | 0.27147 | 0.27314 | 0.27464 | 0.27600 |
| 21 | 0.27342 | 0.28346 | 0.28950 | 0.29386 | 0.29729 | 0.30012 | 0.30254 | 0.30465 | 0.30652 | 0.30821 | 0.30974 |
| 22 | 0.30519 | 0.31640 | 0.32314 | 0.32801 | 0.33184 | 0.33500 | 0.33770 | 0.34005 | 0.34214 | 0.34402 | 0.34573 |
| 23 | 0.33900 | 0.35144 | 0.35894 | 0.36435 | 0.36860 | 0.37211 | 0.37511 | 0.37772 | 0.38004 | 0.38213 | 0.38403 |
| 24 | 0.37487 | 0.38863 | 0.39692 | 0.40290 | 0.40760 | 0.41149 | 0.41480 | 0.41769 | 0.42026 | 0.42257 | 0.42467 |
| 25 | 0.41284 | 0.42800 | 0.43712 | 0.44371 | 0.44889 | 0.45316 | 0.45681 | 0.46000 | 0.46282 | 0.46537 | 0.46768 |
| AIH10 | CC | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.30 | 0.35 | 0.40 | 0.45 | 0.50 | 0.55 | 0.60 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | |
| 2 | 24.92 | 29.74 | 34.67 | 39.68 | 44.79 | 49.96 | 55.21 | 60.52 | 65.90 | 71.33 | 76.81 | 82.35 |
| 3 | 33.65 | 40.16 | 46.81 | 53.59 | 60.48 | 67.47 | 74.56 | 81.73 | 88.99 | 96.33 | 103.73 | 111.21 |
| 4 | 41.64 | 49.70 | 57.93 | 66.32 | 74.85 | 83.50 | 92.27 | 101.15 | 110.13 | 119.21 | 128.38 | 137.63 |
| 5 | 49.13 | 58.64 | 68.35 | 78.25 | 88.30 | 98.51 | 108.86 | 119.34 | 129.93 | 140.64 | 151.46 | 162.37 |
| 6 | 56.23 | 67.12 | 78.24 | 89.56 | 101.08 | 112.76 | 124.61 | 136.60 | 148.73 | 160.99 | 173.37 | 185.86 |
| 7 | 63.04 | 75.24 | 87.70 | 100.40 | 113.31 | 126.41 | 139.68 | 153.13 | 166.72 | 180.46 | 194.34 | 208.35 |
| 8 | 69.59 | 83.06 | 96.82 | 110.84 | 125.09 | 139.55 | 154.21 | 169.05 | 184.06 | 199.23 | 214.55 | 230.02 |
| 9 | 75.94 | 90.64 | 105.65 | 120.95 | 136.50 | 152.28 | 168.27 | 184.47 | 200.85 | 217.40 | 234.12 | 250.99 |
| 10 | 82.10 | 98.00 | 114.23 | 130.77 | 147.58 | 164.64 | 181.94 | 199.45 | 217.16 | 235.05 | 253.13 | 271.37 |
| 11 | 88.11 | 105.17 | 122.59 | 140.34 | 158.38 | 176.69 | 195.25 | 214.04 | 233.04 | 252.25 | 271.65 | 291.23 |
| 12 | 93.98 | 112.17 | 130.75 | 149.68 | 168.93 | 188.46 | 208.25 | 228.29 | 248.56 | 269.05 | 289.74 | 310.62 |
| 13 | 99.72 | 119.03 | 138.74 | 158.83 | 179.25 | 199.97 | 220.98 | 242.24 | 263.75 | 285.49 | 307.44 | 329.60 |
| 14 | 105.35 | 125.74 | 146.57 | 167.79 | 189.37 | 211.26 | 233.45 | 255.92 | 278.64 | 301.60 | 324.80 | 348.20 |
| 15 | 110.88 | 132.34 | 154.26 | 176.59 | 199.30 | 222.34 | 245.69 | 269.34 | 293.25 | 317.42 | 341.83 | 366.47 |
| 16 | 116.31 | 138.82 | 161.82 | 185.24 | 209.06 | 233.23 | 257.73 | 282.53 | 307.62 | 332.97 | 358.57 | 384.42 |
| 17 | 121.65 | 145.20 | 169.25 | 193.76 | 218.66 | 243.95 | 269.57 | 295.51 | 321.75 | 348.27 | 375.05 | 402.08 |
| 18 | 126.91 | 151.48 | 176.57 | 202.14 | 228.12 | 254.50 | 281.23 | 308.30 | 335.67 | 363.33 | 391.27 | 419.47 |
| 19 | 132.10 | 157.67 | 183.79 | 210.40 | 237.45 | 264.90 | 292.73 | 320.90 | 349.39 | 378.19 | 407.27 | 436.62 |
| 20 | 137.22 | 163.78 | 190.91 | 218.55 | 246.65 | 275.16 | 304.07 | 333.33 | 362.92 | 392.83 | 423.04 | 453.53 |
| 21 | 142.27 | 169.81 | 197.94 | 226.59 | 255.73 | 285.29 | 315.26 | 345.60 | 376.28 | 407.30 | 438.62 | 470.23 |
| 22 | 147.26 | 175.76 | 204.88 | 234.54 | 264.69 | 295.30 | 326.31 | 357.72 | 389.48 | 421.58 | 454.00 | 486.72 |
| 23 | 152.19 | 181.65 | 211.74 | 242.39 | 273.56 | 305.18 | 337.24 | 369.70 | 402.52 | 435.70 | 469.20 | 503.01 |
| 24 | 157.07 | 187.47 | 218.52 | 250.16 | 282.32 | 314.96 | 348.05 | 381.54 | 415.42 | 449.65 | 484.23 | 519.13 |
| 25 | 161.89 | 193.23 | 225.24 | 257.84 | 290.99 | 324.63 | 358.73 | 393.26 | 428.17 | 463.46 | 499.10 | 535.07 |
References
- Fang, J.; Chen, A.; Peng, C.; Zhao, S.; Ci, L. Changes in forest biomass carbon storage in China between 1949 and 1998. Science 2001, 292, 2320–2322. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Zhao, P.; Lei, Y.; Zeng, W. Comparison on estimation of wood biomass using forest inventory data. Sci. Silv. Sin. 2012, 48, 44–52. [Google Scholar]
- IPCC (Intergovernmental Panel on Climate Change). 2006 IPCC Guidelines for National Greenhouse Gas Inventories; Institute for Global Environmental Strategies: Kanagawa, Japan, 2006. [Google Scholar]
- Gschwantner, T.; Alberdi, I.; Bauwens, S.; Bender, S.; Borota, D.; Bosela, M.; Bouriaud, O.; Breidenbach, J.; Donis, J.; Fischer, C.; et al. Growing stock monitoring by European National Forest Inventories: Historical origins, current methods and harmonisation. For. Ecol. Manag. 2022, 505, 119868. [Google Scholar] [CrossRef]
- Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Queinnec, M.; Luther, J.E.; Bolton, D.K.; White, J.C.; Wulder, M.A.; van Lier, O.R.; Hermosilla, T. Modelling lidar-derived estimates of forest attributes over space and time: A review of approaches and future trends. Remote Sens. Environ. 2021, 260, 112477. [Google Scholar] [CrossRef]
- Ye, Y.; Coops, N.C.; Wulder, M.A.; Hermosilla, T. A multi-resolution forest stand segmentation algorithm integrating Landsat imagery and forest structural, age, and species attributes. ISPRS J. Photogramm. Remote Sens. 2025, 226, 381–395. [Google Scholar] [CrossRef]
- Zhou, M.; Li, C.A.; Li, Z. Extraction of individual tree attributes using ultra-high-density point clouds acquired by low-cost UAV-LiDAR in Eucalyptus plantations. Ann. For. Sci. 2025, 82, 20. [Google Scholar] [CrossRef]
- Hu, Y.; Sun, R.; He, M.; Zhao, J.; Li, Y.; Huang, S.; Zhang, J. Estimating spatiotemporal dynamics of carbon storage in Roinia pseudoacacia plantations in the Caijiachuan Watershed using sample plots and uncrewed aerial vehicle-borne laser scanning data. Remote Sens. 2025, 17, 1365. [Google Scholar] [CrossRef]
- Lei, L.T.; Chai, G.Q.; Yao, Z.Q.; Li, Y.B.; Jia, X.; Zhang, X.L. A novel self-similarity cluster grouping approach for individual tree crown segmentation using multi-features from UAV-based LiDAR and multi-angle photogrammetry data. Remote Sens. Environ. 2025, 318, 114588. [Google Scholar] [CrossRef]
- Mermoz, S.; Réjou-Méchain, M.; Villard, L.; Le Loan, T.; Rossi, V.; Gourlet-Fleury, S. Decrease of L-band SAR backscatter with biomass of dense forests. Remote Sens. Environ. 2015, 159, 307–317. [Google Scholar] [CrossRef]
- Joshi, N.; Mitchard, E.T.A.; Brolly, M.; Schumacher, J.; Fernández-Landa, A.; Johannsen, V.K.; Marchamalo, M.; Fensholt, R. Understanding ‘saturation’ of radar signals over forests. Sci. Rep. 2017, 7, 3505. [Google Scholar] [CrossRef]
- Oehmcke, S.; Li, L.; Trepekli, K.; Revenga, J.C.; Nord-Larsen, T.; Gieseke, F.; Igel, C. Deep point cloud regression for above-ground forest biomass estimation from airborne LiDAR. Remote Sens. Environ. 2024, 302, 113968. [Google Scholar] [CrossRef]
- Borsah, A.A.; Nazeer, M.; Wong, M.S. LiDAR-based forest biomass remote sensing: A review of metrics, methods, and assessment criteria for the selection of allometric equations. Forests 2023, 14, 2095. [Google Scholar] [CrossRef]
- Beland, M.; Parker, G.; Sparrow, B.; Harding, D.; Chasmer, L.; Phinn, S.; Antonarakis, A.; Strahler, A. On promoting the use of lidar systems in forest ecosystem research. For. Ecol. Manag. 2019, 450, 117484. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Q.; Pang, Y. Review on forest parameters inversion using LiDAR. J. Remote Sens. 2016, 20, 1138–1150. [Google Scholar] [CrossRef]
- Guo, Q.; Liu, J.; Tao, S.; Xue, B.; Li, L.; Xu, G.; Li, W.; Wu, F.; Li, Y.; CHen, L.; et al. Perspectives and prospects of LiDAR in forest ecosystem monitoring and modeling. Chin. Sci. Bull. 2014, 59, 459–478. [Google Scholar] [CrossRef]
- Puliti, S.; Breidenbach, J.; Astrup, R. Estimation of forest growing stock volume with UAV laser scanning data: Can it be done without field data? Remote Sens. 2020, 12, 1245. [Google Scholar] [CrossRef]
- Xu, D.D.; Wang, H.B.; Xu, W.X.; Luan, Z.Q.; Xu, X. LiDAR applications to estimate forest biomass at individual tree scale: Opportunities, challenges and future perspectives. Forests 2021, 12, 550. [Google Scholar] [CrossRef]
- Xu, Q.; Man, A.; Fredrickson, M.; Hou, Z.Y.; Pitkänen, J.; Wing, B.; Ramirez, C.; Li, B.; Greenberg, J.A. Quantification of uncertainty in aboveground biomass estimates derived from small-footprint airborne LiDAR. Remote Sens. Environ. 2018, 216, 514–528. [Google Scholar] [CrossRef]
- Fu, L.Y.; Liu, Q.W.; Sun, H.; Wang, Q.Y.; Li, Z.Y.; Chen, E.X.; Pang, Y.; Song, X.Y.; Wang, G.X. Development of a system of compatible individual tree diameter and aboveground biomass prediction models using error-in-variable regression and airborne LiDAR data. Remote Sens. 2018, 10, 325. [Google Scholar] [CrossRef]
- Salas, C.; Ene, L.; Gregoire, T.G.; Naesset, E.; Gobakken, T. Modelling tree diameter from airborne laser scanning derived variables: A comparison of spatial statistical models. Remote Sens. Environ. 2010, 114, 1277–1285. [Google Scholar] [CrossRef]
- Novotny, J.; Navrátilová, B.; Janoutová, R.; Oulehle, F.; Homolová, L. Influence of site-specific conditions on estimation of forest above ground biomass from airborne laser scanning. Forests 2020, 11, 268. [Google Scholar] [CrossRef]
- Popescu, S.C. Estimating biomass of individual pine trees using airborne lidar. Biomass Bioenergy 2007, 31, 646–655. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, Z.N.; Cao, L. Individual tree structural parameter extraction and volume table creation based on near-field LiDAR data: A case study in a subtropical planted forest. Sensors 2021, 21, 8162. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.; Lee, J. Advancing stem volume estimation using multi-platform LiDAR and taper model integration for precision forestry. Remote Sens. 2025, 17, 785. [Google Scholar] [CrossRef]
- Bornand, A.; Rehush, N.; Morsdorf, F.; Thürig, E.; Abegg, M. Individual tree volume estimation with terrestrial laser scanning: Evaluating reconstructive and allometric approaches. Agric. For. Meteorol. 2023, 341, 109654. [Google Scholar] [CrossRef]
- Zeng, W.; Sun, X.; Wang, L.; Wang, W.; Pu, Y. Development of forest stand volume models based on airborne laser scanning data. Sci. Silv. Sin. 2021, 57, 31–38. [Google Scholar]
- Garcia-Gutierrez, J.; Gonzalez-Ferreiro, E.; Riquelme-Santos, J.C.; Miranda, D.; Dieguez-Aranda, U.; Navarro-Cerrillo, R.M. Evolutionary feature selection to estimate forest stand variables using LiDAR. Int. J. Appl. Earth Observ. Geoinf. 2014, 26, 119–131. [Google Scholar] [CrossRef]
- García-Gutiérrez, J.; Martínez-Alvarez, F.; Troncoso, A.; Riquelme, J.C. A comparison of machine learning regression techniques for LiDAR-derived estimation of forest variables. Neurocomputing 2015, 167, 24–31. [Google Scholar] [CrossRef]
- Xu, C.; Manley, B.; Morgenroth, J. Evaluation of modelling approaches in predicting forest volume and stand age for small-scale plantation forests in New Zealand with RapidEye and LiDAR. Int. J. Appl. Earth Observ. Geoinf. 2018, 73, 386–396. [Google Scholar] [CrossRef]
- Leite, R.V.; do Amaral, C.H.; Pires, R.D.; Silva, C.A.; Soares, C.P.B.; Macedo, R.P.; da Silva, A.A.L.; Broadbent, E.N.; Mohan, M.; Leite, H.G. Estimating stem volume in Eucalyptus plantations using airborne LiDAR: A comparison of area- and individual tree-based approaches. Remote Sens. 2020, 12, 1513. [Google Scholar] [CrossRef]
- Liu, K.; Shen, X.; Cao, L.; Wang, G.B.; Cao, F.L. Estimating forest structural attributes using UAV-LiDAR data in Ginkgo plantations. ISPRS J. Photogramm. Remote Sens. 2018, 146, 465–482. [Google Scholar] [CrossRef]
- Yu, S.H.; Chen, X.Y.; Huang, X.; Chen, Y.C.; Hu, Z.Y.; Liu, J.; Yu, K.Y. Research on the estimation of Chinese fir stand volume based on UAV-LiDAR technology. Forests 2023, 14, 1252. [Google Scholar] [CrossRef]
- Zhou, X.S.; Ma, K.S.; Sun, H.; Li, C.K.; Wang, Y.H. Estimation of forest stand volume in coniferous plantation from individual tree segmentation aspect using UAV-LiDAR. Remote Sens. 2024, 16, 2736. [Google Scholar] [CrossRef]
- Li, C.A.; Lin, X.; Dai, H.B.; Li, Z.; Zhou, M. Effects of plot size on airborne LiDAR-derived metrics and predicted model performances of subtropical planted forest attributes. Forests 2022, 13, 2124. [Google Scholar] [CrossRef]
- Li, C.A.; Yu, Z.; Zhou, X.B.; Zhou, M.; Li, Z. Using the error-in-variable simultaneous equations approach to construct compatible estimation models of forest inventory attributes based on airborne LiDAR. Forests 2023, 14, 65. [Google Scholar] [CrossRef]
- Yuen, J.Q.; Fung, T.; Ziegler, A.D. Review of allometric equations for major land covers in SE Asia: Uncertainty and implications for above- and below-ground carbon estimates. For. Ecol. Manag. 2016, 360, 323–340. [Google Scholar] [CrossRef]
- Sileshi, G.W. A critical review of forest biomass estimation models, common mistakes and corrective measures. For. Ecol. Manag. 2014, 329, 237–254. [Google Scholar] [CrossRef]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.C.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Change Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef]
- Tang, S.; Lang, K.; Li, H. Statistics and Computation of Biomathematical Models (ForStat Course); Science Press: Beijing, China, 2008. [Google Scholar]
- Fu, L.; Tang, S. A general formulation of nonlinear mixed effect models and its application. Sci. Sin. Math. 2020, 50, 15–30. [Google Scholar] [CrossRef]
- Zeng, W. Comparison of different weight functions in weighted regression. For. Grassl. Resour. Res. 2013, 40, 55–61. [Google Scholar]
- Zeng, W.; Tang, S. Evaluation and precision analysis of tree biomass equations. Sci. Silv. Sin. 2011, 47, 106–113. [Google Scholar]
- Wang, Y.L.; Kershaw, J.A.; Ducey, M.J.; Sun, Y.; McCarter, J.B. What diameter? What height? Influence of measures of average tree size on area-based allometric volume relationships. For. Ecosyst. 2024, 11, 100171. [Google Scholar] [CrossRef]
- Balenovic, I.; Milas, A.S.; Marjanovic, H. A comparison of stand-level volume estimates from image-based canopy height models of different spatial resolutions. Remote Sens. 2017, 9, 205. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, R.; Liu, K.; Dong, K.; Gong, Y.; Zhang, B.; Zhou, Y. Effects of thinning on growth and understory vegetation diversity of Chinese fir plantation at different ages. J. Cent. South Univ. For. Technol. 2020, 40, 34–43+82. [Google Scholar]
- Tian, H.L.; Zhu, J.H.; He, X.; Chen, X.Y.; Jian, Z.J.; Li, C.Y.; Ou, Q.X.; Li, Q.; Huang, G.S.; Liu, C.F.; et al. Using machine learning algorithms to estimate stand volume growth of Larix and Quercus forests based on national-scale forest inventory data in China. For. Ecosyst. 2022, 9, 100037. [Google Scholar] [CrossRef]
- Mensah, A.A.; Holmström, E.; Nyström, K.; Nilsson, U. Modelling potential yield capacity in conifers using Swedish long-term experiments. For. Ecol. Manag. 2022, 512, 120162. [Google Scholar] [CrossRef]
- Tang, X.L.; Zhao, X.; Bai, Y.F.; Tang, Z.Y.; Wang, W.T.; Zhao, Y.C.; Wan, H.W.; Xie, Z.Q.; Shi, X.Z.; Wu, B.F.; et al. Carbon pools in China’s terrestrial ecosystems: New estimates based on an intensive field survey. Proc. Natl. Acad. Sci. USA 2018, 115, 4021–4026. [Google Scholar] [CrossRef]
- Sullivan, M.J.P.; Lewis, S.L.; Affum-Baffoe, K.; Castilho, C.; Costa, F.; Sanchez, A.C.; Ewango, C.E.N.; Hubau, W.; Marimon, B.; Monteagudo-Mendoza, A.; et al. Long-term thermal sensitivity of Earth’s tropical forests. Science 2020, 368, 869–874. [Google Scholar] [CrossRef]
- Tong, S.; Liu, J. Management Table and Optimal Density Control of Chinese Fir Forest; China Forestry Press: Beijing, China, 2019. [Google Scholar]

| Level | Variables | Training Set | Test Set | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Mean | Max | Std | Min | Mean | Max | Std | ||
| Tree level | LH (cm) | 2.95 | 13.26 | 23.88 | 3.78 | 3.16 | 13.22 | 23.82 | 3.75 |
| LCW (m) | 0.03 | 2.23 | 6.00 | 1.29 | 0.05 | 2.22 | 5.96 | 1.26 | |
| GSV (m3) | 0.002 | 0.120 | 0.657 | 0.096 | 0.002 | 0.119 | 0.651 | 0.096 | |
| Stand level | AIH10 (m) | 2.12 | 9.08 | 18.70 | 3.75 | 3.37 | 9.00 | 16.38 | 3.19 |
| CC (proportion) | 0.33 | 0.88 | 0.99 | 0.14 | 0.72 | 0.89 | 0.97 | 0.07 | |
| GSV (m3 ha−1) | 10.57 | 276.03 | 718.96 | 132.23 | 102.75 | 273.18 | 729.28 | 122.07 | |
| Level | Model | a/ai | b (LH/AIH10) | c (LCW/CC) |
|---|---|---|---|---|
| Tree level | Base | 0.000222 (0.000008) | 2.367329 (0.014343) | 0.063381 (0.005365) |
| Linear | −0.151763 (0.000209) | 0.019266 (0.000018) | 0.007030 (0.000047) | |
| Dummy variable | 0.000259/0.000243/0.000261/0.000269/0.000275 (0.000012/0.000012/0.000013/0.000014/0.000015) | 2.309164 (0.018917) | 0.065991 (0.005439) | |
| Nonlinear mixed-effects | 0.000223 (0.000016) | 2.363358 (0.023469) | 0.052013 (0.012441) | |
| Stand level | Base | 42.50689 (7.30879) | 0.88988 (0.06887) | 0.85418 (0.23726) |
| Linear | −82.38714 (1.97050) | 28.94223 (0.28611) | 109.61360 (3.68027) | |
| Dummy variable | 41.90878/41.33184/38.30201/40.94594/38.80829 (7.84685/8.73077/8.18430/9.42490/9.12756) | 0.91231 (0.08675) | 0.81914 (0.24603) | |
| Nonlinear mixed-effects | 59.38025 (10.04528) | 0.74094 (0.07265) | 1.14790 (0.25586) |
| Level | Model | R2 | RMSE | MPE | MPSE |
|---|---|---|---|---|---|
| Tree level | Base | 0.677 | 0.055 | 0.82 | 33.33 |
| Linear | 0.639 | 0.058 | 0.86 | 107.35 | |
| Dummy variable | 0.680 | 0.054 | 0.81 | 33.26 | |
| Nonlinear mixed-effects | 0.725 | 0.050 | 0.75 | 30.55 | |
| Stand level | Base | 0.789 | 60.673 | 4.45 | 18.86 |
| Linear | 0.785 | 61.314 | 4.50 | 18.67 | |
| Dummy variable | 0.799 | 59.279 | 4.45 | 18.56 | |
| Nonlinear mixed-effects | 0.879 | 46.052 | 3.44 | 15.50 |
| Level | Model | R2 | RMSE | MPE | MPSE |
|---|---|---|---|---|---|
| Tree level | Base | 0.666 | 0.055 | 1.27 | 33.48 |
| Linear | 0.631 | 0.058 | 1.33 | 91.49 | |
| Dummy variable | 0.669 | 0.055 | 1.26 | 33.43 | |
| Nonlinear mixed-effects | 0.706 | 0.052 | 1.19 | 31.22 | |
| Stand level | Base | 0.792 | 55.623 | 6.70 | 13.32 |
| Linear | 0.781 | 57.070 | 6.87 | 14.06 | |
| Dummy variable | 0.796 | 55.190 | 7.07 | 13.03 | |
| Nonlinear mixed-effects | 0.862 | 45.352 | 5.71 | 11.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Guo, Z.; Zhou, J.; Shen, K.; Zhong, D.; Feng, X.; Ding, S.; Ye, J. Estimating Growing Stock Volume at Tree and Stand Levels for Chinese Fir (Cunninghamia lanceolata) in Southern China Using UAV Laser Scanning. Forests 2025, 16, 1779. https://doi.org/10.3390/f16121779
Yang Z, Guo Z, Zhou J, Shen K, Zhong D, Feng X, Ding S, Ye J. Estimating Growing Stock Volume at Tree and Stand Levels for Chinese Fir (Cunninghamia lanceolata) in Southern China Using UAV Laser Scanning. Forests. 2025; 16(12):1779. https://doi.org/10.3390/f16121779
Chicago/Turabian StyleYang, Zhigang, Zexin Guo, Jianpei Zhou, Kang Shen, Die Zhong, Xinfu Feng, Sheng Ding, and Jinsheng Ye. 2025. "Estimating Growing Stock Volume at Tree and Stand Levels for Chinese Fir (Cunninghamia lanceolata) in Southern China Using UAV Laser Scanning" Forests 16, no. 12: 1779. https://doi.org/10.3390/f16121779
APA StyleYang, Z., Guo, Z., Zhou, J., Shen, K., Zhong, D., Feng, X., Ding, S., & Ye, J. (2025). Estimating Growing Stock Volume at Tree and Stand Levels for Chinese Fir (Cunninghamia lanceolata) in Southern China Using UAV Laser Scanning. Forests, 16(12), 1779. https://doi.org/10.3390/f16121779






