Individual-Tree Crown Width Prediction for Natural Mixed Forests in Northern China Using Deep Neural Network and Height Threshold Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Tree Measurements
2.2. Machine Learning for Predicting CW
2.3. Input Variables
2.4. Model Evaluation and Validation
2.5. Variable-Importance Methodology and Feature Selection
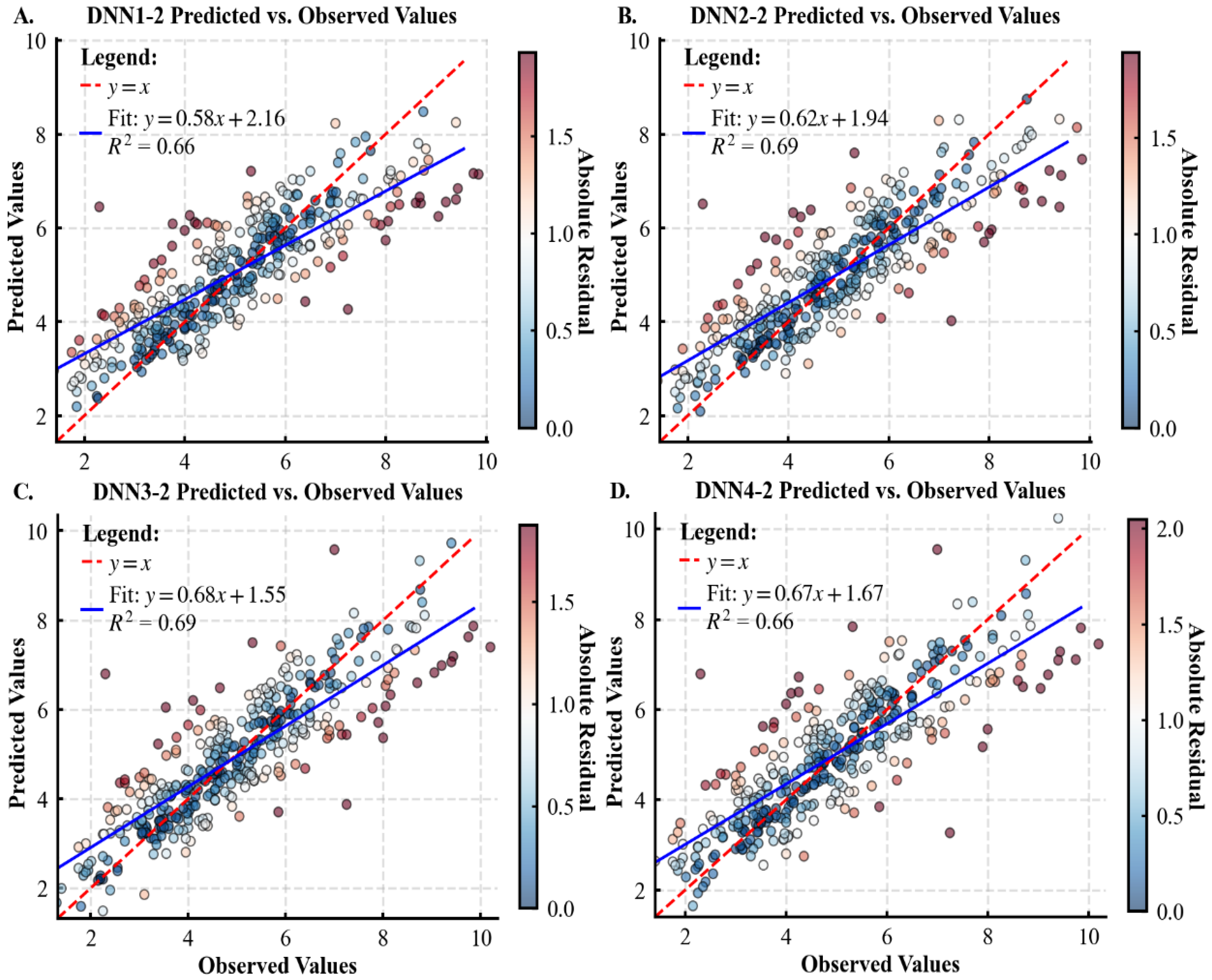
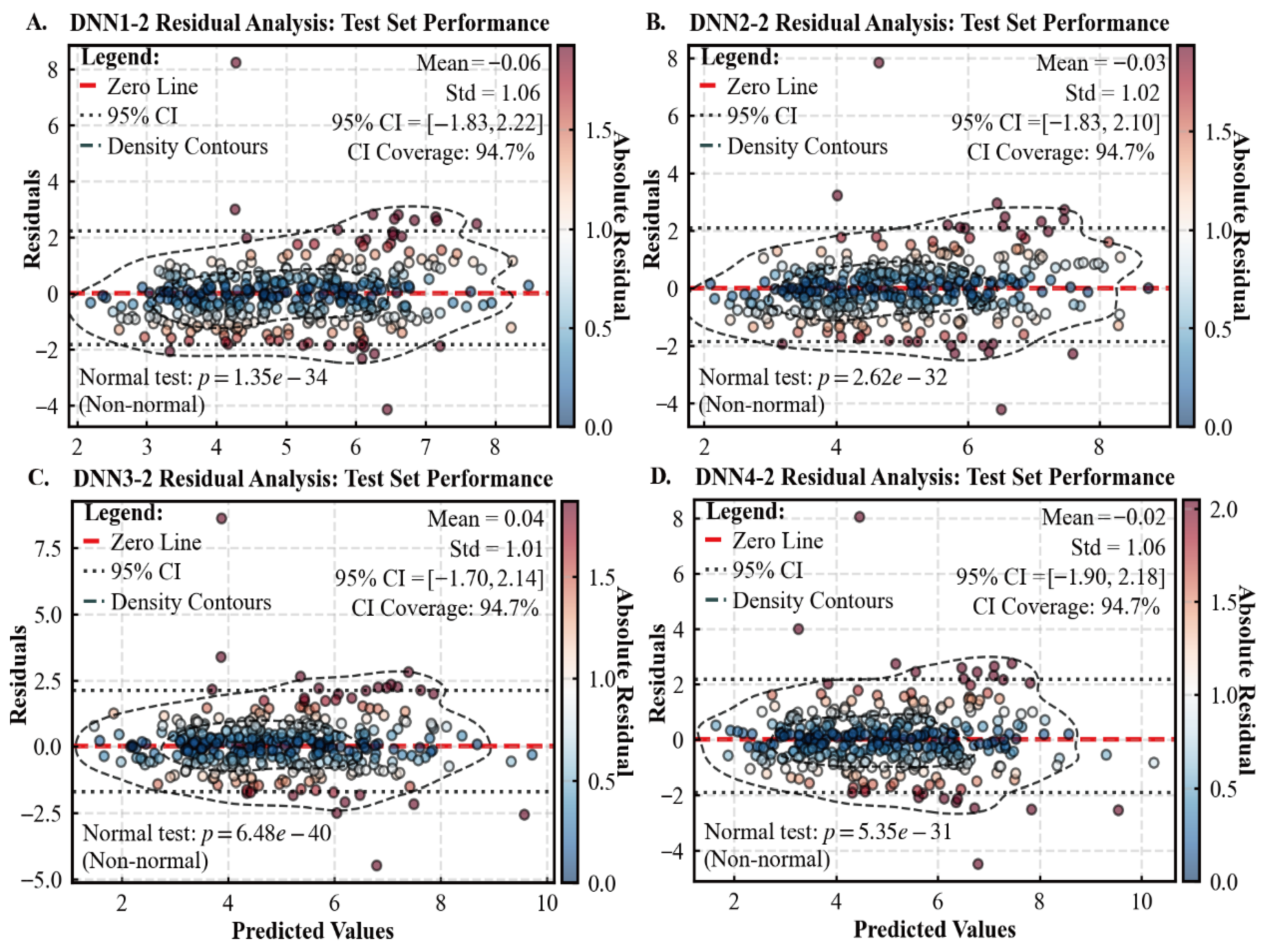
3. Results
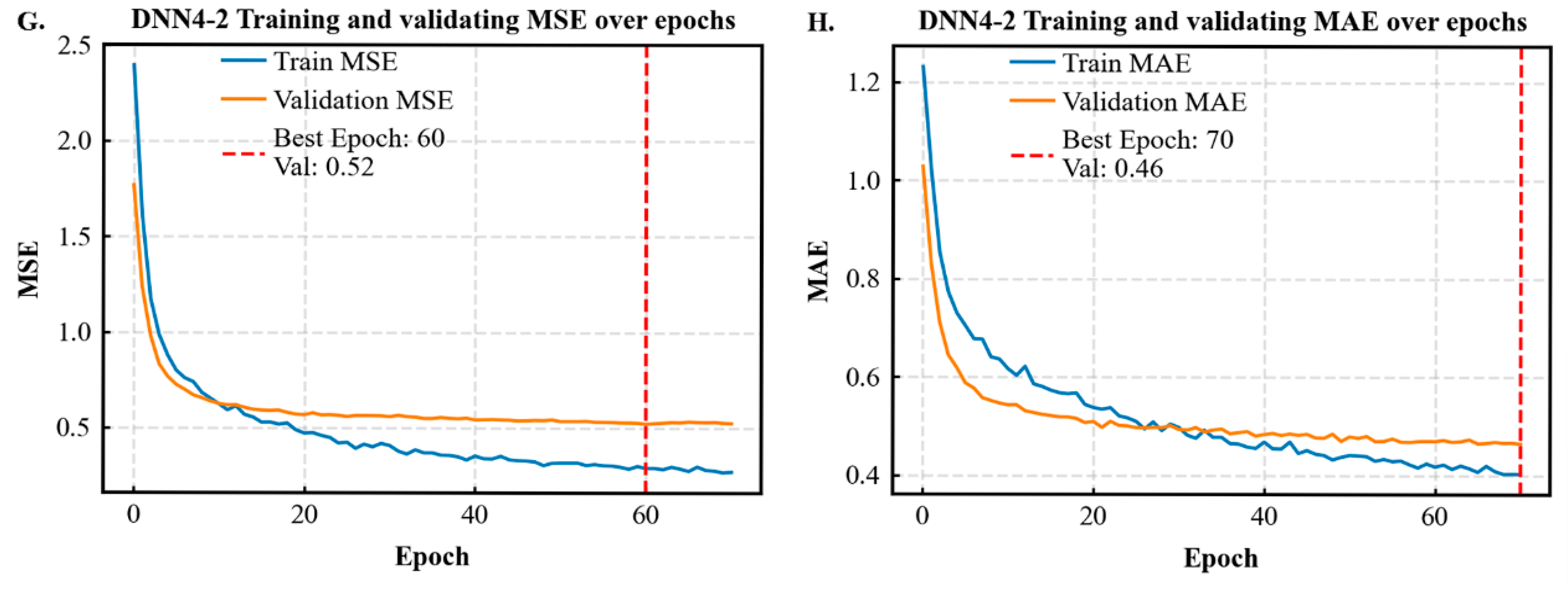
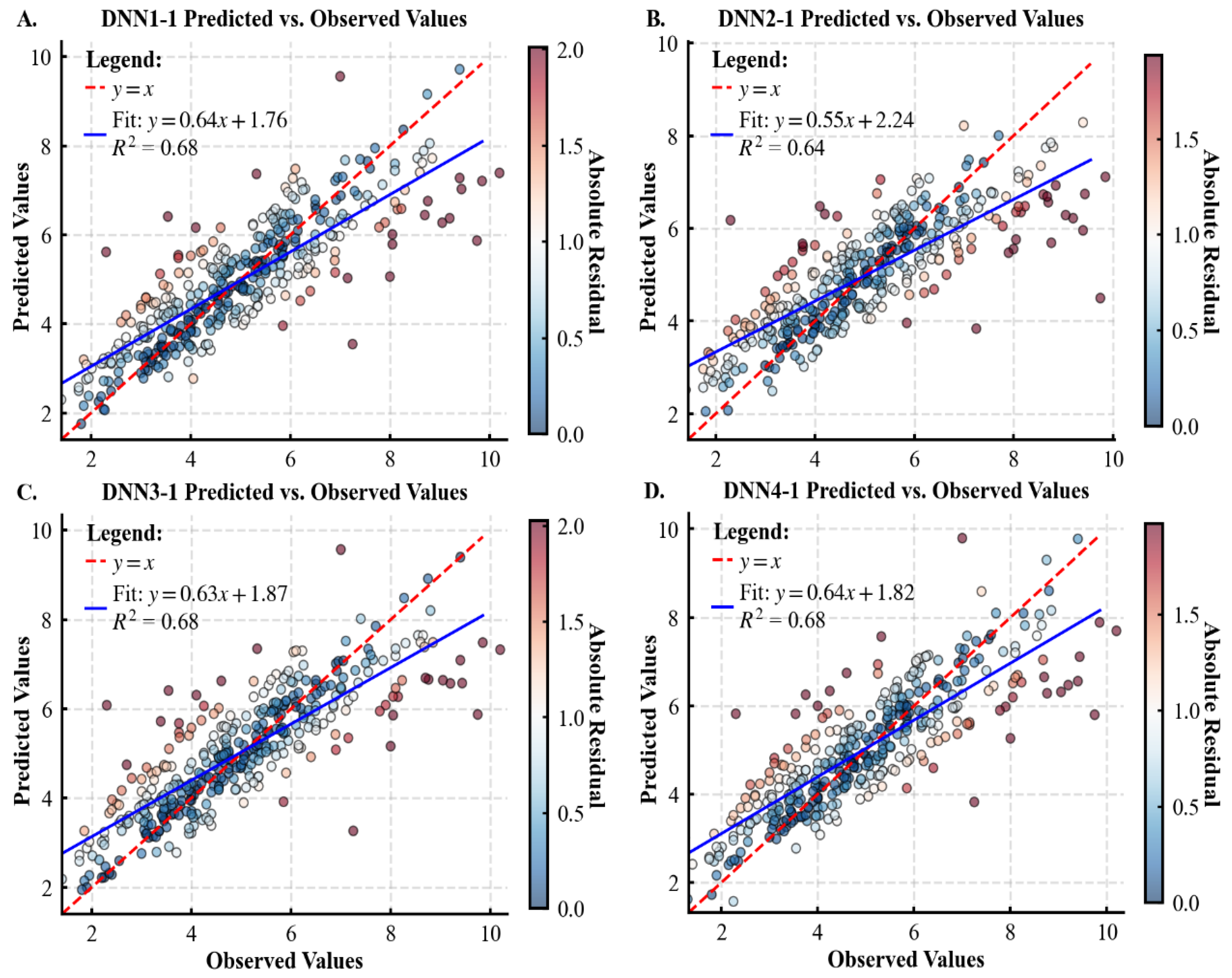
3.1. Performance of Various Models for Predicting Tree CW
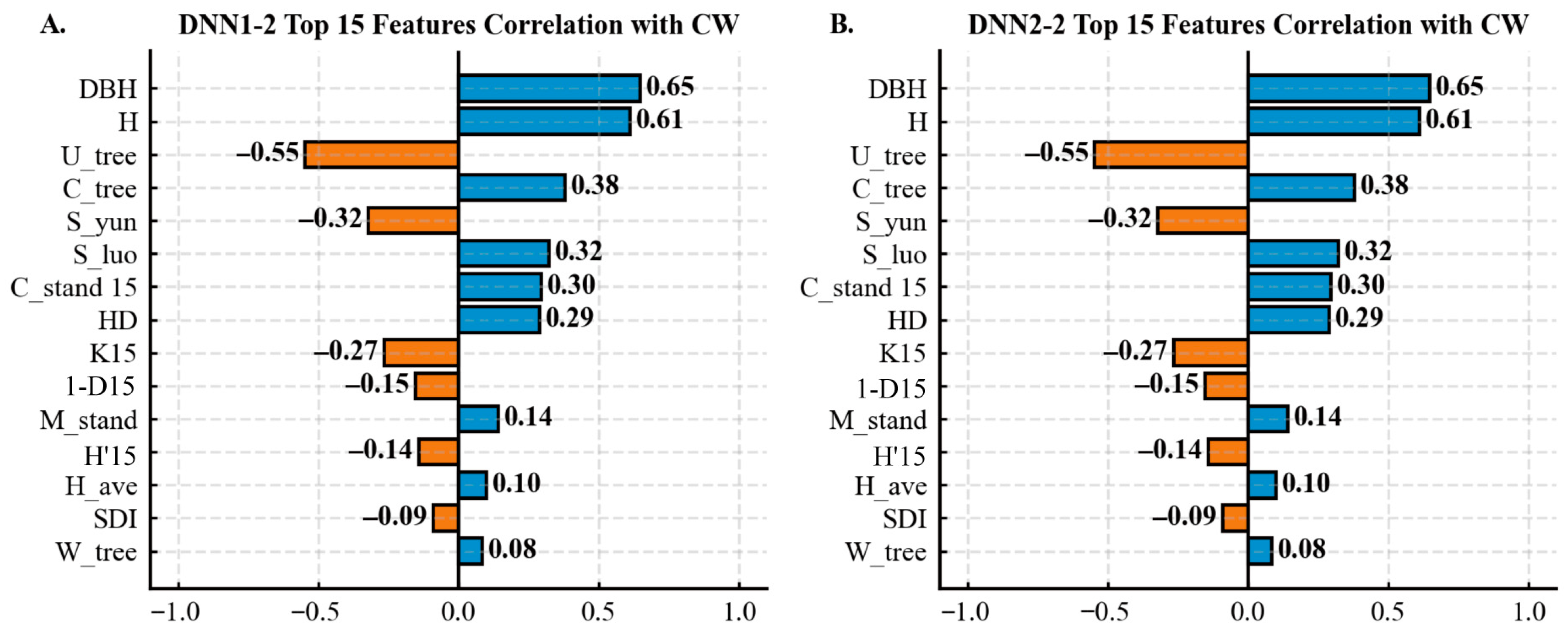
3.2. Effect of Different Input Variables on Tree CW Prediction
4. Discussion
4.1. Deep Learning Algorithm for Tree CW Prediction
4.2. Contributions of Important Input Variables to CW Prediction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CW | Crown width. It represents the horizontal area of influence for a tree, measured through perpendicular crown spread diameters to assess light interception and growing space. |
| DNN | Deep neural network. A DNN is a multi-layered computational model that learns hierarchical patterns from data through backpropagation, capable of approximating complex functions for regression and classification tasks. |
| LME | Linear mixed-effects models. LME models are statistical approaches that incorporate both fixed effects to estimate population-level parameters and random effects to account for variability from grouped or hierarchical data structures. |
| NSUR | Nonlinear seemingly unrelated regression. NLSUR is an econometric technique that simultaneously estimates a system of nonlinear equations with correlated error terms, thereby improving efficiency by accounting for cross-equation dependencies in the stochastic components. |
| GAM | Generalized additive model. A GAM is a statistical framework that extends generalized linear models by incorporating smooth, non-parametric functions of predictors to capture complex nonlinear relationships while maintaining interpretability through its additive structure. |
| NLME | Nonlinear mixed effects models. NLME is hierarchical statistical framework that incorporate both fixed effects describing population-average nonlinear relationships and random effects accounting for individual-specific variations in these nonlinear patterns across grouped or longitudinal data. |
| GNLME | Generalized nonlinear mixed effects models. A GNLME is a comprehensive statistical framework that integrates the flexibility of nonlinear mean structures, the capacity to handle non-normal response distributions through link functions, and the ability to account for between-subject variability through random effects in hierarchical data. |
| DLA | Deep learning algorithms. DLA is a class of machine learning method that utilize multi-layered neural networks with hierarchical feature learning capabilities to automatically extract complex patterns and representations from raw data through successive nonlinear transformations. |
| CNN | Convolutional neural network. A CNN is a specialized deep learning architecture that employs convolutional filters to automatically and adaptively learn spatial hierarchies of features through backpropagation, making it particularly effective for processing grid-like data such as images and time series. |
| RNN | Recurrent neural network. A RNN is a class of artificial neural networks designed to process sequential data by maintaining internal memory through cyclic connections, enabling temporal dynamic behavior and modeling of dependencies across time steps. |
| DBH | Diameter at breast height. DBH is a standard forestry measurement of tree trunk diameter, typically taken at 1.3 m (4.5 feet) above ground level, serving as a fundamental metric for estimating tree volume, growth, and biomass. |
| H | Total height. H is a fundamental tree dimension metric representing the vertical distance from the ground level (or root collar) to the highest point of the tree crown, typically measured using clinometers, hypsometers, or laser rangefinders in forest inventory and ecological studies. |
| N | Stems per hectare. N is a fundamental forest density metric quantifying the number of individual tree stems within a one-hectare area, serving as a crucial measure for assessing stand stocking, competition intensity, and silvicultural treatment requirements. |
| SDI | Stand density index. SDI is a dimensionless measure of stand crowding that quantifies the number of trees per unit area relative to a standard reference diameter. |
| BA | Basal area per hectare. BA is a fundamental metric of stand density that represents the total cross-sectional area of all tree stems measured at breast height (1.3 m) contained within one hectare, providing a comprehensive measure of space occupancy and growing stock in forest ecosystems. |
| Dg | Quadratic mean DBH. Dg is a stand-level metric calculated as the diameter of the tree of average basal area, derived by squaring individual tree DBHs, computing their arithmetic mean, and then taking the square root, providing a biologically meaningful representation of central tendency in forest stands. |
| U | Size ratio. It quantifies the relative dimensional relationship between a subject tree and its competitors, typically calculated as the diameter ratio (DBHj/DBHi) to assess competitive asymmetry within a forest stand. |
| C | Concentration index. C is a statistical measure that quantifies the degree of inequality or clustering in the distribution of resources, individuals, or events within a defined population or geographical area, typically ranging from 0 (perfect equality) to 1 (maximum concentration). |
| GC | Gini coefficient. The GC is a statistical measure of distributional inequality that quantifies the degree of disparity within a given population, ranging from 0 (perfect equality) to 1 (maximum inequality), and is most commonly applied to evaluate income or wealth distribution patterns in economic and social systems. |
| CVd | DBH coefficient of variation. The CVd quantifies the relative variability of tree diameters within a forest stand by expressing the standard deviation of DBH measurements as a percentage of the mean DBH, serving as a key indicator of structural diversity and size inequality in even-aged and uneven-aged stands. |
| 1-D | Simpson’s index. One-dimensional quantifies the probability that two randomly selected individuals from a community will belong to different species, thereby integrating both species richness and abundance evenness into a unified measure of ecological diversity. |
| H′ | Shannon’s index. H′ quantifies ecological diversity by measuring the uncertainty in predicting the species of a randomly selected individual from a community, integrating both species richness and evenness through a logarithmic weighting of relative abundances. |
| W | Neighborhood configuration. W refers to the spatial arrangement, structural composition, and competitive interactions among trees within a defined area surrounding a subject tree, typically quantified through distance-dependent and size-based metrics to assess local competition intensity and resource availability in forest stands. |
| M | Species mingling. M quantifies the spatial diversity of tree species by measuring the proportion of nearest neighbors that differ in species from a focal tree, thereby evaluating the fine-scale spatial intimacy and mixture patterns among species within a forest stand. |
| R | Clark-Evans aggregation index. The R is a spatial point pattern statistic that quantifies the degree of clustering or dispersion in plant populations by comparing the observed mean distance to nearest neighbors with the expected mean distance under a completely random spatial distribution. |
| Dmax | Maximum DBH. Dmax is the largest diameter at breast height (1.3 m above ground) recorded among all living trees within a defined forest stand or sampling area, serving as a critical indicator of stand maturity, site productivity potential, and structural complexity in forest ecosystems. |
| K | Stand crowding index. K quantifies the level of competition for resources within a forest stand by integrating tree density, size distribution, and spatial arrangement, typically expressed as a relative measure comparing actual stand conditions to a reference density for optimal growth. |
| Arithmetic mean height. is a stand-level metric calculated as the simple average of individual tree heights within a defined forest area, obtained by summing all measured tree heights and dividing by the total number of trees, providing a straightforward representation of the central tendency in vertical stand structure. | |
| HD | Mean dominant height. HD is a fundamental forest mensuration parameter representing the average height of the most vigorous trees in a stand—typically defined as the 100 thickest trees per hectare—which serves as a reliable indicator of site productivity potential and is widely used for forest site classification and growth modeling. |
| R2 | Coefficient of determination. The R2 quantifies the proportion of variance in the dependent variable that is predictable from the independent variable(s) in a regression model, serving as a fundamental metric for assessing model fit and explanatory power. |
| MSE | Mean square error. MSE is a fundamental regression metric that quantifies prediction accuracy by calculating the average squared difference between observed and predicted values, thereby emphasizing larger errors through its quadratic penalty term. |
| MAE | Mean absolute error. MAE is a robust regression metric that measures the average magnitude of prediction errors by calculating the arithmetic mean of absolute differences between observed and predicted values, providing an interpretable measure of average model accuracy in the original units of the response variable. |
| MAPE | Mean absolute percentage error. MAPE is a relative accuracy metric that measures the average magnitude of prediction errors expressed as percentages of the actual observed values, calculated as the mean of absolute percentage differences between predicted and true values across all observations. |
References
- Crous, K.Y.; Campany, C.; Lopez, R.; Cano, F.J.; Ellsworth, D.S. Canopy position affects photosynthesis and anatomy in mature Eucalyptus trees in elevated CO2. Tree Physiol. 2021, 41, 206–222. [Google Scholar] [CrossRef]
- Li, Y.; Su, Y.; Zhao, X.; Yang, M.; Hu, T.; Zhang, J.; Liu, J.; Liu, M.; Guo, Q. Retrieval of tree branch architecture attributes from terrestrial laser scan data using a Laplacian algorithm. Agric. For. Meteorol. 2020, 284, 107874. [Google Scholar] [CrossRef]
- Shenkin, A.; Bentley, L.P.; Oliveras, I.; Salinas, N.; Adu-Bredu, S.; Marimon-Junior, B.H.; Marimon, B.S.; Peprah, T.; Choque, E.L.; Rodriguez, L.T.; et al. The influence of ecosystem and phylogeny on tropical tree crown size and shape. Front. For. Glob. Change 2020, 3, 501757. [Google Scholar] [CrossRef]
- Qin, Y.; He, X.; Lei, X.; Feng, L.; Zhou, Z.; Lu, J. Tree size inequality and competition effects on nonlinear mixed effects crown width model for natural spruce-fir-broadleaf mixed forest in northeast China. For. Ecol. Manag. 2022, 518, 120291. [Google Scholar] [CrossRef]
- Li, X.; Yang, X.; Dong, B.; Liu, Q. Predicting 28-day all-cause mortality in patients admitted to intensive care units with pre-existing chronic heart failure using the stress hyperglycemia ratio: A machine learning-driven retrospective cohort analysis. Cardiovasc. Diabetol. 2025, 24, 10. [Google Scholar] [CrossRef]
- Sapijanskas, J.; Paquette, A.; Potvin, C.; Kunert, N.; Loreau, M. Tropical tree diversity enhances light capture through crown plasticity and spatial and temporal niche differences. Ecology 2014, 95, 2479–2492. [Google Scholar] [CrossRef]
- Pretzsch, H. Tree growth as affected by stem and crown structure. Trees 2021, 35, 947–960. [Google Scholar] [CrossRef]
- Krajnc, L.; Farrelly, N.; Harte, A. The influence of crown and stem characteristics on timber quality in softwoods. For. Ecol. Manag. 2019, 435, 8–17. [Google Scholar] [CrossRef]
- Fang, S.; Liu, Y.; Yue, J.; Tian, Y.; Xu, X. Assessments of growth performance, crown structure, stem form and wood property of introduced poplar clones: Results from a long-term field experiment at a lowland site. For. Ecol. Manag. 2021, 479, 118586. [Google Scholar] [CrossRef]
- Liang, R.; Sun, Y.; Zhou, L.; Wang, Y.; Qiu, S.; Sun, Z. Analysis of various crown variables on stem form for Cunninghamia lanceolata based on ANN and taper function. For. Ecol. Manag. 2022, 507, 119973. [Google Scholar] [CrossRef]
- Liu, X.; Su, Y.; Hu, T.; Yang, Q.; Liu, B.; Deng, Y.; Tang, H.; Tang, Z.; Fang, J.; Guo, Q. Neural network guided interpolation for mapping canopy height of China’s forests by integrating GEDI and ICESat-2 data. Remote Sens. Environ. 2022, 269, 112844. [Google Scholar] [CrossRef]
- Rahman, M.F.; Onoda, Y.; Kitajima, K. Forest canopy height variation in relation to topography and forest types in central Japan with LiDAR. For. Ecol. Manag. 2022, 503, 119792. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, H.; Li, F. Using linear mixed-effects models with quantile regression to simulate the crown profile of planted Pinus sylvestris var. Mongolica trees. Forests 2017, 8, 446. [Google Scholar] [CrossRef]
- Zhou, Z.; Fu, L.; Zhou, C.; Sharma, R.P.; Zhang, H. Simultaneous compatible system of models of height, crown length, and height to crown base for natural secondary forests of Northeast China. Forests 2022, 13, 148. [Google Scholar] [CrossRef]
- Ma, A.; Miao, Z.; Xie, L.; Dong, L.; Li, F. Crown width prediction for Larix olgensis plantations in Northeast China based on nonlinear mixed-effects model and quantile regression. Trees 2022, 36, 1761–1776. [Google Scholar] [CrossRef]
- Qin, Y.; Wu, B.; Lei, X.; Feng, L. Prediction of tree crown width in natural mixed forests using deep learning algorithm. For. Ecosyst. 2023, 10, 100109. [Google Scholar] [CrossRef]
- Sharma, R.P.; Bílek, L.; Vacek, Z.; Vacek, S. Modelling crown width-diameter relationship for Scots pine in the central Europe. Trees 2017, 31, 1875–1889. [Google Scholar] [CrossRef]
- Jia, W.; Chen, D. Nonlinear mixed-effects height to crown base and crown length dynamic models using the branch mortality technique for a Korean larch (Larix olgensis) plantations in northeast China. J. For. Res. 2019, 30, 2095–2109. [Google Scholar] [CrossRef]
- Buchacher, R.; Ledermann, T. Interregional crown width models for individual trees growing in pure and mixed stands in Austria. Forests 2020, 11, 114. [Google Scholar] [CrossRef]
- Raptis, D.I.; Kazana, V.; Kechagioglou, S.; Kazaklis, A.; Stamatiou, C.; Papadopoulou, D.; Tsitsoni, T. Nonlinear Quantile Mixed-Effects Models for Prediction of the Maximum Crown Width Fagus sylvatica L., Pinus nigra Arn. and Pinus brutia Ten. Forests 2022, 13, 499. [Google Scholar] [CrossRef]
- Qiu, S.; Gao, P.; Pan, L.; Zhou, L.; Liang, R.; Sun, Y.; Wang, Y. Developing nonlinear additive tree crown width models based on decomposed competition index and tree variables. J. For. Res. 2023, 34, 1407–1422. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, L.; Xin, S.; Wang, Y.; He, P.; Yan, Y. Two new methods applied to crown width additive models: A case study for three tree species in Northeastern China. Ann. For. Sci. 2023, 80, 11. [Google Scholar] [CrossRef]
- Zhou, X.; Li, Z.; Liu, L.; Sharma, R.P.; Guan, F.; Fan, S. Constructing two-level nonlinear mixed-effects crown width models for Moso bamboo in China. Front. Plant Sci. 2023, 14, 1139448. [Google Scholar] [CrossRef] [PubMed]
- Tian, D.; He, P.; Jiang, L.; Sharma, R.P.; Guan, F.; Fan, S. Developing crown width model for mixed forests using soil, climate and stand factors. J. Ecol. 2024, 112, 427–442. [Google Scholar] [CrossRef]
- Onilude, Q.A. Development and evaluation of linear and non-linear models for diameter at breast height and crown diameter of TriplochitonScleroxylon (K. Schum) Plantations in Oyo State, Nigeria. J. Agric. Vet. Sci. 2019, 12, 47–52. [Google Scholar] [CrossRef]
- Calama, R.; Montero, G. Interregional nonlinear height diameter model with random coefficients for stone pine in Spain. Can. J. For. Res. 2004, 34, 150–163. [Google Scholar] [CrossRef]
- Eerikäinen, K. A multivariate linear mixed-effects model for the generalization of sample tree heights and crown ratios in the Finnish National Forest Inventory. For. Sci. 2009, 55, 480–493. [Google Scholar] [CrossRef]
- Hao, X.; Yujun, S.; Xinjie, W.; Jin, W.; Yao, F. Linear mixed-effects models to describe individual tree crown width for China-fir in Fujian province, southeast China. PLoS ONE 2015, 10, e0122257. [Google Scholar] [CrossRef]
- Leite, R.V.; Silva, C.A.; Mohan, M.; Cardil, A.; de Almeida, D.R.A.; Carvalho, S.d.P.C.e.; Jaafar, W.S.W.M.; Guerra-Hernández, J.; Weiskittel, A.; Hudak, A.T.; et al. Individual tree attribute estimation and uniformity assessment in fast-growing Eucalyptus Spp. forest plantations using Lidar and linear mixed-effects models. Remote Sens. 2020, 12, 3599. [Google Scholar] [CrossRef]
- Sattler, D.F.; LeMay, V. A system of nonlinear simultaneous equations for crown length and crown radius for the forest dynamics model SORTIE-ND. Can. J. For. Res. 2011, 41, 1567–1576. [Google Scholar] [CrossRef]
- Fu, L.; Sun, H.; Sharma, R.P.; Lei, Y.; Zhang, H.; Tang, S. Nonlinear mixed-effects crown width models for individual trees of Chinese fir (Cunninghamia lanceolata) in south-central China. For. Ecol. Manag. 2013, 302, 210–220. [Google Scholar] [CrossRef]
- Chen, Q.; Duan, G.; Liu, Q.; Ye, Q.; Sharma, R.P.; Chen, Y.; Liu, H.; Fu, L. Estimating crown width in degraded forest: A two-level nonlinear mixed-effects crown width model for Dacrydium pierrei and Podocarpus imbricatus in tropical China. For. Ecol. Manag. 2021, 497, 119486. [Google Scholar] [CrossRef]
- Wang, W.; Ge, F.; Hou, Z.; Meng, J. Predicting crown width and length using nonlinear mixed-effects models: A test of competition measures using Chinese fir (Cunninghamia lanceolata (Lamb.) Hook.). Ann. For. Sci. 2021, 78, 77. [Google Scholar] [CrossRef]
- Sharma, R.P.; Vacek, Z.; Vacek, S. Generalized nonlinear mixed-effects individual tree crown ratio models for Norway spruce and European beech. Forests 2018, 9, 555. [Google Scholar] [CrossRef]
- Pan, L.; Mei, G.; Wang, Y.; Saeed, S.; Chen, L.; Cao, Y.; Sun, Y. Generalized nonlinear mixed-effect model of individual TREE height to crown base for Larix olgensis Henry in northeast China. J. Sustain. For. 2020, 39, 827–840. [Google Scholar] [CrossRef]
- Ashraf, M.I.; Zhao, Z.; Bourque, C.P.-A.; MacLean, D.A.; Meng, F.-R. Integrating biophysical controls in forest growth and yield predictions with artificial intelligence technology. Can. J. For. Res. 2013, 43, 1162–1171. [Google Scholar] [CrossRef]
- Salehnasab, A.; Bayat, M.; Namiranian, M.; Khaleghi, B.; Omid, M.; Awan, H.U.M.; Al-Ansari, N.; Jaafari, A. Machine learning for the estimation of diameter increment in mixed and uneven-aged forests. Sustainability 2022, 14, 3386. [Google Scholar] [CrossRef]
- Zhao, Q.; Yu, S.; Zhao, F.; Tian, L.; Zhao, Z. Comparison of machine learning algorithms for forest parameter estimations and application for forest quality assessments. For. Ecol. Manag. 2019, 434, 224–234. [Google Scholar] [CrossRef]
- Qiu, S.; Liang, R.; Wang, Y.; Luo, M.; Sun, Y. Comparative analysis of machine learning algorithms and statistical models for predicting crown width of Larix olgensis. Earth Sci. Inf. 2022, 15, 2415–2429. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Sothe, C.; De Almeida, C.; Schimalski, M.; Liesenberg, V.; La Rosa, L.E.C.; Castro, J.D.B.; Feitosa, R.Q. A comparison of machine and deep-learning algorithms applied to multisource data for a subtropical forest area classification. Int. J. Remote Sens. 2020, 41, 1943–1969. [Google Scholar] [CrossRef]
- Hayder, I.M.; Al-Amiedy, T.A.; Ghaban, W.; Saeed, F.; Nasser, M.; Al-Ali, G.A.; Younis, H.A. An intelligent early flood forecasting and prediction leveraging machine and deep learning algorithms with advanced alert system. Processes 2023, 11, 481. [Google Scholar] [CrossRef]
- Latif, S.D.; Ahmed, A.N. Streamflow prediction utilizing deep learning and machine learning algorithms for sustainable water supply management. Water Resour. Manag. 2023, 37, 3227–3241. [Google Scholar] [CrossRef]
- Ercanlı, İ. Innovative deep learning artificial intelligence applications for predicting relationships between individual tree height and diameter at breast height. For. Ecosyst. 2020, 7, 12. [Google Scholar] [CrossRef]
- Ogana, F.N.; Ercanli, I. Modelling height-diameter relationships in complex tropical rain forest ecosystems using deep learning algorithm. J. For. Res. 2022, 33, 883–898. [Google Scholar] [CrossRef]
- Huy, B.; Truong, N.Q.; Khiem, N.Q.; Poudel, K.P.; Temesgen, H. Deep learning models for improved reliability of tree aboveground biomass prediction in the tropical evergreen broadleaf forests. For. Ecol. Manag. 2022, 508, 120031. [Google Scholar] [CrossRef]
- Diez, Y.; Kentsch, S.; Fukuda, M.; Caceres, M.L.L.; Moritake, K.; Cabezas, M. Deep learning in forestry using uav-acquired rgb data: A practical review. Remote Sens. 2021, 13, 2837. [Google Scholar] [CrossRef]
- Hamedianfar, A.; Mohamedou, C.; Kangas, A.; Vauhkonen, J. Deep learning for forest inventory and planning: A critical review on the remote sensing approaches so far and prospects for further applications. Forestry 2022, 95, 451–465. [Google Scholar] [CrossRef]
- Yun, T.; Li, J.; Ma, L.; Zhou, J.; Wang, R.; Eichhorn, M.P.; Zhang, H. Status, advancements and prospects of deep learning methods applied in forest studies. Int. J. Appl. Earth Obs. Geoinf. 2024, 131, 103938. [Google Scholar] [CrossRef]
- Raulier, F.; Lambert, M.-C.; Pothier, D.; Ung, C.-H. Impact of dominant tree dynamics on site index curves. For. Ecol. Manag. 2003, 184, 65–78. [Google Scholar] [CrossRef]
- Lei, Y.; Fu, L.; Affleck, D.L.; Nelson, A.S.; Shen, C.; Wang, M.; Zheng, J.; Ye, Q.; Yang, G. Additivity of nonlinear tree crown width models: Aggregated and disaggregated model structures using nonlinear simultaneous equations. For. Ecol. Manag. 2018, 427, 372–382. [Google Scholar] [CrossRef]
- Draper, F.C.; Costa, F.R.; Arellano, G.; Phillips, O.L.; Duque, A.; Macía, M.J.; ter Steege, H.; Asner, G.P.; Berenguer, E.; Schietti, J.; et al. Amazon tree dominance across forest strata. Nat. Ecol. Evol. 2021, 5, 757–767. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D.; Akay, R. A comprehensive survey on optimizing deep learning models by metaheuristics. Artif. Intell. Rev. 2022, 55, 829–894. [Google Scholar] [CrossRef]
- Pang, B.; Nijkamp, E.; Wu, Y.N. Deep learning with tensorflow: A review. J. Educ. Behav. Stat. 2020, 45, 227–248. [Google Scholar] [CrossRef]
- Aguirre, O.; Hui, G.; von Gadow, K.; Jiménez, J. An analysis of spatial forest structure using neighbourhood-based variables. For. Ecol. Manag. 2003, 183, 137–145. [Google Scholar] [CrossRef]
- Yap, B.W.; Sim, C.H. Comparisons of various types of normality tests. J. Stat. Comput. Simul. 2011, 81, 2141–2155. [Google Scholar] [CrossRef]
- Alibrahim, H.; Ludwig, S.A. Hyperparameter optimization: Comparing genetic algorithm against grid search and bayesian optimization. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June–1 July 2021. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar] [CrossRef]
- Belete, D.M.; Huchaiah, M.D. Grid search in hyperparameter optimization of machine learning models for prediction of HIV/AIDS test results. Int. J. Comput. Appl. 2022, 44, 875–886. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.-Y.; Zhang, H.; Xiong, L.-D.; Lei, H.; Deng, S.-H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar] [CrossRef]
- Jaderberg, M.; Dalibard, V.; Osindero, S.; Czarnecki, W.M.; Donahue, J.; Razavi, A.; Vinyals, O.; Green, T.; Dunning, I.; Simonyan, K.; et al. Population based training of neural networks. arXiv 2017, arXiv:1711.09846. [Google Scholar] [CrossRef]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A novel bandit-based approach to hyperparameter optimization. J. Mach. Learn. Res. 2018, 18, 1–52. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 2951–2959. [Google Scholar] [CrossRef]
- Liu, S.; Liu, S.; Cai, W.; Pujol, S.; Kikinis, R.; Feng, D. Early diagnosis of Alzheimer’s disease with deep learning. In Proceedings of the 2014 IEEE 11th International Symposium on Biomedical Imaging (ISBI), Beijing, China, 29 April–2 May 2014. [Google Scholar] [CrossRef]
- Zhu, A.-X.; Miao, Y.; Wang, R.; Zhu, T.; Deng, Y.; Liu, J.; Yang, L.; Qin, C.-Z.; Hong, H. A comparative study of an expert knowledge-based model and two data-driven models for landslide susceptibility mapping. Catena 2018, 166, 317–327. [Google Scholar] [CrossRef]
- Karaboga, D.; Kaya, E. Adaptive network based fuzzy inference system (ANFIS) training approaches: A comprehensive survey. Artif. Intell. Rev. 2019, 52, 2263–2293. [Google Scholar] [CrossRef]
- Huang, N.; Ding, H.; Hu, R.; Jiao, P.; Zhao, Z.; Yang, B.; Zheng, Q. Multi-time-scale with clockwork recurrent neural network modeling for sequential recommendation. J. Supercomput. 2025, 81, 412. [Google Scholar] [CrossRef]
- Bayat, M.; Bettinger, P.; Hassani, M.; Heidari, S. Ten-year estimation of Oriental beech (Fagus orientalis Lipsky) volume increment in natural forests: A comparison of an artificial neural networks model, multiple linear regression and actual increment. For. Int. J. For. Res. 2021, 94, 598–609. [Google Scholar] [CrossRef]
- Seely, H.; Coops, N.C.; White, J.C.; Montwé, D.; Winiwarter, L.; Ragab, A. Modelling tree biomass using direct and additive methods with point cloud deep learning in a temperate mixed forest. Sci. Remote Sens. 2023, 8, 100110. [Google Scholar] [CrossRef]
- Miseta, T.; Fodor, A.; Vathy-Fogarassy, Á. Surpassing early stopping: A novel correlation-based stopping criterion for neural networks. Neurocomputing 2024, 567, 127028. [Google Scholar] [CrossRef]
- Ziegel, E.R. The Elements of Statistical Learning; Taylor & Francis: London, UK, 2003. [Google Scholar]
- Yang, Z.; Yu, Y.; You, C.; Steinhardt, J.; Ma, Y. Rethinking bias-variance trade-off for generalization of neural networks. Int. Conf. Mach. Learning. 2020, 119, 10767–10777. [Google Scholar] [CrossRef]
- Hoffer, E.; Hubara, I.; Soudry, D. Train longer, generalize better: Closing the generalization gap in large batch training of neural networks. Adv. Neural Inf. Process. Syst. 2017, 30, 1729–1739. [Google Scholar] [CrossRef]
- Zhang, C.; Bengio, S.; Hardt, M.; Recht, B.; Vinyals, O. Understanding deep learning (still) requires rethinking generalization. Commun. ACM 2021, 64, 107–115. [Google Scholar] [CrossRef]
- Asrat, Z.; Eid, T.; Gobakken, T.; Negash, M. Modelling and quantifying tree biometric properties of dry Afromontane forests of south-central Ethiopia. Trees 2020, 34, 1411–1426. [Google Scholar] [CrossRef]
- Raptis, D.; Kazana, V.; Kazaklis, A.; Stamatiou, C. A crown width-diameter model for natural even-aged black pine forest management. Forests 2018, 9, 610. [Google Scholar] [CrossRef]
- Ali, A. Forest stand structure and functioning: Current knowledge and future challenges. Ecol. Indic. 2019, 98, 665–677. [Google Scholar] [CrossRef]
- Dahouda, M.K.; Joe, I. A deep-learned embedding technique for categorical features encoding. IEEE Access 2021, 9, 114381–114391. [Google Scholar] [CrossRef]
- Bechtold, W.A. Largest-crown-width prediction models for 53 species in the western United States. West. J. Appl. For. 2004, 19, 245–251. [Google Scholar] [CrossRef]
- Castaño-Santamaría, J.; López-Sánchez, C.A.; Obeso, J.R.; Barrio-Anta, M. Development of a site form equation for predicting and mapping site quality. A case study of unmanaged beech forests in the Cantabrian range (NW Spain). For. Ecol. Manag. 2023, 529, 120711. [Google Scholar] [CrossRef]
- Raigosa-García, I.; Rathbun, L.C.; Cook, R.L.; Baker, J.S.; Corrao, M.V.; Sumnall, M.J. Rethinking Productivity Evaluation in Precision Forestry through Dominant Height and Site Index Measurements Using Aerial Laser Scanning LiDAR Data. Forests 2024, 15, 1002. [Google Scholar] [CrossRef]
- Rosamond, M.S.; Wellen, C.; Yousif, M.A.; Kaltenecker, G.; Thomas, J.L.; Joosse, P.J.; Feisthauer, N.C.; Taylor, W.D.; Mohamed, M.N. Representing a large region with few sites: The Quality Index approach for field studies. Sci. Total Environ. 2018, 633, 600–607. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, J.; Liu, S.; Gaire, D.; Jiang, L. Modeling the influence of competition, climate, soil, and their interaction on height to crown base for Korean pine plantations in Northeast China. Eur. J. For. Res. 2024, 143, 1627–1640. [Google Scholar] [CrossRef]
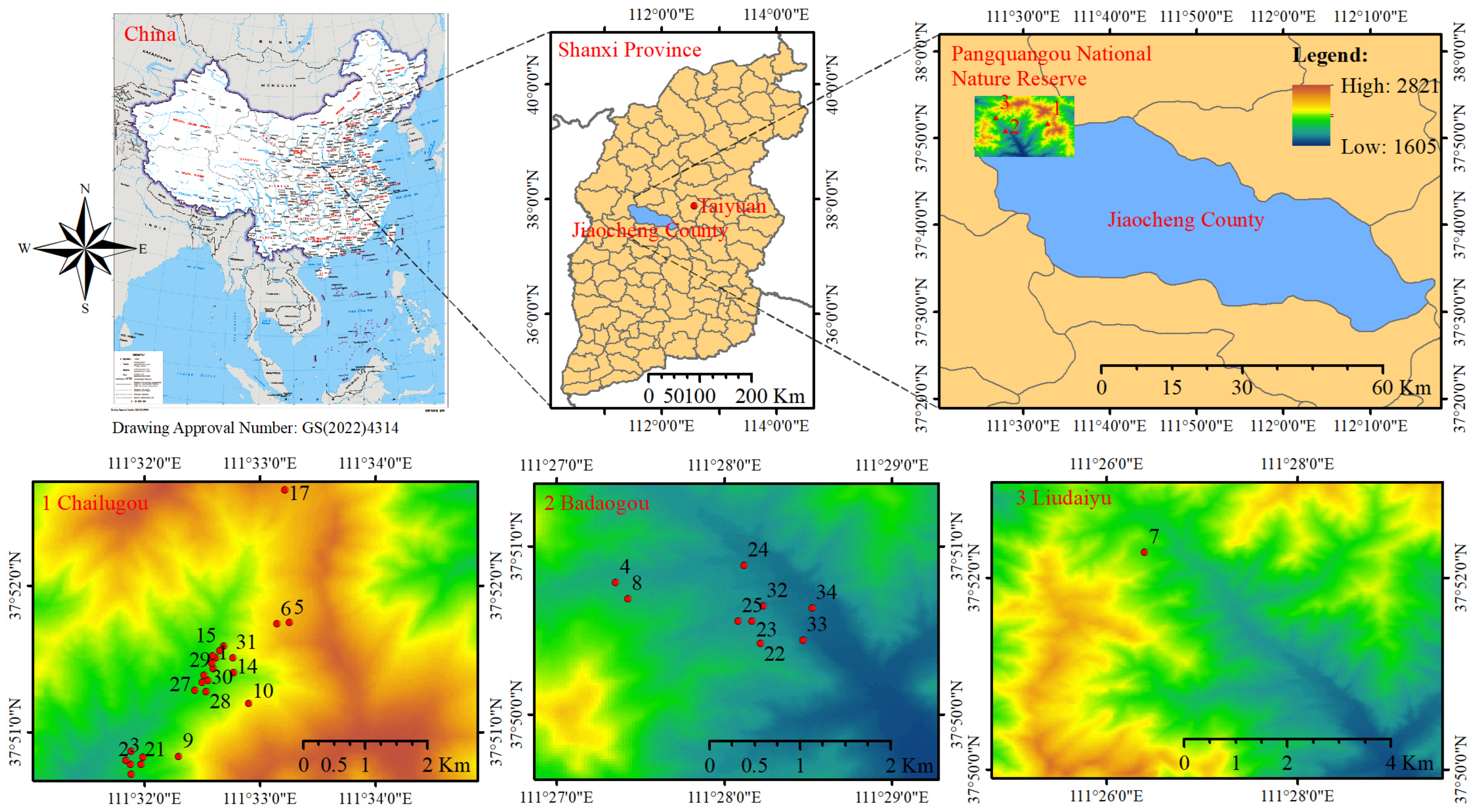
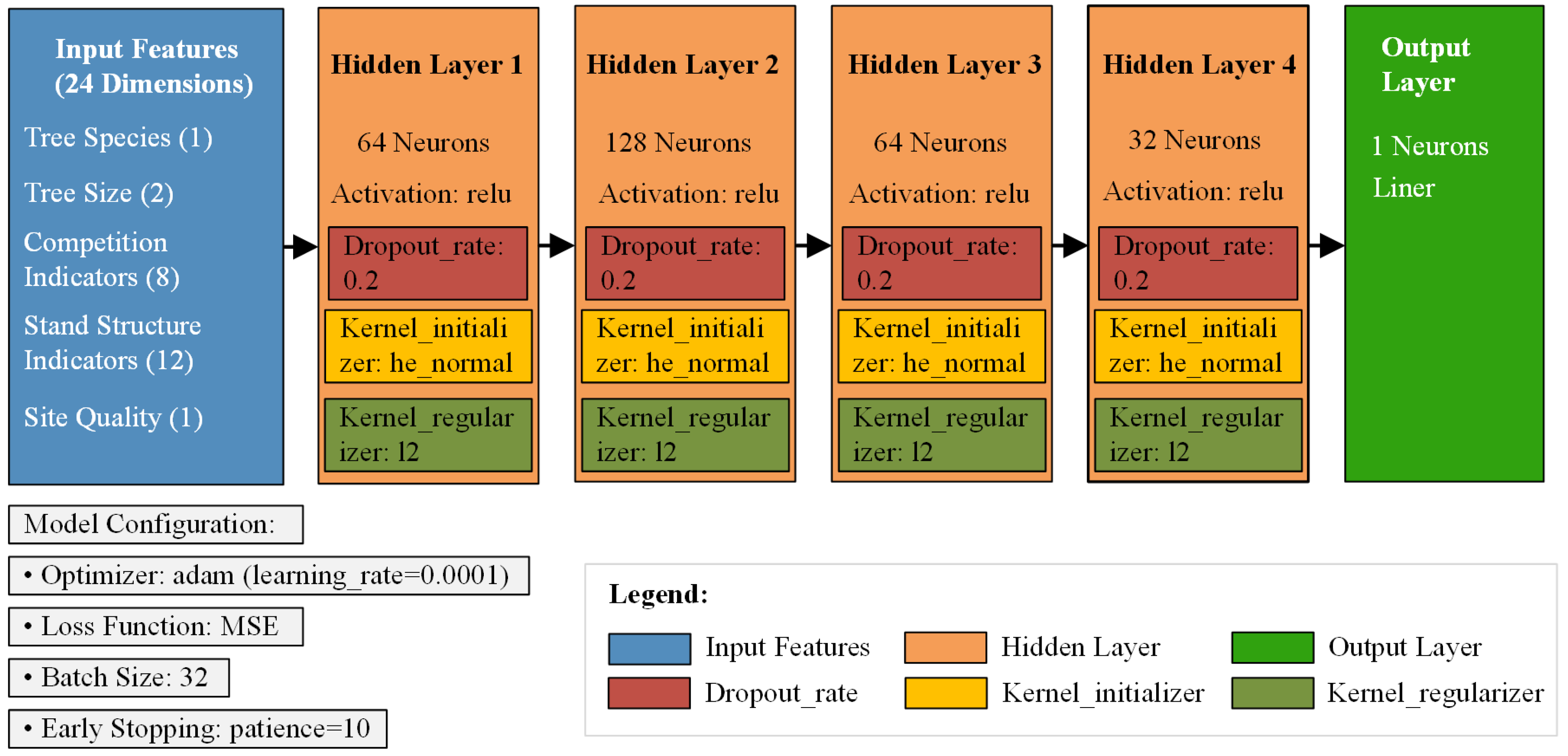






| Statistical Metrics | CW /m | DBH /cm | H /m | HD /m | Stem per Hectare /N | Dg /cm | Arithmetic Average H/m |
|---|---|---|---|---|---|---|---|
| Min. | 1.5 | 5.0 | 5.1 | 19.3 | 108 | 15.7 | 9.7 |
| Max. | 14.4 | 70.3 | 39.8 | 39.2 | 1,000 | 39.6 | 29.8 |
| Ave. ± SD | 5.0 ± 1.9 | 26.7 ± 12.4 | 20.3 ± 8.7 | 27.5 ± 4.2 | 475.6 ± 189.9 | 27.1 ± 4.5 | 18.6 ± 4.4 |
| Tier no. | Hyperparameter | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Hidden_Layers | Units | Kernel_Initializer | Kernel_Regularizer | DropOut_Rate | Optimizer | Learning_Rate | Activation | Batch_Size | |
| 1 | [2,3,4,5] | [1, 2, 4, 8, 16, 32, 64, 128, 256] | [‘he_normal’] | [‘l2(0.0001)’] | [0.2] | [‘adam’] | [1e−4] | [‘relu’] | [32, 64, 96, 128, 256] |
| 2 | [2,3,4,5] | [16, 32, 64, 128] (Data-scaled) | [‘he_normal’] | [‘l2(0.0001)’] | [0.2] | [‘adam’] | [1e−4] | [‘relu’] | [32, 64, 96, 128, 256] |
| 3 | [2,3,4,5] | [16, 32, 64, 128] (Data-scaled) | [‘he_normal’] | ‘l2_reg’, min_value = 1e−6, max_value = 1e−3, sampling = ‘log’ | ‘min’: 0.1, ‘max’: 0.4, ‘sampling’: ‘linear’ | [‘adam’] | [1e−4] | [‘relu’] | [32, 64, 96, 128, 256] |
| 4 | [2,3,4,5] | [16, 32, 64, 128] (Data-scaled) | [‘he_normal’, ‘glorot_uniform’] | ‘l2_reg’, min_value = 1e−6, max_value = 1e−3, sampling = ‘log’ | ‘min’: 0.1, ‘max’: 0.4, ‘sampling’: ‘linear’ | [‘adam’, ‘sgd’, ‘rmsprop’] | ‘min’: 1e−4, ‘max’: 1e−2, ‘sampling’: ‘log’ | [‘relu’, ‘elu’, ‘selu’] ‘beta_1’: ‘min’: 0.8, ‘max’: 0.999, ‘sampling’: ‘log’ ‘beta_2’: ‘min’: 0.9, ‘max’: 0.9999, ‘sampling’: ‘log’ ‘epsilon’: ‘min’: 1e−9, ‘max’: 1e−6, ‘sampling’: ‘log’ ‘momentum’: ‘min’: 0.8, ‘max’: 0.99, ‘sampling’: ‘log’ ‘nesterov’: [True, False] ‘rho’: ‘min’: 0.8, ‘max’: 0.99, ‘sampling’: ‘log’ | [32, 64, 96, 128, 256] |
| Model No. | Comment Variables | Different Variables |
|---|---|---|
| DNN1-1 | DBH, Species, H, N, SDI, BA, Dg, Utree, Ctree, Wtree, Mtree, Mstand, Dmax, , HD | Ustand, Cstand, GC, 1-D, H′, Wstand, R, CVd, K |
| DNN2-1 | ||
| DNN3-1 | ||
| DNN4-1 | ||
| DNN1-2 | DBH, Species, H, N, SDI, BA, Dg, Utree, Ctree, Wtree, Mtree, Mstand, Dmax, , HD | Ustand 15, Cstand 15, GC15, 1-D 15, H′15, Wstand 15, R15, CVd15, K15 |
| DNN2-2 | ||
| DNN3-2 | ||
| DNN4-2 |
| Model No. | Validating Folds Fitting Statistics | Training Fold Fitting Statistics | |||||
|---|---|---|---|---|---|---|---|
| R2 | MSE | MAE/m | MAPE/% | MSE | MAE/m | MAPE/% | |
| DNN1-1 | 0.68 ± 0.05 | 0.31 ± 0.02 | 0.42 ± 0.02 | 715.33 ± 965.41 | 0.30 ± 0.02 | 0.42 ± 0.01 | 558.09 ± 526.73 |
| DNN2-1 | 0.66 ± 0.04 | 0.33 ± 0.04 | 0.44 ± 0.03 | 857.97 ± 1241.28 | 0.36 ± 0.02 | 0.46 ± 0.01 | 649.48 ± 717.86 |
| DNN3-1 | 0.68 ± 0.05 | 0.30 ± 0.02 | 0.42 ± 0.02 | 917.86 ± 1424.77 | 0.27 ± 0.03 | 0.40 ± 0.02 | 560.50 ± 576.08 |
| DNN4-1 | 0.69 ± 0.04 | 0.30 ± 0.02 | 0.41 ± 0.02 | 903.65 ± 1346.82 | 0.30 ± 0.02 | 0.42 ± 0.02 | 513.28 ± 443.82 |
| DNN1-2 | 0.68 ± 0.05 | 0.31 ± 0.02 | 0.43 ± 0.02 | 776.21 ± 1110.31 | 0.32 ± 0.02 | 0.44 ± 0.01 | 829.25 ± 743.02 |
| DNN2-2 | 0.67 ± 0.04 | 0.31 ± 0.01 | 0.43 ± 0.02 | 618.97 ± 777.87 | 0.30 ± 0.03 | 0.42 ± 0.02 | 783.12 ± 719.93 |
| DNN3-2 | 0.70 ± 0.05 | 0.29 ± 0.02 | 0.41 ± 0.01 | 764.40 ± 1053.72 | 0.25 ± 0.02 | 0.38 ± 0.1 | 733.68 ± 634.74 |
| DNN4-2 | 0.71 ± 0.04 | 0.29 ± 0.02 | 0.41 ± 0.02 | 653.75 ± 785.17 | 0.25 ± 0.03 | 0.38 ± 0.02 | 614.02 ± 601.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Cheng, X.; Liu, S.; He, C.; Peng, W.; Zhang, M. Individual-Tree Crown Width Prediction for Natural Mixed Forests in Northern China Using Deep Neural Network and Height Threshold Method. Forests 2025, 16, 1778. https://doi.org/10.3390/f16121778
Zhou L, Cheng X, Liu S, He C, Peng W, Zhang M. Individual-Tree Crown Width Prediction for Natural Mixed Forests in Northern China Using Deep Neural Network and Height Threshold Method. Forests. 2025; 16(12):1778. https://doi.org/10.3390/f16121778
Chicago/Turabian StyleZhou, Lai, Xiaofang Cheng, Shaoyu Liu, Chunxin He, Wei Peng, and Mengtao Zhang. 2025. "Individual-Tree Crown Width Prediction for Natural Mixed Forests in Northern China Using Deep Neural Network and Height Threshold Method" Forests 16, no. 12: 1778. https://doi.org/10.3390/f16121778
APA StyleZhou, L., Cheng, X., Liu, S., He, C., Peng, W., & Zhang, M. (2025). Individual-Tree Crown Width Prediction for Natural Mixed Forests in Northern China Using Deep Neural Network and Height Threshold Method. Forests, 16(12), 1778. https://doi.org/10.3390/f16121778








