Multi-Indicator Drought Variability in Europe (1766–2018)
Abstract
1. Introduction
2. Data and Methods
2.1. Datasets
2.2. Methods
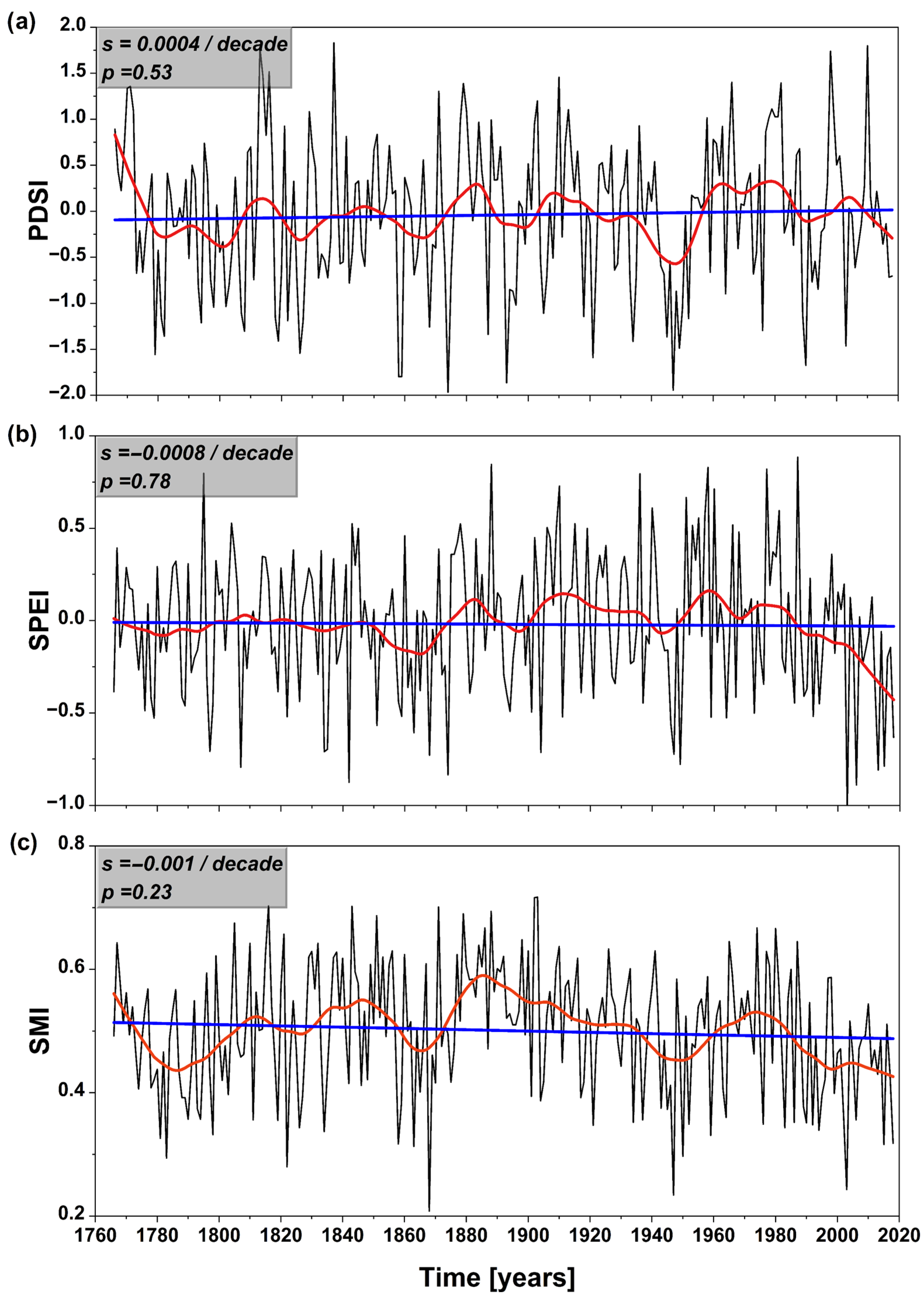
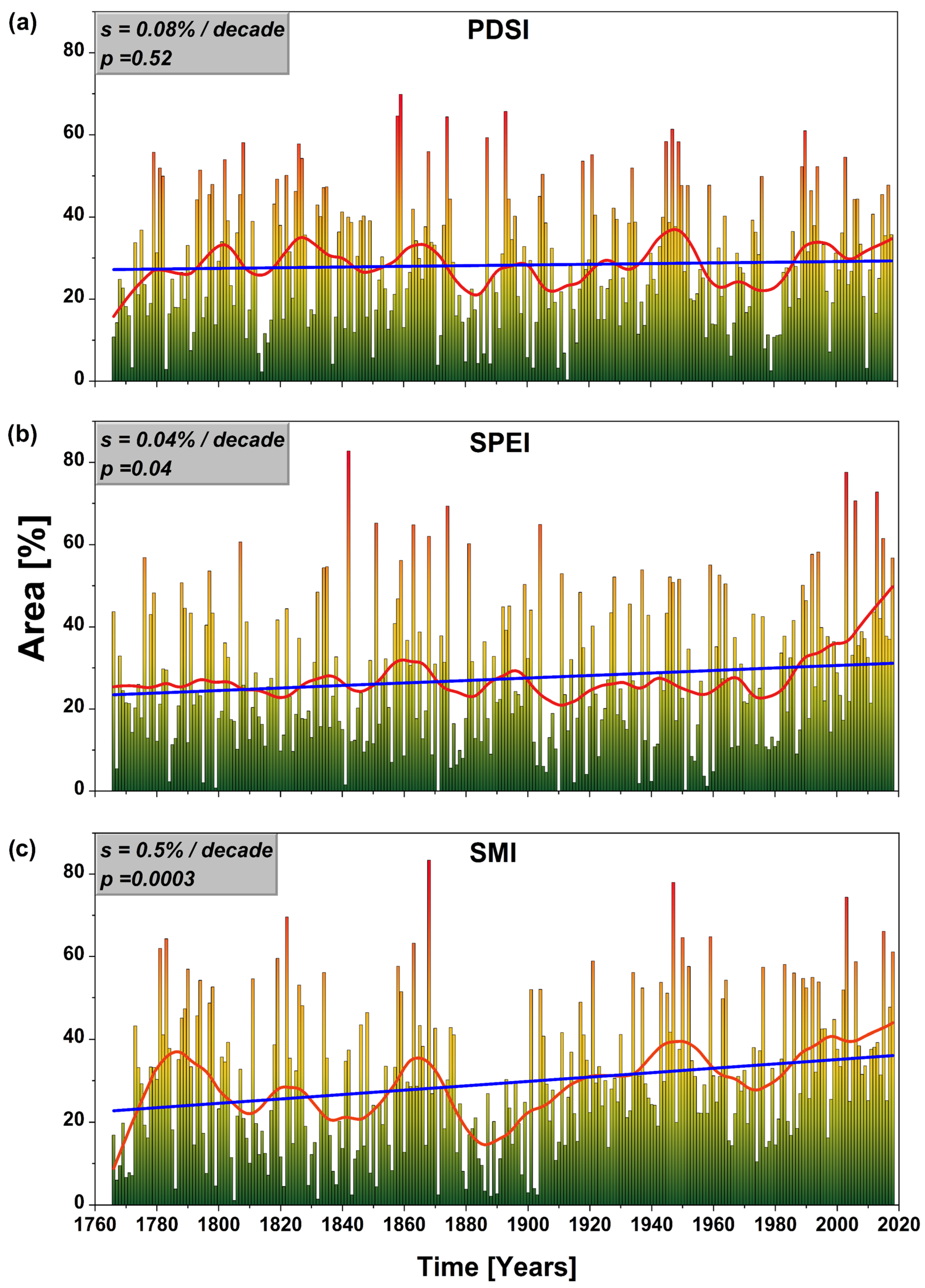
3. Results
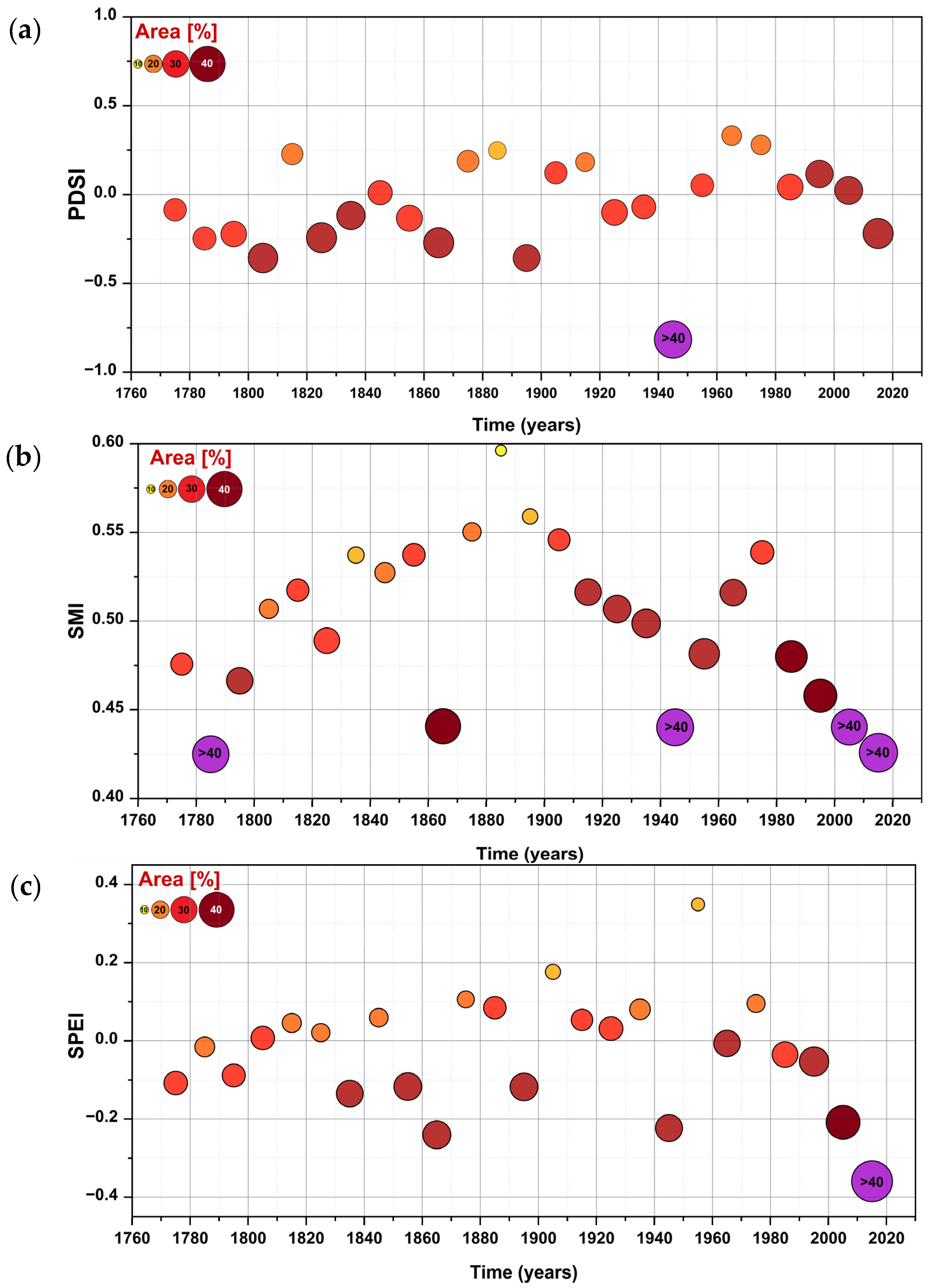
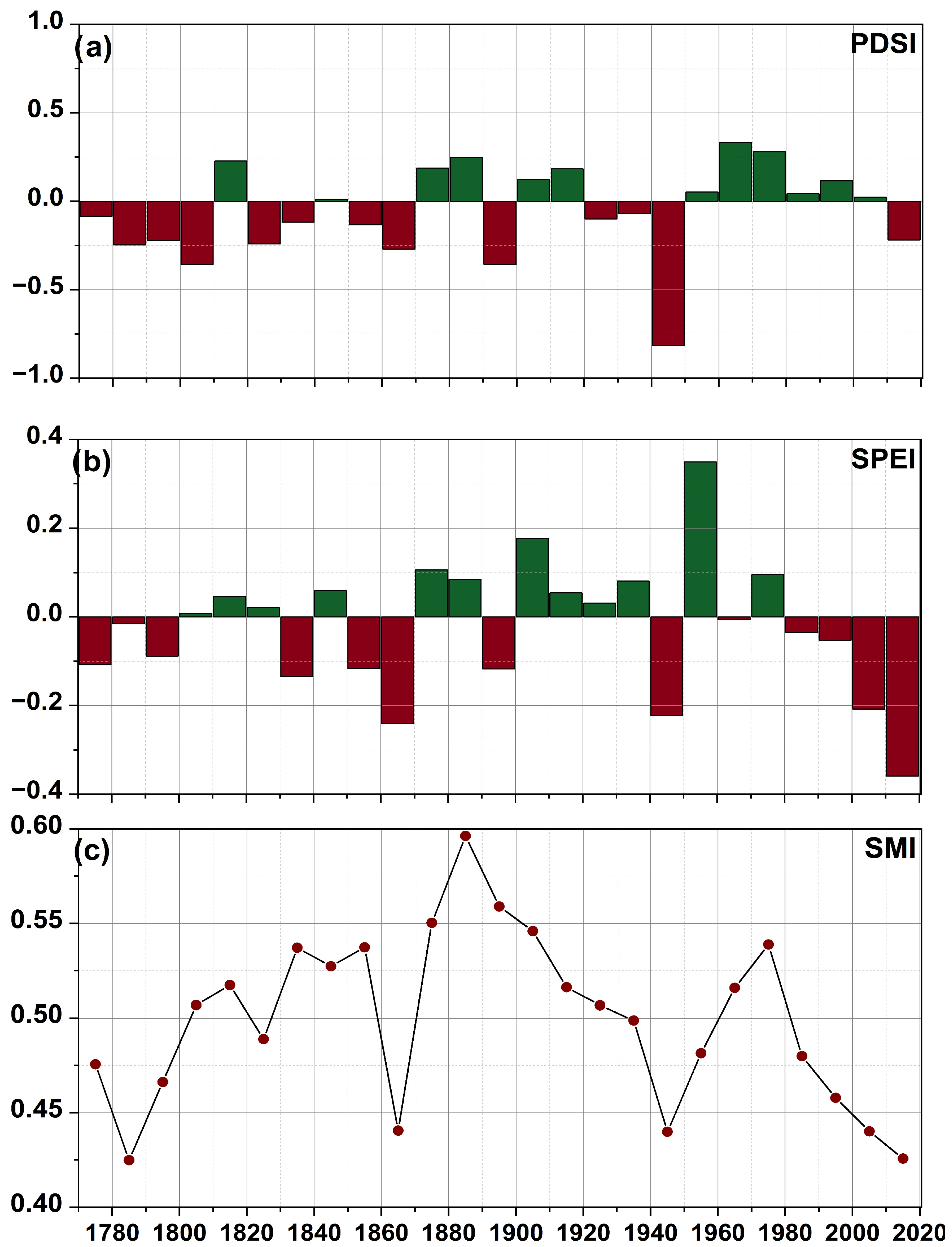
3.1. The Extremities of Individual Years
3.2. European Droughts: A Decadal Perspective
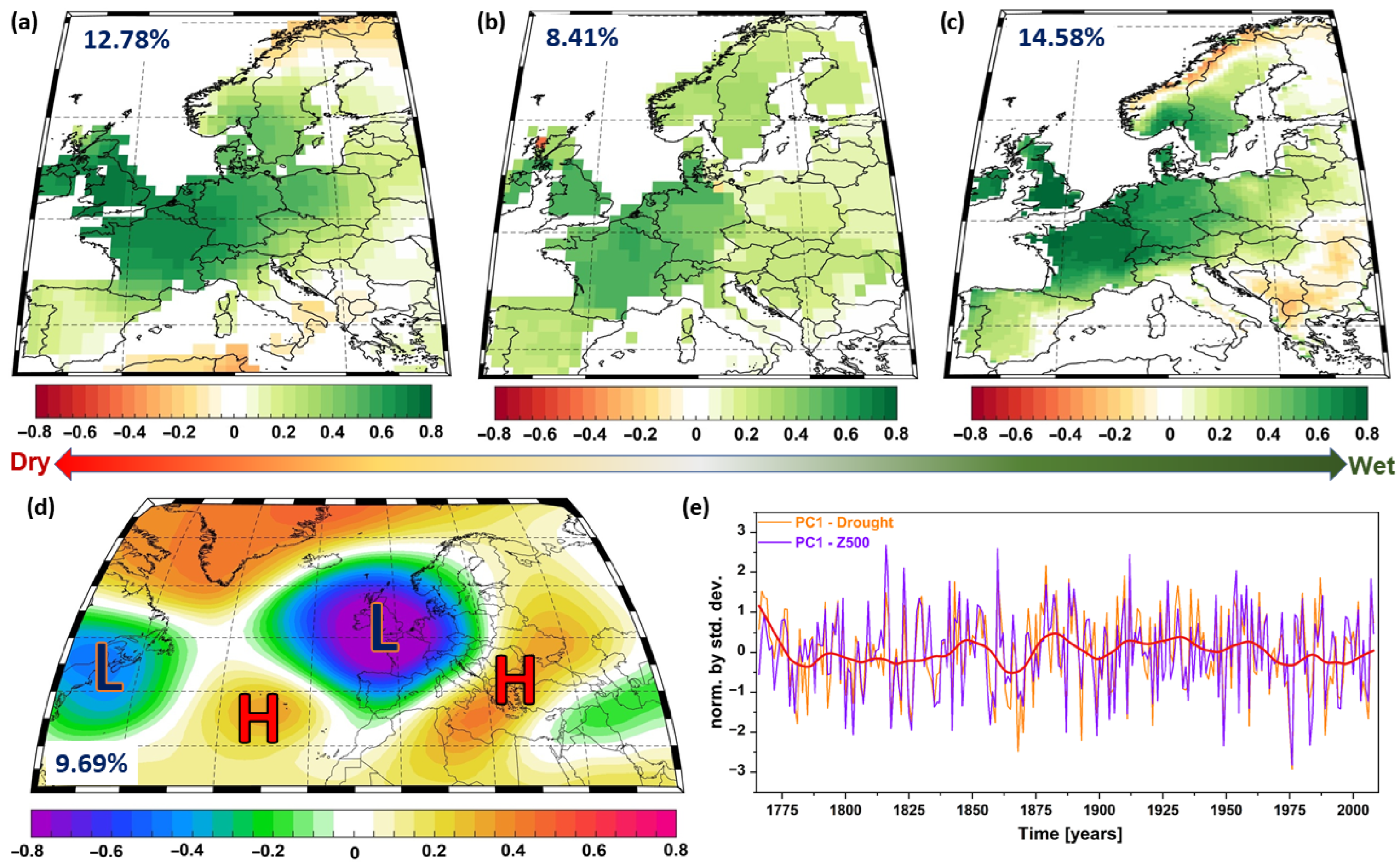
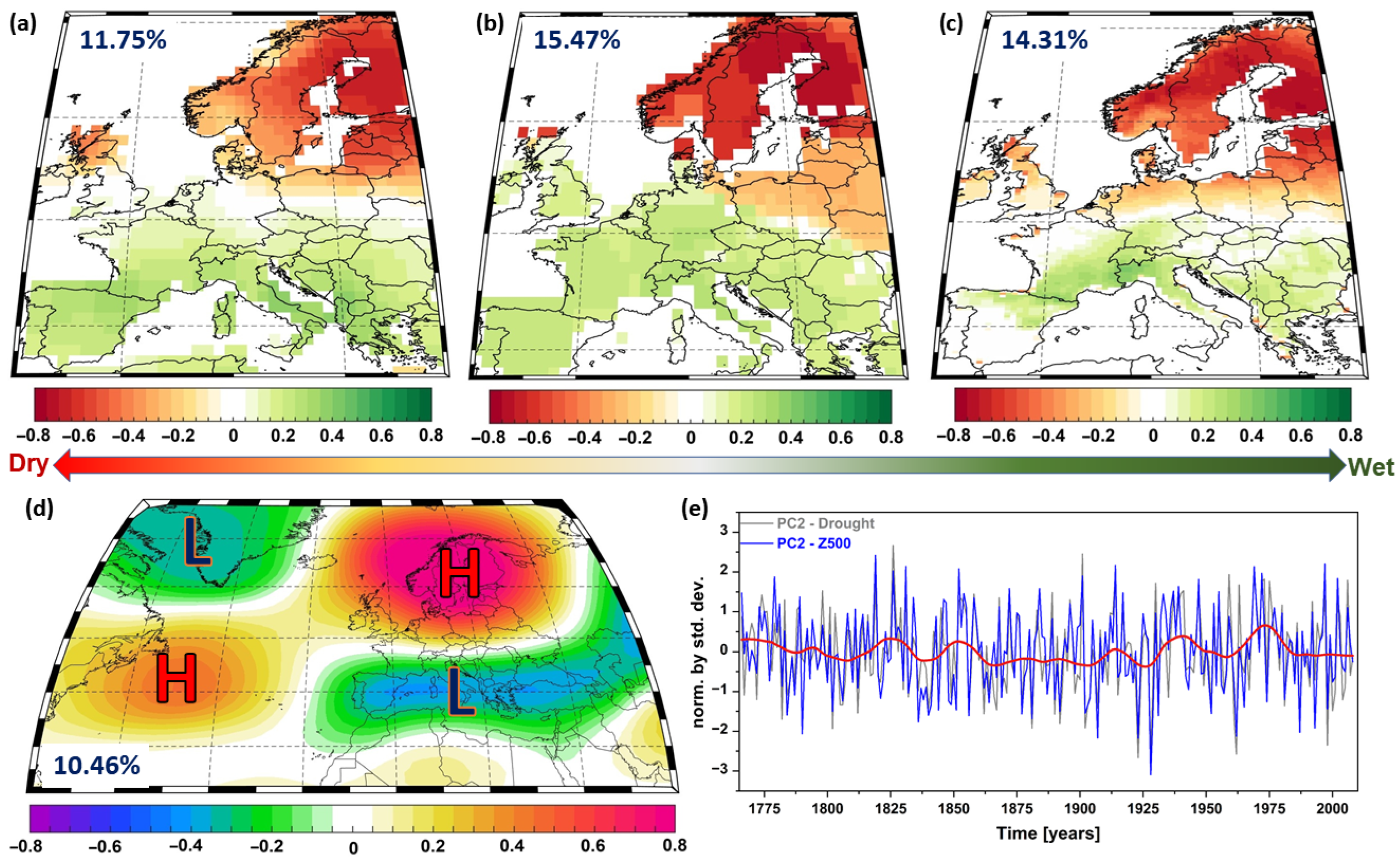
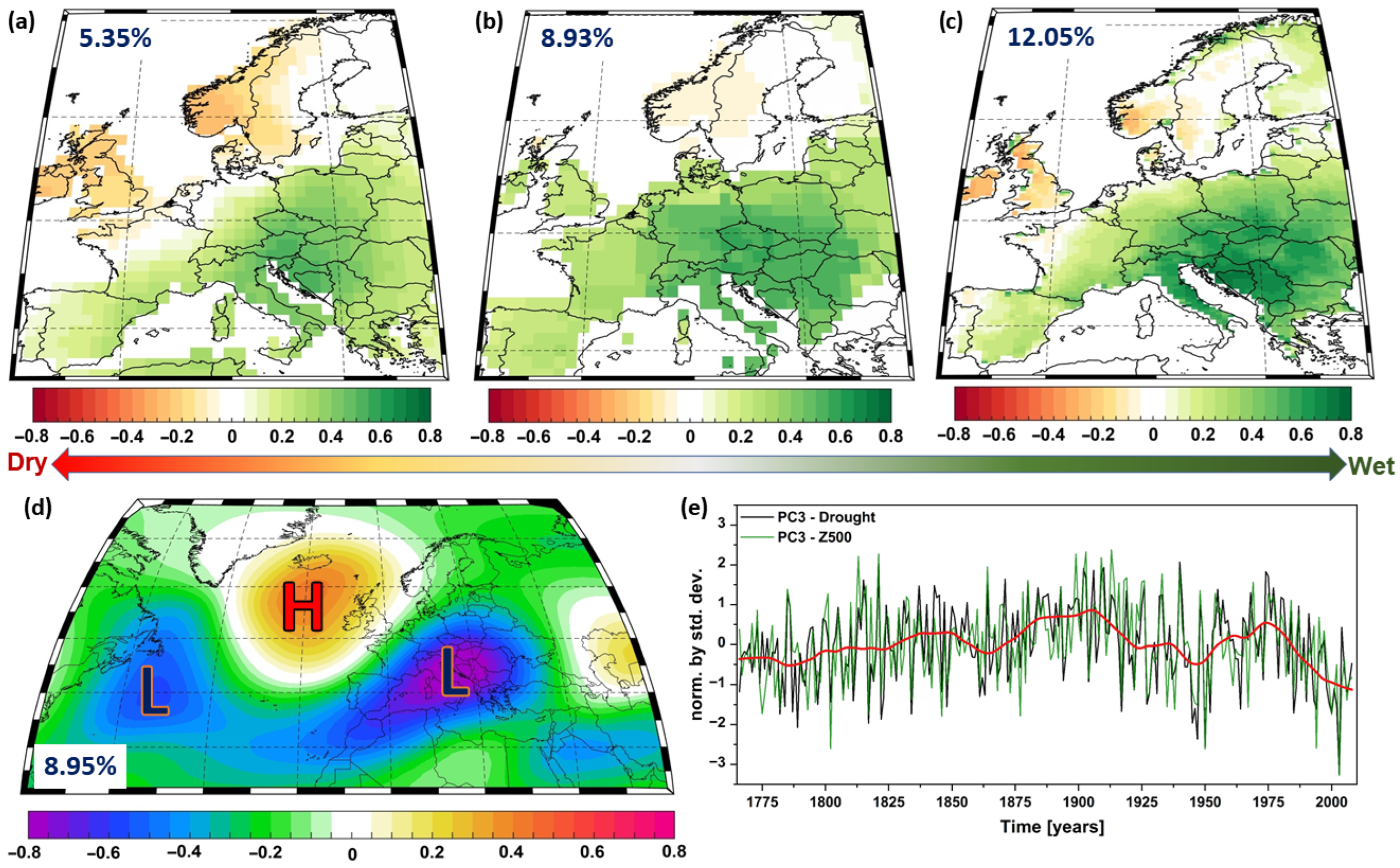
3.3. Large-Scale Drivers of Summer Droughts
4. Discussion and Limitations of the Study
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ionita, M.; Nagavciuc, V. Forecasting Low Flow Conditions Months in Advance through Teleconnection Patterns, with a Special Focus on Summer 2018. Sci. Rep. 2020, 10, 13258. [Google Scholar] [CrossRef]
- Hari, V.; Rakovec, O.; Markonis, Y.; Hanel, M.; Kumar, R. Increased Future Occurrences of the Exceptional 2018–2019 Central European Drought under Global Warming. Sci. Rep. 2020, 10, 12207. [Google Scholar] [CrossRef]
- Ramonet, M.; Ciais, P.; Apadula, F.; Bartyzel, J.; Bastos, A.; Bergamaschi, P.; Blanc, P.E.; Brunner, D.; di Torchiarolo, L.C.; Calzolari, F.; et al. The Fingerprint of the Summer 2018 Drought in Europe on Ground-Based Atmospheric CO2 Measurements. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2020, 375, 20190513. [Google Scholar] [CrossRef]
- Bastos, A.; Ciais, P.; Friedlingstein, P.; Sitch, S.; Pongratz, J.; Fan, L.; Wigneron, J.P.; Weber, U.; Reichstein, M.; Fu, Z.; et al. Direct and Seasonal Legacy Effects of the 2018 Heat Wave and Drought on European Ecosystem Productivity. Sci. Adv. 2020, 6, eaba2724. [Google Scholar] [CrossRef] [PubMed]
- Ionita, M.; Nagavciuc, V. Changes in Drought Features at the European Level over the Last 120 Years. Nat. Hazards Earth Syst. Sci. 2021, 21, 1685–1701. [Google Scholar] [CrossRef]
- Ionita, M.; Antonescu, B.; Roibu, C.; Nagavciuc, V. Drought’s Grip on Romania: A Tale of Two Indices. Int. J. Climatol. 2025, 45, e8876. [Google Scholar] [CrossRef]
- Ghazi, B.; Przybylak, R.; Pospieszyńska, A. Projection of Climate Change Impacts on Extreme Temperature and Precipitation in Central Poland. Sci. Rep. 2023, 13, 18772. [Google Scholar] [CrossRef]
- Knutzen, F.; Averbeck, P.; Barrasso, C.; Bouwer, L.M.; Gardiner, B.; Grünzweig, J.M.; Hänel, S.; Haustein, K.; Johannessen, M.R.; Kollet, S.; et al. Impacts and Damages of the European Multi-Year Drought and Heat Event 2018–2022 on Forests, a Review. Nat. Hazards Earth Syst. Sci. 2025, 25, 77–117. [Google Scholar] [CrossRef]
- Blauhut, V.; Stoelzle, M.; Ahopelto, L.; Brunner, M.I.; Teutschbein, C.; Wendt, D.E.; Akstinas, V.; Bakke, S.J.; Barker, L.J.; Bartošová, L.; et al. Lessons from the 2018–2019 European Droughts: A Collective Need for Unifying Drought Risk Management. Nat. Hazards Earth Syst. Sci. 2022, 22, 2201–2217. [Google Scholar] [CrossRef]
- Rousi, E.; Fink, A.H.; Andersen, L.S.; Becker, F.N.; Beobide-Arsuaga, G.; Breil, M.; Cozzi, G.; Heinke, J.; Jach, L.; Niermann, D.; et al. The Extremely Hot and Dry 2018 Summer in Central and Northern Europe from a Multi-Faceted Weather and Climate Perspective. Nat. Hazards Earth Syst. Sci. 2023, 23, 1699–1718. [Google Scholar] [CrossRef]
- Sinclair, V.A.; Mikkola, J.; Rantanen, M.; Räisänen, J. The Summer 2018 Heatwave in Finland. Weather 2019, 74, 403–409. [Google Scholar] [CrossRef]
- Naumann, G.; Cammalleri, C.; Mentaschi, L.; Feyen, L. Increased Economic Drought Impacts in Europe with Anthropogenic Warming. Nat. Clim. Change 2021, 11, 485–491. [Google Scholar] [CrossRef]
- Rosenzweig, C.; Elliott, J.; Deryng, D.; Ruane, A.C.; Müller, C.; Arneth, A.; Boote, K.J.; Folberth, C.; Glotter, M.; Khabarov, N.; et al. Assessing Agricultural Risks of Climate Change in the 21st Century in a Global Gridded Crop Model Intercomparison. Proc. Natl. Acad. Sci. USA 2014, 111, 3268–3273. [Google Scholar] [CrossRef] [PubMed]
- Estrela, T.; Menéndez, M.; Dimas, M.; Marcuello, C.C.; Rees, G.; Cole, G.; Weber, K.; Grath, J.; Leonard, J.; Ovesen, N.B.; et al. Sustainable Water Use in Europe Part 3: Extreme Hydrological Events: Floods and Droughts; Environmental issue report; European Environment Agency: Copenhagen, Denmark, 2001; pp. 1–84. [Google Scholar]
- IDMP. Drought and Water Scarcity; Global Water Partnership and World Meteorological Organization: Stockholm, Sweden; Geneva, Switzerland, 2022; pp. 1–24. [Google Scholar]
- Cook, B.I.; Smerdon, J.E.; Cook, E.R.; Williams, A.P.; Anchukaitis, K.J.; Mankin, J.S.; Allen, K.; Andreu-Hayles, L.; Ault, T.R.; Belmecheri, S.; et al. Megadroughts in the Common Era and the Anthropocene. Nat. Rev. Earth Environ. 2022, 3, 741–757. [Google Scholar] [CrossRef]
- Ionita, M.; Nagavciuc, V.; Scholz, P.; Dima, M. Long-Term Drought Intensification over Europe Driven by the Weakening Trend of the Atlantic Meridional Overturning Circulation. J. Hydrol. Reg. Stud. 2022, 42, 101176. [Google Scholar] [CrossRef]
- Kingston, D.G.; Lawler, D.M.; McGregor, G.R. Linkages between Atmospheric Circulation, Climate and Streamflow in the Northern North Atlantic: Research Prospects. Prog. Phys. Geogr. 2006, 30, 143–174. [Google Scholar] [CrossRef]
- Schubert, S.D.; Wang, H.; Koster, R.D.; Suarez, M.J.; Groisman, P.Y. Northern Eurasian Heat Waves and Droughts. J. Clim. 2014, 27, 3169–3207. [Google Scholar] [CrossRef]
- Kingston, D.G.; Stagge, J.H.; Tallaksen, L.M.; Hannah, D.M. European-Scale Drought: Understanding Connections between Atmospheric Circulation and Meteorological Drought Indices. J. Clim. 2015, 28, 505–516. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Naumann, G.; Alfieri, L.; Wyser, K.; Mentaschi, L.; Betts, R.A.; Carrao, H.; Spinoni, J.; Vogt, J.; Feyen, L. Global Changes in Drought Conditions Under Different Levels of Warming. Geophys. Res. Lett. 2018, 45, 3285–3296. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Vogt, J.V.; Barbosa, P. Meteorological Droughts in Europe: Events and Impacts—Past Trends and Future Projections; Publications Office of the European Union: Luxembourg, 2016; p. 134. [Google Scholar]
- Kreibich, H.; Loon, A.F.V.; Schröter, K.; Ward, P.J.; Mazzoleni, M.; Sairam, N.; Abeshu, G.W.; Agafonova, S.; AghaKouchak, A.; Aksoy, H.; et al. The Challenge of Unprecedented Floods and Droughts in Risk Management. Nature 2022, 608, 80–86. [Google Scholar] [CrossRef]
- Stagge, J.H.; Kingston, D.G.; Tallaksen, L.M.; Hannah, D.M. Observed Drought Indices Show Increasing Divergence across Europe. Sci. Rep. 2017, 7, 14045. [Google Scholar] [CrossRef] [PubMed]
- Nagavciuc, V.; Ionita, M.; Kern, Z.; McCarroll, D.; Popa, I. A ~700 Years Perspective on the 21st Century Drying in the Eastern Part of Europe Based on δ18O in Tree Ring Cellulose. Commun. Earth Environ. 2022, 3, 277. [Google Scholar] [CrossRef]
- von Storch, H.; Zwiers, F.W. Statistical Analysis in Climate Research; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Tejedor, E.; de Luis, M.; Cuadrat, J.M.; Esper, J.; Saz, M.Á. Tree-Ring-Based Drought Reconstruction in the Iberian Range (East of Spain) since 1694. Int. J. Biometeorol. 2016, 60, 361–372. [Google Scholar] [CrossRef] [PubMed]
- Labuhn, I.; Daux, V.; Girardclos, O.; Stievenard, M.; Pierre, M.; Masson-Delmotte, V. French Summer Droughts since 1326 CE: A Reconstruction Based on Tree Ring Cellulose δ18O. Clim. Past 2016, 12, 1101–1117. [Google Scholar] [CrossRef]
- Cook, E.R.; Seager, R.; Kushnir, Y.; Briffa, K.R.; Büntgen, U.; Frank, D.; Krusic, P.J.; Tegel, W.; van der Schrier, G.; Andreu-Hayles, L.; et al. Old World Megadroughts and Pluvials during the Common Era. Sci. Adv. 2015, 1, e1500561. [Google Scholar] [CrossRef]
- Freund, M.B.; Helle, G.; Balting, D.F.; Ballis, N.; Schleser, G.H.; Cubasch, U. European Tree-Ring Isotopes Indicate Unusual Recent Hydroclimate. Commun. Earth Environ. 2023, 4, 26. [Google Scholar] [CrossRef]
- Rakovec, O.; Samaniego, L.; Hari, V.; Markonis, Y.; Moravec, V.; Thober, S.; Hanel, M.; Kumar, R. The 2018–2020 Multi-Year Drought Sets a New Benchmark in Europe. Earth’s Future 2022, 10, e2021EF002394. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated High-Resolution Grids of Monthly Climatic Observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Wells, N.; Goddard, S.; Hayes, M. A Self-Calibrating Palmer Drought Severity Index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
- Palmer, W. Meteorological Drought; Weather Bureau: Washington, DC, USA, 1965; Volume 45. [Google Scholar]
- Yan, D.; Shi, X.; Yang, Z.; Li, Y.; Zhao, K.; Yuan, Y. Modified Palmer Drought Severity Index Based on Distributed Hydrological Simulation. Math. Probl. Eng. 2013, 2013, 327374. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, Y.; Ma, X.; Ren, L.; Singh, V.P. Drought Analysis in the Yellow River Basin Based on a Short-Scalar Palmer Drought Severity Index. Water 2018, 10, 1526. [Google Scholar] [CrossRef]
- Heim, R. Computing the Monthly Palmer Drought Index on a Weekly Basis: A Case Study Comparing Data Estimation Techniques. Geophys. Res. Lett. 2005, 32, L06401. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS Monthly High-Resolution Gridded Multivariate Climate Dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I.; Angulo, M.; Kenawy, A.E. A New Global 0.5° Gridded Dataset (1901–2006) of a Multiscalar Drought Index: Comparison with Current Drought Index Datasets Based on the Palmer Drought Severity Index. J. Hydrometeorol. 2010, 11, 1033–1043. [Google Scholar] [CrossRef]
- Casty, C.; Raible, C.C.; Stocker, T.F.; Wanner, H.; Luterbacher, J. A European Pattern Climatology 1766–2000. Clim. Dyn. 2007, 29, 791–805. [Google Scholar] [CrossRef]
- Hofstra, N.; Haylock, M.; New, M.; Jones, P.D. Testing E-OBS European High-Resolution Gridded Data Set of Daily Precipitation and Surface Temperature. J. Geophys. Res. Atmos. 2009, 114, D21101. [Google Scholar] [CrossRef]
- Kumar, R.; Samaniego, L.; Attinger, S. Implications of Distributed Hydrologic Model Parameterization on Water Fluxes at Multiple Scales and Locations. Water Resour. Res. 2013, 49, 360–379. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Vanderlinden, K.; Giráldez, J.V.; van Meirvenne, M. Spatial Estimation of Reference Evapotranspiration in Andalusia, Spain. J. Hydrometeorol. 2008, 9, 242–255. [Google Scholar] [CrossRef]
- Valler, V.; Franke, J.; Brugnara, Y.; Brönnimann, S. An Updated Global Atmospheric Paleo-Reanalysis Covering the Last 400 Years. Geosci. Data J. 2022, 9, 89–107. [Google Scholar] [CrossRef]
- Mann, H.B. Non-Parametric Test against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Adamowski, K.; Prokoph, A.; Adamowski, J. Development of a New Method of Wavelet Aided Trend Detection and Estimation. Hydrol. Process. 2009, 23, 2686–2696. [Google Scholar] [CrossRef]
- Dang, V.H.; Tran, D.D.; Cham, D.D.; Hang, P.T.T.; Nguyen, H.T.; Truong, H.V.; Tran, P.H.; Duong, M.B.; Nguyen, N.T.; Le, K.V.; et al. Assessment of Rainfall Distributions and Characteristics in Coastal Provinces of the Vietnamese Mekong Delta under Climate Change and ENSO Processes. Water 2020, 12, 1555. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A.R. A Modified Mann-Kendall Trend Test for Autocorrelated Data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Ionita, M.; Tallaksen, L.M.; Kingston, D.G.; Stagge, J.H.; Laaha, G.; Lanen, H.A.J.V.; Scholz, P.; Chelcea, S.M.; Haslinger, K.; Lanen, H.A.J.V.; et al. The European 2015 Drought from a Climatological Perspective. Hydrol. Earth Syst. Sci. 2017, 21, 1397–1419. [Google Scholar] [CrossRef]
- Parry, S.; Hannaford, J.; Lloyd-Hughes, B.; Prudhomme, C. Multi-Year Droughts in Europe: Analysis of Development and Causes. Hydrol. Res. 2012, 43, 689–706. [Google Scholar] [CrossRef]
- Moravec, V.; Markonis, Y.; Rakovec, O.; Svoboda, M.; Trnka, M.; Kumar, R.; Hanel, M. Europe under Multi-Year Droughts: How Severe Was the 2014–2018 Drought Period? Environ. Res. Lett. 2021, 16, 034062. [Google Scholar] [CrossRef]
- Ionita, M.; Nagavciuc, V.; Kumar, R.; Rakovec, O. On the Curious Case of the Recent Decade, Mid-Spring Precipitation Deficit in Central Europe. NPJ Clim. Atmos. Sci. 2020, 3, 49. [Google Scholar] [CrossRef]
- Ionita, M.; Boroneanṭ, C.; Chelcea, S. Seasonal Modes of Dryness and Wetness Variability over Europe and Their Connections with Large Scale Atmospheric Circulation and Global Sea Surface Temperature. Clim. Dyn. 2015, 45, 2803–2829. [Google Scholar] [CrossRef]
- Brooks, C.E.P.; Glasspoole, J. The Drought of 1921 in the British Isles. Mon. Weather Rev. 1922, 50, 93. [Google Scholar] [CrossRef]
- Büntgen, U.; Urban, O.; Krusic, P.J.; Rybníček, M.; Kolář, T.; Kyncl, T.; Ač, A.; Koňasová, E.; Čáslavský, J.; Esper, J.; et al. Recent European Drought Extremes beyond Common Era Background Variability. Nat. Geosci. 2021, 14, 190–196. [Google Scholar] [CrossRef]
- Ionita, M.; Dima, M.; Nagavciuc, V.; Scholz, P.; Lohmann, G. Past Megadroughts in Central Europe Were Longer, More Severe and Less Warm than Modern Droughts. Commun. Earth Environ. 2021, 2, 61. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Vicente-Serrano, S.M.; Domínguez-Castro, F.; Murphy, C.; Hannaford, J.; Reig, F.; Peña-Angulo, D.; Tramblay, Y.; Trigo, R.M.; Donald, N.M.; Luna, M.Y.; et al. Long-Term Variability and Trends in Meteorological Droughts in Western Europe (1851–2018). Int. J. Climatol. 2021, 41, E690–E717. [Google Scholar] [CrossRef]
- Andreu-Hayles, L.; Lévesque, M.; Guerrieri, R.; Siegwolf, R.T.W.; Körner, C. Limits and Strengths of Tree-Ring Stable Isotopes. In Stable Isotopes in Tree Rings: Inferring Physiological, Climatic and Environmental Responses; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar]
- Gagen, M.; Battipaglia, G.; Daux, V.; Duffy, J.; Dorado-Liñán, I.; Hayles, L.A.; Martínez-Sancho, E.; McCarroll, D.; Shestakova, T.A.; Treydte, K. Climate Signals in Stable Isotope Tree-Ring Records. In Stable Isotopes in Tree Rings. Tree Physiology; Siegwolf, R.T.W., Brooks, J.R., Roden, J., Saurer, M., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 537–579. [Google Scholar]
- Samaniego, L.; Thober, S.; Kumar, R.; Wanders, N.; Rakovec, O.; Pan, M.; Zink, M.; Sheffield, J.; Wood, E.F.; Marx, A. Anthropogenic Warming Exacerbates European Soil Moisture Droughts. Nat. Clim. Change 2018, 8, 421–426. [Google Scholar] [CrossRef]
- McCarroll, D.; Loader, N.J. Stable Isotopes in Tree Rings. Quat. Sci. Rev. 2004, 23, 771–801. [Google Scholar] [CrossRef]
- Levanič, T.; Popa, I.; Poljanšek, S.; Nechita, C. A 323-Year Long Reconstruction of Drought for SW Romania Based on Black Pine (Pinus Nigra) Tree-Ring Widths. Int. J. Biometeorol. 2013, 57, 703–714. [Google Scholar] [CrossRef] [PubMed]
- Nagavciuc, V.; Roibu, C.C.; Ionita, M.; Mursa, A.; Cotos, M.; Popa, I. Different Climate Response of Three Tree Ring Proxies of Pinus Sylvestris from the Eastern Carpathians, Romania. Dendrochronologia 2019, 54, 56–63. [Google Scholar] [CrossRef]
- Barrington, R.M. The Drought of 1887, and Some of Its Effects on Irish Agriculture. J. Stat. Soc. Inq. Soc. Irel. 1888, 9, 223–247. [Google Scholar]
- Bonacina, L.C.W. The European Drought of 1921. Nature 1923, 112, 488–489. [Google Scholar] [CrossRef]
- Brázdil, R.; Kiss, A.; Luterbache, J.; Nash, D.J.; Řezníčková, L. Documentary Data and the Study of Past Droughts: A Global State of the Art. Clim. Past 2018, 14, 1915–1960. [Google Scholar] [CrossRef]
- Brázdil, R.; Dobrovolný, P.; Trnka, M.; Řezníčková, L.; Dolák, L.; Kotyza, O. Extreme Droughts and Human Responses to Them: The Czech Lands in the Pre-Instrumental Period. Clim. Past 2019, 15, 1–24. [Google Scholar] [CrossRef]
- European Environment Agency. Economic Losses from Climate-Related Extremes in Europe; European Environment Agency: Copenhagen, Denmark, 2022. [Google Scholar]
- Glaser, R. Klimageschichte Mitteleuropas; WBG: Washington, DC, USA, 2013. [Google Scholar]
- Ionita, M.; Scholz, P.; Chelcea, S. Assessment of Droughts in Romania Using the Standardized Precipitation Index. Nat. Hazards 2016, 81, 1483–1498. [Google Scholar] [CrossRef]
- Lanen, H.A.J.V.; Laaha, G.; Kingston, D.G.; Gauster, T.; Ionita, M.; Vidal, J.P.; Vlnas, R.; Tallaksen, L.M.; Stahl, K.; Hannaford, J.; et al. Hydrology Needed to Manage Droughts: The 2015 European Case. Hydrol. Process. 2016, 30, 3097–3104. [Google Scholar] [CrossRef]
- Linderholm, H.W.; Molin, T. Early Nineteenth Century Drought in East Central Sweden Inferred from Dendrochronological and Historical Archives. Clim. Res. 2005, 29, 63–72. [Google Scholar] [CrossRef]
- Mihailescu, C. Clima Si Harardele Moldovei. Evolutia, Starea Si Predictia; Licorn: Chisinau, Moldova, 2004. [Google Scholar]
- Možný, M.; Brázdil, R.; Dobrovolný, P.; Trnka, M. April-August Temperatures in the Czech Lands, 1499–2015, Reconstructed from Grape-Harvest Dates. Clim. Past 2016, 12, 1421–1434. [Google Scholar] [CrossRef]
- Noone, S.; Broderick, C.; Duffy, C.; Matthews, T.; Wilby, R.L.; Murphy, C. A 250-Year Drought Catalogue for the Island of Ireland (1765–2015). Int. J. Climatol. 2017, 37, 239–254. [Google Scholar] [CrossRef]
- Schrier, G.V.D.; Allan, R.P.; Ossó, A.; Sousa, P.M.; Vyver, H.V.D.; Schaeybroeck, B.V.; Coscarelli, R.; Pasqua, A.A.; Petrucci, O.; Curley, M.; et al. The 1921 European Drought: Impacts, Reconstruction and Drivers. Clim. Past 2021, 17, 2201–2221. [Google Scholar] [CrossRef]
- Teodoreanu, E. În Căutarea Timpului Trecut Schiță de Climatologie Istorică; Editura Paodeia: Bucuresti, Romania, 2017. [Google Scholar]
- Topor, N. Anii Ploioşi Şi Secetoşi Din Republica Populară Romînă; C.S.A Institutul Meteorologic: Bucureşti, Romania, 1963. [Google Scholar]

| EURO | MED | CEU | NEU | Period | |
|---|---|---|---|---|---|
| PDSI | −1.74 | −1.79 | −1.17 | −1.14 | 1766–2018 |
| SPEI | −0.64 | −0.68 | −0.81 | −0.59 | 1766–2018 |
| SMI | 0.33 | 0.32 | 0.31 | 0.36 | 1766–2018 |
| EURO | MED | CEU | NEU | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PDSI | SPEI | SMI | PDSI | SPEI | SMI | PDSI | SPEI | SMI | PDSI | SPEI | SMI | |
| Magnitude | 1874 | 2003 | 1868 | 1945 | 2012 | 1945 | 1921 | 2015 | 1868 | 1826 | 1868 | 1826 |
| 1947 | 2006 | 1947 | 1779 | 2003 | 2003 | 1835 | 1807 | 2015 | 1818 | 1858 | 1858 | |
| 1893 | 1842 | 2003 | 1874 | 2016 | 1950 | 1952 | 1947 | 1921 | 1976 | 1901 | 1798 | |
| 1858 | 1874 | 1822 | 1893 | 2007 | 1990 | 1964 | 1834 | 1811 | 1940 | 2006 | 2018 | |
| 1859 | 2013 | 1783 | 2017 | 1881 | 2012 | 1827 | 1835 | 2003 | 1969 | 1826 | 1959 | |
| Area | 1859 | 1842 | 1868 | 1945 | 2012 | 1945 | 1921 | 2015 | 1868 | 1826 | 1959 | 1826 |
| 1893 | 2003 | 1947 | 1874 | 2003 | 2003 | 1835 | 1807 | 2015 | 1858 | 2006 | 1798 | |
| 1858 | 2013 | 2003 | 1779 | 1881 | 1950 | 1964 | 1842 | 1921 | 1959 | 1858 | 1858 | |
| 1874 | 2006 | 1822 | 1867 | 1967 | 2015 | 1859 | 1904 | 1819 | 1969 | 1819 | 1901 | |
| 1947 | 1874 | 2015 | 1893 | 1859 | 1990 | 1952 | 2013 | 1811 | 1847 | 1901 | 1959 | |
| EURO | MED | CEU | NEU | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PDSI | SPEI | SMI | PDSI | SPEI | SMI | PDSI | SPEI | SMI | PDSI | SPEI | SMI | |
| Magnitude | 1941–50 | 2011–18 | 1781–90 | 1941–50 | 2011–18 | 2001–10 | 1941–50 | 2011–18 | 1781–90 | 1971–80 | 1851–60 | 1771–80 |
| 1801–10 | 1861–70 | 2011–18 | 1861–70 | 2001–10 | 1991–00 | 2011–18 | 1941–50 | 2011–18 | 1851–60 | 1861–70 | 1941–50 | |
| 1891–00 | 1941–50 | 1941–50 | 1981–90 | 1861–70 | 1941–50 | 1831–40 | 2001–10 | 1861–70 | 1821–30 | 1971–80 | 1791–00 | |
| 1861–70 | 2001–10 | 2001–10 | 2011–18 | 1771–80 | 1981–80 | 1801–10 | 1861–70 | 2001–10 | 1811–20 | 1891–00 | 1851–60 | |
| 1781–90 | 1831–40 | 1861–70 | 1891–00 | 1941–50 | 2011–18 | 1791–00 | 1791–00 | 1991–00 | 1911–20 | 1811–20 | 1911–20 | |
| Area | 1941–50 | 2011–18 | 2011–18 | 1941–50 | 2011–18 | 1991–00 | 1941–50 | 2011–18 | 2011–18 | 1851–60 | 1851–60 | 1851–60 |
| 2011–18 | 2001–10 | 1941–50 | 2011–18 | 2001–10 | 2001–10 | 1831–40 | 2001–10 | 1781–90 | 1821–30 | 1891–00 | 1941–50 | |
| 1821–30 | 1991–00 | 1781–90 | 1981–90 | 1771–80 | 1941–50 | 2011–18 | 1991–00 | 1861–70 | 1971–80 | 1971–80 | 1771–80 | |
| 1861–70 | 1861–70 | 2001–10 | 1861–70 | 1981–90 | 1981–90 | 1801–10 | 1941–50 | 1951–60 | 1771–80 | 1921–30 | 1791–00 | |
| 1801–10 | 1891–00 | 1861–70 | 2001–10 | 1961–70 | 2011–18 | 1861–70 | 1861–70 | 2001–10 | 1931–40 | 1861–70 | 1971–80 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ionita, M.; Scholz, P.; Nagavciuc, V. Multi-Indicator Drought Variability in Europe (1766–2018). Forests 2025, 16, 1739. https://doi.org/10.3390/f16111739
Ionita M, Scholz P, Nagavciuc V. Multi-Indicator Drought Variability in Europe (1766–2018). Forests. 2025; 16(11):1739. https://doi.org/10.3390/f16111739
Chicago/Turabian StyleIonita, Monica, Patrick Scholz, and Viorica Nagavciuc. 2025. "Multi-Indicator Drought Variability in Europe (1766–2018)" Forests 16, no. 11: 1739. https://doi.org/10.3390/f16111739
APA StyleIonita, M., Scholz, P., & Nagavciuc, V. (2025). Multi-Indicator Drought Variability in Europe (1766–2018). Forests, 16(11), 1739. https://doi.org/10.3390/f16111739






