Structural Optimization of Windbreak and Sand-Fixing Forests: A Wind Tunnel Study
Abstract
1. Introduction
2. Materials and Methods
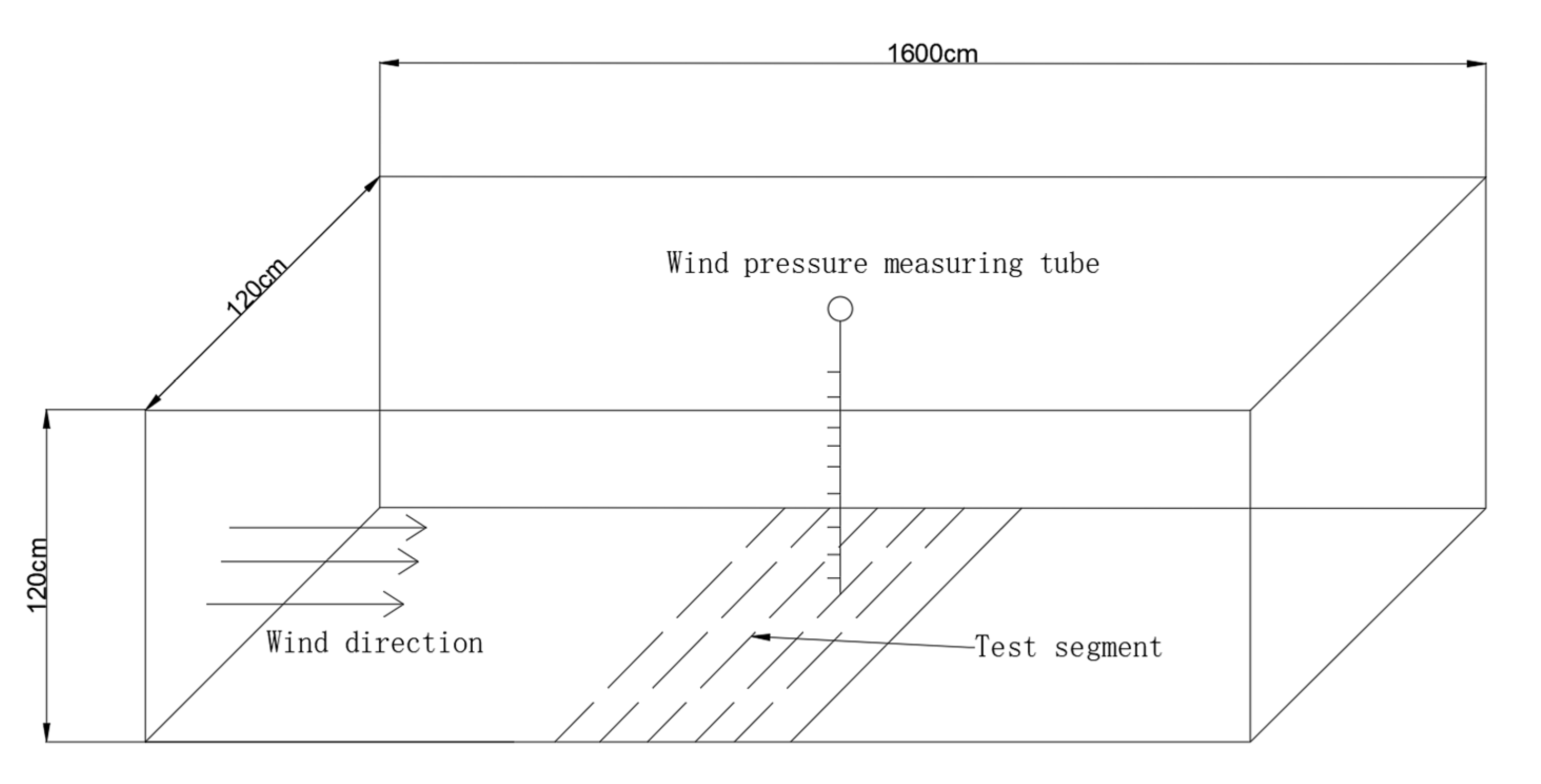
2.1. Experimental Equipment
2.2. Experimental Materials
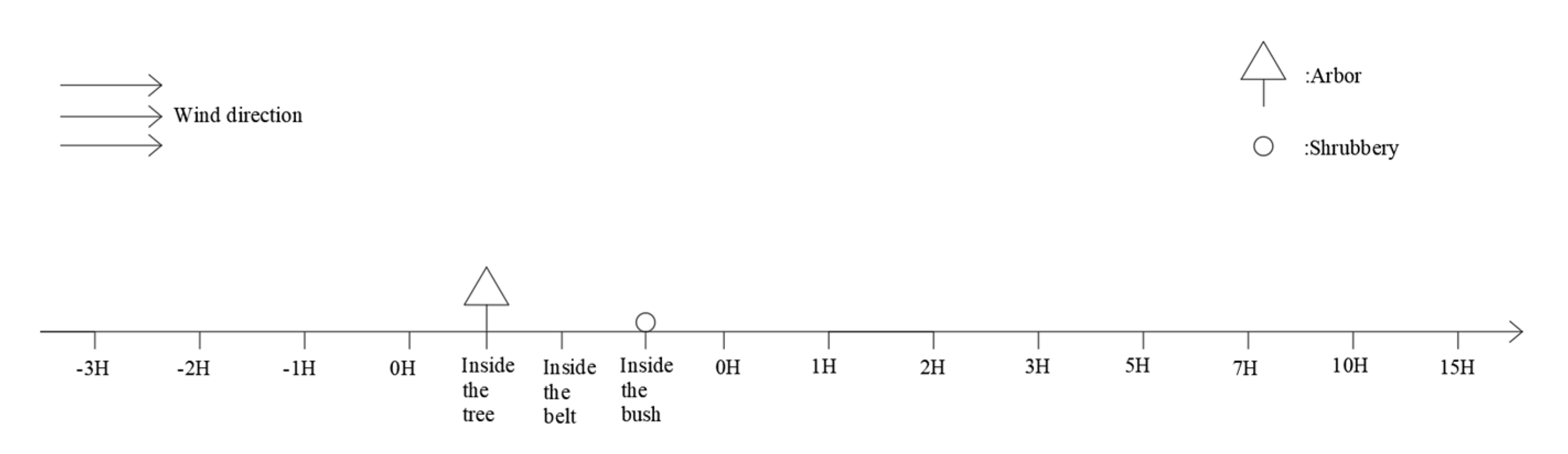
2.3. Model Design
2.4. Wind Speed Measurement
2.5. Data Processing
2.5.1. Relative Wind Speed Calculation
2.5.2. Windbreak Efficiency
- Ewind—Windbreak efficiency;
- Vopen—Average wind speed at height Z in the open area (m s−1);
- Vmeasure—Average wind speed at height Z at a distance of h from the windbreak (m s−1)
2.5.3. Data Analysis and Mapping
3. Results and Analysis
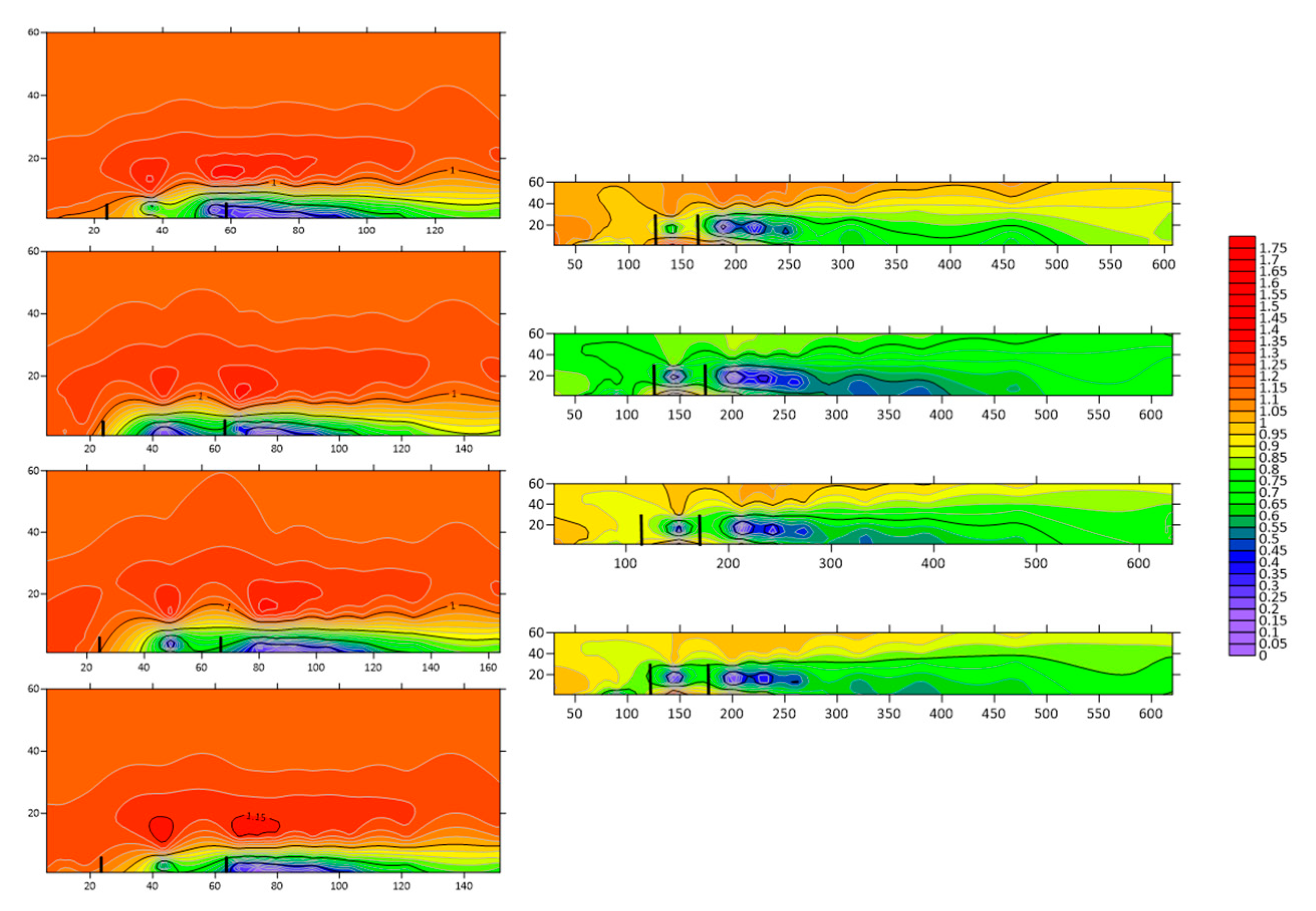
3.1. Initial Wind Field Analysis Without the Model
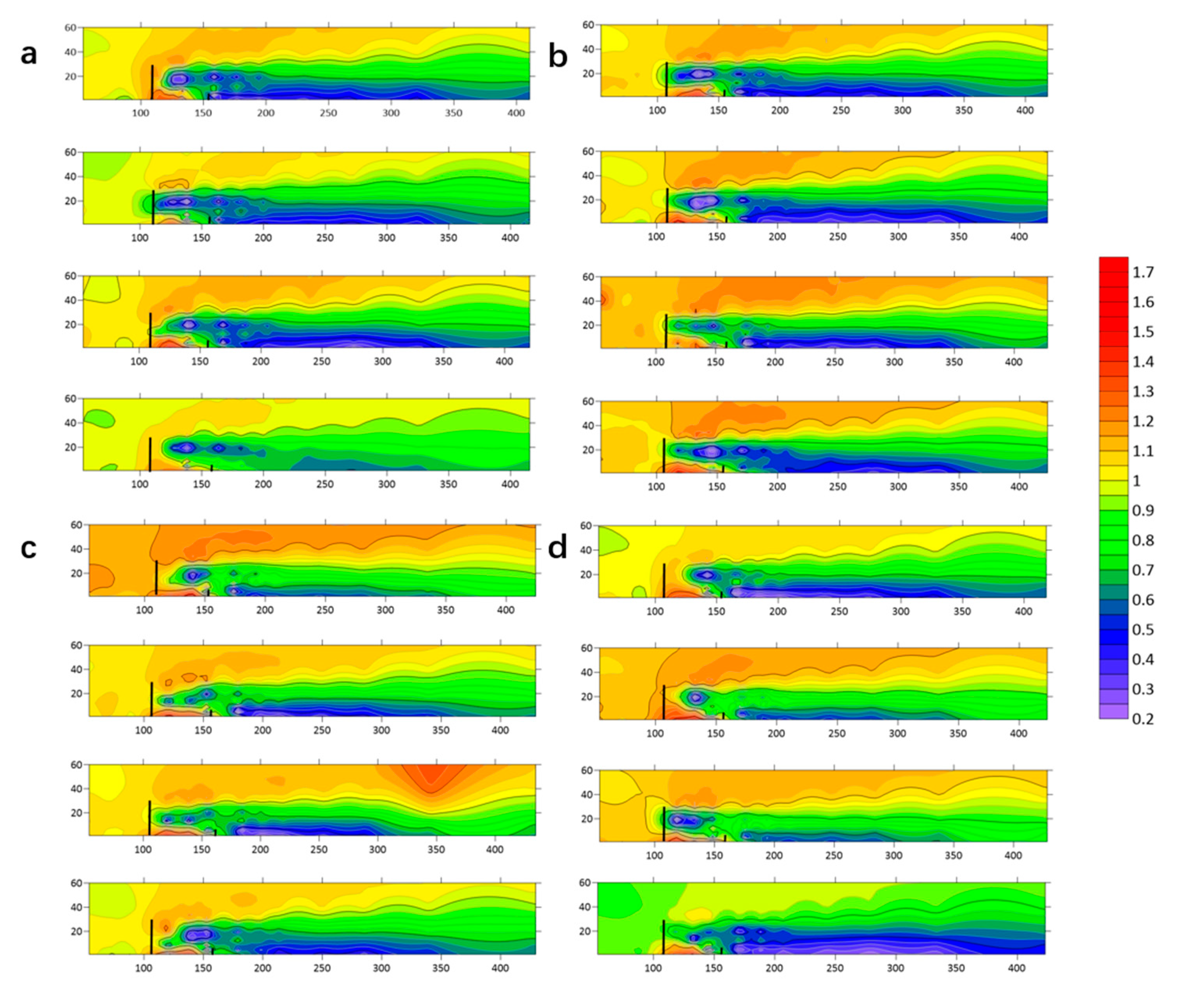
3.2. Flow Field Characteristics of Different Tree-Shrub Windbreak and Sand-Fixing Forests
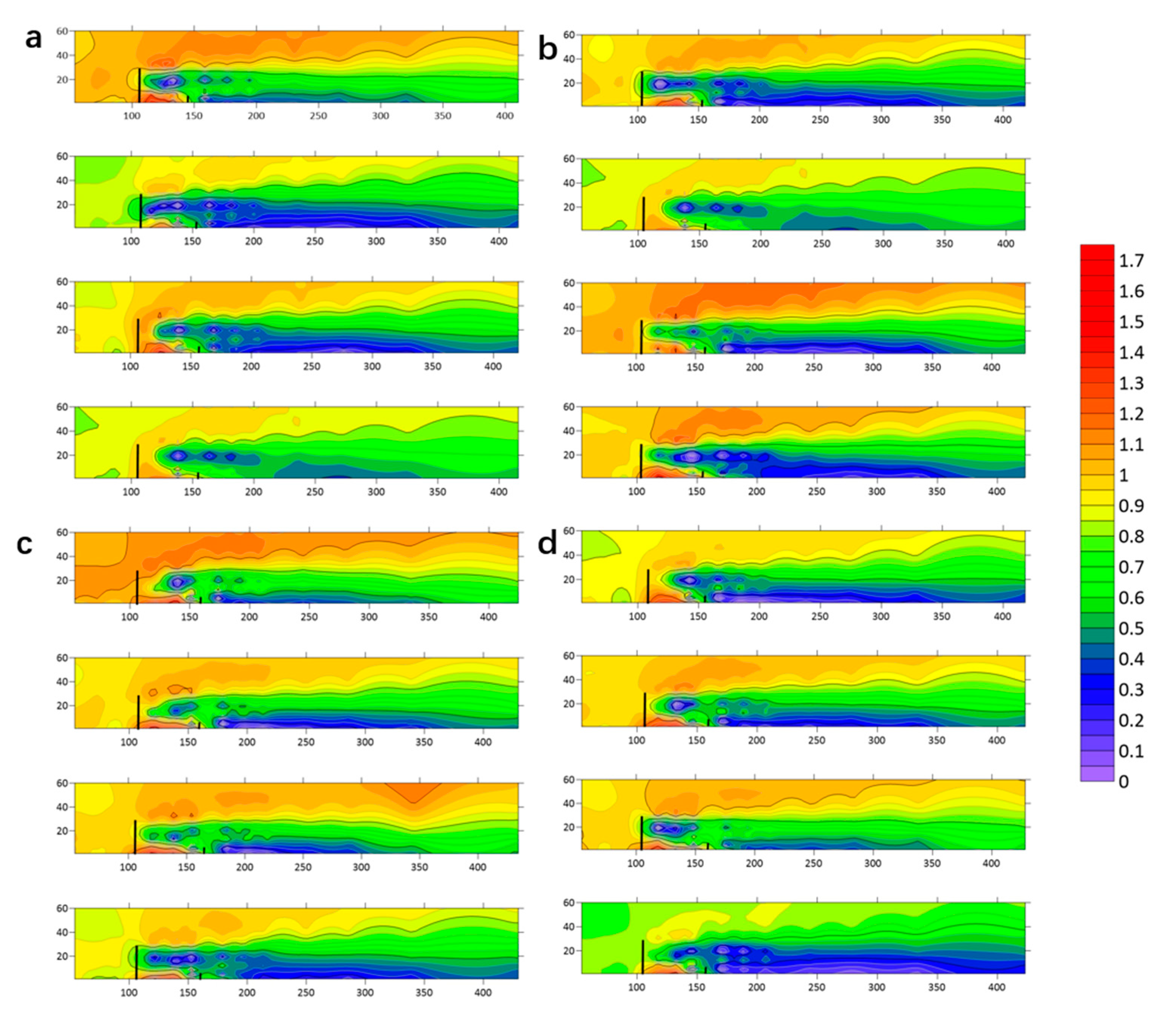
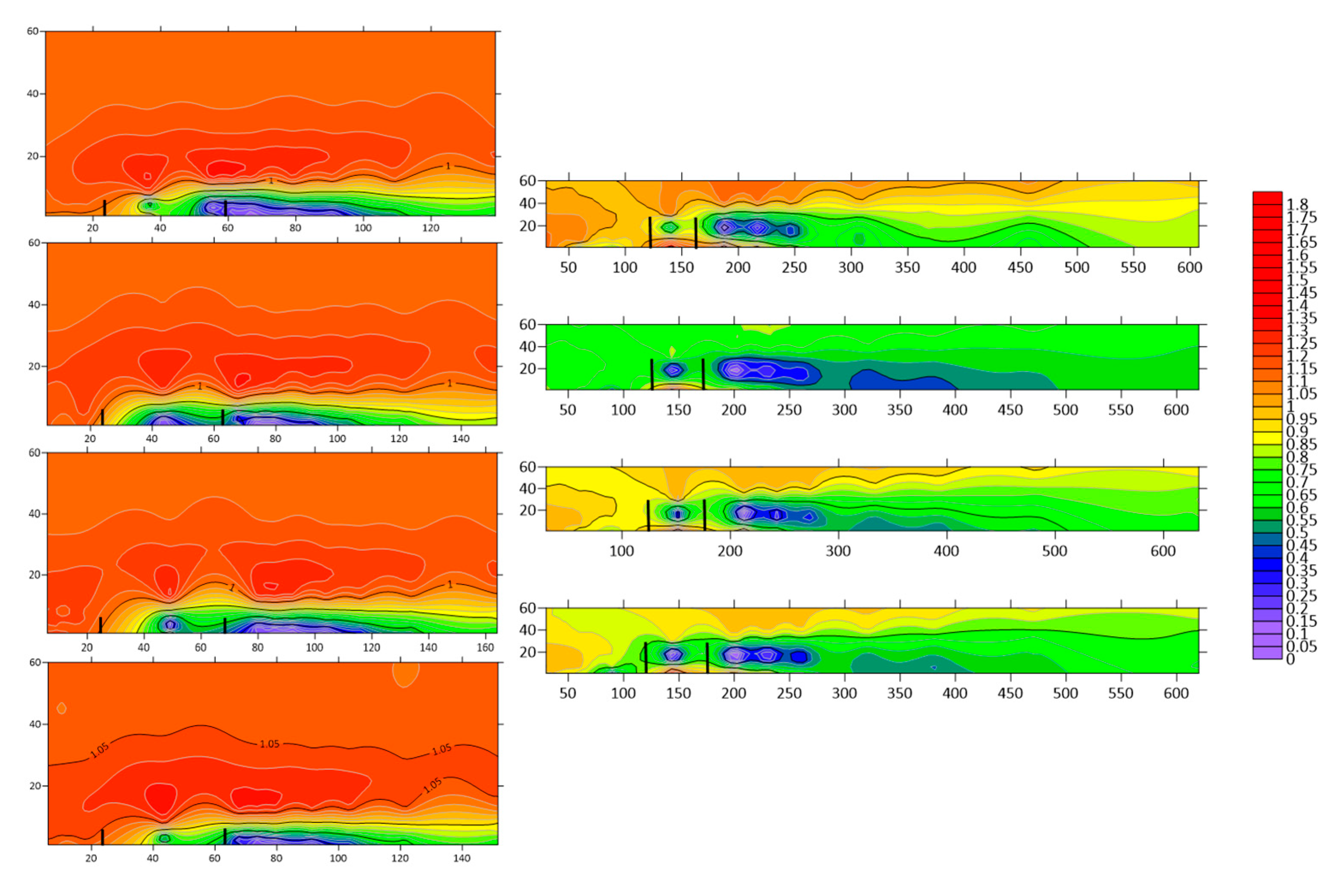
3.2.1. Flow Field Analysis of Different Tree-Shrub Windbreak and Sand-Fixing Forests at 6 m s−1
3.2.2. Flow Field Analysis of Different Tree-Shrub Windbreak and Sand-Fixing Forests at 10 m s−1
3.2.3. Flow Field Analysis of Different Tree-Shrub Windbreak and Sand-Fixing Forests at 15 m s−1
3.3. Windbreak Efficiency Analysis of Different Tree-Shrub Windbreak and Sand-Fixing Forests
3.3.1. Windbreak Efficiency Analysis at 6 m s−1
3.3.2. Windbreak Efficiency Analysis at 10 m s−1
3.3.3. Windbreak Efficiency Analysis at 15 m s−1
4. Discussion
5. Conclusions
- ①
- Proposes and validates a fan-shaped mixed forest belt design (Populus–Tamarix), whose wind tunnel test results demonstrate superior windbreak performance compared to single-species belts and traditional rectangular belts, highlighting the significant advantages of structural innovation.
- ②
- The key to its high-efficiency protection lies in the vertical complementarity of the mixed tree-shrub system: trees reduce upper-layer wind speeds and lift airflow, while shrubs effectively lower near-surface wind speeds, forming a layered protection mechanism that significantly extends the effective distance of the protective strip.
- ③
- The fan-shaped layout employs progressively widening row spacings to dissipate wind energy more gradually, avoiding the turbulence concentration commonly seen in rectangular strips. This design maintains stable protective performance even under strong winds, demonstrating superior adaptability.
- ④
- Moderately dense mixed tree–shrub (P e spaced at 7.5 cm × 10 cm and T c at 5 cm × 10 cm) belts balance protective efficiency with reduced planting density, lowering resource investment costs. This design offers a practical model for shelterbelt construction and ecological restoration in arid regions, possessing significant application value.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol/Abbreviation | Meaning | Unit |
| E | Windbreak efficiency | % |
| H | trees height | m |
| U | Wind speed | m s−1 |
| U0 | Reference (incoming) wind speed | m s−1 |
| U/U0 | Relative wind speed | – |
| P e | Populus euphratica Oliv. | – |
| T c | Tamarix chinensis Lour. | – |
Appendix A. Windbreak Efficiency Across Configurations (6–15 m s−1)
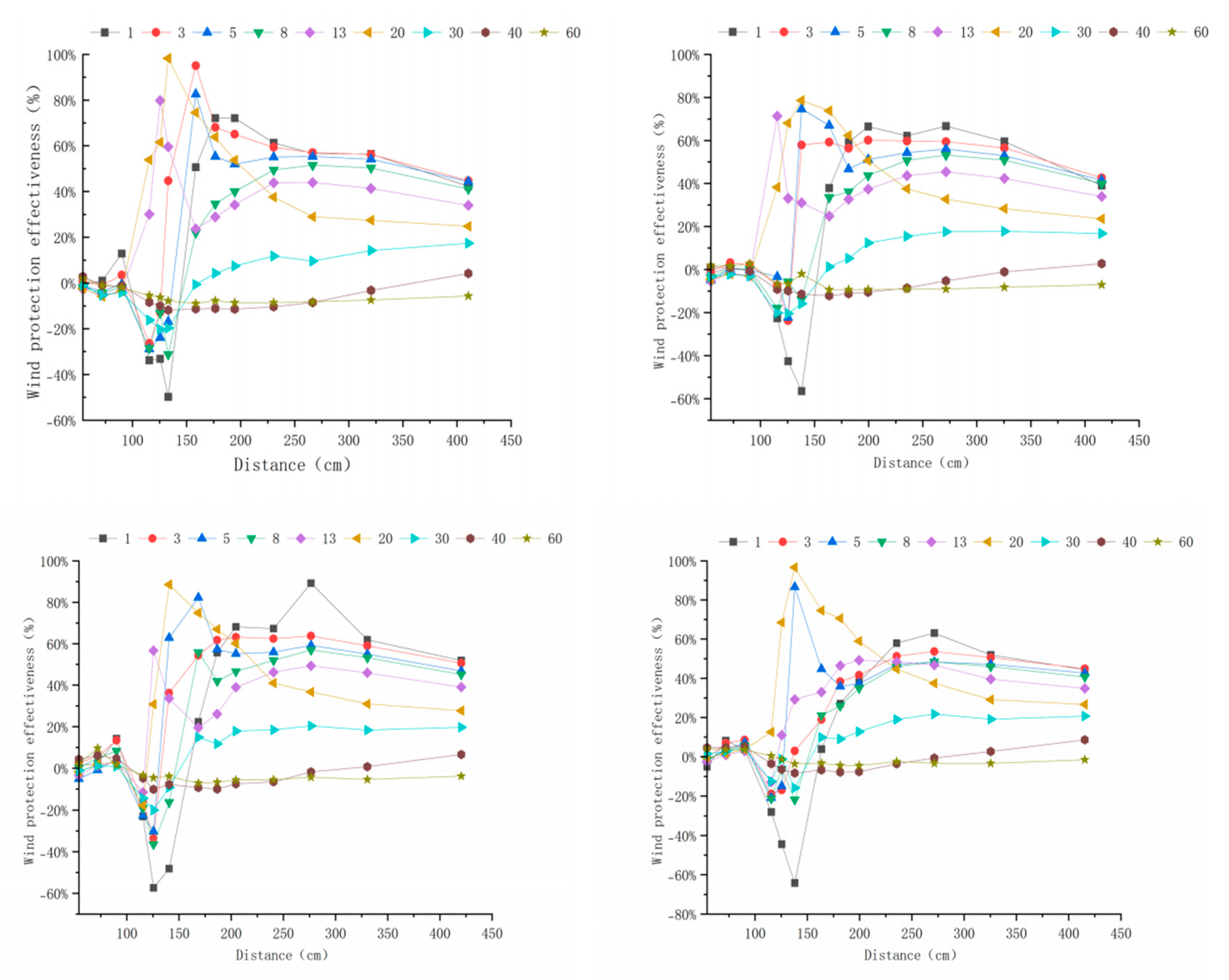
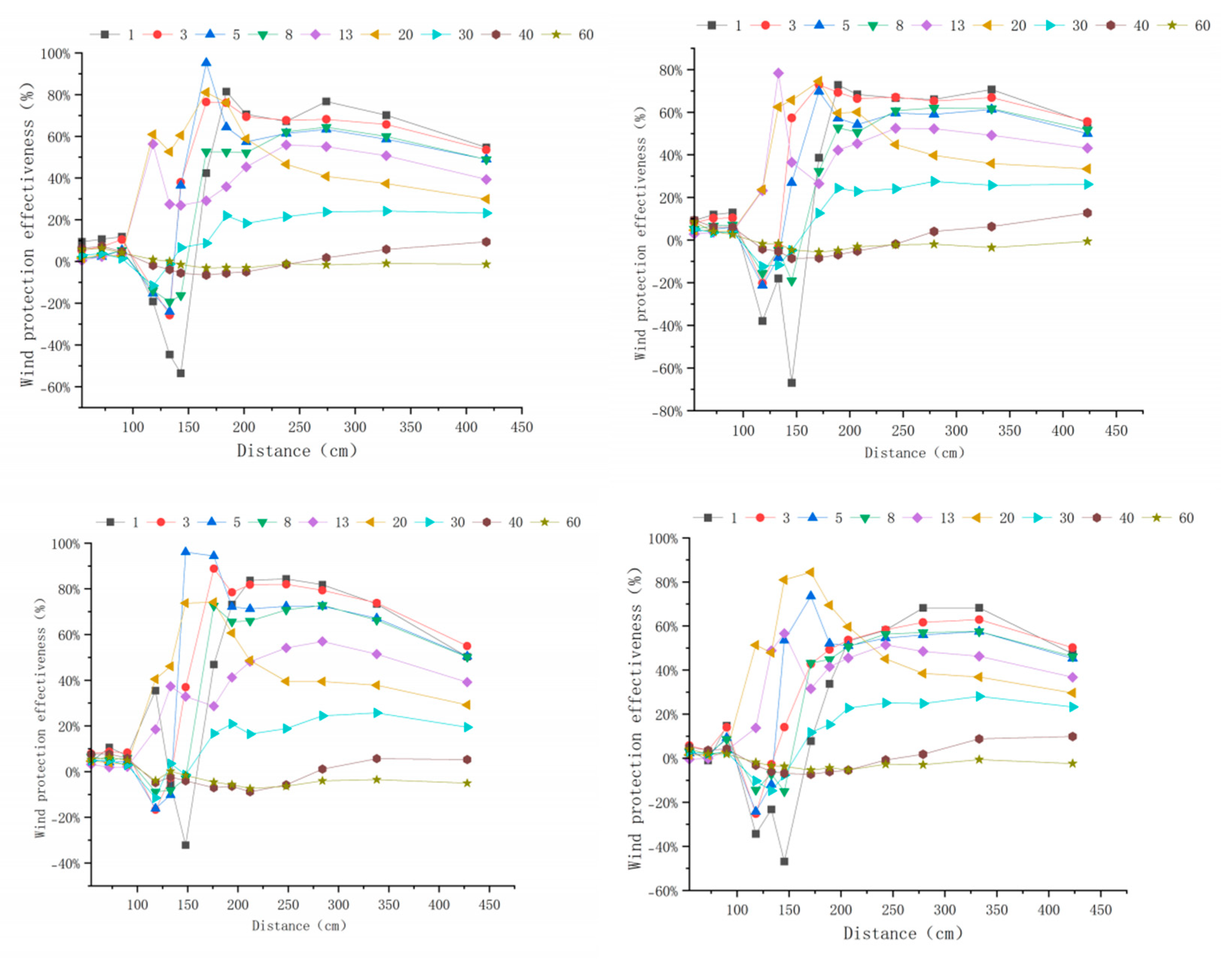
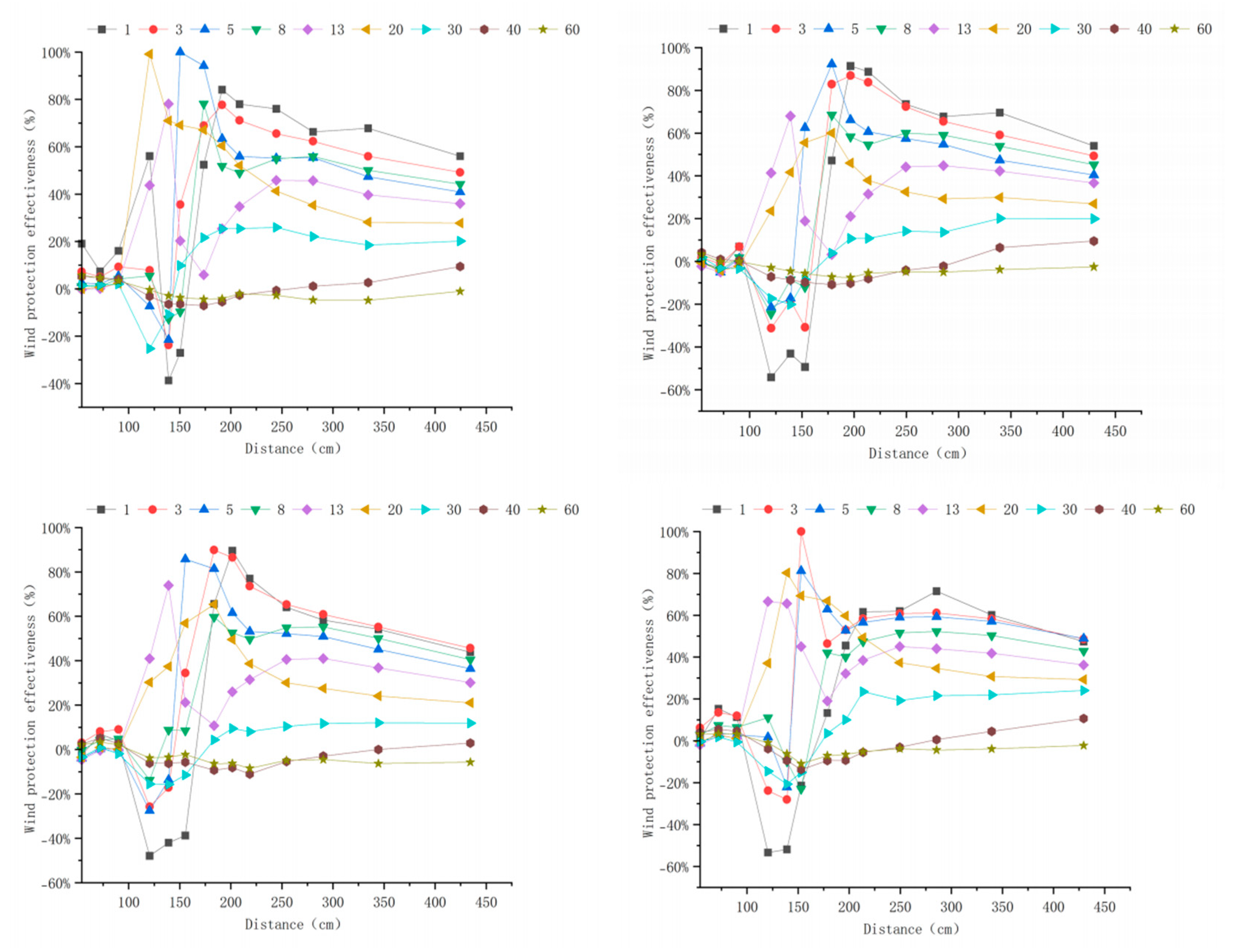
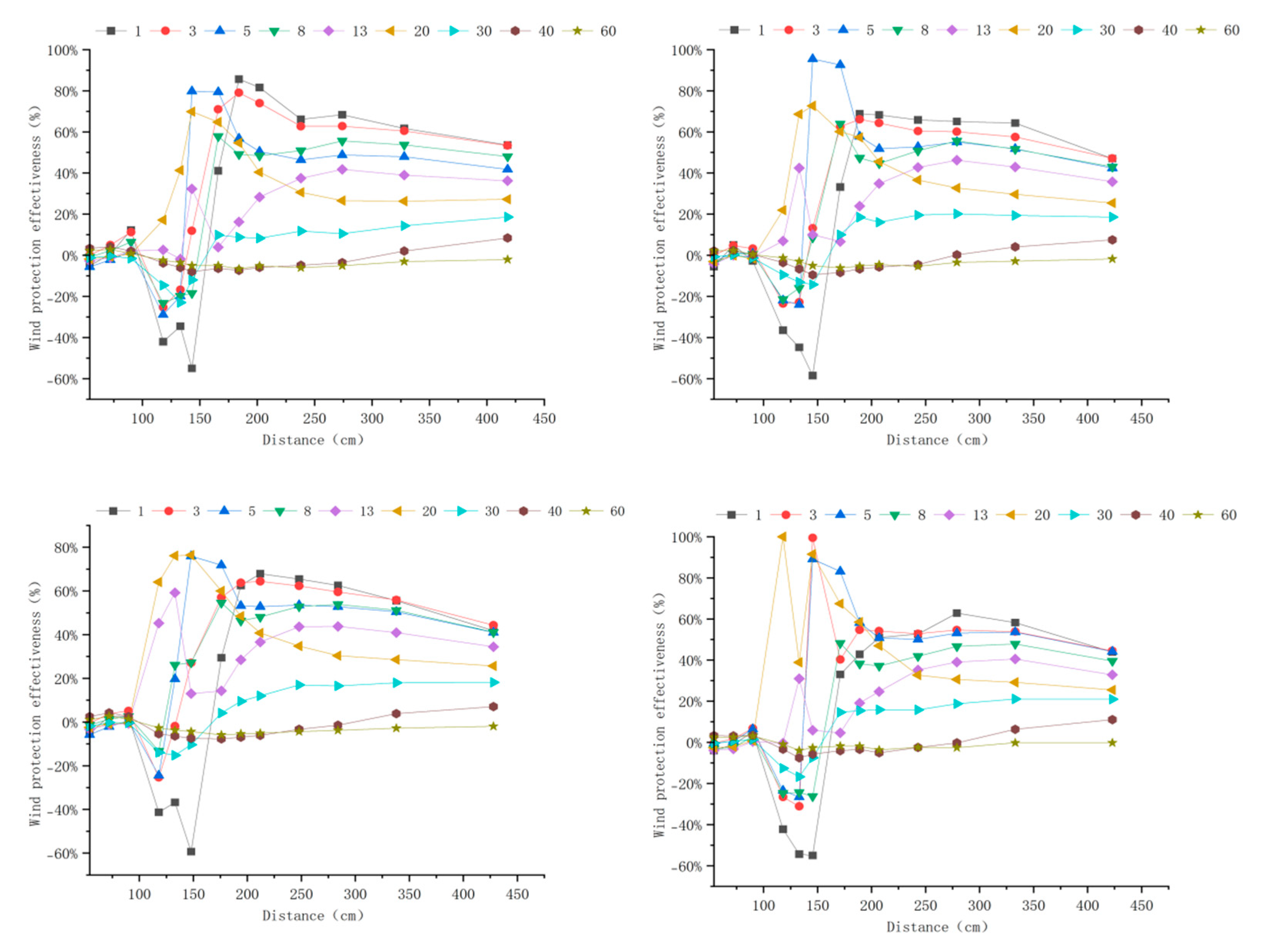
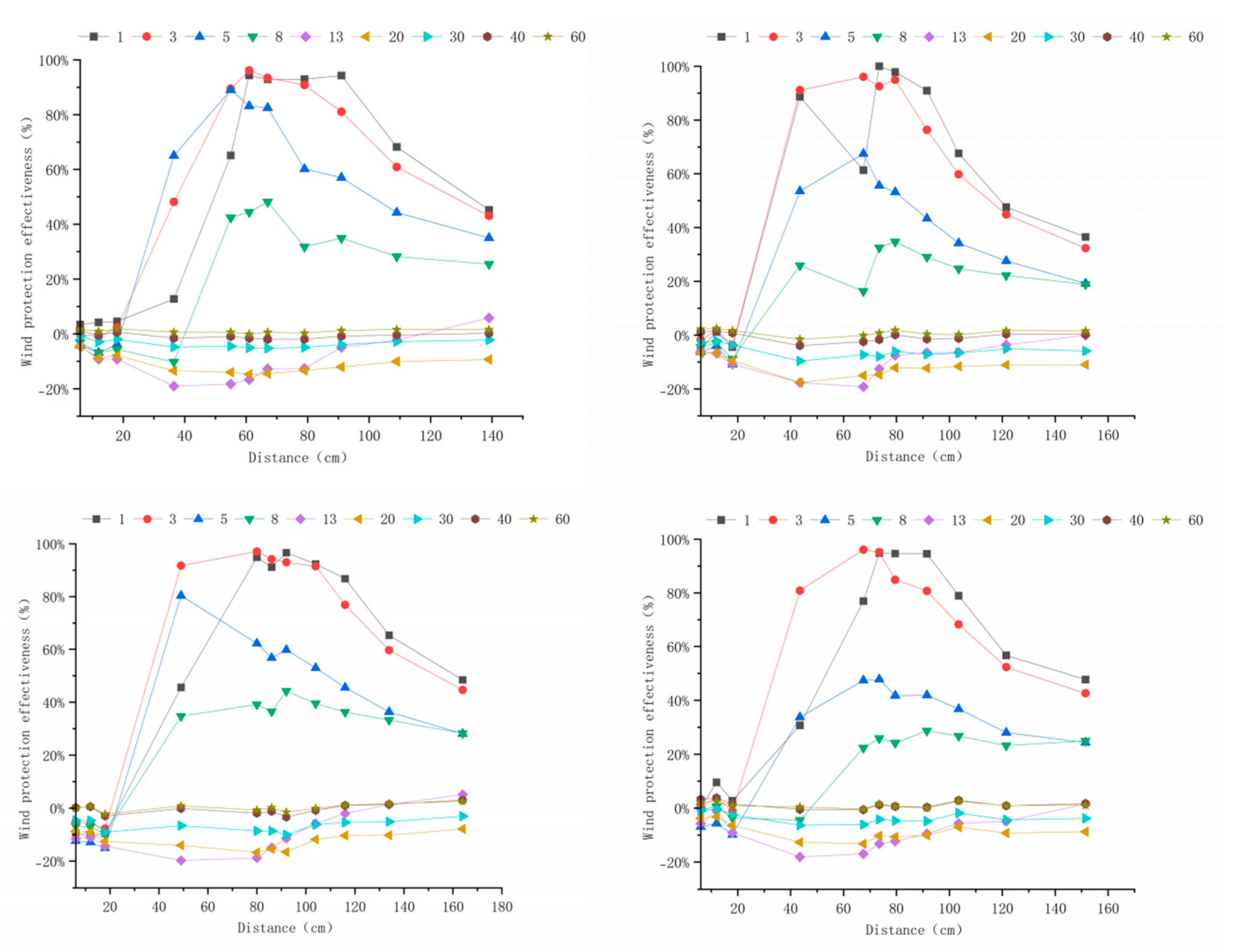
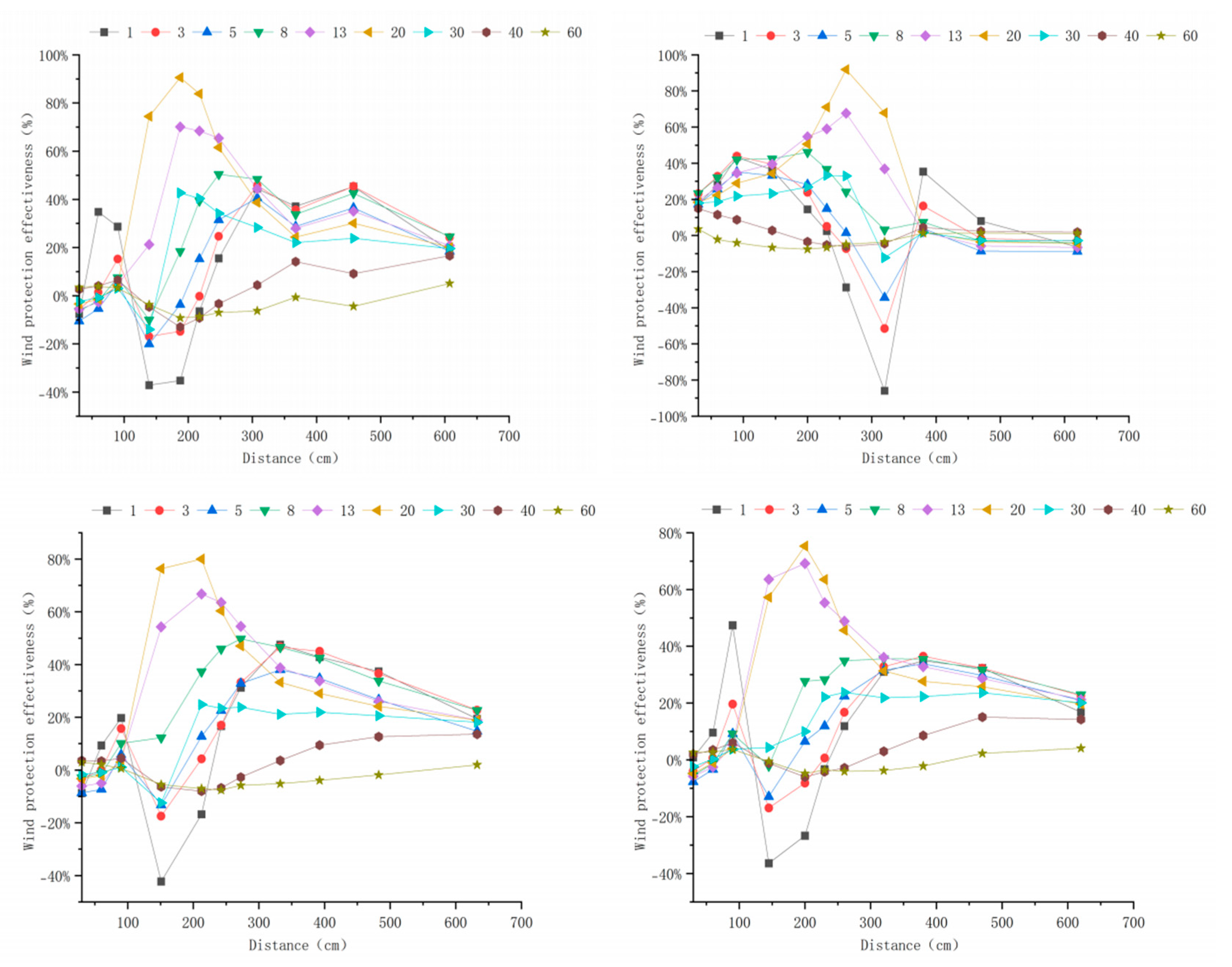
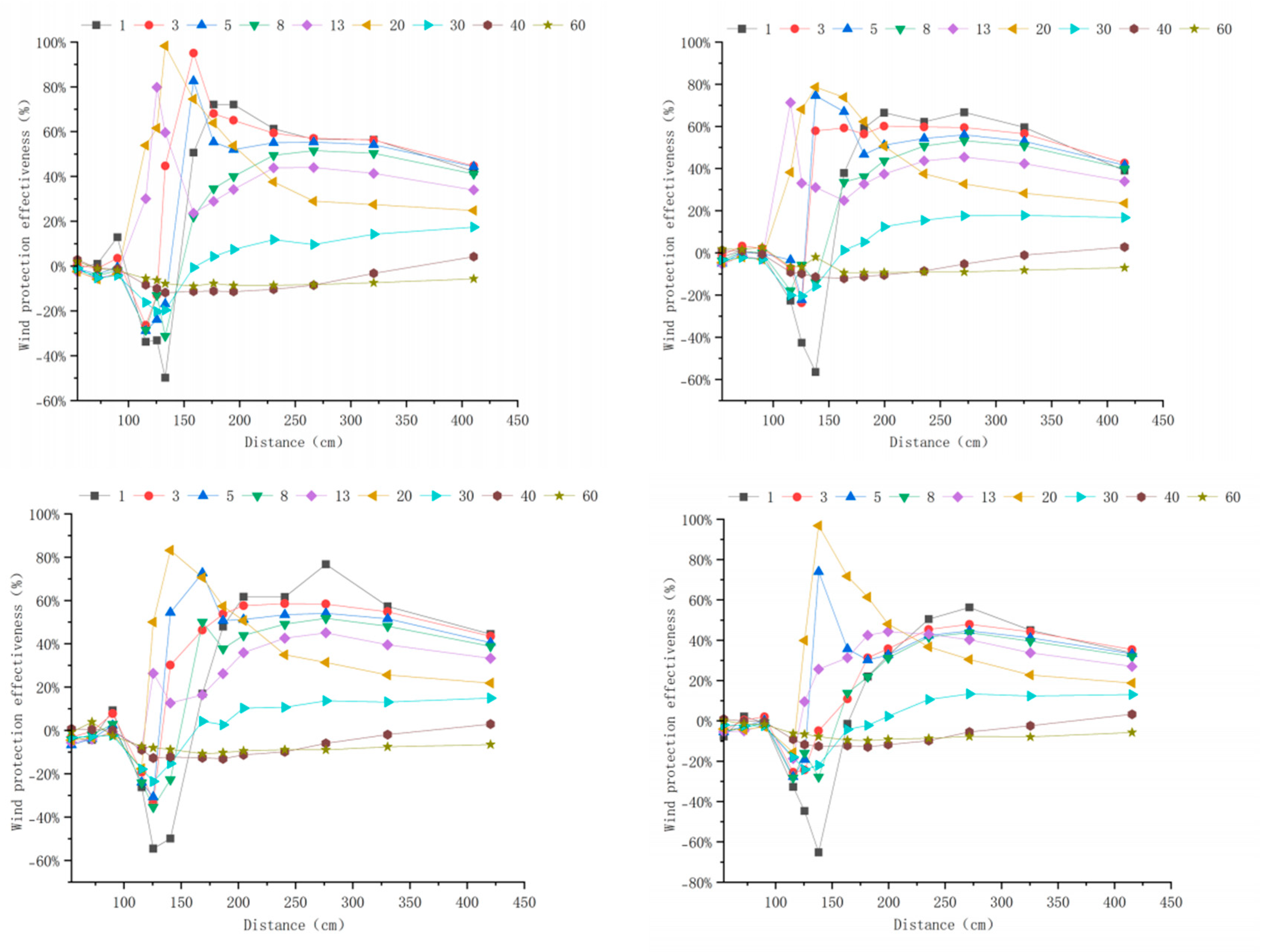
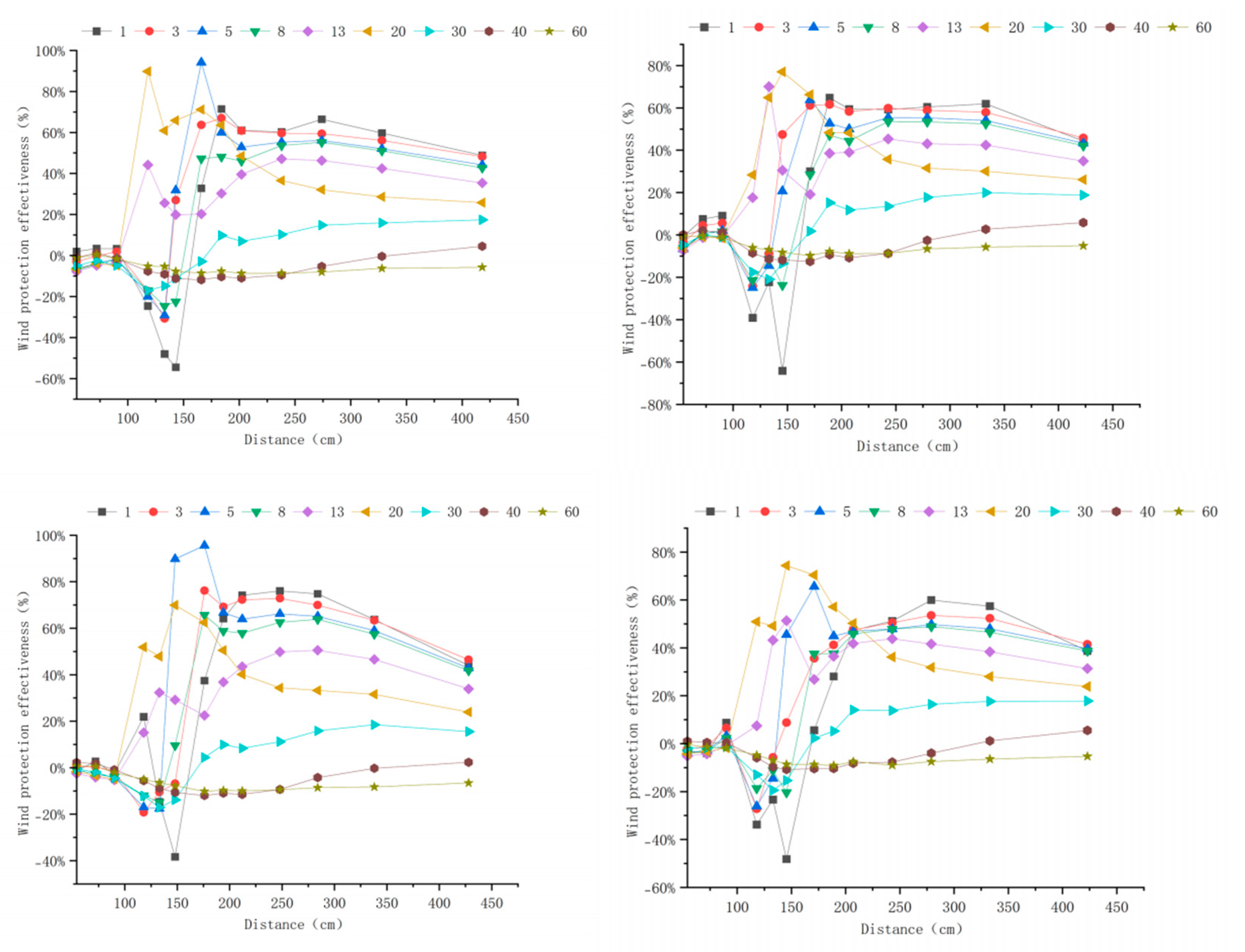
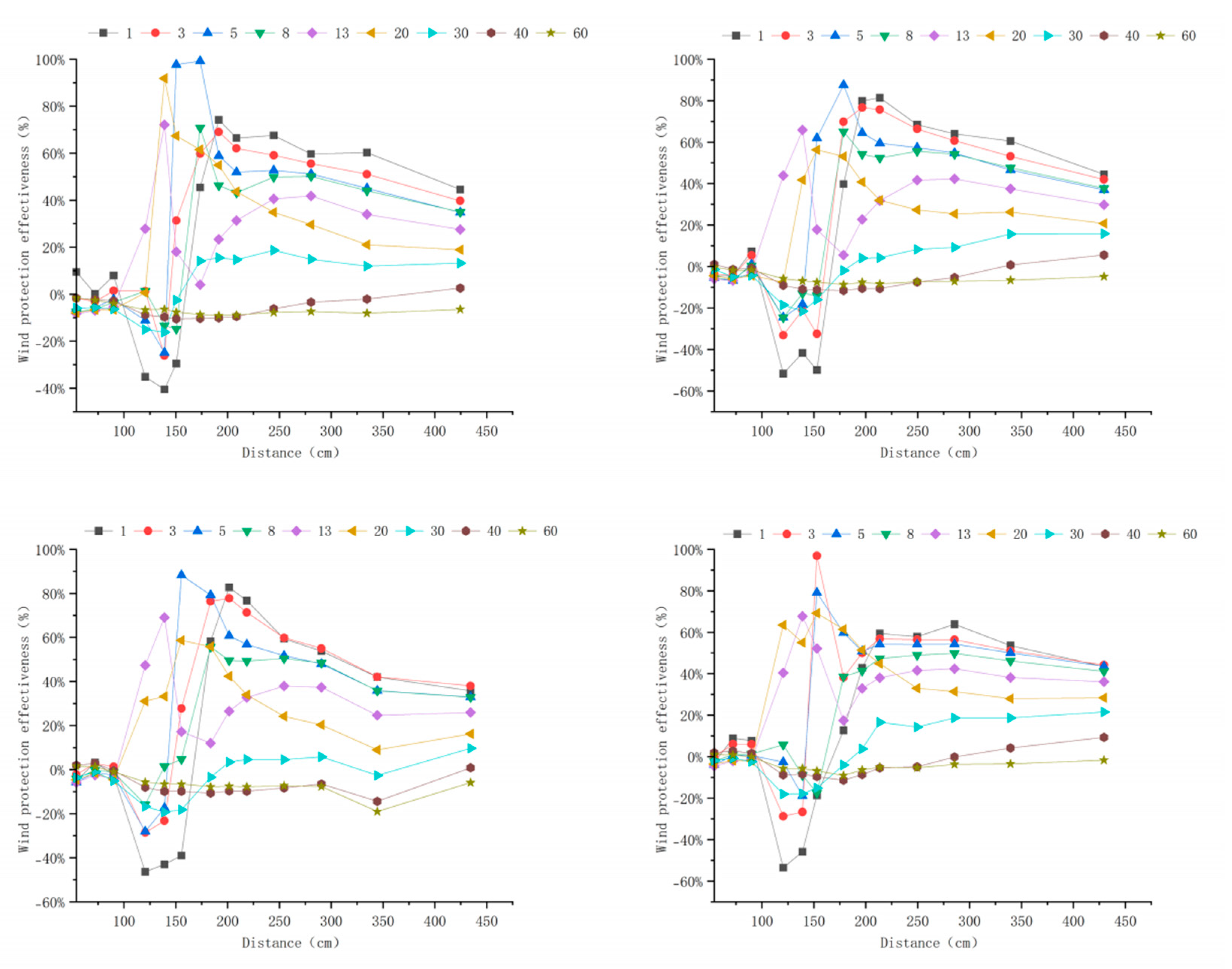
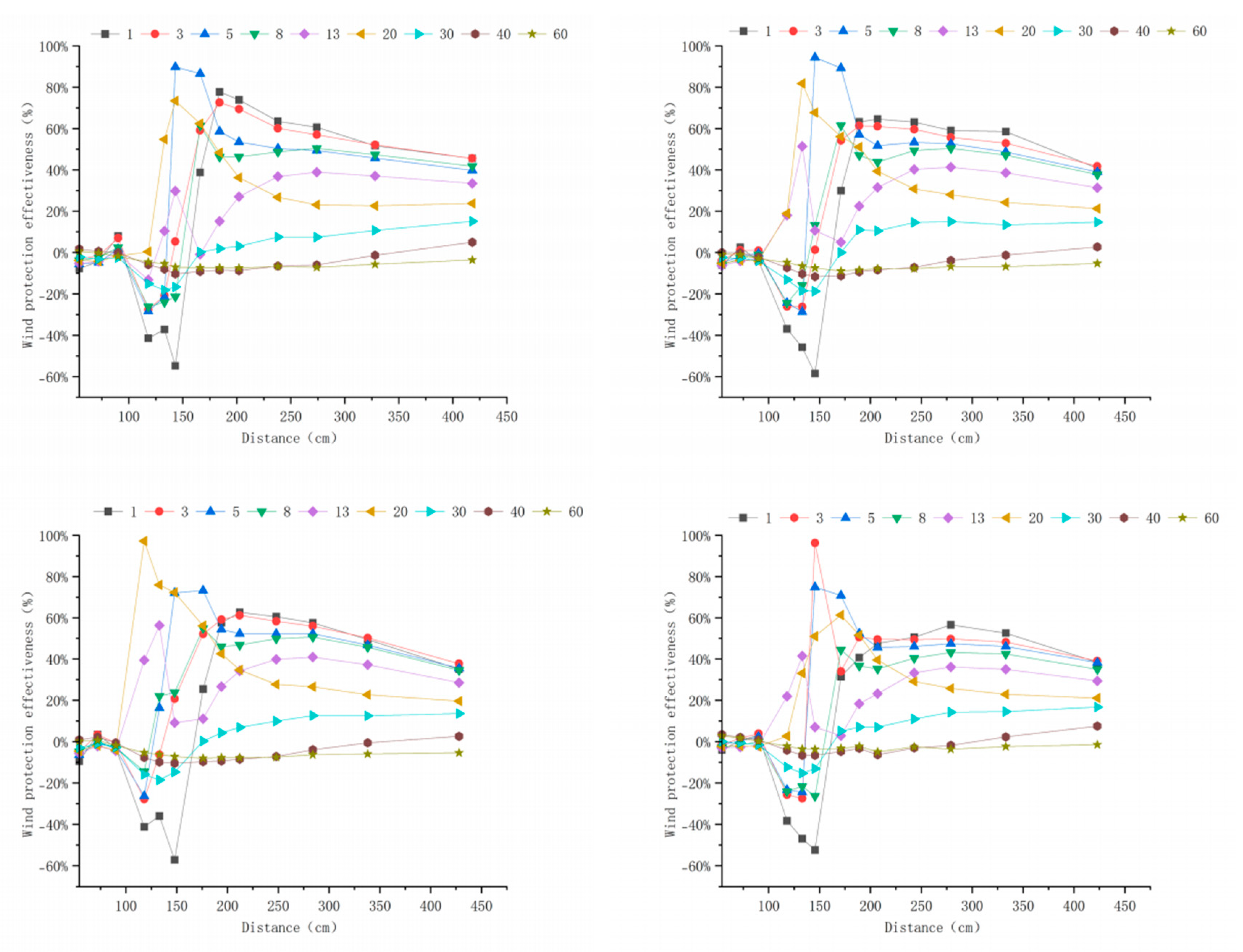
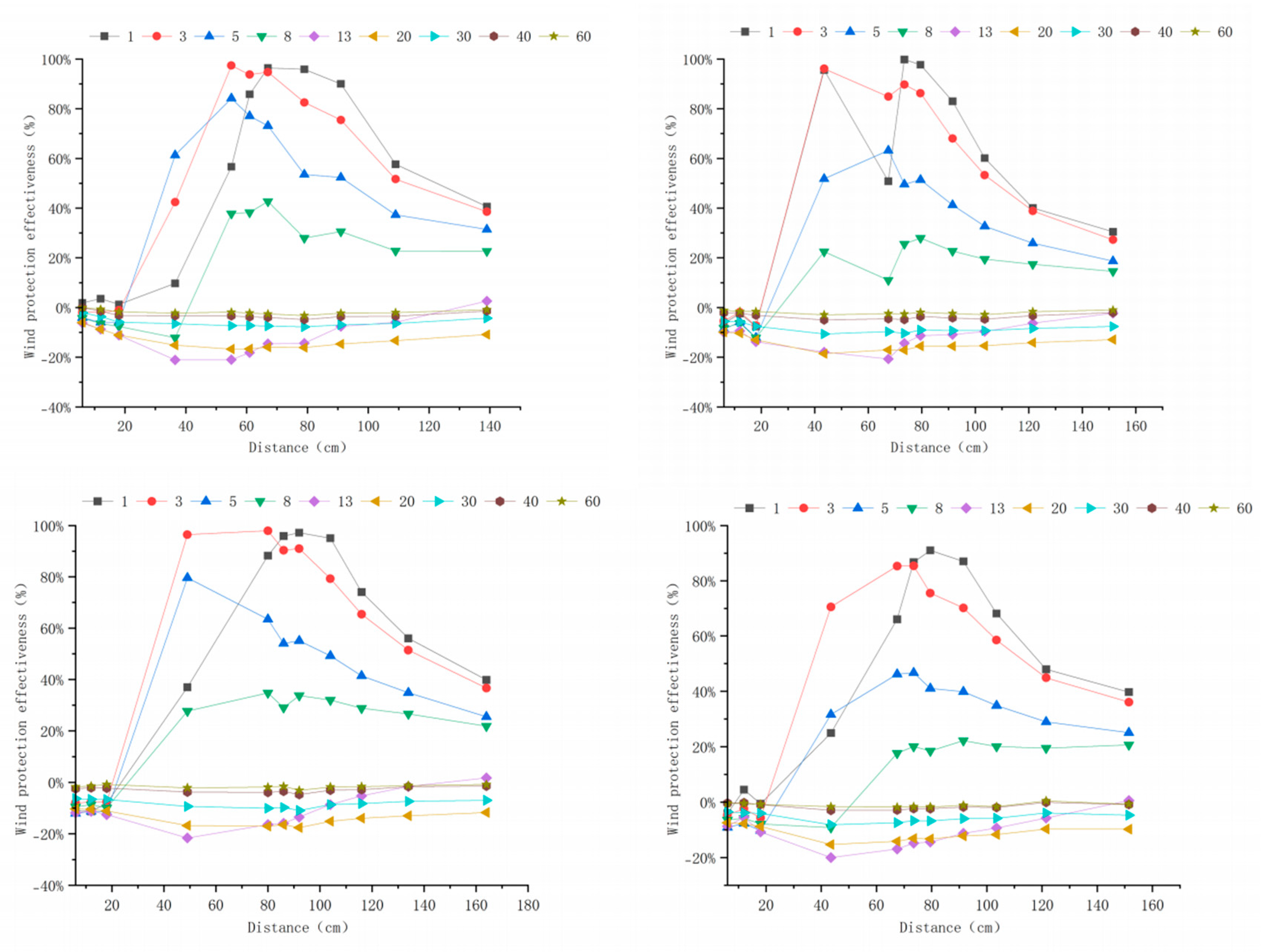
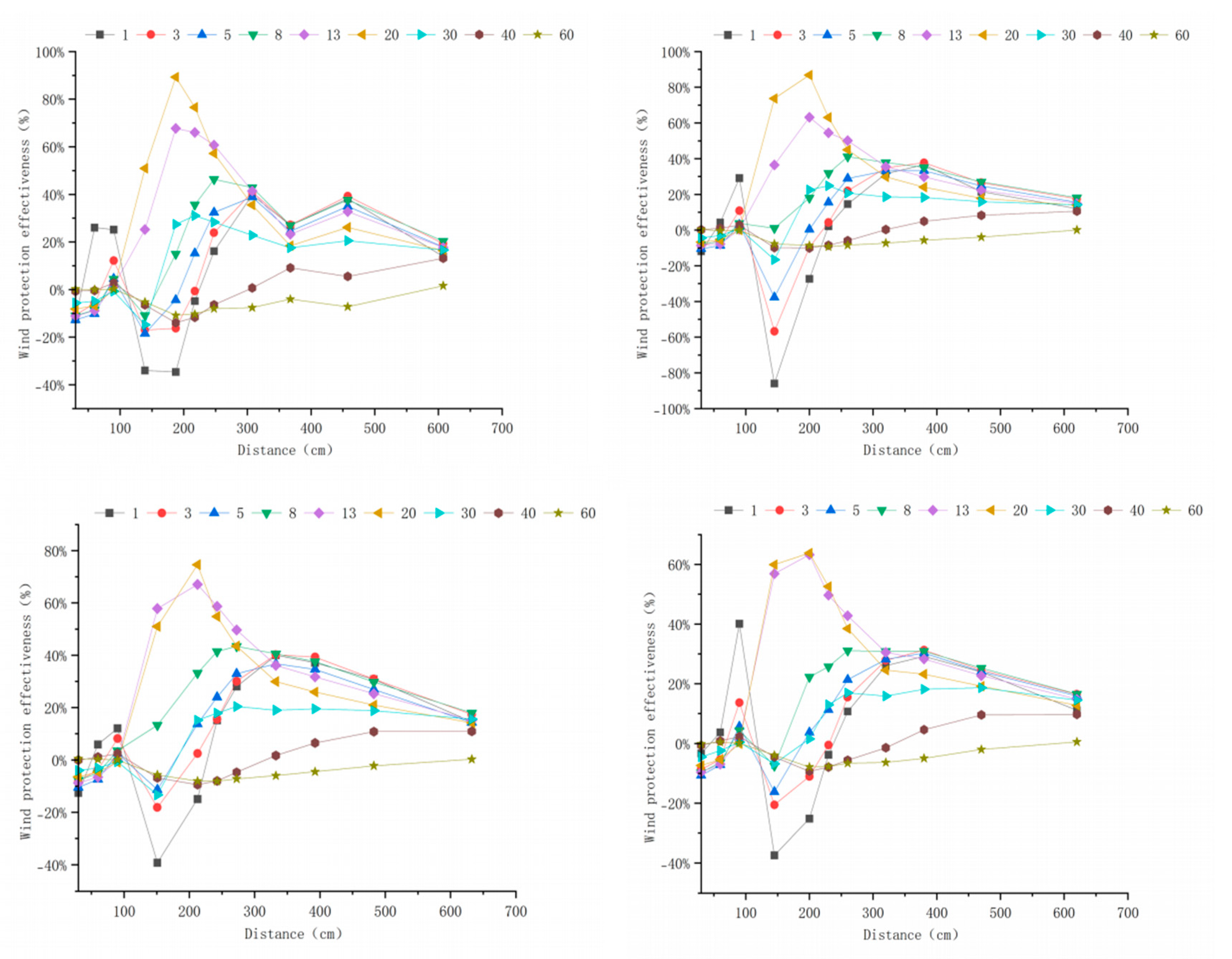
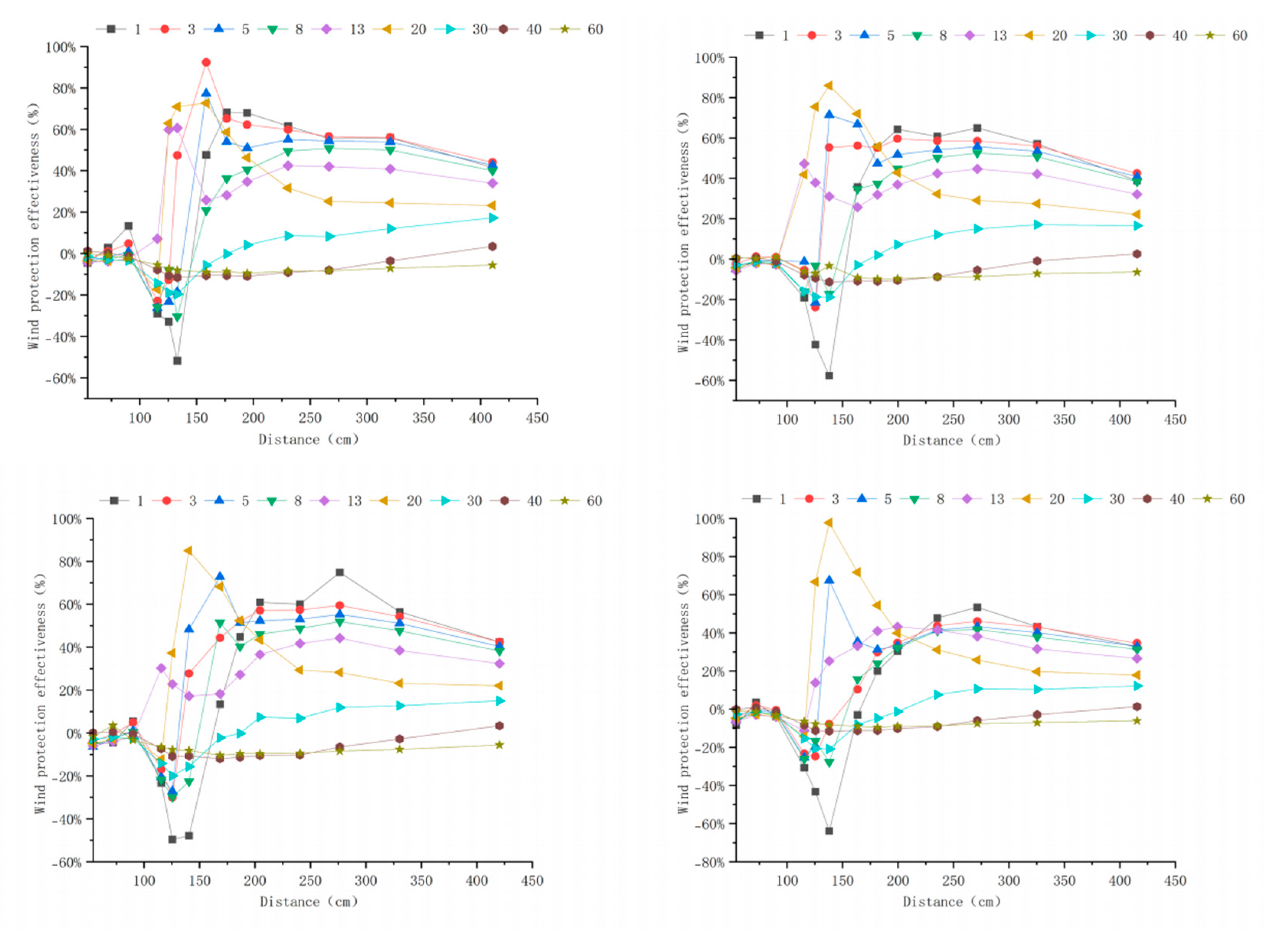
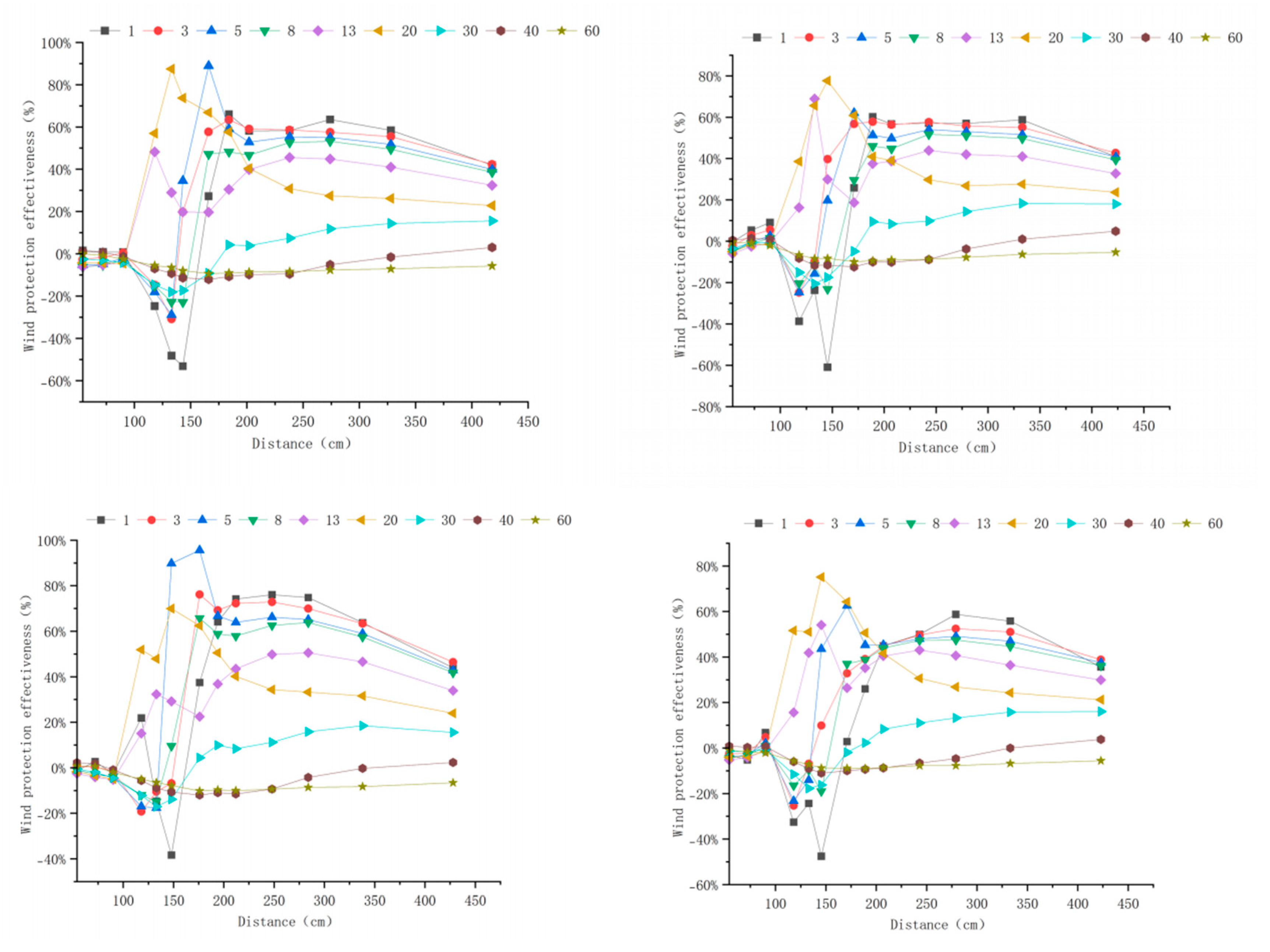
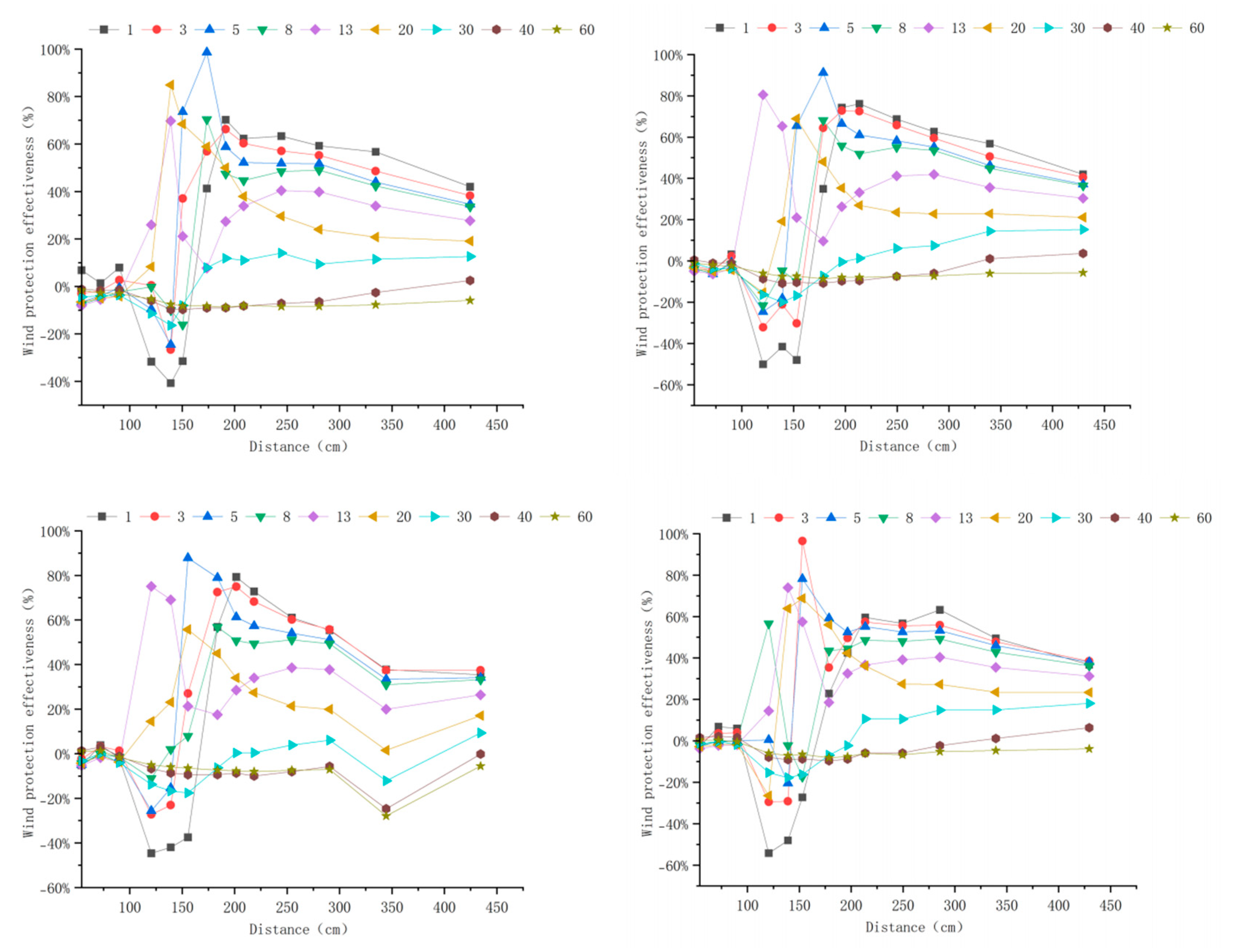


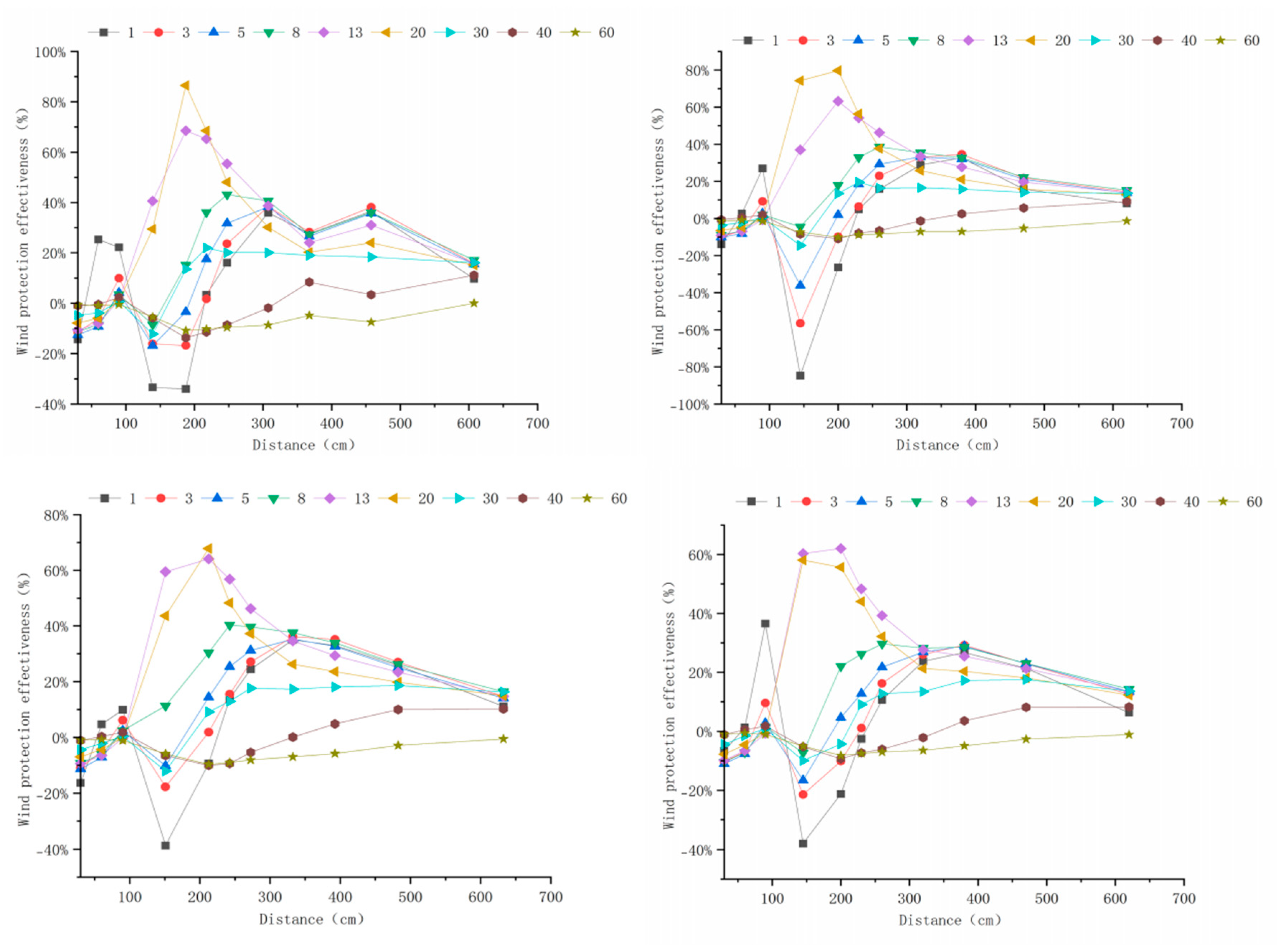
Appendix B. Technical Details
Appendix B.1. Terminology Definition
Appendix B.2. Area Distribution Chart for Relative Wind Speed
| Model | U/U0 | Proportion (%) | Model | U/U0 | Proportion (%) |
|---|---|---|---|---|---|
| T c 5 cm × 5 cm | 0–0.6 | 3.45 | T c 5 cm × 7.5 cm | 0–0.6 | 5.06 |
| 0.6–1 | 31.68 | 0.6–1 | 31.13 | ||
| >1 | 61.78 | >1 | 63.81 | ||
| T c 5 cm × 10 cm | 0–0.6 | 7.07 | T c 7.5 cm × 7.5 cm | 0–0.6 | 4.54 |
| 0.6–1 | 27.5 | 0.6–1 | 41.08 | ||
| >1 | 63.81 | >1 | 54.38 | ||
| P e 7.5 cm × 7.5 cm | 0–0.6 | 7.04 | P e 7.5 cm × 10 cm | 0–0.6 | 4.35 |
| 0.6–1 | 79.05 | 0.6–1 | 79.37 | ||
| >1 | 13.91 | >1 | 16.26 | ||
| P e 7.5 cm × 12.5 cm | 0–0.6 | 5.83 | P e 10 cm × 10 cm | 0–0.6 | 2.97 |
| 0.6–1 | 79.54 | 0.6–1 | 85.94 | ||
| >1 | 14.63 | >1 | 11.09 | ||
| P e 7.5 cm × 7.5 cm, T c 5 cm × 5 cm | 0–0.6 | 21.45 | P e 7.5 cm × 7.5 cm, T c 5 cm × 7.5 cm | 0–0.6 | 23.58 |
| 0.6–1 | 38.98 | 0.6–1 | 55.07 | ||
| >1 | 39.57 | >1 | 21.35 | ||
| P e 7.5 cm × 7.5 cm, T c 5 cm × 10 cm | 0–0.6 | 11.66 | P e 7.5 cm × 7.5 cm, T c 7.5 cm × 7.5 cm | 0–0.6 | 15.62 |
| 0.6–1 | 54.36 | 0.6–1 | 59.35 | ||
| >1 | 33.9 | >1 | 25.03 | ||
| P e 7.5 cm × 10 cm, T c 5 cm × 5 cm | 0–0.6 | 24.56 | P e 7.5 cm × 10 cm, T c 5 cm × 7.5 cm | 0–0.6 | 23.69 |
| 0.6–1 | 57.66 | 0.6–1 | 55.78 | ||
| >1 | 17.78 | >1 | 20.53 | ||
| P e 7.5 cm × 10 cm, T c 5 cm × 10 cm | 0–0.6 | 23.93 | P e 7.5 cm × 10 cm, T c 7.5 cm × 7.5 cm | 0–0.6 | 22.92 |
| 0.6–1 | 53.50 | 0.6–1 | 57.51 | ||
| >1 | 22.57 | >1 | 19.57 | ||
| P e 7.5 cm × 12.5 cm, T c 5 cm × 5 cm | 0–0.6 | 21.25 | P e 7.5 cm × 12.5 cm, T c 5 cm × 7.5 cm | 0–0.6 | 15.81 |
| 0.6–1 | 57.50 | 0.6–1 | 49.41 | ||
| >1 | 21.25 | >1 | 34.78 | ||
| P e 7.5 cm × 12.5 cm, T c 5 cm × 10 cm | 0–0.6 | 11.67 | P e 7.5 cm × 12.5 cm, T c 7.5 cm × 7.5 cm | 0–0.6 | 18.6 |
| 0.6–1 | 54.36 | 0.6–1 | 58.2 | ||
| >1 | 33.97 | >1 | 23.2 | ||
| P e 10 cm × 10 cm, T c 5 cm × 5 cm | 0–0.6 | 14.56 | P e 10 cm × 10 cm, T c 5 cm × 7.5 cm | 0–0.6 | 16.71 |
| 0.6–1 | 54.36 | 0.6–1 | 53.10 | ||
| >1 | 31.82 | >1 | 30.19 | ||
| P e 10 cm × 10 cm, T c 5 cm × 10 cm | 0–0.6 | 14.62 | P e 10 cm × 10 cm, T c 7.5 cm × 7.5 cm | 0–0.6 | 13.23 |
| 0.6–1 | 57.29 | 0.6–1 | 63.25 | ||
| >1 | 28.08 | >1 | 23.52 |
| Model | U/U0 | Proportion (%) | Model | U/U0 | Proportion (%) |
|---|---|---|---|---|---|
| T c 5 cm × 5 cm | 0–0.6 | 5.20 | T c 5 cm × 7.5 cm | 0–0.6 | 4.35 |
| 0.6–1 | 11.73 | 0.6–1 | 12.22 | ||
| >1 | 83.07 | >1 | 83.43 | ||
| T c 5 cm × 10 cm | 0–0.6 | 5.67 | T c 7.5 cm × 7.5 cm | 0–0.6 | 3.27 |
| 0.6–1 | 12.79 | 0.6–1 | 13.41 | ||
| >1 | 81.54 | >1 | 83.32 | ||
| P e 7.5 cm × 7.5 cm | 0–0.6 | 4.55 | P e 7.5 cm × 10 cm | 0–0.6 | 3.14 |
| 0.6–1 | 72.66 | 0.6–1 | 74.61 | ||
| >1 | 22.79 | >1 | 22.25 | ||
| P e 7.5 cm × 12.5 cm | 0–0.6 | 3.12 | P e 10 cm × 10 cm | 0–0.6 | 1.26 |
| 0.6–1 | 76.81 | 0.6–1 | 78.14 | ||
| >1 | 20.07 | >1 | 20.6 | ||
| P e 7.5 cm × 7.5 cm, T c 5 cm × 5 cm | 0–0.6 | 21.45 | P e 7.5 cm × 7.5 cm, T c 5 cm × 7.5 cm | 0–0.6 | 16.56 |
| 0.6–1 | 38.98 | 0.6–1 | 45.72 | ||
| >1 | 39.57 | >1 | 37.72 | ||
| P e 7.5 cm × 7.5 cm, T c 5 cm × 10 cm | 0–0.6 | 14.27 | P e 7.5 cm × 7.5 cm, T c 7.5 cm × 7.5 cm | 0–0.6 | 8.17 |
| 0.6–1 | 43.60 | 0.6–1 | 46.46 | ||
| >1 | 42.13 | >1 | 45.37 | ||
| P e 7.5 cm × 10 cm, T c 5 cm × 5 cm | 0–0.6 | 24.56 | P e 7.5 cm × 10 cm, T c 5 cm × 7.5 cm | 0–0.6 | 16.5 |
| 0.6–1 | 57.66 | 0.6–1 | 47.42 | ||
| >1 | 17.78 | >1 | 36.08 | ||
| P e 7.5 cm × 10 cm, T c 5 cm × 10 cm | 0–0.6 | 17.96 | P e 7.5 cm × 10 cm, T c 7.5 cm × 7.5 cm | 0–0.6 | 13.55 |
| 0.6–1 | 42.58 | 0.6–1 | 48.35 | ||
| >1 | 39.46 | >1 | 38.1 | ||
| P e 7.5 cm × 12.5 cm, T c 5 cm × 5 cm | 0–0.6 | 22.93 | P e 7.5 cm × 12.5 cm, T c 5 cm × 7.5 cm | 0–0.6 | 11.59 |
| 0.6–1 | 57.51 | 0.6–1 | 43.30 | ||
| >1 | 19.56 | >1 | 45.11 | ||
| P e 7.5 cm × 12.5 cm, T c 5 cm × 10 cm | 0–0.6 | 7.09 | P e 7.5 cm × 12.5 cm, T c 7.5 cm × 7.5 cm | 0–0.6 | 14.09 |
| 0.6–1 | 43.84 | 0.6–1 | 55.48 | ||
| >1 | 49.07 | >1 | 30.43 | ||
| P e 10 cm × 10 cm, T c 5 cm × 5 cm | 0–0.6 | 14.56 | P e 10 cm × 10 cm, T c 5 cm × 7.5 cm | 0–0.6 | 11.32 |
| 0.6–1 | 53.62 | 0.6–1 | 44.62 | ||
| >1 | 31.83 | >1 | 44.06 | ||
| P e 10 cm × 10 cm, T c 5 cm × 10 cm | 0–0.6 | 10.85 | P e 10 cm × 10 cm, T c 7.5 cm × 7.5 cm | 0–0.6 | 6.68 |
| 0.6–1 | 50.41 | 0.6–1 | 59.95 | ||
| >1 | 38.74 | >1 | 33.37 |
| Model | U/U0 | Proportion (%) | Model | U/U0 | Proportion (%) |
|---|---|---|---|---|---|
| T c 5 cm × 5 cm | 0–0.6 | 4.65 | T c 5 cm × 7.5 cm | 0–0.6 | 4.04 |
| 0.6–1 | 11.92 | 0.6–1 | 12.49 | ||
| >1 | 83.43 | >1 | 83.47 | ||
| T c 5 cm × 10 cm | 0–0.6 | 4.97 | T c 7.5 cm × 7.5 cm | 0–0.6 | 2.61 |
| 0.6–1 | 12.79 | 0.6–1 | 12.54 | ||
| >1 | 82.22 | >1 | 84.85 | ||
| P e 7.5 cm × 7.5 cm | 0–0.6 | 3.39 | P e 7.5 cm × 10 cm | 0–0.6 | 2.24 |
| 0.6–1 | 70.70 | 0.6–1 | 70.03 | ||
| >1 | 25.91 | >1 | 27.73 | ||
| P e 7.5 cm × 12.5 cm | 0–0.6 | 2.00 | P e 10 cm × 10 cm | 0–0.6 | 0.85 |
| 0.6–1 | 73.97 | 0.6–1 | 74.80 | ||
| >1 | 24.03 | >1 | 24.35 | ||
| P e 7.5 cm × 7.5 cm, T c 5 cm × 5 cm | 0–0.6 | 13.44 | P e 7.5 cm × 7.5 cm, T c 5 cm × 7.5 cm | 0–0.6 | 14.63 |
| 0.6–1 | 42.18 | 0.6–1 | 46.16 | ||
| >1 | 44.38 | >1 | 39.21 | ||
| P e 7.5 cm × 7.5 cm, T c 5 cm × 10 cm | 0–0.6 | 12.30 | P e 7.5 cm × 7.5 cm, T c 7.5 cm × 7.5 cm | 0–0.6 | 6.23 |
| 0.6–1 | 44.42 | 0.6–1 | 47.22 | ||
| >1 | 43.28 | >1 | 46.55 | ||
| P e 7.5 cm × 10 cm, T c 5 cm × 5 cm | 0–0.6 | 14.55 | P e 7.5 cm × 10 cm, T c 5 cm × 7.5 cm | 0–0.6 | 12.86 |
| 0.6–1 | 43.51 | 0.6–1 | 48.97 | ||
| >1 | 41.94 | >1 | 38.17 | ||
| P e 7.5 cm × 10 cm, T c 5 cm × 10 cm | 0–0.6 | 15.07 | P e 7.5 cm × 10 cm, T c 7.5 cm × 7.5 cm | 0–0.6 | 11.05 |
| 0.6–1 | 40.82 | 0.6–1 | 49.31 | ||
| >1 | 44.11 | >1 | 39.64 | ||
| P e 7.5 cm × 12.5 cm, T c 5 cm × 5 cm | 0–0.6 | 10.90 | P e 7.5 cm × 12.5 cm, T c 5 cm × 7.5 cm | 0–0.6 | 10.32 |
| 0.6–1 | 43.85 | 0.6–1 | 43.37 | ||
| >1 | 45.25 | >1 | 46.31 | ||
| P e 7.5 cm × 12.5 cm, T c 5 cm × 10 cm | 0–0.6 | 6.85 | P e 7.5 cm × 12.5 cm, T c 7.5 cm × 7.5 cm | 0–0.6 | 10.09 |
| 0.6–1 | 41.00 | 0.6–1 | 52.68 | ||
| >1 | 52.15 | >1 | 37.23 | ||
| P e 10 cm × 10 cm, T c 5 cm × 5 cm | 0–0.6 | 9.26 | P e 10 cm × 10 cm, T c 5 cm × 7.5 cm | 0–0.6 | 10.16 |
| 0.6–1 | 45.52 | 0.6–1 | 45.20 | ||
| >1 | 45.22 | >1 | 44.64 | ||
| P e 10 cm × 10 cm, T c 5 cm × 10 cm | 0–0.6 | 11.08 | P e 10 cm × 10 cm, T c 7.5 cm × 7.5 cm | 0–0.6 | 4.79 |
| 0.6–1 | 50.23 | 0.6–1 | 54.17 | ||
| >1 | 38.69 | >1 | 41.04 |
References
- Durán Zuazo, V.H.; Rodríguez Pleguezuelo, C.R. Soil-erosion and runoff prevention by plant covers. A review. Agron. Sustain. Dev. 2008, 28, 65–86. [Google Scholar] [CrossRef]
- Gadiga, B.L.; Dan, Y. Evaluating the Role of Shelterbelt in Vegetation Development in a Semi Arid Zone of Yobe State, Nigeria. J. Geogr. Inf. Syst. 2015, 7, 541–550. [Google Scholar] [CrossRef]
- Zhan, K.; Liu, S.; Yang, Z.; Fang, E.; Zhou, L.; Huang, N. Effects of sand-fixing and windbreak forests on wind flow: A synthesis of results from field experiments and numerical simulations. J. Arid Land 2017, 9, 1–12. [Google Scholar] [CrossRef]
- Jones, R.E.; Vere, D.T.; Campbell, M.H. The external costs of pasture weed spread: An economic assessment of serrated tussock control. Agric. Econ. 2000, 22, 91–103. [Google Scholar] [CrossRef]
- Boldes, U.; Golberg, A.; Di Leo, J.M.; Colman, J.; Scarabino, A. Canopy flow and aspects of the response of plants protected by herbaceous shelterbelts and wood fences. J. Wind Eng. Ind. Aerodyn. 2002, 90, 1253–1270. [Google Scholar] [CrossRef][Green Version]
- Cleugh, H.A. Effects of windbreaks on airflow, microclimates and crop yields. Agrofor. Syst. 1998, 41, 55–84. [Google Scholar] [CrossRef]
- Torita, H.; Satou, H. Relationship between shelterbelt structure and mean wind reduction. Agric. For. Meteorol. 2007, 145, 186–194. [Google Scholar] [CrossRef]
- Raine, J.K.; Stevenson, D.C. Wind protection by model fences in a simulated atmospheric boundary layer. J. Wind Eng. Ind. Aerodyn. 1977, 2, 159–180. [Google Scholar] [CrossRef]
- Bitog, J.P.; Lee, I.-B.; Hwang, H.-S.; Shin, M.-H.; Hong, S.-W.; Seo, I.-H.; Kwon, K.-S.; Mostafa, E.; Pang, Z. Numerical simulation study of a trees windbreak. Biosyst. Eng. 2012, 111, 40–48. [Google Scholar] [CrossRef]
- Heisler, G.M.; Dewalle, D.R. Effects of windbreak structure on wind flow. Agric. Ecosyst. Environ. 1988, 22–23, 41–69. [Google Scholar] [CrossRef]
- Sun, Q.; Zheng, B.; Liu, T.; Zhu, L.; Hao, X.; Han, Z. The optimal spacing interval between principal shelterbelts of the farm-shelter forest network. Environ. Sci. Pollut. Res. 2022, 29, 12680–12693. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Henderson, M.; Wang, L.; Su, Y.; Liu, B. Shelterbelt Structure and Crop Protection from Increased Typhoon Activity in Northeast China. Agriculture 2021, 11, 995. [Google Scholar] [CrossRef]
- Pretzsch, H.; Del Río, M.; Schütze, G.; Ammer, C.; Annighöfer, P.; Avdagic, A.; Barbeito, I.; Bielak, K.; Brazaitis, G.; Coll, L.; et al. Mixing of Scots pine (Pinus sylvestris L.) and European beech (Fagus sylvatica L.) enhances structural heterogeneity, and the effect increases with water availability. For. Ecol. Manag. 2016, 373, 149–166. [Google Scholar] [CrossRef]
- Frank, C.; Ruck, B. Double-Arranged Mound-Mounted Shelterbelts: Influence of Porosity on Wind Reduction between the Shelters. Environ. Fluid Mech. 2005, 5, 267–292. [Google Scholar] [CrossRef]
- Li, H.; Wang, Y.; Li, S.; Askar, A.; Wang, H. Shelter Efficiency of Various Shelterbelt Configurations: A Wind Tunnel Study. Atmosphere 2022, 13, 1022. [Google Scholar] [CrossRef]
- Balakin, V.V. Formation of linear-strip greening objects in urban environmental systems. IOP Conf. Ser. Mater. Sci. Eng. 2018, 451, 012166. [Google Scholar] [CrossRef]
- Guyot, G. Brise-vent, pare-feu et sylviculture. Rev. For. Française 1990, 42, 93. [Google Scholar] [CrossRef]
- Wilson, J.D. Numerical studies of flow through a windbreak. J. Wind Eng. Ind. Aerodyn. 1985, 21, 119–154. [Google Scholar] [CrossRef]
- Zhang, K.; Qu, J.; Zhang, X.; Zhao, L.; Li, S. Protective Efficiency of Railway Arbor-Shrub Windbreak Forest Belts in Gobi Regions: Numerical Simulation and Wind Tunnel Tests. Front. Environ. Sci. 2022, 10, 885070. [Google Scholar] [CrossRef]
- Chen, C.; Chen, J. Remote sensing analysis on the regional differentiation of land types in the Loess Plateau of the North Shaanxi Province. Natl. Remote Sens. Bull. 1992, 1, 1–8. [Google Scholar] [CrossRef]
- Zhang, S.; Yuan, W.; Yu, Y.; Zhang, Y.; Wang, W.; Wang, L.; Yang, Y.; Wang, H. Shrubs plays an important role in configuration of shelterbelt in windy and sandy areas. Front. Ecol. Evol. 2024, 12, 1347714. [Google Scholar] [CrossRef]
- Judd, M.J.; Raupach, M.R.; Finnigan, J.J. A wind tunnel study of turbulent flow around single and multiple windbreaks, part I: Velocity fields. Bound.-Layer Meteorol. 1996, 80, 127–165. [Google Scholar] [CrossRef]
- Mayaud, J.; Webb, N. Vegetation in Drylands: Effects on Wind Flow and Aeolian Sediment Transport. Land 2017, 6, 64. [Google Scholar] [CrossRef]
- Raupach, M.R.; Finnigan, J.J.; Brunet, Y. Coherent eddies and turbulence in vegetation canopies: The mixing-layer analogy. Bound.-Layer Meteorol. 1996, 78, 351–382. [Google Scholar] [CrossRef]
- Mayaud, J.R.; Wiggs, G.F.S.; Bailey, R.M. Characterizing turbulent wind flow around dryland vegetation. Earth Surf. Process. Landf. 2016, 41, 1421–1436. [Google Scholar] [CrossRef]
- Nepf, H.M.; Vivoni, E.R. Flow structure in depth–limited, vegetated flow. J. Geophys. Res. Ocean. 2000, 105, 28547–28557. [Google Scholar] [CrossRef]
- Horne, W.J. Flow Around a Solitary Trees in a Large Field Under Neutral Atmospheric Stratification. Ph.D. Thesis, University of Utah, Salt Lake City, UT, USA, 2012. [Google Scholar]
- Brandle, J.R.; Hodges, L.; Zhou, X.H. Windbreaks in North American agricultural systems. Agrofor. Syst. 2004, 61, 65–78. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, C.; Jiang, H. Wind tunnel experiments on airflow patterns and wind erosion behind different windbreak structures. Aeolian Res. 2018, 31, 79–87. [Google Scholar] [CrossRef]
- Tustin, D.S.; Van Hooijdonk, B.M.; Breen, K.C. The Planar Cordon—New planting systems concepts to improve light utilisation and physiological function to increase apple orchard yield potential. Acta Hortic. 2018, 1228, 1–12. [Google Scholar] [CrossRef]
- Kegley, N.F. Toward the Preservation of Rural Cultural Historic Landscapes: Amethod for Evaluating Nineteenth Century Blue Ridge Farms. Master’s Thesis, Virginia Polytechnic Institute State University, Blacksburg, VA, USA, 1986. Available online: https://vtechworks.lib.vt.edu/bitstreams/7b8571e3-eccd-4946-859c-4cd1524486ab/download (accessed on 1 October 2025).
- Zhang, H.; Pei, L.; Li, J.; Wang, F. Numerical simulation of wind and sand resistance in three typical shrubs. Sustainability 2025, 17, 5481. [Google Scholar] [CrossRef]
- Messier, C.; Bauhus, J.; Doyon, F.; Maure, F.; Sousa-Silva, R.; Nolet, P.; Puettmann, K. The functional complex network approach to foster forest resilience to global changes. For. Ecosyst. 2019, 6, 21. [Google Scholar] [CrossRef]
- MacLean, D.A.; Clark, K.L. Mixedwood management positively affects forest health during insect infestations in eastern North America. Can. J. For. Res. 2021, 51, 910–920. [Google Scholar] [CrossRef]
- Singh, J.; Roy, A.K. CFD simulation of the wind field around pyramidal roofed single-story buildings. SN Appl. Sci. 2019, 1, 1425. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.H.W. Analysis of creeping sand trajectories using high-speed photography. Chin. Sci. Bull. 2010, 55, 3186–3192. [Google Scholar] [CrossRef]
- Sankaran, A.; Hain, R.; Kähler, C. Assessing the dispersion characteristics of ship exhausts in neutral boundary layers: Wind tunnel testing. In PHYSMOD 2024, Proceedings of the International Workshop on Physical Modelling of Flow and Dispersion Phenomena, Lyon, France, 28–30 August 2024; HAL Open Science: Lyon, France, 2024; pp. 118–126. [Google Scholar]
- Cui, K.; Li, S.; Wang, H.; Fan, J. Three dimensional flow field characteristics of two typical blowouts in the dry lake basin of Taitema Lake and their influence on wind erosion. Arid Land. Geogr. 2022, 45, 1784–1794. [Google Scholar] [CrossRef]
- Ma, R.; Wang, J.; Qu, J.; Liu, H. Effectiveness of shelterbelt with a non-uniform density distribution. J. Wind Eng. Ind. Aerodyn. 2010, 98, 767–771. [Google Scholar] [CrossRef]
- Lampartová, I.; Schneider, J.; Vyskot, I.; Rajnoch, M.; Litschmann, T. Impact of protective shelterbelt microclimate characteristics. Ekológia 2015, 34, 101–110. [Google Scholar] [CrossRef]
- Dong, Z.; Luo, W.; Qian, G.; Wang, H. Experimental investigation of the sheltering effect of porous fences on sand flux profiles. Geomorphology 2018, 310, 74–83. [Google Scholar] [CrossRef]
- Cheng, H.; He, W.; Liu, C.; Zou, X.; Kang, L.; Chen, T.; Zhang, K. Transition model for airflow fields from single plants to multiple plants. Agric. For. Meteorol. 2019, 266–267, 29–42. [Google Scholar] [CrossRef]
- Li, J.; Dong, S.; Li, Y. Comparative study on windbreak effects of two different configuration shelterbelts. IOP Conf. Ser. Earth Environ. Sci. 2021, 895, 012020. [Google Scholar] [CrossRef]
- Kainkwa, R.M.R.; Stigter, C.J. Wind reduction downwind from a savanna woodland edge. Neth. J. Agric. Sci. 1994, 42, 145–157. [Google Scholar] [CrossRef]
- Liu, B.; Zhou, X.; Brandle, J. Effects of multiple-row trees–shrub shelterbelts on wind speed reduction and crop yield improvement in arid regions. Agrofor. Syst. 2019, 93, 541–554. [Google Scholar] [CrossRef]
- Leenders, J.K.; Boxel, J.H.V.; Sterk, G. The effect of single vegetation elements on wind speed and sediment transport in the Sahelian zone of Burkina Faso. Earth Surf. Process. Landf. 2007, 32, 1454–1474. [Google Scholar] [CrossRef]
- Ghisalberti, M.; Nepf, H. The Structure of the Shear Layer in Flows over Rigid and Flexible Canopies. Environ. Fluid Mech. 2006, 6, 277–301. [Google Scholar] [CrossRef]
- Mukherjee, A.; Cajas, J.C.; Houzeaux, G.; Lehmkuhl, O.; Suckale, J.; Marras, S. Forest density is more effective than trees rigidity at reducing the onshore energy flux of tsunamis. Coast. Eng. 2023, 182, 104286. [Google Scholar] [CrossRef]
- Lup, A.; Miron, L. Fighting Against Drought in Dobrogea by Protective Forest Belts. Munich Personal RePEc Archive (MPRA), No. 61724, Ovidius University of Constanta. 20 November 2014. Available online: https://mpra.ub.uni-muenchen.de/61724 (accessed on 1 October 2025).
- Foster, D.R.; Boose, E.R. Patterns of Forest Damage Resulting from Catastrophic Wind in Central New England, USA. J. Eco. 1992, 80, 79–98. [Google Scholar] [CrossRef]
- Finnigan, J. Turbulence in plant canopies. Ann. Rev. Fluid Mech. 2000, 32, 519–791. [Google Scholar] [CrossRef]



| P e Plant Spacing | T c Plant Row Spacing | Belt Width (cm) |
|---|---|---|
| 7.5 cm × 7.5 cm | 5 cm × 5 cm | 40.5 |
| 5 cm × 7.5 cm | 45.5 | |
| 5 cm × 10 cm | 50.5 | |
| 7.5 cm × 7.5 cm | 45.5 | |
| 7.5 cm × 10 cm | 5 cm × 5 cm | 48 |
| 5 cm × 7.5 cm | 53 | |
| 5 cm × 10 cm | 58 | |
| 7.5 cm × 7.5 cm | 53 | |
| 7.5 cm × 12.5 cm | 5 cm × 5 cm | 55.5 |
| 5 cm × 7.5 cm | 60.5 | |
| 5 cm × 10 cm | 65.5 | |
| 7.5 cm × 7.5 cm | 60.5 | |
| 10 cm × 10 cm | 5 cm × 5 cm | 48 |
| 5 cm × 7.5 cm | 53 | |
| 5 cm × 10 cm | 58 | |
| 7.5 cm × 7.5 cm | 53 |
| Height (cm) Speed (m s−1) | 6 | 10 | 15 |
|---|---|---|---|
| 1 | 4.14 | 6.89 | 9.88 |
| 3 | 5.05 | 8.18 | 11.68 |
| 5 | 5.42 | 8.72 | 12.46 |
| 8 | 5.67 | 9.08 | 12.95 |
| 13 | 6.05 | 9.61 | 13.69 |
| 20 | 6.40 | 10.36 | 14.83 |
| 30 | 7.05 | 11.11 | 15.87 |
| 40 | 8.11 | 12.75 | 18.06 |
| 60 | 8.91 | 13.89 | 19.50 |
| Wind Speed Profile Equation | u = 1.07928769ln(z) + 3.72818485 R2 = 0.91 | u = 1.5986ln(z) + 6.2403 R2 = 0.91 | u = 2.53ln(z) + 8.06 R2 = 0.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Yang, J.; Chen, R.; Hou, P.; Wang, Z.; Qin, Y.; He, M.; Luo, Q. Structural Optimization of Windbreak and Sand-Fixing Forests: A Wind Tunnel Study. Forests 2025, 16, 1710. https://doi.org/10.3390/f16111710
Li F, Yang J, Chen R, Hou P, Wang Z, Qin Y, He M, Luo Q. Structural Optimization of Windbreak and Sand-Fixing Forests: A Wind Tunnel Study. Forests. 2025; 16(11):1710. https://doi.org/10.3390/f16111710
Chicago/Turabian StyleLi, Feng, Jianjun Yang, Rui Chen, Peng Hou, Zhixi Wang, Yao Qin, Miao He, and Qinghong Luo. 2025. "Structural Optimization of Windbreak and Sand-Fixing Forests: A Wind Tunnel Study" Forests 16, no. 11: 1710. https://doi.org/10.3390/f16111710
APA StyleLi, F., Yang, J., Chen, R., Hou, P., Wang, Z., Qin, Y., He, M., & Luo, Q. (2025). Structural Optimization of Windbreak and Sand-Fixing Forests: A Wind Tunnel Study. Forests, 16(11), 1710. https://doi.org/10.3390/f16111710






