Application of Climate Sensitivity Transfer Matrix Growth Model in Qinghai Province
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sources
2.3. Model Structure
2.4. Model Evaluation and Validation
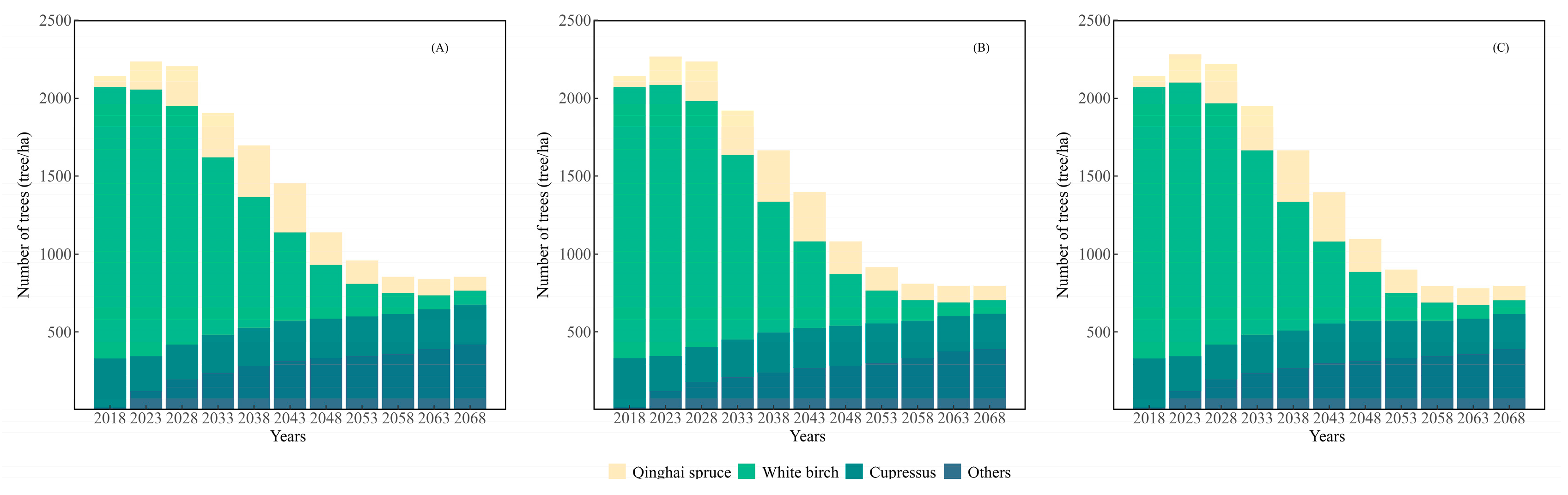
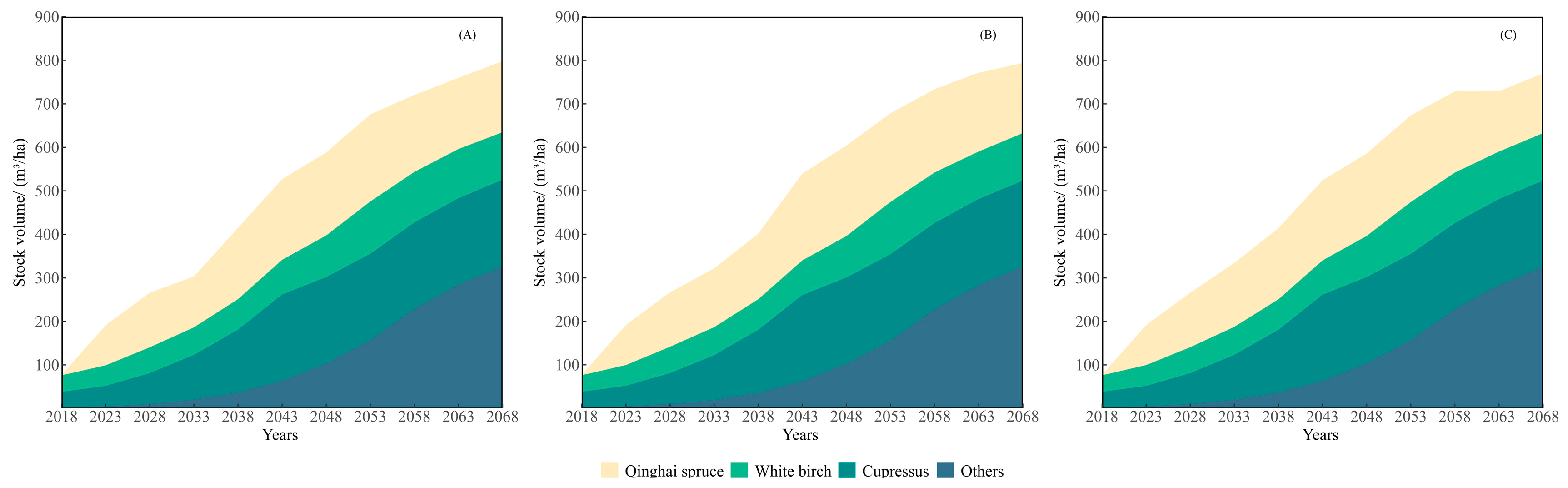
2.5. Growth Prediction
3. Results
3.1. Model Parameters and Validation
3.2. Growth Simulation
4. Discussion
4.1. Model Parameters and Validation Results
4.2. Forest Growth Prediction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, C.; Li, D.; Wang, D.; Zhang, L. Quantification and assessment of changes in ecosystem service in the Three-River Headwaters Region, China as a result of climate variability and land cover change. Ecol. Indicat. 2016, 66, 199–211. [Google Scholar] [CrossRef]
- Qi, Y.; Lian, X.; Wang, H.; Zhang, J.; Yang, R. Dynamic mechanism between human activities and ecosystem services: A case study of Qinghai lake watershed, China. Ecol. Indicat. 2020, 117, 106528. [Google Scholar] [CrossRef]
- Lin, S.; Li, Y.; Li, Y.; Chen, Q.; Wang, Q.; He, K. Influence of tree size, local forest structure, topography, and soil resource availability on plantation growth in Qinghai Province, China. Ecol. Indicat. 2021, 120, 106957. [Google Scholar] [CrossRef]
- Gao, Q.; Guo, Y.; Xu, H.; Ganjurjav, H.; Li, Y.; Wan, Y.; Qin, X.; Ma, X.; Liu, S. Climate change and its impacts on vegetation distribution and net primary productivity of the alpine ecosystem in the Qinghai-Tibetan Plateau. Sci. Total Environ. 2016, 554–555, 34–41. [Google Scholar] [CrossRef]
- Lindner, M.; Maroschek, M.; Netherer, S.; Kremer, A.; Barbati, A.; Garcia-Gonzalo, J.; Seidl, R.; Delzon, S.; Corona, P.; Kolström, M.; et al. Climate change impacts, adaptive capacity, and vulnerability of European forest ecosystems. For. Ecol. Manag. 2010, 259, 698–709. [Google Scholar] [CrossRef]
- Wang, S.; Che, Y.; Pang, H.; Du, J.; Zhang, Z. Accelerated changes of glaciers in the Yulong Snow Mountain, Southeast Qinghai-Tibetan Plateau. Reg. Environ. Change 2020, 20, 38. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, R.; Singh, V.; Xu, C.; Fan, K.; Shen, Z.; Wang, G.; Zhao, J. Dynamic vulnerability of ecological systems to climate changes across the Qinghai-Tibet Plateau, China. Ecol. Indicat. 2022, 134, 108483. [Google Scholar] [CrossRef]
- Fu, M.; Wang, J.; Zhu, Y.; Zhang, Y. Evaluation of the Protection Effectiveness of Natural Protected Areas on the Qinghai–Tibet Plateau Based on Ecosystem Services. Int. J. Environ. Res. Public Health 2023, 20, 2605. [Google Scholar] [CrossRef]
- Zhao, Z.; Guo, Y.; Wei, H.; Ran, Q.; Liu, J.; Zhang, Q.; Gu, W. Potential distribution of Notopterygium incisum Ting ex H. T. Chang and its predicted responses to climate change based on a comprehensive habitat suitability model. Ecol. Evol. 2020, 10, 3004–3016. [Google Scholar] [CrossRef]
- Mori, A.; Lertzman, K.; Gustafsson, L. Biodiversity and ecosystem services in forest ecosystems: A research agenda for applied forest ecology. J. Appl. Ecol. 2017, 54, 12–27. [Google Scholar] [CrossRef]
- Führer, E. Forest functions, ecosystem stability and management. For. Ecol. Manag. 2000, 132, 29–38. [Google Scholar] [CrossRef]
- Myers, N.; Goreau, T. Tropical forests and the greenhouse effect: A management response. Clim. Change 1991, 19, 215–225. [Google Scholar] [CrossRef]
- Jandl, R.; Bauhus, J.; Bolte, A.; Schindlbacher, A.; Schüler, S. Effect of climate-adapted forest management on carbon pools and greenhouse gas emissions. Curr. For. Rep. 2015, 1, 1–7. [Google Scholar] [CrossRef]
- Yan, K.; Wang, W.; Li, Y.; Wang, X.; Jin, J.; Jiang, J.; Yang, H.; Wang, L. Identifying priority conservation areas based on ecosystem services change driven by Natural Forest Protection Project in Qinghai province, China. J. Clean. Prod. 2022, 362, 132453. [Google Scholar] [CrossRef]
- Peng, C. Understanding the role of forest simulation models in sustainable forest management. Environ. Impact Assess. Rev. 2000, 10, 481–501. [Google Scholar] [CrossRef]
- Carrijo, J.; Ferreira, A.; Ferreira, M. The growth and production modeling of individual trees of Eucalyptus urophylla plantations. J. For. Res. 2020, 31, 1663–1672. [Google Scholar] [CrossRef]
- Ma, F.; Jia, L. Advances in the Researches of Stand Growth and Yield Model. J. For. Res. 2008, 21, 21–27. [Google Scholar]
- Burkhart, H.E.; Margarida, T. Modeling Forest Trees and Stands; Burkhart, H.E., Tomé, M., Eds.; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Peng, C. Growth and yield models for uneven-aged stands: Past, present and future. For. Ecol. Manag. 2000, 132, 259–279. [Google Scholar] [CrossRef]
- Burkhart, H.E.; Tomé, M. Whole-Stand Models for Even-Aged Stands. In Modeling Forest Trees and Stands; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Liang, J.; Picard, N. Matrix Model of Forest Dynamics: An Overview and Outlook. For. Sci. 2013, 59, 359–378. [Google Scholar] [CrossRef]
- Mabvurira, D.; Miina, J. Individual-tree growth and mortality models for Eucalyptus grandis (Hill) Maiden plantations in Zimbabwe. For. Ecol. Manag. 2002, 161, 231–245. [Google Scholar] [CrossRef]
- Palahí, M.; Pukkala, T. Optimising the management of Scots pine (Pinus sylvestris L.) stands in Spain based on individual-tree models. Ann. For. Sci. 2003, 60, 105–114. [Google Scholar] [CrossRef]
- Pukkala, T.; Lähde, E.; Laiho, O. Using optimization for fitting individual-tree growth models for uneven-aged stands. Eur. J. For. Res. 2011, 130, 829–839. [Google Scholar] [CrossRef]
- Subedi, N.; Sharma, M. Individual-tree diameter growth models for black spruce and jack pine plantations in northern Ontario. For. Ecol. Manag. 2011, 261, 2140–2148. [Google Scholar] [CrossRef]
- Hamidi, S.K.; Weiskittel, A.; Bayat, M.; Fallah, A. Development of individual tree growth and yield model across multiple contrasting species using nonparametric and parametric methods in the Hyrcanian forests of northern Iran. Eur. J. For. Res. 2021, 140, 421–434. [Google Scholar] [CrossRef]
- Rosa, R.; Soares, P.; Tomé, M. Evaluating the Economic Potential of Uneven-aged Maritime Pine Forests. Ecol. Econ. 2018, 143, 210–217. [Google Scholar] [CrossRef]
- Ek, A.R.; Monserud, R.A. Performance and comparison of stand growth models based on individual tree and diameter-class growth. Can. J. For. Res. 1979, 9, 231–244. [Google Scholar] [CrossRef]
- Jou, Y.; Huang, C.; Cho, H. A VIF-based optimization model to alleviate collinearity problems in multiple linear regression. Comput. Stat. 2014, 29, 1515–1541. [Google Scholar] [CrossRef]
- Ma, W.; Domke, G.M.; D’Amato, A.W.; Woodall, C.W.; Walters, B.F.; Deo, R.K. Using matrix models to estimate aboveground forest biomass dynamics in the eastern USA through various combinations of LiDAR, Landsat, and forest inventory data. Environ. Res. Lett. 2018, 13, 125004. [Google Scholar] [CrossRef]
- Solomon, D.; Hosmer, R.; Hayslett, H. A two-stage matrix model for predicting growth of forest stands in the Northeast. Can. J. For. Res. 1986, 16, 521–528. [Google Scholar] [CrossRef]
- Wang, G.; Bai, W.; Li, N.; Hu, H. Climate changes and its impact on tundra ecosystem in Qinghai-Tibet Plateau, China. Clim Change 2001, 106, 463–482. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, Y.; Zhu, J.; Liu, Y.; Zu, J.; Zhang, J. The Influences of Climate Change and Human Activities on Vegetation Dynamics in the Qinghai-Tibet Plateau. Remote Sens. 2016, 8, 876. [Google Scholar] [CrossRef]
- Weber, M.; Flannigan, M. Canadian boreal forest ecosystem structure and function in a changing climate: Impact on fire regimes. Environ. Rev. 1997, 5, 145–166. [Google Scholar] [CrossRef]
- Ramdane, A.; Alessandro, C. Biophysical climate impacts of recent changes in global forest cover. Science 2016, 351, 600–604. [Google Scholar] [CrossRef] [PubMed]
- Keenan, R. Climate change impacts and adaptation in forest management: A review. Ann. For. Sci. 2015, 72, 145–167. [Google Scholar] [CrossRef]
- Condit, R.; Hubbell, S.P.; Foster, R. Changes in tree species abundance in a Neotropical forest: Impact of climate change. J. Trop. Ecol. 1996, 12, 231–256. [Google Scholar] [CrossRef]
- Ammer, C. Diversity and forest productivity in a changing climate. N. Phytol. 2019, 221, 50–66. [Google Scholar] [CrossRef]
- Liang, J.; Zhou, M.; Verbyla, D.L.; Zhang, L.; Springsteen, A.L.; Malone, T. Mapping forest dynamics under climate change: A matrix model. For. Ecol. Manag. 2011, 262, 2250–2262. [Google Scholar] [CrossRef]
- Stage, A.R. An Expression for the Effect of Aspect, Slope, and Habitat Type on Tree Growth. For. Sci. 1976, 22, 457–460. [Google Scholar] [CrossRef]
- Tobin, J. Estimation of Relationships for Limited Dependent Variables. Econometrica 1958, 26, 24–36. [Google Scholar] [CrossRef]
- Ai, C.; Norton, E. Interaction terms in logit and probit models. Econ. Lett. 2003, 80, 123–129. [Google Scholar] [CrossRef]
- Henningsen, A. Estimating censored regression models in R using the censReg Package. R Package Vignettes 2010, 5, 12. [Google Scholar]
- Taylor, K.; Stouffer, R.; Meehl, G. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Du, X.; Chen, X.; Zeng, W.; Meng, J. A climate-sensitive transition matrix growth model for uneven-aged mixed-species oak forests in North China. Forestry 2021, 94, 258–277. [Google Scholar] [CrossRef]
- Wang, W.; Bai, Y.; Jiang, C.; Yang, H.; Jing, M. Development of a linear mixed-effects individual-tree basal area increment model for masson pine in Hunan Province, South-central China. J. Sustain. For. 2020, 39, 526–541. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, Q.; Sharma, R.; Wang, Y.; He, P.; Guo, J.; Lei, Y.; Fu, L. A climate sensitive mixed-effects diameter class mortality model for Prince Rupprecht larch (Larix gmelinii var. principis-rupprechtii) in northern China. For. Ecol. Manag. 2021, 491, 119091. [Google Scholar] [CrossRef]
- Coomes, D.A.; Allen, R.B. Effects of size, competition and altitude on tree growth. J. Ecol. 2007, 95, 1084–1097. [Google Scholar] [CrossRef]
- Forrester, D.; Bauhus, J. A Review of Processes Behind Diversity—Productivity Relationships in Forests. Curr. For. Rep. 2016, 2, 45–61. [Google Scholar] [CrossRef]
- Searle, E.; Chen, H.; Paquette, A. Higher tree diversity is linked to higher tree mortality. Proc. Natl. Acad. Sci. USA 2022, 119, e2013171119. [Google Scholar] [CrossRef]
- Edgar, C.B.; Burk, T.E. Productivity of aspen forests in northeastern Minnesota, U.S.A., as related to stand composition and canopy structure. Can. J. For. Res. 2001, 31, 1019–1029. [Google Scholar] [CrossRef]
- Pretzsch, H. Facilitation and competition reduction in tree species mixtures in Central Europe: Consequences for growth modeling and forest management. Ecol. Model. 2022, 464, 109812. [Google Scholar] [CrossRef]
- Jonczak, J.; Jankiewicz, U.; Kondras, M.; Kruczkowska, B.; Oktaba, L.; Oktaba, J.; Olejniczak, I.; Pawłowicz, E.; Polláková, N.; Raab, T.; et al. The influence of birch trees (Betula spp.) on soil environment—A review. For. Ecol. Manag. 2020, 477, 118486. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, H. Competition, species interaction and ageing control tree mortality in boreal forests. J. Ecol. 2011, 99, 1470–1480. [Google Scholar] [CrossRef]
- Young, B.; Liang, J.; Chapin, F. Effects of species and tree size diversity on recruitment in the Alaskan boreal forest: A geospatial approach. For. Ecol. Manag. 2011, 262, 1608–1617. [Google Scholar] [CrossRef]
- Vencurik, J.; Bosela, M.; Sedmáková, D.; Pittner, J.; Kucbel, S.; Jaloviar, P.; Parobeková, Z.; Saniga, M. Tree species diversity facilitates conservation efforts of European yew. Biodivers. Conserv. 2019, 28, 791–810. [Google Scholar] [CrossRef]
- Liang, J.; Buongiorno, J.; Monserud, R.; Kruger, E.; Zhou, M. Effects of diversity of tree species and size on forest basal area growth, recruitment, and mortality. For. Ecol. Manag. 2007, 243, 116–127. [Google Scholar] [CrossRef]
- Liang, J.; Buongiorno, J.; Monserud, R.A. Growth and yield of all-aged Douglas-fir western hemlock forest stands: A matrix model with stand diversity effects. Can. J. For. Res. 2005, 35, 2368–2381. [Google Scholar] [CrossRef]
- Lei, X.; Wang, W.; Peng, C. Relationships between stand growth and structural diversity in spruce-dominated forests in New Brunswick, Canada. Can. J. For. Res. 2009, 39, 1835–1847. [Google Scholar] [CrossRef]
- Tan, L.; Fan, C.; Fan, X. Relationships between species diversity or community structure and productivity of woody-plants in a broad-leaved Korean pine forest in Jiaohe, Jilin, China. Chin. J. Plant Ecol. 2017, 41, 1149–1156. [Google Scholar]
- Wang, W.; Lei, X.; Ma, Z.; Kneeshaw, D.; Peng, C. Positive relationship between aboveground carbon stocks and structural diversity in spruce-dominated forest stands in New Brunswick, Canada. For. Sci. 2011, 57, 506–515. [Google Scholar] [CrossRef]
- Madrigal-González, J.; Ruiz-Benito, P.; Ratcliffe, S.; Calatayud, J.; Kändler, G.; Lehtonen, A.; Dahlgren, J.; Wirth, C.; Zavala, M.A. Complementarity effects on tree growth are contingent on tree size and climatic conditions across Europe. Sci. Rep. 2016, 6, 32233. [Google Scholar] [CrossRef]
- Rozendaal, D.; Phillips, O.; Lewis, S.; Affum-Baffoe, K.; Alvarez-Davila, E. Competition influences tree growth, but not mortality, across environmental gradients in Amazonia and tropical Africa. Ecology 2020, 101, e03052. [Google Scholar] [CrossRef]
- Kaber, Y.; Meyer, P.; Stillhard, J.; De Lombaerde, E.; Zell, J.; Stadelmann, G.; Bugmann, H.; Bigler, C. Tree recruitment is determined by stand structure and shade tolerance with uncertain role of climate and water relations. Ecol. Evol. 2021, 11, 12182–12203. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Zhang, L.; Fu, S. Effects of tree age and basal area on boreal forest tree mortality in Canada. Chin. J. Ecol. 2011, 22, 2477–2481. [Google Scholar]
- Raich, J.; Russell, A.; Kitayama, K.; Parton, W.; Vitousek, P. Temperature Influences Carbon Accumulation in Moist Tropical Forests. Ecology 2006, 87, 76–87. [Google Scholar] [CrossRef] [PubMed]
- Toledo, M.; Poorter, L.; Peña-Claros, M.; Alarcón, A.; Balcázar, J.; Leaño, C.; Licona, J.C.; Llanque, O.; Vroomans, V.; Zuidema, P.; et al. Climate is a stronger driver of tree and forest growth rates than soil and disturbance. J. Ecol. 2011, 99, 254–264. [Google Scholar] [CrossRef]
- Liu, J.; Li, Z.; Keyimu, M.; Wang, X.; Liang, H.; Feng, X.; Gao, G.; Fu, B. Accelerated warming in the late 20th century promoted tree radial growth in the Northern Hemisphere. J. Plant Ecol. 2023, 16, rtac077. [Google Scholar] [CrossRef]
- Gradel, A.; Haensch, C.; Ganbaatar, B.; Dovdondemberel, B.; Nadaldorj, O.; Günther, B. Response of white birch (Betula platyphylla Sukaczev) to temperature and precipitation in the mountain forest steppe and taiga of Northern Mongolia. Dendrochronologia 2017, 41, 24–33. [Google Scholar] [CrossRef]
- Gradel, A.; Ganbaatar, B.; Nadaldorj, O.; Dovdondemberel, B.; Kusbach, A. Climate-growth relationships and pointer year analysis of a Siberian larch (Larix sibirica Ledeb.) chronology from the Mongolian mountain forest steppe compared to white birch (Betula platyphylla Sukaczev). For. Ecosyst. 2017, 4, 22. [Google Scholar] [CrossRef]
- Anderegg, W.; Kane, J.; Anderegg, L. Consequences of widespread tree mortality triggered by drought and temperature stress. Nat. Clim. Change 2013, 3, 30–36. [Google Scholar] [CrossRef]
- Park Williams, A.; Allen, C.; Macalady, A.; Griffin, D.; Woodhouse, C.; Meko, D.; Swetnam, T.W.; Rauscher, S.A.; Seager, R.; Grissino-Mayer, H.D.; et al. Temperature as a potent driver of regional forest drought stress and tree mortality. Nat. Clim. Change 2013, 3, 292–297. [Google Scholar] [CrossRef]
- Sarris, D.; Christodoulakis, D.; Koerner, C. Recent decline in precipitation and tree growth in the eastern Mediterranean. Glob. Change Biol. 2007, 13, 1187–1200. [Google Scholar] [CrossRef]
- Trouet, V.; Coppin, P.; Beeckman, H. Annual growth ring patterns in Brachystegia spiciformis reveal influence of precipitation on tree growth. Biotropica 2006, 38, 375–382. [Google Scholar] [CrossRef]
- Van Mantgem, P.; Stephenson, N. Apparent climatically induced increase of tree mortality rates in a temperate forest. Ecol. Lett. 2007, 10, 909–916. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.; Ma, Z.; Lei, X.; Zhou, Q.; Chen, H.; Wang, W.; Liu, S.; Li, W.; Fang, X.; Zhou, X. A drought-induced pervasive increase in tree mortality across Canada’s boreal forests. Nat. Clim. Change 2011, 1, 467–471. [Google Scholar] [CrossRef]
- Gao, X.; Zheng, Z.; Diao, Z.; Zhang, Y.; Wang, Y.; Ma, L. The effects of litter input and increased precipitation on soil microbial communities in a temperate grassland. Front. Microbiol. 2024, 15, 1347016. [Google Scholar] [CrossRef]
- Petrie, M.; Wildeman, A.; Bradford, J.; Hubbard, R.; Lauenroth, W. A review of precipitation and temperature control on seedling emergence and establishment for ponderosa and lodgepole pine forest regeneration. For. Ecol. Manag. 2016, 361, 328–338. [Google Scholar] [CrossRef]
- Wang, J.; Sun, Z.; Hui, D.; Yang, L.; Wang, F.; Liu, N.; Ren, H. Responses of seedling performance to altered seasonal precipitation in a secondary tropical forest, southern China. For. Ecol. Manag. 2018, 410, 27–34. [Google Scholar] [CrossRef]
- Du, H.; Li, M.H.; Rixen, C.; Zong, S.; Stambaugh, M.; Huang, L.; He, H.S.; Wu, Z. Sensitivity of recruitment and growth of alpine treeline birch to elevated temperature. Agric. For. Meteorol. 2021, 304, 108403. [Google Scholar] [CrossRef]
- Gao, L.; Gou, X.; Deng, Y.; Wang, Z.; Gu, F.; Wang, F. Increased growth of Qinghai spruce in northwestern China during the recent warming hiatus. Agr. For. Meteorol. 2018, 260–261, 9–16. [Google Scholar] [CrossRef]
- Zuo, Y.; Yang, L.; Wang, Q.; Zhu, B.; Xia, C.; Zhang, H.; Li, W.; Zhang, Z.; Deng, H. Divergent Fungal Community Dynamics of Thuja sutchuenensis in Arid Environments. Microorganisms 2024, 12, 446. [Google Scholar] [CrossRef]
- Oikonomakis, N.; Ganatsas, P. Secondary forest succession in Silver birch (Betula pendula Roth) and Scots pine (Pinus sylvestris L.) southern limits in Europe, in a site of Natura 2000 network—An ecogeographical approach. For. Syst. 2020, 29, e010. [Google Scholar] [CrossRef]
- Ali, A.; Wang, L. Big-sized trees and forest functioning: Current knowledge and future perspectives. Ecol. Indic. 2021, 127, 107760. [Google Scholar] [CrossRef]
- Bannister, P.; Neuner, G. Frost Resistance and the Distribution of Conifers. In Conifer Cold Hardiness; Bigras, F.J., Colombo, S.J., Eds.; Tree Physiology; Springer: Dordrecht, The Netherlands, 2001; Volume 1. [Google Scholar]
- Yang, Y.; Watanabe, M.; Li, F.; Zhang, J.; Zhang, W.; Zhai, J. Factors affecting forest growth and possible effects of climate change in the Taihang Mountains, northern China. Forestry 2006, 79, 135–147. [Google Scholar] [CrossRef]
- Peng, J.; Gou, X.; Chen, F.; Li, J.; Liu, P.; Zhang, Y.; Fang, K. Difference in tree growth responses to climate at the upper treeline: Qilian Juniper in the Anyemaqen Mountains. J. Integr. Plant Biol. 2008, 50, 982–990. [Google Scholar] [CrossRef]
- García-Nieto, A.; García-Llorente, M.; Iniesta-Arandia, I.; Martín-López, B. Mapping forest ecosystem services: From providing units to beneficiaries. Ecosyst. Serv. 2013, 4, 126–138. [Google Scholar] [CrossRef]
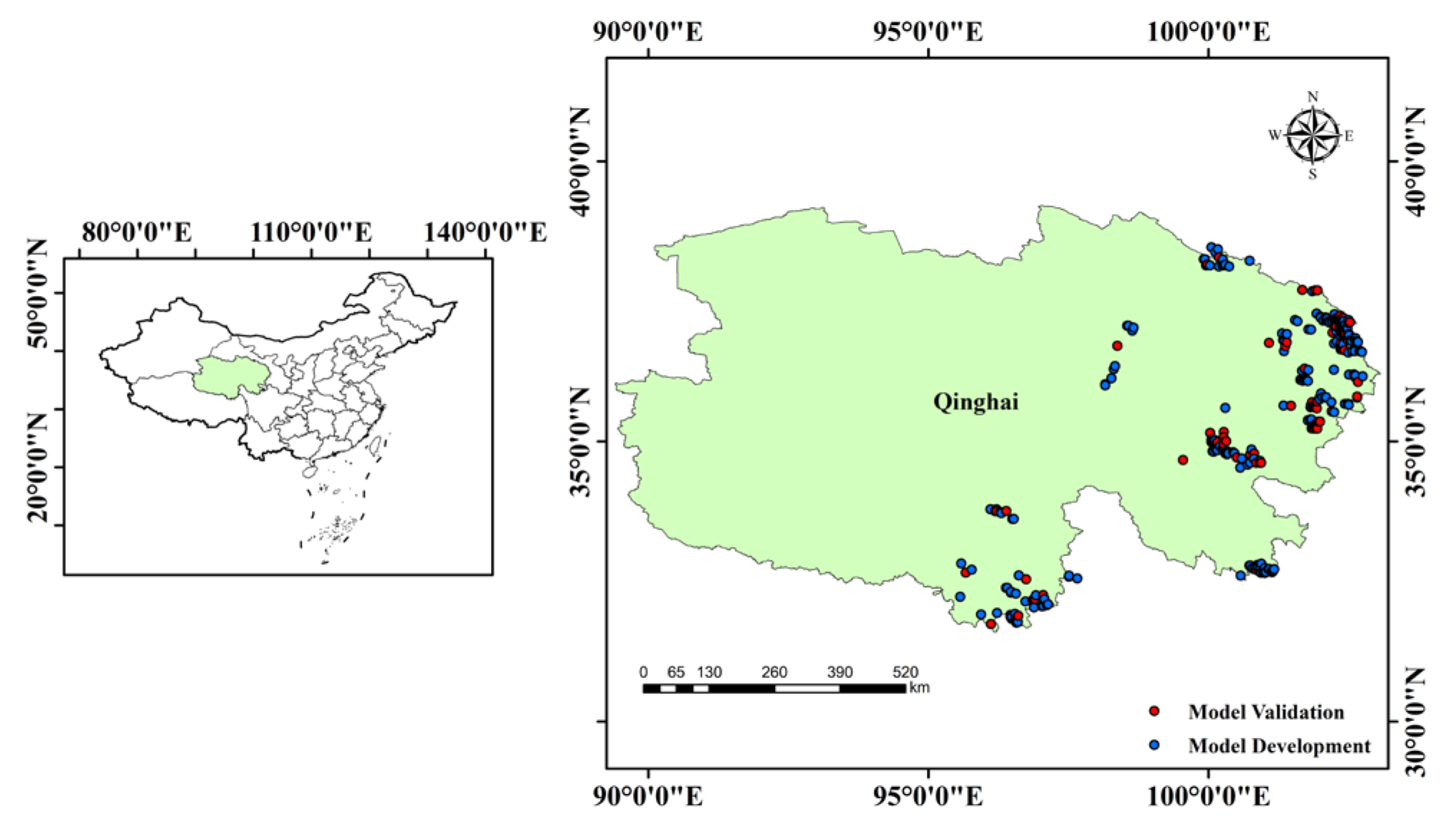
| MAT (°C) | MAP (mm) | DBH | Sd | Dc | SLcos | Ba (m2/ha) | N (Trees/ha) | ||
|---|---|---|---|---|---|---|---|---|---|
| Model Development (227 Plots) | Max | 5.02 | 786.00 | 76.40 | 1.03 | 2.40 | 37.00 | 65.72 | 2400 |
| Min | −2.80 | 308.60 | 5.00 | 0.00 | 0.00 | −43.00 | 1.92 | 465 | |
| Mean | 1.52 | 535.31 | 14.75 | 0.28 | 1.68 | −1.73 | 26.89 | 1255 | |
| SD | 1.40 | 86.77 | 9.40 | 0.31 | 0.44 | 22.31 | 15.14 | 525 | |
| Model Validation (100 Plots) | Max | 5.98 | 835.20 | 90.80 | 1.34 | 2.37 | 45.00 | 83.03 | 3120 |
| Min | −2.40 | 296.00 | 5.00 | 0.00 | 0.00 | −43.00 | 1.58 | 465 | |
| Mean | 1.70 | 550.98 | 15.23 | 0.19 | 1.66 | −3.18 | 26.59 | 1190 | |
| SD | 1.42 | 95.72 | 9.92 | 0.30 | 0.39 | 21.88 | 15.65 | 544 |
| Qinghai Spruce | White Birch | Cupressus | Others | |
|---|---|---|---|---|
| Intercept | 3.938 × 10−2 | 5.435 × 10−1 *** | 3.558 × 10−1 *** | 5.347 × 10−1 *** |
| DBH | 7.968 × 10−3 *** | 1.171 × 10−2 *** | 1.346 × 10−3 *** | 6.90 × 10−3 *** |
| SLcos 1 | 8.961 × 10−4 ** | −6.989 × 10−4 *** | 3.419 × 10−4 *** | 2.813 × 10−3 *** |
| Sd | 1.488 × 10−1 *** | −8.197 × 10−2 *** | −5.896 × 10−2 *** | −1.971 × 10−1 *** |
| Dc | 3.150 × 10−1 *** | 9.960 × 10−2 *** | 4.878 × 10−2 *** | 1.264 × 10−2 |
| MAT | 6.075 × 10−2 *** | −1.619 × 10−2 *** | 1.565 × 10−2 *** | 1.069 × 10−2 * |
| MAP | 2.128 × 10−4 *** | −3.358 × 10−4 *** | 8.679 × 10−4 *** | 4.484 × 10−4 *** |
| Ba | −9.965 × 10−3 *** | −5.432 × 10−3 *** | −1.314 × 10−3 *** | −7.811 × 10−3 *** |
| R2 2 | 0.44 | 0.29 | 0.22 | 0.30 |
| AIC 3 | 371.33 | 91.30 | −4610.09 | 270.41 |
| BIC 4 | 424.52 | 148.48 | −4561.69 | 322.71 |
| LogLik 5 | −64.56 | −865.59 | 2314.05 | −75.15 |
| Qinghai Spruce | White Birch | Cupressus | Others | |
|---|---|---|---|---|
| Intercept | −1.479 × 100 *** | −2.78 × 100 *** | −2.085 × 100 *** | −2.682 × 100 *** |
| DBH | −2.635 × 10−2 *** | −3.052 × 10−2 *** | −1.579 × 10−2 *** | −3.043 × 10−2 *** |
| SLcos | 3.371 × 10−3 | −7.136 × 10−3 *** | −3.587 × 10−3 *** | 6.382 × 10−4 |
| Sd | 1.063 × 10−1 | −4.770 × 10−1 *** | 5.846 × 10−1 *** | 1.827 × 10−1 |
| Dc | −3.186 × 10−1 | 5.963 × 10−1 *** | −7.463 × 10−3 | 2.505 × 10−1 |
| MAT | 8.475 × 10−2 * | 6.262 × 10−2 ** | 1.580 × 10−3 | 8.940 × 10−2 |
| MAP | −1.269 × 10−3 | 7.612 × 10−4 ** | 4.533 × 10−4 | −1.181 × 10−3 |
| Ba | 2.833 × 10−2 *** | 1.669 × 10−2 * | 1.092 × 10−3 | 1.001 × 10−2 *** |
| R2 | 0.28 | 0.27 | 0.24 | 0.19 |
| AIC | 707.51 | 3032.59 | 1841.78 | 553.91 |
| BIC | 756.74 | 3085.98 | 1897.76 | 602.33 |
| LogLik | −345.76 | −1508.29 | −912.89 | −268.96 |
| Qinghai Spruce | White birch | Others | |
|---|---|---|---|
| Intercept | −4.511 × 102 *** | 2.28 × 102 *** | −8.62 × 101 *** |
| N 1 | 2.41 × 10−1 *** | 8.03 × 10−2 *** | 1.14 × 10−2 *** |
| SLcos | 2.77 × 100 *** | 1.32 × 100 *** | 2.13 × 10−1 ** |
| Sd | −4.85 × 10−1 | −4.73 × 101 *** | 7.54 × 101 *** |
| Dc | 2.42 × 102 *** | −2.19 × 101 ** | −2.74 × 101 *** |
| MAT | 8.00 × 100 *** | −3.70 × 101 *** | 1.11 × 101 *** |
| MAP | 2.17 × 10−1 *** | 7.29 × 10−2 ** | 3.37 × 10−1 *** |
| Ba | −9.15 × 100 *** | −4.88 × 100 *** | −5.64 × 100 *** |
| LogSigma 2 | 4.97 × 100 *** | 4.97 × 100 *** | 4.74 × 100 *** |
| R2 | 0.42 | 0.33 | 0.19 |
| AIC | 28,369.25 | 30,196.09 | 41,308.93 |
| BIC | 28,424.63 | 30,250.56 | 41,369.01 |
| LogLik | −14,175.62 | −15,089.05 | −20,645.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.; Yan, N.; He, Y.; Wang, J. Application of Climate Sensitivity Transfer Matrix Growth Model in Qinghai Province. Forests 2025, 16, 1695. https://doi.org/10.3390/f16111695
Chen K, Yan N, He Y, Wang J. Application of Climate Sensitivity Transfer Matrix Growth Model in Qinghai Province. Forests. 2025; 16(11):1695. https://doi.org/10.3390/f16111695
Chicago/Turabian StyleChen, Keyi, Ni Yan, Youjun He, and Jianjun Wang. 2025. "Application of Climate Sensitivity Transfer Matrix Growth Model in Qinghai Province" Forests 16, no. 11: 1695. https://doi.org/10.3390/f16111695
APA StyleChen, K., Yan, N., He, Y., & Wang, J. (2025). Application of Climate Sensitivity Transfer Matrix Growth Model in Qinghai Province. Forests, 16(11), 1695. https://doi.org/10.3390/f16111695





