Age-Based Biomass Carbon Estimation and Soil Carbon Assessment in Rubber Plantations Integrating Geospatial Technologies and IPCC Tier 1–2 Guidelines
Abstract
1. Introduction
2. Materials and Methods
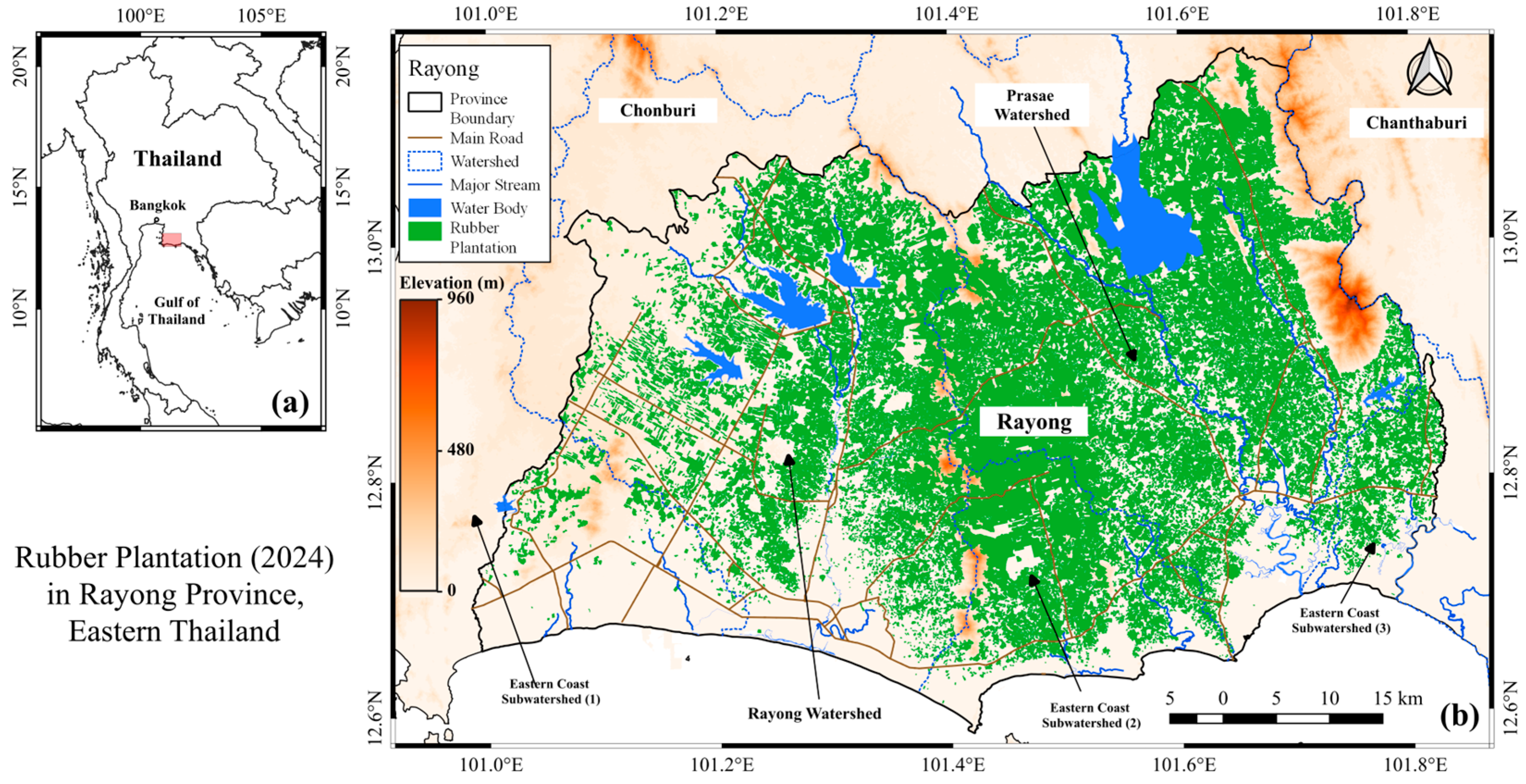
2.1. Study Area
2.2. Data
2.2.1. Landsat Time Series
2.2.2. Land Use and Land Cover (LULC) Data
2.2.3. Soil Series
2.2.4. Rubber Farmer Registration Database
2.2.5. Rubber Tree Inventory Survey Data
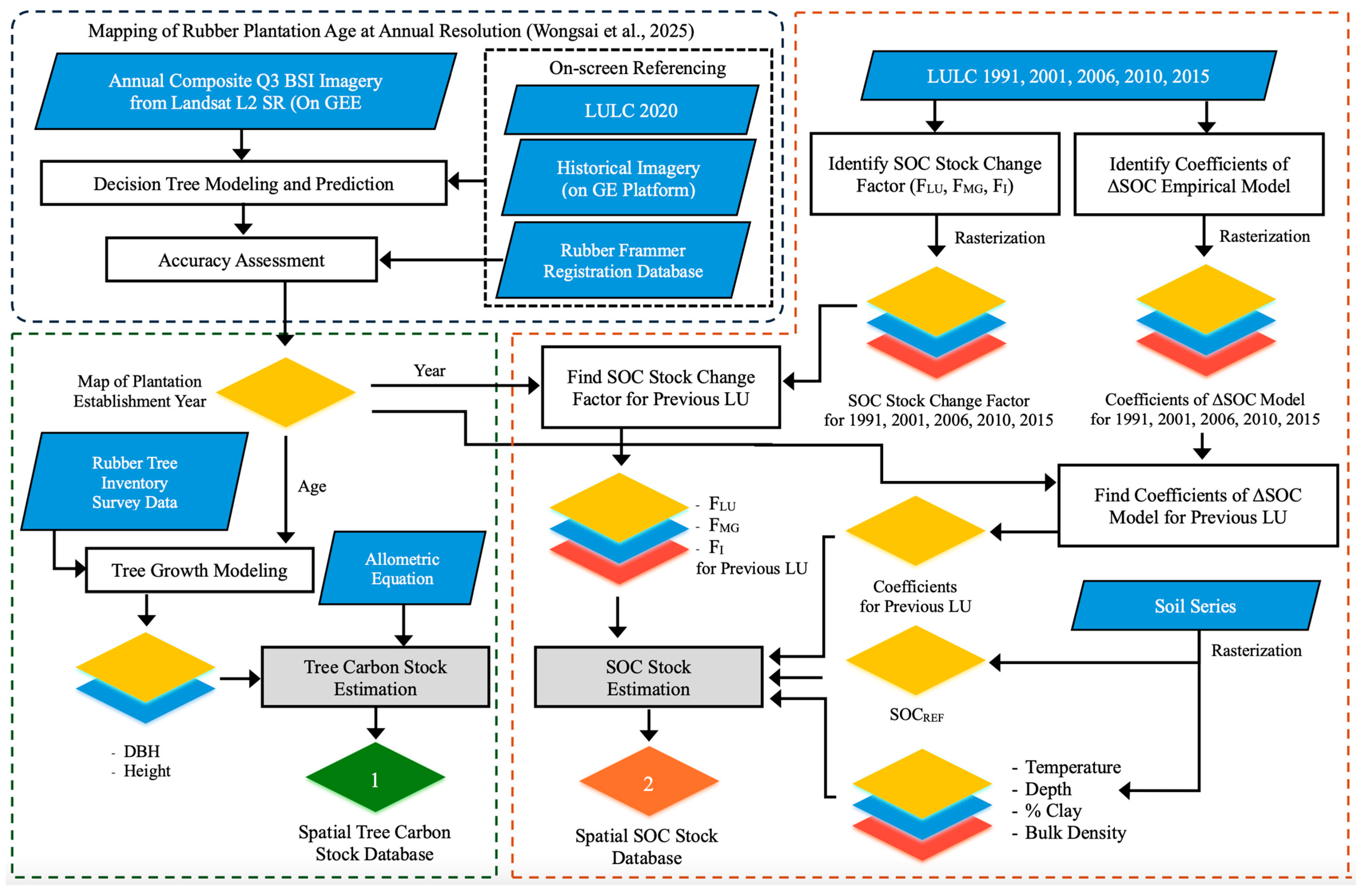
2.3. Tree and Soil Carbon Stock Estimation Framework for Rubber Plantations
2.4. Data Preparation
2.4.1. Annual BSI Time Series for Predicting Rubber Plantation Establishment Year
2.4.2. Soil Organic Carbon Stock Map
2.4.3. Change in Carbon Stock Before and After Land-Use Conversion
2.5. Mapping Para Rubber Stand Age
2.6. Carbon Stock Estimation
2.6.1. Above- and Below-Ground Biomass
- (1)
- Witthawatchutikul and Jirasuktaveekul (1988) model [44]
- (2)
- Chiarawipa et al. (2024) model [45]
- (3)
- Hytönen et al. (2018) model [46]
2.6.2. Estimating Carbon Stock from Rubber Tree Biomass
2.6.3. Inventory of Soil Organic Carbon (SOC)
2.7. Estimation of Overall 95% Confidence Intervals Using the Delta Method
2.7.1. Uncertainty of Tree Carbon Stock
2.7.2. Uncertainty of the Inherited SOC Stock from Pre-Conversion Land Use
2.7.3. Uncertainty of the Changed SOC Stock
3. Results
3.1. Prediction of Rubber Plantation Establishment Year
3.2. Map of Rubber Plantation Age
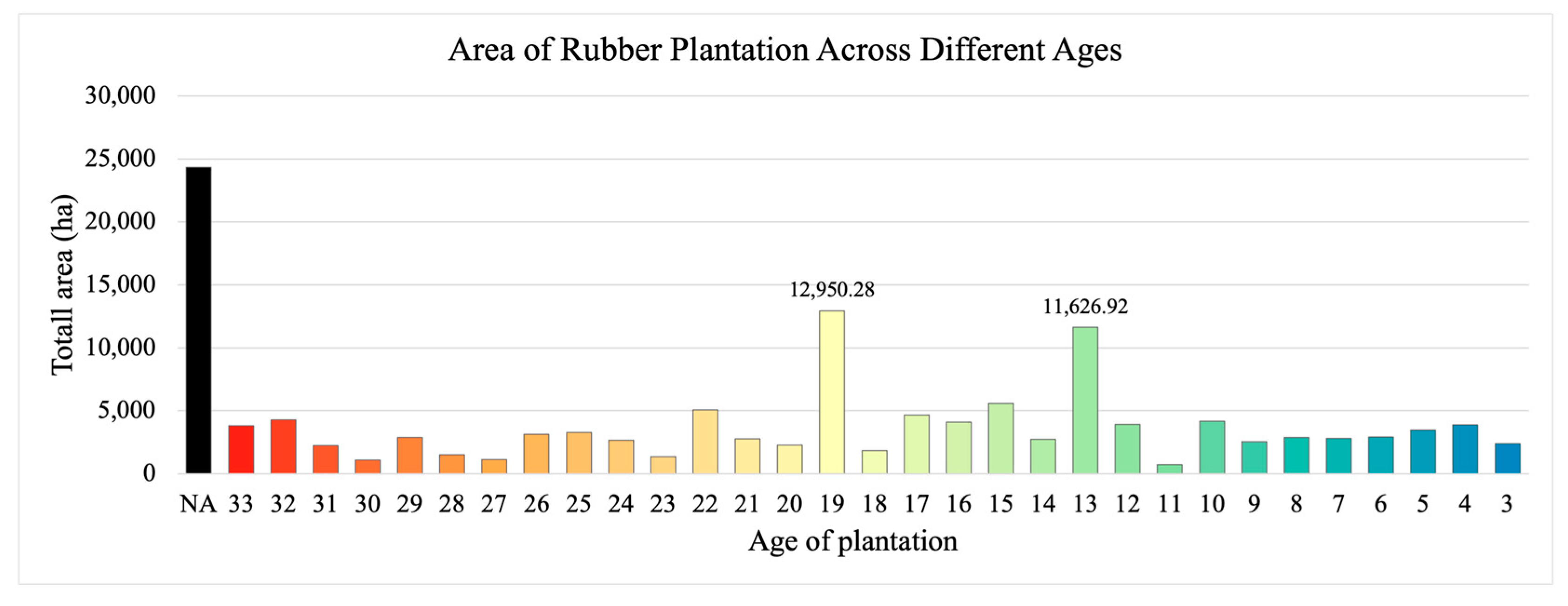
3.3. Rubber Tree Growth Model
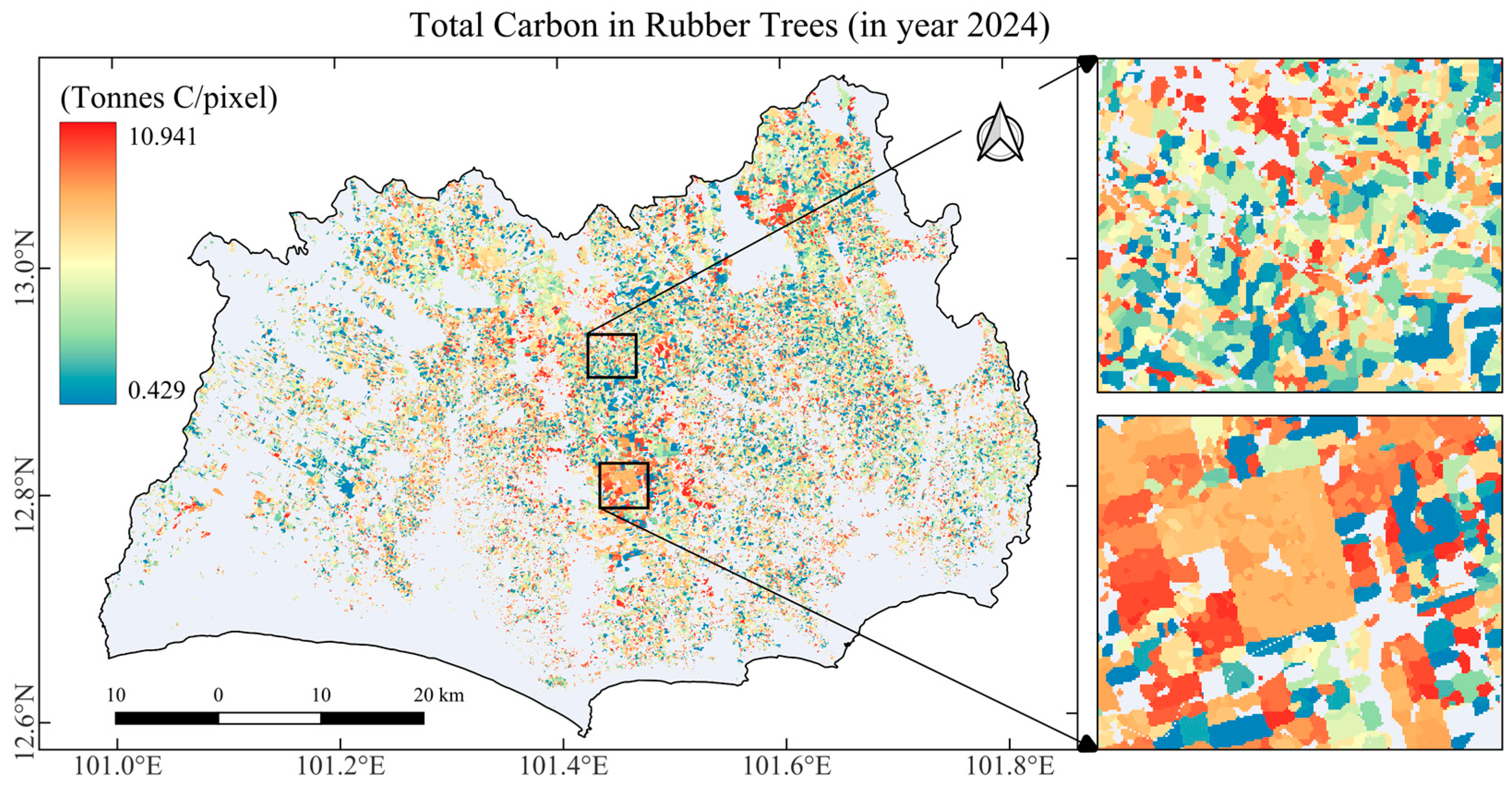
3.4. Carbon Stock in Rubber Plantations
3.4.1. Tree Carbon Stock
3.4.2. Soil Organic Carbon Stock
4. Discussion
4.1. Comparison with IPCC Default Values and Field Studies
4.1.1. Tree Carbon Stock
4.1.2. SOC Stock
4.2. Drivers of Carbon Dynamics
4.2.1. Effects of Spatial Resolution on Age Prediction and Carbon Estimates
4.2.2. Input Data Variability
4.2.3. Age-Related Tree Productivity Declines
4.3. Limitations and Model Uncertainty
4.3.1. Limitations of the Age–DBH/Height Cubic Model
4.3.2. Uncertainty in Tree Carbon and SOC Inventory
4.3.3. Limitations of the Empirical Model
4.4. Ecological Trade-Offs and Management Implications
4.4.1. Ecological Trade-Offs Tied to Carbon Results
4.4.2. Alternative Management Practices
4.4.3. Policy Implications and Uncertainty in SOC Estimates
5. Conclusions
- Tree carbon stocks derived from the Hytönen et al. (2018) model (mean 66.94 t C ha−1) were broadly consistent with national field studies, while improving age-specific estimates compared to IPCC Tier 1 defaults.
- SOC stocks averaged 46.85 t C ha−1, aligning with regional observations but showing much lower modeled than field-based measurements, reflecting limitations of the empirical Ledo et al. (2020) model.
- Provincial inventories confirm that inherited SOC () dominates totals, while plantation-driven SOC changes remain small and highly uncertain.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| IPCC Soil Class | Soil Texture(s) Observed in Study Area | (t C ha−1) |
|---|---|---|
| HAC: High-activity clay | Clay | 40 ± 7% |
| LAC: Low-activity clay | Sandy loam; clay loam mixed with fine sand or sand; fine sandy loam; sandy loam mixed with gravel; clay loam; sandy clay loam mixed with gravel; loam mixed with clay and gravel | 38 ± 5% |
| SAN: Sandy soils | Sandy soils mixed with loam | 27 ± 12% |
| POD: Spodic soils | Not found in the study area | NA |
| VOL: Volcanic soils | Not found in the study area | 70 ± 90% |
| WET: Wetland soils | Excluded from analysis | 49 ± 19% |
| Factor | Pre-Conversion Land Use /Management | IPCC Default | Reference |
|---|---|---|---|
| Long-term cultivated cropland | 0.83 ± 11% | [31] (Table 5.5, pp. 5.27–5.28) | |
| Paddy rice | 1.35 ± 4% | ||
| Perennial/tree cropland | 1.01 ± 25% | ||
| Set-aside (<20 years) | 0.82 ± 17% | ||
| Native forest or grassland (non-degraded) * | 1.00 ± NA | [31] (Table 5.10, pp. 5.44–5.45) | |
| Managed forest | 1.00 ± NA | ||
| Managed grassland | 1.00 ± NA | [31] (Table 6.2, p. 6.6) | |
| Settlements and other lands | 1.00 | Assumed unchanged | |
| Full tillage cropland | 1.00 ± NA | [31] (Table 5.5, pp. 5.27–5.28) | |
| Reduced tillage cropland | 1.04 ± 7% | ||
| No-tillage cropland | 1.10 ± 5% | ||
| Native forest or grassland (non-degraded) | 1.00 ± NA | [31] (Table 5.10, pp. 5.44–5.45) | |
| Nominally managed grassland (non-degraded) * | 1.00 ± NA | [31] (Table 6.2, p. 6.6) | |
| Settlements and other lands | 1.00 | Assumed unchanged | |
| Low fertilization cropland | 0.92 ± 14% | [31] (Table 5.5, pp. 5.27–5.28) | |
| Medium fertilization cropland | 1.00 ± NA | ||
| High fertilization (without manure) | 1.11 ± 10% | ||
| High fertilization (with manure) | 1.44 ± 10% | ||
| Native forest or grassland (non-degraded) | 1.00 ± NA | [31] (Table 5.10, pp. 5.44–5.45) | |
| Nominally managed grassland (non-degraded) * | 1.00 ± NA | [31] (Table 6.2, p. 6.6) | |
| Settlements and other lands | 1.00 | assumed unchanged |
| Previous Land Use | |||
|---|---|---|---|
| Annual crop | Fallow | Gasland | Natural Forest |
| 10−05 | 10−05 | 10−04 | 10−04 |
| Current land use | |||
| Agroforestry | Bioenergy grass | Food (and bio-products) | |
| 10−06 | 10−04 | 10−04 | |
| Density Scenario | Relative Carbon Stock * | Change vs. Baseline ** |
|---|---|---|
| Sparse: 419 trees ha−1 | 83.8 | −16.2% |
| Moderate: 475 trees ha−1 | 95.0 | −5.0% |
| Standard: 500 trees ha−1 | 100.0 | 0.0% |
| Dense: 556 trees ha−1 | 111.2 | +11.2% |
| Very dense: 569 trees ha−1 | 113.8 | +13.8% |
References
- Cornish, K. Similarities and differences in rubber biochemistry among plant species. Phytochemistry 2001, 57, 1123–1134. [Google Scholar] [CrossRef] [PubMed]
- Min, S.; Huang, J.; Waibel, H.; Yang, X.; Cadisch, G. Rubber Boom, Land Use Change and the Implications for Carbon Balances in Xishuangbanna, Southwest China. Ecol. Econ. 2019, 156, 57–67. [Google Scholar] [CrossRef]
- Warren-Thomas, E.; Dolman, P.M.; Edwards, D.P. Increasing demand for natural rubber necessitates a robust sustainability initiative to mitigate impacts on tropical biodiversity. Conserv. Lett. 2015, 8, 230–241. [Google Scholar] [CrossRef]
- de Blécourt, M.; Brumme, R.; Xu, J.; Corre, M.D.; Veldkamp, E. Soil carbon stocks decrease following conversion of secondary forests to rubber (Hevea brasiliensis) plantations. PLoS ONE 2013, 8, e69357. [Google Scholar] [CrossRef]
- Yang, X.; Blagodatsky, S.; Liu, F.; Beckschäfer, P.; Xu, J.; Cadisch, G. Rubber tree allometry, biomass partitioning and carbon stocks in mountainous landscapes of sub-tropical China. For. Ecol. Manag. 2017, 404, 84–99. [Google Scholar] [CrossRef]
- Wang, Y.; Hollingsworth, P.M.; Zhai, D.; West, C.D.; Green, J.M.H.; Chen, H.; Hurni, K.; Su, Y.; Warren-Thomas, E.; Xu, J.; et al. High-resolution maps show that rubber causes substantial deforestation. Nature 2023, 623, 340–346. [Google Scholar] [CrossRef]
- Brahma, B.; Sileshi, G.W.; Nath, A.J.; Das, A.K. Development and evaluation of robust tree biomass equations for rubber tree (Hevea brasiliensis) plantations in India. For. Ecosyst. 2017, 4, 14. [Google Scholar] [CrossRef]
- Sone, K.; Watanabe, N.; Takase, M.; Hosaka, T.; Gyokusen, K. Carbon sequestration, tree biomass growth and rubber yield of PB260 clone of rubber tree (Hevea brasiliensis) in north Sumatra. J. Rubber Res. 2014, 17, 115–127. [Google Scholar]
- Mesike, C.S.; Idoko, S.O. An overview of Carbon sequestration potential of Rubber tree plantations. Clim. Change 2024, 10, e10cc1043. [Google Scholar] [CrossRef]
- Lal, R. Soil carbon sequestration impacts on global climate change and food security. Science 2004, 304, 1623–1627. [Google Scholar] [CrossRef]
- Ledo, A.; Smith, P.; Zerihun, A.; Whitaker, J.; Vicente-Vicente, J.L.; Qin, Z.C.; McNamara, N.P.; Zinn, Y.L.; Llorente, M.; Liebig, M.; et al. Changes in soil organic carbon under perennial crops. Glob. Change Biol. 2020, 26, 4158–4168. [Google Scholar] [CrossRef]
- Don, A.; Schumacher, J.; Freibauer, A. Impact of tropical land-use change on soil organic carbon stocks—A meta-analysis. Glob. Change Biol. 2011, 17, 1658–1670. [Google Scholar] [CrossRef]
- Paustian, K.; Lehmann, J.; Ogle, S.; Reay, D.; Robertson, G.P.; Smith, P. Climate-smart soils. Nature 2016, 532, 49–57. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.K.; Liu, W.; Zhu, X.; Chen, C.; Khan, M.N.; Yang, B.; Jiang, X.J. The detrimental effect of rainforest conversion to rub-ber plantations on soil dissolved organic carbon and C:N stoichiometry, mediated by altered soil biogeochemistry. J. Environ. Manag. 2024, 370, 122965. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.B.; Gifford, R.M. Soil carbon stocks and land use change: A meta-analysis. Glob. Change Biol. 2002, 8, 345–360. [Google Scholar] [CrossRef]
- Liu, Y.; Shen, J.; Zhang, C.; Chen, Z. Impact of rubber-based land use changes on soil properties and carbon pools: A me-ta-analysis. CATENA 2023, 227, 107121. [Google Scholar] [CrossRef]
- Toriyama, J.; Imaya, A.; Hirai, K.; Lim, T.K.; Hak, M.; Kiyono, Y. Effects of forest conversion to rubber plantation and of re-planting rubber trees on soil organic carbon pools in a tropical moist climate zone. Agric. Ecosyst. Environ. 2022, 323, 107699. [Google Scholar] [CrossRef]
- Razaq, M.; Huang, Q.; Wang, F.; Liu, C.; Gnanamoorthy, P.; Liu, C.; Tang, J. Carbon Stock Dynamics in Rubber Plantations Along an Elevational Gradient in Tropical China. Forests 2024, 15, 1933. [Google Scholar] [CrossRef]
- Xu, H.; Pham, T.D.; Wu, Q.; Chai, P.; Lu, D.; Li, D.; Chen, Y. Rubber Plantation Expansion Leads to Increase in Soil Erosion in the Middle Lancang-Mekong River Basin During the Period 2003–2022. Remote Sens. 2025, 17, 2220. [Google Scholar] [CrossRef]
- Charoenjit, K.; Zuddas, P.; Allemand, P.; Pattanakiat, S.; Pachana, K. Estimation of biomass and carbon stock in Para rubber plantations using object-based classification from Thaichote satellite data in Eastern Thailand. J. Appl. Remote Sens. 2015, 9, 096072. [Google Scholar] [CrossRef]
- Fu, Y.; Tan, H.; Kou, W.; Xu, W.; Wang, H.; Lu, N. Estimation of rubber plantation biomass based on variable optimization from Sentinel-2 remote sensing imagery. Forests 2024, 15, 900. [Google Scholar] [CrossRef]
- Tan, H.; Kou, W.; Xu, W.; Wang, L.; Wang, H.; Lu, N. Improved Estimation of Aboveground Biomass in Rubber Plantations Using Deep Learning on UAV Multispectral Imagery. Drones 2025, 9, 32. [Google Scholar] [CrossRef]
- Liang, Y.; Kou, W.; Lai, H.; Wang, J.; Wang, Q.; Xu, W.; Wang, H.; Lu, N. Improved estimation of aboveground biomass in rubber plantations by fusing spectral and textural information from UAV-based RGB imagery. Ecol. Indic. 2022, 142, 109286. [Google Scholar] [CrossRef]
- Chen, B.; Xiao, X.; Wu, Z.; Yun, T.; Kou, W.; Ye, H.; Lin, Q.; Doughty, R.; Dong, J.; Ma, J.; et al. Identifying Establishment Year and Pre-Conversion Land Cover of Rubber Plantations on Hainan Island, China Using Landsat Data during 1987–2015. Remote Sens. 2018, 10, 1240. [Google Scholar] [CrossRef]
- Somching, N.; Wongsai, S.; Wongsai, N.; Koedsin, W. Using machine learning algorithm and Landsat time series to identify establishment year of para rubber plantations: A case study in Thalang district, Phuket Island, Thailand. Int. J. Remote Sens. 2020, 41, 9075–9100. [Google Scholar] [CrossRef]
- Wongsai, S.; Sanpayao, M.; Jirakajohnkool, S.; Wongsai, N. Pixel-Based Mapping of Rubber Plantation Age at Annual Reso-lution Using Supervised Learning for Forest Inventory and Monitoring. Forests 2025, 16, 672. [Google Scholar] [CrossRef]
- Phiri, D.; Simwanda, M.; Salekin, S.; Nyirenda, V.R.; Murayama, Y.; Ranagalage, M. Sentinel-2 Data for Land Cover/Use Mapping: A Review. Remote Sens. 2020, 12, 2291. [Google Scholar] [CrossRef]
- Li, H.; Zhao, L.; Sun, L.; Li, X.; Wang, J.; Han, Y.; Liang, S.; Chen, J. Capability of Phenology-Based Sentinel-2 Composites for Rubber Plantation Mapping in a Large Area with Complex Vegetation Landscapes. Remote Sens. 2022, 14, 5338. [Google Scholar] [CrossRef]
- Ahrends, A.; Hollingsworth, P.M.; Ziegler, A.D.; Fox, J.M.; Chen, H.; Su, Y.; Xu, J. Current trends of rubber plantation expansion may threaten biodiversity and livelihoods. Glob. Environ. Change 2015, 34, 48–58. [Google Scholar] [CrossRef]
- IPCC. 2019 Refinement to the 2006 IPCC Guidelines for National Greenhouse Gas Inventories; IPCC: Geneva, Switzerland, 2019; Available online: https://www.ipcc-nggip.iges.or.jp/public/2019rf/vol4.html (accessed on 19 June 2024).
- IPCC. 2006 IPCC Guidelines for National Greenhouse Gas Inventories; Prepared by the National Greenhouse Gas Inventories Programme; IGES: Kanagawa, Japan, 2006; Available online: https://www.ipcc-nggip.iges.or.jp/public/2006gl/vol4.html (accessed on 14 June 2023).
- Office of Agriculture Economics (OAE). Para Rubber: Total and Tapping Areas, Productivity in Provinces, Regions and Entire Countries in 2023. Available online: https://oae.go.th/uploads/files/2025/06/13/3fab62450dcb2284.pdf (accessed on 10 July 2025).
- Agri-Map: Online Agricultural Mapping System for Proactive Management. Para Rubber Cultivation Area in Rayong Province (2021). Available online: https://agri-map-online.moac.go.th/ (accessed on 10 July 2025).
- Diek, S.; Fornallaz, F.; Schaepman, M.E.; de Jong, R. Barest Pixel Composite for Agricultural Areas Using Landsat Time Series. Remote Sens. 2017, 9, 1245. [Google Scholar] [CrossRef]
- Chiarawipa, R.; Pechkeo, S.; Keawdoung, M.; Prommee, W. Assessment of carbon stock and the potential income of the carbon offset in rubber plantation. Burapha Sci. J. 2012, 17, 91–102. [Google Scholar]
- Nattharom, N.; Roongtawanreongsri, S.; Bumrungsri, S. The economic value of ecosystem services of rubber-based agoforest plantation in south Thailand. J. Sustain. Sci. Manag. 2021, 16, 247–262. [Google Scholar] [CrossRef]
- Wentzel, K. Determination of the overall soil erosion potential in the Nsikazi District (Mpumalanga Province, South Africa) using remote sensing and GIS. Can. J. Remote Sens. 2002, 28, 322–327. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Chen, W.; Liu, L.; Zhang, C.; Wang, J.; Wang, J.; Pan, Y. Monitoring the seasonal bare soil areas in Beijing using multi-temporal TM images. Int. Geosci. Remote Sens. Symp. 2004, 5, 3379–3382. [Google Scholar] [CrossRef]
- Jamalabd, M.S.; Abkar, A.A. Forest Canopy Density Monitoring, Using Satellite Images. In Proceedings of the International Society for Photogrammetry and Remote Sensing (ISPRS)—ISPRS Congress, Istanbul, Turkey, 12–23 July 2004; pp. 12–23. Available online: https://www.isprs.org/proceedings/xxxv/congress/comm7/papers/48.pdf (accessed on 7 August 2025).
- Nguyen, C.T.; Chidthaisong, A.; Kieu Diem, P.; Huo, L.-Z. A Modified Bare Soil Index to Identify Bare Land Features during Agricultural Fallow-Period in Southeast Asia Using Landsat 8. Land 2021, 10, 231. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, D.; Zhang, Z.; Liu, Q.; Zhang, D.; Xu, Z. Modeling Free Branch Growth with the Competition Index for a Larix principis-rupprechtii Plantation. Forests 2023, 14, 1495. [Google Scholar] [CrossRef]
- Seo, Y.; Lee, D.; Choi, J. Developing and Comparing Individual Tree Growth Models of Major Coniferous Species in South Korea Based on Stem Analysis Data. Forests 2023, 14, 115. [Google Scholar] [CrossRef]
- Lolupiman, T.; Nakhapakorn, K.; Ussawarujikulchai, A.; Kanchanasoontorn, S.; Jirakajohnkool, S. Estimation of above ground carbon stock in para rubber plantation by application of remote sensing, Rayong province. Thai Sci. Technol. J. 2016, 24, 914–926. Available online: https://li01.tci-thaijo.org/index.php/tstj/article/view/67019/54717 (accessed on 7 August 2025). (In Thai).
- Chiarawipa, R.; Somboonsuke, B.; Wandao, S.; Thongsong, A.; Jirakajohnkool, S. Investigating Drivers Impacting Carbon Stock and Carbon Offset in a Large-Scale Rubber Plantation in the Middle South of Thailand. Trop. Life Sci. Res. 2024, 35, 139–160. [Google Scholar] [CrossRef]
- Hytönen, J.; Kaakkurivaara, N.; Kaakkurivaara, T.; Nurmi, J. Biomass equations for rubber tree (Hevea brasiliensis) components in Southern Thailand. J. Trop. For. Sci. 2018, 30, 588–5966. [Google Scholar] [CrossRef]
- Goslee, K.; Walker, S.M.; Grais, A.; Murray, L.; Casarim, F.; Brown, S. Winrock’s REDD+ Technical Guidance, Module C-CS: Calculations for Estimating Carbon Stocks; Winrock International: Arlington, VA, USA, 2013; Available online: https://winrock.org/wp-content/uploads/2018/08/Winrock-Guidance-on-calculating-carbon-stocks-1.pdf (accessed on 11 July 2025).
- Petaja, G.; Bārdule, A.; Zalmanis, J.; Lazdiņa, D.; Daugaviete, M.; Skranda, I.; Zvaigzne, Z.A.; Purviņa, D. Changes in Organic Carbon Stock in Soil and Whole Tree Biomass in Afforested Areas in Latvia. Plants 2023, 12, 2264. [Google Scholar] [CrossRef] [PubMed]
- Ledo, A.; Hillier, J.; Smith, P.; Aguilera, E.; Blagodatskiy, S.; Brearley, F.Q.; Datta, A.; Diaz-Pines, E.; Don, A.; Dondini, M.; et al. A global, empirical, harmonised dataset of soil organic carbon changes under perennial crops. Sci. Data. 2019, 6, 57. [Google Scholar] [CrossRef] [PubMed]
- Siddique, I.A.; Grados, D.; Chen, J.; Lærke, P.E.; Jørgensen, U. Soil organic carbon stock change following perennialization: A meta-analysis. Agron. Sustain. Dev. 2023, 43, 58. [Google Scholar] [CrossRef]
- Næss, J.S.; Hu, X.; Gvein, M.H.; Iordan, C.-M.; Cavalett, O.; Dorber, M.; Giroux, B.; Cherubini, F. Climate change mitigation potentials of biofuels produced from perennial crops and natural regrowth on abandoned and degraded cropland in Nordic countries. J. Environ. Manag. 2023, 325, 116474. [Google Scholar] [CrossRef]
- Martani, E.; Ferrarini, A.; Hastings, A.; Amaducci, S. Soil Organic Carbon Significantly Increases When Perennial Biomass Plantations Are Reverted Back to Annual Arable Crops. Agronomy 2023, 13, 447. [Google Scholar] [CrossRef]
- Oehlert, G.W. A Note on the Delta Method. Am. Stat. 1992, 46, 27–29. [Google Scholar] [CrossRef]
- Ver Hoef, J.M. Who Invented the Delta Method? Am. Stat. 2012, 66, 124–127. [Google Scholar] [CrossRef]
- Laganiére, J.; Angers, D.A.; Paré, D. Carbon accumulation in agricultural soils after afforestation: A meta-analysis. Glob. Change Biol. 2010, 16, 439–453. [Google Scholar] [CrossRef]
- Zhang, K.; Dang, H.; Tan, S.; Cheng, X.; Zhang, Q. Change in soil organic carbon following the ‘Grain-for-Green’ programme in China. Land Degrad. Dev. 2010, 21, 13–23. [Google Scholar] [CrossRef]
- Dou, F.G.; Hons, F.M.; Ocumpaugh, W.R.; Read, J.C.; Hussey, M.A.; Muir, J.P. Soil Organic Carbon Pools Under Switchgrass Grown as a Bioenergy Crop Compared to Other Conventional Crops. Pedosphere 2013, 23, 409–416. [Google Scholar] [CrossRef]
- Blagodatsky, S.; Xu, J.; Cadisch, G. Carbon balance of rubber (Hevea brasiliensis) plantations: A review of uncertainties at plot, landscape and production level. Agric. Ecosyst. Environ. 2016, 221, 8–19. [Google Scholar] [CrossRef]
- Bridhikitti, A. Soil and biomass carbon stocks in forest and agricultural lands in tropical climates. Songklanakarin J. Sci. Technol. 2017, 39, 697–707. [Google Scholar] [CrossRef]
- Saengruksawong, C.; Khamyong, S.; Anongrak, N.; Pinthong, J. Growths and carbon stocks of Para rubber plantations on Phonpisai soil series in Northeastern Thailand. Rubber Thai J. 2012, 1, 1–18. [Google Scholar]
- Saengruksawong, C.; Khamyong, S.; Anongrak, N.; Pinthong, J. Growths and carbon stocks in rubber plantations on Chakkarat soil series, Northeastern Thailand. Suranaree J. Sci. Technol. 2012, 19, 271–278. [Google Scholar]
- Sudjarit, W. Estimation of soil carbon flux in cultivated areas with Aquilaria crassna, Hevea brasiliensis, and Oryza sativa L. J. Sci. Technol. Mahasarakham Univ. 2014, 34, 161–170. (In Thai) [Google Scholar]
- Qin, Z.; Dunn, J.B.; Kwon, H.; Mueller, S.; Wander, M.M. Soil carbon sequestration and land use change associated with biofuel production: Empirical evidence. GCB Bioenergy 2016, 8, 66–80. [Google Scholar] [CrossRef]
- McGowan, A.R.; Nicoloso, R.S.; Diop, H.E.; Roozeboom, K.L.; Rice, C.W. Soil Organic Carbon, Aggregation, and Microbial Community Structure in Annual and Perennial Biofuel Crops. Agronomy 2019, 111, 128–142. [Google Scholar] [CrossRef]
- Martani, E.; Ferrarini, A.; Serra, P.; Pilla, M.; Marcone, A.; Amaducci, S. Belowground biomass C outweighs soil organic C of perennial energy crops: Insights from a long-term multispecies trial. GCB Bioenergy 2021, 13, 459–472. [Google Scholar] [CrossRef]
- Dheri, G.S.; Lal, R.; Moonilall, N.I. Soil carbon stocks and water stable aggregates under annual and perennial biofuel crops in central Ohio. Agric. Ecosyst. Environ. 2022, 324, 107715. [Google Scholar] [CrossRef]
- Suleymanov, A.; Shagaliev, R.; Belan, L.; Bogdan, E.; Tuktarova, I.; Nagaev, E.; Muftakhina, D. Forest growing stock volume mapping with accompanying uncertainty in het-erogeneous landscapes using remote sensing data. Earth Sci. Inform. 2024, 17, 5359–5369. [Google Scholar] [CrossRef]
- Suleymanov, A.; Bogdan, E.; Gaysin, I.; Volkov, A.; Tuktarova, I.; Belan, L.; Shagaliev, R. Spatial high-resolution modelling and uncertainty assessment of forest growing stock volume based on remote sensing and environmental covariates. For. Ecol. Manag. 2024, 554, 121676. [Google Scholar] [CrossRef]
- Qiu, T.; Aravena, M.C.; Andrus, R.; Ascoli, D.; Bergeron, Y.; Berretti, R.; Bogdziewicz, M.; Boivin, T.; Bonal, R.; Caignard, T.; et al. Is there tree senescence? The fecundity evidence. Proc. Natl. Acad. Sci. USA 2021, 118, e2106130118. [Google Scholar] [CrossRef] [PubMed]
- Cannon, C.H.; Piovesan, G.; Munné-Bosch, S. Old and ancient trees are life history lottery winners and vital evolutionary resources for long-term adaptive capacity. Nat. Plants 2022, 8, 136–145. [Google Scholar] [CrossRef]
- Weiner, J.; Thomas, S.C. The nature of tree growth and the “age-related decline in forest productivity”. OIKOS 2001, 94, 374–376. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, L.; Chen, J.; Ju, W.; Feng, X.; Wu, W. Relationships between net primary productivity and stand age for several forest types and their influence on China’s carbon balance. J. Environ. Manag. 2011, 92, 1651–1662. [Google Scholar] [CrossRef]
- Vangi, E.; Dalmonech, D.; Cioccolo, E.; Marano, G.; Bianchini, L.; Puchi, P.F.; Grieco, E.; Cescatti, A.; Colantoni, A.; Chirici, G.; et al. Stand age diversity (and more than climate change) affects forests’ resilience and stability, although unevenly. J. Environ. Manag. 2024, 366, 121822. [Google Scholar] [CrossRef]
- Tian, L.; Tao, Y.; Joanna, S.; Mäkelä, A.; Li, M. How forest age impacts on net primary productivity: Insights from future mul-ti-scenarios. For. Ecosyst. 2024, 11, 100228. [Google Scholar] [CrossRef]
- Casella, G.; Berger, R.L. Statistical Inference, 2nd ed.; Duxbury Press: Pacific Grove, CA, USA, 2002. [Google Scholar]
- Doetterl, S.; Stevens, A.; Six, J.; Merckx, R.; Van Oost, K.; Casanova Pinto, M.; Casanova-Katny, A.; Muñoz, C.; Boudin, M.; Zagal Venegas, E.; et al. Soil carbon storage controlled by interactions between geochemistry and climate. Nat. Geosci. 2015, 8, 780–783. [Google Scholar] [CrossRef]
- Zinn, Y.L.; Lal, R.; Resck, D.V.S. Changes in soil organic carbon stocks under agriculture in Brazil. Soil Till. Res. 2005, 84, 28–40. [Google Scholar] [CrossRef]
- Gray, J.M.; Bishop, T.F.A.; Wilson, B.R. Factors Controlling Soil Organic Carbon Stocks with Depth in Eastern Australia. Soil Sci. Soc. Am. J. 2015, 79, 1741–1751. [Google Scholar] [CrossRef]
- Guillaume, T.; Damris, M.; Kuzyakov, Y. Losses of soil carbon by converting tropical forest to plantations: Erosion and de-composition estimated by δ13C. Glob. Change Biol. 2015, 21, 3548–3560. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Ou, X.; Chen, D.; Wu, J. Rubber Intercropped with Coffea liberica Increases Carbon and Nitrogen Stocks in Soils in Xishuangbanna, China. Forests 2025, 16, 13. [Google Scholar] [CrossRef]
- Guardiola-Claramonte, M.; Troch, P.A.; Ziegler, A.D.; Giambelluca, T.W.; Durcik, M.; Vogler, J.B.; Nullet, M.A. Local hydrologic effects of introducing non-native vegetation in a tropical catchment. Ecohydrology 2008, 1, 13–22. [Google Scholar] [CrossRef]
- Ziegler, A.D.; Fox, J.M.; Xu, J. The rubber juggernaut. Science 2009, 324, 1024–1025. [Google Scholar] [CrossRef]
- Yuan, X.; Yang, B.; Liu, W.; Wu, J.; Li, X. Intercropping with cash crops promotes sustainability of rubber agroforestry: Insights from litterfall production and associated carbon and nutrient fluxes. Eur. J. Agron. 2024, 154, 127071. [Google Scholar] [CrossRef]
- Villamor, G.B.; Le, W.B.; Djanibekov, U.; Noordwijk, M.V.; Vlek, P.L.G. Biodiversity in rubber agroforests, carbon emissions, and rural livelihoods: An agent-based model of land-use dynamics in lowland Sumatra. Environ. Model. Softw. 2014, 61, 151–165. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations (FAO). World Reference Base for Soil Resources. 2006. Available online: https://www.fao.org/3/a0510e/a0510e.pdf (accessed on 22 January 2025).
- Chicco, D.; Warrens, M.J.; Jurman, G. The Matthews Correlation Coefficient (MCC) is More Informative Than Cohen’s Kappa and Brier Score in Binary Classification Assessment. IEEE Access 2021, 9, 78368–78381. [Google Scholar] [CrossRef]
- Powers, D.M.W. What the F-Measure Doesn’t Measure: Features, Flaws, Fallacies and Fixes. arXiv 2015, arXiv:1503.06410. [Google Scholar] [CrossRef]
- Frosst, N.; Hinton, G. Distilling a Neural Network Into a Soft Decision Tree. arXiv 2017, arXiv:1711.09784. [Google Scholar] [CrossRef]



| Model | Mean | SD | Median | IQR | Min–Max |
|---|---|---|---|---|---|
| Witthawatchutikul and Jirasuktaveekul (1998) | 220.0 | 122.9 | 225.8 | 208.7 | 15.9–502.2 |
| Chiarawipa et al. (2024) | 242.4 | 134.9 | 241.2 | 202.9 | 22.8–609.1 |
| Hytönen et al. (2018) | 257.0 | 159.3 | 249.4 | 238.3 | 15.0–715.5 |
| Estimated Method | Carbon Stock (t C ha−1) | 95% Confidence Interval (t C ha−1) | Relative Uncertainty |
|---|---|---|---|
| Witthawatchutikul and Jirasuktaveekul (1988) | 58.40 | 53.59–63.73 | –8.2%, +9.1% |
| Chiarawipa et al. (2024) | 62.80 | 55.77–69.83 | ±11.2% |
| Hytönen et al. (2018) | 66.94 | 58.19–75.69 | ±13.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jirakajohnkool, S.; Wongsai, S.; Sanpayao, M.; Wongsai, N. Age-Based Biomass Carbon Estimation and Soil Carbon Assessment in Rubber Plantations Integrating Geospatial Technologies and IPCC Tier 1–2 Guidelines. Forests 2025, 16, 1652. https://doi.org/10.3390/f16111652
Jirakajohnkool S, Wongsai S, Sanpayao M, Wongsai N. Age-Based Biomass Carbon Estimation and Soil Carbon Assessment in Rubber Plantations Integrating Geospatial Technologies and IPCC Tier 1–2 Guidelines. Forests. 2025; 16(11):1652. https://doi.org/10.3390/f16111652
Chicago/Turabian StyleJirakajohnkool, Supet, Sangdao Wongsai, Manatsawee Sanpayao, and Noppachai Wongsai. 2025. "Age-Based Biomass Carbon Estimation and Soil Carbon Assessment in Rubber Plantations Integrating Geospatial Technologies and IPCC Tier 1–2 Guidelines" Forests 16, no. 11: 1652. https://doi.org/10.3390/f16111652
APA StyleJirakajohnkool, S., Wongsai, S., Sanpayao, M., & Wongsai, N. (2025). Age-Based Biomass Carbon Estimation and Soil Carbon Assessment in Rubber Plantations Integrating Geospatial Technologies and IPCC Tier 1–2 Guidelines. Forests, 16(11), 1652. https://doi.org/10.3390/f16111652









