Integrating Social Conflicts into Sustainable Decision-Making of the Forest-to-Lumber Supply Chain
Abstract
1. Introduction
- (i)
- How do logistical decisions in the forest-to-lumber supply chain influence exposure to territorial conflicts in socially sensitive regions?
- (ii)
- Which operational strategies can balance economic, environmental, and social sustainability in conflict-affected territories?
1.1. Contributions of This Study
- (1)
- It introduced a novel social conflict exposure index for the forest-to-lumber supply chain. The index is derived from region-specific historical data and expert weightings, providing a quantitative measure of territorial risk not addressed in previous optimization models
- (2)
- It integrated this social dimension into a multi-objective mixed-integer linear programming (MILP) model, together with economic and environmental objectives, allowing for an explicit balance among the three pillars of sustainability.
- (3)
- It presented extensive computational experiments, including trade-off analyses and sensitivity tests, to evaluate how changes in the conflict exposure index affect network configuration, supply chain efficiency, and social vulnerability.
1.2. Literature Review
2. Materials and Methods
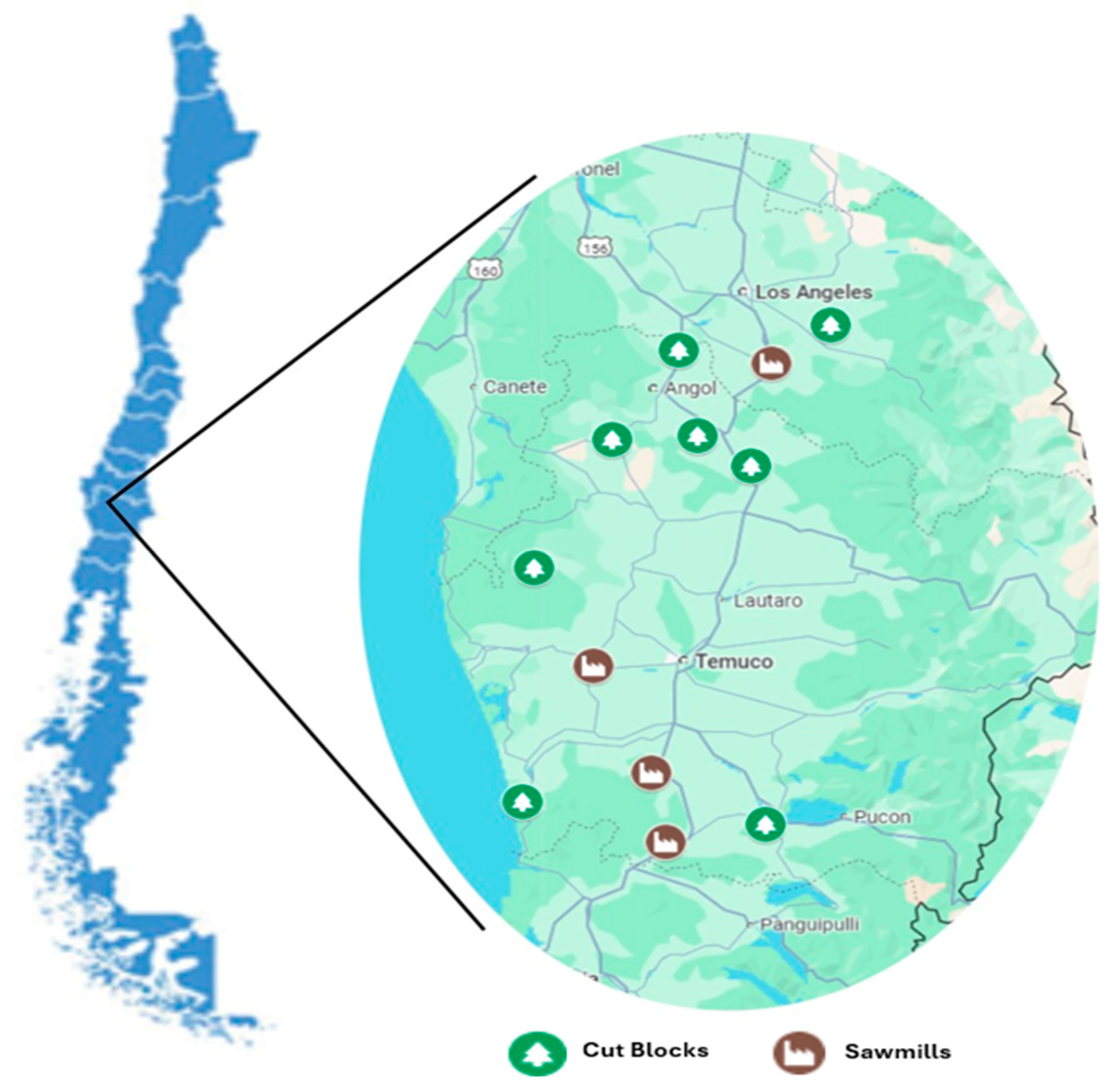
2.1. Study Area
2.2. Forest-to-Lumber Supply Chain
- Data collection: Secondary information was compiled from news articles, institutional reports, and historical records of events associated with the supply chain’s nodes and arcs.
- Event classification: Events were grouped into 14 categories, including fire, armed attack, machinery burning, truck burning, occupation, police action, court of guarantee, communiqués, roadblocks, threats, explosions, fatalities, protests, and robberies.
- Severity weighting: Conflict severity weights were established through a combination of secondary data analysis and expert assessment. Three professionals with experience in Chile’s southern macrozone participated in this process: two logistics managers from the forestry sector and one territorial conflict analyst. These experts were selected for their extensive, on-the-ground knowledge of conflict-related disruptions affecting forest operations.
- Each expert independently assigned severity scores on a 0–10 scale to the 14 event types, considering three main criteria: (i) operational impact, (ii) frequency of occurrence, and (iii) potential risk escalation. To ensure consistency, a comparative analysis was carried out, and final weights were obtained by averaging the scores. This method provided a balanced representation of both technical and territorial perspectives. Table 2 summarizes the assigned weights.
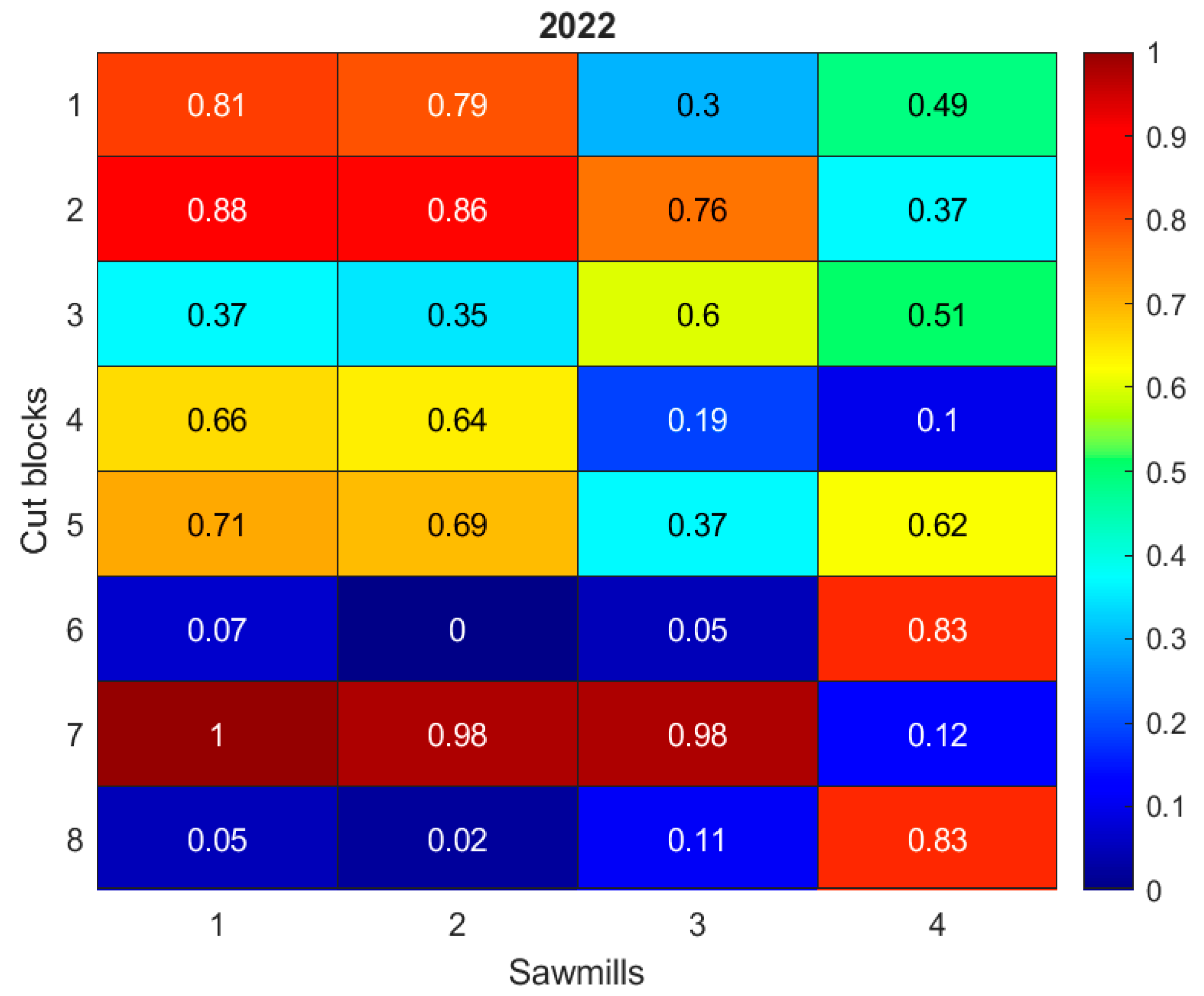
- Conflict index calculation: The total degree of exposure to conflict for each arc was computed using Equation (1), which aggregates the weighted number of events:
- 6.
- Normalization: The normalized exposure index () is obtained by dividing each arc’s total conflict score by the maximum value observed across all arcs, as shown in Equation (2). This normalization makes the values dimensionless and comparable across all routes, enabling consistent integration into the optimization model’s third objective function (z3), which minimizes social conflict risk along transportation routes.
2.3. Mathematical Model
2.4. Computational Experiments
2.4.1. Experiment I—Multi-Objective Optimization with a Focus on Territorial Sustainability
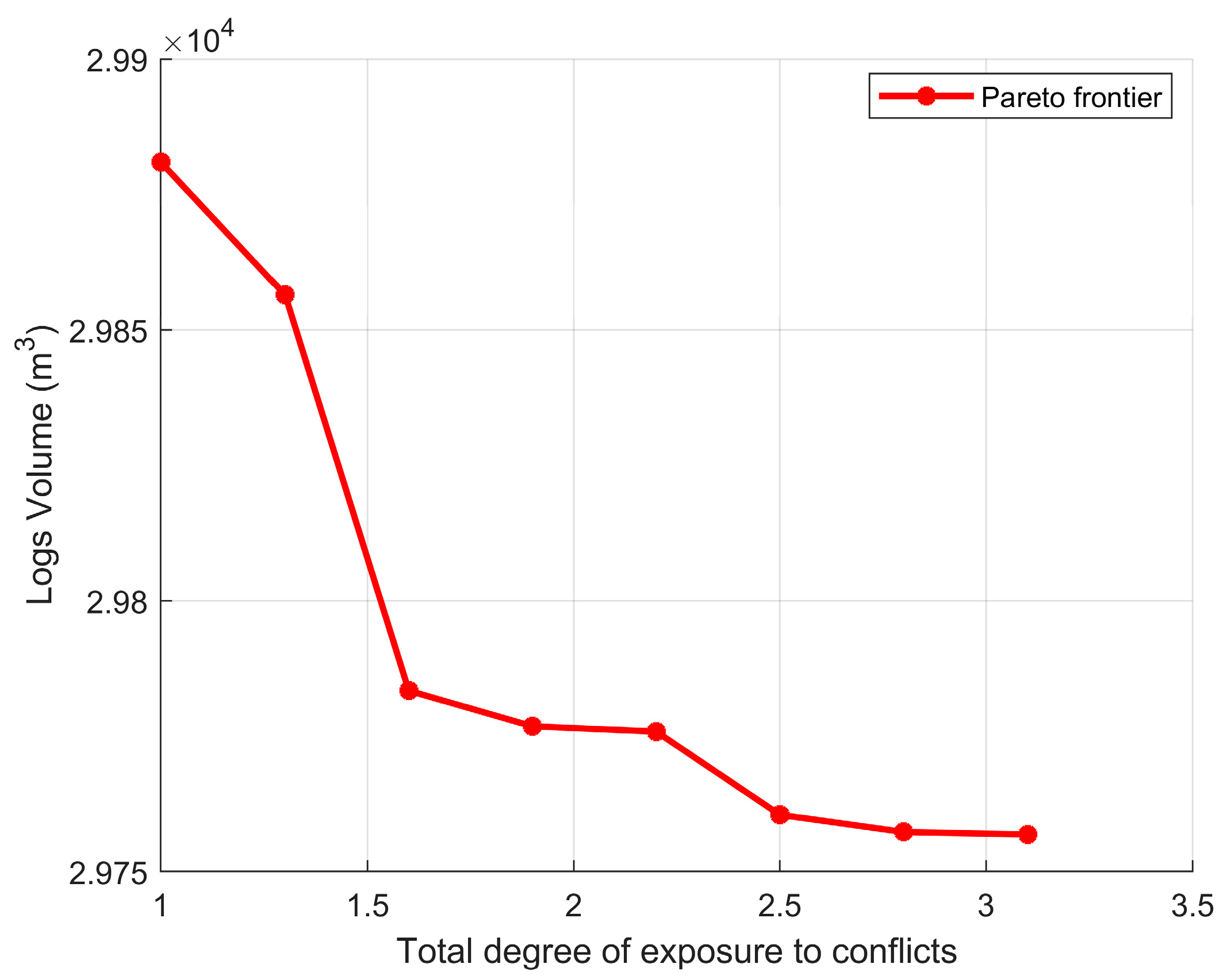
- Experiment I-A: Logs consumed vs. territorial exposure to social conflicts (z1 vs. z3)Objective: Examine how minimizing log consumption (z1) is affected when the degree of exposure to social conflicts (z3) is progressively constrained.Method: ε-constraint with z1 as the primary objective, z3 as the constrained objective.
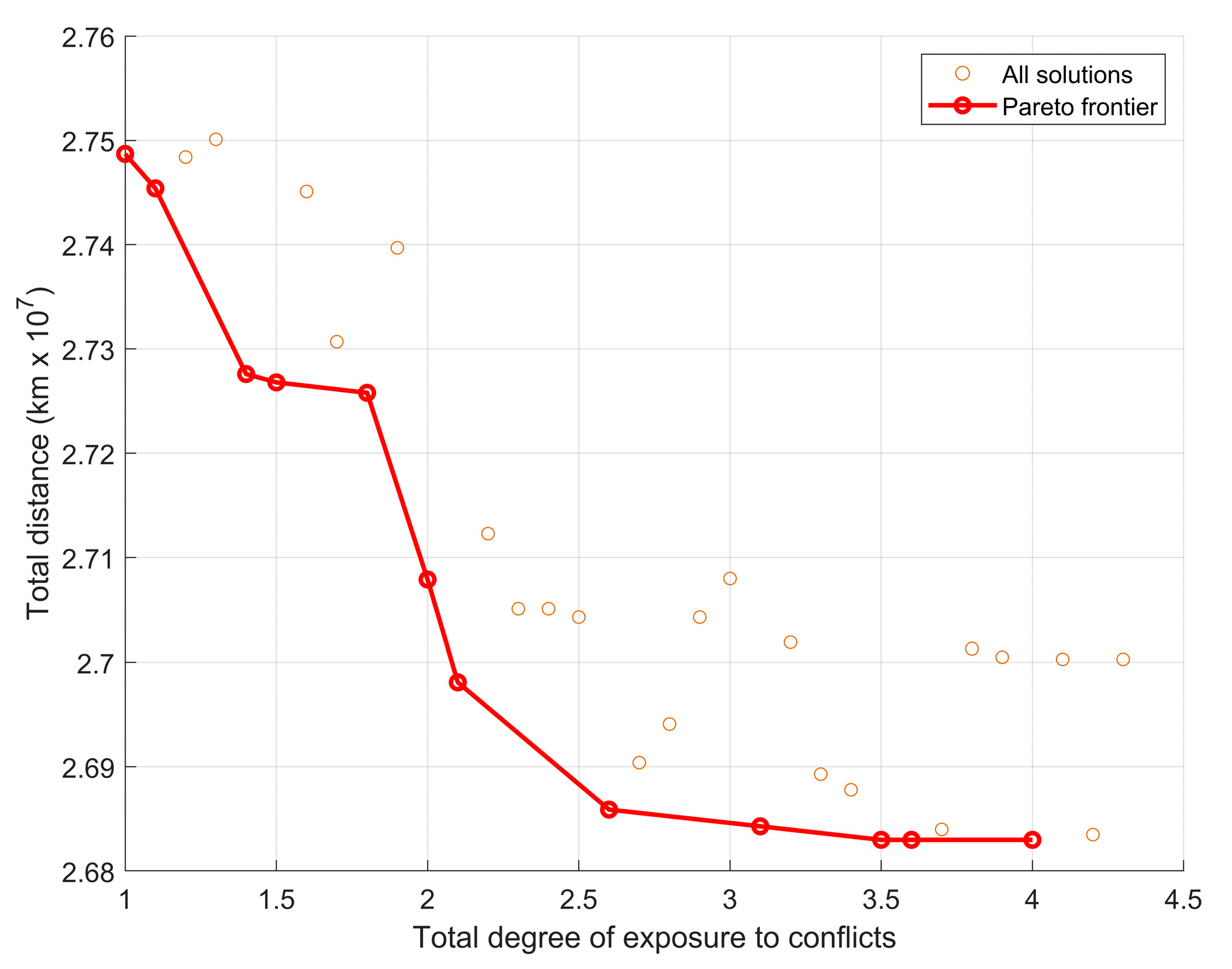
- Experiment I-B: Transportation distance vs. territorial exposure to social conflicts (z2 vs. z3)Objective: Explore trade-offs between minimizing transportation distance (z2) and reducing exposure to social conflicts (z3).Method: ε-constraint with z2 as the primary objective, z3 as the constrained objective.
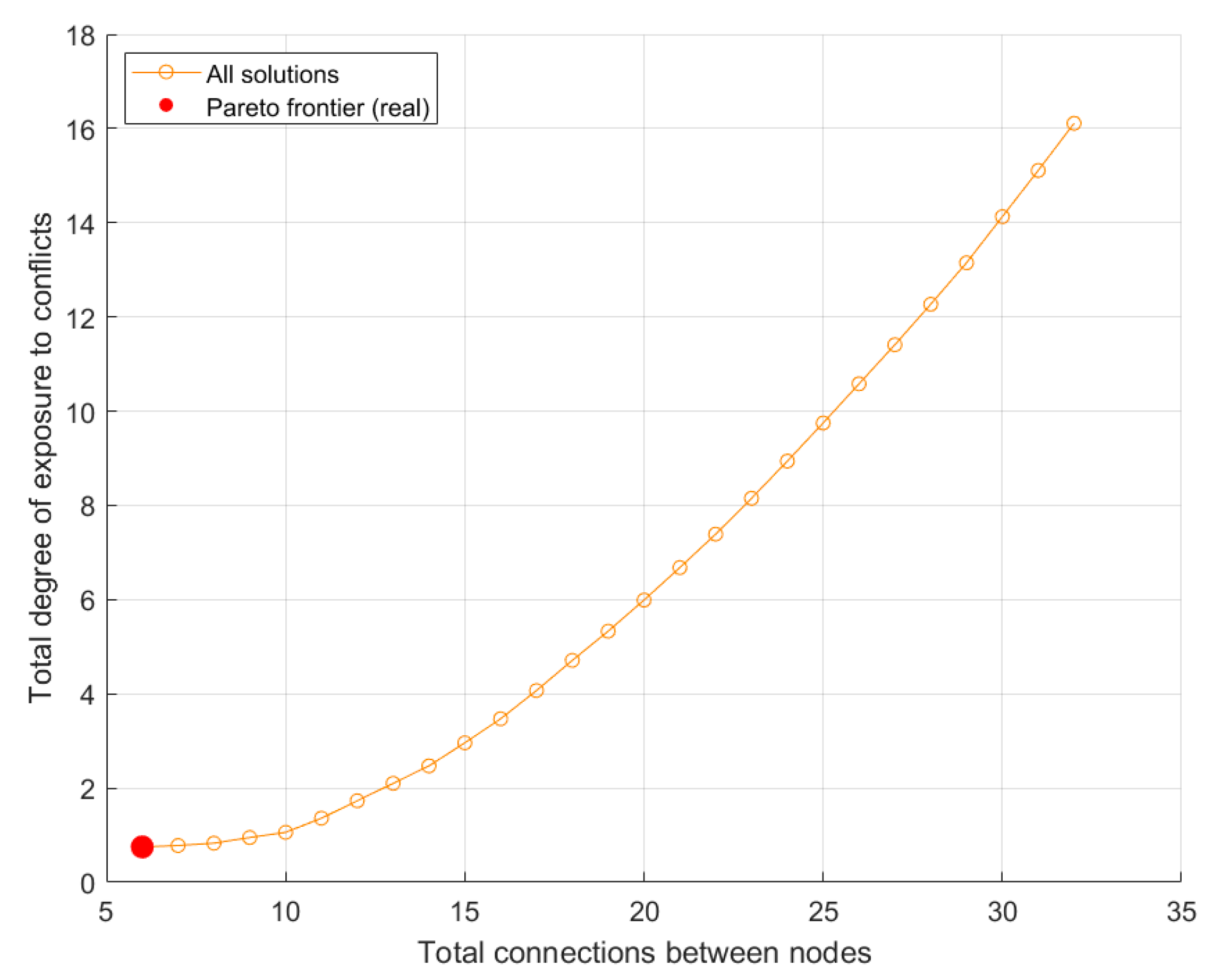
- Experiment I-C: Territorial exposure to social conflicts vs. number of active connections (z3 vs. z4)Objective: Analyze the relationship between the exposure to social conflicts (z3) and the number of active connections (z4).Method: ε-constraint with z3 as the primary objective, z4 as the constrained objective.
2.4.2. Experiment II—Strategic Priorities Analysis
- z1: log consumption (economic)
- z5: surplus products (economic)
- z6: cutting loss (environmental)
2.4.3. Experiment III—Individual Evaluation of Performance Measure
- Six supply scenarios: variations in spatial distribution of log availability.
- Four demand scenarios: variations in product type requirements.
- Supply instances:
- Homogeneous Supply (units)
- Random Supply (units)
- Homogeneous Log Supply in 2 Clusters (units)
- Normally Distributed Log Supply in 2 Clusters (units)
- Homogeneous Log Supply in 3 Clusters (units)
- Normally Distributed Log Supply in 3 Clusters (units)
- Demand scenarios:
- Homogeneous Demand (units)
- Demand Concentrated on Lower-Volume Products (units)
- Demand Concentrated on Higher-Volume Products (units)
- Demand Concentrated on Medium-Volume Products (units)
3. Results
3.1. Social Conflicts in the Southern Macrozone
3.2. Solution Method
3.3. Computational Results
3.3.1. Experiment I, Multi-Objective Optimization with a Focus on Territorial Sustainability
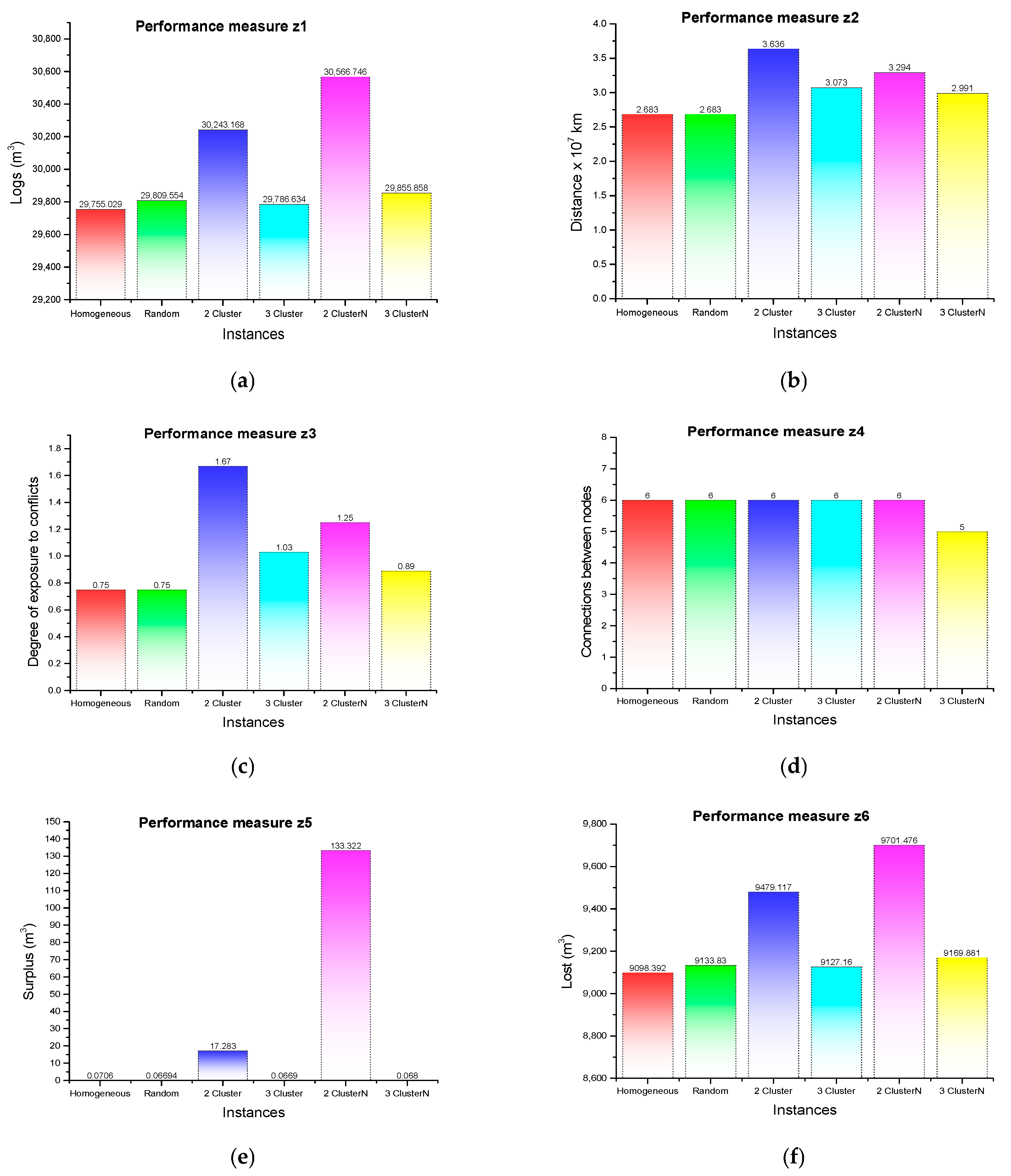
3.3.2. Experiment II, Strategic Priorities Analysis
- z1: log consumption (economic).
- z5: surplus products (economic).
- z6: cutting loss (environmental).
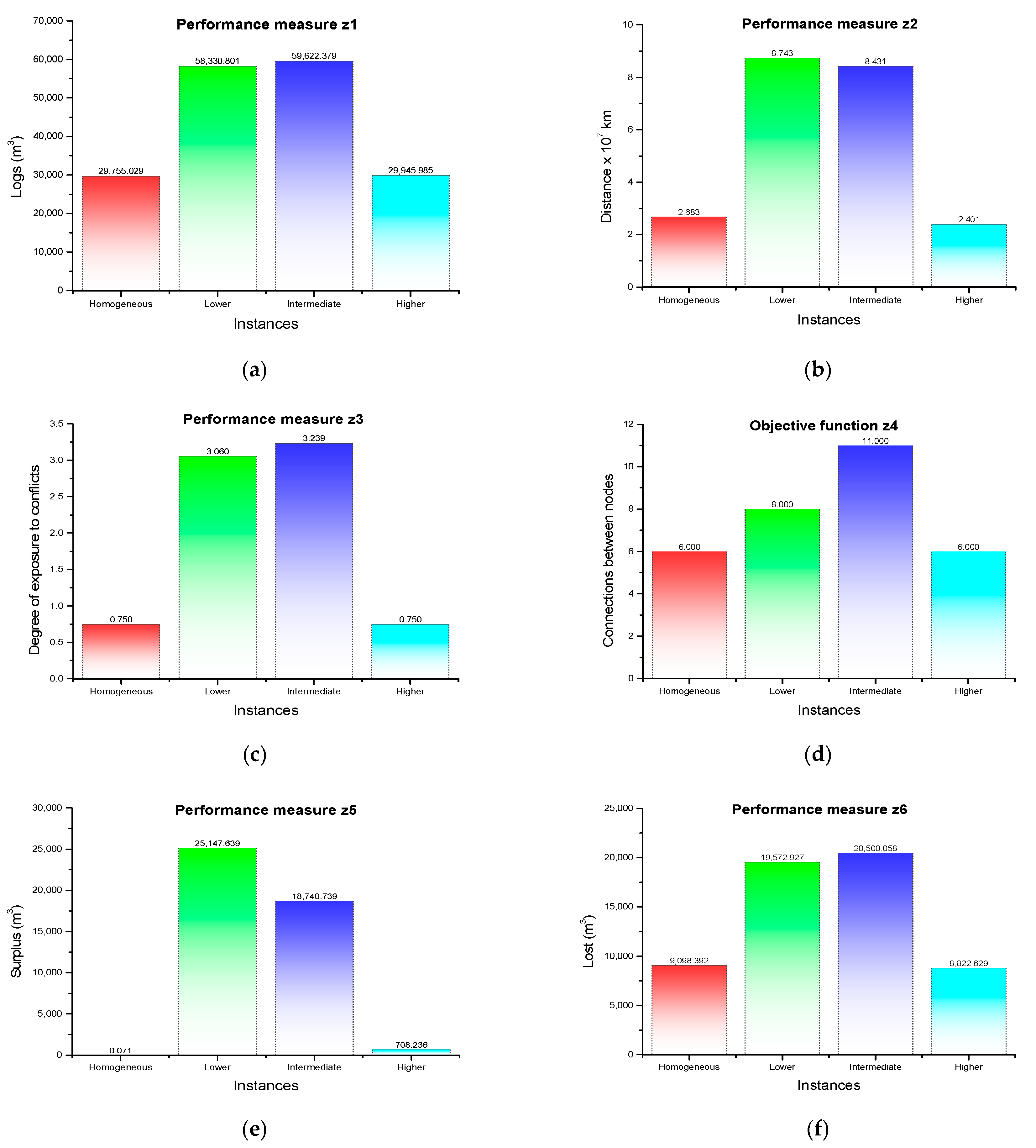
3.3.3. Experiment III, Individual Evaluation of Performance Measures
- Six supply scenarios: variations in spatial distribution of log availability.
- Four demand scenarios: variations in product type requirements.
4. Discussion
4.1. Discussion of Experiment I: Multi-Objective Optimization with ε-Constraint Method
4.2. Discussion of Experiment II: Strategic Priorities Analysis
4.3. Discussion of Experiment III: Individual Evaluation of Performance Measures
4.4. Limitations and Projections of the Study
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beamon, B.M. Supply Chain Design and Analysis: Models and Methods. Int. J. Prod. Econ. 1998, 55, 281–294. [Google Scholar] [CrossRef]
- D’Amours, S.; Rönnqvist, M.; Weintraub, A. Using Operational Research for Supply Chain Planning in the Forest Products Industry. INFOR Inf. Syst. Oper. Res. 2008, 46, 265–281. [Google Scholar] [CrossRef]
- Rönnqvist, M. Optimization in Forestry. Math. Program. 2003, 97, 267–284. [Google Scholar] [CrossRef]
- Weintraub, A.; Romero, C.; Bjørndal, T.; Epstein, R.; Miranda, J. Handbook of Operations Research in Natural Resources; Springer: Berlin/Heidelberg, Germany, 2007; Volume 99. [Google Scholar]
- Acuna, M.; Sessions, J.; Zamora, R.; Boston, K.; Brown, M.; Ghaffariyan, M.R. Methods to Manage and Optimize Forest Biomass Supply Chains: A Review. Curr. For. Rep. 2019, 5, 124–141. [Google Scholar] [CrossRef]
- Wang, S.; Tian, X. Research on Sustainable Closed-Loop Supply Chain Synergy in Forest Industry Based on High-Quality Development: A Case Study in Northeast China. Forests 2022, 13, 1587. [Google Scholar] [CrossRef]
- Uusitalo, J.; Pearson, M. Introduction to Forest Operations and Technology; JVP Forest Systems Oy: Hämeenlinna, Finland, 2010; ISBN 952-92-5269-2. [Google Scholar]
- Scholz, J.; De Meyer, A.; Marques, A.S.; Pinho, T.M.; Boaventura-Cunha, J.; Van Orshoven, J.; Rosset, C.; Künzi, J.; Kaarle, J.; Nummila, K. Digital Technologies for Forest Supply Chain Optimization: Existing Solutions and Future Trends. Environ. Manag. 2018, 62, 1108–1133. [Google Scholar] [CrossRef]
- Santos, A.; Carvalho, A.; Barbosa-Póvoa, A.P.; Marques, A.; Amorim, P. Assessment and Optimization of Sustainable Forest Wood Supply Chains—A Systematic Literature Review. For. Policy Econ. 2019, 105, 112–135. [Google Scholar] [CrossRef]
- Mena-Reyes, J.F.; Vergara, F.; Linfati, R.; Escobar, J.W. Quantitative Techniques for Sustainable Decision Making in Forest-to-Lumber Supply Chain: A Systematic Review. Forests 2024, 15, 297. [Google Scholar] [CrossRef]
- Pulkki, R. Role of Supply Chain Management in the Wise Use of Wood Resources. S. Afr. For. J. 2001, 191, 89–95. [Google Scholar] [CrossRef]
- Boston, K. Forestry Raw Materials Supply Chain Management. In The Management of Industrial Forest Plantations: Theoretical Foundations and Applications; Borges, J.G., Diaz-Balteiro, L., McDill, M.E., Rodriguez, L.C.E., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 467–487. ISBN 978-94-017-8899-1. [Google Scholar]
- Larsson, M.; Stendahl, M.; Roos, A. Supply Chain Management in the Swedish Wood Products Industry—A Need Analysis. Scand. J. For. Res. 2016, 31, 777–787. [Google Scholar] [CrossRef]
- Fuentealba, S.; Pradenas, L.; Linfati, R.; Ferland, J.A. Forest Harvest and Sawmills: An Integrated Tactical Planning Model. Comput. Electron. Agric. 2019, 156, 275–281. [Google Scholar] [CrossRef]
- Rodríguez-Dorna, A.; Alonso, L.; Picos, J.; Armesto, J. Mapping Feasibility for Wood Supply: A High-Resolution Geospatial Approach to Enhance Sustainable Forest Management in Galicia (NW Spain). Forests 2023, 14, 2124. [Google Scholar] [CrossRef]
- Lämås, T.; Sängstuvall, L.; Öhman, K.; Lundström, J.; Årevall, J.; Holmström, H.; Nilsson, L.; Nordström, E.-M.; Wikberg, P.-E.; Wikström, P.; et al. The Multi-Faceted Swedish Heureka Forest Decision Support System: Context, Functionality, Design, and 10 Years Experiences of Its Use. Front. For. Glob. Change 2023, 6, 1163105. [Google Scholar] [CrossRef]
- Auger, M.; LeBel, L.; Brotherton, E. Benefits and Requirements of Mathematical Optimization in the Allocation of Wood to a Network of Forest Product Mills. Forests 2023, 14, 140. [Google Scholar] [CrossRef]
- Kogler, C. Discrete Event Simulation-Based Risk Analysis for Efficient, Sustainable and Resilient Transportation. Soud. Inž. 2023, 34, 74–78. [Google Scholar] [CrossRef]
- Simard, V.; Rönnqvist, M.; LeBel, L.; Lehoux, N. Improving the Decision-Making Process by Considering Supply Uncertainty—A Case Study in the Forest Value Chain. Int. J. Prod. Res. 2024, 62, 665–684. [Google Scholar] [CrossRef]
- Westlund, K.; Sundström, L.E.; Eliasson, L. An Optimization and Discrete Event Simulation Framework for Evaluating Delivery Performance in Swedish Wood Supply Chains under Stochastic Weather Variations. Int. J. For. Eng. 2024, 35, 326–337. [Google Scholar] [CrossRef]
- Teymourifar, A.; Trindade, M.A.M. A Framework to Design and Evaluate Green Contract Mechanisms for Forestry Supply Chains. Sustainability 2023, 15, 7668. [Google Scholar] [CrossRef]
- Sacchelli, S.; Bernetti, I. Integrated Management of Forest Ecosystem Services: An Optimization Model Based on Multi-Objective Analysis and Metaheuristic Approach. Nat. Resour. Res. 2019, 28, 5–14. [Google Scholar] [CrossRef]
- Deng, D.; Ye, C.; Tong, K.; Zhang, J. Evaluation of the Sustainable Forest Management Performance in Forestry Enterprises Based on a Hybrid Multi-Criteria Decision-Making Model: A Case Study in China. Forests 2023, 14, 2267. [Google Scholar] [CrossRef]
- Tang, C.S. Socially Responsible Supply Chains in Emerging Markets: Some Research Opportunities. J. Oper. Manag. 2018, 57, 1–10. [Google Scholar] [CrossRef]
- Qiu, H.; Zhang, H.; Lei, K.; Hu, X.; Yang, T.; Jiang, X. A New Tree-Level Multi-Objective Forest Harvest Model (MO-PSO): Integrating Neighborhood Indices and PSO Algorithm to Improve the Optimization Effect of Spatial Structure. Forests 2023, 14, 441. [Google Scholar] [CrossRef]
- Baghizadeh, K.; Zimon, D.; Jum’a, L. Modeling and Optimization Sustainable Forest Supply Chain Considering Discount in Transportation System and Supplier Selection under Uncertainty. Forests 2021, 12, 964. [Google Scholar] [CrossRef]
- Zhang, W.; Shao, H.; Sun, H.; Zhang, W.; Yan, Q. Optimizing Carbon Sequestration in Forest Management Plans Using Advanced Algorithms: A Case Study of Greater Khingan Mountains. Forests 2023, 14, 1785. [Google Scholar] [CrossRef]
- Alcalde-Calonge, A.; Ruiz-Palomino, P.; Sáez-Martínez, F.J. The Circularity of the Business Model and the Performance of Bioeconomy Firms: An Interactionist Business-Environment Model. Cogent Bus. Manag. 2022, 9, 2140745. [Google Scholar] [CrossRef]
- Munoz, M.F.; Zhang, K.; Shahzad, A.; Ouhimmou, M. LogLog: A Blockchain Solution for Tracking and Certifying Wood Volumes. In Proceedings of the 2021 IEEE International Conference on Blockchain and Cryptocurrency (ICBC), Sydney, Australia, 3–6 May 2021; IEEE: Sydney, Australia, 2021; pp. 1–9. [Google Scholar]
- Hoppen, M.; Chen, J.; Kemmerer, J.; Baier, S.; Bektas, A.R.; Schreiber, L.J.; Mayer, D.G.; Kaulen, A.; Ziesak, M.; Rossmann, J. Smart Forestry—A Forestry 4.0 Approach to Intelligent and Fully Integrated Timber Harvesting. Int. J. For. Eng. 2024, 35, 137–152. [Google Scholar] [CrossRef]
- González-Hidalgo, M.; Zografos, C. How Sovereignty Claims and “Negative” Emotions Influence the Process of Subject-Making: Evidence from a Case of Conflict over Tree Plantations from Southern Chile. Geoforum 2017, 78, 61–73. [Google Scholar] [CrossRef]
- Medvedev, S.; Zyryanov, M.; Dudin, P. Interaction Model of Forestry Enterprises with Society and Environment. BIO Web Conf. 2024, 93, 01016. [Google Scholar] [CrossRef]
- Infante, F. Social Capital and Landscape: Effects of Monoculture Forest Plantations on Small Producers in the Mediterranean Dryland of South-Central Chile. Rural Soc. 2023, 32, 151–168. [Google Scholar] [CrossRef]
- Maher, R.; Pedemonte-Rojas, N.; Gálvez, D.; Banerjee, S.B. The Role of Multistakeholder Initiatives in the Radicalization of Resistance: The Forest Stewardship Council and the Mapuche Conflict in Chile. J. Manag. Stud. 2024, 61, 2961–2991. [Google Scholar] [CrossRef]
- Garrido, M.C.; Alarcón, A.M. The Commoditization of Ecosystems within Chile’s Mapuche Territory: A Violation of the Human Right to Health. Health Hum. Rights 2023, 25, 95. [Google Scholar]
- Meyer, R.; Campanella, S.; Corsano, G.; Montagna, J.M. Optimal Design of a Forest Supply Chain in Argentina Considering Economic and Social Aspects. J. Clean. Prod. 2019, 231, 224–239. [Google Scholar] [CrossRef]
- Maring, P. Conflict Transformation and Collaboration in Developing Social Forestry in Flores, Indonesia. For. Soc. 2022, 6, 40–66. [Google Scholar] [CrossRef]
- Wang, M.; Radics, R.; Islam, S.; Hwang, K.-S. Towards Forest Supply Chain Risks. Oper. Supply Chain Manag. Int. J. 2023, 97–108. [Google Scholar] [CrossRef]
- Berasaluce, M.; Díaz-Siefer, P.; Rodríguez-Díaz, P.; Mena-Carrasco, M.; Ibarra, J.T.; Celis-Diez, J.L.; Mondaca, P. Social-Environmental Conflicts in Chile: Is There Any Potential for an Ecological Constitution? Sustainability 2021, 13, 12701. [Google Scholar] [CrossRef]
- Carte, L.; Hofflinger, Á.; Polk, M.H. Expanding Exotic Forest Plantations and Declining Rural Populations in La Araucanía, Chile. Land 2021, 10, 283. [Google Scholar] [CrossRef]
- Braun, A.C. Encroached by Pine and Eucalyptus? A Grounded Theory on an Environmental Conflict between Forest Industry and Smallholder Livelihoods in Chile. J. Rural. Stud. 2021, 82, 107–120. [Google Scholar] [CrossRef]
- Schmalz, S.; Graf, J.; Julián-Vejar, D.; Sittel, J.; Alister Sanhueza, C. Challenging the Three Faces of Extractivism: The Mapuche Struggle and the Forestry Industry in Chile. Globalizations 2023, 20, 365–383. [Google Scholar] [CrossRef]
- Pawlak, Z. An Inquiry into Anatomy of Conflicts. Inf. Sci. 1998, 109, 65–78. [Google Scholar] [CrossRef]
- Forestal (Chile), I. El Sector Forestal Chileno 2024 = Chilean Forestry Sector 2024; Instituto Forestal: Santiago, Chile, 2024. [Google Scholar] [CrossRef]
- Pareja Arellano, N.; Riquelme Brevis, H.; Sandoval Obando, E. El problema económico-social de la tierra en el espacio rural de la Araucanía: Un análisis histórico (1910–1998). Rev. CUHSO 2025, 35, 1–25. [Google Scholar] [CrossRef]
- Ramos-Maldonado, M.; Muñoz, F.T.; Mora, P.; Venegas-Vásconez, D. Optimizing Cutting Log Operations in Softwood Sawmills: A Multi-Objective Approach Tailored for SMEs. IEEE Access 2024, 12, 128141–128150. [Google Scholar] [CrossRef]
- Dias, G.P.; Silva, M.E.; Viana, F.L.E. Contributions of Social Capital to Supply Chain Sustainability Practices: Conceptual Framework and Propositions. Clean. Logist. Supply Chain 2024, 11, 100151. [Google Scholar] [CrossRef]
- Miettinen, K. Nonlinear Multiobjective Optimization; Springer Science & Business Media: Berlin, Germany, 1999; ISBN 978-0-7923-8278-2. [Google Scholar]
- Ehrgott, M. Multicriteria Optimization; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]


| Study | Approach | Sustainability Dimensions | Key Contribution/Limitation |
|---|---|---|---|
| [9] | Systematic review of sustainable forest supply chains | Economic, Environmental | No explicit social indicators included |
| [36] | MILP optimization model for forest supply chains (Argentina) | Economic, Social | No territorial conflict dimension considered |
| [26] | Sustainable supply chain optimization under uncertainty | Economic, Environmental | Social aspects not incorporated |
| [24] | Conceptual framework for socially responsible supply chains | Social | Lacks quantitative or mathematical modeling |
| [23] | Multi-criteria model for evaluating enterprise sustainability | Economic, Environmental, Social | Limited to corporate-level scope |
| This study | Multi-objective MILP model for forest-to-lumber supply chain | Economic, Environmental, Social | Explicitly integrates a social conflict exposure index |
| Event Type | (0–10) |
|---|---|
| Fatalities | 10 |
| Attack or explosion | 10 |
| Armed attack | 10 |
| Machinery burning | 9 |
| Truck burning | 8 |
| Fire | 8 |
| Occupation | 7 |
| Roadblock | 6 |
| Robbery | 6 |
| Menace | 5 |
| Police action | 5 |
| Protests | 4 |
| Court of guarantee | 4 |
| Communiqués | 3 |
| Notation | Description |
|---|---|
| i | |
| j | |
| k | |
| l | |
| n |
| Notation | Description |
|---|---|
| Volume logs l (in m3). | |
| Volume products n (in m3). | |
| Volume loss of the cutting pattern k (in m3). | |
| Supply of logs from cut block i of logs class l (in units). | |
| Number of products n obtained by applying the cutting pattern k (in units). | |
| Demand for products n in the sawmill j (in units). | |
| Degree of exposure to social conflicts when connecting cut block i to sawmill j (dimensionless on a scale from 0 no conflict to 1 high conflict). | |
| Set of cutting patterns compatible with the log class l, index-based (unitless) | |
| Distance to transport from cut block i to sawmill j (in km). | |
| BigM | A larger number (in units). |
| Parameter | Symbol | Value | Description |
|---|---|---|---|
| Number of cut blocks | nb | 8 | Log origin zones. |
| Number of sawmills | na | 4 | Processing plants in the network. |
| Number of cutting patterns | np | 160 | Patterns documented/used in the optimization. |
| Number of product types | nt | 23 | Final products (by dimensions) considered in the demand. |
| Number of log classes | nd | 14 | Classification by diameter (20–46 cm). |
| Notation | Description |
|---|---|
| Number of logs obtained from cut block i, sent to sawmill j, processed with cutting pattern k (in units). | |
| Difference between the demand of products n and total products production n at sawmill j (in units). |
| Objective | Description | Sustainability Dimension | Applied Experiment(s) |
|---|---|---|---|
| z1 | Minimize volume of logs consumed | Economic | E I-A, E II, E III |
| z2 | Minimize total transportation distance | Environmental | E I-B, E III |
| z3 | Minimize exposure to social conflicts | Social | E I-A, I-B, I-C, E III |
| z4 | Minimize the number of active network connections | Environmental/ Social | E I-C |
| z5 | Minimize surplus of non-demanded products | Economic | E II, E III |
| z6 | Minimize volume loss due to cutting patterns | Environmental | E II, E III |
| Code | Experiment | Dimension Evaluated | Purpose |
|---|---|---|---|
| E I-A | Multi-objective resolution with ε-constraint method | Economic-Environmental vs. Social | Explore trade-offs between log consumption and conflict exposure. |
| E I-B | Multi-objective resolution with ε-constraint method | Economic-Environmental vs. Social | Explore trade-offs between transportation distance and conflict exposure. |
| E I-C | Multi-objective resolution with ε-constraint method | Economic-Environmental vs. Social | Evaluate the relationship between network complexity and conflict exposure to identify efficient configurations. |
| E II | Scalar aggregate resolution (by weightings) | Economic, Environmental | Analyze the impact of different prioritization strategies on consumption, surplus, and cutting loss. |
| E III | Mono objective resolution | Economic, Environmental, Social | Evaluate the individual behavior of each performance measure under different supply and demand scenarios. |
| Scenario | Δz2 (%) | % Coincident Arcs | Leaving | Entering |
|---|---|---|---|---|
| α = 0.8 | −0.0052 | 87.5 | 1 | 2 |
| α = 0.9 | −0.00953 | 87.5 | 1 | 2 |
| Base | — | — | — | — |
| α = 1.1 | +0.05336 | 87.5 | 1 | 0 |
| α = 1.2 | +0.05525 | 87.5 | 1 | 0 |
| α = 1.5 | +1.58193 | 75.0 | 2 | 2 |
| Data | |||
|---|---|---|---|
| Testing | z1 | z5 | z6 |
| 1 | 29,771.131 | 0.071 | 9131.030 |
| 2 | 29,755.029 | 2.094 | 9112.905 |
| 3 | 29,860.625 | 122.202 | 9098.392 |
| Computation Times (In Seconds) | ||||||
|---|---|---|---|---|---|---|
| Performance Measure | Homogeneous | Random | 2 Cluster | 3 Cluster | 2 ClusterN | 3 ClusterN |
| z1 | 0.19 | 1.53 | 1.47 | 1.76 | 0.24 | 0.15 |
| z2 | 0.15 | 0.20 | 0.12 | 0.14 | 0.11 | 0.11 |
| z3 | 1.13 | 9.14 | 11.27 | 8.13 | 4.17 | 3.46 |
| z4 | 8.80 | 57.53 | 101.24 | 29.59 | 65.82 | 64.68 |
| z5 | 66.59 | 66.90 | 66.82 | 91.42 | 300 * | 300 * |
| z6 | 1.35 | 0.13 | 0.32 | 0.13 | 0.12 | 0.16 |
| Computation Times (In Seconds) | ||||
|---|---|---|---|---|
| Performance Measure | Homogeneous | Lower | Intermediate | Higher |
| z1 | 0.19 | 0.14 | 0.19 | 1.54 |
| z2 | 0.15 | 0.11 | 0.12 | 0.16 |
| z3 | 1.13 | 3.80 | 6.62 | 1.37 |
| z4 | 8.80 | 1.68 | 88.18 | 2.39 |
| z5 | 66.59 | 0.82 | 0.54 | 294.28 |
| z6 | 1.35 | 1.26 | 0.19 | 0.13 |
| Performance Measures | Supply | Demand |
|---|---|---|
| z1: Log volume consumed | Higher consumption in configurations with greater spatial concentration. | Higher consumption with lower and intermediate volume products. |
| z2: Total distance traveled | Shorter distances in configurations with greater spatial dispersion. | Shorter distances with higher-volume products. |
| z3: Degree of exposure to social conflicts | Lower exposure in configurations with greater spatial dispersion. | Higher exposure with lower-volume products. |
| z4: Number of active arcs | Decreases by only one arc under highly concentrated supply. | More arcs with lower volume products. |
| z5: Surplus of non-demand products | Higher surplus in more spatially concentrated configurations; low in the others. | Higher surplus with lower-volume products. |
| z6: Cutting losses | Higher losses in configurations with greater spatial concentration. | Higher losses with lower- and medium-volume products. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mena-Reyes, J.F.; Soto-Concha, R.; Vergara, F.P.; Ortiz-Araya, V.; Escobar, J.W.; Linfati, R. Integrating Social Conflicts into Sustainable Decision-Making of the Forest-to-Lumber Supply Chain. Forests 2025, 16, 1644. https://doi.org/10.3390/f16111644
Mena-Reyes JF, Soto-Concha R, Vergara FP, Ortiz-Araya V, Escobar JW, Linfati R. Integrating Social Conflicts into Sustainable Decision-Making of the Forest-to-Lumber Supply Chain. Forests. 2025; 16(11):1644. https://doi.org/10.3390/f16111644
Chicago/Turabian StyleMena-Reyes, Jorge Félix, Raúl Soto-Concha, Francisco P. Vergara, Virna Ortiz-Araya, John Willmer Escobar, and Rodrigo Linfati. 2025. "Integrating Social Conflicts into Sustainable Decision-Making of the Forest-to-Lumber Supply Chain" Forests 16, no. 11: 1644. https://doi.org/10.3390/f16111644
APA StyleMena-Reyes, J. F., Soto-Concha, R., Vergara, F. P., Ortiz-Araya, V., Escobar, J. W., & Linfati, R. (2025). Integrating Social Conflicts into Sustainable Decision-Making of the Forest-to-Lumber Supply Chain. Forests, 16(11), 1644. https://doi.org/10.3390/f16111644







