Enhancing Distance-Independent Forest Growth Models Using National-Scale Forest Inventory Data
Abstract
1. Introduction
2. Materials and Methods
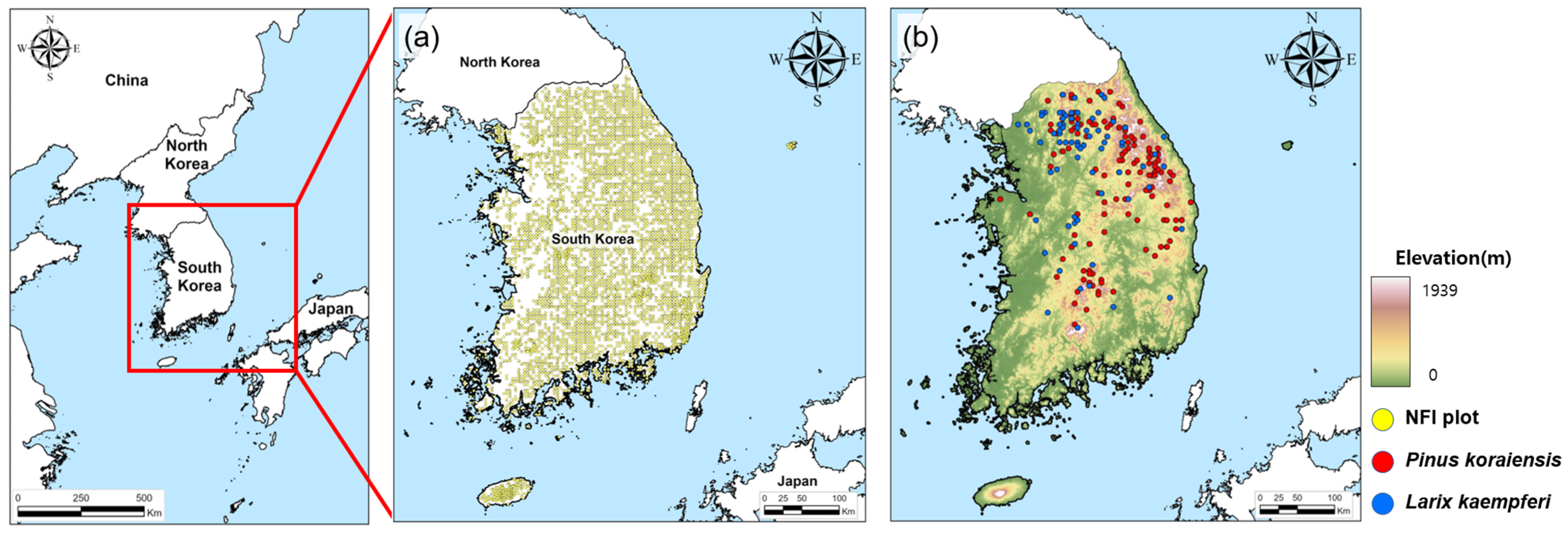
2.1. Study Area and Target Species
2.2. Data Collection and Preprocessing
- (1)
- Plots in which forest management activities were implemented more than twice across the three survey cycles (5th to 7th NFIs), which complicated the tracking of individual tree growth over time.
- (2)
- Plots with missing individual tree data owing to survey omissions (including cases where dead trees were identified), which resulted in decreased total DBH and hindered the confirmation of accurate growth.
2.3. Distance Independent Model Fitting
2.4. Model Evaluation and Validation
3. Results
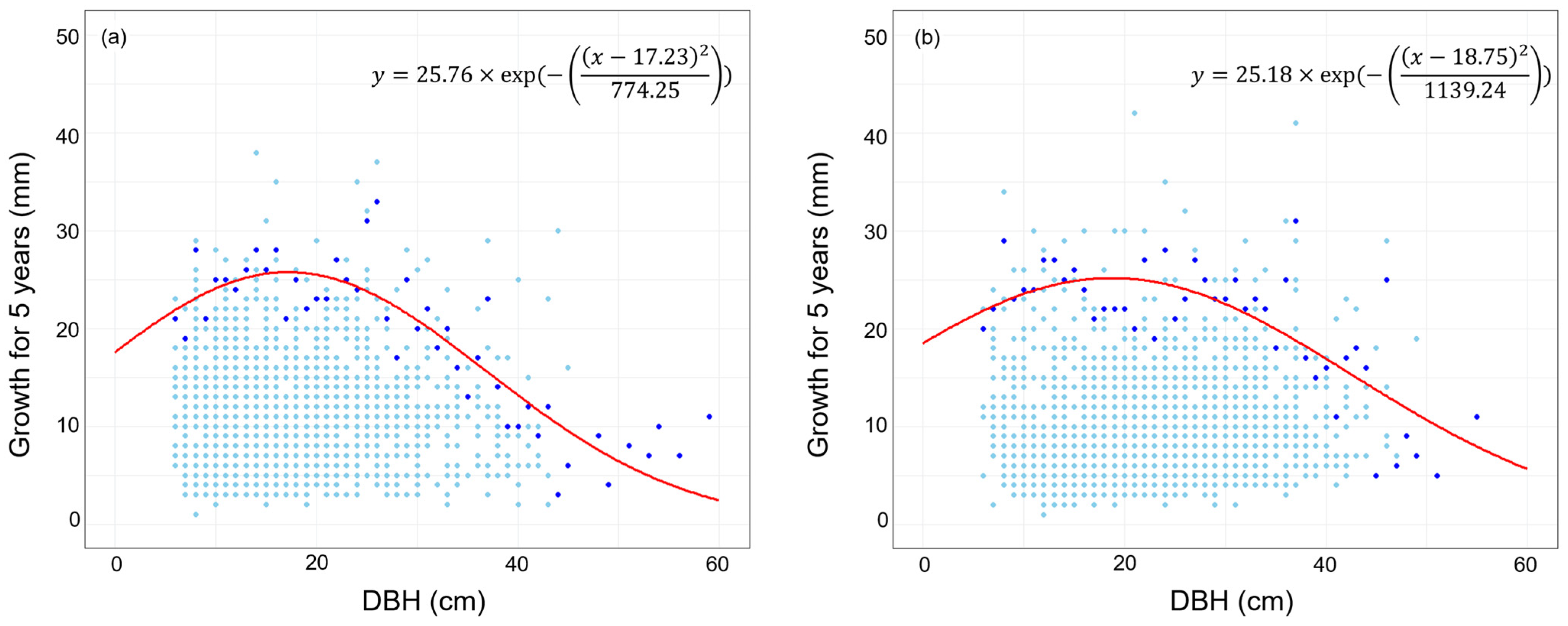
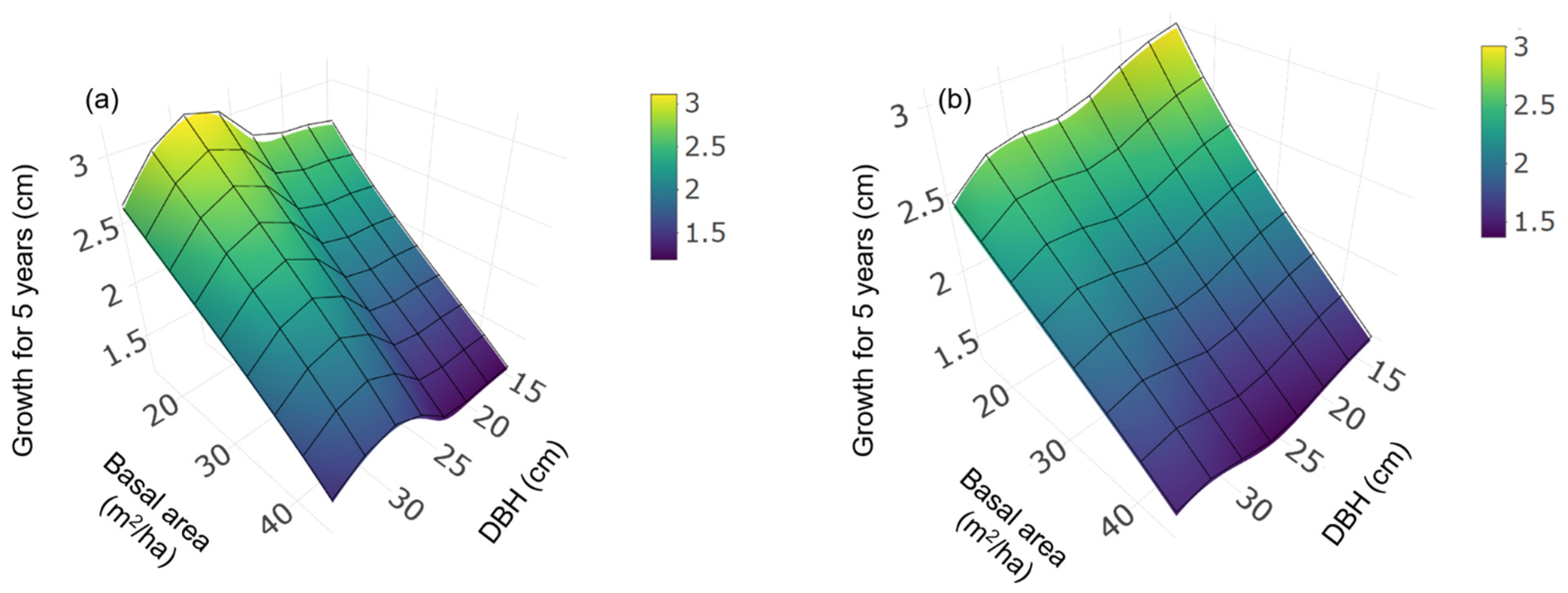
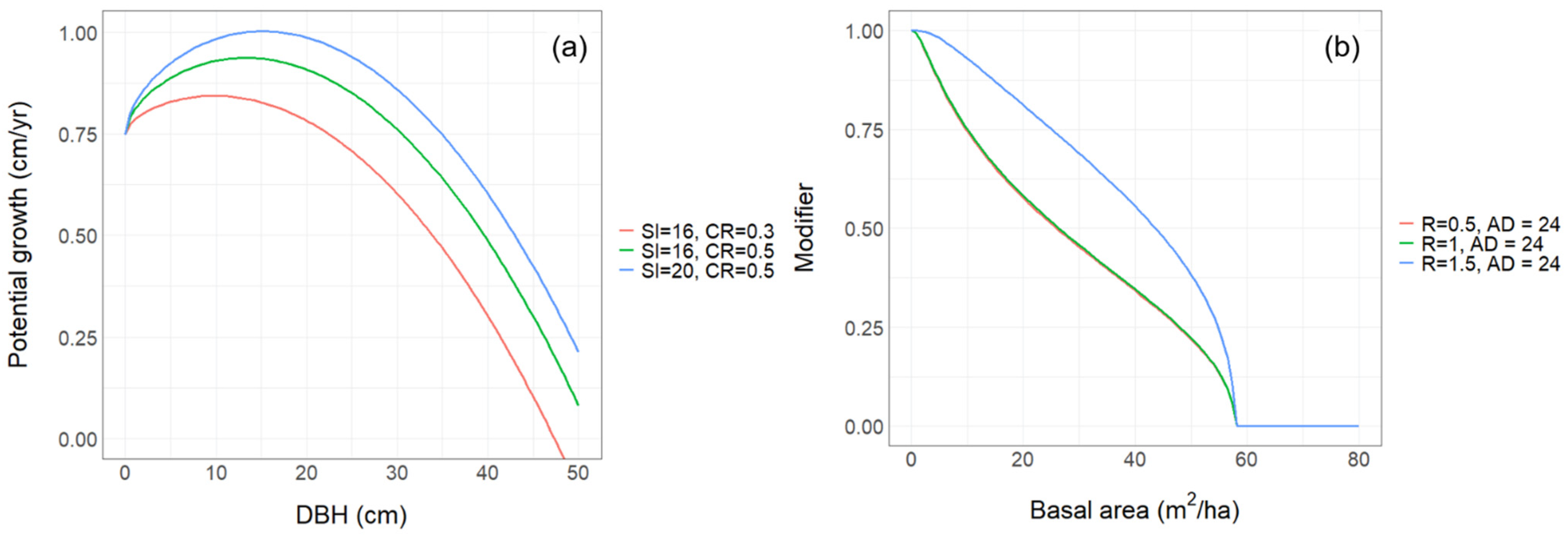
3.1. Growth Model Based on a Potential Diameter Growth and a Modifier Function
3.2. Model Evaluation and Validation
4. Discussion
4.1. Applicability of the Distance-Independent Growth Model
4.2. Sustainable Individual-Level Growth Model Based on NFI
4.3. Limitations and Future Studies
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AD | Average Diameter |
| BA | Basal Area |
| BAmax | Maximum Basal Area |
| CR | Crown Ratio |
| DBH | Diameter at Breast Height |
| MOD | Modifier Function |
| NFI | National Forest Inventory |
| PG | Potential Growth |
| SI | Site Index |
References
- Lämås, T.; Sängstuvall, L.; Öhman, K.; Lundström, J.; Årevall, J.; Holmström, H.; Nilsson, L.; Nordström, E.-M.; Wikberg, P.-E.; Wikström, P.; et al. The Multi-Faceted Swedish Heureka Forest Decision Support System: Context, Functionality, Design, and 10 Years Experiences of Its Use. Front. For. Glob. Change 2023, 6, 1163105. [Google Scholar] [CrossRef]
- Nguyen, D.; Henderson, E.; Wei, Y. PRISM: A Decision Support System for Forest Planning. Environ. Model. Softw. 2022, 157, 105515. [Google Scholar] [CrossRef]
- Söderbergh, I.; Ledermann, T. Algorithms for Simulating Thinning and Harvesting in Five European Individual-Tree Growth Simulators: A Review. Comput. Electron. Agric. 2003, 39, 115–140. [Google Scholar] [CrossRef]
- Crookston, N.L.; Dixon, G.E. The Forest Vegetation Simulator: A Review of Its Structure, Content, and Applications. Comput. Electron. Agric. 2005, 49, 60–80. [Google Scholar] [CrossRef]
- Thrippleton, T.; Temperli, C.; Krumm, F.; Mey, R.; Zell, J.; Stroheker, S.; Gossner, M.M.; Bebi, P.; Thürig, E.; Schweier, J. Balancing Disturbance Risk and Ecosystem Service Provisioning in Swiss Mountain Forests: An Increasing Challenge under Climate Change. Reg. Environ. Chang. 2023, 23, 29. [Google Scholar] [CrossRef]
- Mutterer, S.; Schweier, J.; Bont, L.G.; Pezzatti, G.B.; Conedera, M.; Temperli, C.; Griess, V.C.; Blattert, C. Integrating Fire Predisposition Assessment into Decision Support Systems for Mountain Forest Management. MethodsX 2025, 14, 103332. [Google Scholar] [CrossRef]
- Seidl, R.; Rammer, W. Climate Change Amplifies the Interactions between Wind and Bark Beetle Disturbances in Forest Landscapes. Landsc. Ecol. 2017, 32, 1485–1498. [Google Scholar] [CrossRef] [PubMed]
- Twery, M.J.; Knopp, P.D.; Thomasma, S.A.; Rauscher, H.M.; Nute, D.E.; Potter, W.D.; Maier, F.; Wang, J.; Dass, M.; Uchiyama, H.; et al. NED-2: A Decision Support System for Integrated Forest Ecosystem Management. Comput. Electron. Agric. 2005, 49, 24–43. [Google Scholar] [CrossRef]
- Weiskittel, A.R.; Hann, D.W.; Kershaw, J.A., Jr.; Vanclay, J.K. Forest Growth and Yield Modeling; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Pretzsch, H.; Grote, R.; Reineking, B.; Rötzer, T.; Seifert, S. Models for Forest Ecosystem Management: A European Perspective. Ann. Bot. 2008, 101, 1065–1087. [Google Scholar] [CrossRef]
- Pretzsch, H.; Forrester, D.I.; Rötzer, T. Representation of Species Mixing in Forest Growth Models: A Review and Perspective. Ecol. Model. 2015, 313, 276–292. [Google Scholar] [CrossRef]
- Boukhris, I.; Marano, G.; Dalmonech, D.; Valentini, R.; Collalti, A. Modeling Forest Growth under Current and Future Climate. Curr. For. Rep. 2025, 11, 17–36. [Google Scholar] [CrossRef]
- Henttonen, H.M.; Nöjd, P.; Mäkinen, H. Environment-Induced Growth Changes in Forests of Finland Revisited—A Follow-Up Using an Extended Data Set from the 1960s to the 2020s. For. Ecol. Manag. 2024, 551, 121515. [Google Scholar] [CrossRef]
- Lu, J. Individual Tree Diameter Growth Modelling for Natural Secondary Forest in Changbai Mountains, Northeast China. Sci. Rep. 2024, 14, 18695. [Google Scholar] [CrossRef]
- Zhang, Z.; Papaik, M.J.; Wang, X.; Hao, Z.; Ye, J.; Lin, F.; Yuan, Z. The Effect of Tree Size, Neighborhood Competition and Environment on Tree Growth in an Old-Growth Temperate Forest. J. Plant Ecol. 2017, 10, 970–980. [Google Scholar] [CrossRef]
- Ma, P.; Han, X.H.; Lin, Y.; Moore, J.; Guo, Y.X.; Yue, M. Exploring the Relative Importance of Biotic and Abiotic Factors That Alter the Self-Thinning Rule: Insights from Individual-Based Modelling and Machine-Learning. Ecol. Model. 2019, 397, 16–24. [Google Scholar] [CrossRef]
- Pacala, S.W.; Canham, C.D.; Saponara, J.; Silander, J.A., Jr.; Kobe, R.K.; Ribbens, E. Forest Models Defined by Field Measurements: Estimation, Error Analysis and Dynamics. Ecol. Monogr. 1996, 66, 1–43. [Google Scholar] [CrossRef]
- Pretzsch, H.; Biber, P.; Ďurský, J. The Single Tree-Based Stand Simulator SILVA: Construction, Application and Evaluation. For. Ecol. Manag. 2002, 162, 3–21. [Google Scholar] [CrossRef]
- Seidl, R.; Rammer, W.; Scheller, R.M.; Spies, T.A. An Individual-Based Process Model to Simulate Landscape-Scale Forest Ecosystem Dynamics. Ecol. Model. 2012, 231, 87–100. [Google Scholar] [CrossRef]
- Landsberg, J.J.; Waring, R.H. A Generalised Model of Forest Productivity Using Simplified Concepts of Radiation-Use Efficiency, Carbon Balance and Partitioning. For. Ecol. Manag. 1997, 95, 209–228. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef]
- Hoover, C.M.; Bush, R.; Palmer, M.; Treasure, E. Using Forest Inventory and Analysis Data to Support National Forest Management: Regional Case Studies. J. For. 2020, 118, 313–323. [Google Scholar] [CrossRef]
- Shannon, E.S.; Finley, A.O.; Domke, G.M.; May, P.B.; Andersen, H.-E.; Gaines, G.C., III; Banerjee, S. Toward Spatio-Temporal Models to Support National-Scale Forest Carbon Monitoring and Reporting. Environ. Res. Lett. 2024, 20, 014052. [Google Scholar] [CrossRef]
- Combaud, M.; Cordonnier, T.; Dupire, S.; Vallet, P. Climate Change Altered the Dynamics of Stand Dominant Height in Forests during the Past Century—Analysis of 20 European Tree Species. For. Ecol. Manag. 2024, 553, 121601. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Winter, S.; Chirici, G.; LaPoint, E. Assessing Forest Naturalness. For. Sci. 2012, 58, 294–309. [Google Scholar] [CrossRef]
- Domke, G.M.; Walters, B.F.; Giebink, C.L.; Greenfield, E.J.; Smith, J.E.; Nichols, M.C.; Knott, J.A.; Ogle, S.M.; Coulston, J.W.; Steller, J. Greenhouse Gas Emissions and Removals from Forest Land, Woodlands, Urban Trees, and Harvested Wood Products in the United States, 1990–2021; Resource Bulletin WO-101; U.S. Department of Agriculture, Forest Service, Washington Office: Washington, DC, USA, 2023. [CrossRef]
- Breidenbach, J.; Astrup, R. Small Area Estimation of Forest Attributes in the Norwegian National Forest Inventory. Eur. J. For. Res. 2012, 131, 1255–1267. [Google Scholar] [CrossRef]
- Borghi, C.; Francini, S.; McRoberts, R.E.; Parisi, F.; Lombardi, F.; Nocentini, S.; Maltoni, A.; Travaglini, D.; Chirici, G. Country-Wide Assessment of Biodiversity, Naturalness and Old-Growth Status Using National Forest Inventory Data. Eur. J. For. Res. 2024, 143, 271–303. [Google Scholar] [CrossRef]
- Ryu, D.; Park, M.; Park, J.; Moon, M.; Yim, J.; Kim, H.S. Quantification of Tree Growth Change under Climate Change Using National Forest Inventory of Korea. For. Ecol. Manag. 2024, 568, 122112. [Google Scholar] [CrossRef]
- Kim, M.; Kraxner, F.; Son, Y.; Jeon, S.W.; Shvidenko, A.; Schepaschenko, D.; Ham, B.-Y.; Lim, C.-H.; Song, C.; Hong, M.; et al. Quantifying Impacts of National-Scale Afforestation on Carbon Budgets in South Korea from 1961 to 2014. Forests 2019, 10, 579. [Google Scholar] [CrossRef]
- Hong, M.; Song, C.; Kim, M.; Kraxner, F.; Ko, Y.; Son, J.; Lee, W.-K. Realizing Climate Resilient Development Pathways in Forestry: A Focus on Carbon Management in Republic of Korea. Environ. Impact Assess. Rev. 2025, 110, 107665. [Google Scholar] [CrossRef]
- Shin, J.; Chang, Y.; Lee, K.; Kim, D.; Han, H. Sample Selection Bias Due to Omitting Short Trees for Tree Height Estimation in Forest Inventories: A Case Study on Pinus koraiensis Plantations in South Korea. PLoS ONE 2025, 20, e0321160. [Google Scholar] [CrossRef]
- Wykoff, W.R. A basal area increment model for individual conifers in the northern Rocky Mountains. For. Sci. 1990, 36, 1077–1104. [Google Scholar] [CrossRef]
- Korea Forest Service. Statistical Yearbook of Forestry 2024; Korea Forest Service: Daejeon, Republic of Korea, 2023. Available online: https://kfss.forest.go.kr/ (accessed on 1 October 2024).
- Ryu, D. Estimation of Growth and Mortality Rate of Major 6 Tree Species Using NFI 5–7th. Ph.D. Thesis, Seoul National University, Seoul, Republic of Korea, 2022. [Google Scholar]
- Bragg, D.C. Potential Relative Increment (PRI): A New Method to Empirically Derive Optimal Tree Diameter Growth. Ecol. Model. 2001, 137, 77–92. [Google Scholar] [CrossRef]
- Härkönen, S.; Mäkinen, A.; Tokola, T.; Rasinmäki, J.; Kalliovirta, J. Evaluation of Forest Growth Simulators with NFI Permanent Sample Plot Data from Finland. For. Ecol. Manag. 2010, 259, 573–582. [Google Scholar] [CrossRef]
- Padfield, D.; Matheson, G.; Windram, F. nls.multstart: Robust Non-Linear Regression Using AIC Scores, R Package, version 2.0.0; R Foundation for Statistical Computing: Vienna, Austria, 2025; Available online: https://CRAN.R-project.org/package=nls.multstart (accessed on 1 January 2025).
- Monserud, R.A.; Sterba, H. A Basal Area Increment Model for Individual Trees Growing in Even- and Uneven-Aged Forest Stands in Austria. For. Ecol. Manag. 1996, 80, 57–80. [Google Scholar] [CrossRef]
- Hahn, J.T.; Leary, R.A. Potential Diameter Growth Functions; USDA Forest Service; General Technical Report NC-49; U.S. Department of Agriculture, Forest Service, North Central Forest Experiment Station: St. Paul, MN, USA, 1979.
- Leary, R.A.; Holdaway, M.R. Modifier Function. In A Generalized Forest Growth Projection System Applied to the Lake States Region; General Technical Report NC-49; USDA Forest Service: St. Paul, MN, USA, 1979. [Google Scholar]
- National Institute of Forest Science (NIFoS). 2023 Tree Volume, Biomass, and Stand Yield Table (Research Report No. 1092); National Institute of Forest Science: Seoul, Republic of Korea, 2023. [Google Scholar]
- Kwon, S.D.; Lee, K.H.; Kim, H.H.; Chung, J.S. Development of Individual-Tree/Distance-Independent Growth-and-Mortality Prediction Equations for Pinus koraiensis Stands. J. Korean For. Soc. 2003, 92, 590–597. [Google Scholar]
- Sterba, H. Estimating Potential Density from Thinning Experiments and Inventory Data. For. Sci. 1987, 33, 1022–1034. [Google Scholar] [CrossRef]
- Kim, M.; Lee, W.-K.; Choi, G.-M.; Song, C.; Lim, C.-H.; Moon, J.; Piao, D.; Kraxner, F.; Shvidenko, A.; Forsell, N. Modeling Stand-Level Mortality Based on Maximum Stem Number and Seasonal Temperature. For. Ecol. Manag. 2017, 386, 37–50. [Google Scholar] [CrossRef]
- Lee, K.; Yun, S.J.; Kim, M.; Yang, H.M.; Kim, A.R. The Effect of Thinning on Trade-Offs in Ecosystem Services: The Case Study of a Korean Pine Plantation on Mt. Gari. J. Ecol. Environ. 2024, 48, 137–143. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024; Available online: https://www.R-project.org/ (accessed on 1 October 2024).
- Kwon, S.D.; Chung, J.S. Development of Individual-Tree Distance-Independent Simulation Model for Growth Prediction of Pinus koraiensis Stands. J. Korean For. Soc. 2004, 93, 43–49. [Google Scholar]
- Kim, S.; Seol, A.; Chung, J. Development of Diameter Growth and Mortality Prediction Models of Pinus koraiensis Based on Periodic Annual Increment. J. Korean Soc. For. Sci. 2011, 100, 1–7. [Google Scholar] [CrossRef]
- Kwon, K.; Han, H.; Seol, A.; Chung, H.; Chung, J. Analyzing Thinning Effects on Growth and Carbon Absorption for Cryptomeria japonica Stands Using Distance-Independent Growth Simulations. J. Korean Soc. For. Sci. 2016, 105, 132–138. [Google Scholar] [CrossRef]
- Craine, J.M.; Fargione, J.; Sugita, S. Supply Pre-Emption, Not Concentration Reduction, Is the Mechanism of Competition for Nutrients. New Phytol. 2005, 166, 933–940. [Google Scholar] [CrossRef] [PubMed]
- Hong, M.; Song, C.; Kim, M.; Kim, J.; Roh, M.; Ko, Y.; Cho, K.; Son, Y.; Jeon, S.; Kraxner, F.; et al. Modeling-Based Risks Assessment and Management of Climate Change in South Korean Forests. Forests 2023, 14, 745. [Google Scholar] [CrossRef]
- Lee, S.-J.; Lee, Y.-J.; Ryu, J.-Y.; Kwon, C.-G.; Seo, K.-W.; Kim, S.-Y. Prediction of Wildfire Fuel Load for Pinus densiflora Stands in South Korea Based on the Forest-Growth Model. Forests 2022, 13, 1372. [Google Scholar] [CrossRef]
- Ager, A.A.; Barros, A.M.G.; Houtman, R.; Seli, R.; Day, M.A. Modelling the Effect of Accelerated Forest Management on Long-Term Wildfire Activity. Ecol. Model. 2020, 421, 108962. [Google Scholar] [CrossRef]
- Dhakal, A.S.; Sidle, R.C. Long-Term Modelling of Landslides for Different Forest Management Practices. Earth Surf. Process. Landf. 2003, 28, 853–868. [Google Scholar] [CrossRef]
- McCullagh, A.; Black, K.; Nieuwenhuis, M. Evaluation of Tree and Stand-Level Growth Models Using National Forest Inventory Data. Eur. J. For. Res. 2017, 136, 251–258. [Google Scholar] [CrossRef]
- Mehtätalo, L.; Räty, M.; Mehtätalo, J. A New Growth Curve and Fit to the National Forest Inventory Data of Finland. Ecol. Model. 2025, 501, 111006. [Google Scholar] [CrossRef]
- Cho, Y.C.; Seol, J.; Lim, C.H. Climate-Induced Distribution Dynamics and Niche Adaptation of South Korean Endemic Plants across the Korean Peninsula. Sci. Rep. 2024, 14, 22253. [Google Scholar] [CrossRef]
- Jevšenak, J.; Skudnik, M. A Random Forest Model for Basal Area Increment Predictions from National Forest Inventory Data. For. Ecol. Manag. 2021, 479, 118601. [Google Scholar] [CrossRef]
- Leite e Lopes, I.; Sousa da Mata, A.; Oliveira Castro, R.V.; Viana da Páscoa, K.J.; Souza Jarochinski e Silva, C.; Rezende Gomide, L. Applying Complex Network Metrics to Individual-Tree Diameter Growth Modeling. iForest 2025, 18, 176–182. [Google Scholar] [CrossRef]
- Kwon, S. Development of a simulation model for stand-level forest management. Ph.D. Thesis, Seoul National University Graduate School, Seoul, Republic of Korea, 2003. [Google Scholar]


| Category | Pinus koraiensis | Larix kaempferi | ||||
|---|---|---|---|---|---|---|
| 5th | 6th | 7th | 5th | 6th | 7th | |
| Number of plots | 171 | 165 | 158 | 249 | 230 | 207 |
| Age | 29.40 ± 9.68 | 33.40 ± 10.50 | 37.60 ± 10.80 | 30.80 ± 10.50 | 35.60 ± 10.40 | 39.60 ± 11.60 |
| Height (m) | 12.15 ± 3.58 | 14.23 ± 3.23 | 15.74 ± 3.37 | 17.47 ± 4.35 | 20.12 ± 4.24 | 21.96 ± 4.19 |
| Diameter at breast height (cm) | 20.77 ± 7.44 | 23.72 ± 7.47 | 25.95 ± 7.69 | 22.16 ± 6.77 | 24.56 ± 6.81 | 26.34 ± 7.08 |
| Tree density (trees/ha) | 713.96 ± 473.55 | 606.00 ± 434.55 | 566.47 ± 396.40 | 602.41 ± 355.03 | 534.59 ± 334.59 | 468.35 ± 283.40 |
| Tree growing stocks (m3/ha) | 130.89 ± 78.85 | 166.21 ± 91.04 | 204.68 ± 96.53 | 181.34 ± 91.79 | 220.16 ± 104.79 | 241.73 ± 117.88 |
| Management Type | Area (ha) | Age in 2006 (year) | Tree Density (trees/ha) | Average DBH (cm) | Basal Area (m2/ha) | |||
|---|---|---|---|---|---|---|---|---|
| Before Thinning | After Thinning | Before Thinning | After Thinning | Before Thinning | After Thinning | |||
| Light thinning | 13.9 | 46 | 937.5 | 525.0 | 24.5 ± 0.7 | 28.7 ± 0.9 | 46.9 | 35.5 |
| Intensive thinning | 14.9 | 46 | 737.5 | 275.0 | 25.7 ± 0.8 | 31.4 ± 1.6 | 40.2 | 22.4 |
| No thinning | 3.9 | 46 | 975.0 | 975.0 | 20.3 ± 0.7 | 21.5 ± 0.8 | 33.4 | 37.6 |
| Species | Function | Parameter Estimates | R2 | RMSE | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| b1 | b2 | b3 | b4 | b5 | b6 | BAmax | |||||
| Pinus koraiensis | Crown Ratio | 0.1733 | 0.0312 | 0.4414 | 0.1864 | - | - | - | - | 0.98 | 1.15 |
| Potential Growth | 2.5740 | 0.0000011 | 3.9810 | 0.05378 | 0.4870 | - | - | 0.16 | |||
| Modifier | 0.3723 | −9.3770 | 37,600 | 0.4703 | 0.7939 | 0.1896 | 57.91 | 0.98 | |||
| Larix kaempferi | Crown Ratio | 0.0630 | 0.0091 | 0.7540 | 0.0198 | - | - | - | - | 0.98 | 1.14 |
| Potential Growth | 3.7389 | 0.0009831 | 2.2258 | 0.0376 | 0.5526 | - | - | 0.13 | |||
| Modifier | 0.5497 | −4.4901 | 406.71 | 0.3597 | 0.6727 | 0.2949 | 65.01 | 0.98 | |||
| Management | R2 | RMSE | Bias | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2016 | 2021 | 2011 | 2016 | 2021 | 2011 | 2016 | 2021 | |
| Light thinning | 0.97 | 0.94 | 0.90 | 0.87 | 1.38 | 1.86 | −0.35 | −0.68 | −0.80 |
| Intensive thinning | 0.98 | 0.93 | 0.90 | 0.82 | 1.48 | 1.80 | −0.42 | 0.25 | 0.24 |
| No thinning | 0.98 | 0.89 | 0.86 | 0.92 | 2.29 | 2.81 | −0.77 | −1.81 | −2.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, B.; Park, S.; Kim, H.; Ko, D.W.; Lee, K.; Kim, A.-R.; Cho, W. Enhancing Distance-Independent Forest Growth Models Using National-Scale Forest Inventory Data. Forests 2025, 16, 1567. https://doi.org/10.3390/f16101567
Hwang B, Park S, Kim H, Ko DW, Lee K, Kim A-R, Cho W. Enhancing Distance-Independent Forest Growth Models Using National-Scale Forest Inventory Data. Forests. 2025; 16(10):1567. https://doi.org/10.3390/f16101567
Chicago/Turabian StyleHwang, Byungmook, Sinyoung Park, Hyemin Kim, Dongwook W. Ko, Kiwoong Lee, A-Reum Kim, and Wonhee Cho. 2025. "Enhancing Distance-Independent Forest Growth Models Using National-Scale Forest Inventory Data" Forests 16, no. 10: 1567. https://doi.org/10.3390/f16101567
APA StyleHwang, B., Park, S., Kim, H., Ko, D. W., Lee, K., Kim, A.-R., & Cho, W. (2025). Enhancing Distance-Independent Forest Growth Models Using National-Scale Forest Inventory Data. Forests, 16(10), 1567. https://doi.org/10.3390/f16101567







