Simulation of the Radial Sawing Technique for Pedunculata Oak (Quercus robur L.) Logs
Abstract
1. Introduction
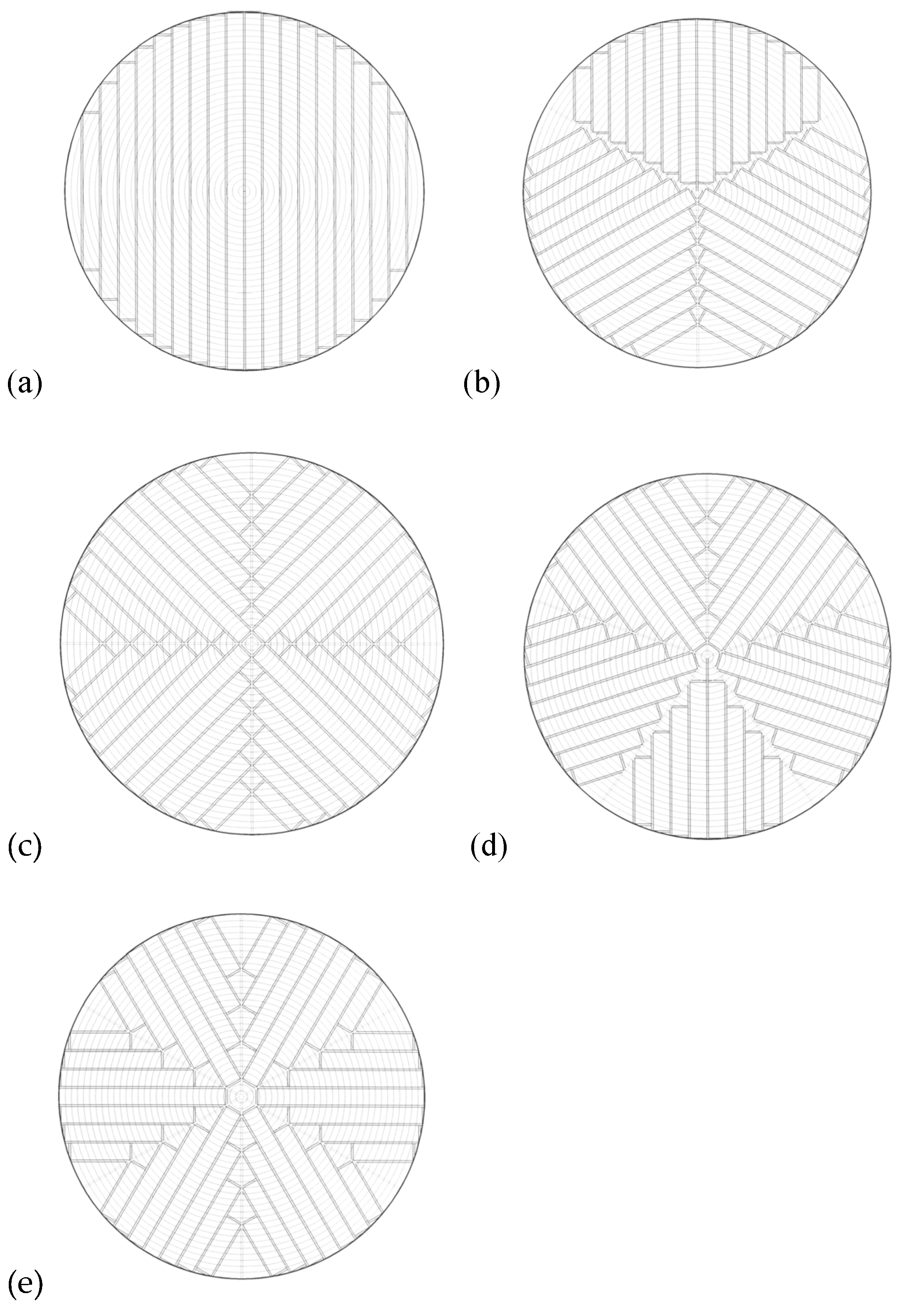
- live sawing;
- radial sawing third sections;
- radial sawing fourth sections;
- radial sawing fifth sections;
- radial sawing sixth sections.
2. Materials and Methods
2.1. Description of the Simulated Method of Sawing
2.2. Simulation Parameters
3. Results and Discussion
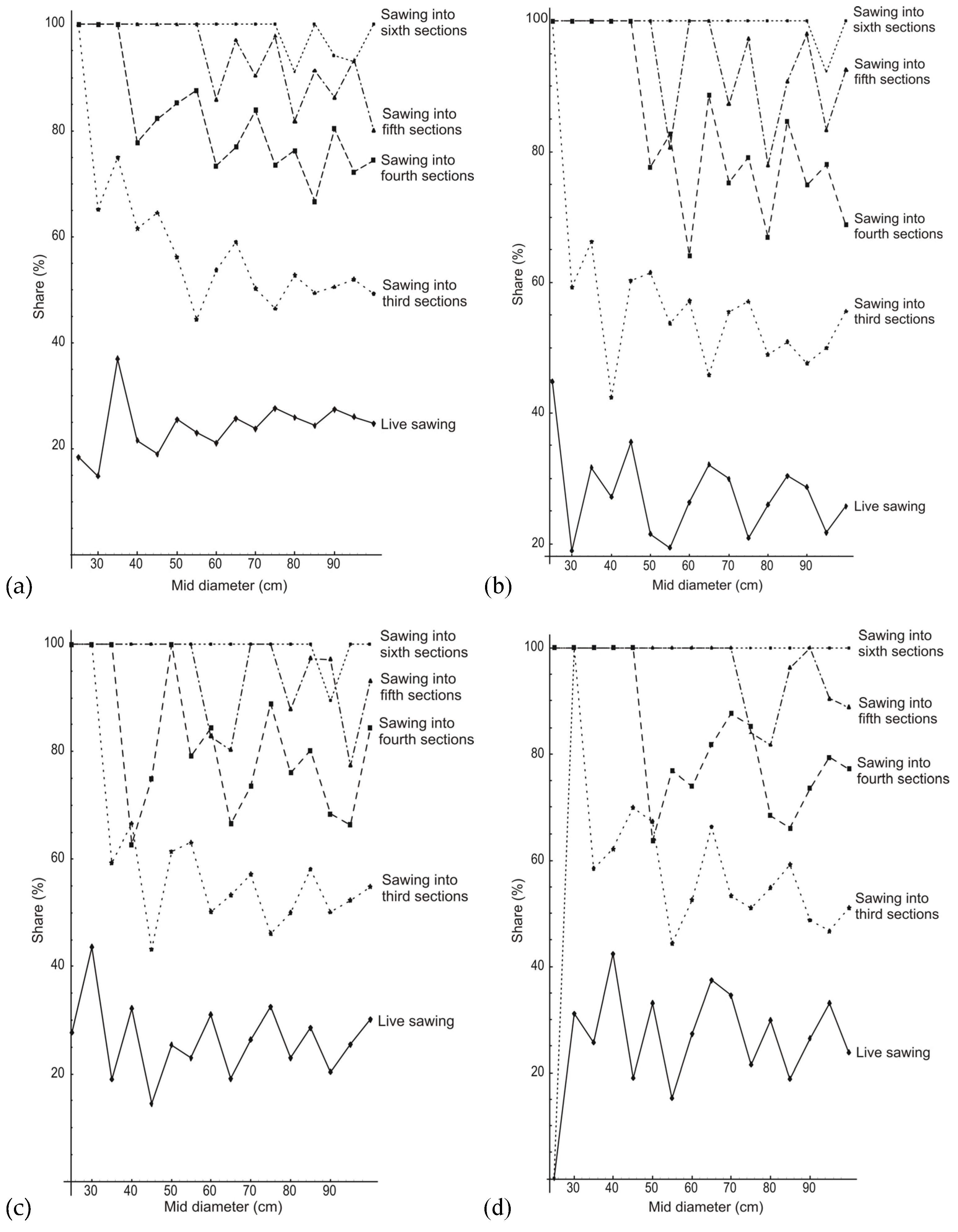
3.1. Share of Radially Sawn Boards
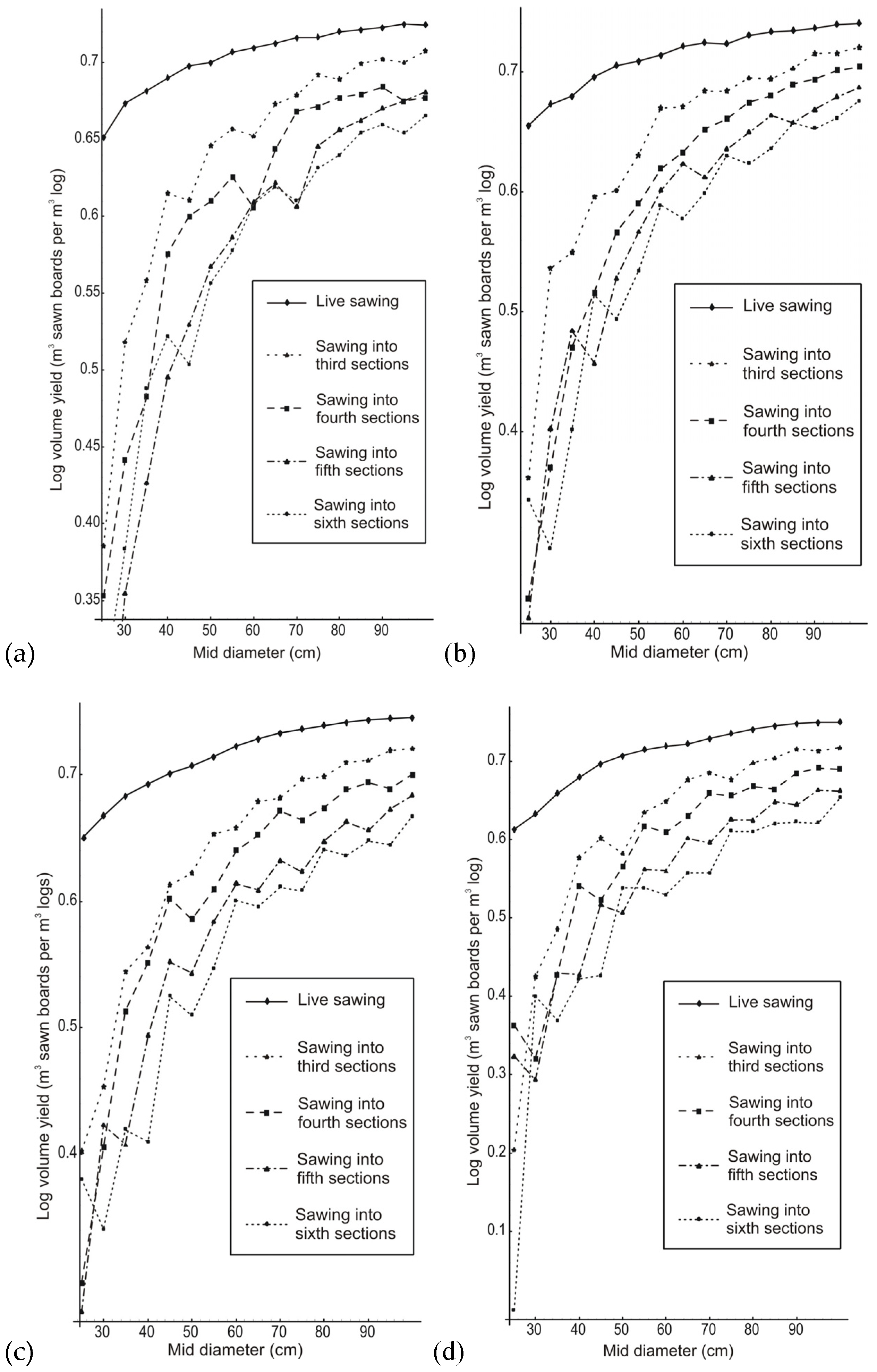
3.2. Log Volume Yield
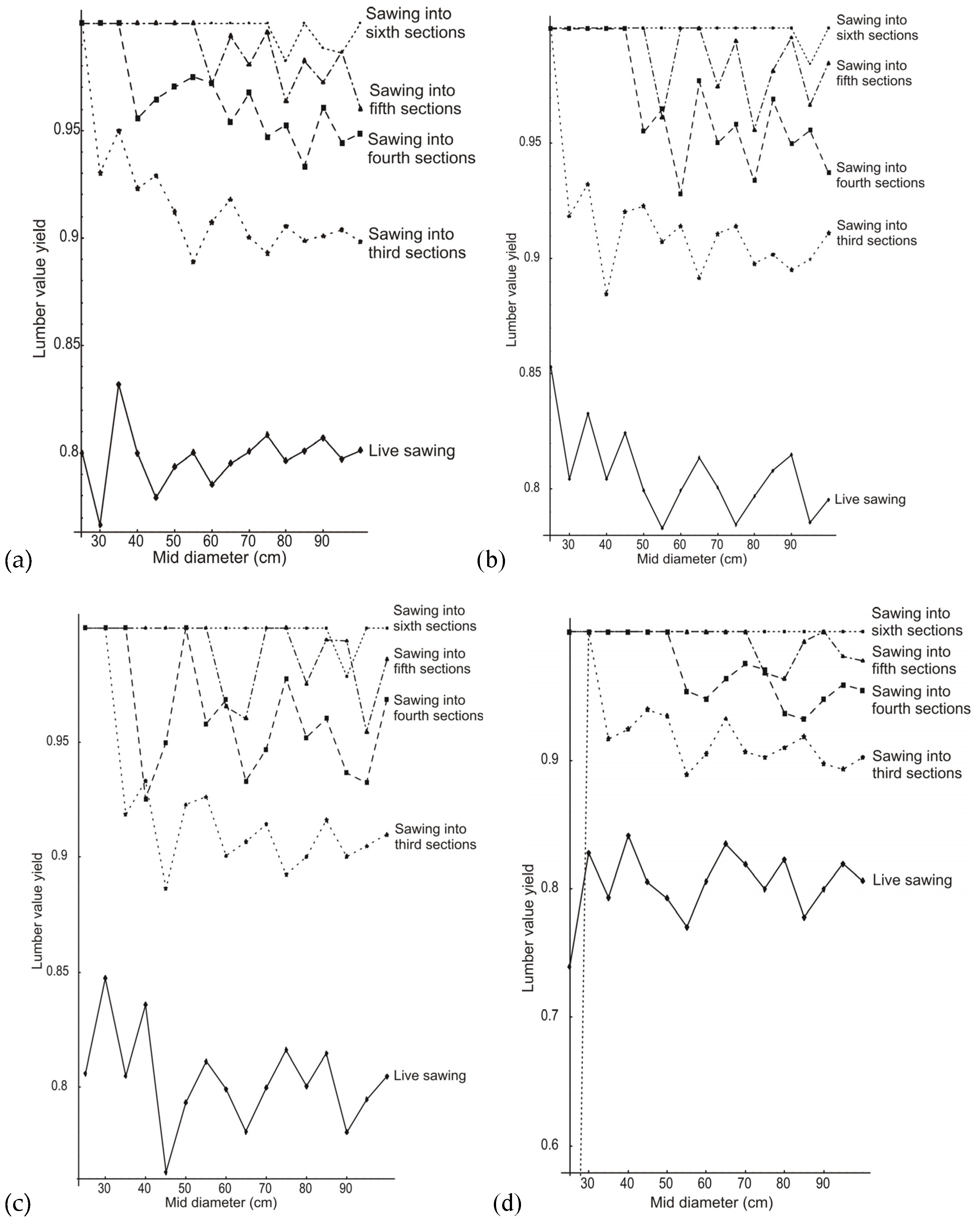
3.3. Lumber Value Yield
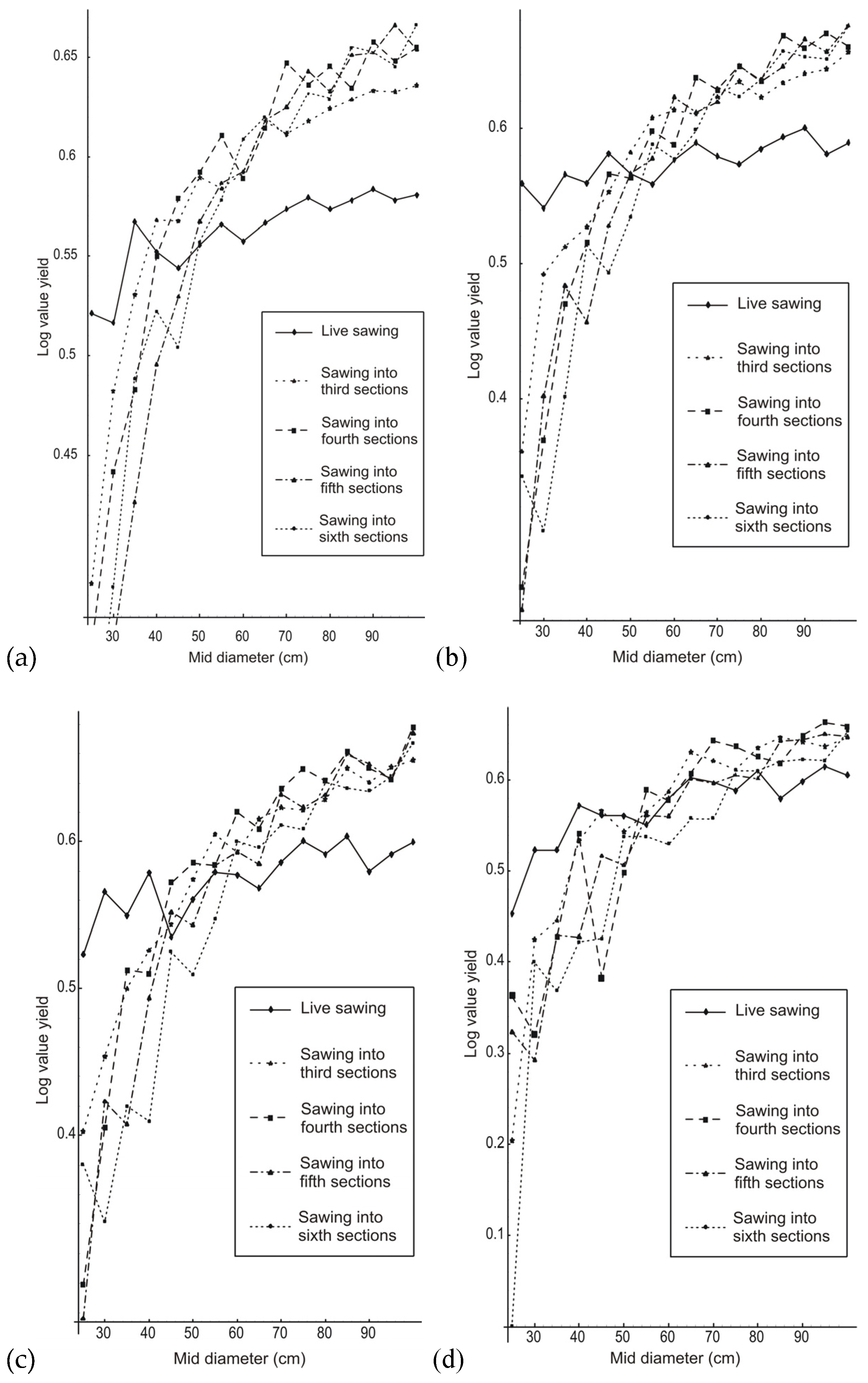
3.4. Log-Value Yield
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Herjavec, S.; Jeromel, A.; Da Silva, A.; Orlic, S.; Redzepovic, S. The quality of white wines fermented in Croatian oak barrels. Food Chem. 2007, 100, 124–128. [Google Scholar] [CrossRef]
- Gregić, M. Development of timber conversion and utilization of Slavonian oak and other hardwood species in Croatia from 1699 to 1984. Drv. Ind. 1987, 38, 195–210. [Google Scholar]
- Prka, T. Development of oak wood sawmilling—Part I. Drv. Ind. 1988, 39, 217–222. [Google Scholar]
- Carvalho, D.E.; Rocha, M.P.; Timofeiczyk, R.; Klitzke, R.J. Production costs in the log processing of Eucalyptus spp. wood. An. Acad. Bras. Cienc. 2020, 92, e20180486. [Google Scholar] [CrossRef] [PubMed]
- Butković, J. Comparison of the yield for three methods of fir/spruce logs sawing. Drv. Ind. 1998, 49, 3–7. [Google Scholar]
- Xiang, Z.; Peralta, P.; Peszlen, I. Lumber drying stresses and mitigation of cross-sectional deformation. Wood Fiber Sci. 2012, 44, 94–102. [Google Scholar]
- Venäläinen, M.; Hu, Y.; Verkasalo, E. Checking of radially sawn Scots pine and Norway spruce wood. Nat. Resour. 2016, 7, 505–514. [Google Scholar] [CrossRef]
- Vilkovský, P.; Klement, I.; Vilkovská, T. The impact of the log-sawing patterns on the quantitative and qualitative yield of beech timber (Fagus sylvatica L.). Appl. Sci. 2023, 13, 8262. [Google Scholar] [CrossRef]
- Klement, I.; Vilkovský, P.; Vilkovská, T. Impact of sawmill processing on the yield and longitudinal warping of beech blanks. BioResources 2023, 18, 8311–8322. [Google Scholar] [CrossRef]
- Klement, I.; Vilkovská, T.; Vilkovský, P. Effects of beech wood dimensions and quality on edge-glued boards yield. BioResources 2025, 20, 910–922. [Google Scholar] [CrossRef]
- Sandberg, D. Radially sawn timber. Star sawing—A new method for producing timber with vertical annual rings. Holz Roh-Werkst. 1996, 54, 145–151. [Google Scholar] [CrossRef]
- Sandberg, D. Radially sawn timber—The Primwood Method for improved properties. Holz Roh-Werkst. 2005, 63, 94–101. [Google Scholar] [CrossRef]
- Knörr, K.A. New developments in radial milling—What they mean for tree growers in a changing industry. In Proceedings of the Australian Forest Growers National Conference, Albury Wodonga, Australia, 19–22 October 2008. [Google Scholar]
- Begunkova, N.O. Predicting the yield of radially sawn timber. Int. Sci. Res. J. 2021, 6, 44–48. [Google Scholar] [CrossRef]
- Ištvanić, J.; Piljak, K.; Antonović, A.; Lučić, R.B.; Jambreković, V.; Pervan, S. The theory and mathematical model underlying the radial sawing simulator—RadSawSim. Forest Prod. J. 2010, 60, 48–56. [Google Scholar] [CrossRef]
- Riesco Muñoz, G.; Remacha Gete, A.; Gasalla Regueiro, M. Variation in log quality and prediction of sawing yield in oak wood (Quercus robur). Ann. For. Sci. 2013, 70, 695–706. [Google Scholar] [CrossRef]
- Li, R.; Cao, P.; Guo, X.; Futang, J.; Ekevad, M.; Wang, A.X. A Novel Sawing Method for Small-Diameter Log. Wood Res. 2015, 60, 293–300. [Google Scholar]
- Popadić, R.; Šoškić, B.; Milić, G.; Todorović, N.; Furtula, M. Influence of the Sawing Method on Yield of Beech Logs with Red Heartwood. Drv. Ind. 2014, 65, 1–8. [Google Scholar] [CrossRef]
- Popadić, R.; Todorović, N. The Influence of Sawing Method and Beech Roundwood Quality on the Radial, Radial–Tangential and Tangential Lumber Participation. Prer. Drv. 2009, 28, 28–34. [Google Scholar]
- Gergeľ, T.; Bucha, T.; Gejdoš, M.; Vyhnáliková, Z. Computed tomography log scanning–high technology for forestry and forest based industry. Cent. Eur. For. J. 2019, 65, 51–59. [Google Scholar] [CrossRef]
- Gejdoš, M.; Gergeľ, T.; Michajlová, K.; Bucha, T.; Gracovský, R. The accuracy of CT scanning in the assessment of the internal and external qualitative features of wood logs. Sensors 2023, 23, 8505. [Google Scholar] [CrossRef] [PubMed]
| Mid Diameter (cm) | Board Thickness (mm) | |||
|---|---|---|---|---|
| 25 | 32 | 38 | 50 | |
| 25 | n2 0.521 | n2 0.560 | n2 0.524 | n2 0.456 |
| 30 | n2 0.515 | n2 0.541 | n2 0.568 | n2 0.522 |
| 35 | n2 0.567 | n2 0.548 | n2 0.550 | n2 0.522 |
| 40 | n3 0.568 | n2 0.560 | n2 0.579 | n2 0.570 |
| 45 | n4 0.578 | n2 0.580 | n4 0.572 | n3 0.563 |
| 50 | n4 0.592 | n3 0.582 | n4 0.586 | n2 0.560 |
| 55 | n4 0.610 | n3 0.609 | n3 0.605 | n4 0.589 |
| 60 | n6 0.609 | n5 0.622 | n4 0.621 | n3 0.586 |
| 65 | n6 0.619 | n4 0.638 | n3 0.614 | n3 0.629 |
| 70 | n4 0.648 | n4 and n6 0.629 | n4 0.638 | n4 0.642 |
| 75 | n5 0.642 | n4 and n5 0.630 | n4 0.640 | n4 0.639 |
| 80 | n4 0.645 | n4, n5 and n6 0.635 | n4 and n6 0.642 | n3 0.638 |
| 85 | n6 0.655 | n4 0.675 | n4 0.661 | n3 0.640 |
| 90 | n4 0.658 | n5 0.670 | n5 0.652 | n4 0.650 |
| 95 | n5 0.655 | n4 0.676 | n3 0.660 | n4 0.660 |
| 100 | n6 0.665 | n5 and n6 0.678 | n4 0.680 | n4 0.658 |
| Method of Sawing | Posterior Mean (Value Yield) | 95% Credible Interval Lower | 95% Credible Interval Upper |
|---|---|---|---|
| Live sawing (n2) | 0.544 | 0.529 | 0.558 |
| Radial sawing—thirds (n3) | 0.609 | 0.590 | 0.627 |
| Radial sawing—fourths (n4) | 0.634 | 0.622 | 0.647 |
| Radial sawing—fifths (n5) | 0.645 | 0.621 | 0.670 |
| Radial sawing—sixths (n6) | 0.645 | 0.618 | 0.672 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ištvanić, J.; Pervan, D.; Antonović, A.; Piljak, K.; Obućina, M.; Klarić, M. Simulation of the Radial Sawing Technique for Pedunculata Oak (Quercus robur L.) Logs. Forests 2025, 16, 1538. https://doi.org/10.3390/f16101538
Ištvanić J, Pervan D, Antonović A, Piljak K, Obućina M, Klarić M. Simulation of the Radial Sawing Technique for Pedunculata Oak (Quercus robur L.) Logs. Forests. 2025; 16(10):1538. https://doi.org/10.3390/f16101538
Chicago/Turabian StyleIštvanić, Josip, Dario Pervan, Alan Antonović, Krunoslav Piljak, Murčo Obućina, and Miljenko Klarić. 2025. "Simulation of the Radial Sawing Technique for Pedunculata Oak (Quercus robur L.) Logs" Forests 16, no. 10: 1538. https://doi.org/10.3390/f16101538
APA StyleIštvanić, J., Pervan, D., Antonović, A., Piljak, K., Obućina, M., & Klarić, M. (2025). Simulation of the Radial Sawing Technique for Pedunculata Oak (Quercus robur L.) Logs. Forests, 16(10), 1538. https://doi.org/10.3390/f16101538







