Abstract
Quasistatic nanoindentation is a proven tool that provides information on the micromechanical behavior of wood cell walls. However, quasistatic tests cannot probe the time-dependent mechanical behavior shown by wood. Nanoindentation dynamic mechanical analysis (nanoDMA) can measure the viscoelastic properties of wood cell walls. This research aimed to study the quasistatic and viscoelastic properties of individual radiata pine wood (Pinus radiata D. Don) cell wall layers. To minimize variability and retrieve both properties at the same locations, a load function composed of a multiload-quasistatic function followed by dynamic reference frequency segments was developed. Nanoindentations were then performed on the S2 layer and compound corner middle lamella (CCML) of unembedded latewood cells. Because the S2 layer is anisotropic, both transverse and longitudinal–tangential wood planes were studied. In the transverse plane, the average results of the quasistatic elastic moduli for the S2 layer and CCML were 15.7 GPa and 4.6 GPa, respectively. In the longitudinal–tangential plane, the was 3.9 GPa. In the transverse section, the hardness of the S2 layer and CCML were 331 MPa and 277 MPa, respectively, and in the longitudinal–tangential section H was 244 MPa. To acquire the viscoelastic properties, measurements were made over more than three decades of frequency. An increase of the storage modulus and a reduction of the loss modulus and loss factor as frequency increased were found in both wood orientations. The quasi-static and dynamic indentations equivalent at 0.1 Hz showed similar values for and E′. This study contributes to our knowledge of wood cell wall micromechanical properties.
1. Introduction
Wood is a versatile, environmentally friendly material with remarkable mechanical properties that make it a sustainable alternative to other materials such as plastic, steel, and concrete. Its advantageous properties stem from wood’s complex multiscale structure and chemical composition. The wood cell wall is made up of polymeric components, primarily cellulose, hemicelluloses, and lignin. Each polymer has different chemical and physical properties, and they form an intricate network with one another providing strength to wood [1,2]. These wood components exhibit certain mechanical and viscoelastic behavior depending on the conditions they are exposed to, such as temperature, humidity, load type, and time [3,4,5,6]. As summarized in [7], the elastic behavior of wood is influenced mainly by the crystalline cellulose microfibrils. Additionally, the amorphous components of the matrix such as lignin and hemicelluloses contribute mainly to the viscous and plastic behavior of the wood. The hydrophilic nature of wood results in the mechanical and viscoelastic properties being highly influenced by the moisture content. Dry wood has greater dimensional stability, and therefore lower shrinkage or expansion, compared to wet wood. As wood reduces its moisture content under the fiber saturation point, its mechanical properties increase and are more stable [8]. On the other hand, water changes drastically the point of wood softening at determined temperatures because it produces the mobility of wood macromolecules. As a result, the wood material changes from stiff to soft. The amorphous polymers of wood, both hemicelluloses and lignin, differ in functional groups and sensitivity to water; therefore, they have different glass transition temperatures. In wet conditions, these polymers have their glass transition at low temperatures [9].
Bulk wood mechanical properties have been evaluated under various laboratory tests [10,11]. At the micrometer scale, the mechanical properties have been studied using novel characterization techniques and state-of-the-art technologies. Studying the mechanical behavior of wood at the nanometer scale can help us understand the molecular-scale processes responsible for the phenomena we observe at the macroscopic level [12].
Nanoindentation has proven to be a useful tool to evaluate the micrometer-scale mechanical properties of the S2 layer and compound corner middle lamella (CCML) of the cell walls of different wood species [13,14,15,16,17,18]. In a typical nanoindentation test, a carefully shaped probe is pressed into a sample following a prescribed loading protocol, with which both applied load and displacement are continuously measured [19]. Many indentation tests in wood cell walls include load functions comprising a three-segment loading ramp (loading, holding, and unloading) in which each segment employs at different times. The short period of time aims to reduce the possible effects of plastic deformations in wood on the unloading segment. The step-wise load functions use a force-controlled mode, with maximum forces ranging from 250 μN to 400 μN [13,15,16,20,21,22]. On the other hand, multiload nanoindentation load functions have been developed to measure properties as a function of nanoindentation size in a single location [18]. The multiload functions consist of a series of loading cycles; therefore, a series of nanoindentations is obtained instead of single nanoindentations. Similarly to the single load function, the number of segments per cycle is three [23]; however, a four-segment cycle has also been reported. This includes a final segment to hold the partial unloads before beginning the next cycle [18]. The test can be quasistatic or dynamic. In the quasistatic test, the elastic modulus of a material is obtained from the contact area and initial slope of the unloading segment in a load vs. displacement ( graph, whereas the hardness is calculated from the maximum load and contact area [24]. The calculations assume that during the unloading segment the material has a purely elastic behavior [25].
However, wood cell walls are polymeric materials, and, thus, exhibit time-dependent elastic and plastic mechanical behavior. Therefore, elastic modulus and hardness measurements made using quasistatic nanoindentations are unique values that correspond to the chosen time-scales of the loading, the hold at maximum load, and the unloading segments in the load function [26,27]. Capturing time-dependent mechanical properties using quasistatic nanoindentation requires a series of nanoindentations while systematically varying times for the different segments in each load function [26,27]. It is also not straightforward to calculate mechanical damping using quasistatic nanoindentation. Therefore, quasistatic nanoindentation has limitations in describing the full magnitude of the mechanical response of a viscoelastic material during the indentation process [28].
Nanoscale Dynamic Mechanical Analysis (nanoDMA) is complementary to quasistatic nanoindentation testing. The nanoDMA technique involves a small sinusoidal load superimposed on the quasistatic nanoindentation loading. By measuring the corresponding displacement amplitude and time lag between the displacement and load measurements, dynamic properties are obtained: storage modulus and loss modulus, each representing two different components of the material’s behavior [25]. The specimens are subjected to the application and release of stresses for a given time. Being a cyclic experiment, different orders of magnitude of frequencies ranging from millihertz to hundreds of hertz can be used. The storage modulus is related to the stiffness or the sample’s in-phase response to the applied force. Therefore, it is related to the elastic recovery of the material, which represents the amount of energy stored after an oscillation loading cycle. The loss modulus , also called the viscous modulus, is a parameter related to the viscous energy dissipation of a material due to the internal movement of polymeric chains [29]. The viscous state, or mechanical damping, of the material is obtained by the ratio of these two parameters and is known as the loss tangent , which is zero for an ideal elastic material and extends to infinity for an ideal liquid [30].
The nanoDMA technique has been used to quantify mechanical changes in various materials [28,31]. This trend continues with the incorporation of additional materials with broad potential for different applications [32,33,34,35]. The viscoelastic properties of Carapa procera wood cell walls have been studied using various nanoindentation tests, including nanoDMA, in a frequency range of 10 to 240 Hz. The reduced storage modulus and measured at 50 locations ranged from 7 to 15 GPa and 0.01 to 0.04, respectively [36]. Nano-DMA has also been used to investigate the effects of accelerated aging on the cell wall micromechanics of loblolly pine wood (Pinus taeda) [37]. Moreover, the modulus mapping method has been used to obtain the storage modulus in Norway spruce wood [38,39]. Similarly, using the dynamic mapping technique, micromechanical variations in phenol formaldehyde-impregnated Pinus massoniana samples [40] and individual phases within sapwood tissues of Larix gmelinii [20] have been analyzed. Dynamic nanoindentation has also been used to study the correlations of heat-treated bamboo cells and heat treatment conditions [41]. In addition to a more thorough characterization of time-dependent mechanical properties, viscoelastic characterization over wide ranges of frequency can also provide insights into microphysical processes causally linked to material properties [42]. Jakes used nanoDMA to measure the moisture-dependent in latewood loblolly pine wood cell walls across more than three decades of frequency [43]. The results revealed a peak in at high moisture content, which was used to causally link polymer segmental motions to intra-cell wall mineral ion diffusion. These nanoDMA results led to the discovery that mineral ion diffusion though a wood cell wall is a solid polymer diffusion process.
Nanoindentation and nanoDMA have proven to be very useful tools for studying mechanical properties in wood cell walls. However, the high variability in the mechanical properties among different wood species makes it difficult to make accurate predictions about the mechanical behavior of one species based on the data from another. In Chile, radiata pine wood accounts for 60% of the 3.11 million hectares of forest plantations [44]; therefore, it is the main species used there for structural applications. Thus, it is important to study the mechanical behavior at the microscale, which will contribute to a complete picture for the design of timber structures that will be exposed to different service conditions. Yet, to the best of our knowledge there are no reports of nanoDMA for this species. Furthermore, the anisotropic over greater than three decades of frequency have never been reported for wood cell wall layers. The objective of this research was to study the viscoelastic properties over a frequency range of 0.1 to 200 Hz of radiata pine compound corner middle lamella (CCML) and S2 layer. The S2 layer was measured in both the transverse and longitudinal orientations. Quasistatic elastic modulus and hardness measurements were also made on the same cell wall layers. The obtained results allowed a comparison of quasistatic nanoindentation and nanoDMA measurements on the same locations in wood cell wall layers.
2. Materials and Methods
2.1. Sample Origin and Preparation
Samples were obtained from a strip of a radiata pine tree (Pinus radiata D. Don) from a 26-year-old plantation located in Los Ángeles, Bío-Bío Province, VIII region, Chile. The strip was dried to 12% moisture content in an industrial dryer. The basic bulk wood density of 0.39 was determined according to the ASTM D2395-14 standard [45]. Small latewood blocks of 5 mm in length and a cross-sectional area of 4 × 4 mm were cut with a fine tooth saw and bonded to a steel disc using a 5-min epoxy such that either a transverse or a tangential–longitudinal plane was facing up. Due to the bordered pits present in the longitudinal radial walls of the tracheids, the radial longitudinal direction was not considered. These pits can significantly affect the micromechanical properties in this direction due to the non-uniformity of the microfibril angle around the boarded pits [15,46]. Samples were not embedded in low viscosity resin to avoid possible unwanted chemical modifications by the resin [47,48]. Nanoindentation surface preparation in the unembedded wood followed the protocols described in Jakes and Stone [18]. Briefly, the specimens were fit into a Leica (Wetzlar, Germany) EM UC7 ultramicrotome equipped with a Micro Star (Huntsville, TX, USA) 45° diamond knife. A hand razor was used to trim a pyramid with an apex in the region of interest. To obtain smooth block face surfaces for nanoindentations, sections were cut from the apex using the diamond knife with the final sections only 100 nm thick.
2.2. Nanoindentation
Nanoindentation was performed using a Bruker Hysitron (Minneapolis, MN, USA) TriboIndenter equipped with a diamond Berkovich probe and upgraded with the nanoDMA III package. The relative humidity (RH) inside of the enclosure was maintained at 60% ± 1% RH using an InstruQuest (Coconut Creek, FL, USA) HumiSys HF RH generator. The temperature was not controlled but measured to be maintained between 20°C ± 1 °C. The calibration of the RH and temperature sensor was verified using a Control Company (Webster, TX, USA) 4085 Traceable® Hygrometer Thermometer Dew Point Meter. The machine compliance, probe area function, and tip roundness effects were determined using the procedures in [49,50] and a series of 80 nanoindentations in a fused silica calibration standard. Following the calibration reporting procedure prescribed in [49], values for the square root of the Joslin–Oliver parameter of 1.254 ± 0.002 µm/N½, elastic modulus of 72.0 ± 0.2 GPa, and Meyer’s hardness of 9.72 ± 0.03 GPa were obtained for nanoindentations with contact depths between 30 and 186 nm. No systematic variations of machine compliance or Joslin–Oliver parameter were observed in the systematic SYS plot analysis over this range of contact depths. Uncertainties in calibration measurements correspond to standard errors.
For nanoindentation, an open-loop, two-part load function was created consisting of a quasistatic multiload segment followed by a dynamic reference frequency segment (Figure 1). This load function design facilitated both quasistatic and viscoelastic micromechanical measurements from the same nanoindentation locations. A pre-nanoindentation 25 nm lift-off, 2 stage offset, and reapproach were used to accurately detect the undeformed specimen surface. The multiload part was based on the multiload load function described in detail in [18]. It was designed to provide data needed for employing the structural compliance method and to measure depth-dependent elastic modulus and hardness. It consisted of eight cycles with each cycle containing four segments: (1) a 2 s loading segment, (2) a 5 s hold at the cycle maximum load, (3) a 1.4 s unloading segment to 30% of the cycle maximum load, and (4) a 1 s hold at 30% of the cycle maximum load before starting the next cycle. The quasistatic multiload part ended with a loading segment after the eighth cycle that loaded to the overall nanoindentation maximum load. The multiload cycle maximum loads ranged from 4 to 81% of the overall nanoindentation maximum load. The dynamic reference frequency part was designed to assess viscoelastic properties, including storage modulus , loss modulus , and mechanical damping , from 0.1 to 200 Hz. Assessing properties over such a large frequency range required about 30 min. Reference frequency load functions are advantageous for long duration experiments because the reference frequency segments are used to determine contact areas instead of depth [51,52]. The depth measurements become unreliable during long nanoindentation experiments because of displacement drift uncertainties. The dynamic part began with a 17 s segment at 220 Hz, then an initial 10 s reference frequency segment at 220 Hz. The remaining dynamic part consisted of a series of alternating testing frequency and 10 s reference frequency segments, before ending with a 5 s unload. There were 11 testing frequencies, which were evenly positioned on a logarithmic scale from 200 to 0.1 Hz [43]. Figure 2 shows a representative load-depth trace of a quasistatic and dynamic test on the transverse plane in the S2 layer of radiata pine wood cell wall.

Figure 1.
Load function comprises of a multiload function and a reference frequency segment.
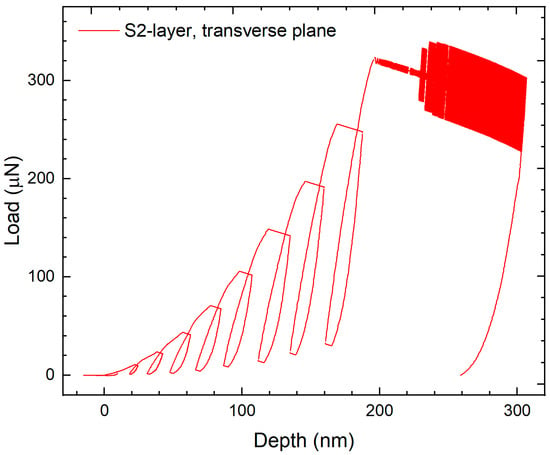
Figure 2.
Load depth trace of a quasistatic and dynamic experiment on the transverse plane in the S2 layer of radiata pine wood cell wall.
Nanoindentation experiments followed the best practices described in [18] to minimize errors arising from misplaced nanoindentations, surface detection errors, dirty probes, displacement drift, and nanoindenter calibration or performance issues as well as structural compliances caused by nearby free edges and cellular flexing. In brief, wood specimens were placed inside of the nanoindenter enclosure and left to equilibrate 48 h before testing. Areas for nanoindentation were chosen using the optical microscope in the TriboIndenter. Scanning probe microscopy images obtained using the nanoindentation probe were used to both place the nanoindentations in the cell wall layer of interest and to verify their placement after experiments (Figure 3). Any nanoindentation overlapping an interface was discarded. In the multiload part, unloading segments with contact depths lower than 30 nm were excluded from further analysis because tip roundness effects were detected in the fused silica calibrations below that depth. The structural compliance method [48,53] was employed using the quasistatic multiload part of the experiment to remove potential artifacts arising from nearby edges and specimen-scale flexing. Both the quasistatic and dynamic parts were corrected using the structural compliance measurement from the analysis of the multiload segments.
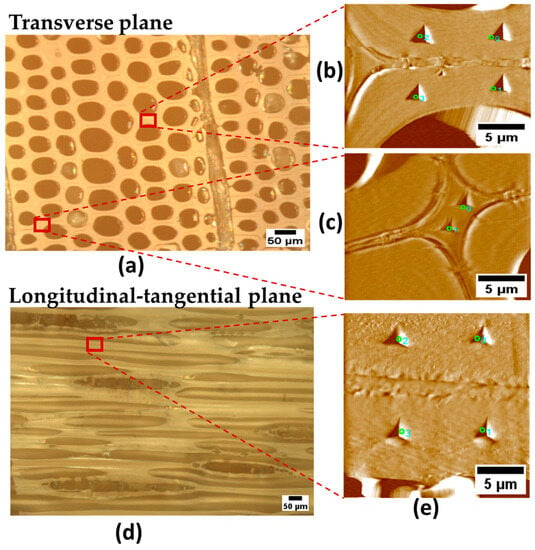
Figure 3.
Cutting planes in radiata pine wood. (a) Transverse plane with nanoindentations on (b) S2 layer and (c) CCML, (d) Longitudinal–tangential plane with nanoindentations on (e) S2 layer.
The quasistatic reduced elastic modulus () and hardness (H) of the cell wall layers were then calculated using the following equations:
where S is the contact stiffness of the unloading segment, is the projected contact area, and Pmax is the maximum load immediately prior to unloading. To evaluate the specimen elastic modulus of the sample (), while considering the probe contributions to the , the following equation was used:
where is the elastic modulus of the diamond probe (1137 GPa), and are the Poisson’s ratio of diamond probe and sample, respectively. For this work, and were used [54].
The storage modulus , loss modulus , and the mechanical damping were obtained directly from [55]:
and are the dynamic stiffness and damping coefficients, respectively, is the radial frequency, is the Poisson’s ratio of the sample, , and is the reference contact area calculated using the following:
where is the E′ calculated from the initial reference frequency segment. For each testing frequency segment, was calculated using the Ks from the reference frequency segment immediately following the testing segment.
3. Results and Discussion
3.1. Quasistatic Nanoindentations
In this investigation, unembedded specimens were used. Therefore, nanoindentations in wood cell wall layers were always nearby heterophase interfaces, such as the free edge of a lumen surface, and the entire open cellular structure could flex under loading. Thus, for each nanoindentation, the structural compliance method was employed using the initial quasistatic multiload segments. This allowed for reducing or eliminating the effects associated with the heterophase interfaces and specimen-scale flexing, which, if left unaccounted for, can lead to an overestimation or underestimation of hardness and elastic modulus [18]. Because the structural compliance correction is location-dependent, the structural compliance correction calculated from the quasistatic multiload portion was applied to the entire nanoindentation experiment, including the dynamic portions. Therefore, both the quasistatic multiload and dynamic viscoelastic experiments were corrected for structural compliances.
Figure 4 shows the behavior of the elastic modulus and hardness in the multiload segments as a function of the contact depth of each of the indentations performed. It is observed that the results lower than 30 nm were discarded because of tip roundness effects. It is clear that the hardness and elastic modulus values for samples are almost constant throughout the indentation depth. The scatter in each nanonidentation results in a good part from the variability of the S2 layer and CCML of the samples. Although variability is present in all the quasistatic results, no systematic trends in mechanical behavior with contact depth could be observed. In relation to the elastic modulus in the transverse orientation, an average of 15.7 ± 1.9 GPa was obtained, with a coefficient of variation of 12.5% (Figure 4a). This variation is generated by the orientation of the microfibril angles (MFA), which is the dominant parameter of microstructural influence on wood stiffness. Jäger et al. found different results in the elastic modulus evaluated over the range of MFA from 0 to 90° [56]. The same variation in mechanical properties was observed by [57] but in a range from 15 to 36°. The degree of inclination of the microfibril angle can be affected by the proximity to the cell lumen and pits [15]. The elastic modulus values found in this research are slightly higher than those reported by [58,59]. On the other hand, the hardness presented an average of 331.1 ± 26.3 MPa (Figure 4b). The variation in the hardness measurements was 7.9%. This result is slightly lower than that reported by Moon (2009) in non-impregnated radiata pine latewood cells [60], but it is within the range of hardness reported for another pine species [17]. This discrepancy in results in both elastic modulus and hardness could be due to variability in wood structure and more specifically microfibril angles, which can vary even between different growth rings, resin embedment, or differences in the RH of the testing environment.
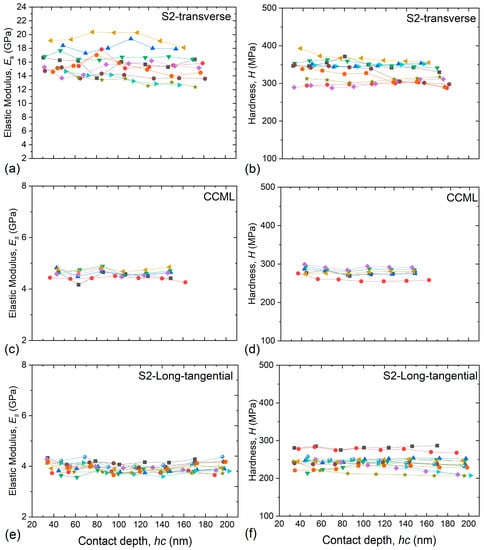
Figure 4.
Elastic modulus and hardness of wood cell walls obtained from individual nanoindentations. (a,b) S2 layer in the transverse orientation; (c,d) CCML in the transverse orientation; (e,f) S2 layer in the longitudinal–tangential orientation. Each colored curve represents the complete multiload segment of a nanoindentation.
The average value of the elastic modulus of the CCML was 4.6 ± 0.2 GPa, and the coefficient of variation was 3.6%. Other authors have found values of 6.8 GPa in the CCML of Norway spruce [15] and 5.0 GPa in loblolly pine [53]. The value of the elastic modulus for radiata pine is clearly reduced in the middle lamella, which is approximately 30% of the result found in the S2 layer (Figure 4c). These differences between the mechanical properties of the secondary wall and the middle lamella are due to the proportion of structural components [61]. Concerning the hardness of the CCML, an average of 277.6 ± 11.4 MPa and a coefficient of variation of 4.1% were found (Figure 4d). This low variability is justified by the fact that the middle lamella is mainly constituted by lignin, around 86% [62], while in the S2 layer, apart from cellulose, there is also the presence of lignin and hemicelluloses. Likewise, the higher coefficient of variation of the hardness in the S2 layer is due to the spatial variation in the distribution of lignin in the cell wall [63]. Some authors have found no difference between the hardness of the S2 layer and the middle lamella [15,61]. However, the results here showed a contrast since the hardness values in the CCML are approximately 16% lower. This may be due to a higher lignin concentration contributing in two ways: indirectly by increasing the packing density of the cell wall by filling the space between hemicellulose and cellulose fibrils and directly by contributing to the higher cell wall hardness [63]. The difference could also be caused by resin embedment in previous experiments or differences in the RH of the testing environment.
The quantitative analysis of the indentations performed on the S2 layer in the longitudinal-tangential plane revealed average values of the elastic transverse modulus of 3.9 ± 0.2 GPa, with a coefficient of variation of 4.4% (Figure 4e), while the hardness presented average values of 243.9 ± 19.8 MPa and a coefficient of variation of 8.9% (Figure 4f). The average value of the elastic modulus is four times lower than the longitudinal elastic modulus. Similarly, [64] found in the S2 layer of spruce wood up to 5.8 times higher values in the longitudinal elastic modulus than the transversal elastic modulus. This is because the direction of application of the indenter probe is perpendicular to the arrangement of the cellulose fibrils in the S2 layer. Thus, when performing an indentation in this orientation, the fibrils are in a mechanical series with the more compliant amorphous polymers in the matrix, which therefore have the greatest influence on the transverse elastic modulus [1].
3.2. NanoDMA
When wood is put into service, it can be subjected to different time scales of stresses, and the mechanical behavior of material varies as a function of frequency. Thus, depending on the application of the oscillatory loads, it will exhibit different properties. The viscoelastic response of wood is a result of the structure and relaxations of the structural wood polymer components and their interactions with environmental conditions (humidity and temperature). This leads to a complex deformation mechanism in response to stress. Figure 5 shows the viscoelastic properties of radiata pine wood S2 layer in the transverse direction. The influence of temperature on storage modulus has been extensively studied. It has been found that the modulus decreases with increasing temperature [65]. However, this behavior is opposite to the frequency—that is, the storage modulus increases as the frequency increases—obtaining lower values of 14.3 and 14.7 GPa for frequencies lower than 1 Hz, and the maximum value (16.9 GPa) was found at higher frequencies. However, it is observed that, at the frequency of 93.5 Hz, the value of the storage modulus is similar to that at the frequency of 200 Hz. This value is higher than that reported by [39] on Norway Spruce wood cell wall. These researchers obtained an average storage modulus of 15.5 GPa and 12.4 GPa for air-dried and artificially dried wood, respectively, using modulus mapping at a frequency of 80 Hz. The increase of storage modulus with frequency was also observed in the Carapa species cell wall using nanoDMA in a frequency range of 10 to 240 Hz [36] and in Chinese fir wood [66].
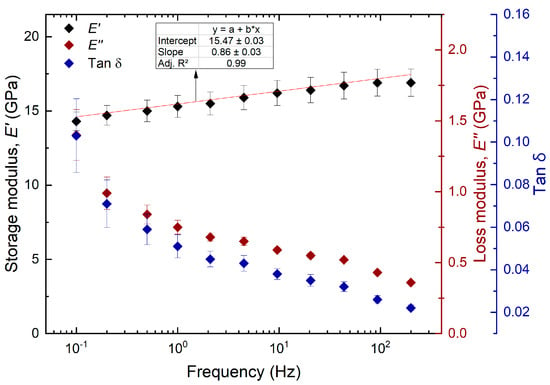
Figure 5.
Viscoelastic properties of the S2 cell wall layer in the transverse plane. Error bars are the standard error.
As seen in Figure 5, the increase in the modulus is linear and fits the logarithmic scale of the frequency with an adjusted coefficient of determination of 0.99. The reason for this increase in storage modulus is due to the shorter exposure times (cycle/s) of the material to the load. Therefore, the polymer chains will be able to recover faster, and the amount of stored energy is higher. The polymer chains have minimal movements, and this makes it behave as a rigid material. In contrast to the storage modulus, it is observed that the amount of dissipated energy or loss modulus increases as the frequency decreases, with values from 1.40 GPa for the lowest frequency to 0.36 GPa at 200 Hz. Therefore, it is evident that the material has a stiffer behavior at high frequencies because the viscous response is related to the relaxation time of the material. At high frequencies, the duration of each cycle time is shorter; therefore, there is less time for the chains to relax, begin to move, and reach new conformations in response to the applied stress. Consequently, the viscous response of the material is lost [67]. On the other hand, when wood is subjected to cyclic loading, it loses energy during the deformation process. This loss factor is smaller as the frequency becomes larger, since there is less energy dissipated due to the small molecular movement. Here, the tan decreased from 0.10 at the lowest frequency to 0.02 at 200 Hz. A decrease in tan was also observed by [36,43].
Similarly, for the CCML (Figure 6), the values of the storage modulus increased as the frequency increased. A linear correlation was obtained with an . Compared to the S2 layer, the storage modulus values are considerably lower. At the maximum frequency, 200 Hz, the storage modulus was 5.7 GPa. This value decreased until it reached 4.4 GPa at the frequency of 0.1 Hz. Likewise, as indicated in the quasistatic indentations section, the decrease in modulus is related to the chemical composition of the CCML, which is mostly constituted by lignin with some hemicelluloses and lacks the highly organized stiff cellulose fibrils. On the other hand, following the same order of the frequency described above, the loss modulus presented values of 0.22 GPa and 0.39 GPa, respectively. Evidently, the loss modulus decreased as the frequency increased. However, unlike the S2 layer this was not a featureless decrease in the loss modulus with increasing frequency. There is a decrease in the loss modulus from 0.1 to 0.5 Hz, followed by an increase until 4.5 Hz, and another decrease in the loss modulus until reaching the maximum frequency. The variation of the tan as a function of frequency is also shown. The plateau in tan here is very similar to that previously observed in the loblolly pine CCML [43]. Jakes [43] also tested under higher RH conditions and observed that the plateau in Figure 6 is actually a peak in tan that clearly emerges at higher frequencies under higher RH conditions.
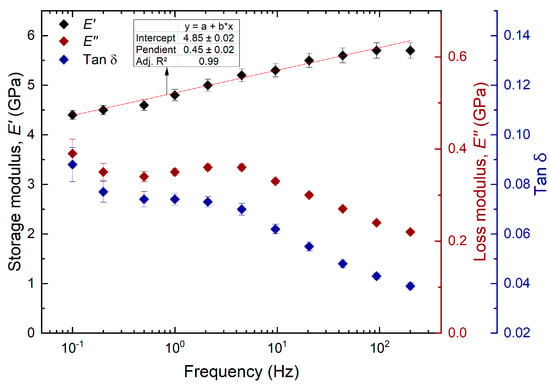
Figure 6.
Viscoelastic properties of the CCML in the transverse plane. Error bars are the standard error.
Figure 7 shows the viscoelastic properties for the S2 layer in the longitudinal–tangential orientation. The storage modulus in this direction increased with frequency. A strong linear correlation = 0.99 is shown. It is observed that the storage modulus at the maximum frequency (200 Hz) is slightly lower than the value reported for the CCML and up to three times lower than the elastic modulus of the S2 layer in the transverse direction. This trend is maintained for the remaining frequencies. The loss modulus increases with increasing frequency until it reaches a peak at frequency 4.5 Hz, then decreases with increasing frequency. The tan changes with frequency, it tends to decrease towards higher frequencies. However, it is observed that there is a plateau. Again, this plateau in tan here is very similar to that previously observed in the loblolly pine S2 layer tested in a longitudinal plane, which was attributed to a tan peak that emerges at higher frequencies under higher RH conditions [43]. In general, the CCML and the S2 layer tested in the longitudinal–tangential plane behave similarly, despite the marked differences in the proportions of their underlying structural components. However, during testing on the longitudinal plane, the stress is applied in the direction perpendicular to the long, stiff axis of the cellulose fibrils in the S2 layer. Thus, the fibrils are in a mechanical series with the more compliant amorphous polymers in the matrix, which therefore have the greatest influence on the transverse elastic modulus. The similarity between the transverse S2 layer and the CCML viscoelastic properties is likely because the mechanical responses are both being similarly dominated by the matrix polymers lignin and hemicelluloses.
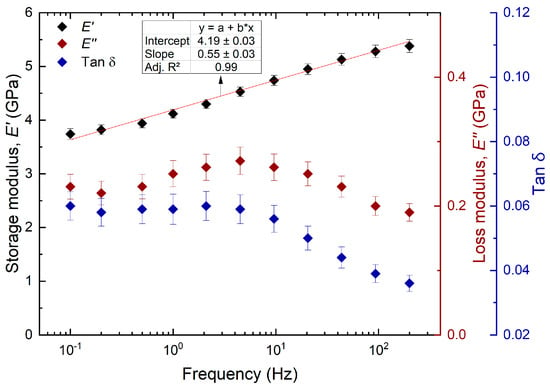
Figure 7.
Viscoelastic properties of the S2 layer in the longitudinal–tangential plane. Error bars are the standard error.
The load function used made it possible to obtain both quasistatic and dynamic properties at the same nanoindentation locations. For comparison, a frequency is estimated for the quasistatic experiments using the transformation f = 1/2πtul where tul is the 2 s unloading time [26,42]. Therefore, the approximate frequency corresponding to the quasistatic results is about 0.08 Hz. When comparing the values obtained for quasi-static and dynamic indentations equivalent at a frequency of 0.1 Hz, it is found that the elastic and storage moduli are relatively similar. When there is no damping, the elastic modulus is similar to the storage modulus [68]. However, when it comes to wood, this does not occur markedly due to its viscoelastic nature, which was evident in the results shown. Table 1 shows the results of the elastic and dynamic moduli for the S2 layer and CCML.

Table 1.
Elastic and storage moduli for the S2 layer and CCML in the different wood planes.
4. Conclusions
The application of a load function composed of a multiload segment and a reference frequency segment provided results for the quasistatic and dynamic mechanical properties of the S2 layer and CCML of radiata pine wood. It is important to note that several nanoindentations were performed in different cell walls, but for each nanoindentation, both types of properties were obtained, which allows having thorough data on the mechanical behavior of the wood cell walls that can be used for both engineering applications as well as investigating causal links between microphysical processes and material properties. The small variations in the nanoindentations performed reflected the inhomogeneities of the wood structure. The mechanical properties of wood are a function of the chemical composition and the arrangement of the polymeric chains. The chemical nature of each structural component gives the wood a viscoelastic behavior, which is dependent on the service conditions of the wood. When subjected to cyclic loading, the material will respond according to the intensity of the stress. In this investigation, for the S2 layer and CCML, the storage modulus increased with frequency, while the viscous response of the material remained relatively constant or decreased. When comparing the values of the elastic and storage moduli obtained at a frequency of 0.1 Hz from all the planes studied in this work, it is observed that they are very similar, other than for the elastic modulus of the S2 layer in the transverse orientation, whose value is higher than the storage modulus. Radiata pine is a species that has a high projection for structural use.
This study contributes to the generation of information on microscale properties. The data on the mechanical and dynamic properties can be used to model and simulate the structural behavior of wood, providing a better understanding, for example, of the stress distribution throughout the wood and its load-bearing capacity. This contributes to optimizing a design. Additionally, from a dynamic perspective, a material such as wood can suffer significant damage when exposed to cyclic loads, making it a critical factor in the durability and stability of the structure. Therefore, the values reported here can be used in models that design damping systems and impact reduction for external loads—that is, modeling the vibratory behavior of wood-based structural elements in order to minimize the risk of structural failures due to the dynamic loads.
Author Contributions
Conceptualization, O.E. and J.E.J.; methodology, J.E.J.; validation, J.E.J., O.E. and W.G.; formal analysis, O.E., J.E.J. and N.Z.P.; investigation, O.E., J.E.J. and W.G.; resources, W.G.; data curation, J.E.J. and O.E.; writing—original draft preparation, O.E.; writing—review and editing, O.E., J.E.J., N.Z.P., W.G., J.V.-F. and P.V.; visualization, O.E., J.E.J., N.Z.P., W.G., J.V.-F. and P.V.; supervision, J.E.J.; project administration, W.G.; funding acquisition, W.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Agency for Research and Development (ANID) through the Research Project FONDECYT No. 1191228.
Data Availability Statement
Data can be available upon reasonable request to the corresponding author.
Acknowledgments
The authors would like to acknowledge the USDA Forest Service, Forest Products Laboratory for the support of the Nanoindentation testing. Oswaldo Erazo would like to thank the University of Bío Bío for the Doctoral Scholarship and Research Grant.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bergander, A.; Salmén, L. Cell Wall Properties and Their Effects on the Mechanical Properties of Fibers. J. Mater. Sci. 2002, 37, 151–156. [Google Scholar] [CrossRef]
- Winandy, J.E.; Rowell, R.M. Chemistry of Wood Strength; CRC Press: Boca Raton, FL, USA, 2012; ISBN 9781439853818. [Google Scholar]
- Kaboorani, A.; Blanchet, P.; Laghdir, A. A Rapid Method to Assess Viscoelastic and Mechanosorptive Creep in Wood. Wood Fiber Sci. 2013, 45, 370–382. [Google Scholar]
- Fathi, H.; Kazemirad, S.; Nasir, V. A Nondestructive Guided Wave Propagation Method for the Characterization of Moisture-Dependent Viscoelastic Properties of Wood Materials. Mater. Struct. Constr. 2020, 53, 147. [Google Scholar] [CrossRef]
- Sharma, M.; Brennan, M.; Chauhan, S.S.; Entwistle, K.M.; Altaner, C.M.; Harris, P.J. Wood Quality Assessment of Pinus radiata (Radiata pine) Saplings by Dynamic Mechanical Analysis. Wood Sci. Technol. 2015, 49, 1239–1250. [Google Scholar] [CrossRef]
- Pearson, H.; Gabbitas, B.; Ormarsson, S. Tensile Behaviour of Radiata Pine with Different Moisture Contents at Elevated Temperatures. Holzforschung 2012, 66, 659–665. [Google Scholar] [CrossRef]
- Fortino, S.; Metsäjoki, J.; Ronkainen, H.; Bjurhager, I.; Heinemann, S.; Salminen, L.I. Scratch Resistance of PEG-Impregnated Green Wood: A Method for Evaluation of Swollen Wood Properties. Wood Sci. Technol. 2020, 54, 715–735. [Google Scholar] [CrossRef]
- Soares, L.S.Z.R.; Fraga, I.F.; Paula, L.D.S.E.; Arroyo, F.N.; Ruthes, H.C.; Aquino, V.B.D.M.; Molina, J.C.; Panzera, T.H.; Branco, L.A.M.N.; Christoforo, A.L.; et al. Influence of Moisture Content on Physical and Mechanical Properties of Cedrelinga Catenaeformis Wood. BioResources 2021, 16, 6758–6765. [Google Scholar] [CrossRef]
- Olsson, A.-M.; Salmén, L. The Effect of Lignin Composition on the Viscoelastic Properties of Wood. Nord. Pulp Pap. Res. J. 1997, 12, 140–144. [Google Scholar] [CrossRef]
- Hu, W.; Chen, B.; Zhang, T. Experimental and Numerical Studies on Mechanical Behaviors of Beech Wood under Compressive and Tensile States. Wood Res. 2021, 66, 27–38. [Google Scholar] [CrossRef]
- Nowak, T.; Patalas, F.; Karolak, A. Estimating Mechanical Properties of Wood in Existing Structures—Selected Aspects. Materials 2021, 14, 1941. [Google Scholar] [CrossRef]
- Eder, M.; Arnould, O.; Dunlop, J.W.C.; Hornatowska, J.; Salmén, L. Experimental Micromechanical Characterisation of Wood Cell Walls. Wood Sci. Technol. 2013, 47, 163–182. [Google Scholar] [CrossRef]
- Gindl, W.; Gupta, H.S.; Schöberl, T.; Lichtenegger, H.C.; Fratzl, P. Mechanical Properties of Spruce Wood Cell Walls by Nanoindentation. Appl. Phys. A Mater. Sci. Process. 2004, 79, 2069–2073. [Google Scholar] [CrossRef]
- Gacitua, W.; Bahr, D.; Wolcott, M. Damage of the Cell Wall during Extrusion and Injection Molding of Wood Plastic Composites. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1454–1460. [Google Scholar] [CrossRef]
- Wagner, L.; Bader, T.K.; De Borst, K. Nanoindentation of Wood Cell Walls: Effects of Sample Preparation and Indentation Protocol. J. Mater. Sci. 2014, 49, 94–102. [Google Scholar] [CrossRef]
- Li, J.; Yu, Y.; Feng, C.; Wang, H. Mechanical Characterization of Pinus massoniana Cell Walls Infected by Blue-Stain Fungi Using in Situ Nanoindentation. J. For. Res. 2020, 31, 661–665. [Google Scholar] [CrossRef]
- Vincent, M.; Tong, Q.; Terziev, N.; Daniel, G.; Bustos, C.; Escobar, W.G.; Duchesne, I. A Comparison of Nanoindentation Cell Wall Hardness and Brinell Wood Hardness in Jack Pine (Pinus banksiana Lamb.). Wood Sci. Technol. 2014, 48, 7–22. [Google Scholar] [CrossRef]
- Jakes, J.E.; Stone, D.S. Best Practices for Quasistatic Berkovich Nanoindentation of Wood Cell Walls. Forests 2021, 12, 1696. [Google Scholar] [CrossRef]
- Oliver, W.; Pharr, G. An Improved Technique for Determining Hardness and Elastic Modulus Using Load and Displacement Sensing Indentation Experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Qin, L.; Lin, L.; Fu, F.; Fan, M. Micromechanical Properties of Wood Cell Wall and Interface Compound Middle Lamella Using Quasi-Static Nanoindentation and Dynamic Modulus Mapping. J. Mater. Sci. 2018, 53, 549–558. [Google Scholar] [CrossRef]
- Prošek, Z.; Topič, J.; Tesárek, P.; Indrová, K.; Nežerka, V.; Králik, V.; Klapálek, P. Micromechanical Properties of Spruce Tissues Using Static Nanoindentation and Modulus Mapping. Appl. Mech. Mater. 2015, 732, 115–118. [Google Scholar] [CrossRef]
- Xing, D.; Wang, X.; Wang, S. Temperature-Dependent Creep Behavior and Quasi-Static Mechanical Properties of Heat-Treatedwood. Forests 2021, 12, 968. [Google Scholar] [CrossRef]
- Muñoz, F.; Valenzuela, P.; Gacitúa, W. Eucalyptus Nitens: Nanomechanical Properties of Bark and Wood Fibers. Appl. Phys. A Mater. Sci. Process. 2012, 108, 1007–1014. [Google Scholar] [CrossRef]
- Schuh, C.A. Nanoindentation Studies of Materials. Mater. Today 2006, 9, 32–40. [Google Scholar] [CrossRef]
- Hayes, S.A.; Goruppa, A.A.; Jones, F.R. Dynamic Nanoindentation as a Tool for the Examination of Polymeric Materials. J. Mater. Res. 2004, 19, 3298–3306. [Google Scholar] [CrossRef]
- Jakes, J.E.; Lakes, R.S.; Stone, D.S. Broadband Nanoindentation of Glassy Polymers: Part I. Viscoelasticity. J. Mater. Res. 2012, 27, 463–474. [Google Scholar] [CrossRef]
- Jakes, J.E.; Lakes, R.S.; Stone, D.S. Broadband Nanoindentation of Glassy Polymers: Part II. Viscoplasticity. J. Mater. Res. 2012, 27, 475–484. [Google Scholar] [CrossRef]
- Nayar, V.T.; Weiland, J.D.; Nelson, C.S.; Hodge, A.M. Elastic and Viscoelastic Characterization of Agar. J. Mech. Behav. Biomed. Mater. 2012, 7, 60–68. [Google Scholar] [CrossRef]
- Placet, V.; Passard, J.; Perré, P. Viscoelastic Properties of Green Wood across the Grain Measured by Harmonic Tests in the Range 0–95 °C: Hardwood vs. Softwood and Normal Wood vs. Reaction Wood. Holzforschung 2007, 61, 548–557. [Google Scholar] [CrossRef]
- Łukomski, M.; Bridarolli, A.; Fujisawa, N. Nanoindentation of Historic and Artists’ Paints. Appl. Sci. 2022, 12, 1018. [Google Scholar] [CrossRef]
- Chakravartula, A.; Komvopoulos, K. Viscoelastic Properties of Polymer Surfaces Investigated by Nanoscale Dynamic Mechanical Analysis. Appl. Phys. Lett. 2006, 88, 7–22. [Google Scholar] [CrossRef]
- Venugopal, G.; Veetil, J.C.; Raghavan, N.; Singh, V.; Kumar, A.; Mukkannan, A. Nano-Dynamic Mechanical and Thermal Responses of Single-Walled Carbon Nanotubes Reinforced Polymer Nanocomposite Thinfilms. J. Alloys Compd. 2016, 688, 454–459. [Google Scholar] [CrossRef]
- Liu, K.; Ostadhassan, M.; Bubach, B.; Dietrich, R.; Rasouli, V. Nano-Dynamic Mechanical Analysis (Nano-DMA) of Creep Behavior of Shales: Bakken Case Study. J. Mater. Sci. 2018, 53, 4417–4432. [Google Scholar] [CrossRef]
- Mallikarjunachari, G.; Ghosh, P. Pile-up Response of Polymer Thin Films to Static and Dynamic Loading. Thin Solid Films 2019, 677, 1–12. [Google Scholar] [CrossRef]
- Panchal, V.; Dobryden, I.; Hangen, U.D.; Simatos, D.; Spalek, L.J.; Jacobs, I.E.; Schweicher, G.; Claesson, P.M.; Venkateshvaran, D. Mechanical Properties of Organic Electronic Polymers on the Nanoscale. Adv. Electron. Mater. 2022, 8, 2101019. [Google Scholar] [CrossRef]
- Zhang, T.; Bai, S.L.; Zhang, Y.F.; Thibaut, B. Viscoelastic Properties of Wood Materials Characterized by Nanoindentation Experiments. Wood Sci. Technol. 2012, 46, 1003–1016. [Google Scholar] [CrossRef][Green Version]
- Wang, X.; Zhao, L.; Xu, B.; Li, Y.; Wang, S.; Deng, Y. Effects of Accelerated Aging Treatment on the Microstructure and Mechanics of Wood-Resin Interphase. Holzforschung 2017, 72, 235–241. [Google Scholar] [CrossRef]
- Prošek, Z.; Králík, V.; Topic, J.; Nežerka, V.; Indrová, K.; Tesárek, P. A Description of the Microstructure and the Micromechanical Properties of Spruce Wood. Acta Polytech. 2015, 55, 39–49. [Google Scholar] [CrossRef]
- Prošek, Z.; Topič, J.; Tesárek, P.; Nežerka, V.; Králik, V. Modulus Mapping and Its Use to Determine the Effect Process of Drying on the Cells of Spruce. Key Eng. Mater. 2016, 714, 25–28. [Google Scholar] [CrossRef]
- Wang, X.; Chen, X.; Xie, X.; Yuan, Z.; Cai, S.; Li, Y. Effect of Phenol Formaldehyde Resin Penetration on the Quasi-Static and Dynamic Mechanics Ofwood Cellwalls Using Nanoindentation. Nanomaterials 2019, 9, 1409. [Google Scholar] [CrossRef]
- Li, Y.; Yin, L.; Huang, C.; Meng, Y.; Fu, F.; Wang, S.; Wu, Q. Quasi-Static and Dynamic Nanoindentation to Determine the Influence of Thermal Treatment on the Mechanical Properties of Bamboo Cell Walls. Holzforschung 2015, 69, 909–914. [Google Scholar] [CrossRef]
- Lakes, R. Viscoelastic Materials; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Jakes, J.E. Mechanism for Diffusion through Secondary Cell Walls in Lignocellulosic Biomass. J. Phys. Chem. B 2019, 123, 4333–4339. [Google Scholar] [CrossRef]
- CONAF Plantaciones Forestales. Available online: https://www.conaf.cl/nuestros-bosques/plantaciones-forestales/ (accessed on 18 April 2023).
- ASTM D2395:14; Standard Test Methods for Density and Specific Gravity (Relative Density) of Wood and Wood-Based Materials. American Society for Testing Materials: West Conshohocken, PA, USA, 2014; Volume 93, pp. 1–13. [CrossRef]
- Sedighi-Gilani, M.; Sunderland, H.; Navi, P. Within-Fiber Nonuniformities of Microfibril Angle. Wood Fiber Sci. 2006, 38, 132–138. [Google Scholar]
- Meng, Y.; Wang, S.; Cai, Z.; Young, T.M.; Du, G.; Li, Y. A Novel Sample Preparation Method to Avoid Influence of Embedding Medium during Nano-Indentation. Appl. Phys. A Mater. Sci. Process. 2012, 110, 361–369. [Google Scholar] [CrossRef]
- Jakes, J.E.; Frihart, C.R.; Beecher, J.F.; Moon, R.J.; Stone, D.S. Experimental Method to Account for Structural Compliance in Nanoindentation Measurements. J. Mater. Res. 2008, 23, 1113–1127. [Google Scholar] [CrossRef]
- Jakes, J.E. Improved Methods for Nanoindentation Berkovich Probe Calibrations Using Fused Silica. J. Mater. Sci. 2018, 53, 4814–4827. [Google Scholar] [CrossRef]
- Stone, D.S.; Yoder, K.B.; Sproul, W.D. Hardness and Elastic Modulus of TiN Based on Continuous Indentation Technique and New Correlation. J. Vac. Sci. Technol. A Vac. Surf. Film. 1991, 9, 2543–2547. [Google Scholar] [CrossRef]
- Asif, S.A.S.; Pethica, J.B. Nano-Scale Viscoelastic Properties of Polymer Materials. Mater. Res. Soc. Symp. Proc. 1997, 505, 103–108. [Google Scholar] [CrossRef]
- Syed Asif, S.A.; Pethica, J.B. Nanoindentation Creep of Single-Crystal Tungsten and Gallium Arsenide. Philos. Mag. A 1997, 76, 1105–1118. [Google Scholar] [CrossRef]
- Jakes, J.E.; Frihart, C.R.; Beecher, J.F.; Moon, R.J.; Resto, P.J.; Melgarejo, Z.H.; Suárez, O.M.; Baumgart, H.; Elmustafa, A.A.; Stone, D.S. Nanoindentation near the Edge. J. Mater. Res. 2009, 24, 1016–1031. [Google Scholar] [CrossRef]
- Baradit, E.; Fuentealba, C.; Yáñez, M. Elastic Constants of Chilean Pinus radiata Using Ultrasonic. Maderas Cienc. y Tecnol. 2021, 23, 1–10. [Google Scholar] [CrossRef]
- Herbert, E.G.; Oliver, W.C.; Pharr, G.M. Nanoindentation and the Dynamic Characterization of Viscoelastic Solids. J. Phys. D Appl. Phys. 2008, 41, 074021. [Google Scholar] [CrossRef]
- Jäger, A.; Bader, T.; Hofstetter, K.; Eberhardsteiner, J. The Relation between Indentation Modulus, Microfibril Angle, and Elastic Properties of Wood Cell Walls. Compos. Part A Appl. Sci. Manuf. 2011, 42, 677–685. [Google Scholar] [CrossRef]
- Tze, W.T.Y.; Wang, S.; Rials, T.G.; Pharr, G.M.; Kelley, S.S. Nanoindentation of Wood Cell Walls: Continuous Stiffness and Hardness Measurements. Compos. Part A Appl. Sci. Manuf. 2007, 38, 945–953. [Google Scholar] [CrossRef]
- Liu, M.; Lyu, S.; Peng, L.; Fan, Z.; Cai, L.; Huang, Z.; Lyu, J. Study on Properties of Radiata Pine Wood Treated with Furfuryl Alcohol as Fretboard Materials for String Instruments. Eur. J. Wood Wood Prod. 2022, 80, 1185–1200. [Google Scholar] [CrossRef]
- Erazo, O.; Moreno, P.; Valenzuela, P.; Gacitúa, W. Propriedades Nanomecânicas de Pinus radiata D. Don Para Uso Em Produtos de Alto Valor/Nanomechanical Properties of Pinus radiata D. Don for Use in High Value Products. Braz. J. Dev. 2021, 7, 109892–109905. [Google Scholar] [CrossRef]
- Moon, R.J.; Jakes, J.E.; Beecher, J.F.; Frihart, C.R.; Stone, D.S. Relating Nanoindentation to Macroindentation of Wood. In Advanced Biomass Science and Technology for Bio-Based Products; Research, Station; Hse, C., Jiang, Z., Kuo, M.L., Eds.; Chinese Academy of Forestry: Beijing, China; USDA Forest Service: Washington, DC, USA; Southern Research Station: Washington, DC, USA, 2009; pp. 145–160. [Google Scholar]
- Wimmer, R.; Lucas, B. Comparing Mechanical Properties of Secondary Cell Wall and Cell Corner Middle Lamella in Spruce Wood. IAWA J. 1997, 18, 77–88. [Google Scholar] [CrossRef]
- Donaldson, L.A. S3 Lignin Concentration in Radiata Pine Tracheids. Wood Sci. Technol. 1987, 21, 227–234. [Google Scholar] [CrossRef]
- Gindl, W.; Gupta, H.S.; Grünwald, C. Lignification of Spruce Tracheid Secondary Cell Walls Related to Longitudinal Hardness and Modulus of Elasticity Using Nano-Indentation. Can. J. Bot. 2002, 80, 1029–1033. [Google Scholar] [CrossRef]
- Jäger, A.; Hofstetter, K.; Buksnowitz, C.; Gindl-Altmutter, W.; Konnerth, J. Identification of Stiffness Tensor Components of Wood Cell Walls by Means of Nanoindentation. Compos. Part A Appl. Sci. Manuf. 2011, 42, 2101–2109. [Google Scholar] [CrossRef]
- Jiang, J.; Lu, J.; Yan, H. Dynamic Viscoelastic Properties of Wood Treated by Three Drying Methods Measured at High-Temperature Range. Wood Fiber Sci. 2008, 40, 72–79. [Google Scholar]
- Jiang, J.; Lu, J. Impact of Temperature on the Linear Viscoelastic Region of Wood. Can. J. For. Res. 2009, 39, 2092–2099. [Google Scholar] [CrossRef]
- Menard, K.P. Dynamic Mechanical Analysis: A Pratical Introduction; CRC Press: Boca Raton, FL, USA, 1999; ISBN 0849386888. [Google Scholar]
- Hay, J.; Herbert, E. Measuring the Complex Modulus of Polymers by Instrumented Indentation Testing. Exp. Tech. 2013, 37, 55–61. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).