Next Article in Journal
The Relationships between Root Traits and the Soil Erodibility of Farmland Shelterbelts in the Bashang Region of China
Previous Article in Journal
Reevaluating Near-Infrared Reflectance as a Tool for the Study of Plant Water Status in Holm Oak (Quercus ilex subsp. rotundifolia)
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 14
Issue 9
10.3390/f14091826
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Geographical Variation Reveals Strong Genetic Differentiation in Cryptomeria japonica var. sinensis

by
Xinyu Li
,
Minjun Dai
,
Minqiu Wang
,
Xingtong Wu
,
Mengying Cai
,
Yiling Tao
,
Jiadi Huang
and
Yafeng Wen
*
College of Landscape and Architecture, Central South University of Forestry and Technology, Changsha 410004, China
*
Author to whom correspondence should be addressed.
Forests 2023, 14(9), 1826; https://doi.org/10.3390/f14091826
Submission received: 22 June 2023 / Revised: 29 August 2023 / Accepted: 2 September 2023 / Published: 7 September 2023
(This article belongs to the Section Genetics and Molecular Biology)
Browse Figures
Versions Notes

Abstract

:
The adaptive capacity of tree species is crucial for their survival under environmental change. Liushan (Cryptomeria japonica var. sinensis), an allogamous conifer species, is widely distributed across southern China. However, despite its broad distribution, there have been few investigations on the geographical variation and environmental adaptability of this species. Here, we combined the phenotypic (eight needle traits) and genetic data (14 nSSR loci) to fill this gap by assessing the genetic variation of geographical populations and exploring environmental adaptations of this species. Both phenotypic and molecular genetic analyses indicated a strong genetic differentiation among geographic populations. All populations could be clustered into three groups that were consistent with their geography. Most of the needle traits showed significantly correlated with geography and environmental factors. Geographical isolation and environmental differences are the main factors that have shaped current morphological traits and patterns of genetic variation. We suggest conservation measures to be implemented on a population level with existing populations, especially those with rare phenotypes as the main goal. Our findings shed light on the geographic variation in Liushan and expanded the knowledge of its putative adaptive mechanisms, ultimately benefiting the conservation of this species.

1. Introduction

Biodiversity has become seriously threatened during rapid global climate change, and many plant and animal species are locally extinct or endangered [1,2]. To avoid population extinction, species must spread into new habitats or adapt to environmental changes via phenotypic plasticity or heritable variations and mutations [3]. Compared to animal species, migration is difficult for plant species. Long-lived forest trees normally have wide distribution and strong potential to adapt environmental change due to phenotypic plasticity and local adaptation or combination of these two mechanisms. Selection over time results in changes of allele frequencies at the specific loci underlying those traits and, finally, fixed locally adapted populations [4,5]. Therefore, these variation patterns of morphological and genetic are an effective tool for understanding the adaptive potential of plant resources to environmental changes and are of great significance for their protection and utilization. Classically, the phenotypic patterns have long been observed for centuries. In recent years, environmental data and genetic data have also been widely used to understand the genetic variation of plant populations, spatial distribution, and its relationship with environmental conditions from different perspectives. These approaches can be combined to understand how genetic data complement or overlap with environmental data and phenotypic data in characterizing geographical variation among different populations.
Cryptomeria (family Cupressaceae, subfamily Taxodioideae) is a monotypic Tertiary relict genus that was widespread in North America and Eurasia during the Tertiary period. As consequence of climate changes in the Quaternary, the only extant species in the genus is Cryptomeria japonica, which has adapted to a wide range of environmental conditions in Japan and China. Two Japanese varieties, var. radicans (ura-sugi) and var. japonica (omote-sugi), occur from Aomori Prefecture to Yakushima Island on the Japanese archipelago [6]. Outside of Japan, var. sinensis, also called Liushan, is a separate variety endemic to China and widely distributed in Fujian, Zhejiang, Jiangxi, Hunan, and other provinces in the south of China [7]. This variety has been long cultivated in China owing to its rapid growth rate and high-quality wood [8,9]. Since Liushan has high ecological, economic, and ornamental value, it has become one of the most important forest trees used for afforestation, timber production, and landscaping in China.
Cryptomeria japonica, as a “nation tree” species in Japan [10], has been the subject of investigations of geographical variation among natural forests in Japan, with a focus on its morphological traits [11], diterpene compounds [12], reproductive system [13], and molecular genetic variation [14,15]. Those studies supported that two varieties, ura-sugi and omote-sugi, are strongly shaped by local environments, namely heavy snowfall during winter along the coast of the Sea of Japan and dry climate in winter along the coast of the Pacific Ocean, respectively [16]. It is well known that the historical demographic process, such as range expansion or colonization, could determine the geographical structure and phenotypic traits divergence, finally leading to local populations. Compared with C. japonica in Japan, Liushan (C. Japonica var. sinensis) has a more extensive distribution and occupies more diverse climate environments in China; however, it possesses a lower genetic diversity with strong genetic differentiation, as revealed by our previous study [17,18]. Natural forests of Liushan were seriously damaged due to climate-induced range reduction during the Quaternary period and intensive human interference since the Holocene period. As a result, only limited ancient trees can be found in a few provinces of China. Moreover, the climate has warmed dramatically over the past decades and is expected to continue to intensify in the future, further leading to a series of changes in plant species distributions, vegetation types, plant species richness, etc. [19,20,21]. The precautious status of genetic resources highlight the urgent need for exploring the phenotypic differentiation and genetic structure among different Liushan populations, proposing protection suggestions, and understanding its adaptability to environmental changes, especially under dramatical climate change in the near future.
Identifying the level and spatial distribution of genetic variation among geographical populations is important for the conservation and breeding of this species. However, because of the difficulty in evaluating phenotypes in the field and the limited genomic information available, there are few studies on the geographical variation trends among populations of this species. The aims of this study were to evaluate the phenotypic and molecular genetic diversity of six geographical populations. We focused on the following questions: (1) What is the geographical variation pattern of Liushan populations? (2) Do environmental factors affect genetic variation? (3) How does the phenotypic variation change along environmental gradients? Our results broadly benefit efforts in germplasm collection, breeding improvement, and sustainable conservation of this species and are also valuable for understanding the response of this variety and other trees to climate change.

2. Materials and Methods

2.1. Population Sites and Plant Materials

From among the whole distribution of Liushan in China, we selected six populations from different areas, including a total of 90 individuals. These populations were collected from local forests with a clear genetic background and covered the entire distribution from east to west in China (Figure 1A; Table 1). In each population, 15 individuals were sampled, with 1–2 g of fresh needles collected from each individual for DNA extraction. We collected 30 needle leaves from the middle of two-year-old branchlets for needle trait analyses of each populations. The latitude and longitude information was recorded. Data characterizing 19 bioclimatic variables (Bio1–Bio19) for the current period (1970–2000) with a 30-arc-second spatial resolution were downloaded from the WorldClim website (http://www.worldclim.org/, accessed on 13 July 2022) and were extracted using ArcGIS version 10.7 (Esri, Redlands, CA, USA).

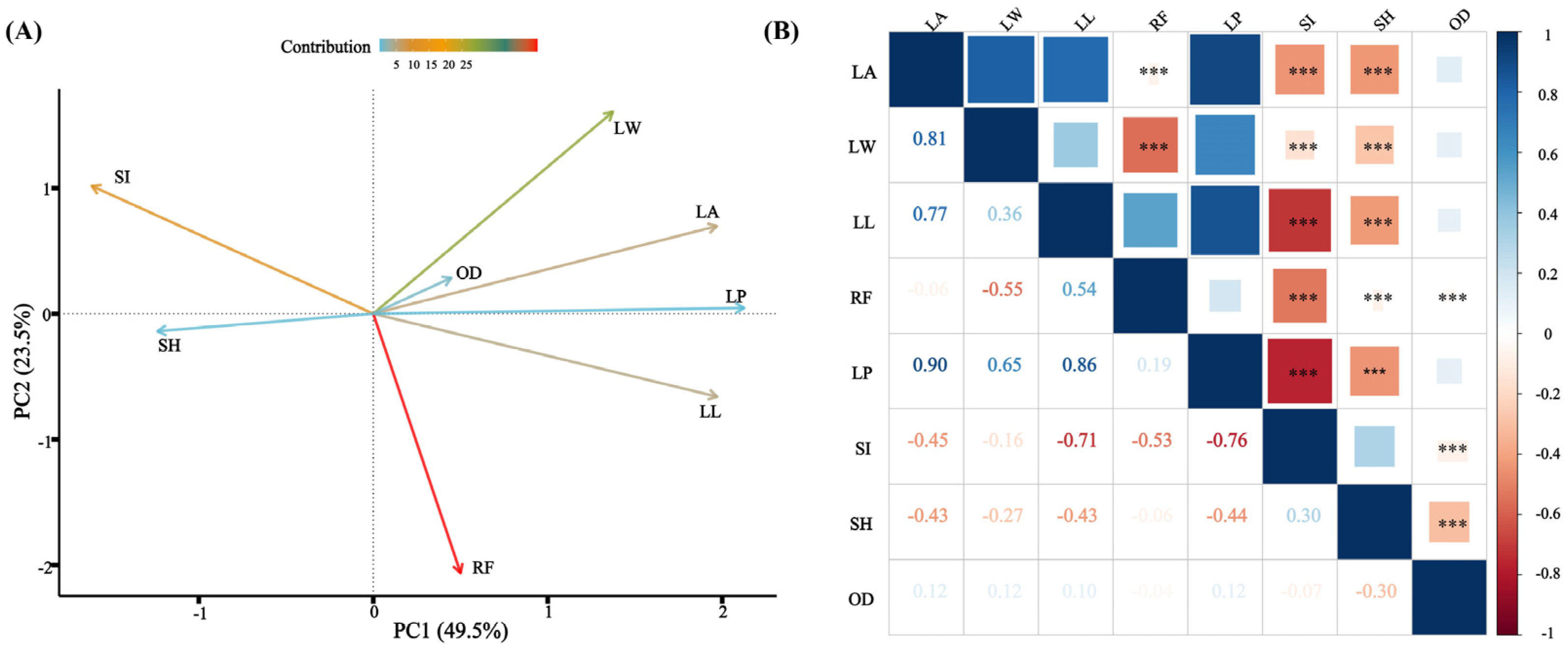
2.2. Needle Trait Analyses

Needle leaf data were collected using the AM350 Portable Leaf Area Meter (ADC Bioscientific Ltd., Hoddesdon, UK), which consists of a high-resolution scanner and scanboard. Needle leaves were placed on the scanboard of the instrument. The scanner chops the image into tiny dots, 1/100″ square4, and the needle data measurements were completed using the high-resolution scanner by identifying the number of tiny dots (LA) and the length or width of continuous dots (LL, LW). The perimeter measurement was made on the compressed image following a scan based on an algorithm developed by Steve Prashker of Carleton University, Canada. Six quantitative traits were measured with 0.1 mm accuracy (except for 0.1 mm2 accuracy for needle area), including leaf area (LA), leaf width (LW), leaf length (LL), ratio of leaf length to width (RF), leaf perimeter (LP), and shape index (SI). Leaf length (LL) is the length measured from the base of the needle up to the tip, and the leaf width (LW) is the maximum width of the needle (Figure S2). The ratio of leaf length to width (RF) is the ratio of leaf length (LL) to leaf width (LW). The shape index (SI) is the ratio of the leaf area (LA) to the leaf perimeter (LP). Furthermore, two qualitative traits of conifer species, namely the softness or hardness of needles (hardness, SH) and the opening degree of needles (opening degree, OD), were also observed. All measurement data were statistically analyzed using Microsoft Excel 2016 (Microsoft Corp., Redmond, WA, USA).
Tests of normality (Shapiro–Wilk) and homogeneity of variance (Levene’s test) were conducted using SPSS 25.0 (IBM Corp., Armonk, NY, USA). Data for all traits exhibited a normal distribution with homogeneous variance. Mean and coefficient of variation (CV) values for each phenotypic trait were calculated using SPSS 25.0. The coefficient of variation, which indicates the degree of trait dispersion, was calculated using the following formula: CV = Standard deviation (SD)/Mean × 100%. Analysis of variance (ANOVA) was conducted also using SPSS 25.0. The Euclidean distance of six geographical Liushan populations was calculated in the R ‘readxl’ package. Based on the Euclidean distances, cluster analysis was performed to explore the relationships among geographical populations. Principal component analysis (PCA) of phenotypic data was performed in the R ‘vegan’ package, and the percentage of contribution of phenotypic traits to each principal component was calculated using the ‘rda’ object. In addition, we also calculated the Pearson correlation coefficients between needle traits and 20 environmental variables (Bio1–Bio19 and elevation) using SPSS 25.0 in order to screen environmental factors that might affect phenotypic traits. For QST analysis, we selected four traits with continuous measurement values and excluded two ratio quantitative traits and two qualitative traits. A mixed linear model was performed in R ‘lme4’ package to calculate phenotypic differences among populations and within population of four quantitative trait (LA, LW, LL, and LP). Longitude and latitude of different populations was considered as fixed effect and population as random effect. Quantitative trait divergence indices (QST) were calculated using the following formula: QST = Va/(Va + 2Vw), where Va is the phenotypic differences among populations and Vw the phenotypic differences within populations [22].

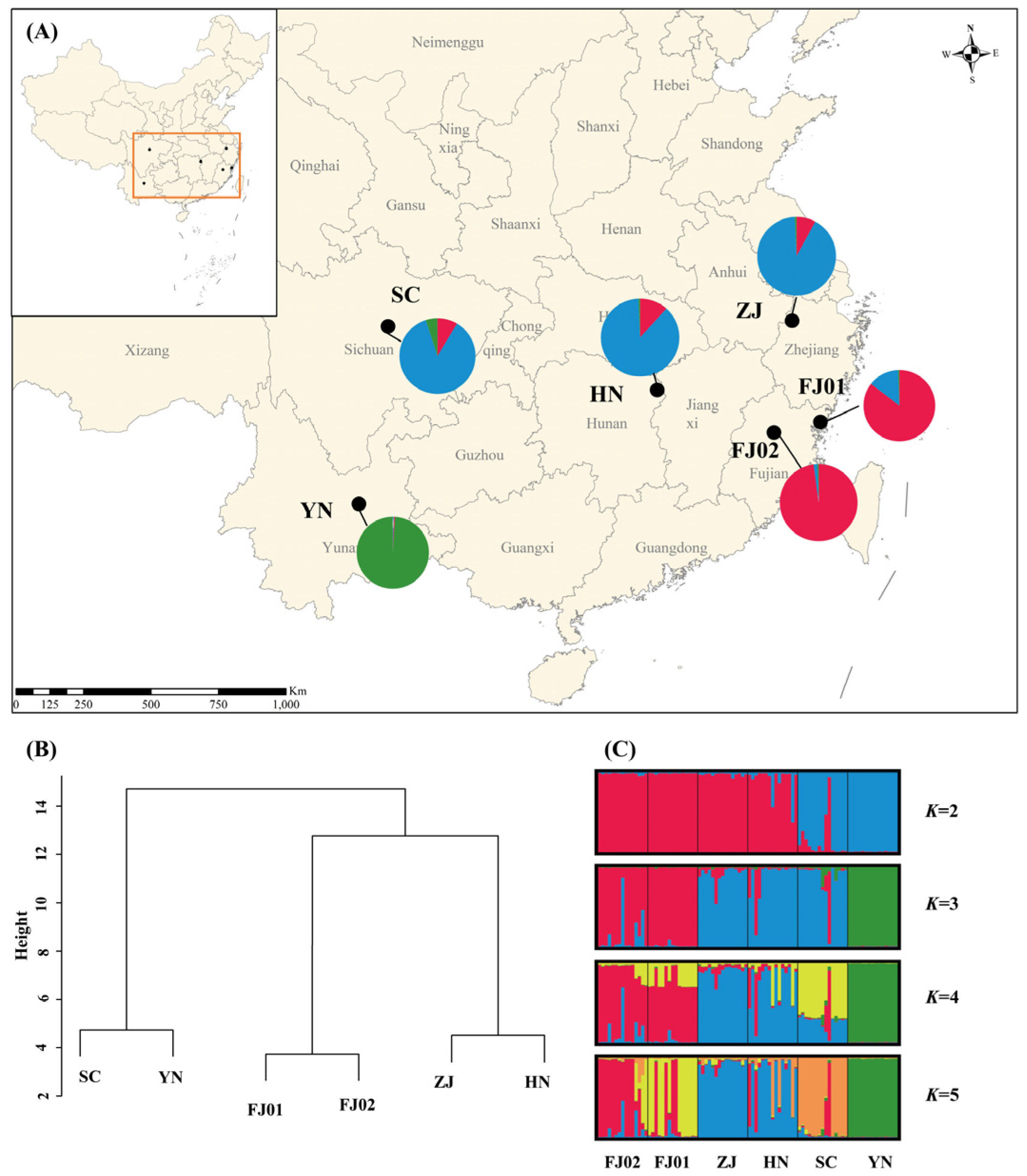
2.3. Genetic Diversity and Population Structure

Genomic DNA was extracted using a modified CTAB method [23], and its quality and concentration were assessed by 1.0% agarose gel electrophoresis and Nano-400 (Hangzhou Allsheng Instruments Co., Ltd., Hangzhou, China), followed by dilution to a concentration of 20–50 ng·μL−1. Fourteen nuclear microsatellites (nSSR) of C. japonica with high polymorphism were selected for subsequent genotyping experiments (Table S1) [24,25,26]. These markers were pre-screened to confirm without null alleles by Micro-Checker 2.2.3 [27]. The primers were labelled at the 5′ end with FAM and HEX fluorescent dyes (Applied Biosystems, Waltham, MA, USA) for polymerase chain reaction (PCR). PCR amplification was conducted in reaction volumes of 15 μL, containing 7.5 μL of 2 × Taq PCR Master Mix (Tiangen, Beijing, China), 0.75 μL of forward primer (10 μmol·L−1) and reverse primer (10 μmol·L−1), 3 μL of ddH2O, and 3 μL of 20–50 ng·μL−1 DNA template. The PCR amplification procedure was performed as follows: 94 °C for 4 min; 34 cycles of 94 °C for 45 s, 55 °C for 45 s, and 72 °C for 45 s; and a final extension at 72 °C for 10 min. The PCR products were visualized on a 1.0% agarose gel, and fluorescence-labeled PCR products were subsequently sized on an ABI 3730xL DNA Analyzer (Applied Biosystems, Waltham, MA, USA) using a GeneScan 500 LIZ internal size standard (Applied Biosystems, Waltham, MA, USA). The software GeneMarker v.1.9 was used to read the peaks observed from the fluorescence-labeled primers of all samples [28].
Genetic diversity parameters were analyzed within each population using GenAlEx 6.5 [29], including the number of alleles (Na), the number of effective alleles (Ne), Shannon’s information index (I), the observed heterozygosity (Ho), the expected heterozygosity (He), and the fixation index (FIS). Genepop 4.3 [30] was used to infer the statistical significance of either heterozygote deficit or excess. Analysis of molecular variance (AMOVA) was performed, and the genetic differentiation coefficient FST was calculated based on Weir and Cockerham’s method using Arlequin 3.0 [31,32]. Genetic structure was estimated in STRUCTURE 2.3.4 [33]. Structure analyses were performed under the Admixture model and the correlated allele frequency model. The burn-in iterations and the Markov chain Monte Carlo (MCMC) iterations were 50,000 and 100,000, respectively. The K values representing the number of ancestral populations ranged from 1 to 6 with ten independent runs for each K value. Structure Harvester [34] was used to calculate the distribution of ΔK and mean LnK to determine the optimal K value [35]. The population Q-matrix (the average of membership coefficients for each cluster across individuals) of the optimal K value was calculated using CLUMPP v.1.1 [36] and graphically displayed by Distruct v.1.1 [37].

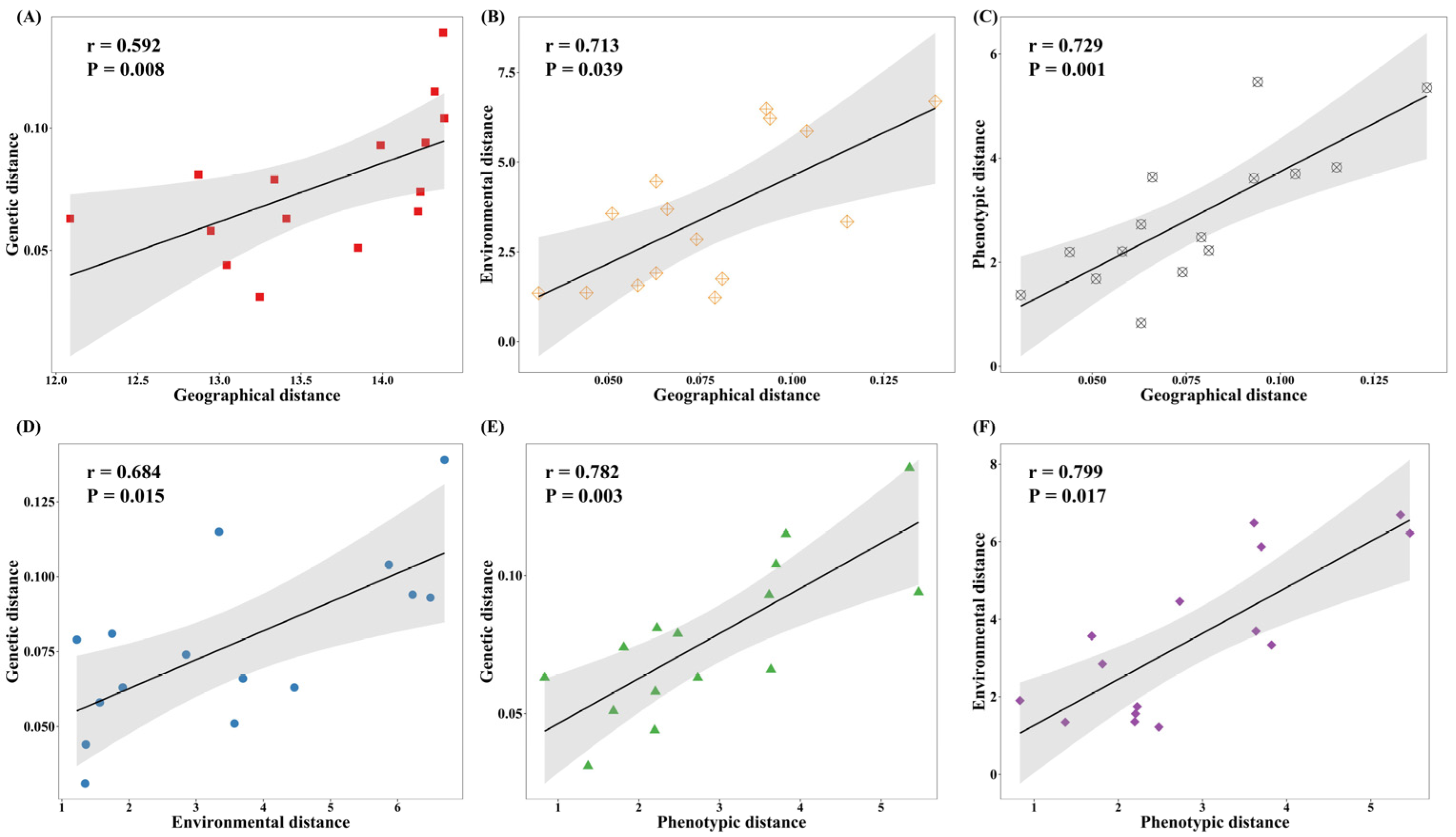
2.4. Mantel Test and QST–FST Comparisons

The Mantel test was used to detect relationships among the genetic, phenotypic, and site characteristic (i.e., geographic and environmental) distance matrices by using the ‘vegan’ package in R with default settings and parameters (999 permutation steps), as recommended by the package documentation. Geographic distance matrixes (LnKm) for different geographical populations were calculated using the ‘geosphere’ package in R and subsequently log-transformed. For the genetic distance matrix, an FST’ matrix was obtained from GenAlEx 6.5 and generated according to the formula FST/(1 − FST). Furthermore, based on the results of the correlation between the phenotypic traits and environmental factors, a phenotypic matrix was constructed using five phenotypic traits (LA, LW, LP, SH, and OD) by the Euclidean method in SPSS 25.0. For this analysis, we selected eight environment variables with significant correlations for construction of the environmental factor distance matrix (Euclidean distance, ED). We also conducted QST–FST comparisons for the distinction between natural selection and genetic drift as causes of population differentiation [24].

3. Results

3.1. Phenotypic Variation

The coefficient of variation (CV) of each trait ranged from 23.25% to 40.88%, with an average of 29.67%, confirming that Liushan populations have abundant phenotypic variation among different geographical populations (Table 2). Among them, the largest coefficient of variation was that of leaf area (LA), reaching 40.88%, and the smallest was that of leaf length (LL, 23.25%) (Table 2). However, the extent to which phenotypic traits were differentiated across the six geographical populations was varied. Compared to other populations, the YN population had the highest variation in LA (31.80%), SC had the highest variation in LW (25.93%) and SH (35.16%), and FJ02 had the most variation in LL (33.78%), RF (47.30%), LP (28.80%), SI (34.33%), and OD (35.96%). ANOVA results showed that there was a significant variation in the eight traits (p < 0.001), and the phenotypic differentiation among populations was greater than that within populations, revealing that the phenotypic variation mainly occurs among geographical populations (Table 3). Cluster analysis results showed clear differentiation among the eastern populations (FJ01 and FJ02), western populations (SC and YN), and central populations (ZJ and HN) (Figure 1B). The first two PCA axes explained 49.50% and 23.50% of the total phenotypic variation, respectively. RF, LW, SI, LA, and LL were the main traits affecting phenotypic differentiation of Liushan populations (Figure 2A and Table S3). The value of QST ranges from 0.244 (RF) to 0.425 (LA), with an average of 0.331 (Table 2).

3.2. Correlations of Phenotypic Traits with Environmental Factors

The correlation analysis results of needle traits showed that RF had significant negative correlations with LA (r = −0.06) and LW (r = −0.55). A high negative correlation of SI with LP (r = −0.76), LL (r = −0.71), RF (r = −0.53), and LA (r = −0.45) was also found. Except for SI, there was a significant negative correlation between SH and other traits, and it was observed to have a high negative correlation with LA (r = −0.43), LL (r = −0.43), and LP (r = −0.44). OD was significantly negatively correlated with RF and SI but had a lower correlation coefficient (Figure 2B).
Eight environmental factors associated with phenotypic traits were found, including mean diurnal range (mean of monthly) (Bio2), isothermality (Bio3), max temperature of warmest month (Bio5), annual precipitation (Bio12), precipitation of driest month (Bio14), precipitation of driest quarter (Bio17), precipitation of coldest quarter (Bio19), and elevation (elevation) (Table 4). A high negative correlation was observed between LA and Bio12 (r = −0.863), Bio14 (r = −0.904), Bio17 (r = −0.820), and Bio19 (r = −0.902). Similar to LA, leaf width (LW) had a high negative correlation with Bio5, Bio12, Bio14, and Bio19 (r > 0.8, p < 0.05). SH showed a significant positive correlation with precipitation variables (Bio12, Bio14, and Bio 19, p < 0.05), but it showed a significant negative correlation with elevation (r = −0.825). A high negative correlation was observed between OD and Bio12 (r = −0.905), but OD had significant positive correlation with Bio2 (r = 0.930), Bio3 (r = 0.927), and elevation (r = 0.843) (Table 4).

3.3. Genetic Diversity and Population Structure

Based on 14 nSSR loci, the number of alleles (Na) ranged from 3.214 to 4.286, with an average of 3.988. The effective number of alleles (Ne) of each population ranged from 2.369 to 2.869, with an average of 2.652 (Table 1). The average of Shannon’s information index (I) was 0.968, with the highest and lowest values found in the HN population (I = 1.040) and YN population (I = 0.891), respectively. The overall observed heterozygosity (Ho) and the expected heterozygosity (He) were 0.525 and 0.516, respectively. FJ01, FJ02, HN, and SC populations exhibited significant inbreeding; the fixation index (FIS) values of these populations were positive, and a heterozygote deficit was observed (Table 1).
Structure analysis results suggested that the optimal K value, representing the number of ancestral populations, was 2 (Figure S3). When K = 2, all populations were divided into two gene pools; SC and YN were grouped into one gene pool (blue), and the other populations were grouped into another gene pool (red). When K = 3, the YN population was allocated to a new separate gene pool (green). When K = 4, a new gene pool (yellow) appeared in five populations but not the YN population. When K = 5, two gene pools were separated, namely FJ01 (yellow) and SC (orange).
AMOVA results showed that genetic variation among groups, among populations within groups, and within populations accounted for 6.12%, 6.94%, and 86.95% of the total genetic variation (p < 0.001), respectively (Table 5). According to the results of phenotypic cluster and genetic structure analysis, six Liushan populations could also be reasonably divided into three groups, and the genetic differentiation coefficient was calculated (FST = 0.130), indicating that there was obvious genetic differentiation among groups (Table 5).

3.4. Mantel Test and QST–FST Comparisons

The Mantel test showed significant correlations between geographical and genetic distance (r = 0.592, p = 0.008) (Figure 3A), environmental distance (r = 0.713, p = 0.039) (Figure 3B), and phenotypic distance (r = 0.729, p = 0.001) (Figure 3C). A significant correlation between genetic distance and environmental distance (r = 0.684, p = 0.015) was identified as well (Figure 3D). We also detected significant correlations between phenotypic distance and both genetic distance (r = 0.782, p = 0.003) (Figure 3E) and environmental distance (r = 0.799, p = 0.017) (Figure 3F). We found that total QST = 0.331 was greater than FST (0.130) (Table 2). The QST of four traits (LA, LP, LL, and LW) were also greater than FST (Table 2 and Figure S4).

4. Discussion

4.1. Geographical Variation

Liushan (C. japonica var. sinensis) is an important greening and afforestation tree species with a wide distribution and strong adaptability in southern of China. Varied living environments have increased variation in Liushan. Based on our analysis of phenotypic and genetic data, we found that Liushan populations have abundant phenotypic variation (CV = 30.62%) and moderate genetic variation (Ho = 0.525, He = 0.516) with strong differentiation among different geographical populations (QST = 0.331, FST = 0.130), revealing that Liushan has strong adaptability to the environment and thus possesses great potential for breeding. At the morphological and molecular levels, there is strong genetic differentiation among populations, which might be a result of the distant distances between populations in this study. Structure results obtained by Evanno et al. (2005) [35] indicated the optimal K value was 2. However, based on the phenotypic clustering results, we inferred that results based on K = 3 may provide a more accurate capture of the geographic pattern of genetic variation. Therefore, the six geographical populations were assigned into three groups, which was consistent with their geographic origin (K = 3, Figure 1C).
In terms of evergreen trees, especially widely distributed tree species, complex habitat climates, long-term geographical isolation, and natural selection can promote geographically differentiated variation within species [38]. The Mantel test results in this study also supported this point. We found obvious isolation by distance (IBD, r = 0.592, p = 0.008) and isolation by environment (IBE, r = 0.684, p = 0.015) for Liushan populations in China, which was, however, inconsistent with the findings of Cai et al. (2020) [17] and Li et al. (2022) [18]. This discordance of results might be related to our inclusion of newly sampled populations from southwest China (SC and YN, Table 1). The present study expanded the sampling range compared to previous studies, and correspondingly, the geographical distance between populations increased. The Mantel test results also reflected the environmental (r = 0.799, p = 0.017) and genetic (r = 0.782, p = 0.003) effects on phenotypic divergence, indicating that genetic variations caused by environmental changes promote phenotypic differentiation among populations. In addition, we clearly observed that the YN population, which is relatively distinct from the other Liushan populations, has unique phenotypic and genetic characteristics (Figure 1C and Table 2). Thus, Liushan populations contain abundant variation, a clear geographical structure, and significant differentiation among populations, which is inseparable from its wide distribution range and broad adaptation to diverse ecological environments. Abundant geographical variation and broad adaptive ranges have laid an ample foundation for the selection, cultivation, and utilization of excellent varieties of Liushan. In addition, previous studies have shown that the genetic diversity of natural Liushan forests was largely impoverished by human interference in past decades [17]. In our field survey, most Liushan populations were found to be located in natural scenic spots or around villages and temples, with only a few forests located in inaccessible areas. Therefore, the influence of human interference on the geographical variation of this species merits further investigation.

4.2. Effects of Environment on Geographical Variation

Phenotypic divergence among populations is particularly evident for long-lived forest species, which often show strong genetic differences and environmental adaptation with profound effects on the evolution of species [39,40]. In this study, we utilized a combination of phenotypic and genetic data to explore geographic variation and its driving forces shaping Liushan populations. Previous studies have shown that QST–FST comparison was an indirect approach to investigating whether environmental pressure might potentially be involved in the phenotypic divergence of populations [41]. In the case of QST ≈ FST, it can be inferred that the trait divergence among populations may be explained by genetic drift alone. If QST > FST, trait divergence exceeds neutral expectations and is likely to have been caused by positive directional natural selection in different populations. If QST < FST, trait divergence among populations is less than expected by genetic drift alone, and this pattern is suggestive of uniform selection or stabilizing selection across the populations [24,41]. Here, the phenotypic differentiation coefficient (QST) and genetic differentiation coefficient (FST) were calculated based on phenotypic traits and neutral molecular markers of different geographic populations, respectively. Although their estimates cannot accurately assess evolutionary adaptation, they provide evidence that directional selection probably caused by heterogeneous environments (QST = 0.331 > FST = 0.130). It is necessary to establish a common garden under a homogenous environment and to measure phenotypic data in order to assess the degree of environmental adaptation in future research.
Leaves are considered to be an important site for photosynthesis and respiration in plants; they are sensitive to the environment and subject to strong genetic control, making them an ideal choice for studying phenotypic diversity [42]. Thus, leaf length, leaf width, and leaf area were recorded as critical leaf traits. In this study, the coefficient of variation results showed that the most differentiated trait was leaf area (LA, 40.88%), and the least differentiated was leaf length (LL, 23.25%). Correlation analysis results between phenotypic traits and environmental factors in Liushan populations have shown that not all phenotypic traits were significantly correlated with environment variables but only leaf area (LA), leaf width (LW), leaf perimeter (LP), softness or hardness of needles (SH), and opening degree of needles (OD). Based on the result of correlation and principal component in this study, we inferred that LA, LW, LP, LL, and SH were the sensitive traits to environmental heterogeneity (Figure 2 and Table S3).
Liushan is an important tree in southern China, as it is well suited to growing in warm and humid mountain environments. This species has a wide distribution from the southeast coast to southwest inland, spanning more than 1700 km, with an elevation range from 200 m to 2000 m (Table 1, Figure 1). From southeast to southwest, the area of Liushan forest exhibits a series of environmental changes, including changes in precipitation, temperature, and elevation. These environmental differences have exerted important selection pressures on Liushan populations. The southeast of China experiences relatively warmer and more humid conditions, while the southwestern region is colder and drier, particularly owing to its higher elevation in comparison to other regions (Table 1 and Table S2). The observed correlation between phenotype and environmental factors indicate that LA, LW, and LP are positively correlated with precipitation, and SH is positively associated with precipitation and negatively associated with elevation. In the present study, we found the YN population in the southwest district had the largest leaf area (61.33 mm2), the longest leaf length (15.15 mm), and relatively soft needles, which might be attributed to this population being located in the area with the highest elevation (2094 m) and the least annual precipitation (975.0 mm) (Table 1, Table 2 and Table S2). In contrast, the FJ01 population, in the southeastern portion of the species range, was located in an area with more precipitation (1591.0 mm) and the lowest elevation (204 m), so its needles were shorter (9.84 mm) and harder with a smaller leaf area (27.73 mm2). Evolutionary adaptation has been previously found in C. japonica populations. There are two varieties of C. japonica endemic to Japan, namely ura-sugi (var. radicans, found near the Sea of Japan) and omote-sugi (var. japonica, found near the Pacific Ocean). Previous studies have shown that the ura-sugi variety has slender branchlets with soft leaves, whereas the omote-sugi variety has rough branchlets with hard leaves [43]. To prevent tree damage from snow accumulation, the var. radicans variety along the Sea of Japan produces these adaptations. Accordingly, we speculate that the current geographically distributed variation of Liushan populations might be attributed to environmental adaptation. The key environmental differences driving this variation are precipitation and elevation, but overall, Liushan is more suited to grow in areas with high elevation, a cool climate (12–14 °C), and a suitable level of precipitation (>1000 mm). In addition, differences in light levels might also have resulted in morphological variation in the needle leaves of Liushan populations. The sunshine duration in the southwest region was greater than that in the southeast region; therefore, longer needle leaves should increase total photosynthesis. However, in this study, we only selected six geographic populations, which might have resulted in an inflation of correlation coefficients, so it is necessary to collect more samples from different populations to eliminate any potential bias caused by sampling.

4.3. Conservation and Breeding Strategy

Exploring the adaptive mechanism of species is helpful in better protecting and utilizing their genetic resources. Liushan, as an economically valuable evergreen tree species, is distributed across a wide range in southern China and has high application value and broad prospects in high-quality wood production and urban greening. Liushan was planted widely in China during the 1950s to the 1960s, but there is a lack of scientifically informed protection and management of its genetic resources. Thus far, the natural resources of Liushan have been severely damaged, and the genetic background of most artificial populations remains unclear. Meanwhile, the natural regeneration of Liushan forests has been slow. Anticipated continuing trends in climate change and human interference will result in a continuous reduction in the number of Liushan populations [17,44]. Significant variation in phenotypic traits and genetic among Liushan populations was observed in this study. Accordingly, we have some suggestions to protect the existing genetic resources and subsequently promote breeding of Liushan. First of all, in view of the fact that Liushan populations had strong genetic differentiation among populations, we recommend that regional seed orchards or germplasm nurseries should be established so as to prohibit inter-regional seed exchanges and maintain existing levels of genetic diversity to the greatest extent possible. Secondly, it is necessary to collect accessions from as many natural populations as possible, especially for populations with unusual germplasm or rare phenotypes, such as the YN, FJ, and SC populations, for ex situ protection. In particular, we found that the YN population had the highest genetic diversity (Ho = 0.614, He = 0.493), with obvious phenotypic differences (i.e., the largest leaf area, longest leaf width, and greatest leaf perimeter). Moreover, this population is genetically distinct, thus demonstrating its uniqueness and emphasizing the importance of conducting further research on this population. Finally, based on the abundant geographic variation of Liushan, it can be inferred that the improvement prospect for this species is broad. The latest genetic breeding techniques should be applied in order to strengthen the selection and breeding of excellent provenances or trees, thus improving the productivity and promoting the genetic improvement of this species.

5. Conclusions

The present study assessed the phenotypic and genetic diversity of six geographical populations of Liushan. The phenotypic variation was abundant, and the genetic diversity was moderate in Liushan populations. We observed strong genetic differentiation and obvious genetic structure among different geographically distributed populations. All populations were clustered into three groups, which was consistent with their geographical distribution. The geographical variation of this species among different geographically distributed populations may reflect its adaptability to environmental conditions (i.e., precipitation and elevation). LA, LW, LP, LL, and SH were the most sensitive needle characters, with likely local adaptive significance. Populations in Fujian (FJ02) and Sichuan (SC) were more phenotypically divergent, while the Yunnan population (YN) had the most unique phenotypic traits and highest genetic diversity; accordingly, it is a key focus for diversity protection and germplasm resource conservation, and it is necessary to strengthen the protection and resource collection of these populations in particular. Our findings provide a key reference for the germplasm collection, breeding, and conservation of this species while helping to understand the adaptability to environmental changes in this important forest species.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/f14091826/s1, Figure S1: The schematic diagram of this study; Figure S2: Measured needle morphological traits: the length measured from the base of the needle up to the tip (leaf length, LL); the maximum width of the needles (leaf width, LW); and the opening degree of needles (opening degree, OD); Figure S3: STRUCTURE analysis results of the C. japonica var. sinensis populations calculated by Evanno et al., 2005; Figure S4: QST–FST comparison; Table S1: The information of nSSR loci used in this study; Table S2: The bioclimatic variables (Bio1–Bio19) of six geographical populations in this study; Table S3: Principal component eigenvectors, eigenvalues, and contribution values.

Author Contributions

Conceptualization, Y.W.; methodology, Y.W. and X.L.; software, X.L., M.D. and X.W.; validation, M.D. and Y.T.; formal analysis, X.L., M.D. and M.W.; investigation, X.L., M.D., M.W., Y.T. and J.H.; resources, Y.W.; data curation, X.L.; writing—original draft preparation, X.L.; writing—review and editing, X.L., M.W., M.C., X.W. and Y.W.; visualization, X.L., M.D. and Y.T.; supervision, Y.W.; project administration, Y.W.; funding acquisition, Y.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the National Key Research and Development Program of China (grant no. 2016YFE0127200), Postgraduate Scientific Research Innovation Project of Hunan Province (grant no. CX20230739), and Scientific Innovation Fund for Post-graduates of Central South University of Forestry and Technology (grant no. 2023CX01004).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Walther, G.R.; Post, E.; Convey, P.; Menzel, A.; Parmesan, C.; Beebee, T.J.; Fromentin, J.M.; Hoegh-Guldberg, O.; Bairlein, F. Ecological responses to recent climate change. Nature 2002, 416, 389–395. [Google Scholar] [CrossRef] [PubMed]
  2. Sang, Y.; Long, Z.; Dan, X.; Feng, J.; Shi, T.; Jia, C.; Zhang, X.; Lai, Q.; Yang, G.; Zhang, H.; et al. Genomic insights into local adaptation and future climate-induced vulnerability of a keystone forest tree in East Asia. Nat. Commun. 2022, 13, 6541. [Google Scholar] [CrossRef] [PubMed]
  3. Aitken, S.N.; Yeaman, S.; Holliday, J.A.; Wang, T.; Curtis-McLane, S. Adaptation, migration or extirpation: Climate change outcomes for tree populations. Evol. Appl. 2008, 1, 95–111. [Google Scholar] [CrossRef]
  4. Sork, V.L. Genomic Studies of Local Adaptation in Natural Plant Populations. J. Hered. 2017, 109, 3–15. [Google Scholar] [CrossRef]
  5. Gao, J.; Liu, Z.L.; Zhao, W.; Tomlinson, K.W.; Xia, S.W.; Zeng, Q.Y.; Wang, X.R.; Chen, J. Combined genotype and phenotype analyses reveal patterns of genomic adaptation to local environments in the subtropical oak Quercus acutissima. J. Syst. Evol. 2021, 59, 541–556. [Google Scholar] [CrossRef]
  6. Hayashi, Y. Taxonomical and Phytogeographical Study of Japanese Conifers; Norin-Shuppan: Tokyo, Japan, 1960. [Google Scholar]
  7. Wang, J.; Liu, J.; Huang, Y.; Yang, J. The origin and natural distribution of Cryptomeria. J. Sichuan For. Sci. Technol. 2007, 28, 92–94. [Google Scholar]
  8. Mo, D.; Wu, Q.; Lin, N.; Zhuo, Y. Carbon and nitrogen storage and their allocation pattern in Cryptomeria fortunei plantations in southeastern Guangxi of South China. Chin. J. Ecol. 2012, 4, 794–799. [Google Scholar]
  9. Zhao, H.; Shuai, W.; Li, J.; Wu, F.; Yang, W.; Tan, B. Distribution Characteristics of Several Typical Plantation Intercept Rainfall in West China Rain Screen Area. J. Soil Water Conserv. 2014, 28, 94–100. [Google Scholar]
  10. Tsumura, Y. Cryptomeria. In Wild Crop Relatives: Genomic and Breeding Resources: Forest Trees; Kole, C., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 49–63. [Google Scholar]
  11. Murai, S. Major Forestry Tree Species in the Tohoku Region and Their Varietal Problems; Kokudo Saiken Zourin Gijutsu Kouenshu: Aomori, Japan, 1947; pp. 131–151. [Google Scholar]
  12. Yasue, M.; Ogiyama, K.; Suto, S.; Tsukahara, H.; Miyahara, F.; Ohba, K. Geographical differentiation of natural Cryptomeria stands analyzed by diterpene hydrocarbon constituents of individual trees. J. Jpn For. Soc. 1987, 69, 152–156. [Google Scholar]
  13. Kimura, M.K.; Kabeya, D.; Saito, T.; Moriguchi, Y.; Uchiyama, K.; Migita, C.; Chiba, Y.; Tsumura, Y. Effects of genetic and environmental factors on clonal reproduction in old-growth natural populations of Cryptomeria japonica. For. Ecol. Manag. 2013, 304, 10–19. [Google Scholar] [CrossRef]
  14. Tsumura, Y.; Kado, T.; Takahashi, T.; Tani, N.; Ujino-Ihara, T.; Iwata, H. Genome scan to detect genetic structure and adaptive genes of natural populations of Cryptomeria japonica. Genetics 2007, 176, 2393–2403. [Google Scholar] [CrossRef]
  15. Tsumura, Y.; Uchiyama, K.; Moriguchi, Y.; Kimura, M.K.; Ueno, S.; Ujino-Ihara, T. Genetic Differentiation and Evolutionary Adaptation in Cryptomeria japonica. G3 Genes Genomes Genet. 2014, 4, 2389–2402. [Google Scholar] [CrossRef]
  16. Moriguchi, N.; Uchiyama, K.; Miyagi, R.; Moritsuka, E.; Takahashi, A.; Tamura, K.; Tsumura, Y.; Teshima, K.M.; Tachida, H.; Kusumi, J. Inferring the demographic history of Japanese cedar, Cryptomeria japonica, using amplicon sequencing. Heredity 2019, 123, 371–383. [Google Scholar] [CrossRef]
  17. Cai, M.; Wen, Y.; Uchiyama, K.; Onuma, Y.; Tsumura, Y. Population Genetic Diversity and Structure of Ancient Tree Populations of Cryptomeria japonica var. sinensis Based on RAD-seq Data. Forests 2020, 11, 1192. [Google Scholar] [CrossRef]
  18. Li, X.Y.; Wang, M.Q.; Yuan, M.L.; Ueno, S.; Wu, X.T.; Cai, M.Y.; Tsumura, Y.; Wen, Y.F. Genetic differentiation and population evolution history of Cryptomeria, a relict plant in East Asia. For. Sci. 2022, 58, 66–78. [Google Scholar]
  19. Parmesan, C. Ecological and evolutionary responses to recent climate change. Annu. Rev. Ecol. Evol. Syst. 2006, 37, 637–669. [Google Scholar] [CrossRef]
  20. Guo, W.; He, H.; Li, X.; Zeng, W. Greater Greening Trend in the Loess Plateau of China Inferred from Long-Term Remote Sensing Data: Patterns, Causes and Implications. Forests 2022, 13, 1630. [Google Scholar] [CrossRef]
  21. Sun, Y.; Sun, Y.; Yao, S.; Akram, M.A.; Hu, W.; Dong, L.; Li, H.; Wei, M.; Gong, H.; Xie, S.; et al. Impact of climate change on plant species richness across drylands in China: From past to present and into the future. Ecol. Indic. 2021, 132, 108288. [Google Scholar] [CrossRef]
  22. Leinonen, T.; McCairns, R.; O’Hara, R.; Merilä, J. QST-FST comparisons: Evolutionary and ecological insights from genomic heterogeneity. Nat. Rev. Genet. 2013, 14, 179–190. [Google Scholar] [CrossRef]
  23. Zhang, J. The Analysis on Genetic Diversity of Superior Cryptomehia Fortunei Resources and Screening of Hybrid Parent. Master’s Thesis, Zhejiang Agriculture and Forestry University, Hangzhou, China, 2014. [Google Scholar]
  24. Tani, N.; Takahashi, T.; Iwata, H.; Mukai, Y.; Ujino-Ihara, T.; Matsumoto, A.; Yoshimura, K.; Yoshimaru, H.; Murai, M.; Nagasaka, K.; et al. A consensus linkage map for sugi (Cryptomeria japonica) from two pedigrees, based on microsatellites and expressed sequence tags. Genetics 2003, 165, 1551–1568. [Google Scholar] [CrossRef]
  25. Moriguchi, Y.; Iwata, H.; Ujino-Ihara, T.; Yoshimura, K.; Taira, H.; Tsumura, Y. Development and characterization of microsatellite markers for Cryptomeria japonica D. Don. Theor. Appl. Genet. 2003, 106, 751–758. [Google Scholar] [CrossRef] [PubMed]
  26. Moriguchi, Y.; Ueno, S.; Higuchi, Y.; Miyajima, D.; Itoo, S.; Futamura, N.; Shinohara, K.; Tsumura, Y. Establishment of a microsatellite panel covering the sugi (Cryptomeria japonica) genome, and its application for localization of a male-sterile gene (ms-2). Mol. Breed. 2014, 33, 315–325. [Google Scholar] [CrossRef]
  27. Van, O.C.; Hutchinson, W.F.; Wills, D.P.M.; Shipley, P. Micro-checker: Software for identifying and correcting genotyping errors in microsatellite data. Mol. Ecol. Resour. 2004, 4, 535–538. [Google Scholar] [CrossRef]
  28. Hulce, D.; Li, X.; Snyder-Leiby, T.; Liu, C.J. GeneMarker® Genotyping Software: Tools to Increase the Statistical Power of DNA Fragment Analysis. J. Biomol. Tech. 2011, 22, S35–S36. [Google Scholar]
  29. Peakall, R.; Smouse, P.E. GenAlEx 6.5: Genetic analysis in Excel. Population genetic software for teaching and research—an update. Bioinformatics 2012, 28, 2537–2539. [Google Scholar] [CrossRef]
  30. Rousset, F. GENEPOP’007: A complete re-implementation of the genepop software for Windows and Linux. Mol. Ecol. Res. 2008, 8, 103–106. [Google Scholar] [CrossRef]
  31. Weir, B.S.; Cockerham, C.C. Estimating F-statistics for the analysis of population structure. Evolution 1984, 38, 1358–1370. [Google Scholar] [CrossRef]
  32. Excoffier, L.; Laval, G.; Schneider, S. Arlequin (version 3.0): An integrated software package for population genetics data analysis. Evol. Bioinform. Online 2005, 1, 47–50. [Google Scholar] [CrossRef]
  33. Pritchard, J.K.; Stephens, M.; Donnelly, P. Inference of Population Structure Using Multilocus Genotype Data. Genetics 2000, 155, 945–959. [Google Scholar] [CrossRef]
  34. Earl, D.A. STRUCTURE HARVESTER: A website and program for visualizing STRUCTURE output and implementing the Evanno method. Conserv. Genet. Resour. 2012, 4, 359–361. [Google Scholar] [CrossRef]
  35. Evanno, G.; Regnaut, S.; Goudet, J. Detecting the number of clusters of individuals using the software STRUCTURE: A simulation study. Mol. Ecol. 2005, 14, 2611–2620. [Google Scholar] [CrossRef] [PubMed]
  36. Jakobsson, M.; Rosenberg, N.A. CLUMPP: A cluster matching and permutation program for dealing with label switching and multimodality in analysis of population structure. Bioinformatics 2007, 23, 1801–1806. [Google Scholar] [CrossRef] [PubMed]
  37. Rosenberg, N.A. DISTRUCT: A program for the graphical display of population structure. Mol. Ecol. Notes 2004, 4, 137–138. [Google Scholar] [CrossRef]
  38. Endler, J.A. Natural Selection in the Wild; Princeton University Press: Princeton, NJ, USA, 1986; p. 358. [Google Scholar]
  39. Leimu, R.; Fischer, M. A meta-analysis of local adaptation in plants. PLoS ONE 2008, 3, e4010. [Google Scholar] [CrossRef]
  40. Savolainen, O.; Pyhäjärvi, T.; Knürr, T. Gene flow and local adaptation in trees. Annu. Rev. Ecol. Evol. Syst. 2007, 38, 595–619. [Google Scholar] [CrossRef]
  41. Marin, S.; Gibert, A.; Archambeau, J.; Bonhomme, V.; Lascoste, M.; Pujol, B. Potential adaptive divergence between subspecies and populations of snapdragon plants inferred from QST-FST comparisons. Mol. Ecol. 2020, 29, 3010–3021. [Google Scholar] [CrossRef] [PubMed]
  42. Cao, D.M.; Zhang, Y.H.; Cheng, X.Q.; Xiang, X.; Zhang, L.; Hu, J. Genetic Variation of Leaf Phenotypic Traits in Different Populations of Populus cathayana. For. Sci. 2021, 57, 56–67. [Google Scholar]
  43. Yamazaki, T. Cryptomeriaceae in Flora of Japan. In Pteridophyta and Gymnospermae; Iwatsuki, K., Yamazaki, T., Boufford, D.E., Ohba, H., Eds.; Kodansha: Tokyo, Japan, 1995; Volume I, p. 264. [Google Scholar]
  44. Dai, M.J.; Li, X.Y.; Wang, M.Q.; Wen, Y.F. Potential suitable area of Cryptomeria japonica var. sinensis and the influence of climate change on its distribution. J. Northwest For. Univ. 2022, 37, 26–33+128. [Google Scholar]
Forests 14 01826 g001
Figure 1. Genetic structure and cluster analysis of Liushan populations based on nSSR loci and phenotypic traits. (A) Geographic distribution of Liushan populations and gene pool distribution map of each population according to the structure (K = 3). (B) Cluster analysis of Liushan populations from different geographical provinces based on eight phenotypic traits. (C) Histogram of the STRUCTURE analysis for the model with K = 2, 3, 4, and 5. Different colors represent different gene pools.
Figure 1. Genetic structure and cluster analysis of Liushan populations based on nSSR loci and phenotypic traits. (A) Geographic distribution of Liushan populations and gene pool distribution map of each population according to the structure (K = 3). (B) Cluster analysis of Liushan populations from different geographical provinces based on eight phenotypic traits. (C) Histogram of the STRUCTURE analysis for the model with K = 2, 3, 4, and 5. Different colors represent different gene pools.
Forests 14 01826 g001
Forests 14 01826 g002
Figure 2. Principal component analysis (A) and correlation (B) of phenotypic traits. The color of the arrow shows the contribution of the variable to the principal component. ***, significance < 0.001.
Figure 2. Principal component analysis (A) and correlation (B) of phenotypic traits. The color of the arrow shows the contribution of the variable to the principal component. ***, significance < 0.001.
Forests 14 01826 g002
Forests 14 01826 g003
Figure 3. Mantel tests of Liushan populations: (A–C) are the correlations between geographical distance and genetic distance, environmental distance, and phenotypic distance, respectively. (D) is the correlation between genetic distance and environmental distance. (E,F) are the correlations between phenotypic distance and genetic distance and environmental distance, respectively.
Figure 3. Mantel tests of Liushan populations: (A–C) are the correlations between geographical distance and genetic distance, environmental distance, and phenotypic distance, respectively. (D) is the correlation between genetic distance and environmental distance. (E,F) are the correlations between phenotypic distance and genetic distance and environmental distance, respectively.
Forests 14 01826 g003
Table 1. Geographic locations and genetic diversity parameters of Liushan populations.
Table 1. Geographic locations and genetic diversity parameters of Liushan populations.
PopSample SizeGeographic RegionLatitude
(°N)		Longitude
(°E)		Elevation
(m)		NaNeIHoHeFIS
FJ0115Fujian26.87119.942044.2142.7220.9970.4950.5110.00 *
FJ0215Fujian26.74118.168664.2142.6011.0100.5090.5340.02 **
ZJ15Zhejiang30.34119.446013.7862.3690.9030.5600.505−0.09
HN15Hunan28.58113.957314.2862.8691.0400.4950.5550.06 ***
SC15Sichuan31.03103.618924.2142.7420.9640.4750.4950.01 *
YN15Yunnan25.10102.6320943.2142.6090.8910.6140.493−0.25
Total90----3.9882.6520.9680.5250.516−0.035
Na, number of alleles; Ne, number of effective alleles; I, Shannon’s information index; Ho, observed heterozygosity; He, expected heterozygosity; FIS, fixation index. *, significance < 0.05; **, significance < 0.01; ***, significance < 0.001.
Table 2. The phenotypic variation of Liushan populations.
Table 2. The phenotypic variation of Liushan populations.
Phenotypic
Traits		Descriptive ParametersGeographical PopulationsTotalQST
FJ01FJ02ZJHNSCYN
Sample Size 15151515151590
LA (mm2)Mean27.7329.0040.9743.0757.4061.3343.250.425
CV28.7226.1518.0213.5131.6331.8040.88
LW (mm)Mean3.653.434.753.974.885.304.330.244
CV18.7920.2018.9816.1425.9325.0127.05
LL (mm)Mean9.8411.2411.9614.4714.8715.1512.920.316
CV16.9233.7813.1411.5610.6215.4823.25
LP (mm)Mean22.0825.2029.3132.0435.2037.7030.250.339
CV22.0428.8018.818.9215.7222.0526.51
RFMean2.753.522.583.783.212.963.13-
CV16.9747.3018.0226.5522.7320.5531.99
SIMean0.750.650.630.540.580.550.62-
CV19.6734.3321.3113.0614.1617.6524.64
SHMean2.002.001.771.501.431.071.63-
CV0.000.0024.3533.9035.1623.7929.78
ODMean1.471.331.431.401.402.001.51-
CV34.6035.9635.1635.5935.590.0033.30
Total Mean19.7128.3220.9819.9023.9419.5429.670.331
LA, leaf area; LW, leaf width; LL, leaf length; RF, rate of leaf length to width; LP, leaf perimeter; SI, shape index; SH, hardness; OD, opening degree; Mean, arithmetic mean; CV, coefficient of variation (%); QST, quantitative trait divergence indices.
Table 3. ANOVA analysis of eight needle traits for Liushan populations.
Table 3. ANOVA analysis of eight needle traits for Liushan populations.
Phenotypic TraitsVariance Componentd.f.SS.MS.F
LA (mm2)Among populations529,289.1835857.83738.234 ***
Within populations17426,658.567153.210
LW (mm)Among populations584.97116.99418.445 ***
Within populations174160.3140.921
LL (mm)Among populations5732.612146.52228.869 ***
Within populations174883.1365.075
RFAmong populations531.5036.3017.395 ***
Within populations174148.2550.852
LP (mm)Among populations55289.2101057.84229.574 ***
Within populations1746223.79835.769
SIAmong populations50.9270.18510.028 ***
Within populations1743.2150.018
SHAmong populations519.9613.99231.432 ***
Within populations17422.1000.127
ODAmong populations59.0941.8198.816 ***
Within populations17435.9000.206
The meaning of index for phenotypic traits are the same as Table 2. d.f., degrees of freedom; SS., sum of squares; MS., mean square; F, F test statistics. ***, significance < 0.001.
Table 4. The correlation between the phenotypic traits and environmental factors.
Table 4. The correlation between the phenotypic traits and environmental factors.
Phenotypic
Traits		Bioclimatic Variables
Bio2Bio3Bio5Bio12Bio14Bio17Bio19Elevation
LA0.5750.564−0.747−0.863 *−0.904 *−0.820 *−0.902 *0.752
LW0.5490.526−0.821 *−0.875 *−0.852 *−0.782−0.855 *0.666
LL0.4850.425−0.572−0.680−0.705−0.583−0.6940.692
RF−0.062−0.1160.2630.3060.2060.2800.2340.070
LP0.5900.538−0.735−0.798−0.813 *−0.700−0.8010.777
SI−0.461−0.3380.5430.5130.4910.3350.465−0.658
SH−0.706−0.6630.7150.898 *0.822 *0.7340.816 *−0.825 *
OD0.930 **0.927 **−0.757−0.905 *−0.698−0.696−0.6860.843 *
The meaning of index for phenotypic traits are the same as Table 2. Bio2, mean diurnal range; Bio3, isothermality; Bio5, max temperature of warmest month; Bio12, annual precipitation; Bio14, precipitation of driest month; Bio17, precipitation of driest quarter; Bio19, precipitation of coldest quarter. *, significance < 0.05; **, significance < 0.01.
Table 5. Analysis of molecular variance (AMOVA) of Liushan populations.
Table 5. Analysis of molecular variance (AMOVA) of Liushan populations.
SourcedfSSVariance ComponentsPercentage of Variation (%)p
Among groups256.0780.2596.12%<0.001
Among populations within groups337.4830.2946.94%<0.001
Within populations174640.6673.68286.95%<0.001
Total179734.2284.235
FST0.130
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Li, X.; Dai, M.; Wang, M.; Wu, X.; Cai, M.; Tao, Y.; Huang, J.; Wen, Y. Geographical Variation Reveals Strong Genetic Differentiation in Cryptomeria japonica var. sinensis. Forests 2023, 14, 1826. https://doi.org/10.3390/f14091826

AMA Style

Li X, Dai M, Wang M, Wu X, Cai M, Tao Y, Huang J, Wen Y. Geographical Variation Reveals Strong Genetic Differentiation in Cryptomeria japonica var. sinensis. Forests. 2023; 14(9):1826. https://doi.org/10.3390/f14091826

Chicago/Turabian Style

Li, Xinyu, Minjun Dai, Minqiu Wang, Xingtong Wu, Mengying Cai, Yiling Tao, Jiadi Huang, and Yafeng Wen. 2023. "Geographical Variation Reveals Strong Genetic Differentiation in Cryptomeria japonica var. sinensis" Forests 14, no. 9: 1826. https://doi.org/10.3390/f14091826

APA Style

Li, X., Dai, M., Wang, M., Wu, X., Cai, M., Tao, Y., Huang, J., & Wen, Y. (2023). Geographical Variation Reveals Strong Genetic Differentiation in Cryptomeria japonica var. sinensis. Forests, 14(9), 1826. https://doi.org/10.3390/f14091826

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop