Heartwood Relationship with Stem Diameter in Pinus canariensis Plantations of Gran Canaria, Spain
Abstract
:1. Introduction
2. Materials and Methods
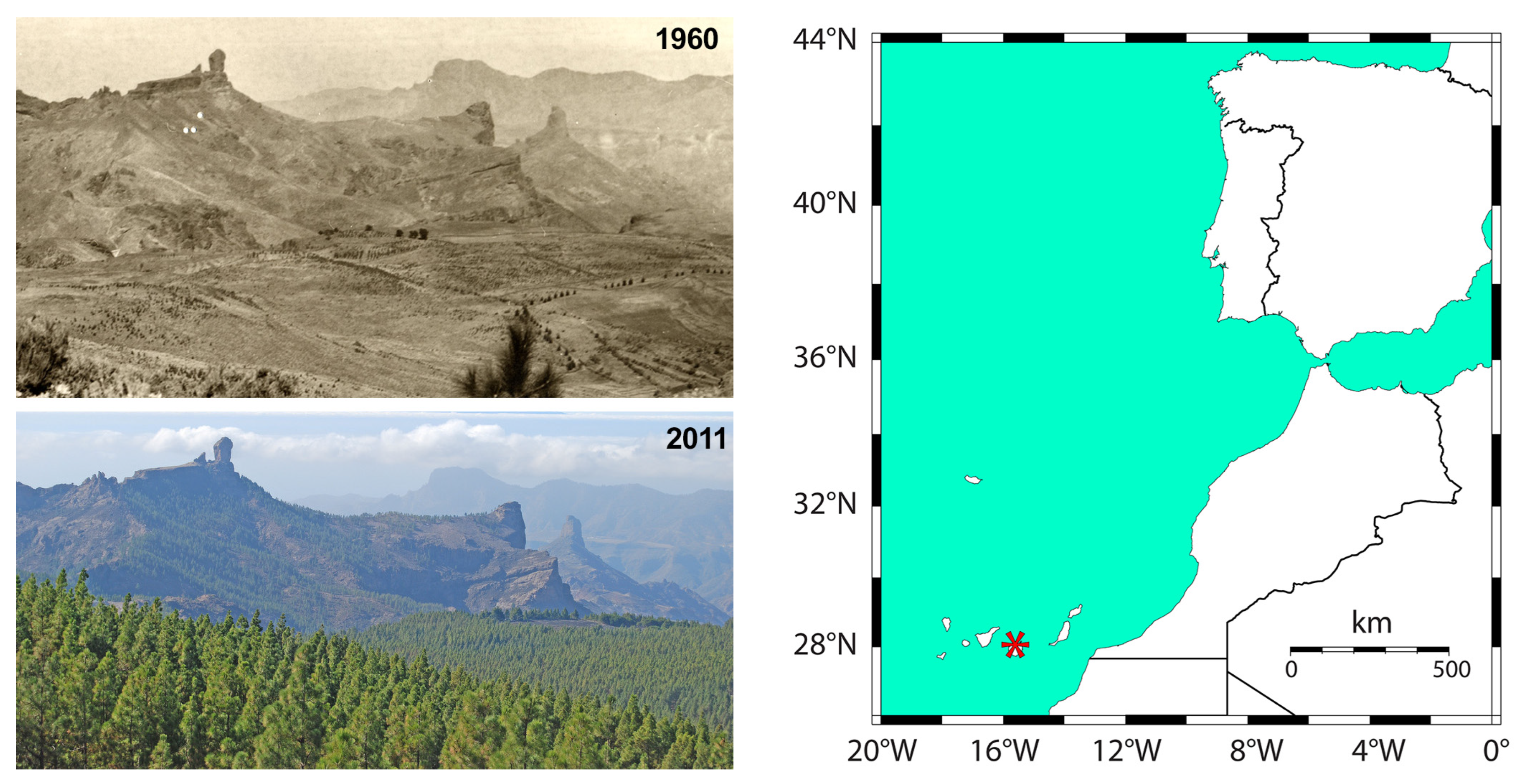
2.1. Study Area
2.2. Field and Laboratory Measurements
2.3. Data Processing and Statistical Model
3. Results
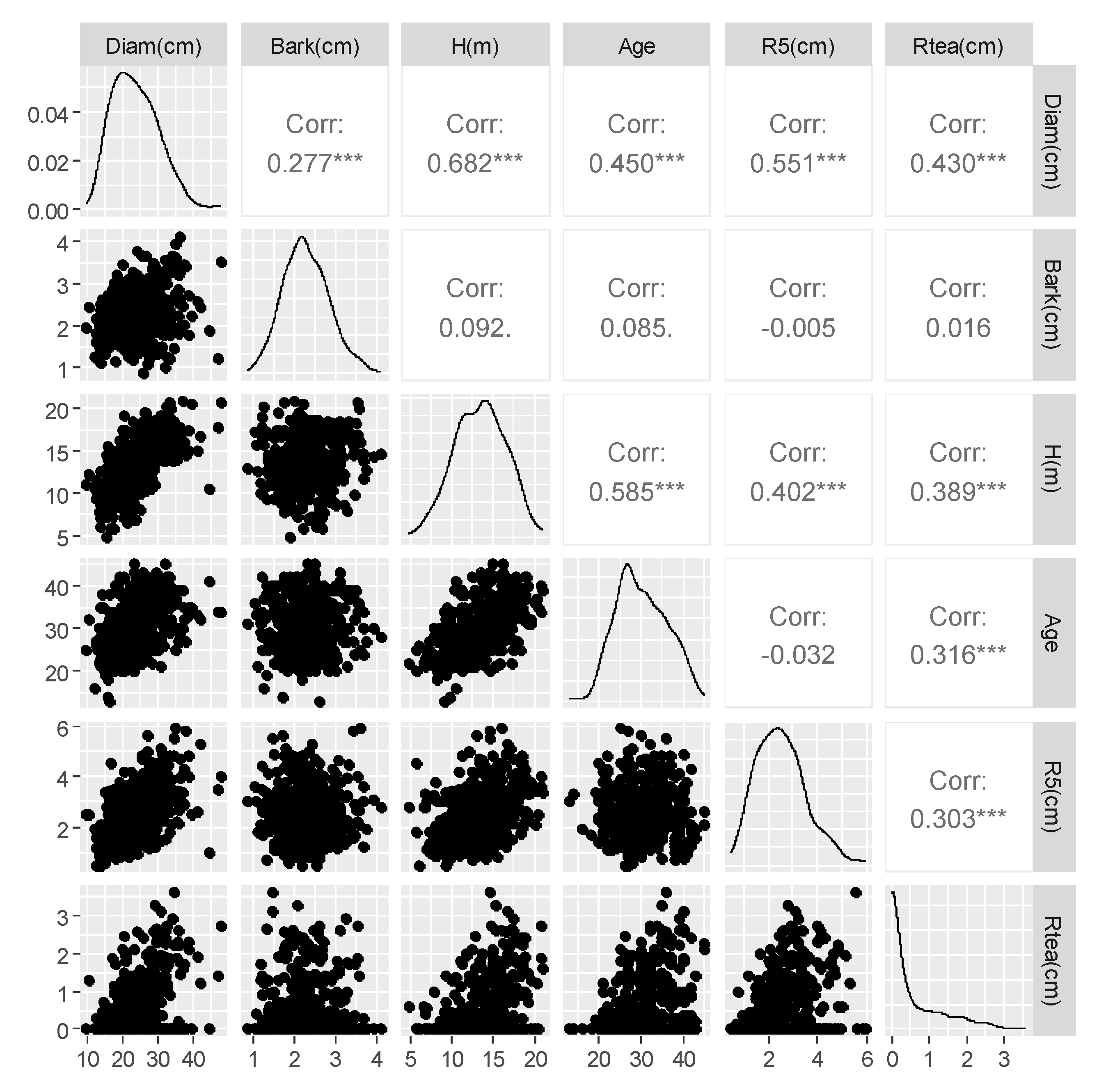
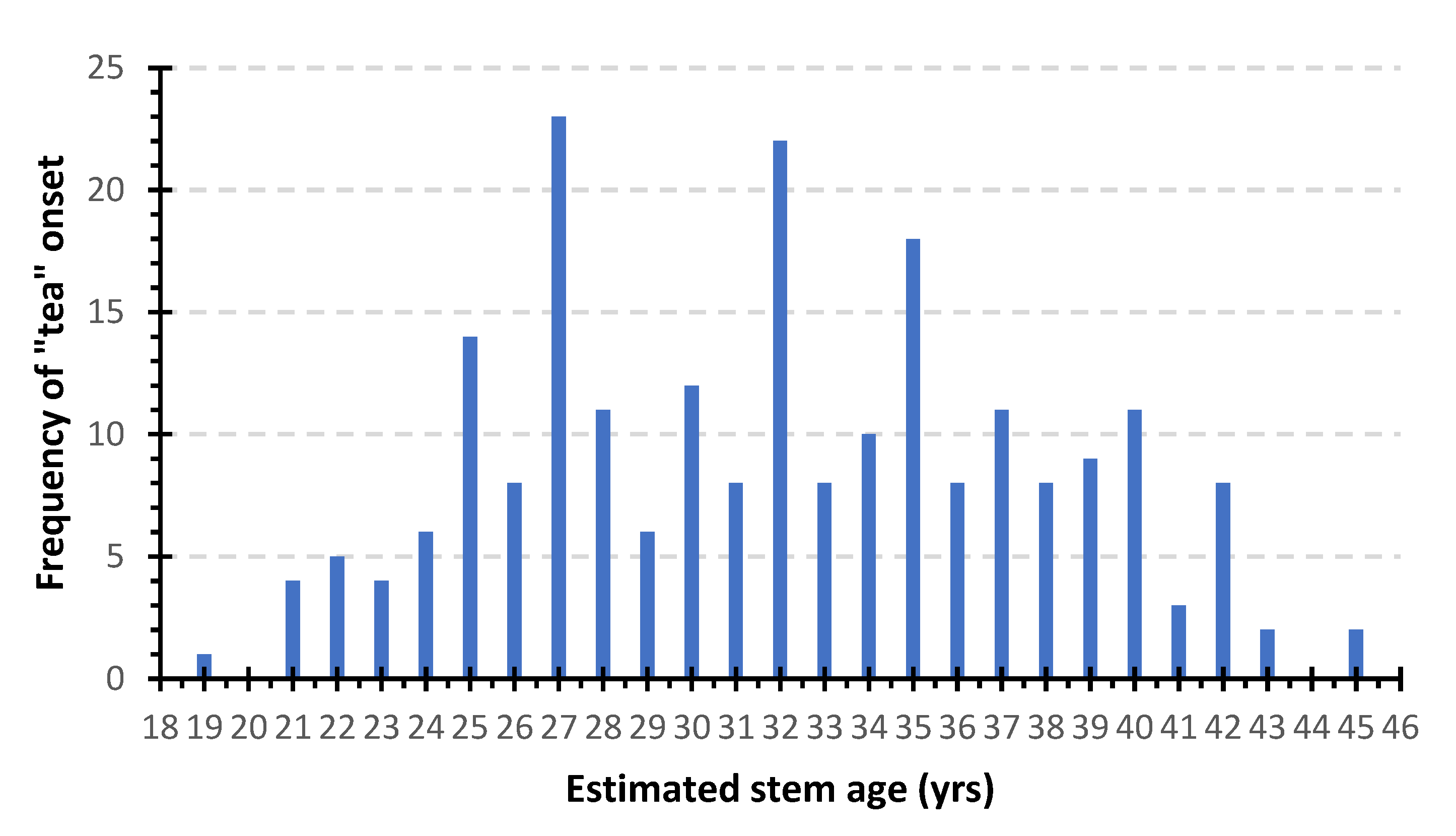
3.1. Sampled Trees and Exploratory Data Analysis
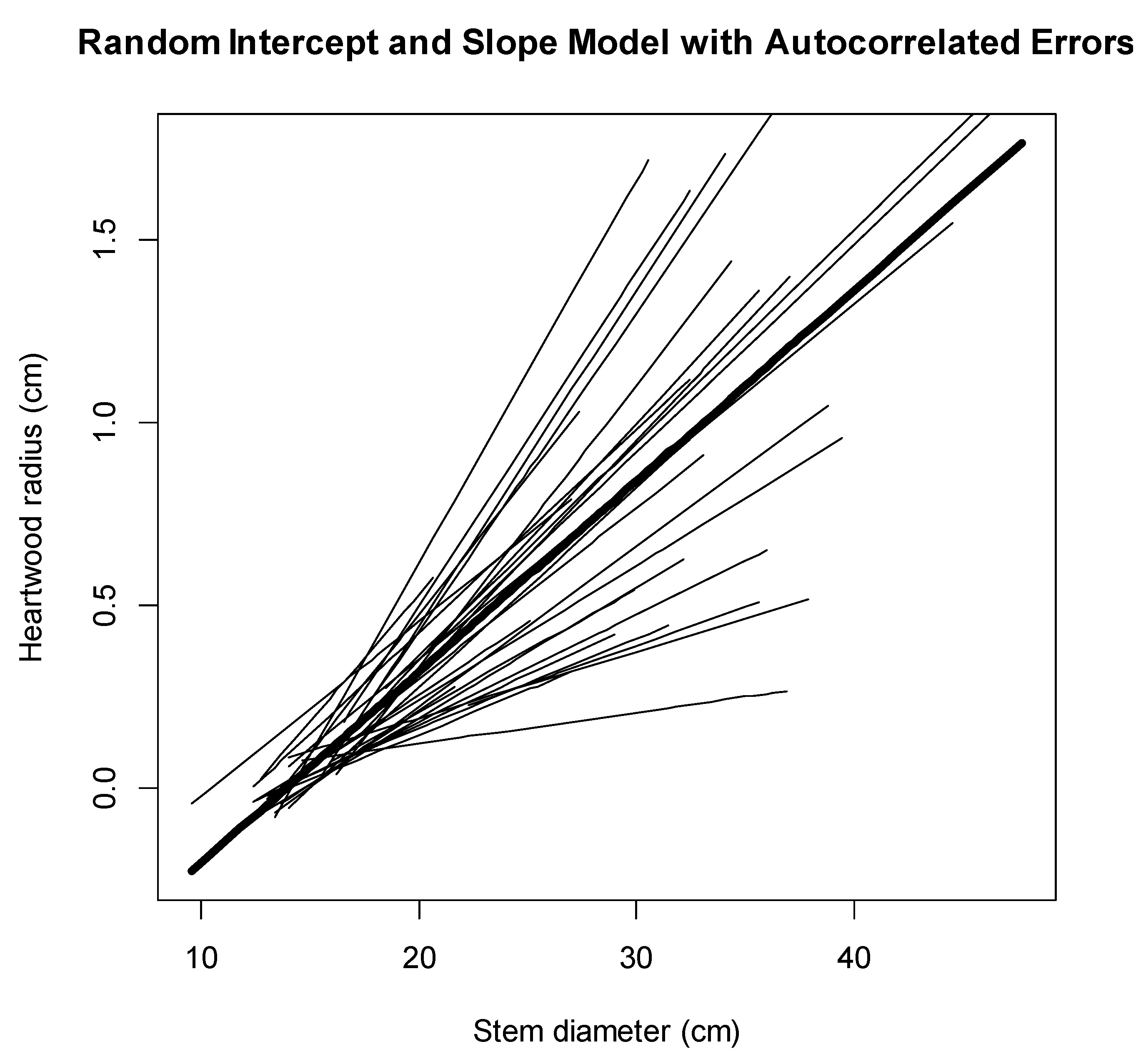
3.2. Mixed-Effect Models
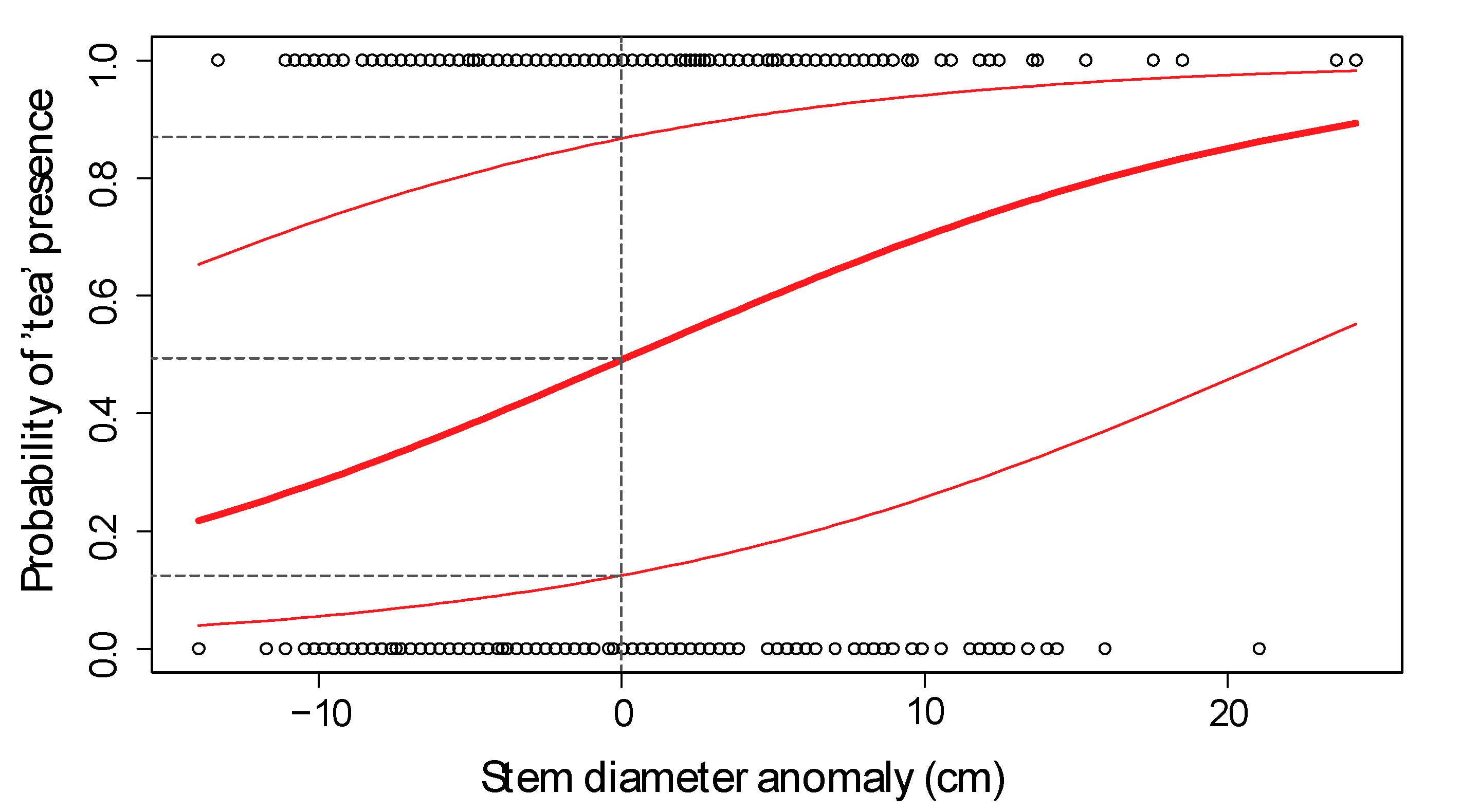
Further Testing of Fixed Effects
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Association of Wood Anatomists (IAWA). Multilingual Glossary of Terms used in Wood Anatomy; Verlagsanstalt Buchdruckere: Winterthur, Switzerland, 1964; Volume 40, p. 26. [Google Scholar]
- Hillis, W.E. Heartwood and Tree Exudates; Springer: Berlin, Germany, 1987; p. 268. [Google Scholar]
- Beekwilder, J.; van Houwelingen, A.; Cankar, K.; van Dijk, A.D.J.; de Jong, R.M.; Stoopen, G.; Bouwmeester, H.; Achkar, J.; Sonke, T.; Bosch, D. Valencene synthase from the heartwood of Nootka cypress (Callitropsis nootkatensis) for biotechnological production of valencene. Plant Biotechnol. J. 2014, 12, 174–182. [Google Scholar] [CrossRef] [PubMed]
- Celedon, J.M.; Chiang, A.; Yuen, M.M.S.; Diaz-Chavez, M.L.; Madilao, L.L.; Finnegan, P.M.; Barbour, E.L.; Bohlmann, J. Heartwood-specific transcriptome and metabolite signatures of tropical sandalwood (Santalum album) reveal the final step of (Z)-santalol fragrance biosynthesis. Plant J. 2016, 86, 289–299. [Google Scholar] [CrossRef] [PubMed]
- Taylor, A.M.; Gartner, B.L.; Morrell, J.J. Heartwood formation and natural durability—A review. Wood Fiber. Sci. 2002, 34, 587–611. [Google Scholar]
- Galibina, N.A.; Moshnikov, S.A.; Nikerova, K.M.; Afoshin, N.V.; Ershova, M.A.; Ivanova, D.S.; Kharitonov, V.A.; Romashkin, I.V.; Semenova, L.I.; Serkova, A.A.; et al. Changes in the intensity of heartwood formation in Scots pine (Pinus sylvestris L.) ontogenesis. IAWA J. 2022, 43, 299–321. [Google Scholar] [CrossRef]
- Bamber, R.K. Sapwood and Heartwood; Forestry Commission of New South Wales: Beecroft, Australia, 1987; p. 7. [Google Scholar]
- Ekeberg, D.; Flæte, P.-O.; Eikenes, M.; Fongen, M.; Naess-Andresen, C.F. Qualitative and quantitative determination of extractives in heartwood of Scots pine (Pinus sylvestris L.) by gas chromatography. J. Chromatogr. A 2006, 1109, 267–272. [Google Scholar] [CrossRef]
- Petit, G.; Mencuccini, M.; Carrer, M.; Prendin, A.L.; Hölttä, T. Axial conduit widening, tree height and height growth rate set the hydraulic transition of sapwood into heartwood. J. Exp. Bot. 2023, erad227. [Google Scholar] [CrossRef]
- Beauchamp, K.; Mencuccini, M.; Perks, M.; Gardiner, B. The regulation of sapwood area, water transport and heartwood formation in Sitka spruce. Plant Ecol. Divers. 2013, 6, 45–56. [Google Scholar] [CrossRef]
- Spicer, R. Senescence in secondary xylem: Heartwood formation as an active developmental program. In Vascular Transport in Plants; Holbrook, N.M., Zwieniecki, M.A., Eds.; Elsevier Academic Press: San Diego, CA, USA, 2005; pp. 457–475. [Google Scholar]
- Frey-Wyssling, A.; Bosshard, H.H. Cytology of the ray cells in sapwood and heartwood. Holzforschung 1959, 13, 129–137. [Google Scholar] [CrossRef]
- Stewart, C.M. Excretion and heartwood formation in living trees. Science 1966, 153, 1068–1074. [Google Scholar] [CrossRef]
- Carrodus, B.B. Carbon dioxide and the formation of heartwood. New Phytol. 1971, 70, 939–943. [Google Scholar] [CrossRef]
- Shain, L.; Mackay, J. Seasonal fluctuation in respiration of aging xylem in relation to heartwood formation in Pinus radiata. Can. J. Bot. 1973, 51, 737–741. [Google Scholar] [CrossRef]
- Bamber, R.K. Heartwood, its function and formation. Wood Sci.Technol. 1976, 10, 1–8. [Google Scholar] [CrossRef]
- Fries, A.; Ericsson, T. Genetic parameters in diallel-crossed Scots pine favor heartwood formation breeding objectives. Can. J. For. Res. 1998, 28, 937–941. [Google Scholar] [CrossRef]
- Long, J.N.; Smith, F.W. Leaf area-sapwood area relations of lodgepole pine as influenced by stand density and site index. Can. J. For. Res. 1988, 18, 247–250. [Google Scholar] [CrossRef]
- Rogers, R.; Hinckley, T. Foliar weight and area related to current sapwood area in oak. For. Sci. 1979, 25, 298–303. [Google Scholar]
- Waring, R.; Gholz, H.; Grier, C.; Plummer, M. Evaluating stem conducting tissue as an estimator of leaf area in four woody angiosperms. Can. J. Bot. 2011, 55, 1474–1477. [Google Scholar] [CrossRef]
- Shinozaki, K.; Yoda, K.; Hozumi, K.; Kira, T. A quantitative analysis of plant form-the pipe model theory: I. Basic analyses. Jpn. J. Ecol. 1964, 14, 97–105. [Google Scholar] [CrossRef]
- Marchand, P.J. Sapwood area as an estimator of foliage biomass and projected leaf area for Abies balsamea and Picea rubens. Can. J. For. Res. 1984, 14, 85–87. [Google Scholar] [CrossRef]
- Whitehead, D.; Edwards, W.R.N.; Jarvis, P.G. Conducting sapwood area, foliage area, and permeability in mature trees of Picea sitchensis and Pinus contorta. Can. J. For. Res. 1984, 14, 940–947. [Google Scholar] [CrossRef]
- Waring, R.H.; Schroeder, P.E.; Oren, R. Application of the pipe model theory to predict canopy leaf area. Can. J. For. Res. 1982, 12, 556–560. [Google Scholar] [CrossRef]
- Morataya, R.; Galloway, G.; Berninger, F.; Kanninen, M. Foliage biomass-sapwood (area and volume) relationships of Tectona grandis L.F. and Gmelina arborea Roxb.: Silvicultural implications. For. Ecol. Manag. 1999, 113, 231–239. [Google Scholar] [CrossRef]
- Todorovski, S. Effect of certain factors on the proportion of sapwood and heartwood in the stem of Pinus sylvestris and Pinus nigra. For. Abstr. 1968, 2908. [Google Scholar]
- Yang, K.C.; Hazenberg, G. Relationship between tree age and sapwood/heartwood width in Populus tremuloides Michx. Wood Fiber Sci. 1991, 23, 247–252. [Google Scholar]
- Yang, K.C.; Hazenberg, G. Sapwood and heartwood width relationship to tree age in Pinus banksiana. Can. J. For. Res. 1991, 21, 521–525. [Google Scholar] [CrossRef]
- Sellin, A. Sapwood amount in Picea abies (L.) Karst. determined by tree age and radial growth rate. Holzforschung 1996, 50, 291–296. [Google Scholar] [CrossRef]
- Björklund, L. Identifying heartwood-rich stands or stems of Pinus sylvestris by using inventory data. Silva Fenn. 1999, 33, 611. [Google Scholar] [CrossRef]
- Boanza, M.V.; Gutiérrez, A.; Grau, J.M. Variación de la densidad, la humedad, el duramen y la corteza con la altura en el tronco de pino laricio. In Proceedings of the III Congreso Forestal Español, Granada, Spain, 25–28 September 2001; p. 5. [Google Scholar]
- Koch, P. Utilization of the Southern Pines—Volume 2; USDA-Forest Service, Southern Forest Experiment Station: Asheville, NC, USA, 1972; pp. 735–1663. [Google Scholar]
- Knapic, S.; Pereira, H. Within-tree variation of heartwood and ring width in maritime pine (Pinus pinaster Ait.). For. Ecol. Manag. 2005, 210, 81–89. [Google Scholar] [CrossRef]
- Moya, R.; Calvo-Alvarado, J. Variation of wood color parameters of Tectona grandis and its relationship with physical environmental factors. Ann. For. Sci. 2012, 69, 947–959. [Google Scholar] [CrossRef]
- Climent, J.; Gil, L.; Pardos, J. Heartwood and sapwood development and its relationship to growth and environment in Pinus canariensis Chr.Sm ex DC. For. Ecol. Manag. 1993, 59, 165–174. [Google Scholar] [CrossRef]
- Córdoba, L.C.; de Medina, F.O.F. Estudio Sobre la Vegetación y Flora Forestal de las Canarias Occidentales; Ministerio de Agricultura, Dirección General de Montes, Caza y Pesca Fluvial, Instituto Forestal de Investigaciones y Experiencias: Madrid, Spain, 1951; p. 465. [Google Scholar]
- Parsons, J.J. Human influences on the pine and laurel forests of the Canary Islands. Geogr. Rev. 1981, 71, 253–271. [Google Scholar] [CrossRef]
- Arévalo, J.R.; Fernández-Palacios, J.M. 9550-Pinares endémicos canarios. In Bases Ecológicas Preliminares Para la Conservación de los Tipos de Hábitat de Interés Comunitario en España; Dirección General de Medio Natural y Política Forestal, Ministerio de Medio Ambiente y Medio Rural y Marino: Madrid, Spain, 2009; p. 74. [Google Scholar]
- Rodríguez, R.A.L. Diferenciación Adaptativa Entre Poblaciones de Pinus Canariensis Chr. Sm. ex DC. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2009. [Google Scholar]
- Climent, J.; Chambel, M.R.; Pérez, E.; Gil, L.; Pardos, J. Relationship between heartwood radius and early radial growth, tree age, and climate in Pinus canariensis. Can. J. For. Res. 2002, 32, 103–111. [Google Scholar] [CrossRef]
- Wilkes, J. Heartwood development and its relationship to growth in Pinus radiata. Wood Sci.Technol. 1991, 25, 85–90. [Google Scholar] [CrossRef]
- Arístegui, J.; Barton, E.D.; Álvarez-Salgado, X.A.; Santos, A.M.P.; Figueiras, F.G.; Kifani, S.; Hernández-León, S.; Mason, E.; Machú, E.; Demarcq, H. Sub-regional ecosystem variability in the Canary Current upwelling. Prog. Oceanog. 2009, 83, 33–48. [Google Scholar] [CrossRef]
- del Arco Aguilar, M.J.; Delgado, O.R. Vegetation of the Canary Islands; Springer International Publishing: Cham, Switzerland, 2018; p. 429. [Google Scholar]
- Puyol, D.G.; Herrera, R.G.; Martín, E.H.; Presa, L.G.; Rodríguez, P.R. Major influences on precipitation in the Canary Islands. In Climatic Change: Implications for the Hydrological Cycle and for Water Management; Beniston, M., Ed.; Springer: Dordrecht, The Netherlands, 2002; pp. 57–73. [Google Scholar]
- García, M.B. Manual de Dasometría; Organismo Autónomo Parques Nacionales: Madrid, Spain, 2011; p. 135. [Google Scholar]
- Applequist, M.B. A simple pith locator for use with off center increment cores. J. For. Res. 1958, 56, 141. [Google Scholar]
- QGIS.org. QGIS Geographic Information System; 3.28.4-Firenze; QGIS Association: Florence, Italy, 2022. [Google Scholar]
- Kopecký, M.; Macek, M.; Wild, J. Topographic Wetness Index calculation guidelines based on measured soil moisture and plant species composition. Sci. Total Environ. 2021, 757, 143785. [Google Scholar] [CrossRef]
- Böhner, J.; Antonić, O. Land-surface parameters specific to topo-climatology. In Developments in Soil Science; Hengl, T., Reuter, H.I., Eds.; Elsevier: Amsterdam, The Netherlands, 2009; Volume 33, pp. 195–226. [Google Scholar]
- Sokal, R.R.; Rohlf, F.J. Biometry, 4th ed.; W.H. Freeman and Co.: New York, NY, USA, 2012; p. 937. [Google Scholar]
- Isaaks, E.H.; Srivastava, R.M. An Introduction to Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Biondi, F.; Myers, D.E.; Avery, C.C. Geostatistically modeling stem size and increment in an old-growth forest. Can. J. For. Res. 1994, 24, 1354–1368. [Google Scholar] [CrossRef]
- Venables, W.N.; Dichmont, C.M. GLMs, GAMs and GLMMs: An overview of theory for applications in fisheries research. Fish. Res. 2004, 70, 319–337. [Google Scholar] [CrossRef]
- Bolker, B.M.; Brooks, M.E.; Clark, C.J.; Geange, S.W.; Poulsen, J.R.; Stevens, M.H.H.; White, J.-S.S. Generalized linear mixed models: A practical guide for ecology and evolution. Trends Ecol. Evol. 2009, 24, 127–135. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer Science+Business Media: New York, NY, USA, 2002; p. 495. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Zuur, A.F.; Ieno, E.N.; Walker, N.J.; Saveliev, A.A.; Smith, G.M. Mixed Effects Models and Extensions in Ecology with R; Springer Science+Business Media: New York, NY, USA, 2009; p. 574. [Google Scholar]
- Gelman, A.; Hill, J. Data Analysis Using Regression and Multilevel/Hierarchical Models; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing, 4.1.2; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; Eispack, A.; Heisterkamp, S.; Van Willigen, B.; Ranke, J.; R Core Team. Package ‘nlme’: Linear and Nonlinear Mixed Effects Models; R Package Version 3.1-162; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Broström, G.; Jin, J.; Holmberg, H. Package ‘glmmML’: Generalized Linear Models with Clustering; R Package Version 1.1.4; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Ripley, B.D.; Venables, W.N.; Bates, D.M.; Hornik, K.; Gebhardt, A.; Firth, D. Package ‘MASS’: Support Functions and Datasets for Venables and Ripley’s MASS; R Package Version 7.3-60; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Wang, X.; Wang, C.; Zhang, Q.; Quan, X. Heartwood and sapwood allometry of seven Chinese temperate tree species. Ann. For. Sci. 2010, 67, 410. [Google Scholar] [CrossRef]
- Kokutse, A.D.; Baillères, H.; Stokes, A.; Kokou, K. Proportion and quality of heartwood in Togolese teak (Tectona grandis L.f.). For. Ecol. Manag. 2004, 189, 37–48. [Google Scholar] [CrossRef]
- Knapic, S.; Tavares, F.; Pereira, H. Heartwood and sapwood variation in Acacia melanoxylon R. Br. trees in Portugal. Forestry 2006, 79, 371–380. [Google Scholar] [CrossRef]
- Gominho, J.; Pereira, H. The influence of tree spacing in heartwood content in Eucalyptus globulus Labill. Wood Fiber Sci. 2005, 582–590. [Google Scholar]
- Climent, J.; Chambel, M.R.; Gil, L.; Pardos, J.A. Vertical heartwood variation patterns and prediction of heartwood volume in Pinus canariensis Sm. For. Ecol. Manag. 2003, 174, 203–211. [Google Scholar] [CrossRef]
- Hillis, W.E.; Ditchburne, N. The prediction of heartwood diameter in radiata pine trees. Can. J. For. Res. 1974, 4, 524–529. [Google Scholar] [CrossRef]
- Graham, M.H. Confronting multicollinearity in ecological multiple regression. Ecology 2003, 84, 2809–2815. [Google Scholar] [CrossRef]
- Bergström, B.; Gref, R.; Ericsson, A. Effects of pruning on heartwood formation in Scots pine trees. J. For. Sci. 2004, 50, 11–16. [Google Scholar] [CrossRef]
- Jakubowski, M.; Kałuziński, D.; Tomczak, A.; Jelonek, T. Proportion of heartwood and sapwood in Scots pine (Pinus sylvestris L.) stems grown in different site conditions. Ann. WULS-SGGW For. Wood Technol. 2015, 92, 122–126. [Google Scholar]
- Tarelkina, T.V.; Galibina, N.A.; Moshnikov, S.A.; Nikerova, K.M.; Moshkina, E.V.; Genikova, N.V. Anatomical and morphological features of Scots pine heartwood formation in two forest types in the middle taiga subzone. Forests 2022, 13, 17. [Google Scholar] [CrossRef]
- Almeida, M.N.F.d.; Vidaurre, G.B.; Pezzopane, J.E.M.; Lousada, J.L.P.C.; Silva, M.E.C.M.; Câmara, A.P.; Rocha, S.M.G.; Oliveira, J.C.L.d.; Campoe, O.C.; Carneiro, R.L.; et al. Heartwood variation of Eucalyptus urophylla is influenced by climatic conditions. For. Ecol. Manag. 2020, 458, 117743. [Google Scholar] [CrossRef]
- Pk, T.; Km, B. Log characteristics and sawn timber recovery of home-garden teak from wet and dry localities of Kerala, India. Small-Scale For. 2009, 8, 15–24. [Google Scholar] [CrossRef]
- Amoah, M.; Inyong, S. Comparison of some physical, mechanical and anatomical properties of smallholder plantation teak (Tectona grandis Linn. f.) from dry and wet localities of Ghana. J. Indian Acad. Wood Sci. 2019, 16, 125–138. [Google Scholar] [CrossRef]
- Krause, C.; Gagnon, R. The relationship between site and tree characteristics and the presence of wet heartwood in black spruce in the boreal forest of Quebec, Canada. Can. J. For. Res. 2011, 36, 1519–1526. [Google Scholar] [CrossRef]
- Vidal-Matutano, P.; Delgado-Darias, T.; López-Dos Santos, N.; Henríquez-Valido, P.; Velasco-Vázquez, J.; Alberto-Barroso, V. Use of decayed wood for funerary practices: Archaeobotanical analysis of funerary wooden artefacts from Prehispanic (ca. 400–1500 CE) Gran Canaria (Canary Islands, Spain). Quatern. Int. 2021, 593, 384–398. [Google Scholar] [CrossRef]
- Thurner, M.; Beer, C.; Crowther, T.; Falster, D.; Manzoni, S.; Prokushkin, A.; Schulze, E.-D. Sapwood biomass carbon in northern boreal and temperate forests. Glob. Ecol. Biogeogr. 2019, 28, 640–660. [Google Scholar] [CrossRef]
- Lamlom, S.; Savidge, R. A reassessment of carbon content in wood: Variation within and between 41 North American species. Biomass Bioenerg. 2003, 25, 381–388. [Google Scholar] [CrossRef]
- Roebroek, C.T.J.; Duveiller, G.; Seneviratne, S.I.; Davin, E.L.; Cescatti, A. Releasing global forests from human management: How much more carbon could be stored? Science 2023, 380, 749–753. [Google Scholar] [CrossRef]
- Terrer, C.; Phillips, R.P.; Hungate, B.A.; Rosende, J.; Pett-Ridge, J.; Craig, M.E.; van Groenigen, K.J.; Keenan, T.F.; Sulman, B.N.; Stocker, B.D.; et al. A trade-off between plant and soil carbon storage under elevated CO2. Nature 2021, 591, 599–603. [Google Scholar] [CrossRef]
- Climate-Data.org. TEJEDA CLIMATE (SPAIN): Data and Graphs for Weather & Climate. Available online: https://en.climate-data.org/europe/spain/canary-islands/tejeda-199883/ (accessed on 5 March 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilar, L.F.A.; Rodríguez, P.R.; Biondi, F. Heartwood Relationship with Stem Diameter in Pinus canariensis Plantations of Gran Canaria, Spain. Forests 2023, 14, 1719. https://doi.org/10.3390/f14091719
Aguilar LFA, Rodríguez PR, Biondi F. Heartwood Relationship with Stem Diameter in Pinus canariensis Plantations of Gran Canaria, Spain. Forests. 2023; 14(9):1719. https://doi.org/10.3390/f14091719
Chicago/Turabian StyleAguilar, Luis Fernando Arencibia, Priscila Rodríguez Rodríguez, and Franco Biondi. 2023. "Heartwood Relationship with Stem Diameter in Pinus canariensis Plantations of Gran Canaria, Spain" Forests 14, no. 9: 1719. https://doi.org/10.3390/f14091719
APA StyleAguilar, L. F. A., Rodríguez, P. R., & Biondi, F. (2023). Heartwood Relationship with Stem Diameter in Pinus canariensis Plantations of Gran Canaria, Spain. Forests, 14(9), 1719. https://doi.org/10.3390/f14091719






