Abstract
Quantifying forest aboveground biomass (AGB) is essential for elucidating the global carbon cycle and the response of forest ecosystems to climate change. Over the past five decades, remote-sensing techniques have played a vital role in forest AGB estimation at different scales. Here, we present an overview of the progress in remote sensing-based forest AGB estimation. More in detail, we first describe the principles of remote sensing techniques in forest AGB estimation: that is, the construction and use of parameters associated with AGB (rather than the direct measurement of AGB values). Second, we review forest AGB remotely sensed data sources (including passive optical, microwave, and LiDAR) and methods (e.g., empirical, physical, mechanistic, and comprehensive models) alongside their limitations and advantages. Third, we discuss possible sources of uncertainty in resultant forest AGB estimates, including those associated with remote sensing imagery, sample plot survey data, stand structure, and statistical models. Finally, we offer forward-looking perspectives and insights on prospective research directions for remote sensing-based forest AGB estimation. Remote sensing is anticipated to play an increasingly important role in future forest AGB estimation and carbon cycle studies. Overall, this comprehensive review may (1) benefit the research communities focused on carbon cycle, remote sensing, and climate change elucidation, (2) provide a theoretical basis for the study of the carbon cycle and global climate change, (3) inform forest ecosystems and carbon management, and (4) aid in the elucidation of forest feedbacks to climate change.
1. Introduction
The rapidly changing climate has severely impacted natural ecosystems and human societies worldwide, resulting in a series of ecological issues, including rising global sea levels [1], accelerated glacial melting at high latitudes and elevations [2,3,4], extremely severe weather [5,6], reduced food production [7], species extinction [8], and deleterious human health effects [9] which directly threaten the survival and security of human beings [10]. Global climate change imposes serious, long-term challenges to the sustainable development of human societies and has evolved into a political, economic, and environmental issue of global concern [11,12].
Forest ecosystems comprise the largest terrestrial carbon pool, storing approximately 76%–98% of terrestrial organic carbon (approximately 80% of above- and 40% of belowground carbon) [13,14]. Moreover, forest ecosystems play a crucial role in the global carbon cycle by absorbing greenhouse gases (GHG) such as atmospheric CO2, thereby reducing GHG concentrations and mitigating global climate change [15,16,17,18].
Forest aboveground biomass (AGB, the aboveground part of forest biomass) reflects the complicated relationship between the nutrient cycle and energy flow [19], providing the necessary nutrient sources and energy base for the functionality of the entire forest ecosystem [20]. In addition, AGB is a key indicator of forest ecosystem carbon sequestration capacity [21,22], productivity, structural function [23,24], and carbon sources and sinks [21,25,26]. Forest AGB estimates have been used as surrogates for aboveground carbon measurements [27]. Accordingly, AGB variations reflect the quality and condition of forest ecosystems [28,29], as well as the effects of ecological succession, natural disturbances, human activities, and climate change on forests [21,30,31]. Therefore, forest AGB estimations in the context of climate change could provide a theoretical basis for the study of the carbon cycle in terrestrial ecosystems and global climate change [18,22,32], which plays a crucial role in understanding and monitoring the response of forest ecosystems to GHG emissions [13,28,33]. In addition, the estimation of forest AGB has contributed to providing strategic guidelines for sustainable forest management [24,34], as well as rational utilization of forest resources and improvement of the forest ecological environment [14,28,29,35].
A rapid and accurate estimation of forest AGB remains challenging in forestry research [25,30]. In general, forest AGB estimation methods can be categorized as field measurements, remote sensing-based approaches, and ecological model simulations [25,36]. Field measurements entail the construction of allometric equations using tree height and diameter data measured via National Forest Inventory (NFI) data or auxiliary field plots [19,37,38,39]. To date, field measurements are considered the most accurate means of obtaining forest biomass data [19,40]; however, these measurements are also the most challenging on a regional scale because of the lengthy and arduous nature of ground-based measurements [30,41]. In addition, the actual amount of land inventoried tends to be quite small; for example, the United States Department of Agriculture (USDA) Forest Service Forest Inventory and Analysis program uses 1 plot per 2400 ha of land. Alternatively, remote sensing-based approaches combine ground measurement data with remotely sensed data to estimate parameters that highly correlate with AGB. This is achieved by obtaining spectral features and vegetation metrics from multi-source remotely sensed data, such as vegetation indices (VIs), canopy cover and height, texture, shaded fraction, leaf and basal area, and timber volume [31,42,43,44,45], whereafter an AGB estimation model is constructed for regional AGB mapping [37]. In addition to the two aforementioned methods, ecological model simulation is a promising tool for the dynamic assessment of regional AGB [46]. However, this approach is often location-specific, has poor applicability, and requires a large number of input parameters for which appropriate values may be difficult to obtain [47,48]. Therefore, remote sensing-based approaches remain the dominant data source for AGB mapping and estimation in different environments [30,36,49,50].
Optical remote sensing images with varying spatial, spectral, and temporal resolutions are freely available and are widely used to estimate AGB at different scales [49,51,52]. For example, moderate- and coarse-resolution data, such as those obtained from the moderate resolution imaging spectroradiometer (MODIS), are typically employed in large-scale AGB estimates for global, continental, or national regions [53,54]. Conversely, medium-resolution data, such as those obtained from Sentinel-2 and Landsat, are mainly used to estimate AGB at local scales [55,56,57,58]. Finer-resolution commercial satellite data, such as those obtained from IKONOS, QuickBird, and WorldView-2, have been employed for AGB estimation at the forest stand scale [59,60,61]. In addition, microwave radar remotely sensed data, including synthetic aperture radar (SAR), interferometric SAR (InSAR), and polarimetric InSAR (PolInSAR) data, have also been used to estimate AGB at regional scales with moderate spatial resolutions [62,63,64,65,66]. However, optical and radar data generally suffer from signal saturation at high AGB, which limits their ability to estimate AGB in dense tropical and subtropical forests [40,67]. Recently, measurements collected using LiDAR, which is capable of acquiring tree height, canopy area, and stand density data, have improved AGB estimations in dense forests [68,69]. Furthermore, unmanned aerial vehicles (UAVs) have emerged as promising remote sensing tools over the last few decades, demonstrating enhanced applications in forest AGB estimation [70,71,72,73].
In an assimilate effort, this review aims to (1) introduce the principles of forest AGB estimation using remotely sensed data, (2) expound and assess several forest AGB data sources and estimation methods, (3) summarize the current sources of uncertainty in forest AGB estimation, and (4) encapsulate possible directions to improve the accuracy of AGB estimation.
2. Principles of AGB Estimation via Remote Sensing
As opposed to direct forest biomass estimations, remote sensing techniques generally evaluate forest AGB through the construction and use of parameters such as optical sensor-derived surface reflectance, VIs, leaf area index (LAI), coverage, and tree and canopy height, with the aim to establish relationships that serve as a proxy for the AGB [36]. The remote sensing techniques used to estimate forest AGB are illustrated in Figure 1. Over the past decades, remote sensing has played a critical role in estimating forest AGB at various spatial and temporal scales [18].
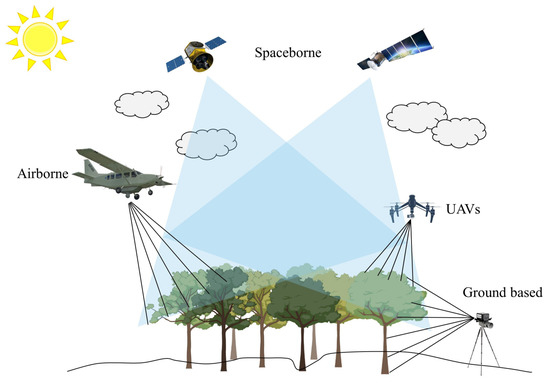
Figure 1.
Illustration of forest aboveground biomass estimation using remote sensing techniques. Note: UAVs, unmanned aerial vehicles.
In addition to single-band information obtained via optical remote sensing, AGB estimations are commonly obtained using VIs based on live green vegetation absorbing solar radiation in red wavelengths to support photosynthesis, which include the normalized difference vegetation index (NDVI), difference vegetation index (DVI), and enhanced vegetation index (EVI) [18,74,75]. However, as green vegetation increases, the strong absorption of red wavelengths leads to a saturation effect, thereby decreasing the AGB estimation accuracy [36]. Nonetheless, several VIs, such as the renormalized DVI (RNDVI) and modified simple ratio (MSR), have been developed to improve the accuracy of biomass estimation in dense vegetation areas [76,77]. For sparse vegetation covers, the orthogonal transform-based perpendicular VI (PVI), soil-adjusted VI (SAVI), and modified SAVI (MSAVI) are used to minimize interference from the atmosphere and soil background [78,79,80]. Moreover, remote sensing-derived texture information has been increasingly used in the estimation of forest AGB [81,82].
Additional parameters that are essential for AGB estimation include those describing the forest structure, such as tree height, diameter at breast height (DBH), and canopy height. Tree height not only reflects the biological characteristics and growth capacity of trees, but also indicates the stand quality [83]. Previous studies have demonstrated a constant AGB-to-tree height ratio (10.6 t/(hm2·m)) in closed-canopy forests using global sampling site survey data on forest age and average tree height [84]. In other words, the density of AGB per forest space was constant (1.0 kg/m3). This phenomenon (called constant aboveground biomass per forest space, BPS) was more pronounced between regions, demonstrating a small mean variation of 9.4–10.5 Mg/(hm2·m) and a global mean value of 9.9 Mg/(hm2·m) [84]. However, it is difficult to determine tree height at the plot scale, especially in tall and closed-canopy forests; therefore, it is often more practical to determine the tree height of only some individuals and then estimate the overall tree height by establishing a growth correlation between tree height and DBH [83]. Furthermore, the power law allometric equation of AGB and tree height constructed at the plot scale remains applicable on a large scale [85], which is a significant advantage of estimating AGB using remote sensing combined with ground measurements [25,36,50]. In recent years, microwave and LiDAR remote sensing have been widely used to estimate AGB. Tree height can be accurately and conveniently obtained from InSAR and LiDAR data, which has significant potential for advancement [86,87,88]. In addition, canopy height has been shown to provide accurate AGB estimations [89,90]. Notably, canopy height is not tree height; it depends not only on tree height, but also on the canopy and stand density of each tree [36].
LAI and forest coverage are also valuable indicators for estimating AGB [52,91]. LAI refers to the total area of plant leaves per unit land area as a multiple of the land area; thus, it mainly reflects leaf biomass [92]. At large scales, LAI-based estimation of AGB requires preliminary establishment of the relationship between leaf biomass and AGB, whereafter AGB is obtained via extrapolation [93]. At small scales, however, total AGB usually refers to the sum of the wood and foliage biomass [94]. Forest coverage refers to the vertical projection of the aboveground portion of trees as a percentage of the sample area and is commonly used for closed-canopy forests to express the tree layer coverage, which is the ratio of the area covered by the forest canopy to the ground surface area [83]. Generally, in uniform forests, a higher coverage represents a higher biomass [52]. Nevertheless, as forest coverage approaches saturation (reaching 1), biomass may continue to increase, which, to some extent, reduces the biomass estimation accuracy in high forest coverage areas [36].
After solar radiation-induced excitation, green leaves emit solar-induced chlorophyll fluorescence (SIF), an electromagnetic signal in the red and far-red spectral portions, from the core of their photosynthetic machinery. Therefore, SIF is mechanically connected to photosynthesis and thus provides a better representation of vegetation growth conditions compared to other biophysical parameters or VIs [95]. Previous studies have found that SIF is strongly related to the gross primary production (GPP) [96,97,98], and GPP can provide direct AGB estimations. Therefore, GPP can be obtained via SIF–GPP correlation analyses, whereafter forest AGB can be estimated from the GPP data [18,98,99,100]. Currently, several global SIF products are available that permit forest biomass estimations [101], including the SIF datasets of Global Monitoring Ozone Experiment 2 (GOME-2) [102,103,104], Orbiting Carbon Observatory 2 (OCO-2) [105] and the Chinese Carbon Dioxide Observation Satellite (TanSat) [106]. Despite the low spatial resolution (40 km × 40 km at best) of the GOME-2 SIF dataset, it is the most widely used owing to its continuous spatial sampling, global coverage, and long time series. For example, Hu et al. [107] developed a method to upscale SIF from instantaneous clear-sky observations to all-sky sums, adopting the absorbed photosynthetically active radiation (APAR) to correct for the effect of clouds on SIF, thereby deriving all-sky SIF (ASSIF) products from GOME-2 in 8-day and monthly intervals during 2007 and 2018 (Figure 2). Moreover, a good correspondence between the temporal trajectories of SIF and GPP [108] has been demonstrated on a global scale by Li et al. [109], who assessed OCO-2-detected SIF data and flux tower GPP data. They showed that a strong relationship between SIF and GPP exists at the ecosystem level and is nearly universal across various biomes. Nevertheless, when using SIF data to estimate GPP and AGB, the influence of environmental conditions and vegetation structure must be considered. Accordingly, SIF yields may be less sensitive than photosynthetic yields under stress conditions [110]; and the relationship between photosynthesis and top-of-canopy SIF measurements is complicated by leaf and plant structural effects [111].
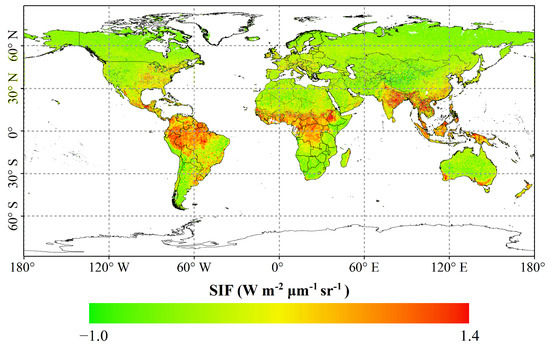
Figure 2.
Global upscaling of the GOME-2 solar-induced chlorophyll fluorescence (SIF) map based on averaged daily values over an 8-day period on the 265th day in 2018, (https://zenodo.org/record/4049762#.X3P9H2gzZPY, accessed on 26 July 2022.) [107].
Overall, forest AGB is estimated using remotely sensed data acquired over a broad electromagnetic wavelength range, from visible light to microwaves (Figure 3). In addition to the above ecological process parameters, environmental (e.g., precipitation, temperature, and atmospheric pressure), topographic (e.g., elevation and slope), and biotic (e.g., species diversity) factors also affect forest AGB estimates. Specifically, factors such as precipitation, temperature, elevation, and slope drive tree species distribution patterns, while soil resources and radiation intensity determine vegetation growth conditions, all of which influence forest AGB [112]. In addition, by taking succession, disturbance, and ecosystem processes into account, forest AGB estimation accuracy may be improved [36,113].
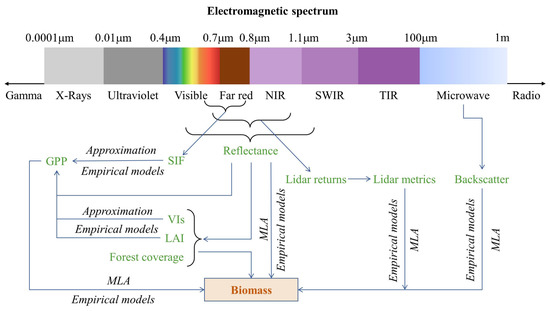
Figure 3.
Electromagnetic spectrum and remote sensing of forest aboveground biomass (AGB). Note: MLA, machine learning approaches; NIR, near-infrared; SWIR, shortwave infrared; TIR, thermal infrared; VIs, vegetation indices; LAI, leaf area index; SIF, solar-induced chlorophyll fluorescence; GPP, gross primary production (adapted from Xiao et al. [18]).
3. Remote Sensing Procedures in Forest AGB Estimation
Forest AGB can be quantified using various remotely sensed data and methods [18,36,114,115,116]. Data sources include passive optical remotely sensed data, microwave remotely sensed data and LiDAR remotely sensed data, etc., estimation methods can be mainly classified into empirical models, physical models, mechanistic models and comprehensive models, etc.
3.1. Remotely Sensed Data Sources
3.1.1. Passive Optical Remote Sensing of AGB
Passive remote sensing is where the detection system of a remote sensing system does not itself carry a source of radiation. Specifically, it is a remote sensing system in which the instrument acquires and records electromagnetic information emitted by the target object itself or reflected from a natural source of radiation (e.g., the sun) during remote sensing. In contrast to passive remote sensing, active remote sensing refers to a remote sensing system that emits a certain form of electromagnetic wave from an artificial radiation source on a remote sensing platform to a target, whose reflected waves are then received and recorded by a sensor. Passive optical remote sensing is widely employed to estimate forest AGB because it is highly sensitive to vegetation canopy properties. Coarse-resolution data (250–8000 m, e.g., MODIS, AVHRR, and SPOT vegetation) are often used to estimate forest AGB at a regional or global scale [50,53,93,117]. Moreover, medium spatial resolution data (~30 m), mainly from the Landsat series (Thematic Mapper, TM; Enhanced Thematic Mapper plus, ETM+; and Operational Land Imager, OLI), Sentinel-2 Multispectral Imager (MSI), and Terra/Aqua ASTER data are applied to local- and regional-scale forest AGB estimates for different ecosystems [58,118,119,120,121]. High spatial resolution data (<5 m), such as IKONOS, QuickBird, and WorldView-2, are frequently used to calculate stand scale forest AGB [59,60,61]. However, such data are generally collected by commercial satellites, which limits their broader application in the field of forest AGB estimation.
Spectral reflectance, VIs, spatial texture, and forest canopy properties are the main variables derived via passive optical remote sensing for AGB estimation. VIs have been developed to minimize the influence of contributing factors that represent vegetation conditions, such as soil background, atmosphere, and sun-target-sensor geometry [122,123,124,125]. In addition to the commonly used VIs (e.g., NDVI, EVI, simple ratio (SR), and chlorophyll difference index), tasseled cap (TC) transformation, and principal component analysis (PCA) are also commonly used for AGB estimation [18]. Spatial texture information describes the spatial features of an image and can reflect the amount of forest AGB to some extent. This texture information can be extracted using a grayscale co-occurrence matrix, which generally uses a 3 × 3 window size [60,126]. In addition, previous studies have improved the accuracy of AGB estimates by including indicators that reflect forest canopy attributes, such as LAI, forest canopy density (FCD), and forest coverage [52,91,127].
Passive optical remote sensing provides one of the best tools for forest AGB estimation in terms of its multiple spatial resolutions, high temporal validity, global coverage, and low cost. However, the optical remote sensing signal has poor penetration, and mainly records information on the horizontal structure, thereby poorly representing the vertical one. Moreover, most vegetation attributes, especially tree height and DBH, are difficult to deduce from passive optical remotely sensed data. Nevertheless, some studies have combined field survey data with QuickBird panchromatic and multispectral data to map tree canopies, obtain canopy area–DBH relationships, and estimate the AGB of mangrove forests in southern Thailand [61]. Unfortunately, implementing this AGB estimation method in other regions is difficult. Furthermore, the passive optical remote sensing signal becomes saturated in very dense forests, resulting in the under- and overestimation of high and low biomass densities, respectively. Therefore, it remains difficult to accurately estimate forest AGB using passive optical remotely sensed data [18].
3.1.2. Microwave Remote Sensing of AGB
As opposed to passive optical remote sensing, microwave remote sensing technology is capable of day-and-night imaging, penetrating clouds and vegetation, obtaining information on the internal structure of forests, and is unaffected by meteorological conditions and sunlight levels. Therefore, it carries certain advantages in estimating forest AGB [21,128]. SAR mainly estimates forest AGB based on the backscatter coefficient. Different SAR backscatter wavelengths (or frequencies) and polarizations originate from different tree parts, resulting in varying AGB estimation abilities. Moreover, forest AGB is mainly estimated using the SAR X-(9.6 G, 3.0 cm), C-(5.6 G, 5.7 cm), S-(3.0 G, 10 cm), L-(1.27 G, 23.5 cm), and P-bands (0.435 G, 70.0 cm), and the HH, HV, VH, and VV polarization signals. The X-band interacts with the leaves and vegetation canopy and extracts information from the surface layer of the forest canopy, whereas the C-band penetrates the leaves and is dispersed by small branches and understory features. The L-band has a high penetration capability through the canopy surface layer and is dispersed by the main trunk and branches of the forest. Finally, the P-band, which has the greatest penetration capability, can penetrate the entire canopy, and the majority of the P-band backscattered signals are generated by the main trunk and its interaction with the ground. The four polarization combinations of SAR data are (1) HH polarization, where both the transmitted and backscattered signals are horizontally polarized; (2) HV polarization, where the transmitted and backscattered signals are horizontally and vertically polarized, respectively; (3) VH polarization, where the transmitted and backscattered signals are vertically and horizontally polarized, respectively; and (4) VV polarization, where both the transmitted and backscattered signals are vertically polarized [129].
Previous studies have found that co-polarization (HH and VV) data at longer wavelengths (e.g., P-band) are highly sensitive to changing surface conditions. Conversely, the backscattered signal from cross-polarization (HV and VH) mainly includes multiple scattering within the canopy and is less influenced by surface conditions [130,131,132]. For low biomass areas, such as grasslands, swamps, post-allotment stands, regenerated stands, and young forests, the backscattered signal at longer wavelengths is lower than that of the C-band; therefore, the C-band is preferred for biomass estimation in lower vegetation biomass areas [129]. Luckman et al. [133] estimated forest biomass in the central Amazon basin and noted that the long-band (L-band) cross-polarized backscatter coefficient was more sensitive to forest AGB changes than that of the C-band, which is limited in distinguishing vegetation from bare soil under soil drought conditions. Following SAR-based forest biomass estimations in central Queensland, Australia, Lucas et al. [134] found that the C-, L-, and P-bands were saturated at varying degrees. Moreover, they demonstrated that the L-band HV polarization data obtained at incidence angles near or above 45° were the most suitable for AGB estimation at saturation levels of 80–85 Mg/ha. Hamdan et al. [135] estimated biomass via ALOS/PALSAR and found that the HV polarization backscatter coefficients had a stronger correlation with dense forests than those of HH polarization did, and the L-band backscatter coefficients had a good AGB estimation ability in mature tropical forests. Furthermore, using airborne SAR data, Schlund and Davidson [136] demonstrated that combined L- and P-band data had a higher biomass estimation accuracy than single-band data, owing to the high sensitivity of the L- and P-bands to low and high biomass, respectively.
The C-band is limited by its inability to effectively penetrate the canopy, and by its saturation level (approximately 60–70 Mg/ha). Nevertheless, these limitations can be overcome by using longer bands capable of higher forest canopy penetration (e.g., L-band and P-band) [137]. Studies have shown that the L-band and P-band usually saturate at 100 Mg/ha for complex heterogeneous tropical forest structures [138]; however, this saturation level increases to approximately 250 Mg/ha for stands with simple structures and few dominant species [134]. Moreover, in an L-band saturation study, Mermoz et al. [139] explored the relationship between the backscatter coefficient and tropical forest biomass. They found that biomass increased with increasing forest canopy density; however, the SAR backscatter coefficient showed a decreasing trend after initially increasing to a certain value and tended to underestimate high biomass values.
Although microwave radar penetration is capable of extracting vertical structure information of forest stands and is widely used in forest biomass estimation, many difficulties exist in SAR-based forest biomass estimation. SAR reflects the roughness of the land cover surface and, therefore, cannot distinguish between vegetation types. Moreover, the SAR signal is susceptible to interference from high wind speed, humidity, and temperature conditions, thereby complicating biomass estimation [21]. In addition, SAR signal saturation also affects the forest biomass estimation accuracy [130,140,141]. Fortunately, PolInSAR and tomographic SAR (TomoSAR) data, which includes BIOMASS (Europe, P-band, scheduled 2022) [142], NISAR (USA, L-band; India, S-band, postponed to 2022) [143], and TanDEM-L (Germany, L-band, scheduled 2022) [144] can effectively overcome the saturation issues in AGB estimation by directly measuring forest spatial structures [18]. Therefore, the use of PolInSAR and TomoSAR shows great promise in the near future.
3.1.3. LiDAR Remote Sensing of AGB
The two-dimensional (2D) nature of optical remotely sensed data limits their application in the direct quantification of vegetation parameters, such as tree height, canopy height, and wood volume. LiDAR is a relatively new and advanced technology that helps overcome this limitation owing to its ability to perform three-dimensional (3D) spatial analyses. LiDAR directly measures the height and vertical structure of forests by emitting laser pulses and measuring the signal return time [145,146,147]. Available terrestrial, aircraft, and spacecraft LiDAR data have been applied to forest AGB estimation and include two main types: small-footprint waveform LiDAR (discrete return LiDAR) and large-footprint waveform LiDAR (full-waveform LiDAR) [148,149]. The small-footprint waveform LiDAR generally has a diameter less than 1 m and a spot size smaller than the canopy width of the stand. Therefore, its practical application necessitates the addition of horizontal sampling points to compensate for the lack of vertical direction, thereby forming complete single-wood (an individual tree) sampling data to estimate stand parameters suitable for inversion of the forest parameter estimation at single-wood and sample plot scales [150]. Large-footprint waveform LiDAR, such as the National Aeronautics and Space Administration’s (NASA) Geoscience Laser Altimeter System (GLAS) (spaceborne) [151] and the Laser Vegetation Imaging Sensor (LVIS) (airborne) [152], generally have spot diameters larger than the canopy width of standing trees, and are suitable for estimating inversions of large-scale forest parameters [153].
Terrestrial laser scanning (TLS) sensors provide very dense point cloud data at millimeter intervals for tree trunks, branches, and leaves [154]. Branch and foliage volumes are then estimated based on the shape information fitted from the point cloud [155,156], thereby providing a non-destructive method to estimate forest AGB and for allometric equation development [156,157]. Apart from AGB estimation at the individual tree level, forest AGB at the stand level has also been successfully estimated using TLS data [154,158].
Airborne laser scanners (ALS) can accurately measure forest canopy height and density. Additionally, by segmenting the canopy height model (CHM) or high-density point cloud data, ALS data can be used to quantify tree height, crown width, and crown volume that, in turn, can be used to estimate the biomass of individual trees [159,160]. For example, Garcia et al. [161] compared waveform- and CHM-based data obtained for different community biomass estimations and point cloud density effects, and pointed out that point cloud density had a greater effect on the CHM. When the point density exceeded 5 points/m2, the CHM- and waveform-based data models performed similarly during the forest AGB estimation. Recently, an increasing amount of LiDAR data acquired from UAVs has been used to estimate forest AGB at the landscape scale [70,162]. Furthermore, low point density ALS data are generally suitable for forest AGB estimation at the stand level or over large areas, and are combined with biomass data from field plots to build biomass estimation models [163,164]. LiDAR-based regional-scale biomass surveys may require less field sampling than other remote sensing methods.
The main advantage of airborne LiDAR is its ability to collect data over large regions or even globally; however, its accuracy in forest parameter inversion estimation is affected by topographic factors, the influence of which numerous studies have aimed to reduce [165]. For example, to reduce the effect of terrain slope on biomass estimation during GLAS application, Wang et al. [166] proposed a novel slope-adaptive waveform metric that obtained a forest AGB estimation accuracy (R2 = 0.92) unparalleled by that of previous methods. Regardless, LiDAR is limited by its high data acquisition costs, discontinuous data coverage, and small coverage area; therefore, research on its forest parameters remains restricted to specific areas and has not been widely applied for continuous biomass distribution estimation and mapping of larger areas. Nevertheless, an increasing availability of LiDAR data has accompanied the development of next-generation LiDAR systems, including the Advanced Terrain Laser Altimeter System (ATLAS) and Global Ecosystem Dynamics Investigation (GEDI). GEDI (launched December 5, 2018) is the first satellite-based LiDAR mission designed to study forests [167] and, in conjunction with ATLAS on board ICESat-2 [168], could facilitate large-scale forest AGB estimates. Indeed, there have been studies that have used GEDI data to estimate biomass at regional and global scales [169,170].
3.1.4. Multi-Source Remote Sensing of AGB
Forest AGB depends on four parameters: tree height, density, DBH, and canopy width. However, measuring DBH directly using air- and spaceborne data is challenging. A single data source usually only enables the combined or individual observation of the other three parameters. Therefore, to facilitate accurate forest AGB estimations, the fusion of multi-source remotely sensed data is inevitable. To achieve this, passive, active, and combined passive and active remotely sensed data have been used. The forest detection parameters associated with these different remotely sensed data sources are shown in Figure 4.
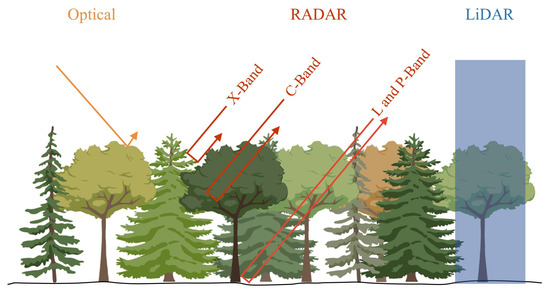
Figure 4.
Diagram of the detection of forest parameters from different sources of remotely sensed data.
Forest AGB estimations via multi-source passive optical remote sensing mainly focus on texture information provided by high-resolution optical remotely sensed data that is supplemented by medium- and high-resolution spectral information or vegetation indices. Nichol and Sarker [171] extracted texture information using two high-resolution optical datasets, AVNIR-2 and SPOT-5, to estimate forest AGB in Hong Kong, China. They observed a higher estimation accuracy based on texture information than that based on multispectral and vegetation indices, and achieved the highest estimation accuracy by combining the texture information from the two sensors. Bastin et al. [172] used Fourier-based textural ordination (FOTO) to extract Geoeye-1 and QuickBird-2 texture information to invert the forest AGB in the African Congo region. Accordingly, they found that the texture information extracted by optical remote sensing could largely minimize the effect of biomass saturation points.
Forest AGB estimation via multi-source active remote sensing is mainly based on field measurement or LiDAR data as a benchmark, combined with different bands of SAR/InSAR data to permit area extension. For example, Duncanson et al. [173] evaluated the biomass simulated by three NASA missions (GEDI, ICESAT-2, and NISAR) over Sonoma County, CA, USA, using high-resolution, locally calibrated, airborne LiDAR maps as reference data. By using these LiDAR reference maps, their method provided guidance for the inter-comparison and validation of spatial biomass estimates. Moreover, the method could be repeated for on-orbit estimates in any area with high-quality field plots and ALS data, providing good technical support for the synergistic inversion of LiDAR and SAR. Accordingly, Joshi et al. [174] estimated forest AGB in Denmark using airborne wall-to-wall discrete return LiDAR and field species trial plot data as a benchmark combined with L-band ALOS/PALSAR HV backscatter data.
The combination of active and passive remote sensing for the collaborative estimation of forest AGB predominantly relies on biomass data obtained from field sampling points or LiDAR as the benchmark and passive remote sensing or SAR data as the independent variables. Laurin et al. [175] combined ALSO-2-extracted SAR backscatter and texture information with Landsat 8-derived NDVI data for mixed forest AGB estimations in California (Tahoe) and the Alps (Asiago). Their model (R2 = 0.66) confirmed that the combination of SAR and optical data complemented each other, thereby improving the estimation accuracy and reducing the saturation problem. Moreover, these results were similar to those of the LiDAR data model in the Alpine region, indicating that the combination of SAR and optical data could provide low-cost, wide-coverage, and highly accurate estimation results at the regional scale. Furthermore, Navarro et al. [176] used UAVs, Sentinel-1, and Sentinel-2 data to study mangrove AGB in Senegal. Accordingly, the use of UAV-obtained, highly accurate parameters of individual trees and the subsequent combination of Sentinel-1 and Sentinel-2 data provided more accurate forest AGB estimates than those obtained by single-sensor Sentinel-1 or Sentinel-2 at the sample level. These findings may facilitate the prospective advancement of biomass estimation in areas with poor accessibility.
Although remote sensing significantly reduces the time and costs of forest AGB estimation, additional field and data measurements are indispensable for both model construction and result validation of forest AGB estimations. In addition, considering the acquisition costs, area coverage (swath width), and limited availability of various sensors, the selection of a suitable sensor in accordance with the specific data availability, project budget, and technical skill requirements for data interpretation remains a practical challenge [177]. Table 1 summarizes the advantages and limitations of the main remote sensing sensors used for AGB estimations. The aforementioned issues should be considered alongside the information presented in Table 1, when applying remote sensing to forest AGB estimation studies to facilitate the selection of appropriate remote sensing technology/data according to the specifics of the study area.

Table 1.
Summary of limitations and advantages of optical, microwave, and LiDAR sensors used for forest AGB estimations, as adapted from Issa et al. [177]. Notes: AGB, aboveground biomass; ETM+, Enhanced Thematic Mapper plus; InSAR, interferometric synthetic aperture radar; MODIS, moderate resolution imaging spectroradiometer; OLI, Operational Land Imager; PolInSAR, polarimetric interferometric synthetic aperture radar; SAR, synthetic aperture radar; TM, Thematic Mapper; TomoSAR, tomographic synthetic aperture radar.
3.2. AGB Estimation Methods
With its rapid and continuing development, remote sensing technology has gradually replaced the traditional forest AGB estimation method. Forest AGB remote sensing estimation methods are mainly categorized into empirical, physical, mechanistic, and comprehensive models. Table 2 summarizes the advantages and limitations of these categories in terms of AGB estimation studies.

Table 2.
A summary of limitations and advantages of the main methods used for estimating forest aboveground biomass (AGB). Notes: ANN, artificial neural networks; GB, gradient boosting; KNN, k-nearest neighbor; LR, linear regression; ME, maximum entropy; MR, multiple regression; RF, random forest; SVM, support vector machine.
3.2.1. Empirical Modeling
Empirical modeling is the most common approach for estimating forest AGB. Specifically, a statistical model is constructed between variables from remotely sensed data and field samples, and the model is used to predict AGB for areas [40,58,119]. Empirical models are classified as being either parametric or non-parametric. Parametric models mainly refer to linear regression (LR), multiple regression (MR), and non-linear regression approaches, whereby the parametric equations and functions serve as model descriptions. Although empirical models are straightforward and understandable, which facilitates the comprehension and analysis of the findings, their estimation accuracy is typically not very high [178,179,180,181]. For instance, Safari et al. [179] used various spectral variables derived from the Landsat 8 OLI to remotely estimate the AGB using nine modeling techniques, including parametric, semi-parametric and non-parametric methods, and compared the accuracy of the different modeling techniques. Based on cross-validation statistics, SVM and Cubist regression are more accurate in the estimation of AGB and are good modeling choices if the degree of under- or over-estimation is not a problematic.
The MR model can enhance AGB estimations by integrating surface reflectance, VIs, and biophysical factors [206]. Accordingly, Eckert [60] created a biomass and carbon estimation model based on stepwise multiple linear regression using texture measurements, VIs, and forest inventory data from the WorldView-2 satellite. They demonstrated that the texture measurements had a stronger correlation with carbon and biomass than spectral characteristics. Zaki et al. [182] used a non-linear regression equation of quadratic functions to estimate the accuracy of AGB and carbon stocks in the tropical lowland dipterocarp forest of the Ayer Hitam Forest Reserve, Selangor. Their results showed a strong relationship between the projected canopy area and carbon stocks. Nevertheless, forest AGB and carbon stocks may be quantified over a wider sample area using Worldview-3 images in conjunction with CHM raster-based LiDAR. Model variable optimization is dependent on the study region, which restricts the applicability despite numerous MR models having been established for forest AGB prediction [18,183]. Additionally, MR assumes that the data variables from remote sensors at various spectral bands are uncorrelated, which is rarely the case in remote sensing. Therefore, Lu et al. [207] suggested the use of the correlation coefficient and stepwise regression analyses to identify remotely sensed data variables that are highly correlated with biomass while being weakly autocorrelated.
Parametric models are constructed based on ideal data distribution assumptions, such that the data distribution follows a normal distribution. However, the interactions between the remote sensing component variables used to estimate forest AGB are complicated, and the data distribution is either difficult to assess or lacks distinguishing features. In contrast, non-parametric models involve direct statistical data analyses without relying on generalizations of the sample’s distribution as a whole. Non-parametric models, which are commonly applied in machine learning, are the most currently used models in remote sensing-based forest AGB estimations and mainly include k-nearest neighbor (KNN) [54], artificial neural networks (ANN) [184], support vector machine (SVM) [185], random forest (RF) [186], gradient boosting (GB) [29], and maximum entropy (ME) [187]. RF and ME methods are increasingly being applied to AGB mapping in complex environments because they can effectively integrate variables with different statistical distributions to provide stable and valid models. In addition, deep learning (DL) methods also have shown great potential in the field of forest AGB estimation [188,189,190,208]. For example, DL methods not only automate many of the steps involved in AGB estimation, e.g., data processing and feature extraction, but also integrate multiple data sources such as satellite imagery, LiDAR data, and ground-based measurements to improve the accuracy of AGB estimation. Moreover, DL models have a high transferability, i.e., DL models trained on one forest can be transferred to other forests with similar characteristics, saving time and effort in model development. However, DL methods still have some limitations, such as high data requirements, complex models and low interpretability. Therefore, it is important to carefully evaluate the advantages and disadvantages of DL methods and consider them in the context of specific applications and datasets.
The relationship between the output results and the input variables is typically complex in non-parametric models because they lack empirical formulae similar to those found in parametric models; however, it is frequently possible to achieve high model estimation accuracies. Reese et al. [209] used Landsat 5 TM and SPOT-3 imagery in combination with digital map data and forest inventory plot data to continuously estimate forest parameters (wood volume, age, and biomass) in five Swedish regions using the KNN method. Their validation results showed that the forest parameter estimation errors were lower in larger areas than in smaller areas. Gao et al. [184] used Landsat 5 TM and ALOS/PALSAR images to estimate the AGB of subtropical forests in Zhejiang Province using ANN, SVM, RF, KNN, and LR models. After comparing the estimation performance of the different models, they demonstrated that Landsat TM imagery provided more accurate AGB estimates than ALOS/PALSAR. Moreover, the combination of TM and PALSAR data performed similarly for ANN and SVM, worse for RF and KNN, and slightly better for LR.
RF improves prediction accuracy by building a “forest” of multiple categorical decision trees through an exhaustive scheme, where both samples and variables are processed simultaneously via the bootstrap method and “bagging algorithm,” respectively [29,210]. In addition, RF achieves optimal segmentation at each node using classification and regression trees. Although individual trees may be weak, the combination of all trees is more robust than the other algorithms and is not limited by the occurrence of over-learning [210]. Accordingly, Chi et al. [211] used Landsat TM, ICESat/GLAS, and ground elevation data combined with ground survey data to collaboratively estimate forest AGB in the Changbai Mountain region based on statistical regression and RF. The results showed that VI contributed more to forest AGB < 150 t/hm2, whereas canopy depression contributed the most when biomass ≥150 t/hm2. Furthermore, Li et al. [29] constructed and comparatively analyzed the ability of LR, RF, and extreme gradient boosting (XGBoost) models to estimate forest AGB in the Hunan Province using Landsat 8 OLI imagery and forest resource survey data. Accordingly, they highlighted the importance of variable selection to improve the performance of models, especially for machine learning algorithms, and that the influence of variable selection on XGBoost is significantly greater than that of RF. Therefore, AGB modeling based on forest type is a very advantageous for improving performance at lower and higher values of AGB.
The ME algorithm is a general statistical method used to predict values from incomplete sample datasets. It fundamentally estimates the probability distribution function of a target from a finite number of samples. The information describing the probability distribution function of the target is called “features”, with the constraint that the expected value of each feature should match its empirical mean (average value obtained from the sampling points). For forest AGB estimation using remotely sensed data, the environmental constraint information can be derived from the spectral information of remote sensing image data (e.g., MODIS, ALOS, shuttle radar topography mission, SRTM, Landsat). Furthermore, the ME model could contain many attributes and thus is highly suitable for large-scale forest AGB mapping [212]. Saatchi et al. [213] successfully developed a global, tropical forest biomass (aboveground and belowground) distribution map using an ME algorithm based on fourteen remotely sensed variables (five MODIS NDVI, three MODIS LAI, four quick scatter meter, QSCAT, and two SRTM derived metrics). Additionally, Rodriguez-Veiga et al. [214] used the ME algorithm to generate forest AGB distribution maps, corresponding biomass uncertainty distribution maps, and forest probability distribution maps for Mexico based on MODIS VI products (NDVI, EVI, blue, red, MIR, and NIR), ALOS/PALSAR mosaic data (HH, HV; two backscatter intensities), and SRTM DEM data. The analysis revealed that ALOS/PALSAR data had the highest relative contribution to AGB estimation (50.9%), followed by MODIS VI (32.9%), whereas SRTM DEM had the lowest contribution. In addition, the forest probability distribution map obtained by the ME algorithm produced the most accurate statistical results for forest AGB.
3.2.2. Physical Modeling
Biomass can be estimated by physical modeling via the inversion of remote sensing information using the relationship between bidirectional vegetation characteristics and biomass. Physical models used for forest AGB estimation primarily include the radiative transfer and geometric optical models. Koetz et al. [191] used LiDAR and optical remotely sensed data to estimate forest AGB by inverting forest structural parameters, such as vegetation cover, LAI, and tree height, using a radiative transfer model. Accordingly, a priori information on canopy structure obtained from large-footprint LiDAR data significantly improved the forest AGB estimation accuracy. Additionally, Chopping et al. [192] used multi-angle reflectance data from the NASA multi-angle imaging spectroradiometer on the Terra satellite as a geometric optical model to invert the canopy cover and mean canopy height and derive the forest AGB by linear transformation in the forests of Arizona and New Mexico, USA. The retrieved distributions of forest crown cover, mean canopy height, and AGB were similar to maps obtained from the USDA Forest Service. Although the physical model has a clear physical meaning and a good stability and applicability, the calculation is complicated and is currently only applicable to small-scale AGB estimations [193].
3.2.3. Mechanistic Modeling
Mechanistic (or process) modeling is generally used to simulate the net primary productivity (NPP) of a forest, and is based on the principles of plant physiology and ecology. Models in this category estimate the productivity of vegetation by simulating the conversion of solar energy to chemical energy during vegetation growth, photosynthesis and evapotranspiration in the plant canopy, and the accompanying water loss from the plant body and soil [194]. Common mechanistic models include climate-related, physiological–ecological process, and light use efficiency models [193,195]. Climate-related models estimate the NPP of different zones based on the average annual temperature, precipitation, and soil moisture [196]. Furthermore, the physiological–ecological process model uses information, such as vegetation cover and soil moisture, provided by remotely sensed data to simulate ecological and physiological factors related to the environment and to plant growth, respectively, to form a hybrid biochemical and biophysical model [197]. Light use efficiency models estimate vegetation NPP by utilizing the relationship between vegetation NPP and photosynthetically active radiation absorbed by vegetation, which is converted to organic matter [197,198].
Opposed to empirical models, mechanistic models emphasize the simulation and description of various processes acting within the ecosystem; therefore, the estimation results are more reliable. However, mechanistic approaches are highly complex and require the input of numerous parameters, such as plant physiology and ecology, soil, meteorology, and solar radiation, some of which are not readily available, thereby limiting their applicability [194].
3.2.4. Comprehensive Modeling
Comprehensive models use ecologically significant estimation models combined with remotely sensed data to estimate forest AGB. These models employ ecological succession as the theoretical basis and allow dynamic simulation of forest vegetation changes [204], including the widely used FAREAST, LANDIS/LANDIS-II, FVS, and SORTIE-ND models [199,200,201,202,203]. For instance, based on the FAREAST model, Wang et al. [205] used the distribution range of Picea crassifolia on different elevation gradients to simulate the elevation distribution characteristics of biomass carbon in young and middle-aged forests in the western, central, and eastern Qilian Mountains. Their results showed that the biomass carbon of P. crassifolia, which was distributed between 2800 and 3100 m above sea level, was higher in the central part of the Qilian Mountains than in the eastern and western parts, thereby identifying the best area for P. crassifolia growth and potential distribution. Wu et al. [199] used a loose-coupling of PnET-II with LANDIS-II to simulate changes in forest AGB and composition under climate change scenarios (current climate, RCP2.6, RCP4.5, RCP6.0, and RCP8.5) with harvest disturbances. The simulation results demonstrated that forest AGB and composition were significantly affected by climate change in both landscapes. Changes in forest AGB was mostly driven by succession and harvest, but climate change also greatly contribute to the variation in AGB of deciduous broad-leaved forests, and coniferous forests. Overall, comprehensive models are logical, flexible in structure, and diverse in form; however, when the spatial resolution of the remotely sensed data is low, the extracted remote sensing information, such as light, moisture, soil nutrients, and temperature, cannot reflect the forest ecological succession law. Comprehensive models require the input of parameters of many tree species. Therefore, the model accuracy not only depends on that of the remotely sensed data, but also on the accuracy of these parameters. This makes the estimation of forest AGB challenging in areas without comprehensive information on the biological characteristics of tree species [193].
4. Uncertainty in Remote Sensing Estimation of Forest AGB
To date, a large, global body of research exists wherein increasingly reliable forest AGB estimations have been achieved using various remotely sensed data and techniques [43,48,91,137,180]. However, the accuracy of remote sensing-based AGB estimations has been a cause of great concern because accurate forest AGB estimation is required to effectively study the global carbon cycle and climate change [18,25]. The forest AGB calculation accuracy is affected by a variety of possible errors and uncertainties, which lead to underestimation of high and overestimation of low AGB values [215,216]. In general, the causative factors of the errors and uncertainties in remote sensing-based forest AGB estimations include remote sensing images, sample plot survey data, stand structure, and statistical models [217,218].
Remotely sensed data errors are primarily related to image complications (e.g., image surface reflectance, VI, SIF, and LAI products) brought on by environmental factors (e.g., atmosphere and humidity), sensor degradation, faulty image processing techniques, and faulty matching of image acquisition time with sample sites, among others [219,220]. Errors in sample plot survey data include faulty measurements of single trees (e.g., DBH and height), allometric growth equation calculations of the sample plot biomass, and sample plot location matching to remote sensing image data [218]. In addition, different sources of forest inventory data may also cause uncertainties in the AGB estimates [218]. For example, in the United States, the USDA Forest Service, Forest Inventory and Analysis program provides NFI data collected as a probability-based (semi-systematic) sample to be used for the purpose of, among others, calibration of forest biomass estimation and mapping. Similarly, ecological research networks such as the National Ecological Observatory Network (NEON), Forest Global Ecosystem Observatory (ForestGEO), and others provide fewer sampling locations but a wealth of data (including commissioning their own remote sensing). Different sources of field survey data use inconsistent measurement methods or approaches, which is one of the sources of the uncertainties in the final AGB estimates. Stand structure errors primarily refer to the inability of information, such as stand canopy, stand age, tree height, and tree diameter structure, to fully portray the stand state on remote sensing imagery. Finally, statistical model errors are mostly caused by the model’s failure to accurately link the stand information with remote sensing image components, leading to estimation issues. Examples of such errors include errors in input data other than remotely sensed data (e.g., meteorological data), errors in the model structure (e.g., incomplete or flawed underlying processes and assumptions), and errors in model parameters (e.g., incomplete or poorly defined parameters due to a lack of information) [18].
Numerous studies have evaluated the uncertainty of remote sensing forest AGB estimations [214,215,216,221]. Accordingly, Saatchi, Houghton, Alvala, Soares and Yu [41] used a regression model to examine the spatial distribution of forest biomass in the Amazon basin and found a significant correlation between forest AGB distribution and the length of the dry season, as well as a 20% uncertainty in the estimated total carbon. Using Landsat TM images and permanent sample plot data from the national forest inventory, Zhang et al. [222] investigated the calculation uncertainty of the aboveground forest carbon (AGFC) owing to sample plot location errors. The findings demonstrated that the accuracy of the anticipated AGFC values decreased with increasing perturbation of the plot location distance. In addition, it was discovered that upscaled spatial data reduced the effects of plot location errors on the map accuracy compared to those without upscaled spatial data. Fassnacht et al. [223] examined the effects of sample size, statistical models, and different remotely sensed data on forest AGB estimation. They found that the sensor type was the most significant factor affecting the accuracy of AGB estimation (LiDAR outperformed hyperspectral results), and that using hyperspectral data in conjunction with LiDAR did not improve the prediction accuracy, and that the prediction models, which usually had a greater impact than the sample size, had a significant impact on the accuracy of the estimation result. Fu et al. [224] examined the biomass estimation uncertainty caused by sampling and model estimation errors in the anisotropic growth equation from continuous forest inventory data of the Chinese fir in Jiangxi Province. Accordingly, they found that the sampling error had a greater effect than the model estimation error on biomass estimations. Furthermore, Gao et al. [184] explored the effects of different models on forest AGB estimation and found that high value underestimation and low value overestimation occurs with different models and images from different data sources (Landsat and SAR). The effect of models on AGB estimation is significant, however, the ability of different models to portray different AGB intervals varies. Therefore, model selection is an important consideration to ensure accurate AGB estimation. In addition, the forest AGB estimates for some specific areas are also of interest, such as the wildland–urban interface (WUI) [225]. WUI, where built-up intermingles with wildland vegetation, is the fastest-growing land use type in the United States [226]. Some studies have shown that forest in the WUI had greater carbon storage, with greater aboveground biomass, relative stand density, and more live trees per hectare than non-WUI forest, suggesting a greater capacity to sequester carbon compared to non-WUI forest [226].
Forest stand structures include both horizontal and vertical structures, and the structure of forest ecosystems is relatively complex. Remote sensing-based forest biomass estimations are carried out using stand structure information, which is, therefore, an important factor affecting forest biomass estimation errors and inaccuracies. To establish empirical correlations between continuous estimates of forest structural features and remotely sensed image data (described as spectral response variables), Hall et al. [56] proposed BioSTRUCT (Estimating Biomass from Stand STRUCTure) to estimate forest AGB. Their results suggested that stand structure may significantly improve the accuracy of AGB estimation. Additionally, Zheng et al. [227] developed a polynomial model to improve the accuracy of forest AGB estimations by combining the spectral variables of Landsat images with the age of the forest stands. Similarly, Ou, Li, Lv, Wei, Xiong, Xu and Wang [186] improved alpine pine forest AGB estimation accuracies by adding age group independent variables to the model. Specifically, different vegetation types are represented in remote sensing images as having different spectral information, and in this case, the forest needs to be classified into types to improve the accuracy of remote sensing-based forest AGB estimations [228]. Nevertheless, forest stands contain not only tree layers, but also shrub and herb layers. In underdeveloped stands, the remote sensing images also contain shrub and herb information to a certain extent, which affects the forest AGB estimation accuracy.
Forest AGB mapping based on different remote sensing data and methods may vary significantly. Several forest AGB maps, some of which are based on ground-measured forest data, optical remote sensing data, or products, have been developed for China (Figure 5). For instance, Piao et al. [229] developed a satellite-based method to estimate the total forest biomass carbon stocks in China based on forest inventory data from three periods (1984–1988, 1989–1993, and 1994–1998) and synchronous NDVI data, thereby successfully estimating these forest AGB changes over two decades (1981–1999). Du et al. [230] estimated the spatially explicit distribution of forest AGB in China based on forest inventory statistics (2004–2008) and the spatially explicit MODIS land cover type product (MCD12C1). Moreover, Yin et al. [231] integrated the plot-level ground-measured forest AGB database with geospatial information from a MODIS dataset (1 km spatial resolution) into a model tree ensemble algorithm to estimate forest AGB in China during 2001–2013. Interestingly, some maps combine ground-based measurements, optical remote sensing, spaceborne LiDAR, and SAR data to estimate forest AGB. Su et al. [232] developed a 1000 m resolution forest AGB map of China using forest ground survey data, GLAS/ICESat data, optical imagery, climate surfaces, and topographic data. Furthermore, Huang et al. [25] developed a finer-resolution spatially continuous forest AGB map for China. They developed novel forest type- and ecozone-specific allometric models based on 1607 field plots, and subsequently applied these models to GLAS data to calculate AGB at the footprint level. This GLAS footprint AGB was related to various variables extracted from Landsat and PALSAR L-band data to map the 30 m resolution national forest AGB. Nevertheless, other studies have conducted global forest AGB mapping based on previously published land-cover biomass products. Spawn et al. [233] developed a global 300 m spatial-resolution, vegetation biomass, carbon-density product based on GlobBiomass AGB density maps [234], and African vegetation AGB density maps [44]. Numerous studies have obtained significantly different average forest AGB values (69.88–120 Mg/ha) for China (Figure 5 and Table 3). Notably, we used an AGB-to-carbon conversion factor of 0.5, and the forest biomass (above- and belowground)-to-AGB conversion factor of 0.81, thereby converting forest biomass and carbon-to-forest AGB [235]. The highest average AGB was observed for the product of Su et al. [232], and that of Yin et al. [231] was similar. It is essential to quantify and reduce uncertainty in the remote sensing of forest AGB products to assess regional and global carbon storage to inform the management and climate policy making.
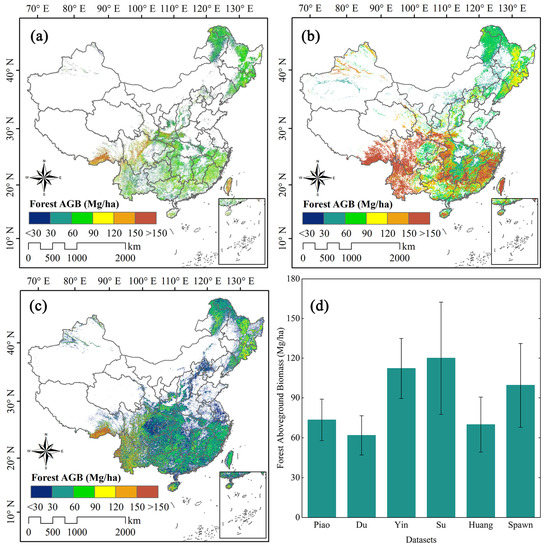
Figure 5.
Forest aboveground biomass (AGB) maps of China based on different datasets: (a) the Huang et al. map [25]; (b) the Su et al. map [232]; (c) the Spawn et al. map [233]; (d) the average AGB of six China forest AGB products.

Table 3.
Comparison of average forest AGB of China derived from various studies.
Quantifying and reducing the uncertainty in forest AGB estimates remains a significant challenge. Considering the different sources of uncertainty, it is important to comprehensively quantify the uncertainty of these estimates in order to reduce or eliminate its effect on forest AGB estimation accuracy. This provides an important direction for future research on forest AGB estimation. Furthermore, the accuracy of forest AGB estimates could be improved by using high-quality resolution, and better methodological remotely sensed data while considering succession, disturbance, and ecosystem processes.
5. Prospects for Remote Sensing of Forest AGB Estimation
The urgent need for society to elucidate Earth’s carbon cycle has motivated recent studies to focus on the numerous factors that change the observed atmospheric CO2 composition; however, numerous gaps remain in our knowledge of these processes. Furthermore, terrestrial vegetation contains carbon stocks comparable to the total amount of atmospheric CO2, and plays an important role in the Earth’s carbon cycle.
Earth observation satellites and other remote sensing sources are the only means to obtain high spatial and temporal resolution data on a global scale. Passive optical, microwave, and LiDAR remote sensing will remain in use for AGB estimations. The utilization of remote sensing combined with field observation data allows for the assessment of global forest AGB changes. Passive optical remote sensing, with its high spatial and temporal resolution, and continuous spatial and temporal coverage, remains an important data source for AGB estimation. For example, the Harmonized Landsat and Sentinel-2 (HLS) data generated by combining Landsat 8 and Sentinel-2 data can provide data with a time interval of up to 5 days and a spatial resolution of 30 m. This enhances our capacity to estimate the AGB consistently from the local to the global scales by enabling us to estimate the AGB at a field scale of 30 m using an ideal time series [236]. Nevertheless, the large amounts of accurately measured AGB data required for empirical models based on passive optical remotely sensed data, as well as for AGB estimation models built using machine learning algorithms, remain lacking at the regional and global scales. Fortunately, high-resolution passive remotely sensed data (e.g., QuickBird, IKONOS, and UAVs) and LiDAR data can generate a large number of AGB samples to train AGB estimation models. Furthermore, the fusion of multi-source remotely sensed data (i.e., passive optical remote sensing with LiDAR and microwave remotely sensed data) is expected to partially overcome the saturation problem in passive optimal remote sensing biomass estimation [18].
To assess forest AGB and monitor forest change, data from airborne- and satellite-based SAR have become crucial resources during the past three decades. Three limitations of SAR forest AGB estimation now exist at the regional scale: the saturation problem, topographic effects, and the mismatch between the base unit of the SAR data and the field sample plot area. The saturation problem associated with AGB estimation using the radar backscatter intensity of a forest with a complex spatial structure may be significantly improved by exploiting spatial structure information obtained from other data, such as InSAR data or optical stereo images [237]. Digital surface model (DSM) data obtained using TanDEM-X satellite X-band radar interferometric data with nearly no temporal decoherence provides, when combined with a high-precision digital terrain model (DTM), a CHM that improves forest AGB estimation accuracy [238]. In addition, NASA’s NISAR provides global L-band InSAR data, as well as either PolInSAR or TomoSAR data, which will soon be widely available free of charge. In particular, the L- and P-band data can directly invert the 3D structure of the forest canopy without requiring a DTM, providing a promising solution for mapping global biomass and monitoring forest disturbances. In practice, the terrain effects can be corrected by developing a relationship between the radar backscatter coefficient and the incidence angle of the main surface types. This involves calculating the incidence angle of each image element based on the radar incidence angle, the slope angle, and slope direction information of the local terrain. Moreover, the terrain effects will likely be overcome by the development of theoretical models and simulations [239], whereas the scale-mismatch problem may be overcome by the synergy of SAR with other types of data such as LiDAR [240] and stereo images [241].
In the last decade and beyond, LiDAR-based technology advancements have enabled the acquisition of accurate understory topography data and forest structure parameters. Furthermore, TLS integration with mobile systems have resulted in the development of mobile laser scanning (MLS) and backpack laser scanning (BLS). The increasing integration of ALS with hyperspectral sensors and the decreasing cost of data capture enables the use of ALS for large-scale sampling [242] and forest AGB estimation [164]. Moreover, because more satellite-based LiDAR systems are used to facilitate global carbon cycle research, AGB estimation models based on LiDAR data will require more consideration to allow regional and global biomass mapping. For example, the new LiDAR aboard ICESat-2 will provide global coverage data to assess carbon stocks, whereas GEDI will use a geodetic-grade LiDAR laser system with 25 m coverage to provide high-resolution laser-ranging observations of the 3D structure of the Earth’s surface.
The integration of passive optical remotely sensed data, SAR, and spaceborne LiDAR is expected to provide seamless and accurate AGB estimates on a global scale. Specifically, at local and regional scales, airborne acquisition techniques, such as imaging spectrometry, LiDAR, SAR, and optical photogrammetry, provide high spatial resolution data. Conversely, spaceborne sensors, including those on Landsat, MODIS, SRTM, ALOS/PALSAR, ICESAT/GLAS, and the L-band SAR carried by ALOS-2, provide observations at intercontinental and global scales.
Clearly, many forest AGB estimation methods exist based on remotely sensed data. The selection of an appropriate method depends on the coverage of the specific project and the availability of various data types. Although the established algorithms have achieved some results, improving the prediction accuracy and reducing uncertainty in the face of complex conditions is still a key direction for future research. Additionally, the use of MR models to estimate local and regional biomass is still relatively popular; however, non-parametric or machine learning approaches have a greater advantage for regional- and global-scale projects. In addition, canopy structure, tree species, and other environmental factors are important considerations for the development of biomass estimation algorithms and models, and the interference of these factors should be reduced to improve the biomass estimation accuracy.
6. Conclusions
In the context of global climate change, forest AGB estimation provides a theoretical basis to study the carbon cycle; however, rapid, accurate AGB estimation remains challenging in forestry research. Remote sensing is an advanced biomass estimation method that enables the estimation of forest AGB at different scales. At present, remotely sensed data from various platforms/sensors are widely applied to estimate forest AGB, including passive optical, microwave, and LiDAR remote sensing, which has resulted in various AGB estimation methods being proposed, including empirical, physical, mechanistic, and comprehensive models. Forest AGB-related parameters, such as surface reflectance, VIs, LAI, coverage, tree height, and canopy height, are used to develop forest AGB estimation models. However, the limitations of different remotely sensed data sources and forest AGB estimation methods remain a major challenge in carbon cycle research. Therefore, reliable forest AGB estimation necessitates the reduction or elimination of uncertainty sources.
Combining remotely sensed data from multiple sources is the most promising strategy for AGB estimation. In such a strategy, VIs, spectral, and texture information are extracted from passive optical remotely sensed data and combined with SAR/LiDAR-extracted tree height, DHB, and canopy height data to estimate forest AGB, which is expected to partially overcome the saturation problem. Forest AGB estimation methods should be selected according to the specific conditions of the study area. To date, MR models remain a relatively popular approach to estimate local and regional biomass; however, non-parametric or machine learning approaches provide added advantages for regional- and global-scale projects. Here, the key finding of this paper is that canopy structure, tree species, and other environmental factors should be considered when developing biomass estimation algorithms or models. On this basis, the interference of these factors should be reduced to improve the accuracy of biomass estimations. Overall, passive optical remotely sensed data, SAR, and airborne LiDAR remain useful for AGB estimation, while the integration of multi-source data is expected to provide seamless and highly accurate AGB estimates on a global scale.
Author Contributions
Conceptualization, L.T. and M.L.; visualization, L.T., X.W. and Y.T.; formal analysis, X.W., C.Q., L.L. and W.F.; writing—original draft preparation and editing, L.T., Y.T. and M.L.; funding acquisition, L.T., M.L. and C.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Postgraduate Research & Practice Innovation Program of Jiangsu Province, the National Natural Science Foundation of China (31770679), and the Suzhou Polytechnic Institute of Agriculture Doctoral Promotion Program Research Fund (BS2022-15).
Acknowledgments
The authors would like to thank Yingchang Li and Chao Li for helpful discussion on forest AGB estimation methods. And we are thankful for all of the helpful comments provided by the reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
AGB, aboveground biomass; AGFC, aboveground forest carbon; ALS, airborne laser scanners; ANN, artificial neural networks; APAR, absorbed photosynthetically active radiation; ASSIF, all-sky solar-induced chlorophyll fluorescence; ATLAS, Advanced Terrain Laser Altimeter System; BLS, backpack laser scanning; BPS, aboveground biomass per forest space; CHM, canopy height model; DBH, diameter at breast height; DL, deep learning; DSM, digital surface model; DTM, digital terrain model; DVI, difference vegetation index; ETM+, Enhanced Thematic Mapper plus; EVI, enhanced vegetation index; FCD, forest canopy density; ForestGEO, Forest Global Ecosystem Observatory; FOTO, Fourier-based textural ordination; GB, gradient boosting; GEDI, Global Ecosystem Dynamics Investigation; GHG, greenhouse gasses; GLAS, Geoscience Laser Altimeter System; GOME-2, Global Monitoring Ozone Experiment 2; GPP, gross primary production; HLS, harmonized Landsat and Sentinel-2; InSAR, interferometric synthetic aperture radar; KNN, k-nearest neighbor; LAI, leaf area index; LR, linear regression; ME, maximum entropy; MLS, mobile laser scanning; MODIS, moderate resolution imaging spectroradiometer; MR, multiple regression; MSAVI, modified soil-adjusted vegetation index; MSI, Multispectral Imager; MSR, modified simple ratio; NASA, National Aeronautics and Space Administration; NDVI, normalized difference vegetation index; NEON, National Ecological Observatory Network; NFI, National Forest Inventory; NISAR, NASA-ISRO SAR Mission; NPP, net primary productivity; OCO-2, Orbiting Carbon Observatory-2; OLI, Operational Land Imager; PCA, principal component analysis; PolInSAR, polarimetric interferometric synthetic aperture radar; PVI, perpendicular vegetation index; QSCAT, quick scatter meter; RF, random forest; RNDVI, renormalized difference vegetation index; SAR, synthetic aperture radar; SAVI, soil-adjusted vegetation index; SIF, solar-induced chlorophyll fluorescence; SR, simple ratio; SRTM, shuttle radar topography mission, SVM, support vector machine; TanSat, Chinese Carbon Dioxide Observation Satellite; TC, tasseled cap; TLS, terrestrial laser scanning; TM, Thematic Mapper; TomoSAR, tomographic synthetic aperture radar; UAVs, unmanned aerial vehicles; USDA, United States Department of Agriculture; VIs, vegetation indices; WUI, wildland-urban interface; XGBoost, extreme gradient boosting.
References
- Nerem, R.S.; Beckley, B.D.; Fasullo, J.T.; Hamlington, B.D.; Masters, D.; Mitchum, G.T. Climate-change-driven accelerated sea-level rise detected in the altimeter era. Proc. Natl. Acad. Sci. USA 2018, 115, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Radic, V.; Bliss, A.; Beedlow, A.C.; Hock, R.; Miles, E.; Cogley, J.G. Regional and global projections of twenty-first century glacier mass changes in response to climate scenarios from global climate models. Clim. Dynam. 2014, 42, 37–58. [Google Scholar] [CrossRef]
- Zheng, G.X.; Allen, S.K.; Bao, A.; Ballesteros-Canovas, J.A.; Huss, M.; Zhang, G.Q.; Li, J.L.; Yuan, Y.; Jiang, L.L.; Yu, T.; et al. Increasing risk of glacial lake outburst floods from future Third Pole deglaciation. Nat. Clim. Change 2021, 11, 411–417. [Google Scholar] [CrossRef]
- Kang, S.C.; Zhang, Q.G.; Qian, Y.; Ji, Z.M.; Li, C.L.; Cong, Z.Y.; Zhang, Y.L.; Guo, J.M.; Du, W.T.; Huang, J.; et al. Linking atmospheric pollution to cryospheric change in the Third Pole region: Current progress and future prospects. Natl. Sci. Rev. 2019, 6, 796–809. [Google Scholar] [CrossRef]
- Yin, J.B.; Gentine, P.; Zhou, S.; Sullivan, S.C.; Wang, R.; Zhang, Y.; Guo, S.L. Large increase in global storm runoff extremes driven by climate and anthropogenic changes. Nat. Commun. 2018, 9, 4389. [Google Scholar] [CrossRef]
- Ebi, K.L.; Vanos, J.; Baldwin, J.W.; Bell, J.E.; Hondula, D.M.; Errett, N.A.; Hayes, K.; Reid, C.E.; Saha, S.; Spector, J.; et al. Extreme Weather and Climate Change: Population Health and Health System Implications. In Annual Review of Public Health; Fielding, J.E., Ed.; Annual Review of Public Health: San Mateo, CA, USA, 2021; Volume 42, pp. 293–315. [Google Scholar] [CrossRef]
- Hasegawa, T.; Fujimori, S.; Havlik, P.; Valin, H.; Bodirsky, B.L.; Doelman, J.C.; Fellmann, T.; Kyle, P.; Koopman, J.F.L.; Lotze-Campen, H.; et al. Risk of increased food insecurity under stringent global climate change mitigation policy. Nat. Clim. Change 2018, 8, 699–703. [Google Scholar] [CrossRef]
- Bellard, C.; Bertelsmeier, C.; Leadley, P.; Thuiller, W.; Courchamp, F. Impacts of climate change on the future of biodiversity. Ecol. Lett. 2012, 15, 365–377. [Google Scholar] [CrossRef]
- Frumkin, H.; Haines, A. Global Environmental Change and Noncommunicable Disease Risks. In Annual Review of Public Health; Fielding, J.E., Ed.; Annual Review of Public Health: San Mateo, CA, USA, 2019; Volume 40, pp. 261–282. [Google Scholar] [CrossRef]
- Gosling, S.N.; Arnell, N.W. A global assessment of the impact of climate change on water scarcity. Clim. Change 2016, 134, 371–385. [Google Scholar] [CrossRef]
- Hoegh-Guldberg, O.; Jacob, D.; Taylor, M.; Guillen Bolanos, T.; Bindi, M.; Brown, S.; Camilloni, I.; Diedhiou, A.; Djalante, R.; Ebi, K.; et al. The human imperative of stabilizing global climate change at 1.5 °C. Science 2019, 365, 1263. [Google Scholar] [CrossRef]
- Sippel, S.; Meinshausen, N.; Fischer, E.M.; Szekely, E.; Knutti, R. Climate change now detectable from any single day of weather at global scale. Nat. Clim. Change 2020, 10, 35–41. [Google Scholar] [CrossRef]
- Pan, Y.D.; Birdsey, R.A.; Fang, J.Y.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Houghton, R.A.; Hall, F.; Goetz, S.J. Importance of biomass in the global carbon cycle. J. Geophys. Res.-Biogeosci. 2009, 114, G00E03. [Google Scholar] [CrossRef]
- Molotoks, A.; Stehfest, E.; Doelman, J.; Albanito, F.; Fitton, N.; Dawson, T.P.; Smith, P. Global projections of future cropland expansion to 2050 and direct impacts on biodiversity and carbon storage. Glob. Change Biol. 2018, 24, 5895–5908. [Google Scholar] [CrossRef] [PubMed]
- Tian, L.; Tao, Y.; Fu, W.X.; Li, T.; Ren, F.; Li, M.Y. Dynamic Simulation of Land Use/Cover Change and Assessment of Forest Ecosystem Carbon Storage under Climate Change Scenarios in Guangdong Province, China. Remote Sens. 2022, 14, 2330. [Google Scholar] [CrossRef]
- Payne, N.J.; Cameron, D.A.; Leblanc, J.D.; Morrison, I.K. Carbon storage and net primary productivity in Canadian boreal mixedwood stands. J. For. Res. 2019, 30, 1667–1678. [Google Scholar] [CrossRef]
- Xiao, J.F.; Chevallier, F.; Gomez, C.; Guanter, L.; Hicke, J.A.; Huete, A.R.; Ichii, K.; Ni, W.J.; Pang, Y.; Rahman, A.F.; et al. Remote sensing of the terrestrial carbon cycle: A review of advances over 50 years. Remote Sens. Environ. 2019, 233, 111383. [Google Scholar] [CrossRef]
- Chave, J.; Rejou-Mechain, M.; Burquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Change Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef]
- Chang, F.C.; Ko, C.H.; Yang, P.Y.; Chen, K.S.; Chang, K.H. Carbon sequestration and substitution potential of subtropical mountain Sugi plantation forests in central Taiwan. J. Clean. Prod. 2017, 167, 1099–1105. [Google Scholar] [CrossRef]
- Li, D.R.; Wang, C.W.; Hu, Y.M.; Liu, S.G. General Review on Remote Sensing-Based Biomass Estimation. Geomat. Inform. Sci. Wuhan Univ. 2012, 37, 631–635. [Google Scholar] [CrossRef]
- Brown, S.; Sathaye, J.; Cannell, M.; Kauppi, P.E. Mitigation of carbon emissions to the atmosphere by forest management. Commonw. For. Rev. 1996, 75, 80–91. [Google Scholar]
- Lu, D.S.; Batistella, M.; Moran, E. Satellite estimation of aboveground biomass and impacts of forest stand structure. Photogramm. Eng. Remote Sens. 2005, 71, 967–974. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, X.; Chen, R.X.; He, Q.S. Review of methods on estimating forest above ground biomass. J. Beijing For. Univ. 2011, 33, 144–150. [Google Scholar] [CrossRef]
- Huang, H.B.; Liu, C.X.; Wang, X.Y.; Zhou, X.L.; Gong, P. Integration of multi-resource remotely sensed data and allometric models for forest aboveground biomass estimation in China. Remote Sens. Environ. 2019, 221, 225–234. [Google Scholar] [CrossRef]
- Myneni, R.B.; Dong, J.; Tucker, C.J.; Kaufmann, R.K.; Kauppi, P.E.; Liski, J.; Zhou, L.; Alexeyev, V.; Hughes, M.K. A large carbon sink in the woody biomass of Northern forests. Proc. Natl. Acad. Sci. USA 2001, 98, 14784–14789. [Google Scholar] [CrossRef] [PubMed]
- Nelson, R.; Gobakken, T.; Naesset, E.; Gregoire, T.G.; Stahl, G.; Holm, S.; Flewelling, J. Lidar sampling—Using an airborne profiler to estimate forest biomass in Hedmark County, Norway. Remote Sens. Environ. 2012, 123, 563–578. [Google Scholar] [CrossRef]
- Houghton, R.A. Aboveground Forest Biomass and the Global Carbon Balance. Glob. Change Biol. 2005, 11, 945–958. [Google Scholar] [CrossRef]
- Li, Y.C.; Li, C.; Li, M.Y.; Liu, Z.Z. Influence of Variable Selection and Forest Type on Forest Aboveground Biomass Estimation Using Machine Learning Algorithms. Forests 2019, 10, 1073. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, X.H.; Ouyang, Z.T.; Avitabile, V.; Qi, J.G.; Chen, J.Q.; Giannico, V. Estimating aboveground biomass in subtropical forests of China by integrating multisource remote sensing and ground data. Remote Sens. Environ. 2019, 232, 111341. [Google Scholar] [CrossRef]
- Narine, L.L.; Popescu, S.; Neuenschwander, A.; Zhou, T.; Srinivasan, S.; Harbeck, K. Estimating aboveground biomass and forest canopy cover with simulated ICESat-2 data. Remote Sens. Environ. 2019, 224, 1–11. [Google Scholar] [CrossRef]
- Fan, W.Y.; Li, M.Z.; Yang, J.M. Forest Biomass Estimation Models of Remote Sensing in Changbai Mountain Forests. Sci. Silvae Sinicae 2011, 47, 16–20. [Google Scholar] [CrossRef]
- Sarker, M.L.R.; Nichol, J.; Iz, H.B.; Bin Ahmad, B.; Rahman, A.A. Forest Biomass Estimation Using Texture Measurements of High-Resolution Dual-Polarization C-Band SAR Data. IEEE Trans. Geosci. Remote 2013, 51, 3371–3384. [Google Scholar] [CrossRef]
- Ali, A.; Lin, S.L.; He, J.K.; Kong, F.M.; Yu, J.H.; Jiang, H.S. Climate and soils determine aboveground biomass indirectly via species diversity and stand structural complexity in tropical forests. For. Ecol. Manag. 2019, 432, 823–831. [Google Scholar] [CrossRef]
- Deng, L.; Liu, S.G.; Kim, D.G.; Peng, C.H.; Sweeney, S.; Shangguan, Z.P. Past and future carbon sequestration benefits of China’s grain for green program. Glob. Environ. Change 2017, 47, 13–20. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Liang, S.L.; Yang, L. A Review of Regional and Global Gridded Forest Biomass Datasets. Remote Sens. 2019, 11, 2744. [Google Scholar] [CrossRef]
- Cartus, O.; Santoro, M.; Kellndorfer, J. Mapping forest aboveground biomass in the Northeastern United States with ALOS PALSAR dual-polarization L-band. Remote Sens. Environ. 2012, 124, 466–478. [Google Scholar] [CrossRef]
- Ketterings, Q.M.; Coe, R.; van Noordwijk, M.; Ambagau, Y.; Palm, C.A. Reducing uncertainty in the use of allometric biomass equations for predicting above-ground tree biomass in mixed secondary forests. For. Ecol. Manag. 2001, 146, 199–209. [Google Scholar] [CrossRef]
- Kenzo, T.; Furutani, R.; Hattori, D.; Kendawang, J.J.; Tanaka, S.; Sakurai, K.; Ninomiya, I. Allometric equations for accurate estimation of above-ground biomass in logged-over tropical rainforests in Sarawak, Malaysia. J. For. Res. 2009, 14, 365–372. [Google Scholar] [CrossRef]
- Lu, D.S.; Chen, Q.; Wang, G.X.; Liu, L.J.; Li, G.Y.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Houghton, R.A.; Alvala, R.; Soares, J.V.; Yu, Y. Distribution of aboveground live biomass in the Amazon basin. Global Change Biol. 2007, 13, 816–837. [Google Scholar] [CrossRef]
- Baccini, A.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, D.; Hackler, J.; Beck, P.S.A.; Dubayah, R.; Friedl, M.A.; et al. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nat. Clim. Change 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Badreldin, N.; Sanchez-Azofeifa, A. Estimating Forest Biomass Dynamics by Integrating Multi-Temporal Landsat Satellite Images with Ground and Airborne LiDAR Data in the Coal Valley Mine, Alberta, Canada. Remote Sens. 2015, 7, 2832–2849. [Google Scholar] [CrossRef]
- Bouvet, A.; Mermoz, S.; Toan, T.L.; Villard, L.; Mathieu, R.; Naidoo, L.; Asner, G.P. An above-ground biomass map of African savannahs and woodlands at 25 m resolution derived from ALOS PALSAR. Remote Sens. Environ. 2018, 206, 156–173. [Google Scholar] [CrossRef]
- Santoro, M.; Beaudoin, A.; Beer, C.; Cartus, O.; Fransson, J.B.S.; Hall, R.J.; Pathe, C.; Schmullius, C.; Schepaschenko, D.; Shvidenko, A.; et al. Forest growing stock volume of the northern hemisphere: Spatially explicit estimates for 2010 derived from Envisat ASAR. Remote Sens. Environ. 2015, 168, 316–334. [Google Scholar] [CrossRef]
- Tian, X.; Yan, M.; van der Tol, C.; Li, Z.; Su, Z.B.; Chen, E.X.; Li, X.; Li, L.H.; Wang, X.F.; Pan, X.D.; et al. Modeling forest above-ground biomass dynamics using multi-source data and incorporated models: A case study over the qilian mountains. Agric. For. Meteorol. 2017, 246, 1–14. [Google Scholar] [CrossRef]
- Hurtt, G.C.; Fisk, J.; Thomas, R.Q.; Dubayah, R.; Moorcroft, P.R.; Shugart, H.H. Linking models and data on vegetation structure. J. Geophys. Res.-Biogeosci. 2010, 115, G00E10. [Google Scholar] [CrossRef]
- Waring, R.H.; Coops, N.C.; Landsberg, J.J. Improving predictions of forest growth using the 3-PGS model with observations made by remote sensing. For. Ecol. Manag. 2010, 259, 1722–1729. [Google Scholar] [CrossRef]
- Yan, F.; Wu, B.; Wang, Y.J. Estimating spatiotemporal patterns of aboveground biomass using Landsat TM and MODIS images in the Mu Us Sandy Land, China. Agric. For. Meteorol. 2015, 200, 119–128. [Google Scholar] [CrossRef]
- Chopping, M.; Wang, Z.S.; Schaaf, C.; Bull, M.A.; Duchesne, R.R. Forest aboveground biomass in the southwestern United States from a MISR multi-angle index, 2000–2015. Remote Sens. Environ. 2022, 275, 112964. [Google Scholar] [CrossRef]
- Foody, G.M.; Boyd, D.S.; Cutler, M.E.J. Predictive relations of tropical forest biomass from Landsat TM data and their transferability between regions. Remote Sens. Environ. 2003, 85, 463–474. [Google Scholar] [CrossRef]
- Blackard, J.A.; Finco, M.V.; Helmer, E.H.; Holden, G.R.; Hoppus, M.L.; Jacobs, D.M.; Lister, A.J.; Moisen, G.G.; Nelson, M.D.; Riemann, R.; et al. Mapping US forest biomass using nationwide forest inventory data and moderate resolution information. Remote Sens. Environ. 2008, 112, 1658–1677. [Google Scholar] [CrossRef]
- Baccini, A.; Walker, W.; Carvalho, L.; Farina, M.; Sulla-Menashe, D.; Houghton, R.A. Tropical forests are a net carbon source based on aboveground measurements of gain and loss. Science 2017, 358, 230–233. [Google Scholar] [CrossRef]
- Beaudoin, A.; Bernier, P.Y.; Guindon, L.; Villemaire, P.; Guo, X.J.; Stinson, G.; Bergeron, T.; Magnussen, S.; Hall, R.J. Mapping attributes of Canada’s forests at moderate resolution through kNN and MODIS imagery. Can. J. For. Res. 2014, 44, 521–532. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O. Evaluating the utility of the medium-spatial resolution Landsat 8 multispectral sensor in quantifying aboveground biomass in uMgeni catchment, South Africa. ISPRS J. Photogramm. 2015, 101, 36–46. [Google Scholar] [CrossRef]
- Hall, R.J.; Skakun, R.S.; Arsenault, E.J.; Case, B.S. Modeling forest stand structure attributes using Landsat ETM+ data: Application to mapping of aboveground biomass and stand volume. For. Ecol. Manag. 2006, 225, 378–390. [Google Scholar] [CrossRef]
- Powell, S.L.; Cohen, W.B.; Healey, S.P.; Kennedy, R.E.; Moisen, G.G.; Pierce, K.B.; Ohmann, J.L. Quantification of live aboveground forest biomass dynamics with Landsat time-series and field inventory data: A comparison of empirical modeling approaches. Remote Sens. Environ. 2010, 114, 1053–1068. [Google Scholar] [CrossRef]
- Fremout, T.; Vinatea, J.C.D.; Thomas, E.; Huaman-Zambrano, W.; Salazar-Villegas, M.; de la Fuente, D.L.; Bernardino, P.N.; Atkinson, R.; Csaplovics, E.; Muys, B. Site-specific scaling of remote sensing-based estimates of woody cover and aboveground biomass for mapping long-term tropical dry forest degradation status. Remote Sens. Environ. 2022, 276, 113040. [Google Scholar] [CrossRef]
- Dillabaugh, K.A.; King, D.J. Riparian marshland composition and biomass mapping using Ikonos imagery. Can. J. Remote Sens. 2008, 34, 143–158. [Google Scholar] [CrossRef]
- Eckert, S. Improved Forest Biomass and Carbon Estimations Using Texture Measures from WorldView-2 Satellite Data. Remote Sens. 2012, 4, 810–829. [Google Scholar] [CrossRef]
- Hirata, Y.; Tabuchi, R.; Patanaponpaiboon, P.; Poungparn, S.; Yoneda, R.; Fujioka, Y. Estimation of aboveground biomass in mangrove forests using high-resolution satellite data. J. For. Res. 2014, 19, 34–41. [Google Scholar] [CrossRef]
- Cartus, O.; Kellndorfer, J.; Walker, W.; Franco, C.; Bishop, J.; Santos, L.; Fuentes, J.M.M. A National, Detailed Map of Forest Aboveground Carbon Stocks in Mexico. Remote Sens. 2014, 6, 5559–5588. [Google Scholar] [CrossRef]
- Yu, Y.F.; Saatchi, S. Sensitivity of L-Band SAR Backscatter to Aboveground Biomass of Global Forests. Remote Sens. 2016, 8, 522. [Google Scholar] [CrossRef]
- Pham, T.D.; Yokoya, N.; Bui, D.T.; Yoshino, K.; Friess, D.A. Remote Sensing Approaches for Monitoring Mangrove Species, Structure, and Biomass: Opportunities and Challenges. Remote Sens. 2019, 11, 230. [Google Scholar] [CrossRef]
- Luo, H.M.; Chen, R.X.; Li, Z.Y.; Cao, C.X. Forest baove ground biomass estimation methodology based on polarization coherence tomography. Natl. Remote Sens. Bull. 2011, 15, 1138–1155. [Google Scholar]
- Li, W.M.; Chen, R.X.; Li, Z.Y.; Zhao, L. Forest Above-Ground Biomass Estimation Using Polarimetric Interferometry SAR Coherence Tomography. Sci. Silvae Sinicae 2014, 50, 70–77. [Google Scholar]
- Zhao, P.P.; Lu, D.S.; Wang, G.X.; Wu, C.P.; Huang, Y.J.; Yu, S.Q. Examining Spectral Reflectance Saturation in Landsat Imagery and Corresponding Solutions to Improve Forest Aboveground Biomass Estimation. Remote Sens. 2016, 8, 469. [Google Scholar] [CrossRef]
- Baccini, A.; Asner, G.P. Improving pantropical forest carbon maps with airborne LiDAR sampling. Carbon Manag. 2013, 4, 591–600. [Google Scholar] [CrossRef]
- Asner, G.P.; Mascaro, J.; Anderson, C.; Knapp, D.E.; Martin, R.E.; Kennedy-Bowdoin, T.; van Breugel, M.; Davies, S.; Hall, J.S.; Muller-Landau, H.C.; et al. High-fidelity national carbon mapping for resource management and REDD+. Carbon Bal. Manag. 2013, 8, 7. [Google Scholar] [CrossRef]
- Poley, L.G.; McDermid, G.J. A Systematic Review of the Factors Influencing the Estimation of Vegetation Aboveground Biomass Using Unmanned Aerial Systems. Remote Sens. 2020, 12, 1052. [Google Scholar] [CrossRef]
- Fan, X.Y.; Kawamura, K.; Xuan, T.D.; Yuba, N.; Lim, J.; Yoshitoshi, R.; Minh, T.N.; Kurokawa, Y.; Obitsu, T. Low-cost visible and near-infrared camera on an unmanned aerial vehicle for assessing the herbage biomass and leaf area index in an Italian ryegrass field. Grassl. Sci. 2018, 64, 145–150. [Google Scholar] [CrossRef]
- Schirrmann, M.; Giebel, A.; Gleiniger, F.; Pflanz, M.; Lentschke, J.; Dammer, K.H. Monitoring Agronomic Parameters of Winter Wheat Crops with Low-Cost UAV Imagery. Remote Sens. 2016, 8, 706. [Google Scholar] [CrossRef]
- Doughty, C.L.; Cavanaugh, K.C. Mapping Coastal Wetland Biomass from High Resolution Unmanned Aerial Vehicle (UAV) Imagery. Remote Sens. 2019, 11, 540. [Google Scholar] [CrossRef]
- Garroutte, E.L.; Hansen, A.J.; Lawrence, R.L. Using NDVI and EVI to Map Spatiotemporal Variation in the Biomass and Quality of Forage for Migratory Elk in the Greater Yellowstone Ecosystem. Remote Sens. 2016, 8, 404. [Google Scholar] [CrossRef]
- Tian, F.; Brandt, M.; Liu, Y.Y.; Verger, A.; Tagesson, T.; Diouf, A.A.; Rasmussen, K.; Mbow, C.; Wang, Y.J.; Fensholt, R. Remote sensing of vegetation dynamics in drylands: Evaluating vegetation optical depth (VOD) using AVHRR NDVI and in situ green biomass data over West African Sahel. Remote Sens. Environ. 2016, 177, 265–276. [Google Scholar] [CrossRef]
- Durante, P.; Martín-Alcón, S.; Gil-Tena, A.; Algeet, N.; Tomé, J.L.; Recuero, L.; Palacios-Orueta, A.; Oyonarte, C. Improving Aboveground Forest Biomass Maps: From High-Resolution to National Scale. Remote Sens. 2019, 11, 795. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of Vegetation Indices and a Modified Simple Ratio for Boreal Applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Fatehi, P.; Damm, A.; Schaepman, M.E.; Kneubuhler, M. Estimation of Alpine Forest Structural Variables from Imaging Spectrometer Data. Remote Sens. 2015, 7, 16315–16338. [Google Scholar] [CrossRef]
- Luo, S.Z.; Wang, C.; Xi, X.H.; Pan, F.F.; Qian, M.J.; Peng, D.L.; Nie, S.; Qin, H.M.; Lin, Y. Retrieving aboveground biomass of wetland Phragmites australis (common reed) using a combination of airborne discrete-return LiDAR and hyperspectral data. Int. J. Appl. Earth Obs. 2017, 58, 107–117. [Google Scholar] [CrossRef]
- Sadeghi, Y.; St-Onge, B.; Leblon, B.; Prieur, J.F.; Simard, M. Mapping boreal forest biomass from a SRTM and TanDEM-X based on canopy height model and Landsat spectral indices. Int. J. Appl. Earth Obs. 2018, 68, 202–213. [Google Scholar] [CrossRef]
- Kelsey, K.C.; Neff, J.C. Estimates of Aboveground Biomass from Texture Analysis of Landsat Imagery. Remote Sens. 2014, 6, 6407–6422. [Google Scholar] [CrossRef]
- Sarker, L.R.; Nichol, J.E. Improved forest biomass estimates using ALOS AVNIR-2 texture indices. Remote Sens. Environ. 2011, 115, 968–977. [Google Scholar] [CrossRef]
- Fang, J.Y.; Zhu, J.X.; Li, P.; Ji, C.J.; Zhu, J.L.; Jiang, L.; Chen, G.P.; Cai, Q.; Su, H.J.; Feng, Y.H.; et al. Carbon Budgets of Forest Ecosystems in China; Science Press: Beijing, China, 2021. [Google Scholar]
- Fang, J.Y.; Brown, S.; Tang, Y.H.; Nabuurs, G.J.; Wang, X.P.; Shen, H.H. Overestimated biomass carbon pools of the northern mid- and high latitude forests. Clim. Change 2006, 74, 355–368. [Google Scholar] [CrossRef]
- Wu, X.; Wang, X.P.; Wu, Y.L.; Xia, X.L.; Fang, J.Y. Forest biomass is strongly shaped by forest height across boreal to tropical forests in China. J. Plant Ecol. 2015, 8, 559–567. [Google Scholar] [CrossRef]
- Solberg, S.; Nasset, E.; Gobakken, T.; Bollandsas, O.-M. Forest biomass change estimated from height change in interferometric SAR height models. Carbon Bal. Manag. 2014, 9, 5. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.F.; Saatchi, S.; Heath, L.S.; LaPoint, E.; Myneni, R.; Knyazikhin, Y. Regional distribution of forest height and biomass from multisensor data fusion. J. Geophys. Res.-Biogeosci. 2010, 115, G00E12. [Google Scholar] [CrossRef]
- Asner, G.P.; Mascaro, J. Mapping tropical forest carbon: Calibrating plot estimates to a simple LiDAR metric. Remote Sens. Environ. 2014, 140, 614–624. [Google Scholar] [CrossRef]
- Simard, M.; Fatoyinbo, L.; Smetanka, C.; Rivera-Monroy, V.H.; Castaneda-Moya, E.; Thomas, N.; Van der Stocken, T. Mangrove canopy height globally related to precipitation, temperature and cyclone frequency. Nat. Geosci. 2019, 12, 40–45. [Google Scholar] [CrossRef]
- Bouvier, M.; Durrieu, S.; Fournier, R.A.; Renaud, J.P. Generalizing predictive models of forest inventory attributes using an area-based approach with airborne LiDAR data. Remote Sens. Environ. 2015, 156, 322–334. [Google Scholar] [CrossRef]
- Zhang, G.; Ganguly, S.; Nemani, R.R.; White, M.A.; Milesi, C.; Hashimoto, H.; Wang, W.L.; Saatchi, S.; Yu, Y.F.; Myneni, R.B. Estimation of forest aboveground biomass in California using canopy height and leaf area index estimated from satellite data. Remote Sens. Environ. 2014, 151, 44–56. [Google Scholar] [CrossRef]
- Wu, Y.C.; Strahler, A.H. Remote estimation of crown size, stand density, and biomass on the Oregon transect. Ecol. Appl. 1994, 4, 299–312. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Kondragunta, S. Estimating forest biomass in the USA using generalized allometric models and MODIS land products. Geophys. Res. Lett. 2006, 33, L09402. [Google Scholar] [CrossRef]
- Berner, L.T.; Law, B.E. Plant traits, productivity, biomass and soil properties from forest sites in the Pacific Northwest, 1999–2014. Sci. Data 2016, 3, 160002. [Google Scholar] [CrossRef] [PubMed]
- Porcar-Castell, A.; Tyystjarvi, E.; Atherton, J.; van der Tol, C.; Flexas, J.; Pfundel, E.E.; Moreno, J.; Frankenberg, C.; Berry, J.A. Linking chlorophyll a fluorescence to photosynthesis for remote sensing applications: Mechanisms and challenges. J. Exp. Bot. 2014, 65, 4065–4095. [Google Scholar] [CrossRef] [PubMed]
- Gu, L.; Wood, J.D.; Chang, C.Y.Y.; Sun, Y.; Riggs, J.S. Advancing Terrestrial Ecosystem Science with a Novel Automated Measurement System for Sun-Induced Chlorophyll Fluorescence for Integration with Eddy Covariance Flux Networks. J. Geophys. Res.-Biogeosci. 2019, 124, 127–146. [Google Scholar] [CrossRef]
- Damm, A.; Guanter, L.; Paul-Limoges, E.; van der Tol, C.; Hueni, A.; Buchmann, N.; Eugster, W.; Ammann, C.; Schaepman, M.E. Far-red sun-induced chlorophyll fluorescence shows ecosystem-specific relationships to gross primary production: An assessment based on observational and modeling approaches. Remote Sens. Environ. 2015, 166, 91–105. [Google Scholar] [CrossRef]
- Yang, K.; Ryu, Y.; Dechant, B.; Berry, J.A.; Hwang, Y.; Jiang, C.; Kang, M.; Min, J.; Kimm, H.; Kornfeld, A.; et al. Sun-induced chlorophyll fluorescence is more strongly related to absorbed light than to photosynthesis at half-hourly resolution in a rice paddy. Remote Sens. Environ. 2018, 216, 658–673. [Google Scholar] [CrossRef]
- Qin, Y.W.; Xiao, X.M.; Wigneron, J.P.; Ciais, P.; Canadell, J.G.; Brandt, M.; Li, X.J.; Fan, L.; Wu, X.C.; Tang, H.; et al. Large loss and rapid recovery of vegetation cover and aboveground biomass over forest areas in Australia during 2019–2020. Remote Sens. Environ. 2022, 278, 113087. [Google Scholar] [CrossRef]
- Yang, X.; Tang, J.W.; Mustard, J.F.; Lee, J.E.; Rossini, M.; Joiner, J.; Munger, J.W.; Kornfeld, A.; Richardson, A.D. Solar-induced chlorophyll fluorescence that correlates with canopy photosynthesis on diurnal and seasonal scales in a temperate deciduous forest. Geophys. Res. Lett. 2015, 42, 2977–2987. [Google Scholar] [CrossRef]
- Frankenberg, C.; Fisher, J.B.; Worden, J.; Badgley, G.; Saatchi, S.S.; Lee, J.E.; Toon, G.C.; Butz, A.; Jung, M.; Kuze, A.; et al. New global observations of the terrestrial carbon cycle from GOSAT: Patterns of plant fluorescence with gross primary productivity. Geophys. Res. Lett. 2011, 38, L17706. [Google Scholar] [CrossRef]
- Kohler, P.; Guanter, L.; Joiner, J. A linear method for the retrieval of sun-induced chlorophyll fluorescence from GOME-2 and SCIAMACHY data. Atmos. Meas. Tech. 2015, 8, 2589–2608. [Google Scholar] [CrossRef]
- Joiner, J.; Yoshida, Y.; Vasilkov, A.P.; Middleton, E.M.; Campbell, P.K.E.; Yoshida, Y.; Kuze, A.; Corp, L.A. Filling-in of near-infrared solar lines by terrestrial fluorescence and other geophysical effects: Simulations and space-based observations from SCIAMACHY and GOSAT. Atmos. Meas. Tech. 2012, 5, 809–829. [Google Scholar] [CrossRef]
- Wolanin, A.; Rozanov, V.V.; Dinter, T.; Noel, S.; Vountas, M.; Burrows, J.P.; Bracher, A. Global retrieval of marine and terrestrial chlorophyll fluorescence at its red peak using hyperspectral top of atmosphere radiance measurements: Feasibility study and first results. Remote Sens. Environ. 2015, 166, 243–261. [Google Scholar] [CrossRef]
- Sun, Y.; Frankenberg, C.; Jung, M.; Joiner, J.; Guanter, L.; Kohler, P.; Magney, T. Overview of Solar-Induced chlorophyll Fluorescence (SIF) from the Orbiting Carbon Observatory-2: Retrieval, cross-mission comparison, and global monitoring for GPP. Remote Sens. Environ. 2018, 209, 808–823. [Google Scholar] [CrossRef]
- Du, S.S.; Liu, L.Y.; Liu, X.J.; Zhang, X.; Zhang, X.Y.; Bi, Y.M.; Zhang, L.C. Retrieval of global terrestrial solar-induced chlorophyll fluorescence from TanSat satellite. Sci. Bull. 2018, 63, 1502–1512. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.C.; Liu, L.Y.; Yu, H.Y.; Guan, L.L.; Liu, X.J. Upscaling GOME-2 SIF from clear-sky instantaneous observations to all-sky sums leading to an improved SIF-GPP correlation. Agric. For. Meteorol. 2021, 306, 108439. [Google Scholar] [CrossRef]
- Joiner, J.; Yoshida, Y.; Vasilkov, A.; Schaefer, K.; Jung, M.; Guanter, L.; Zhang, Y.; Garrity, S.; Middleton, E.M.; Huemmrich, K.F.; et al. The seasonal cycle of satellite chlorophyll fluorescence observations and its relationship to vegetation phenology and ecosystem atmosphere carbon exchange. Remote Sens. Environ. 2014, 152, 375–391. [Google Scholar] [CrossRef]
- Li, X.; Xiao, J.F.; He, B.B.; Arain, M.A.; Beringer, J.; Desai, A.R.; Emmel, C.; Hollinger, D.Y.; Krasnova, A.; Mammarella, I.; et al. Solar-induced chlorophyll fluorescence is strongly correlated with terrestrial photosynthesis for a wide variety of biomes: First global analysis based on OCO-2 and flux tower observations. Glob. Change Biol. 2018, 24, 3990–4008. [Google Scholar] [CrossRef] [PubMed]
- Wohlfahrt, G.; Gerdel, K.; Migliavacca, M.; Rotenberg, E.; Tatarinov, F.; Müller, J.; Hammerle, A.; Julitta, T.; Spielmann, F.M.; Yakir, D. Sun-induced fluorescence and gross primary productivity during a heat wave. Sci. Rep. 2018, 8, 14169. [Google Scholar] [CrossRef]
- Fournier, A.; Daumard, F.; Champagne, S.; Ounis, A.; Goulas, Y.; Moya, I. Effect of canopy structure on sun-induced chlorophyll fluorescence. ISPRS J. Photogramm. 2012, 68, 112–120. [Google Scholar] [CrossRef]
- McEwan, R.W.; Lin, Y.C.; Sun, I.F.; Hsieh, C.F.; Su, S.H.; Chang, L.W.; Song, G.Z.M.; Wang, H.H.; Hwong, J.L.; Lin, K.C.; et al. Topographic and biotic regulation of aboveground carbon storage in subtropical broad-leaved forests of Taiwan. For. Ecol. Manag. 2011, 262, 1817–1825. [Google Scholar] [CrossRef]
- Frolking, S.; Palace, M.W.; Clark, D.B.; Chambers, J.Q.; Shugart, H.H.; Hurtt, G.C. Forest disturbance and recovery: A general review in the context of spaceborne remote sensing of impacts on aboveground biomass and canopy structure. J. Geophys. Res.-Biogeosci. 2009, 114, G00E02. [Google Scholar] [CrossRef]
- Ryu, Y.; Berry, J.A.; Baldocchi, D.D. What is global photosynthesis? History, uncertainties and opportunities. Remote Sens. Environ. 2019, 223, 95–114. [Google Scholar] [CrossRef]
- Schimel, D.; Pavlick, R.; Fisher, J.B.; Asner, G.P.; Saatchi, S.; Townsend, P.; Miller, C.; Frankenberg, C.; Hibbard, K.; Cox, P. Observing terrestrial ecosystems and the carbon cycle from space. Glob. Change Biol. 2015, 21, 1762–1776. [Google Scholar] [CrossRef]
- Abbas, S.; Wong, M.S.; Wu, J.; Shahzad, N.; Irteza, S.M. Approaches of Satellite Remote Sensing for the Assessment of Above-Ground Biomass across Tropical Forests: Pan-tropical to National Scales. Remote Sens. 2020, 12, 3351. [Google Scholar] [CrossRef]
- Chopping, M.; Schaaf, C.B.; Zhao, F.; Wang, Z.S.; Nolin, A.W.; Moisen, G.G.; Martonchik, J.V.; Bull, M. Forest structure and aboveground biomass in the southwestern United States from MODIS and MISR. Remote Sens. Environ. 2011, 115, 2943–2953. [Google Scholar] [CrossRef]
- Sibanda, M.; Mutanga, O.; Rouget, M. Examining the potential of Sentinel-2 MSI spectral resolution in quantifying above ground biomass across different fertilizer treatments. ISPRS J. Photogramm. 2015, 110, 55–65. [Google Scholar] [CrossRef]
- Luo, M.; Wang, Y.F.; Xie, Y.H.; Zhou, L.; Qiao, J.J.; Qiu, S.Y.; Sun, Y.J. Combination of Feature Selection and CatBoost for Prediction: The First Application to the Estimation of Aboveground Biomass. Forests 2021, 12, 216. [Google Scholar] [CrossRef]
- Taddese, H.; Asrat, Z.; Burud, I.; Gobakken, T.; Orka, H.O.; Dick, O.B.; Naesset, E. Use of Remotely Sensed Data to Enhance Estimation of Aboveground Biomass for the Dry Afromontane Forest in South-Central Ethiopia. Remote Sens. 2020, 12, 3335. [Google Scholar] [CrossRef]
- Muukkonen, P.; Heiskanen, J. Estimating biomass for boreal forests using ASTER satellite data combined with standwise forest inventory data. Remote Sens. Environ. 2005, 99, 434–447. [Google Scholar] [CrossRef]
- Bannari, A.; Morin, D.; Bonn, F.; Huete, A. A review of vegetation indices. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Gao, X.; Huete, A.R.; Ni, W.; Miura, T. Optical–Biophysical Relationships of Vegetation Spectra without Background Contamination. Remote Sens. Environ. 2000, 74, 609–620. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Zeng, Y.L.; Hao, D.L.; Huete, A.; Dechant, B.; Berry, J.; Chen, J.M.; Joiner, J.; Frankenberg, C.; Bond-Lamberty, B.; Ryu, Y.; et al. Optical vegetation indices for monitoring terrestrial ecosystems globally. Nat. Rev. Earth Environ. 2022, 3, 447–493. [Google Scholar] [CrossRef]
- Ploton, P.; Barbier, N.; Couteron, P.; Antin, C.M.; Ayyappan, N.; Balachandran, N.; Barathan, N.; Bastin, J.F.; Chuyong, G.; Dauby, G.; et al. Toward a general tropical forest biomass prediction model from very high resolution optical satellite images. Remote Sens. Environ. 2017, 200, 140–153. [Google Scholar] [CrossRef]
- Li, T.; Li, M.Y.; Ren, F.; Tian, L. Estimation and Spatio-Temporal Change Analysis of NPP in Subtropical Forests: A Case Study of Shaoguan, Guangdong, China. Remote Sens. 2022, 14, 2541. [Google Scholar] [CrossRef]
- Zaki, N.A.M.; Abd Latif, Z. Carbon sinks and tropical forest biomass estimation: A review on role of remote sensing in aboveground-biomass modelling. Geocarto Int. 2017, 32, 701–716. [Google Scholar] [CrossRef]
- Ghasemi, N.; Sahebi, M.; Mohammadzadeh, A. A review on biomass estimation methods using synthetic aperture radar data. Int. J. Geomat. Geosci. 2011, 1, 776–778. [Google Scholar]
- Chen, R.X. Develoment of Forest Biomass Estimation Using SAR Data. World For. Res. 1999, 12, 18–23. [Google Scholar] [CrossRef]
- Wang, Y.; Day, J.L.; Davis, F.W. Sensitivity of Modeled C- and L-Band Radar Backscatter to Ground Surface Parameters in Loblolly Pine Forest. Remote Sens. Environ. 1998, 66, 331–342. [Google Scholar] [CrossRef]
- Huang, Y.P.; Chen, J.S. Advances in the estimation of forest biomass based on SAR data. Remote Sens. Nat. Resour. 2013, 25, 7–13. [Google Scholar] [CrossRef]
- Luckman, A.; Baker, J.; Kuplich, T.M.; da Costa Freitas Yanasse, C.; Frery, A.C. A study of the relationship between radar backscatter and regenerating tropical forest biomass for spaceborne SAR instruments. Remote Sens. Environ. 1997, 60, 1–13. [Google Scholar] [CrossRef]
- Lucas, R.M.; Cronin, N.; Lee, A.; Moghaddam, M.; Witte, C.; Tickle, P. Empirical relationships between AIRSAR backscatter and LiDAR-derived forest biomass, queensland, Australia. Remote Sens. Environ. 2006, 100, 407–425. [Google Scholar] [CrossRef]
- Hamdan, O.; Aziz, H.K.; Abd Rahman, K. Remotely sensed L-band SAR data for tropical forest biomass estimation. J. Trop. For. Sci. 2011, 23, 318–327. [Google Scholar]
- Schlund, M.; Davidson, M.W.J. Aboveground Forest Biomass Estimation Combining L- and P-Band SAR Acquisitions. Remote Sens. 2018, 10, 1151. [Google Scholar] [CrossRef]
- Huang, X.D.; Ziniti, B.; Torbick, N.; Ducey, M.J. Assessment of Forest above Ground Biomass Estimation Using Multi-Temporal C-band Sentinel-1 and Polarimetric L-band PALSAR-2 Data. Remote Sens. 2018, 10, 1424. [Google Scholar] [CrossRef]
- Sandberg, G.; Ulander, L.M.H.; Fransson, J.E.S.; Holmgren, J.; Le Toan, T. L- and P-band backscatter intensity for biomass retrieval in hemiboreal forest. Remote Sens. Environ. 2011, 115, 2874–2886. [Google Scholar] [CrossRef]
- Mermoz, S.; Rejou-Mechain, M.; Villard, L.; Le Loan, T.; Rossi, V.; Gourlet-Fleury, S. Decrease of L-band SAR backscatter with biomass of dense forests. Remote Sens. Environ. 2015, 159, 307–317. [Google Scholar] [CrossRef]
- Wu, Y.R.; Hong, W.; Wang, Y.P. The Current Status and Implications of Polarimetric SAR Interfermetry. J. Electron. Inform. Tech. 2007, 29, 1258–1262. [Google Scholar]
- Liu, X.; Yang, L.; Liu, Q.H.; Li, J. Review of forest above ground biomass inversion methods based on remote sensing technology. Natl. Remote Sens. Bull. 2014, 19, 62–74. [Google Scholar] [CrossRef]
- Le Toan, T.; Quegan, S.; Davidson, M.W.J.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H.; et al. The BIOMASS mission: Mapping global forest biomass to better understand the terrestrial carbon cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
- Rosen, P.; Hensley, S.; Shaffer, S.; Edelstein, W.; Kim, Y.; Kumar, R.; Misra, T.; Bhan, R.; Satish, R.; Sagi, R. An update on the NASA-ISRO dual-frequency DBF SAR (NISAR) mission. In Proceedings of the 36th IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 2106–2108. [Google Scholar] [CrossRef]
- Quegan, S.; Toan, L.T.; Chave, J.; Dall, J.; Exbrayat, J.F.; Minh, D.H.T.; Lomas, M.; D’Alessandro, M.M.; Paillou, P.; Papathanassiou, K.; et al. The European Space Agency BIOMASS mission: Measuring forest above-ground biomass from space. Remote Sens. Environ. 2019, 227, 44–60. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Keller, M.; Pang, Y.; de Camargo, P.B.; Hunter, M.O. Revised method for forest canopy height estimation from Geoscience Laser Altimeter System waveforms. J. Appl. Remote Sens. 2007, 1, 013537. [Google Scholar] [CrossRef]
- Pang, Y.; Lefsky, M.; Andersen, H.E.; Miller, M.E.; Sherrill, K. Validation of the ICEsat vegetation product using crown-area-weighted mean height derived using crown delineation with discrete return lidar data. Can. J. Remote Sens. 2008, 34, S471–S484. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res.-Biogeosci. 2011, 116, G04021. [Google Scholar] [CrossRef]
- Van Aardt, J.A.N.; Wynne, R.H.; Oderwald, R.G. Forest volume and biomass estimation using small-footprint lidar-distributional parameters on a per-segment basis. For. Sci. 2006, 52, 636–649. [Google Scholar]
- Ju, Y.L.; Ji, Y.J.; Huang, J.M.; Zhang, W.F. Inversion of forest aboveground biomass using combination of LiDAR and multispectral data. J. Nanjing For. Univ. 2022, 46, 58–68. [Google Scholar] [CrossRef]
- Xing, Y.Q.; You, H.T.; Huo, D.; Sun, X.T.; Wang, R. Research Progress in Estimating Forest Tree Height Using Small Footprint Lidar Data. World Forestry Res. 2014, 27, 29–34. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, H.L.; Zhang, Y.H.; Li, S.J. Retrieval of Forest LAI Using Airborne LVIS and Spaceborne GLAS Waveform LiDAR Data. Remote Sens. Technol. Appl. 2020, 35, 1004–1014. [Google Scholar]
- Sun, G.; Ranson, K.J.; Kimes, D.S.; Blair, J.B.; Kovacs, K. Forest vertical structure from GLAS: An evaluation using LVIS and SRTM data. Remote Sens. Environ. 2008, 112, 107–117. [Google Scholar] [CrossRef]
- Saatchi, S.; Marlier, M.; Chazdon, R.L.; Clark, D.B.; Russell, A.E. Impact of spatial variability of tropical forest structure on radar estimation of aboveground biomass. Remote Sens. Environ. 2011, 115, 2836–2849. [Google Scholar] [CrossRef]
- Liang, X.L.; Kankare, V.; Hyyppa, J.; Wang, Y.S.; Kukko, A.; Haggren, H.; Yu, X.W.; Kaartinen, H.; Jaakkola, A.; Guan, F.Y.; et al. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Hauglin, M.; Astrup, R.; Gobakken, T.; Naesset, E. Estimating single-tree branch biomass of Norway spruce with terrestrial laser scanning using voxel-based and crown dimension features. Scand. J. Forest. Res. 2013, 28, 456–469. [Google Scholar] [CrossRef]
- Stovall, A.E.L.; Vorster, A.G.; Anderson, R.S.; Evangelista, P.H.; Shugart, H.H. Non-destructive aboveground biomass estimation of coniferous trees using terrestrial LiDAR. Remote Sens. Environ. 2017, 200, 31–42. [Google Scholar] [CrossRef]
- Kankare, V.; Holopainen, M.; Vastaranta, M.; Puttonen, E.; Yu, X.W.; Hyyppa, J.; Vaaja, M.; Hyyppa, H.; Alho, P. Individual tree biomass estimation using terrestrial laser scanning. ISPRS J. Photogramm. 2013, 75, 64–75. [Google Scholar] [CrossRef]
- Astrup, R.; Ducey, M.J.; Granhus, A.; Ritter, T.; von Lupke, N. Approaches for estimating stand-level volume using terrestrial laser scanning in a single-scan mode. Can. J. For. Res. 2014, 44, 666–676. [Google Scholar] [CrossRef]
- Popescu, S.C. Estimating biomass of individual pine trees using airborne lidar. Biomass Bioenerg. 2007, 31, 646–655. [Google Scholar] [CrossRef]
- Tao, S.L.; Guo, Q.H.; Li, L.; Xue, B.L.; Kelly, M.; Li, W.K.; Xu, G.C.; Su, Y.J. Airborne Lidar-derived volume metrics for aboveground biomass estimation: A comparative assessment for conifer stands. Agric. For. Meteorol. 2014, 198, 24–32. [Google Scholar] [CrossRef]
- Garcia, M.; Saatchi, S.; Ferraz, A.; Silva, C.A.; Ustin, S.; Koltunov, A.; Balzter, H. Impact of data model and point density on aboveground forest biomass estimation from airborne LiDAR. Carbon Bal. Manag. 2017, 12, 4. [Google Scholar] [CrossRef]
- Messinger, M.; Asner, G.P.; Silman, M. Rapid Assessments of Amazon Forest Structure and Biomass Using Small Unmanned Aerial Systems. Remote Sens. 2016, 8, 615. [Google Scholar] [CrossRef]
- Zhao, K.G.; Popescu, S.; Nelson, R. Lidar remote sensing of forest biomass: A scale-invariant estimation approach using airborne lasers. Remote Sens. Environ. 2009, 113, 182–196. [Google Scholar] [CrossRef]
- Price, B.; Gomez, A.; Mathys, L.; Gardi, O.; Schellenberger, A.; Ginzler, C.; Thurig, E. Tree biomass in the Swiss landscape: Nationwide modelling for improved accounting for forest and non-forest trees. Environ. Monit. Assess. 2017, 189, 1–14. [Google Scholar] [CrossRef]
- Pang, Y.; Li, Z.Y.; Lefsky, M.; Che, X.J.; Chen, R.X. Effects of Terrain on the Large Footprint Lidar Waveform of Forests. For. Res. 2007, 20, 464–468. [Google Scholar] [CrossRef]
- Wang, Y.; Ni, W.J.; Sun, G.Q.; Chi, H.; Zhang, Z.Y.; Guo, Z.F. Slope-adaptive waveform metrics of large footprint lidar for estimation of forest aboveground biomass. Remote Sens. Environ. 2019, 224, 386–400. [Google Scholar] [CrossRef]
- Stavros, E.N.; Schimel, D.; Pavlick, R.; Serbin, S.; Swann, A.; Duncanson, L.; Fisher, J.B.; Fassnacht, F.; Ustin, S.; Dubayah, R.; et al. ISS observations offer insights into plant function. Nat. Ecol. Evol. 2017, 1, 194. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Dubayah, R.; Armston, J.; Healey, S.P.; Bruening, J.M.; Patterson, P.L.; Kellner, J.R.; Duncanson, L.; Saarela, S.; Stahl, G.; Yang, Z.Q.; et al. GEDI launches a new era of biomass inference from space. Environ. Res. Lett. 2022, 17, 095001. [Google Scholar] [CrossRef]
- Duncanson, L.; Kellner, J.R.; Armston, J.; Dubayah, R.; Minor, D.M.; Hancock, S.; Healey, S.P.; Patterson, P.L.; Saarela, S.; Marselis, S.; et al. Aboveground biomass density models for NASA’s Global Ecosystem Dynamics Investigation (GEDI) lidar mission. Remote Sens. Environ. 2022, 270, 112845. [Google Scholar] [CrossRef]
- Nichol, J.E.; Sarker, M.L.R. Improved Biomass Estimation Using the Texture Parameters of Two High-Resolution Optical Sensors. IEEE Trans. Geosci. Remote 2011, 49, 930–948. [Google Scholar] [CrossRef]
- Bastin, J.F.; Barbier, N.; Couteron, P.; Adams, B.; Shapiro, A.; Bogaert, J.; De Canniere, C. Aboveground biomass mapping of African forest mosaics using canopy texture analysis: Toward a regional approach. Ecol. Appl. 2014, 24, 1984–2001. [Google Scholar] [CrossRef]
- Duncanson, L.; Neuenschwander, A.; Hancock, S.; Thomas, N.; Fatoyinbo, T.; Simard, M.; Silva, C.A.; Armston, J.; Luthcke, S.B.; Hofton, M.; et al. Biomass estimation from simulated GEDI, ICESat-2 and NISAR across environmental gradients in Sonoma County, California. Remote Sens. Environ. 2020, 242, 111779. [Google Scholar] [CrossRef]
- Joshi, N.P.; Mitchard, E.T.A.; Schumacher, J.; Johannsen, V.K.; Saatchi, S.; Fensholt, R. L-Band SAR Backscatter Related to Forest Cover, Height and Aboveground Biomass at Multiple Spatial Scales across Denmark. Remote Sens. 2015, 7, 4442–4472. [Google Scholar] [CrossRef]
- Laurin, G.V.; Pirotti, F.; Callegari, M.; Chen, Q.; Cuozzo, G.; Lingua, E.; Notarnicola, C.; Papale, D. Potential of ALOS2 and NDVI to Estimate Forest Above-Ground Biomass, and Comparison with Lidar-Derived Estimates. Remote Sens. 2017, 9, 18. [Google Scholar] [CrossRef]
- Navarro, J.A.; Algeet, N.; Fernandez-Landa, A.; Esteban, J.; Rodriguez-Noriega, P.; Guillen-Climent, M.L. Integration of UAV, Sentinel-1, and Sentinel-2 Data for Mangrove Plantation Aboveground Biomass Monitoring in Senegal. Remote Sens. 2019, 11, 77. [Google Scholar] [CrossRef]
- Issa, S.; Dahy, B.; Ksiksi, T.; Saleous, N. A Review of Terrestrial Carbon Assessment Methods Using Geo-Spatial Technologies with Emphasis on Arid Lands. Remote Sens. 2020, 12, 2008. [Google Scholar] [CrossRef]
- Tanase, M.A.; Panciera, R.; Lowell, K.; Tian, S.Y.; Garcia-Martin, A.; Walker, J.P. Sensitivity of L-Band Radar Backscatter to Forest Biomass in Semiarid Environments: A Comparative Analysis of Parametric and Nonparametric Models. IEEE Trans. Geosci. Remote 2014, 52, 4671–4685. [Google Scholar] [CrossRef]
- Safari, A.; Sohrabi, H.; Powell, S. Comparison of satellite-based estimates of aboveground biomass in coppice oak forests using parametric, semiparametric, and nonparametric modeling methods. J. Appl. Remote Sens. 2018, 12, 046026. [Google Scholar] [CrossRef]
- Li, C.; Li, Y.C.; Li, M.Y. Improving Forest Aboveground Biomass (AGB) Estimation by Incorporating Crown Density and Using Landsat 8 OLI Images of a Subtropical Forest in Western Hunan in Central China. Forests 2019, 10, 104. [Google Scholar] [CrossRef]
- Li, J.R.; Mao, X.G. Comparison of Canopy Closure Estimation of Plantations Using Parametric, Semi-Parametric, and Non-Parametric Models Based on GF-1 Remote Sensing Images. Forests 2020, 11, 597. [Google Scholar] [CrossRef]
- Zaki, N.A.M.; Abd Latif, Z.; Suratman, M.N.; Zainal, M.Z. Aboveground biomass and carbon stocks modelling using non-linear regression model. In Proceedings of the 8th IGRSM International Conference and Exhibition on Geospatial and Remote Sensing (IGRSM), Kuala Lumpur, Malaysia, 13–14 April 2016. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O. Investigating the robustness of the new Landsat-8 Operational Land Imager derived texture metrics in estimating plantation forest aboveground biomass in resource constrained areas. ISPRS J. Photogramm. 2015, 108, 12–32. [Google Scholar] [CrossRef]
- Gao, Y.K.; Lu, D.S.; Li, G.Y.; Wang, G.X.; Chen, Q.; Liu, L.J.; Li, D.Q. Comparative Analysis of Modeling Algorithms for Forest Aboveground Biomass Estimation in a Subtropical Region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef]
- Tang, J.; Liu, Y.; Li, L.; Liu, Y.F.; Wu, Y.; Xu, H.; Ou, G.L. Enhancing Aboveground Biomass Estimation for Three Pinus Forests in Yunnan, SW China, Using Landsat 8. Remote Sens. 2022, 14, 4589. [Google Scholar] [CrossRef]
- Ou, G.L.; Li, C.; Lv, Y.Y.; Wei, A.C.; Xiong, H.X.; Xu, H.; Wang, G.X. Improving Aboveground Biomass Estimation of Pinus densata Forests in Yunnan Using Landsat 8 Imagery by Incorporating Age Dummy Variable and Method Comparison. Remote Sens. 2019, 11, 738. [Google Scholar] [CrossRef]
- Ferreira, I.J.M.; Campanharo, W.A.; Fonseca, M.G.; Escada, M.I.S.; Nascimento, M.T.; Villela, D.M.; Brancalion, P.; Magnago, L.F.S.; Anderson, L.O.; Nagy, L.; et al. Potential aboveground biomass increase in Brazilian Atlantic Forest fragments with climate change. Glob. Change Biol. 2023, 29, 3098–3113. [Google Scholar] [CrossRef] [PubMed]
- Pascarella, A.E.; Giacco, G.; Rigiroli, M.; Marrone, S.; Sansone, C. ReUse: REgressive Unet for Carbon Storage and Above-Ground Biomass Estimation. J. Imaging 2023, 9, 61. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, L.V.; Amorim, J.G.A.; Guimaraes, L.; Matos, D.M.; da Costa, C.M.; Parraga, A. Above-ground Biomass Wheat Estimation: Deep Learning with UAV-based RGB Images. Appl. Artif. Intell. 2022, 36, 2055392. [Google Scholar] [CrossRef]
- Ghosh, S.M.; Behera, M.D. Aboveground biomass estimates of tropical mangrove forest using Sentinel-1 SAR coherence data—The superiority of deep learning over a semi-empirical model. Comput. Geosci. 2021, 150, 104737. [Google Scholar] [CrossRef]
- Koetz, B.; Sun, G.Q.; Morsdorf, F.; Ranson, K.J.; Kneubuhler, M.; Itten, K.; Allgower, B. Fusion of imaging spectrometer and LIDAR data over combined radiative transfer models for forest canopy characterization. Remote Sens. Environ. 2007, 106, 449–459. [Google Scholar] [CrossRef]
- Chopping, M.; Moisen, G.G.; Su, L.H.; Laliberte, A.; Rango, A.; Martonchik, J.V.; Peters, D.P.C. Large area mapping of southwestern forest crown cover, canopy height, and biomass using the NASA Multiangle Imaging Spectro-Radiometer. Remote Sens. Environ. 2008, 112, 2051–2063. [Google Scholar] [CrossRef]
- Lou, X.T.; Zeng, Y.; Wu, B.F. Advances in the Estimation of Above-ground Biomass of Forest Using Remote Sensing. Remote Sens. Nat. Resour. 2011, 1, 1–8. [Google Scholar] [CrossRef]
- Xu, X.L.; Cao, M.K. An Analysis of the Applications of Remote Sensing Method to the Forest Biomass Estimation. J. Geo-Inf. Sci. 2006, 8, 122–128. [Google Scholar] [CrossRef]
- Smith, B.; Knorr, W.; Widlowski, J.L.; Pinty, B.; Gobron, N. Combining remote sensing data with process modelling to monitor boreal conifer forest carbon balances. For. Ecol. Manag. 2008, 255, 3985–3994. [Google Scholar] [CrossRef]
- Adams, B.; White, A.; Lenton, T.M. An analysis of some diverse approaches to modelling terrestrial net primary productivity. Ecol. Model 2004, 177, 353–391. [Google Scholar] [CrossRef]
- Peng, S.L.; Guo, Z.H.; Wang, B.S. Ues of GIS and RS to extimate the light utilization efficiency of the vagetation in Guangdong, China. Acta Ecol. Sin. 2000, 6, 903–909. [Google Scholar] [CrossRef]
- Piao, S.L.; Fang, J.Y.; Guo, J.H. Application of CASA Model to The Estimation of Chinese Terrestrial Net Primary Productivity. Chin. J. Plant Ecol. 2001, 25, 603–608. [Google Scholar] [CrossRef]
- Wu, Z.; Dai, E.F.; Wu, Z.F.; Lin, M.Z. Assessing differences in the response of forest aboveground biomass and composition under climate change in subtropical forest transition zone. Sci. Total Environ. 2020, 706, 135746. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.D.; Shugart, H.H. FAREAST: A forest gap model to simulate dynamics and patterns of eastern Eurasian forests. J. Biogeogr. 2005, 32, 1641–1658. [Google Scholar] [CrossRef]
- Mladenoff, D.J. LANDIS and forest landscape models. Ecol. Model 2004, 180, 7–19. [Google Scholar] [CrossRef]
- Herbert, C.; Fried, J.S.; Butsic, V. Validation of Forest Vegetation Simulator Model Finds Overprediction of Carbon Growth in California. Forests 2023, 14, 604. [Google Scholar] [CrossRef]
- Brown, M.L.; Canham, C.D.; Murphy, L.; Donovan, T.M. Timber harvest as the predominant disturbance regime in northeastern US forests: Effects of harvest intensification. Ecosphere 2018, 9, e02062. [Google Scholar] [CrossRef]
- Zhang, N.N.; Shugart, H.H.; Yan, X.D. Simulating the effects of climate changes on Eastern Eurasia forests. Clim. Change 2009, 95, 341–361. [Google Scholar] [CrossRef]
- Wang, Q.T.; Zhao, C.Y.; Wang, X.P.; Hu, S.S.; Liu, M.Y.; Shi, W.Y.; Wang, X.Y.; Shan, W.R. Simulating the biomass carbon distribution of young-and-middle aged Picea crassifolia forests based on FAREST model along altitude gradients. Arid Land Geogr. 2020, 40, 1316–1326. [Google Scholar]
- Zheng, D.L.; Rademacher, J.; Chen, J.Q.; Crow, T.; Bresee, M.; le Moine, J.; Ryu, S.R. Estimating aboveground biomass using Landsat 7 ETM+ data across a managed landscape in northern Wisconsin, USA. Remote Sens. Environ. 2004, 93, 402–411. [Google Scholar] [CrossRef]
- Lu, D.S.; Chen, Q.; Wang, G.X.; Moran, E.; Batistella, M.; Zhang, M.Z.; Laurin, G.V.; David, S. Aboveground Forest Biomass Estimation with Landsat and LiDAR Data and Uncertainty Analysis of the Estimates. Int. J. For. Res. 2012, 2012, 436537. [Google Scholar] [CrossRef]
- Narine, L.L.; Popescu, S.C.; Malambo, L. Synergy of ICESat-2 and Landsat for Mapping Forest Aboveground Biomass with Deep Learning. Remote Sens. 2019, 11, 1503. [Google Scholar] [CrossRef]
- Reese, H.; Nilsson, M.; Sandstrom, P.; Olsson, H. Applications using estimates of forest parameters derived from satellite and forest inventory data. Comput. Electron. Agric. 2002, 37, 37–55. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chi, H.; Sun, G.; Huang, J.; Li, R.; Ren, X.; Ni, W.; Fu, A. Estimation of Forest Aboveground Biomass in Changbai Mountain Region Using ICESat/GLAS and Landsat/TM Data. Remote Sens. 2017, 9, 707. [Google Scholar] [CrossRef]
- Saatchi, S.; Buermann, W.; Ter Steege, H.; Mori, S.; Smith, T.B. Modeling distribution of Amazonian tree species and diversity using remote sensing measurements. Remote Sens. Environ. 2008, 112, 2000–2017. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef]
- Rodriguez-Veiga, P.; Saatchi, S.; Tansey, K.; Balzter, H. Magnitude, spatial distribution and uncertainty of forest biomass stocks in Mexico. Remote Sens. Environ. 2016, 183, 265–281. [Google Scholar] [CrossRef]
- Chen, Q.; Laurin, G.V.; Valentini, R. Uncertainty of remotely sensed aboveground biomass over an African tropical forest: Propagating errors from trees to plots to pixels. Remote Sens. Environ. 2015, 160, 134–143. [Google Scholar] [CrossRef]
- Montesano, P.M.; Rosette, J.; Sun, G.; North, P.; Nelson, R.F.; Dubayah, R.O.; Ranson, K.J.; Kharuk, V. The uncertainty of biomass estimates from modeled ICESat-2 returns across a boreal forest gradient. Remote Sens. Environ. 2015, 158, 95–109. [Google Scholar] [CrossRef]
- Lister, A.J.; Andersen, H.; Frescino, T.; Gatziolis, D.; Healey, S.; Heath, L.S.; Liknes, G.C.; McRoberts, R.; Moisen, G.G.; Nelson, M.; et al. Use of Remote Sensing Data to Improve the Efficiency of National Forest Inventories: A Case Study from the United States National Forest Inventory. Forests 2020, 11, 1364. [Google Scholar] [CrossRef]
- Knott, J.A.; Liknes, G.C.; Giebink, C.L.; Oh, S.; Domke, G.M.; McRoberts, R.E.; Quirino, V.F.; Walters, B.F. Effects of outliers on remote sensing-assisted forest biomass estimation: A case study from the United States national forest inventory. Methods Ecol. Evol. 2023, 00, 1–16. [Google Scholar] [CrossRef]
- Van Leeuwen, W.J.D.; Orr, B.J.; Marsh, S.E.; Herrmann, S.M. Multi-sensor NDVI data continuity: Uncertainties and implications for vegetation monitoring applications. Remote Sens. Environ. 2006, 100, 67–81. [Google Scholar] [CrossRef]
- Fang, H.L.; Wei, S.S.; Jiang, C.Y.; Scipal, K. Theoretical uncertainty analysis of global MODIS, CYCLOPES, and GLOBCARBON LAI products using a triple collocation method. Remote Sens. Environ. 2012, 124, 610–621. [Google Scholar] [CrossRef]
- Frazer, G.W.; Magnussen, S.; Wulder, M.A.; Niemann, K.O. Simulated impact of sample plot size and co-registration error on the accuracy and uncertainty of LiDAR-derived estimates of forest stand biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
- Zhang, M.Z.; Lin, H.; Zeng, S.Q.; Li, J.P.; Shi, J.N.; Wang, G.X. Impacts of Plot Location Errors on Accuracy of Mapping and Scaling Up Aboveground Forest Carbon Using Sample Plot and Landsat TM Data. IEEE Geosci. Remote Sens. 2013, 10, 1483–1487. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Hartig, F.; Latifi, H.; Berger, C.; Hernandez, J.; Corvalan, P.; Koch, B. Importance of sample size, data type and prediction method for remote sensing-based estimations of aboveground forest biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
- Fu, Y.; Lei, Y.C.; Zeng, W.S. Uncertainty Assessment in Regional-Scale Above Ground Biomass Estimation of Chinese Fir. Sci. Silvae Sinicae 2014, 50, 79–86. [Google Scholar]
- Scheller, R.M.; Van Tuyl, S.; Clark, K.L.; Hom, J.; Puma, I.L. Carbon Sequestration in the New Jersey Pine Barrens Under Different Scenarios of Fire Management. Ecosystems 2011, 14, 987–1004. [Google Scholar] [CrossRef]
- Sonti, N.F.; Riemann, R.; Mockrin, M.H.; Domke, G.M. Expanding wildland-urban interface alters forest structure and landscape context in the northern United States. Environ. Res. Lett. 2023, 18, 014010. [Google Scholar] [CrossRef]
- Zheng, G.; Chen, J.M.; Tian, Q.; Ju, W.M.; Xia, X.Q. Combining remote sensing imagery and forest age inventory for biomass mapping. J. Environ. Manag. 2007, 85, 616–623. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.; Malhi, Y.; Bhagwat, S. Biomass estimation of mixed forest landscape using a Fourier transform texture-based approach on very-high-resolution optical satellite imagery. Int. J. Remote Sens. 2014, 35, 3331–3349. [Google Scholar] [CrossRef]
- Piao, S.L.; Fang, J.Y.; Zhu, B.; Tan, K. Forest biomass carbon stocks in China over the past 2 decades: Estimation based on integrated inventory and satellite data. J. Geophys. Res.-Biogeosci. 2005, 110, G01006. [Google Scholar] [CrossRef]
- Du, L.; Zhou, T.; Zou, Z.H.; Zhao, X.; Huang, K.C.; Wu, H. Mapping Forest Biomass Using Remote Sensing and National Forest Inventory in China. Forests 2014, 5, 1267–1283. [Google Scholar] [CrossRef]
- Yin, G.D.; Zhang, Y.; Sun, Y.; Wang, T.; Zeng, Z.Z.; Piao, S.L. MODIS Based Estimation of Forest Aboveground Biomass in China. PLoS ONE 2015, 10, e0130143. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.J.; Guo, Q.H.; Xue, B.L.; Hu, T.Y.; Alvarez, O.; Tao, S.L.; Fang, J.Y. Spatial distribution of forest aboveground biomass in China: Estimation through combination of spaceborne lidar, optical imagery, and forest inventory data. Remote Sens. Environ. 2016, 173, 187–199. [Google Scholar] [CrossRef]
- Spawn, S.A.; Sullivan, C.C.; Lark, T.J.; Gibbs, H.K. Harmonized global maps of above and belowground biomass carbon density in the year 2010. Sci. Data 2020, 7, 112. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O.; Mermoz, S.; Bouvet, A.; Le Toan, T.; Carvalhais, N.; Rozendaal, D.; Herold, M.; Avitabile, V.; Quegan, S.; et al. GlobBiomass—Global datasets of forest biomass. PANGAEA 2018, 1594, 979. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, X.; Zhang, X.; Lu, F. Biomass and Its Allocation of Forest Ecosystems in China; Chinese Forestry Publishing House Press: Beijing, China, 2013. [Google Scholar]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.C.; Skakun, S.V.; Justice, C. The Harmonized Landsat and Sentinel-2 surface reflectance data set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Sun, G.Q.; Ranson, K.J.; Guo, Z.; Zhang, Z.; Montesano, P.; Kimes, D. Forest biomass mapping from lidar and radar synergies. Remote Sens. Environ. 2011, 115, 2906–2916. [Google Scholar] [CrossRef]
- Karila, K.; Yu, X.W.; Vastaranta, M.; Karjalainen, M.; Puttonen, E.; Hyyppa, J. TanDEM-X digital surface models in boreal forest above-ground biomass change detection. ISPRS J. Photogramm. 2019, 148, 174–183. [Google Scholar] [CrossRef]
- Ni, W.J.; Zhang, Z.Y.; Sun, G.Q.; Liu, Q.H. Modeling Interferometric SAR Features of Forest Canopies Over Mountainous Area at Landscape Scales. IEEE Trans. Geosci. Remote 2018, 56, 2958–2967. [Google Scholar] [CrossRef]
- Qi, W.L.; Dubayah, R.O. Combining Tandem-X InSAR and simulated GEDI lidar observations for forest structure mapping. Remote Sens. Environ. 2016, 187, 253–266. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Ni, W.J.; Sun, G.Q.; Huang, W.L.; Ranson, K.J.; Cook, B.D.; Guo, Z.F. Biomass retrieval from L-band polarimetric UAVSAR backscatter and PRISM stereo imagery. Remote Sens. Environ. 2017, 194, 331–346. [Google Scholar] [CrossRef]
- Matasci, G.; Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W.; Zald, H.S.J. Large-area mapping of Canadian boreal forest cover, height, biomass and other structural attributes using Landsat composites and lidar plots. Remote Sens. Environ. 2018, 209, 90–106. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).