Predicting the Mechanical Properties of Heat-Treated Woods Using Optimization-Algorithm-Based BPNN
Abstract
1. Introduction
2. Theoretical Analysis of the Algorithm
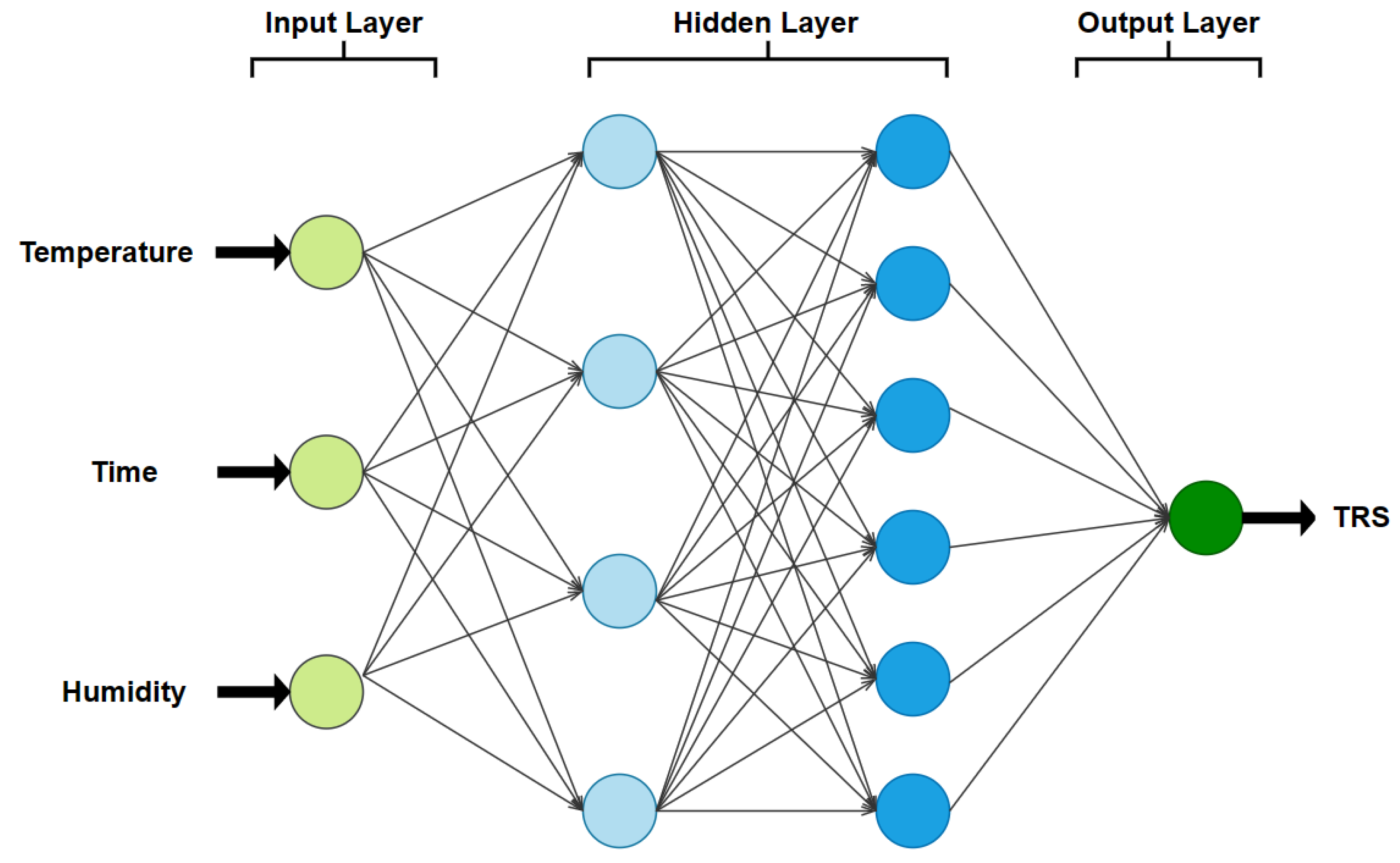
2.1. Back-Propagation (BP) Neural Network Models
2.2. The Traditional DBO Algorithm
2.2.1. Dung Beetle Ball Rolling
Obstacle-Free Mode
Barrier Mode
2.2.2. Dung Beetle Breeding
2.2.3. Dung Beetle Foraging
2.2.4. Dung Beetle Stealing
3. Proposed Method
3.1. Improved Dung Beetle Optimizer
3.1.1. Piece-Wise Linear Chaotic Mapping
3.1.2. Self-Adaptive Parameter Adjustment Tactics
3.1.3. Dimension Learning-Enhanced Foraging Search Strategy
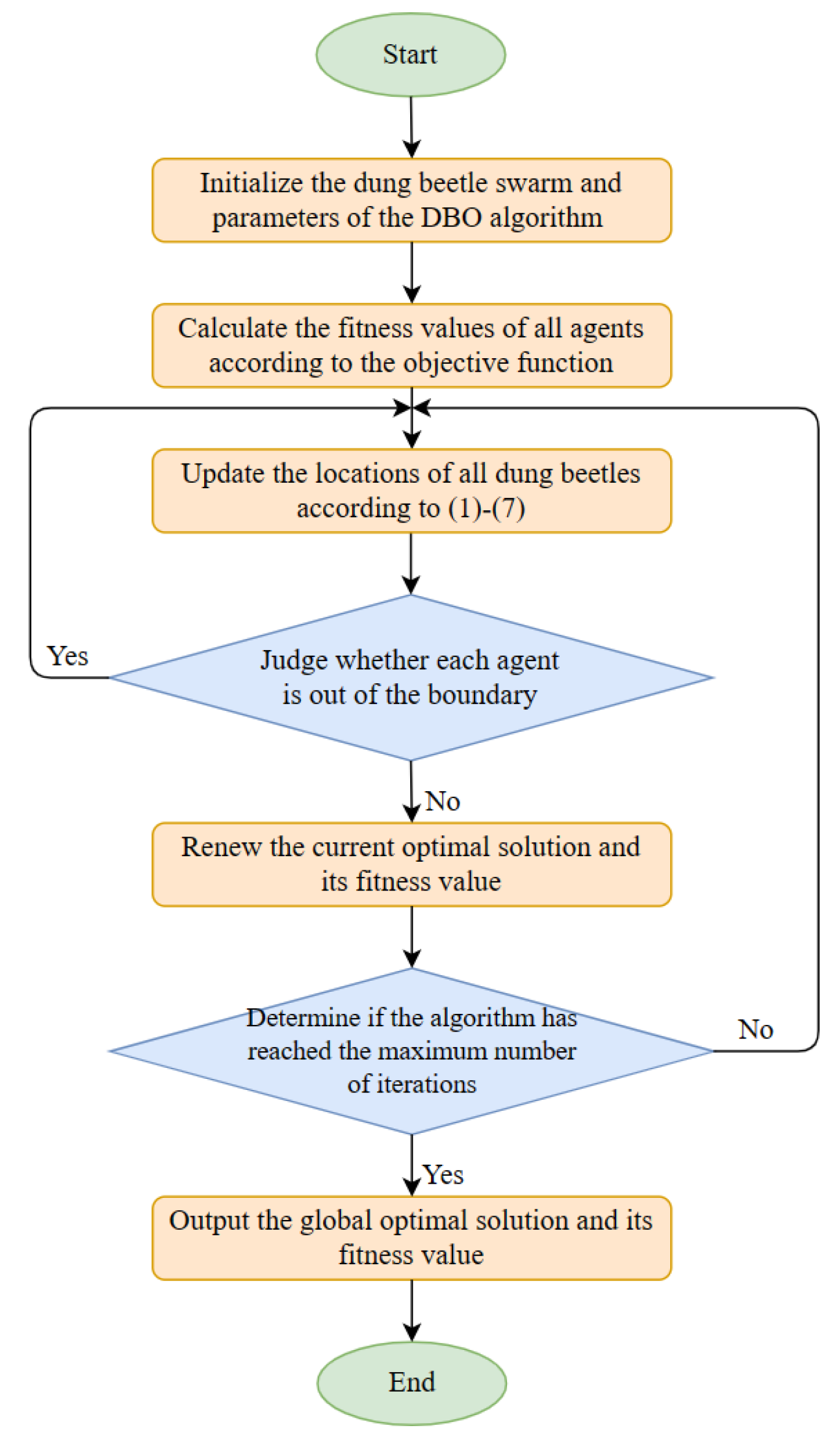
3.2. The IDBO-BP Algorithm
4. Evaluate the Effectiveness of the Suggested IDBO Model
4.1. Benchmark Functions
4.2. Contrast Algorithm and Experimental Parameter Settings
4.3. Evaluation of Exploration and Exploitation
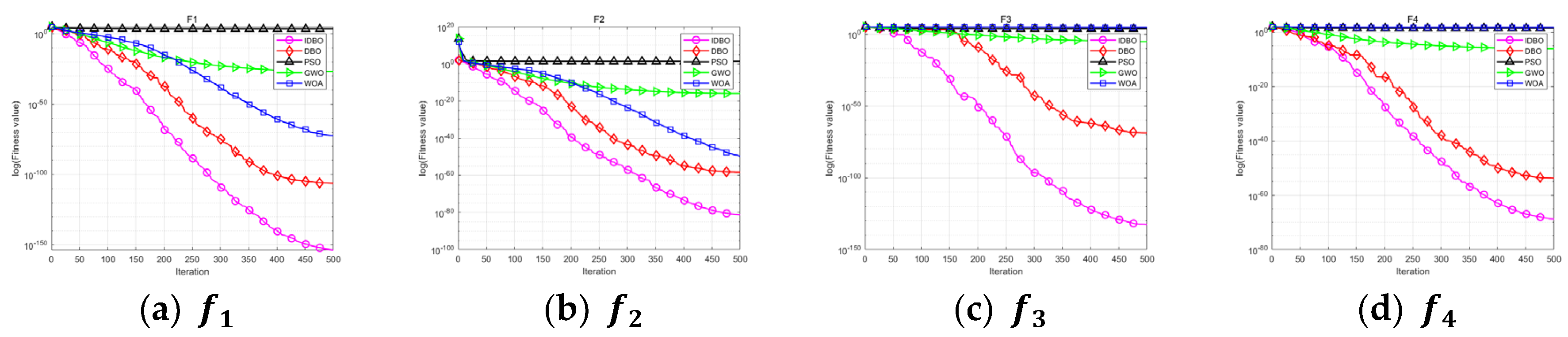
4.4. Evaluation of Convergence Curves
4.5. Local Optimal Circumvention Evaluation
4.6. High-Dimensional Robustness Evaluation
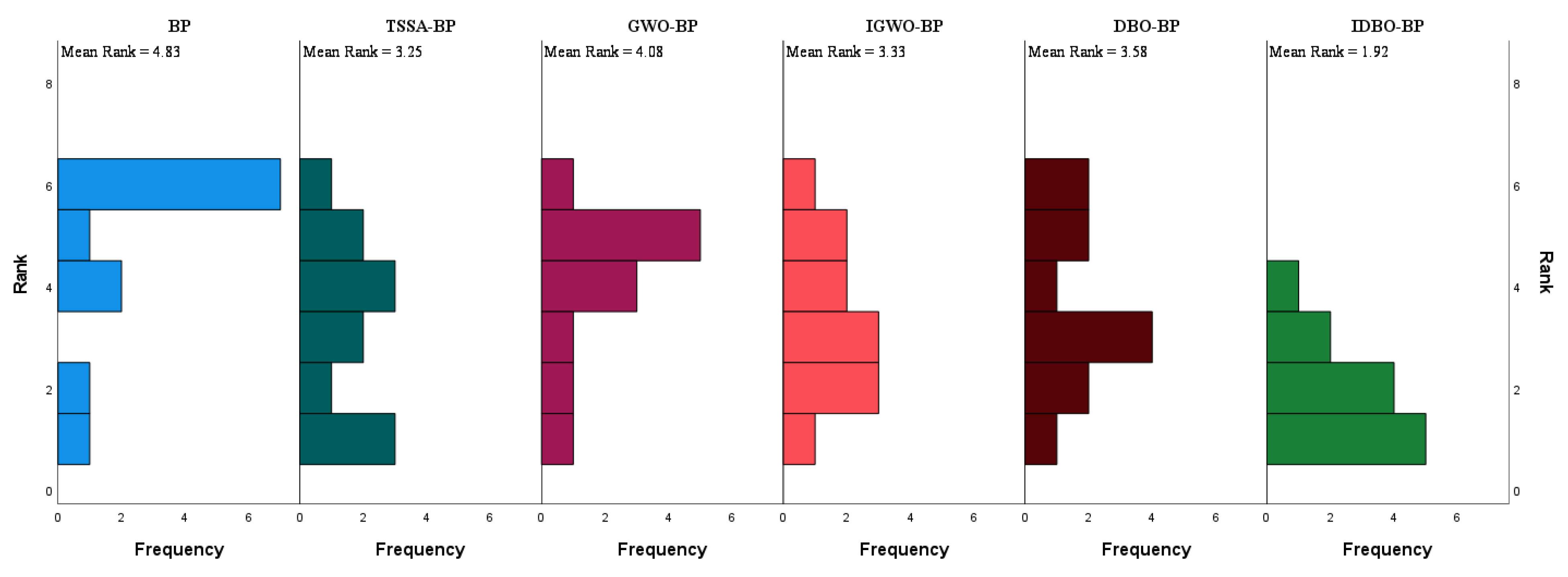
4.7. Statistical Analysis
5. Experimental Research
5.1. Data Preprocessing
5.2. Model Parameter Setting
5.2.1. Selection of Activation Functions
5.2.2. Determination of the Topology
Determination of the Number of Neurons in the Hidden Layer
Determination of the Number of Hidden Layers
5.3. Model Assessment Standards
5.4. Model Performance Comparison Analysis
6. Conclusions
- This article proposes the IDBO algorithm to address the limitations of the DBO algorithm. PWLCM mapping is employed to initialize the population and preserve versatility. An adaptive parameter adjustment strategy is introduced to enhance search range and efficiency. Additionally, a DLF strategy is implemented to equilibrium for exploration and exploitation search capabilities, increasing the likelihood of escaping local optima and improving later searchability. The performance of IDBO is evaluated against four basic meta-heuristic algorithms, including DBO, for 14 benchmark functions. The algorithms are ranked by applying the Wilcoxon signed-rank and Friedman tests. The outcomes demonstrate that IDBO outperforms other algorithms in finding solutions for both low- and high-dimensional functions with a single mode or multiple modes, which verifies the effectiveness of the improvement strategy, and it is highly competitive with other meta-heuristics.
- In this paper, five prediction models are separately developed using the IDBO-BP model to predict the LCS, TRS, TME, RH and TH of larch wood after heat treatment with temperature, duration and relative humidity as input variables. The outcomes indicate that the MAE, MSE and MAPE values of the IDBO-BP model are considerably diminished compared with the primitive BP neural network model. The results show that optimizing neural networks model with IDBO significantly improves the prediction accuracy of wood mechanical properties. In addition to comparing the original BP neural network model, this paper also compares it with the TSSA-BP, GWO-BP, IGWO-BP and DBO-BP models. The results denote that the forecast outcomes of the IDBO-BP model are closer to the true values, indicating significant optimization and improved prediction ability.
- This paper compares the optimal prediction models with different parameters and their corresponding topologies and activation functions, and it shows in Table A3 that the same model with different parameters does not necessarily have the same optimal topology. For the LCS, TRS, TME, RH and TH of heat-treated larch wood predicted in this paper, the five most accurate topologies of IDBO-BP that minimize the error are 3-2-1, 3-4-6-1, 3-4-1, 3-5-1 and 3-4-1, respectively.
- The Friedman test can only reflect the quality of the solution, not the diversity of the solution. Therefore, some algorithms may have significant differences in the diversity of solutions, but not in the quality of solutions. The Friedman test is also less robust in some extreme cases; for example, if an algorithm obtains an exceptionally good or bad solution, it may influence the rank and rank mean of other algorithms, thus obscuring the differences between other algorithms. This is illustrated in Table A5. The original BP model ranks first in MSE for both the training and test sets, which may be more susceptible to outlier data because MSE magnifies the prediction error. However, Table A5 also shows that, although the original BP model performs well for MSE, its overall ranking for both the test and training sets is inferior to that of the other five models.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Test Temperature/°C | Test Time/h | Test Humidity/% | Longitudinal Compressive Strength/MPa | Transverse Rupture Strength/MPa | Transverse Modulus of Elasticity/GPa | Radial Hardness/MPa | Tangential Hardness/MPa |
|---|---|---|---|---|---|---|---|
| 120 | 0.5 | 0 | 41.9 | 67.4 | 9.093 | 14.12 | 15.56 |
| 120 | 0.5 | 40 | 39.8 | 65.3 | 9.038 | 13.02 | 14.69 |
| 120 | 0.5 | 60 | 39.7 | 69.7 | 9.1 | 14.67 | 15.08 |
| 120 | 0.5 | 100 | 39.5 | 67.2 | 8.845 | 14.65 | 15.45 |
| 120 | 1 | 0 | 39.5 | 67.8 | 8.649 | 13.98 | 14.36 |
| 120 | 1 | 40 | 39.5 | 66.4 | 8.752 | 12.98 | 15.59 |
| 120 | 1 | 60 | 39.4 | 67.8 | 9.245 | 13.78 | 15.32 |
| 120 | 1 | 100 | 39.2 | 63.1 | 7.895 | 14.55 | 14.23 |
| 120 | 2 | 0 | 39.2 | 66.9 | 9.074 | 13.33 | 14.23 |
| 120 | 2 | 40 | 39.1 | 68.2 | 8.945 | 12.55 | 14.58 |
| 120 | 2 | 60 | 39.1 | 65.2 | 8.854 | 13.25 | 14.89 |
| 120 | 2 | 100 | 39.1 | 63.2 | 8.933 | 13.36 | 14.56 |
| 120 | 3 | 0 | 39.1 | 66.5 | 8.9 | 13.56 | 14.78 |
| 120 | 3 | 40 | 39.1 | 67.6 | 8.963 | 13.45 | 14.45 |
| 120 | 3 | 60 | 38.9 | 66.6 | 8.745 | 13.01 | 14.69 |
| 120 | 3 | 100 | 38.9 | 64.2 | 8.745 | 12.45 | 14.78 |
| 140 | 0.5 | 0 | 38.9 | 66.7 | 8.978 | 14.69 | 15.56 |
| 140 | 0.5 | 40 | 38.9 | 67.5 | 8.845 | 13.06 | 15.02 |
| 140 | 0.5 | 60 | 38.7 | 66.8 | 9.155 | 14.02 | 14.23 |
| 140 | 0.5 | 100 | 38.7 | 65.3 | 8.877 | 15.02 | 15.01 |
| 140 | 1 | 0 | 38.6 | 66.5 | 9.179 | 14.16 | 15.68 |
| 140 | 1 | 40 | 38.6 | 64.5 | 9.137 | 13.05 | 15.01 |
| 140 | 1 | 60 | 38.5 | 67.2 | 9.024 | 13.49 | 15.17 |
| 140 | 1 | 100 | 38.5 | 63.1 | 8.823 | 13.45 | 15.48 |
| 140 | 2 | 0 | 38.4 | 66.3 | 8.823 | 13.54 | 14.69 |
| 140 | 2 | 40 | 38.4 | 65.7 | 8.852 | 14.69 | 14.58 |
| 140 | 2 | 60 | 38.2 | 67.1 | 8.799 | 13.99 | 14.74 |
| 140 | 2 | 100 | 38.2 | 62.7 | 8.9 | 14.28 | 15.63 |
| 140 | 3 | 0 | 38.2 | 65.4 | 8.811 | 14.39 | 14.23 |
| 140 | 3 | 40 | 38.2 | 64.6 | 8.934 | 13.23 | 14.56 |
| 140 | 3 | 60 | 38.1 | 65.5 | 8.654 | 14.23 | 13.65 |
| 140 | 3 | 100 | 38.1 | 62.1 | 8.798 | 13.56 | 14.02 |
| 160 | 0.5 | 0 | 38.1 | 66.3 | 8.788 | 14.89 | 14.99 |
| 160 | 0.5 | 40 | 38 | 66.9 | 9.011 | 14.87 | 14.36 |
| 160 | 0.5 | 60 | 37.9 | 66.3 | 8.745 | 14.58 | 14.78 |
| 160 | 0.5 | 100 | 37.8 | 65.8 | 8.712 | 14.69 | 15.69 |
| 160 | 1 | 0 | 37.8 | 62.4 | 8.679 | 13.42 | 14.56 |
| 160 | 1 | 40 | 37.6 | 61.4 | 8.645 | 14.09 | 15.3 |
| 160 | 1 | 60 | 37.6 | 62.2 | 8.798 | 14.69 | 15.9 |
| 160 | 1 | 100 | 37.6 | 62.8 | 8.679 | 13.58 | 15.63 |
| 160 | 2 | 0 | 37.6 | 62.2 | 8.727 | 14.63 | 13.92 |
| 160 | 2 | 40 | 37.6 | 62.1 | 8.557 | 14.02 | 14.17 |
| 160 | 2 | 60 | 37.5 | 63.1 | 8.687 | 15.17 | 14.28 |
| 160 | 2 | 100 | 37.5 | 60.9 | 8.611 | 14.65 | 15.09 |
| 160 | 3 | 0 | 37.5 | 61.9 | 8.611 | 13.65 | 14.36 |
| 160 | 3 | 40 | 37.4 | 61.5 | 8.534 | 13.47 | 14.56 |
| 160 | 3 | 60 | 37.3 | 60.8 | 8.601 | 13.58 | 13.89 |
| 160 | 3 | 100 | 37.2 | 60.5 | 8.552 | 13.69 | 14.36 |
| 180 | 0.5 | 0 | 37.2 | 65.9 | 8.601 | 15.21 | 14.03 |
| 180 | 0.5 | 40 | 37.1 | 65.3 | 8.689 | 15.98 | 14.56 |
| 180 | 0.5 | 60 | 37.1 | 66.1 | 8.645 | 16.01 | 13.97 |
| 180 | 0.5 | 100 | 36.9 | 65.7 | 8.599 | 14.32 | 14.33 |
| 180 | 1 | 0 | 36.9 | 65.4 | 8.623 | 15.09 | 13.79 |
| 180 | 1 | 40 | 36.9 | 64.9 | 8.645 | 14.98 | 14.25 |
| 180 | 1 | 60 | 36.7 | 66.3 | 8.579 | 15.45 | 14.08 |
| 180 | 1 | 100 | 36.7 | 64.8 | 8.545 | 14.33 | 13.64 |
| 180 | 2 | 0 | 36.6 | 65.1 | 8.574 | 14.65 | 13.69 |
| 180 | 2 | 40 | 36.5 | 65.8 | 8.6 | 14.13 | 13.59 |
| 180 | 2 | 60 | 36.5 | 64.5 | 8.532 | 13.99 | 14.49 |
| 180 | 2 | 100 | 36.1 | 64.2 | 8.544 | 15.1 | 13.54 |
| 180 | 3 | 0 | 36 | 64.1 | 8.6 | 14.21 | 14.06 |
| 180 | 3 | 40 | 35.9 | 64.2 | 8.541 | 13.99 | 14.21 |
| 180 | 3 | 60 | 35.8 | 64.8 | 8.456 | 14.58 | 13.98 |
| 180 | 3 | 100 | 35.8 | 63.8 | 8.499 | 14.99 | 13.69 |
| 200 | 0.5 | 0 | 35.8 | 62.1 | 8.483 | 12 | 13.6 |
| 200 | 0.5 | 40 | 35.5 | 60.6 | 8.475 | 11.96 | 12.99 |
| 200 | 0.5 | 60 | 35.4 | 59.9 | 8.399 | 11.45 | 13.21 |
| 200 | 1 | 0 | 35.4 | 61.9 | 8.422 | 11.69 | 12.98 |
| 200 | 1 | 40 | 35.1 | 60.8 | 8.489 | 11.46 | 12.64 |
| 200 | 1 | 60 | 34.6 | 61.2 | 8.321 | 11.54 | 12.35 |
| 200 | 2 | 0 | 34.5 | 61.2 | 8.369 | 11.99 | 13.02 |
| 200 | 2 | 40 | 34.5 | 60.8 | 8.354 | 11.15 | 12.69 |
| 200 | 2 | 60 | 34.2 | 60.5 | 8.211 | 10.65 | 12.49 |
| 200 | 3 | 0 | 34.1 | 60.9 | 8.249 | 10.68 | 12.73 |
| 200 | 3 | 40 | 34.1 | 59.8 | 8.231 | 11.05 | 12.57 |
| 200 | 3 | 60 | 34.1 | 58.2 | 8.011 | 10.22 | 12.37 |
| 210 | 0.5 | 0 | 33.9 | 50.1 | 7.856 | 10.23 | 10.98 |
| 210 | 0.5 | 40 | 33.8 | 50.8 | 7.789 | 10.59 | 9.98 |
| 210 | 0.5 | 60 | 33.2 | 49.9 | 7.865 | 10.55 | 10.23 |
| 210 | 1 | 0 | 32.9 | 50.6 | 7.765 | 10.21 | 10.65 |
| 210 | 1 | 40 | 32.9 | 49.8 | 7.712 | 9.98 | 10.21 |
| 210 | 1 | 60 | 32.8 | 48.9 | 7.498 | 10.01 | 10.65 |
| 210 | 2 | 0 | 32.5 | 49.1 | 7.689 | 9.98 | 9.64 |
| 210 | 2 | 40 | 32.1 | 49.5 | 7.712 | 9.65 | 9.35 |
| 210 | 2 | 60 | 31.8 | 49.6 | 7.623 | 10.03 | 9.67 |
| 210 | 3 | 0 | 31.5 | 47.8 | 7.5 | 9.21 | 8.91 |
| 210 | 3 | 40 | 30.8 | 46.5 | 7.412 | 9.1 | 8.21 |
| 210 | 3 | 60 | 30.5 | 45.1 | 7.321 | 9.03 | 8.99 |
| Alg. | D | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | Avg. Rank | Overall Rank |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 30 | 3 | 3 | 5 | 4.67 | 3.67 | 2.5 | 3 | 3 | 1.83 | 2.33 | 3 | 3 | 4.33 | 3.33 | 3.26 | 3 | |
| WOA | 50 | 3 | 2.33 | 5 | 4.67 | 3.67 | 2.5 | 3 | 3 | 2.17 | 3.67 | 3 | 3 | 4.33 | 3.33 | 3.33 | 3 |
| 100 | 3 | 3 | 5 | 4.67 | 3.67 | 2.5 | 3 | 3 | 2.17 | 3.67 | 3 | 3 | 4.33 | 3.33 | 3.38 | 4 | |
| 30 | 4 | 4 | 3 | 3 | 3.33 | 2.5 | 4 | 4 | 3.17 | 4 | 4 | 3.33 | 2.67 | 3.33 | 3.45 | 4 | |
| GWO | 50 | 4 | 4 | 3 | 3 | 3.33 | 2.5 | 4 | 4 | 3.83 | 2.67 | 4 | 2.67 | 2.67 | 3.67 | 3.38 | 4 |
| 100 | 4 | 4 | 3 | 3 | 3.33 | 2.5 | 4 | 4 | 2.83 | 2.67 | 4 | 2.67 | 2.67 | 3.33 | 3.29 | 3 | |
| 30 | 5 | 5 | 4 | 4.33 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 2.67 | 5 | 4.71 | 5 | |
| PSO | 50 | 5 | 5 | 4 | 4.33 | 5 | 5 | 5 | 5 | 4.67 | 5 | 5 | 5 | 2.67 | 5 | 4.69 | 5 |
| 100 | 5 | 5 | 4 | 4.33 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 2.67 | 5 | 4.71 | 5 | |
| 30 | 2 | 2 | 2 | 2 | 1.67 | 2.5 | 2 | 2 | 3.17 | 2.67 | 1.67 | 2.67 | 2.67 | 2.33 | 2.24 | 2 | |
| DBO | 50 | 2 | 2.67 | 2 | 2 | 1.67 | 2.5 | 2 | 2 | 2.83 | 2.67 | 1.67 | 3.33 | 2.67 | 1.67 | 2.26 | 2 |
| 100 | 2 | 2 | 2 | 2 | 1.67 | 2.5 | 2 | 2 | 3.5 | 2.67 | 1.67 | 3.33 | 2.67 | 2.33 | 2.31 | 2 | |
| 30 | 1 | 1 | 1 | 1 | 1.33 | 2.5 | 1 | 1 | 1.83 | 1 | 1.33 | 1 | 2.67 | 1 | 1.33 | 1 | |
| IDBO | 50 | 1 | 1 | 1 | 1 | 1.33 | 2.5 | 1 | 1 | 1.5 | 1 | 1.33 | 1 | 2.67 | 1.33 | 1.33 | 1 |
| 100 | 1 | 1 | 1 | 1 | 1.33 | 2.5 | 1 | 1 | 1.5 | 1 | 1.33 | 1 | 2.67 | 1 | 1.31 | 1 |
| Parms | Model | Neuron Configuration | Topology | Hidden and Output Activations | Train | Test | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | MAPE | R² | MAE | MSE | MAPE | R² | |||||
| LCS | BP | 2 | 3-2-1 | LOGSIG-PURELIN | 0.2206 | 0.0020 | 0.9335% | 0.9770 | 0.1945 | 0.0011 | 0.5332% | 0.9868 |
| GWO-BP | 3 | 3-3-1 | LOGSIG-PURELIN | 0.1956 | 0.1054 | 0.5263% | 0.9785 | 0.1372 | 0.0724 | 0.4919% | 0.9940 | |
| TSSA-BP | 4 | 3-4-1 | LOGSIG-TANSIG | 0.1592 | 0.1282 | 0.4342% | 0.9759 | 0.1481 | 0.0642 | 0.4270% | 0.9887 | |
| DBO-BP | (3, 7) | 3-3-7-1 | LOGSIG-PURELIN | 0.1412 | 0.1052 | 0.3786% | 0.9830 | 0.1503 | 0.0566 | 0.4260% | 0.9879 | |
| IGWO-BP | (2, 2) | 3-2-2-1 | PURELIN-LOGSIG | 0.1652 | 0.1200 | 0.4449% | 0.9805 | 0.1291 | 0.0345 | 0.3591% | 0.9907 | |
| IDBO-BP | 2 | 3-2-1 | LOGSIG-PURELIN | 0.1315 | 0.0996 | 0.3513% | 0.9834 | 0.0856 | 0.0122 | 0.2286% | 0.9978 | |
| TRS | BP | 2 | 3-2-1 | LOGSIG-PURELIN | 1.2157 | 0.0379 | 2.4030% | 0.9363 | 1.1994 | 0.0753 | 2.4487% | 0.9275 |
| TSSA-BP | 2 | 3-2-1 | LOGSIG-PURELIN | 1.2191 | 2.2895 | 1.9534% | 0.9236 | 1.2609 | 2.2655 | 2.0291% | 0.9430 | |
| GWO-BP | (3, 7) | 3-3-7-1 | LOGSIG-PURELIN | 1.1097 | 1.8158 | 1.7920% | 0.9433 | 0.9837 | 1.9907 | 1.5331% | 0.9272 | |
| IGWO-BP | 3 | 3-3-1 | LOGSIG-TANSIG | 1.1020 | 2.2158 | 1.8002% | 0.9310 | 0.9519 | 1.5641 | 1.5302% | 0.9557 | |
| DBO-BP | 7 | 3-7-1 | POSLIN-PURELIN | 1.0349 | 1.7647 | 1.6610% | 0.9510 | 0.9345 | 1.4363 | 1.4881% | 0.9484 | |
| IDBO-BP | (4, 6) | 3-4-6-1 | TANSIG-PURELIN | 0.9032 | 1.4304 | 1.4750% | 0.9601 | 0.8218 | 1.1362 | 1.3392% | 0.9683 | |
| TME | BP | 3 | 3-3-1 | LOGSIG-PURELIN | 0.1710 | 0.0006 | 2.2422% | 0.8260 | 0.0928 | 0.0005 | 1.4955% | 0.8929 |
| GWO-BP | (3, 7) | 3-3-7-1 | LOGSIG-PURELIN | 0.0925 | 0.0306 | 1.0968% | 0.8638 | 0.1010 | 0.0164 | 1.1576% | 0.9002 | |
| TSSA-BP | (2, 2) | 3-2-2-1 | LOGSIG-PURELIN | 0.1207 | 0.0500 | 2.0647% | 0.7992 | 0.0977 | 0.0158 | 1.1322% | 0.7225 | |
| IGWO-BP | 3 | 3-3-1 | LOGSIG-PURELIN | 0.1144 | 0.0324 | 1.3611% | 0.8424 | 0.0923 | 0.0155 | 1.0797% | 0.9018 | |
| DBO-BP | (3, 7) | 3-3-7-1 | LOGSIG-PURELIN | 0.1024 | 0.0273 | 1.2126% | 0.8658 | 0.0879 | 0.0127 | 1.0182% | 0.9053 | |
| IDBO-BP | 4 | 3-4-1 | POSLIN-PURELIN | 0.0849 | 0.0266 | 1.0132% | 0.8743 | 0.0824 | 0.0115 | 0.9340% | 0.9156 | |
| RH | BP | (5, 6) | 3-5-6-1 | POSLIN-PURELIN | 0.4763 | 0.0049 | 3.5198% | 0.9249 | 0.4963 | 0.0078 | 3.8911% | 0.8986 |
| TSSA-BP | (3, 7) | 3-3-7-1 | LOGSIG-PURELIN | 0.4205 | 0.3300 | 4.1028% | 0.8901 | 0.3919 | 0.3644 | 3.8402% | 0.9023 | |
| GWO-BP | 5 | 3-5-1 | POSLIN-PURELIN | 0.4009 | 0.2375 | 2.9805% | 0.9233 | 0.5008 | 0.3834 | 3.8098% | 0.8785 | |
| IGWO-BP | (4, 6) | 3-4-6-1 | TANSIG-PURELIN | 0.4256 | 0.2896 | 3.2035% | 0.9107 | 0.4095 | 0.2953 | 3.0822% | 0.8975 | |
| DBO-BP | 2 | 3-2-1 | TANSIG-PURELIN | 0.3928 | 0.2466 | 2.9423% | 0.8985 | 0.3478 | 0.2053 | 2.5616% | 0.9285 | |
| IDBO-BP | 5 | 3-5-1 | POSLIN-PURELIN | 0.3353 | 0.2122 | 2.5198% | 0.9372 | 0.3236 | 0.1889 | 2.4020% | 0.9458 | |
| TH | BP | (7, 5) | 3-7-5-1 | LOGSIG-LOGSIG | 0.3850 | 0.0024 | 2.8660% | 0.9412 | 0.4308 | 0.0073 | 3.4057% | 0.8996 |
| GWO-BP | 2 | 3-2-1 | LOGSIG-PURELIN | 0.2857 | 0.2283 | 2.8154% | 0.9615 | 0.3720 | 0.2421 | 3.0862% | 0.8625 | |
| TSSA-BP | (4, 6) | 3-4-6-1 | TANSIG-PURELIN | 0.3743 | 0.2175 | 2.8032% | 0.9354 | 0.3839 | 0.2201 | 2.9423% | 0.8896 | |
| IGWO-BP | 4 | 3-4-1 | TANSIG-PURELIN | 0.3156 | 0.1671 | 2.3664% | 0.9566 | 0.3824 | 0.2373 | 2.9295% | 0.8899 | |
| DBO-BP | (7, 5) | 3-7-5-1 | LOGSIG-LOGSIG | 0.3335 | 0.1700 | 2.4652% | 0.9532 | 0.3604 | 0.2092 | 2.6622% | 0.8996 | |
| IDBO-BP | 4 | 3-4-1 | TANSIG-PURELIN | 0.2611 | 0.1249 | 1.9515% | 0.9676 | 0.2962 | 0.1544 | 2.1062% | 0.9399 |
| Parms | Sample1-Sample 2 | Train | Test | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | Adj. Sig.a | MSE | Adj. Sig.a | MAPE | Adj. Sig.a | R² | Adj. Sig.a | MAE | Adj. Sig.a | MSE | Adj. Sig.a | MAPE | Adj. Sig.a | R² | Adj. Sig.a | ||
| LCS | IDBO-BP-DBO-BP | 6.85% | 0.743 | 5.32% | 1 | 7.22% | 0.003 | −0.05% | 0.051 | 43.07% | 0.436 | 78.44% | 0.743 | 46.35% | 0.007 | −1.00% | 0.743 |
| IDBO-BP-IGWO-BP | 20.40% | 1 | 17.05% | 1 | 21.05% | 0.011 | −0.30% | 0.269 | 33.71% | 0.954 | 64.60% | 0.954 | 36.35% | 0.007 | −0.71% | 0.954 | |
| IDBO-BP-GWO-BP | 32.76% | 0.572 | 5.52% | 1 | 33.25% | 0.001 | −0.50% | 1 | 37.65% | 0.068 | 83.14% | 0.132 | 53.53% | 0.001 | −0.38% | 0.011 | |
| IDBO-BP-TSSA-BP | 17.38% | 1 | 22.32% | 1 | 19.10% | 0.096 | −0.77% | 0.945 | 42.21% | 1 | 80.98% | 1 | 46.47% | 0.016 | −0.92% | 0.572 | |
| IDBO-BP-BP | 40.38% | 0.005 | −4858.66% | 0.068 | 62.37% | 0 | −0.66% | 0.103 | 56.00% | 0.002 | −1016.77% | 0.329 | 57.13% | 0 | −1.11% | 0.002 | |
| TRS | IDBO-BP-DBO-BP | 12.73% | 0.44 | 18.94% | 1 | 11.20% | 1 | −0.96% | 0.556 | 12.06% | 0.428 | 20.89% | 1 | 10.01% | 1 | −2.10% | 0.185 |
| IDBO-BP-IGWO-BP | 18.04% | 0.269 | 35.45% | 1 | 18.06% | 1 | −3.13% | 0.269 | 13.67% | 0.945 | 27.36% | 1 | 12.48% | 1 | −1.32% | 0.638 | |
| IDBO-BP-GWO-BP | 18.61% | 0.945 | 21.22% | 1 | 17.69% | 1 | −1.79% | 1 | 16.46% | 0.061 | 42.92% | 1 | 12.65% | 1 | −4.43% | 0.02 | |
| IDBO-BP-TSSA-BP | 25.92% | 0.035 | 37.52% | 1 | 24.49% | 1 | −3.96% | 0.945 | 34.83% | 0.035 | 49.85% | 1 | 34.00% | 0.572 | −2.68% | 1 | |
| IDBO-BP-BP | 25.71% | 0.001 | −3676.83% | 0.001 | 38.62% | 0.096 | −2.55% | 0.103 | 31.48% | 0.006 | −1409.50% | 0 | 45.31% | 0.002 | −4.41% | 0.061 | |
| TME | IDBO-BP-DBO-BP | 17.08% | 0.794 | 2.37% | 1 | 16.44% | 0.164 | −0.98% | 0.393 | 6.20% | 0.132 | 9.71% | 0.572 | 8.27% | 0.005 | −1.13% | 1 |
| IDBO-BP-IGWO-BP | 25.75% | 0.269 | 17.97% | 1 | 25.56% | 0.42 | −3.79% | 0.269 | 10.66% | 0.572 | 25.86% | 1 | 13.49% | 0.954 | −1.53% | 1 | |
| IDBO-BP-GWO-BP | 8.13% | 0.945 | 13.07% | 1 | 7.62% | 0.42 | −1.22% | 1 | 18.36% | 0.002 | 29.85% | 0.034 | 19.31% | 0.181 | −1.71% | 0.007 | |
| IDBO-BP-TSSA-BP | 29.62% | 0.035 | 46.76% | 1 | 50.93% | 0.035 | −9.40% | 0.945 | 15.60% | 0.096 | 27.14% | 0.246 | 17.50% | 0.181 | −26.72% | 0.181 | |
| IDBO-BP-BP | 50.33% | 0.001 | −4103.20% | 0.023 | 54.81% | 0.001 | −5.86% | 0.103 | 11.15% | 0.181 | −2041.22% | 0.436 | 37.55% | 0 | −2.54% | 0.068 | |
| RH | IDBO-BP-DBO-BP | 14.63% | 0.361 | 13.98% | 1 | 14.36% | 1 | −4.30% | 0.185 | 6.97% | 1.000 | 8.00% | 1 | 6.23% | 1 | −1.86% | 0.119 |
| IDBO-BP-IGWO-BP | 21.21% | 0.269 | 26.72% | 1 | 21.34% | 1 | −2.90% | 0.269 | 20.99% | 1 | 36.03% | 1 | 22.07% | 1 | −5.38% | 0.638 | |
| IDBO-BP-GWO-BP | 16.36% | 0.945 | 10.65% | 1 | 15.46% | 1 | −1.50% | 1 | 35.40% | 1 | 50.74% | 1 | 36.95% | 1 | −7.67% | 0.02 | |
| IDBO-BP-TSSA-BP | 20.25% | 0.035 | 35.70% | 0.572 | 38.58% | 1 | −5.29% | 0.945 | 17.44% | 0.096 | 48.18% | 0.954 | 37.45% | 0.572 | −4.82% | 1 | |
| IDBO-BP-BP | 29.60% | 0.001 | −4200.16% | 0.016 | 28.41% | 0.048 | −1.32% | 0.103 | 34.80% | 1.000 | −2308.90% | 0.005 | 38.27% | 0.011 | −5.26% | 0.061 | |
| TH | IDBO-BP-DBO-BP | 21.71% | 0.7 | 26.50% | 1 | 20.84% | 0.087 | −1.50% | 0.556 | 17.83% | 0.366 | 26.17% | 1 | 20.88% | 0.151 | −4.48% | 0.113 |
| IDBO-BP-IGWO-BP | 17.27% | 0.269 | 25.22% | 1 | 17.53% | 0.42 | −1.14% | 0.269 | 22.56% | 0.945 | 34.92% | 1 | 28.10% | 1 | −5.62% | 0.638 | |
| IDBO-BP-GWO-BP | 8.62% | 0.945 | 45.27% | 1 | 30.68% | 0.42 | −0.63% | 1 | 20.39% | 0.061 | 36.20% | 1 | 31.75% | 0.035 | −8.97% | 0.02 | |
| IDBO-BP-TSSA-BP | 30.25% | 0.035 | 42.55% | 1 | 30.38% | 0.035 | −3.44% | 0.945 | 22.87% | 0.035 | 29.84% | 1 | 28.42% | 0.061 | −5.64% | 1 | |
| IDBO-BP-BP | 32.18% | 0.001 | −5117.57% | 1 | 31.91% | 0.001 | −2.80% | 0.103 | 31.25% | 0.006 | −2013.85% | 1 | 38.16% | 0 | −4.48% | 0.061 |
| Parms | Model | Train | Test | Avg. Rank | Overall Rank | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | MAPE | R² | MAE | MSE | MAPE | R² | Include MSE | Exclude MSE | Include MSE | Exclude MSE | ||
| LCS | BP | 5 | 1 | 5.42 | 2.17 | 4.83 | 1 | 5.08 | 2.25 | 2.24 | 2.65 | 5 | 6 |
| TSSA-BP | 2.67 | 4 | 3.08 | 3.92 | 3.25 | 4.08 | 3.5 | 3.58 | 1.64 | 0.83 | 2 | 2 | |
| GWO-BP | 3.83 | 4.5 | 4.08 | 3.33 | 4.08 | 4.75 | 4.08 | 2.58 | 2.43 | 1.69 | 6 | 5 | |
| IGWO-BP | 3.5 | 4.42 | 3.58 | 3.33 | 3.33 | 4.17 | 3.67 | 3.75 | 1.95 | 1.17 | 3 | 3 | |
| DBO-BP | 3.75 | 3.92 | 3.83 | 3.67 | 3.58 | 4.25 | 3.67 | 3.67 | 1.96 | 1.25 | 4 | 4 | |
| IDBO-BP | 2.25 | 3.17 | 1 | 4.58 | 1.92 | 2.75 | 1 | 5.17 | 0.29 | −0.60 | 1 | 1 | |
| TRS | BP | 3.25 | 1 | 5.17 | 3.25 | 4 | 1 | 5.08 | 2.92 | 1.67 | 1.89 | 4 | 6 |
| TSSA-BP | 4.08 | 4.33 | 3.5 | 3 | 3.92 | 4.25 | 3.75 | 3.33 | 2.19 | 1.49 | 6 | 5 | |
| GWO-BP | 4.17 | 4.25 | 3.83 | 3.17 | 3.58 | 4.08 | 3.42 | 3.58 | 2.07 | 1.38 | 5 | 4 | |
| IGWO-BP | 2.83 | 3.75 | 2.67 | 4.33 | 3.5 | 4 | 3.25 | 3 | 1.58 | 0.82 | 2 | 2 | |
| DBO-BP | 3.17 | 3.58 | 2.75 | 3.67 | 3.5 | 3.92 | 3.33 | 3.42 | 1.65 | 0.94 | 3 | 3 | |
| IDBO-BP | 3.5 | 4.08 | 3.08 | 3.58 | 2.5 | 3.75 | 2.17 | 4.75 | 1.34 | 0.49 | 1 | 1 | |
| TME | BP | 4.08 | 1 | 4.75 | 3.83 | 4.67 | 1 | 5.08 | 2.83 | 1.74 | 1.99 | 3 | 6 |
| TSSA-BP | 3.58 | 3.75 | 3.17 | 3.67 | 3.83 | 4.5 | 3.5 | 3.08 | 1.95 | 1.22 | 4 | 3 | |
| GWO-BP | 3.17 | 4.67 | 3.67 | 2.5 | 3.67 | 5 | 4.33 | 2.33 | 2.46 | 1.67 | 6 | 5 | |
| IGWO-BP | 3.25 | 4 | 3 | 3.75 | 3.33 | 3.58 | 3 | 4 | 1.55 | 0.81 | 2 | 2 | |
| DBO-BP | 3.75 | 4.17 | 3.5 | 3.25 | 3.75 | 4.25 | 3.5 | 3.75 | 1.99 | 1.25 | 5 | 4 | |
| IDBO-BP | 3.17 | 3.42 | 2.92 | 4 | 1.75 | 2.67 | 1.58 | 5 | 0.81 | 0.07 | 1 | 1 | |
| RH | BP | 4.58 | 1 | 5.08 | 3.42 | 5.17 | 1 | 5.25 | 3.75 | 1.86 | 2.15 | 4 | 6 |
| TSSA-BP | 3.17 | 5.08 | 3.75 | 2.33 | 3 | 5.17 | 4.25 | 2.08 | 2.50 | 1.63 | 6 | 5 | |
| GWO-BP | 3.5 | 3.83 | 3.08 | 3.42 | 2.92 | 3.5 | 3 | 3.58 | 1.60 | 0.92 | 3 | 3 | |
| IGWO-BP | 3.5 | 4.08 | 3.25 | 3.58 | 3.92 | 4.25 | 3.42 | 3.67 | 1.90 | 1.14 | 5 | 4 | |
| DBO-BP | 3.25 | 3.5 | 3 | 4 | 2.92 | 3.33 | 2.42 | 3.83 | 1.32 | 0.63 | 2 | 2 | |
| IDBO-BP | 3 | 3.5 | 2.83 | 4.25 | 3.08 | 3.75 | 2.67 | 4.08 | 1.31 | 0.54 | 1 | 1 | |
| TH | BP | 4.08 | 1 | 4.75 | 2.08 | 4.17 | 1 | 4.33 | 2.25 | 1.88 | 2.17 | 4 | 6 |
| TSSA-BP | 4.17 | 4.5 | 3.92 | 3 | 3.83 | 4.08 | 3.08 | 3.33 | 2.16 | 1.45 | 5 | 4 | |
| GWO-BP | 3.33 | 3.83 | 3 | 3.67 | 3.92 | 4.17 | 3.75 | 3.58 | 1.84 | 1.13 | 3 | 3 | |
| IGWO-BP | 3.83 | 4.42 | 3.58 | 3.08 | 4.08 | 4.5 | 4 | 3.17 | 2.27 | 1.54 | 6 | 5 | |
| DBO-BP | 3.42 | 3.67 | 3 | 4 | 2.58 | 3.42 | 2.42 | 3.83 | 1.34 | 0.60 | 2 | 2 | |
| IDBO-BP | 3.17 | 3.58 | 2.75 | 3.47 | 2.42 | 3.43 | 2.45 | 3.99 | 1.29 | 0.56 | 1 | 1 | |
References
- Goli, G.; Negro, F.; Emmerich, L.; Militz, H. Thermal and chemical modification of wood—A combined approach for exclusive, high-demanding performance products. Wood Mater. Sci. Eng. 2022, 18, 58–66. [Google Scholar] [CrossRef]
- Bekhta, P. Effect of heat treatment on some physical and mechanical properties of birch plywood. Eur. J. Wood Wood Prod. 2020, 78, 683–691. [Google Scholar] [CrossRef]
- Esteves, B.; Ferreira, H.; Viana, H.; Ferreira, J.; Domingos, I.; Cruz-Lopes, L.; Jones, D.; Nunes, L. Termite Resistance, Chemical and Mechanical Characterization of Paulownia tomentosa Wood before and after Heat Treatment. Forests 2021, 12, 1114. [Google Scholar] [CrossRef]
- Tjeerdsma, B.F.; Militz, H. Chemical changes in hydrothermal treated wood: FTIR analysis of combined hydrothermal and dry heat-treated wood. Eur. J. Wood Wood Prod. 2005, 63, 102–111. [Google Scholar] [CrossRef]
- Kaymakci, A.; Bayram, B. Evaluation of heat treatment parameters’ effect on some physical and mechanical properties of poplar wood with multi-criteria decision making techniques. Bioresources 2021, 16, 4693–4703. [Google Scholar] [CrossRef]
- Suri, I.F.; Purusatama, B.D.; Kim, J.H.; Yang, G.U.; Prasetia, D.; Kwon, G.J.; Hidayat, W.; Lee, S.H.; Febrianto, F.; Kim, N.H. Comparison of physical and mechanical properties of Paulownia tomentosa and Pinus koraiensis wood heat-treated in oil and air. Eur. J. Wood Wood Prod. 2022, 80, 1389–1399. [Google Scholar] [CrossRef]
- Esteves, B.M.; Pereira, H.M. Wood modification by heat treatment: A review. Bioresources 2008, 4, 370–404. [Google Scholar] [CrossRef]
- Korkut, D.S.; Guller, B. The effects of heat treatment on physical properties and surface roughness of red-bud maple (Acer trautvetteri Medw.) wood. Bioresour. Technol. 2008, 99, 2846–2851. [Google Scholar] [CrossRef]
- Içel, B.; Guler, G.; Isleyen, O.; Beram, A.; Mutlubas, M. Effects of Industrial Heat Treatment on the Properties of Spruce and Pine Woods. Bioresources 2015, 10, 5159–5173. [Google Scholar] [CrossRef]
- Xue, J.; Xu, W.; Zhou, J.; Mao, W.; Wu, S. Effects of High-Temperature Heat Treatment Modification by Impregnation on Physical and Mechanical Properties of Poplar. Materials 2022, 15, 7334. [Google Scholar] [CrossRef]
- Boonstra, M.J.; Tjeerdsma, B. Chemical analysis of heat treated softwoods. Eur. J. Wood Wood Prod. 2006, 64, 204–211. [Google Scholar] [CrossRef]
- Hill, C.A.S. Wood Modification; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Kohonen, T. The self-organizing map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Onyiagha, C. From neuronal stochasticity to intelligent resource management of packet data networks. In Proceedings of the Fifth International Conference on Artificial Neural Networks, Venue, UK, 7–9 July 1997. [Google Scholar] [CrossRef]
- Stergios, A.; Anthony, K.; Elli, R.; Dimitris, B. Predicting the properties corrugated base papers using multiple linear regressiom amd artificial neural networks. Drewno 2016, 59, 198. [Google Scholar] [CrossRef]
- You, G.; Wang, B.; Li, J.; Chen, A.; Sun, J. The prediction of MOE of bamboo-wood composites by ANN models based on the non-destructive vibration testing. J. Build. Eng. 2022, 59, 105078. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, W.; Li, N. Prediction of the equilibrium moisture content and specific gravity of thermally modified wood via an Aquila optimization algorithm back-propagation neural network model. Bioresources 2022, 17, 4816–4836. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Elaziz, M.A.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila Optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Chen, Y. Carnivorous Plant Algorithm and BP to Predict Optimum Bonding Strength of Heat-Treated Woods. Forests 2022, 14, 51. [Google Scholar] [CrossRef]
- Ong, K.M.; Ong, P.; Sia, C.K. A carnivorous plant algorithm for solving global optimization problems. Appl. Soft Comput. 2020, 98, 106833. [Google Scholar] [CrossRef]
- Li, N.; Wang, W. Prediction of Mechanical Properties of Thermally Modified Wood Based on TSSA-BP Model. Forests 2022, 13, 160. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Ma, W.; Wang, W.; Cao, Y. Mechanical Properties of Wood Prediction Based on the NAGGWO-BP Neural Network. Forests 2022, 13, 1870. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2022, 79, 7305–7336. [Google Scholar] [CrossRef]
- Tiryaki, S.; Özşahin, Ş..; Yıldırım, I. Comparison of artificial neural network and multiple linear regression models to predict optimum bonding strength of heat treated woods. Int. J. Adhes. Adhes. 2014, 55, 29–36. [Google Scholar] [CrossRef]
- Yan, Y.; Hongzhong, M.; Zhendong, L. An Improved Grasshopper Optimization Algorithm for Global Optimization. Chin. J. Electron. 2021, 30, 451–459. [Google Scholar] [CrossRef]
- Wu, Q. A self-adaptive embedded chaotic particle swarm optimization for parameters selection of Wv-SVM. Expert Syst. Appl. 2011, 38, 184–192. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, S.; Wang, Y. Chaos Encryption Algorithm Based on Kent Mapping and AES Combination. In Proceedings of the 2018 International Conference on Network, Communication, Computer Engineering (NCCE 2018), Chongqing, China, 26–27 May 2018. [Google Scholar] [CrossRef]
- Wang, X.; Jin, C. Image encryption using Game of Life permutation and PWLCM chaotic system. Opt. Commun. 2012, 285, 412–417. [Google Scholar] [CrossRef]
- Bai, H.; Chu, Z.; Wang, D.; Bao, Y.; Qin, L.; Zheng, Y.; Li, F. Predictive control of microwave hot-air coupled drying model based on GWO-BP neural network. Dry. Technol. 2022, 1–11. [Google Scholar] [CrossRef]
- Song, X.; Zhao, M.; Yan, Q.; Xing, S. A high-efficiency adaptive artificial bee colony algorithm using two strategies for continuous optimization. Swarm Evol. Comput. 2019, 50, 100549. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Yang, H.; Cheng, W.; Han, G. Wood Modification at High Temperature and Pressurized Steam: A Relational Model of Mechanical Properties Based on a Neural Network. Bioresources 2015, 10, 5758–5776. [Google Scholar] [CrossRef]



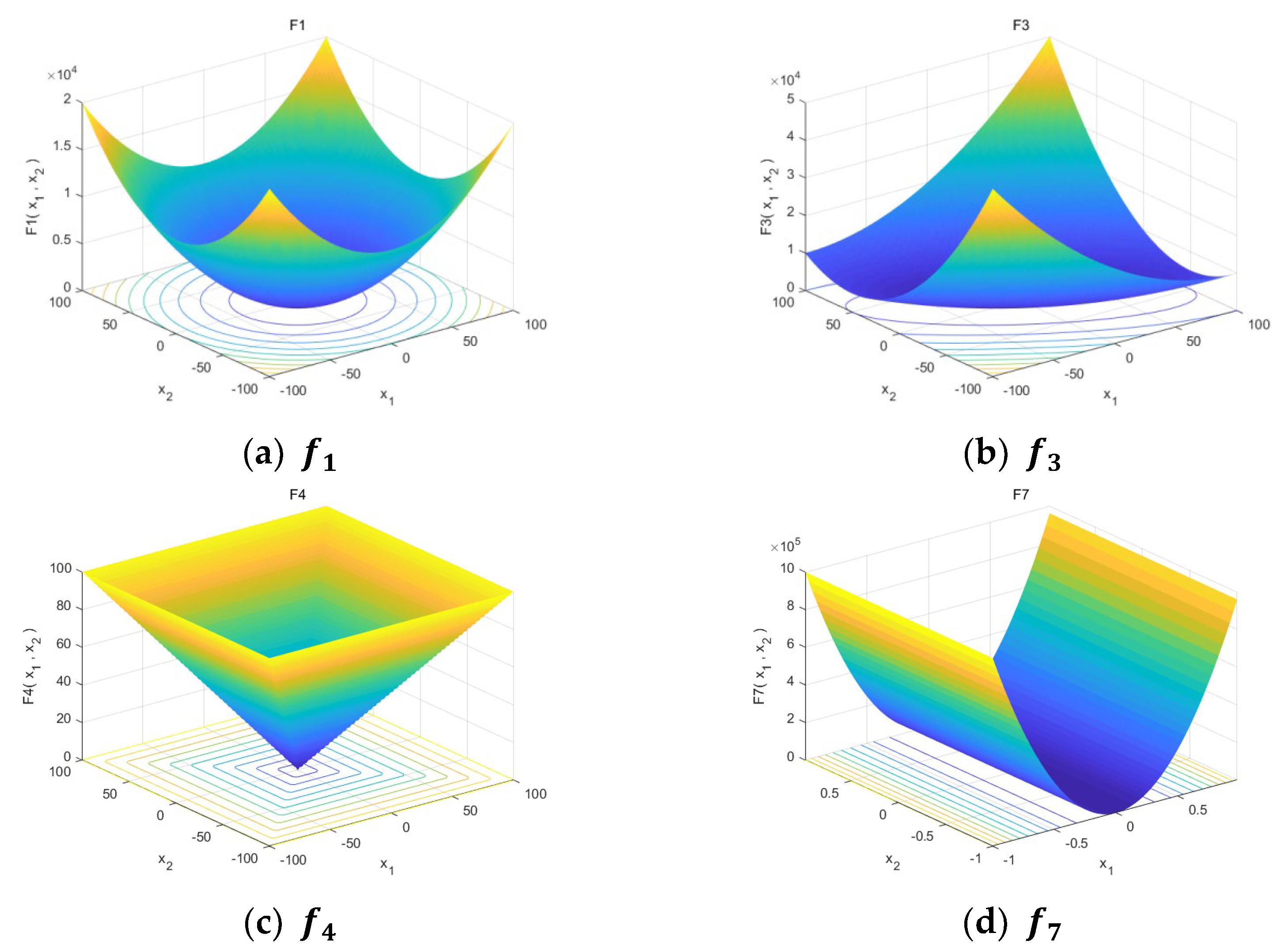
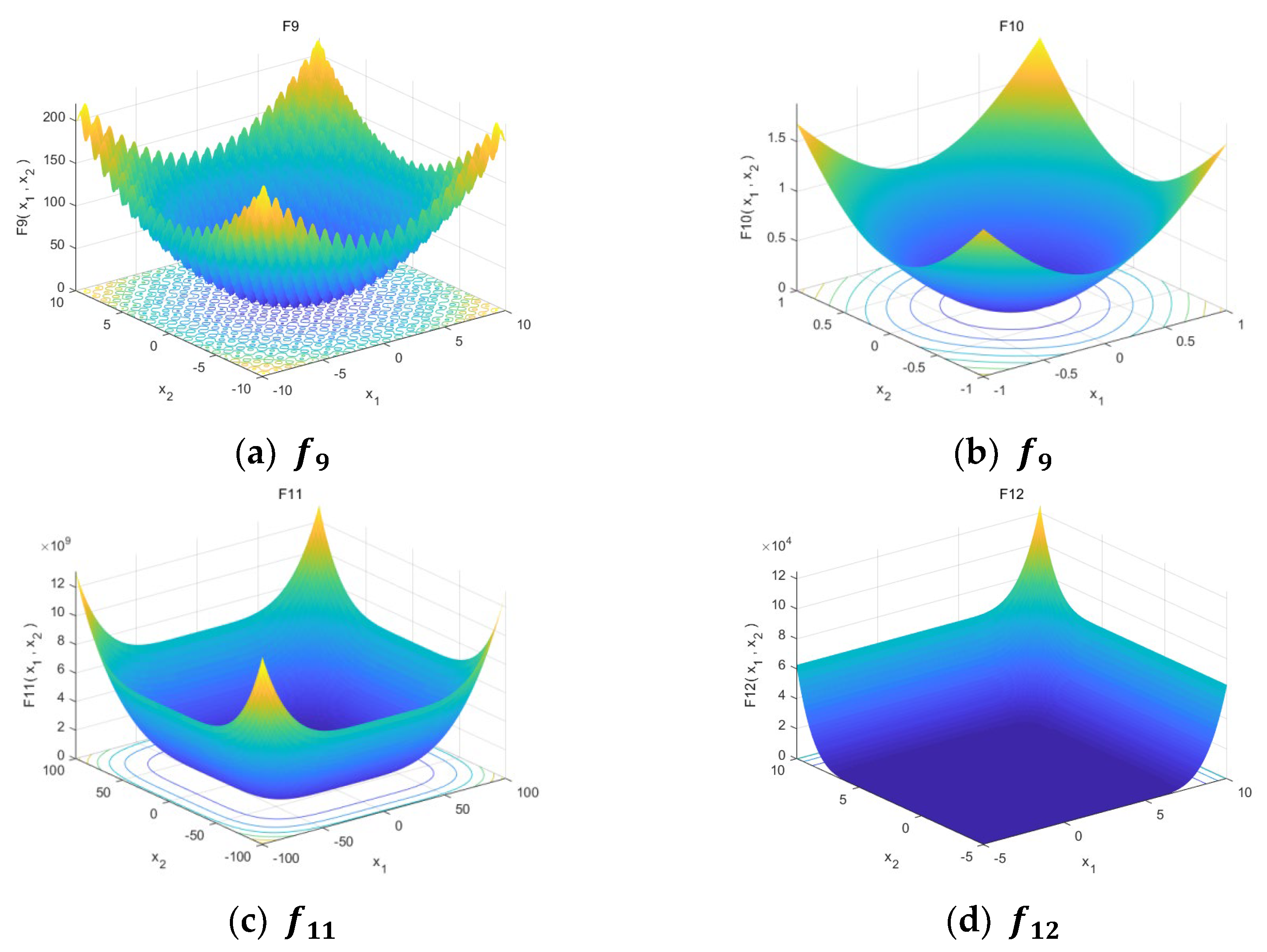


| Function | Dim | Range | |
|---|---|---|---|
| 30/50/100 | [−100, 100] | 0 | |
| 30/50/100 | [−10, 10] | 0 | |
| = | 30/50/100 | [−100, 100] | 0 |
| 30/50/100 | [−100, 100] | 0 | |
| = | 30/50/100 | [−30, 30] | 0 |
| = | 30/50/100 | [−100, 100] | 0 |
| =+ | 30/50/100 | [−100, 100] | 0 |
| = | 30/50/100 | [−5, 10] | 0 |
| Function | Dim | Range | |
|---|---|---|---|
| = | 30/50/100 | [−5.12, 5.12] | 0 |
| = | 30/50/100 | [−10, 10] | 0 |
| =, = 1, for all i = 1, …, n = | 30/50/100 | [−50, 50] | 0 |
| = 0.1 | 30/50/100 | [−50, 50] | 0 |
| = | 30/50/100 | [−100, 100] | 0 |
for all i = 1, …, n | 30/50/100 | [−10, 10] | 0 |
| Algorithm | Parameter | Setting |
|---|---|---|
| WOA | a | Gradually reduced from 2 to 0 |
| GWO | a | Uniformly lowered from 2 to 0 |
| PSO | and | 2 |
| Inertia weight | Linearly decreased from 0.9 to 0.1 | |
| DBO | 0.1 | |
| a and b | 0.3 and 0.5 | |
| IDBO | 0.1 | |
| a and b | 0.3 and 0.5 | |
| The proportions of the ball-rolling dung beetle, the brood ball, the small dung beetle and the thief were , 0.2, 0.2 and | ||
| F | D | Index | WOA | GWO | PSO | DBO | IDBO |
|---|---|---|---|---|---|---|---|
| F1 | 30 | Best | |||||
| Mean | |||||||
| STD | |||||||
| 50 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| 100 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| F2 | 30 | Best | |||||
| Mean | |||||||
| STD | |||||||
| 50 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| 100 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| F3 | 30 | Best | |||||
| Mean | |||||||
| STD | |||||||
| 50 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| 100 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| F4 | 30 | Best | |||||
| Mean | |||||||
| STD | |||||||
| 50 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| 100 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| F5 | 30 | Best | |||||
| Mean | |||||||
| STD | |||||||
| 50 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| 100 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| 30 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| 50 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| 100 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| F7 | 30 | Best | |||||
| Mean | |||||||
| STD | |||||||
| 50 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| 100 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| F8 | 30 | Best | |||||
| Mean | |||||||
| STD | |||||||
| 50 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| 100 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| Rank | 30 | w/t/l | 0/1/7 | 0/1/7 | 0/0/8 | 0/1/7 | 7/1/0 |
| 50 | w/t/l | 0/1/7 | 0/1/7 | 0/0/8 | 0/1/7 | 7/1/0 | |
| 100 | w/t/l | 0/1/7 | 0/1/7 | 0/0/8 | 0/1/7 | 7/1/0 |
| F | D | Index | WOA | GWO | PSO | DBO | IDBO |
|---|---|---|---|---|---|---|---|
| F9 | 30 | Best | |||||
| Mean | |||||||
| STD | |||||||
| 50 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| 100 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| F10 | 30 | Best | |||||
| Mean | |||||||
| STD | |||||||
| 50 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| 100 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| F11 | 30 | Best | |||||
| Mean | |||||||
| STD | |||||||
| 50 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| 100 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| F12 | 30 | Best | |||||
| Mean | |||||||
| STD | |||||||
| 50 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| 100 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| F13 | 30 | Best | |||||
| Mean | |||||||
| STD | |||||||
| 50 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| 100 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| F14 | 30 | Best | |||||
| Mean | |||||||
| STD | |||||||
| 50 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| 100 | Best | ||||||
| Mean | |||||||
| STD | |||||||
| Rank | 30 | w/t/l | 0/1/5 | 0/1/5 | 0/1/5 | 0/1/5 | 4/2/0 |
| 50 | w/t/l | 0/0/6 | 0/1/5 | 0/1/5 | 0/1/5 | 4/2/0 | |
| 100 | w/t/l | 0/0/6 | 0/1/5 | 0/1/5 | 0/1/5 | 4/2/0 |
| WOA | GWO | PSO | DBO | IDBO | |
|---|---|---|---|---|---|
| w/t/l | w/t/l | w/t/l | w/t/l | w/t/l | |
| D = 30 | 0/2/12 | 0/2/12 | 0/1/13 | 0/2/12 | 11/3/0 |
| D = 50 | 0/1/13 | 0/2/12 | 0/1/13 | 0/2/12 | 11/3/0 |
| D = 100 | 0/1/13 | 0/2/12 | 0/1/13 | 0/2/12 | 11/3/0 |
| Total | 0/4/38 | 0/6/36 | 0/3/39 | 0/6/36 | 33/9/0 |
| TP | 9.52% | 14.29% | 7.14% | 14.29% | 100.00% |
| Function | WOA | GWO | PSO | DBO |
|---|---|---|---|---|
| F1 | ||||
| F2 | ||||
| F3 | ||||
| F4 | ||||
| F5 | ||||
| F6 | N/A | N/A | N/A | |
| F7 | ||||
| F8 | ||||
| F9 | N/A | |||
| F10 | ||||
| F11 | ||||
| F12 | ||||
| F13 | N/A | N/A | N/A | |
| F14 | ||||
| +/=/− | 11/3/0 | 12/2/0 | 13/1/0 | 12/2/0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Zhu, Y. Predicting the Mechanical Properties of Heat-Treated Woods Using Optimization-Algorithm-Based BPNN. Forests 2023, 14, 935. https://doi.org/10.3390/f14050935
Zhang R, Zhu Y. Predicting the Mechanical Properties of Heat-Treated Woods Using Optimization-Algorithm-Based BPNN. Forests. 2023; 14(5):935. https://doi.org/10.3390/f14050935
Chicago/Turabian StyleZhang, Runze, and Yujie Zhu. 2023. "Predicting the Mechanical Properties of Heat-Treated Woods Using Optimization-Algorithm-Based BPNN" Forests 14, no. 5: 935. https://doi.org/10.3390/f14050935
APA StyleZhang, R., & Zhu, Y. (2023). Predicting the Mechanical Properties of Heat-Treated Woods Using Optimization-Algorithm-Based BPNN. Forests, 14(5), 935. https://doi.org/10.3390/f14050935







