Allometric Equations to Estimate Aboveground Biomass in Spotted Gum (Corymbia citriodora Subspecies variegata) Plantations in Queensland
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Datasets
2.2. Data Collection
- Prior to sampling, each sample tree was identified and provided with an ID number. Tree diameter over bark at breast height 1.3 m (D, cm) was recorded.
- Most of trees were felled using a chainsaw. However, an excavator was used to push 23 trees onto the ground as these trees were also used to determine belowground biomass [44]. After the tree was felled, total tree height (H, m) was recorded.
- Sample trees were divided into three biomass components: (1) stem; (2) large branches (>2 cm diameter); and (3) small branches (<2 cm diameter), along with foliage, buds, capsules, or flowers. These components were weighed using digital scales and fresh weight (kg) was recorded.
- For each tree, sub-samples (at least 2 kg) of these biomass components were taken to the laboratory for determining moisture content (MC%). From the base of bole to the height of the first limiting defect of each tree, a 40 mm wide disk was taken every 3.0 m for laboratory analysis.
- In the laboratory, the large branch and small branch samples were cut into small pieces and dried at 65–105 °C (as appropriate for the type of sample) until a constant weight was achieved. Stem disks were used to estimate green wood density (ρ, kg m3) prior to drying.
- 6.
- Crown diameter (CD, m) was measured before felling the trees (at step 1). The CD measurements were taken for each tree using a tape measure, averaging the measurements from along and across the planting row.
- 7.
- In the laboratory (at step 5), stem bark was removed from the disks, recording fresh weight of the bark and wood. The samples were dried, and oven-dry weight was determined. In addition, the average width of chainsaw cuts used to collect the discs was used to determine mass of sawdust based on the wood density (ρ kg m−3). The sawdust weight was added to the stem biomass. The formula for estimating stem bark and sawdust was described by Huynh et al. (2021) [45].
2.3. Data Analysis
2.3.1. Variable Selection and Data Preparation
2.3.2. Model Fitting
2.3.3. Model Assessment and Selection
2.3.4. Model Cross Validation
3. Results
3.1. Basic Measurements and Tree Component Biomass
3.2. Data Exploration and Variable Selection
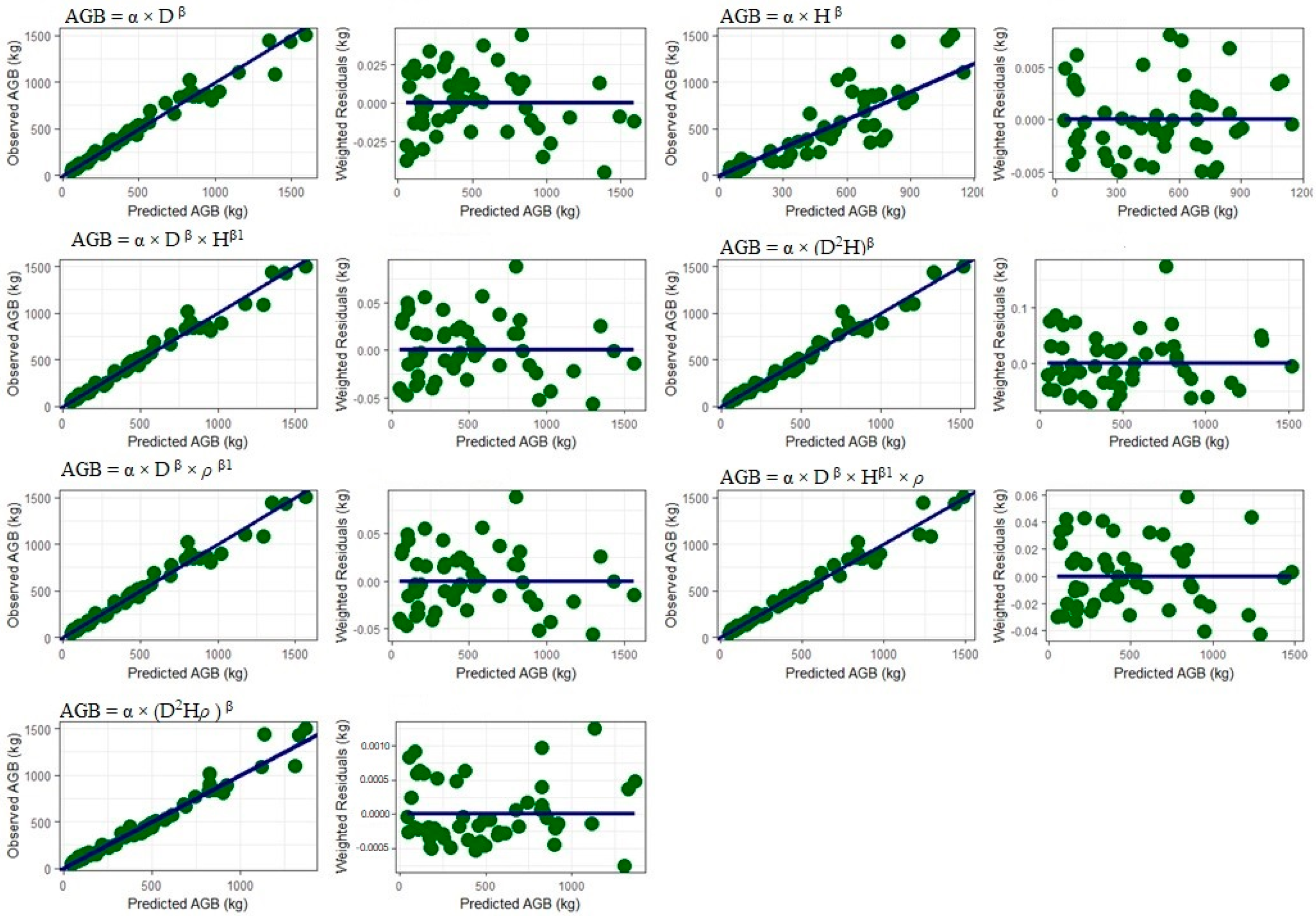
3.3. Allometric Equations for AGB
3.3.1. Including Predictor Variables Height and Wood Density
3.3.2. Including CD and CV in Biomass Equations
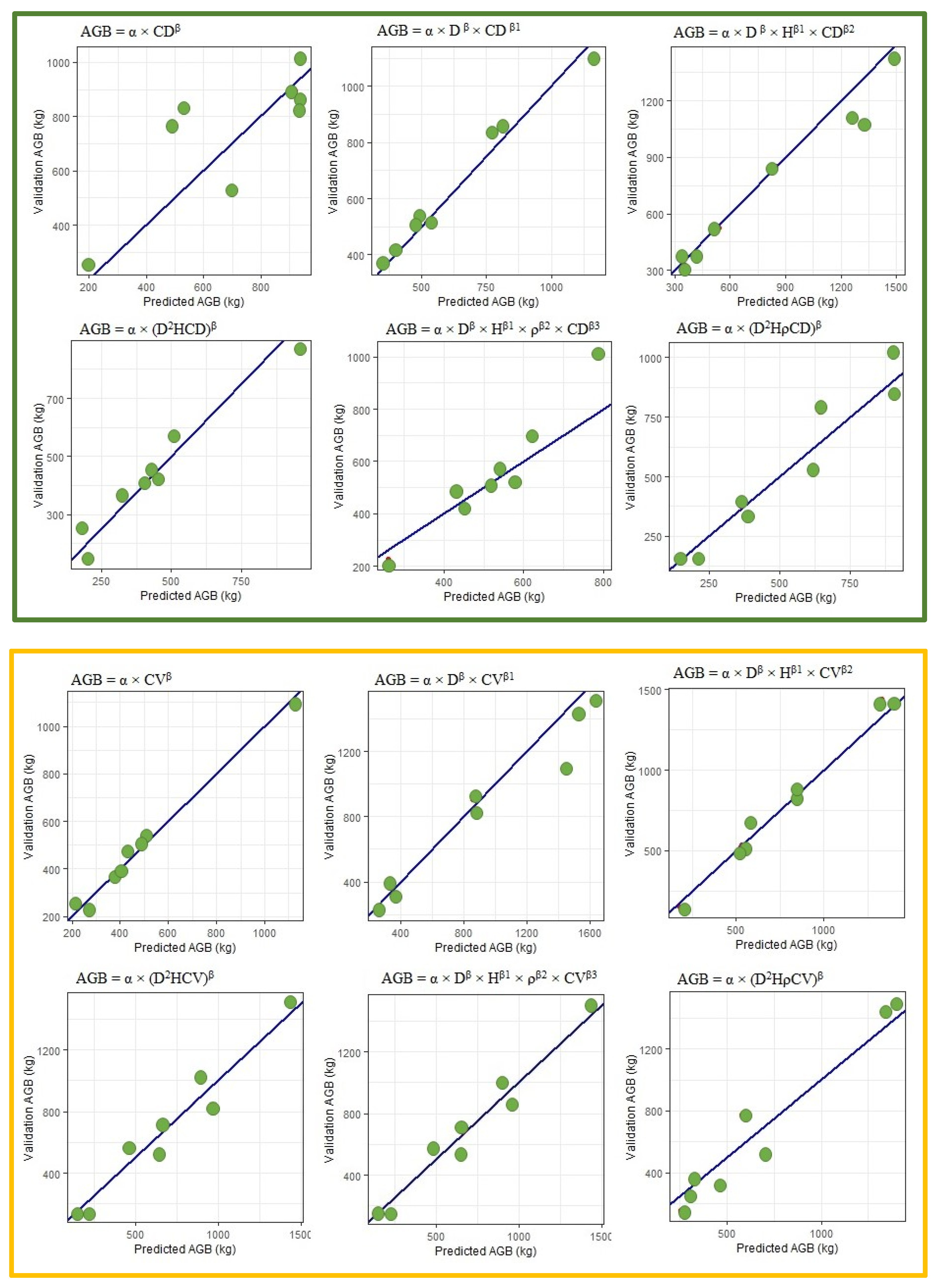
3.4. Cross Validation Biomass Models
3.4.1. Models Using Diameter, Height and Wood Density
3.4.2. Models Using Crown Diameter and Crown Volume
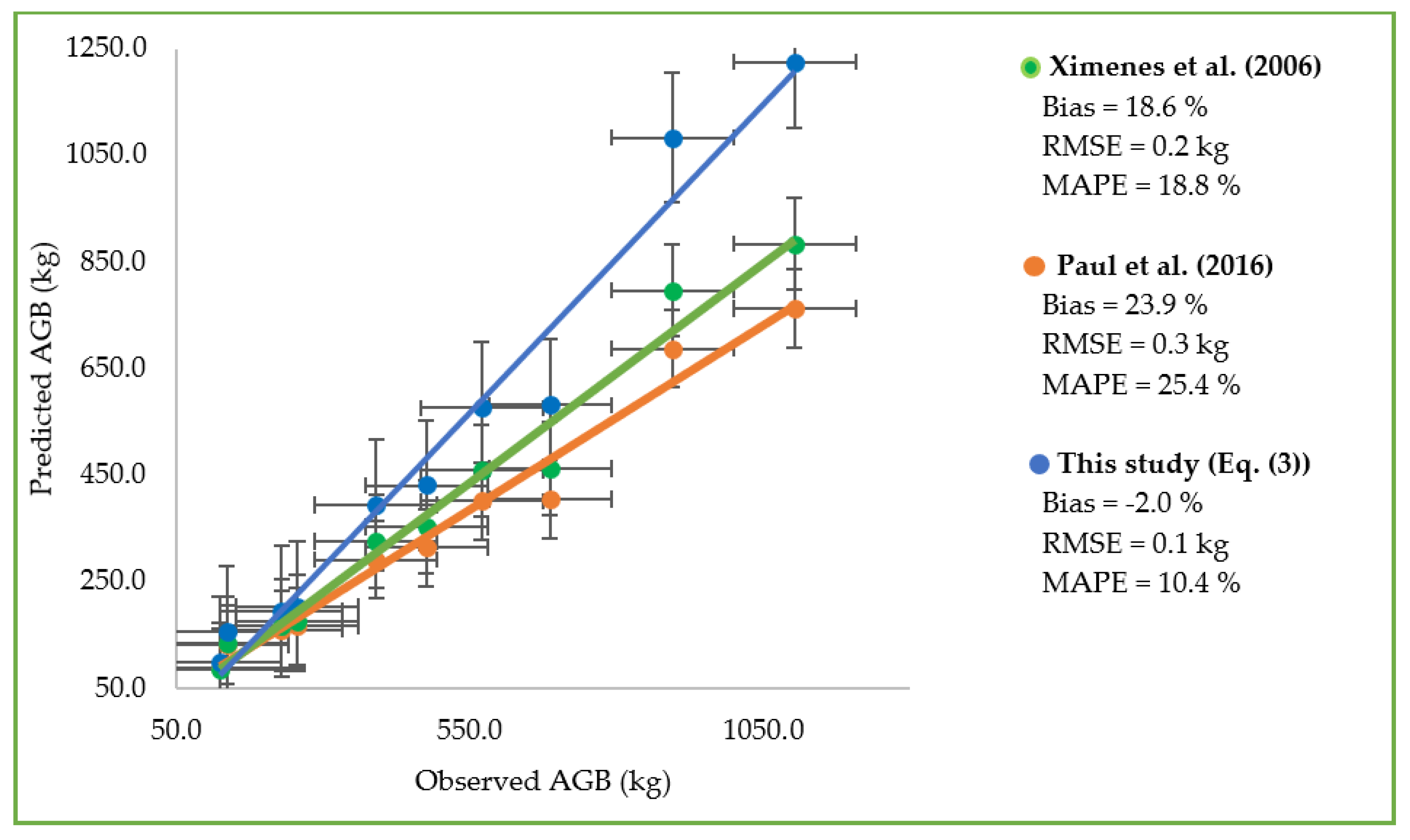
3.4.3. Cross Validation against an Independent Dataset
4. Discussion
4.1. Equation Development and Cross Validation
4.2. Inclusion of Height and Wood Density
4.3. Influence of Crown Diameter and Crown Volume
4.4. Evaluating Existing Applicability Models
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Shao, G.; Shao, G.; Gallion, J.; Saunders, M.R.; Frankenberger, J.R.; Fei, S. Improving Lidar-based aboveground biomass estimation of temperate hardwood forests with varying site productivity. Remote Sens. Environ. 2018, 204, 872–882. [Google Scholar] [CrossRef]
- Eamus, D.; Burrows, W.; McGuinness, K. Review of Allometric Relationships for Estimating Woody Biomass for Queensland, the Northern Territory and Western Australia; Australian Greenhouse Office: Canberra, NSW, Australia, 2000.
- Canadell, J.G.; Raupach, M.R. Managing forests for climate change mitigation. Science 2008, 320, 1456–1457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Phillips, D.L.; Brown, S.L.; Schroeder, P.E.; Birdsey, R.A. Toward error analysis of large-scale forest carbon budgets. Glob. Ecol. Biogeogr. 2000, 9, 305–313. [Google Scholar] [CrossRef]
- IPCC. Guidelines for National Greenhouse Gas Inventories. Agriculture, Forestry and Other Land Use; IGES: Hayama, Japan, 2006; pp. 1–66.
- IPCC. 2019 Refinement to the 2006 IPCC Guidelines for National Greenhouse Gas Inventories. 2019. Available online: https://www.ipcc.ch/report/2019-refinement-to-the-2006-ipcc-guidelines-for-national-greenhouse-gas-inventories/ (accessed on 10 December 2021).
- Lee, D.J. Achievements in forest tree genetic improvement in Australia and New Zealand 2: Development of Corymbia species and hybrids for plantations in eastern Australia. Aust. For. 2007, 70, 11–16. [Google Scholar] [CrossRef]
- Lee, D.J.; Huth, J.R.; Osborne, D.O.; Hogg, B.W. Selecting hardwood varieties for fibre production in Queensland’s subtropics. In Proceedings of the 2nd Australasian Forest Genetics Conference: Book of Abstracts; Forest Products Commission: Kalgoorlie, WA, Australia, 2009. [Google Scholar]
- Salcedo, P.G.; Maraseni, T.N.; McDougall, K. Carbon sequestration potential of spotted gum (Corymbia citriodora subspecies Variegata) in South East Queensland, Australia. Int. J. Environ. Stud. 2012, 69, 770–784. [Google Scholar] [CrossRef]
- McMahon, L.; George, B.; Hean, R. Corymbia maculata, Corymbia citriodora subsp. variegata and Corymbia henryi; Industry and Investment, New South Wales Government: Sydney, NSW, Australia, 2010.
- Garcia Florez, L.; Vanclay, J.K.; Glencross, K.; Nichols, J.D. Developing biomass estimation models for above-ground compartments in Eucalyptus dunnii and Corymbia citriodora plantations. Biomass Bioenergy 2019, 130, 105353. [Google Scholar] [CrossRef]
- Lee, D.J.; Brawner, J.T.; Smith, T.E.; Hogg, B.W.; Meder, R.; Osborne, D.O. Productivity of Plantation Hardwood Tree Species in North-Eastern Australia: A Report from the Forest Adaptation and Sequestration Alliance; The Australian Government Department of Agriculture, Fisheries and Forestry: Canberra, NSW, Australia, 2011.
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Change Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef]
- Keith, H.; Barrett, D.; Keenan, R. Review of Allometric Relationships for Estimating Woody Biomass for New South Wales, the Australian Capital Territory, Victoria, Tasmania and South Australia; Australian Greenhouse Office: Canberra, NSW, Australia, 2000.
- Applegate, G.B.; Richards, B.; Charley, J.; Bevege, I. Biomass of Blackbutt (‘Eucalyptus pilularis’ Sm.) Forests on Fraser Island. Master’s Thesis, University of New England, Armidale, NSW, Australia, 1984. [Google Scholar]
- McKenzie, N.; Ryan, P.; Fogarty, P.; Wood, J. Sampling, Measurement and Analytical Protocols for Carbon Estimation in Soil, Litter and Coarse Woody Debris; Australian Greenhouse Office: Canberra, NSW, Australia, 2000.
- Williams, R.J.; Zerihun, A.; Montagu, K.D.; Hoffman, M.; Hutley, L.B.; Chen, X. Allometry for estimating aboveground tree biomass in tropical and subtropical eucalypt woodlands: Towards general predictive equations. Aust. J. Bot. 2005, 53, 607–619. [Google Scholar] [CrossRef]
- Ximenes, F.; Bi, H.; Cameron, N.; Coburn, R.; Maclean, M.; Matthew, D.S.; Roxburgh, S.; Ryan, M.; Williams, J.; Ken, B. Carbon Stocks and Flows in Native Forests and Harvested Wood Products in SE Australia; Project No: PNC285-1112; Forest Wood Products Australia: Melbourne, VIC, Australia, 2016. [Google Scholar]
- Paul, K.I.; Roxburgh, S.H.; Chave, J.; England, J.R.; Zerihun, A.; Specht, A.; Lewis, T.; Bennett, L.T.; Baker, T.G.; Adams, M.A. Testing the generality of above-ground biomass allometry across plant functional types at the continent scale. Glob. Change Biol. 2016, 22, 2106–2124. [Google Scholar] [CrossRef]
- Paul, K.I.; Larmour, J.; Specht, A.; Zerihun, A.; Ritson, P.; Roxburgh, S.H.; Sochacki, S.; Lewis, T.; Barton, C.V.; England, J.R.; et al. Testing the generality of below-ground biomass allometry across plant functional types. For. Ecol. Manag. 2019, 432, 102–114. [Google Scholar] [CrossRef]
- Ximenes, F.A.; Gardner, W.D.; Richards, G.P. Total above-ground biomass and biomass in commercial logs following the harvest of spotted gum (Corymbia maculata) forests of SE NSW. Aust. For. 2006, 69, 213–222. [Google Scholar] [CrossRef]
- Forrester, D.I.; Dumbrell, I.C.; Elms, S.R.; Paul, K.I.; Pinkard, E.A.; Roxburgh, S.H.; Baker, T.G. Can crown variables increase the generality of individual tree biomass equations? Trees 2020, 35, 15–26. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A.; Ewel, J.J.; Clark, D.B. Estimation of tropical rain forest aboveground biomass with small-footprint lidar and hyperspectral sensors. Remote Sens. Environ. 2011, 115, 2931–2942. [Google Scholar] [CrossRef]
- Kumar, L.; Mutanga, O. Remote Sensing of Above-Ground Biomass. Remote Sens. 2017, 9, 935. [Google Scholar] [CrossRef] [Green Version]
- Morel, A.C.; Saatchi, S.S.; Malhi, Y.; Berry, N.J.; Banin, L.; Burslem, D.; Nilus, R.; Ong, R.C. Estimating aboveground biomass in forest and oil palm plantation in Sabah, Malaysian Borneo using ALOS PALSAR data. For. Ecol. Manag. 2011, 262, 1786–1798. [Google Scholar] [CrossRef]
- Van Niekerk, P.; Drew, D.; Dovey, S.; Du Toit, B. Allometric relationships to predict aboveground biomass of 8–10-year-old Eucalyptus grandis × E. nitens in south-eastern Mpumalanga, South Africa. South. For. J. For. Sci. 2020, 82, 15–23. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef]
- Picard, N.; Rutishauser, E.; Ploton, P.; Ngomanda, A.; Henry, M. Should tree biomass allometry be restricted to power models? For. Ecol. Manag. 2015, 353, 156–163. [Google Scholar] [CrossRef]
- Xu, Q.-S.; Liang, Y.-Z.; Du, Y.-P. Monte Carlo cross-validation for selecting a model and estimating the prediction error in multivariate calibration. J. Chemom. 2004, 18, 112–120. [Google Scholar] [CrossRef]
- Paul, K.I.; Radtke, P.J.; Roxburgh, S.H.; Larmour, J.; Waterworth, R.; Butler, D.; Brooksbank, K.; Ximenes, F. Validation of allometric biomass models: How to have confidence in the application of existing models. For. Ecol. Manag. 2018, 412, 70–79. [Google Scholar] [CrossRef]
- Xu, Y.; Goodacre, R. On splitting training and validation set: A comparative study of cross-validation, bootstrap and systematic sampling for estimating the generalization performance of supervised learning. J. Anal. Test. 2018, 2, 249–262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brown, S.; Gillespie, A.J.R.; Lugo, A.E. Biomass estimation methods for tropical forests with applications to forest inventory data. For. Sci. 1989, 35, 881–902. [Google Scholar] [CrossRef]
- Brown, S.; Iverson, L.R. Biomass estimates for tropical forests. World Resour. Rev. 1992, 4, 366–384. [Google Scholar]
- Brown, S. Estimating Biomass and Biomass Change of Tropical Forests: A Primer; Food & Agriculture Organization: Rome, Italy, 1997; Volume 134. [Google Scholar]
- Brown, S. Geographical Distribution of Biomass Carbon in Tropical Southeast Asian Forests: A Database; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2002. [Google Scholar]
- Burrows, W.H.; Hoffmann, M.B.; Compton, J.F.; Back, P.V.; Tait, L.J. Allometric relationships and community biomass estimates for some dominant eucalypts in Central Queensland woodlands. Aust. J. Bot. 2000, 48, 707–714. [Google Scholar] [CrossRef]
- Ketterings, Q.M.; Coe, R.; van Noordwijk, M.; Palm, C.A. Reducing uncertainty in the use of allometric biomass equations for predicting above-ground tree biomass in mixed secondary forests. For. Ecol. Manag. 2001, 146, 199–209. [Google Scholar] [CrossRef]
- Basuki, T.M.; van Laake, P.E.; Skidmore, A.K.; Hussin, Y.A. Allometric equations for estimating the above-ground biomass in tropical lowland Dipterocarp forests. For. Ecol. Manag. 2009, 257, 1684–1694. [Google Scholar] [CrossRef]
- Diédhiou, I.; Diallo, D.; Mbengue, A.; Hernandez, R.; Bayala, R.; Diémé, R.; Diédhiou, P.; Sène, A. Allometric equations and carbon stocks in tree biomass of Jatropha curcas L. in Senegal’s Peanut Basin. Glob. Ecol. Conserv. 2017, 9, 61–69. [Google Scholar] [CrossRef]
- Sileshi, G.W. A critical review of forest biomass estimation models, common mistakes and corrective measures. For. Ecol. Manag. 2014, 329, 237–254. [Google Scholar] [CrossRef]
- Picard, R.R.; Cook, R.D. Cross-validation of regression models. J. Am. Stat. Assoc. 1984, 79, 575–583. [Google Scholar] [CrossRef]
- Brown, S. Measuring carbon in forests: Current status and future challenges. Environ. Pollut. 2002, 116, 363–372. [Google Scholar] [CrossRef]
- Huynh, T.; Applegate, G.; Lewis, T.; Pachas, A.N.A.; Hunt, M.A.; Bristow, M.; Lee, D.J. Species-Specific Allometric Equations for Predicting Belowground Root Biomass in Plantations: Case Study of Spotted Gums (Corymbia citriodora subspecies variegata) in Queensland. Forests 2021, 12, 1210. [Google Scholar] [CrossRef]
- Huynh, T.; Lee, D.J.; Applegate, G.; Lewis, T. Field methods for above and belowground biomass estimation in plantation forests. MethodsX 2021, 8, 101192. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Kleinn, C.; Nölke, N. Assessing tree crown volume—A review. For. Int. J. For. Res. 2021, 94, 18–35. [Google Scholar] [CrossRef]
- Xiao, X.; White, E.P.; Hooten, M.B.; Durham, S.L. On the use of log-transformation vs. nonlinear regression for analyzing biological power laws. Ecology 2011, 92, 1887–1894. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Z.; Gamarra, J.; Birigazzi, L. Inventory of Allometric Equations for Estimation Tree Biomass—A Database for China; UNREDD Programme: Rome, Italy, 2014. [Google Scholar]
- Huy, B.; Thanh, G.T.; Poudel, K.P.; Temesgen, H. Individual Plant Allometric Equations for Estimating Aboveground Biomass and Its Components for a Common Bamboo Species (Bambusa procera A. Chev. and A. Camus) in Tropical Forests. Forests 2019, 10, 316. [Google Scholar] [CrossRef] [Green Version]
- Moore, J.R. Allometric equations to predict the total above-ground biomass of radiata pine trees. Ann. For. Sci. 2010, 67, 806. [Google Scholar] [CrossRef] [Green Version]
- Fordjour, P.; Rahmad, Z. Development of allometric equation for estimating above-ground liana biomass in tropical primary and secondary forest, Malaysia. Int. J. Ecol. 2013, 2013, 658140. [Google Scholar] [CrossRef] [Green Version]
- Furnival, G.M. An index for comparing equations used in constructing volume tables. For. Sci. 1961, 7, 337–341. [Google Scholar]
- Picard, N.; Saint-André, L.; Henry, M. Manual for Building Tree Volume Biomapass Allometric Equations: From Field Measurement to Prediction; FAO Food Agricultural Organization of the United Nations: Rome, Italy, 2012. [Google Scholar]
- Huy, B.; Kralicek, K.; Poudel, K.P.; Phuong, V.T.; Van Khoa, P.; Hung, N.D.; Temesgen, H. Allometric equations for estimating tree aboveground biomass in evergreen broadleaf forests of Viet Nam. For. Ecol. Manag. 2016, 382, 193–205. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R.C. Team. nlme: Linear and nonlinear mixed effects models. R Package Version 2013, 3, 111. [Google Scholar]
- Stegmann, G.; Jacobucci, R.; Harring, J.R.; Grimm, K.J. Nonlinear mixed-effects modeling programs in R. Struct. Equ. Model. 2018, 25, 160–165. [Google Scholar] [CrossRef]
- Wickham, H.; Chang, W.; Wickham, M.H. Package ‘ggplot2’. Create Elegant Data Visualisations Using the Grammar of Graphics. R Package Version 2016, 2, 1–189. [Google Scholar]
- Fonseca-Delgado, R.; Gómez-Gil, P. An assessment of ten-fold and Monte Carlo cross validations for time series forecasting. In Proceedings of the 10th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Mexico City, Mexico, 30 September–4 October 2013. [Google Scholar]
- Temesgen, H.; Zhang, C.; Zhao, X. Modelling tree height–diameter relationships in multi-species and multi-layered forests: A large observational study from Northeast China. For. Ecol. Manag. 2014, 316, 78–89. [Google Scholar] [CrossRef]
- Huy, B.; Tinh, N.T.; Poudel, K.P.; Frank, B.M.; Temesgen, H. Taxon-specific modeling systems for improving reliability of tree aboveground biomass and its components estimates in tropical dry dipterocarp forests. For. Ecol. Manag. 2019, 437, 156–174. [Google Scholar] [CrossRef]
- Paul, K.I.; Adams, M.; Applegate, G.; Attiwill, P.; Baker, T.; Barton, C.; Bastin, G.; Battaglia, M.; Bradford, M.; Bradstock, R.; et al. Australian Individual Tree Biomass Library, Version 2. ÆKOS Data Portal, Rights Owned by Commonwealth Scientific and Industrial Research Organisation. 2016. Available online: https://researchdata.edu.au/australian-individual-tree-biomass-library/1340678 (accessed on 7 November 2021). [CrossRef]
- Brown, S.; Sathaye, J.; Cannell, M.; Kauppi, P. Management of Forests for Mitigation of Greenhouse Gas Emissions; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Montagu, K.; Düttmer, K.; Barton, C.; Cowie, A. Developing general allometric relationships for regional estimates of carbon sequestration—An example using Eucalyptus pilularis from seven contrasting sites. For. Ecol. Manag. 2005, 204, 115–129. [Google Scholar] [CrossRef]
- Bi, H.; Turner, J.; Lambert, M.J. Additive biomass equations for native eucalypt forest trees of temperate Australia. Trees 2004, 18, 467–479. [Google Scholar] [CrossRef]
- Ledermann, T.; Neumann, M. Biomass equations from data of old long-term experimental plots. Austrian J. For. Sci. 2006, 123, 47–64. [Google Scholar]
- António, N.; Tomé, M.; Tomé, J.; Soares, P.; Fontes, L. Effect of tree, stand, and site variables on the allometry of Eucalyptus globulus tree biomass. Can. J. For. Res. 2007, 37, 895–906. [Google Scholar] [CrossRef]
- Veiga, P. Allometric Biomass Equations for Plantations of Eucalyptus globulus and Eucalyptus nitens in Australia; Albert-Ludwigs University Freiburg, Faculty of Forest and Environmental Sciences: Freiburg, Switzerland, 2008. [Google Scholar]
- Xiang, W.; Liu, S.; Deng, X.; Shen, A.; Lei, X.; Tian, D.; Zhao, M.; Peng, C. General allometric equations and biomass allocation of Pinus massoniana trees on a regional scale in southern China. Ecol. Res. 2011, 26, 697–711. [Google Scholar] [CrossRef]
- Goodman, R.C.; Phillips, O.; Baker, T.R. The importance of crown dimensions to improve tropical tree biomass estimates. Ecol. Appl. 2014, 24, 680–698. [Google Scholar] [CrossRef] [Green Version]
- Molto, Q.; Rossi, V.; Blanc, L. Error propagation in biomass estimation in tropical forests. Methods Ecol. Evol. 2013, 4, 175–183. [Google Scholar] [CrossRef]
- Kuyah, S.; Dietz, J.; Muthuri, C.; van Noordwijk, M.; Neufeldt, H. Allometry and partitioning of above-and below-ground biomass in farmed eucalyptus species dominant in Western Kenyan agricultural landscapes. Biomass Bioenergy 2013, 55, 276–284. [Google Scholar] [CrossRef]
- Poorter, H.; Nagel, O. The role of biomass allocation in the growth response of plants to different levels of light, CO2, nutrients and water: A quantitative review. Funct. Plant Biol. 2000, 27, 1191. [Google Scholar] [CrossRef] [Green Version]
- Banin, L.; Feldpausch, T.R.; Phillips, O.; Baker, T.R.; Lloyd, J.; Affum-Baffoe, K.; Arets, E.; Berry, N.J.; Bradford, M.J.; Brienen, R.J.W.; et al. What controls tropical forest architecture? Testing environmental, structural and floristic drivers. Glob. Ecol. Biogeogr. 2012, 21, 1179–1190. [Google Scholar] [CrossRef]
- Baker, T.R.; Phillips, O.L.; Malhi, Y.; Almeida, S.; Arroyo, L.; Di Fiore, A.; Erwin, T.; Killeen, T.J.; Laurance, S.G.; Laurance, W.F.; et al. Variation in wood density determines spatial patterns in Amazonian forest biomass. Glob. Change Biol. 2004, 10, 545–562. [Google Scholar] [CrossRef]

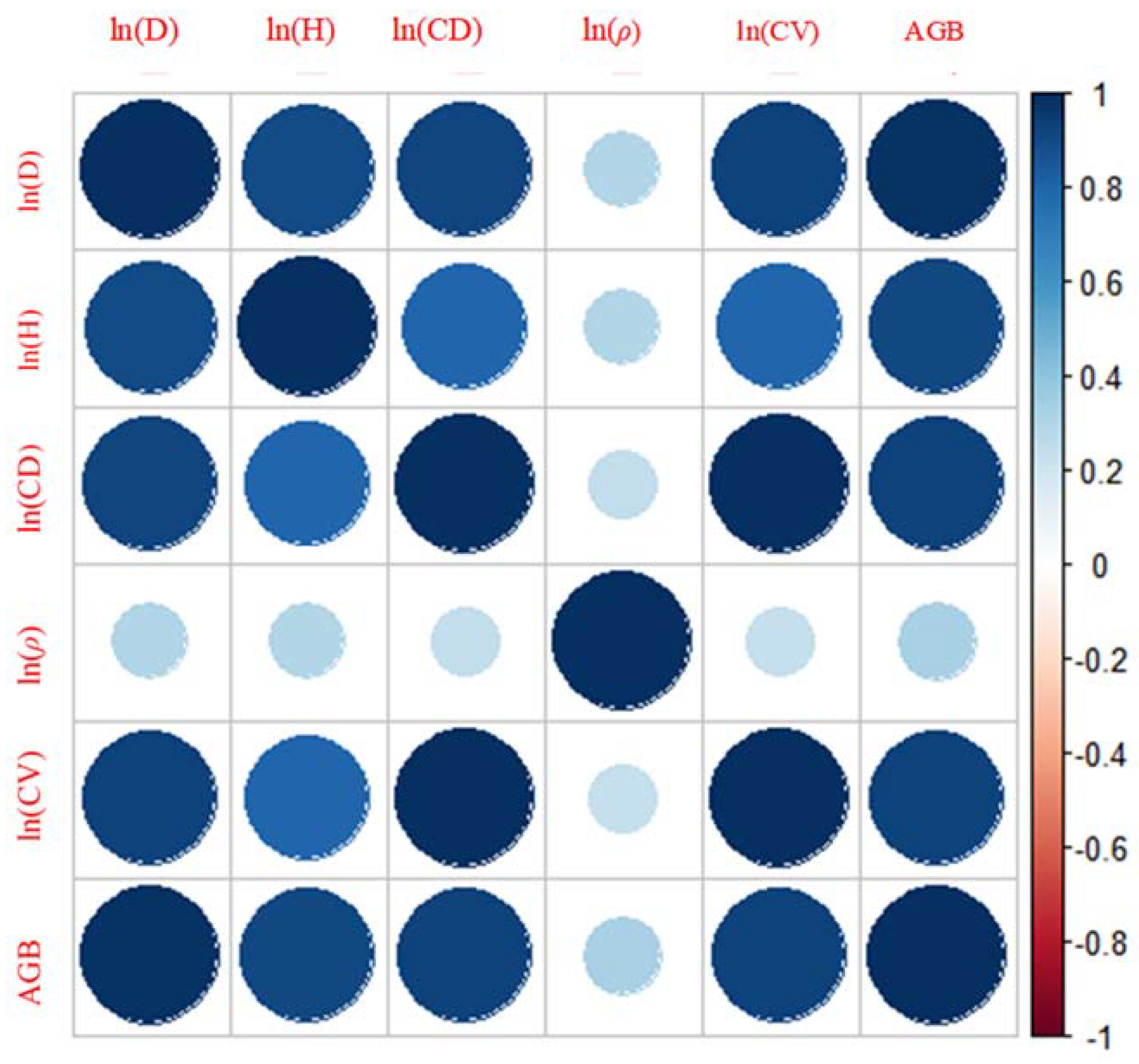

| Sites (Age) | n | Mean (min, max) | |||
|---|---|---|---|---|---|
| D (cm) | H (m) | CD (m) | ρ (kg m−3) | ||
| 451G (7) | 3 | 17.8 (11.8–17.6) | 17.4 (15.3–20.4) | NA | 702.6 (646.8–752.8) |
| 13PHY (8) | 6 | 15.3 (12.5–18.2) | 15.4 (13.1–16.4) | NA | 676.7 (613.0–738.8) |
| 451D (9) | 3 | 14.4 (12.0–17.8) | 15.5 (12.6–17.5) | NA | 663.8 (631.1–713.1) |
| 451G (18) | 13 | 27.1 (17.6–39.9) | 27.0 (22.1–29.9) | 5.3 (3.0–7.9) | 730.8 (671.5–813.5) |
| 451D (20) | 27 | 28.6 (17.1–42.0) | 25.8 (20.2–32.0) | 6.1 (2.8–9.9) | 736.5 (625.7–801.0) |
| Total | 52 | 25.9 (11.8–42.0) | 23.9 (12.6–32.0) | 5.9 (2.8–9.9) | 722.0 (613.0–813.5) |
| Input Variable | Equation No. | Model Form | Weight Variable |
|---|---|---|---|
| Model set 1: Compound predictor variables including D, H and ρ, n = 52 trees | |||
| D | (3) | AGB = α × Dβ | 1/Dδ |
| H | (4) | AGB = α × Hβ | 1/Hδ |
| D and H | (5) | AGB = α × Dβ × Hβ1 | 1/Dδ |
| (6) | AGB = α × (D2H)β | 1/(D2H)δ | |
| D and ρ | (7) | AGB = α × Dβ × ρβ1 | 1/Dδ |
| D, H and ρ | (8) | AGB = α × Dβ × Hβ1 × ρβ2 | 1/(D)δ |
| (9) | AGB = α × (D2Hρ)β | 1/(D2Hρ)δ | |
| Model set 2a: Compound predictor variables including D, H, ρ and CD, n = 40 trees | |||
| D | (10) | AGB = α × Dβ | 1/Dδ |
| H | (11) | AGB = α × Hβ | 1/Hδ |
| CD | (12) | AGB = α × CDβ | 1/CDδ |
| D and CD | (13) | AGB = α × Dβ × CDβ1 | 1/Dδ |
| D, H and CD | (14) | AGB = α × Dβ × Hβ1 × CDβ2 | 1/Dδ |
| (15) | AGB = α × (D2HCD)β | 1/(D2HCD)δ | |
| D, H, ρ and CD | (16) | AGB = α × Dβ × Hβ1 × ρβ2 × CDβ3 | 1/Dδ |
| (17) | AGB = α × (D2Hρ CD)β | 1/(D2HρCD)δ | |
| Model set 2b: Compound predictor variables including D, H, ρ and CV, n = 40 trees | |||
| CV | (18) | AGB = α × CVβ | 1/CVδ |
| D and CV | (19) | AGB = α × Dβ × CVβ1 | 1/Dδ |
| D, H and CV | (20) | AGB = α × Dβ × Hβ1 × CVβ2 | 1/Dδ |
| (21) | AGB = α × (D2HCV)β | 1/(D2H CV)δ | |
| D, H, ρ and CV | (22) | AGB = α × Dβ × Hβ1 × ρβ2 × CVβ3 | 1/Dδ |
| (23) | AGB = α × (D2HρCV)β | 1/(D2HρCV)δ | |
| Sites | n | Mean (min, max), kg | ||||
|---|---|---|---|---|---|---|
| Stem | Bark | Large Branches | Small Branches and Leaves | Total AGB | ||
| 451G (7) | 3 | 67.8 (29.0–110.0) | 16.4 (8.7–23.4) | 10.6 (5.5–16.3) | 5.3 (2.3–7.2) | 100.0 (45.5–156.8) |
| 13PHY (8) | 6 | 70.8 (40.1–101.9) | 12.0 (7.9–16.1) | 28.5 (8.8–44.7) | 8.9 (4.6–13.4) | 120.2 (73.3–174.1) |
| 451D (9) | 3 | 59.4 (26.4–98.0) | 17.0 (10.8–24.6) | 3.6 (2.1–5.4) | 4.8 (3.3–7.7) | 84.8 (43.9–135.6) |
| 451G (18) | 13 | 417.1 (99.0–845.9) | 55.1 (19.8–109.9) | 179.1 (21.0–666.4) | 51.1 (9.6–109.7) | 702.5 (149.4–1503.7) |
| 451D (20) | 27 | 329.9 (92.2–682.1) | 44.3 (18.8–75.5) | 159.1 (17.2–501.2) | 43.1 (7.2–172.5) | 576 (149.7–1431.3) |
| Total | 52 | 291.1 (26.4–845.9) | 40.1 (7.9–109.9) | 131.5 (2.1–666.4) | 36.8 (2.3–172.5) | 499.4 (43.9–1503.7) |
| Equation No. | Parameter Estimates | AIC | Adj. R2 | Bias (%) | RMSE (kg) | MAPE (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| α | β | β1 | β2 | β3 | ||||||
| Model set 1: Compound predictor variables including D, H and ρ (n = 52 trees) | ||||||||||
| (3) | 0.08220 | 2.64134 | 544.1 | 0.963 | −0.0025 | 0.0200 | 0.0085 | |||
| (4) | 0.00622 | 3.49873 | 670.8 | 0.720 | 0.0001 | 0.0034 | 0.0012 | |||
| (5) | 0.05251 | 2.40238 | 0.38285 | 546.3 | 0.973 | −0.0023 | 0.0316 | 0.0132 | ||
| (6) | 0.02533 | 1.00656 | 554.0 | 0.975 | 0.0212 | 0.0500 | 0.0186 | |||
| (7) | 0.05252 | 2.40266 | 0.38253 | 546.3 | 0.973 | −0.0023 | 0.0316 | 0.0132 | ||
| (8) | 0.00233 | 2.42585 | 0.30576 | 0.49890 | 551.8 | 0.972 | 0.0001 | 0.0248 | 0.0106 | |
| (9) | 0.00004 | 0.99037 | 561.6 | 0.963 | 0.0004 | 0.0004 | 0.0002 | |||
| Model set 2a: Compound predictor variables including D, H, ρ and CD (n = 40 trees) | ||||||||||
| (10) | 0.10606 | 2.56803 | 442.3 | 0.950 | 0.0000 | 0.0043 | 0.0009 | |||
| (11) | 0.00027 | 4.45063 | 545.9 | 0.614 | 0.0000 | 0.0002 | 0.0000 | |||
| (12) | 33.24309 | 1.61825 | 532.6 | 0.769 | 4.3446 | 30.0835 | 6.1784 | |||
| (13) | 2.30247 | 1.07425 | 450.2 | 0.947 | −0.0003 | 0.0032 | 0.0007 | |||
| (14) | 0.05153 | 2.18627 | 0.54648 | 0.11719 | 456.7 | 0.964 | 0.0007 | 0.0259 | 0.0050 | |
| (15) | 0.19568 | 0.68009 | 460.3 | 0.961 | −1.0183 | 1.6823 | 0.3358 | |||
| (16) | 0.00079 | 2.07194 | 0.69202 | 0.60292 | 0.18009 | 463.1 | 0.967 | 0.0031 | 0.0318 | 0.0060 |
| (17) | 0.00156 | 0.69886 | 455.2 | 0.965 | 0.0347 | 0.1618 | 0.0326 | |||
| Model set 2b: Compound predictor variables including D, H, ρ and CV (n = 40 trees) | ||||||||||
| (18) | 15.35139 | 0.53941 | 532.6 | 0.781 | 2.7223 | 18.9797 | 3.8982 | |||
| (19) | 0.09881 | 2.61161 | −0.01109 | 450.2 | 0.950 | −0.0003 | 0.0032 | 0.0007 | ||
| (20) | 0.04872 | 2.18625 | 0.54650 | 0.03907 | 456.7 | 0.966 | 0.0007 | 0.0259 | 0.0050 | |
| (21) | 0.95382 | 0.38323 | 496.5 | 0.908 | −0.5644 | 5.6982 | 1.1344 | |||
| (22) | 0.00072 | 2.07191 | 0.69205 | 0.60293 | 0.06004 | 463.1 | 0.970 | 0.0030 | 0.0318 | 0.0060 |
| (23) | 0.06581 | 0.38942 | 494.9 | 0.907 | 0.1717 | 1.2739 | 0.2542 | |||
| Equation No. | Model Form | AIC | Adj. R2 | Bias | RMSE | MAPE |
|---|---|---|---|---|---|---|
| (3) | AGB = α × Dβ | 434.4 | 0.823 | −2.2 | 0.115 | 7.2 |
| (4) | AGB = α × Hβ | 533.1 | 0.642 | −41.7 | 0.679 | 55.3 |
| (10) | AGB = α × Dβ | 357.2 | 0.880 | −6.0 | 0.114 | 6.8 |
| (12) | AGB = α × CDβ | 430.4 | 0.964 | −6.5 | 0.428 | 25.4 |
| (18) | AGB = α × CVβ | 428.3 | 0.964 | −14.8 | 0.348 | 23.1 |
| Δ AIC | Δ Adj. R2 | Δ Bias | Δ RMSE | Δ MAPE | ||
| Model set 1: Compound predictor variables including D, H and ρ | ||||||
| (4) | AGB = α × Hβ | −98.7 | 0.181 | 39.4 | −0.564 | −48.1 |
| (5) | AGB = α × Dβ × Hβ1 | −6.7 | −0.099 | 1.2 | 0.016 | −0.1 |
| (6) | AGB = α × (D2H)β | −13.2 | −0.149 | 6.2 | −0.011 | −3.4 |
| (7) | AGB = α × Dβ × ρβ1 | −4.0 | −0.098 | 1.1 | 0.011 | 0.8 |
| (8) | AGB = α × Dβ × Hβ1 × ρβ2 | −13.4 | −0.130 | 1.9 | 0.021 | 0.7 |
| (9) | AGB = α × (D2Hρ)β | −19.8 | −0.135 | 8.6 | −0.023 | −4.2 |
| Model set 2a: Compound predictor variables including D, H, ρ and CD | ||||||
| (11) | AGB = α × Hβ | −86.9 | 0.255 | 9.9 | −0.096 | −11.4 |
| (12) | AGB = α × CDβ | −73.2 | −0.084 | 0.5 | −0.315 | −18.6 |
| (13) | AGB = α × D β × CDβ1 | −7.8 | 0.054 | 0.2 | −0.012 | −0.3 |
| (14) | AGB = α × D β × Hβ1 × CDβ2 | −19.7 | 0.003 | −1.2 | 0.021 | −0.7 |
| (15) | AGB = α × (D2HCD)β | −16.6 | −0.084 | −2.6 | −0.010 | −0.9 |
| (16) | AGB = α × D β × Hβ1 × ρβ2 × CDβ3 | −24.4 | −0.047 | −1.7 | 0.017 | −1.7 |
| (17) | AGB = α × (D2HρCD)β | −12.8 | −0.083 | −2.9 | −0.075 | −6.5 |
| Model set 2b: Compound predictor variables including D, H, ρ and CV | ||||||
| (18) | AGB = α × CVβ | −71.1 | −0.084 | 8.8 | −0.234 | −16.3 |
| (19) | AGB = α × Dβ × CVβ1 | −9.3 | −0.046 | 0.2 | −0.026 | −4.2 |
| (20) | AGB = α × Dβ × Hβ1 × CVβ2 | −16.2 | 0.004 | −1.2 | −0.031 | −4.5 |
| (21) | AGB = α × (D2HCV)β | −45.7 | −0.084 | −2.2 | −0.039 | −4.2 |
| (22) | AGB = α × D β × Hβ1 × ρβ2 × CVβ3 | −11.8 | −0.047 | −1.7 | −0.026 | −3.9 |
| (23) | AGB = α × (D2HρCV)β | −44.2 | −0.084 | −2.4 | −0.039 | −10.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huynh, T.; Lewis, T.; Applegate, G.; Pachas, A.N.A.; Lee, D.J. Allometric Equations to Estimate Aboveground Biomass in Spotted Gum (Corymbia citriodora Subspecies variegata) Plantations in Queensland. Forests 2022, 13, 486. https://doi.org/10.3390/f13030486
Huynh T, Lewis T, Applegate G, Pachas ANA, Lee DJ. Allometric Equations to Estimate Aboveground Biomass in Spotted Gum (Corymbia citriodora Subspecies variegata) Plantations in Queensland. Forests. 2022; 13(3):486. https://doi.org/10.3390/f13030486
Chicago/Turabian StyleHuynh, Trinh, Tom Lewis, Grahame Applegate, Anibal Nahuel A. Pachas, and David J. Lee. 2022. "Allometric Equations to Estimate Aboveground Biomass in Spotted Gum (Corymbia citriodora Subspecies variegata) Plantations in Queensland" Forests 13, no. 3: 486. https://doi.org/10.3390/f13030486
APA StyleHuynh, T., Lewis, T., Applegate, G., Pachas, A. N. A., & Lee, D. J. (2022). Allometric Equations to Estimate Aboveground Biomass in Spotted Gum (Corymbia citriodora Subspecies variegata) Plantations in Queensland. Forests, 13(3), 486. https://doi.org/10.3390/f13030486







