Spectral Pre-Processing and Multivariate Calibration Methods for the Prediction of Wood Density in Chinese White Poplar by Visible and Near Infrared Spectroscopy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Samples Preparation
2.2. Vis-NIR Spectra Collection and Density Measurement
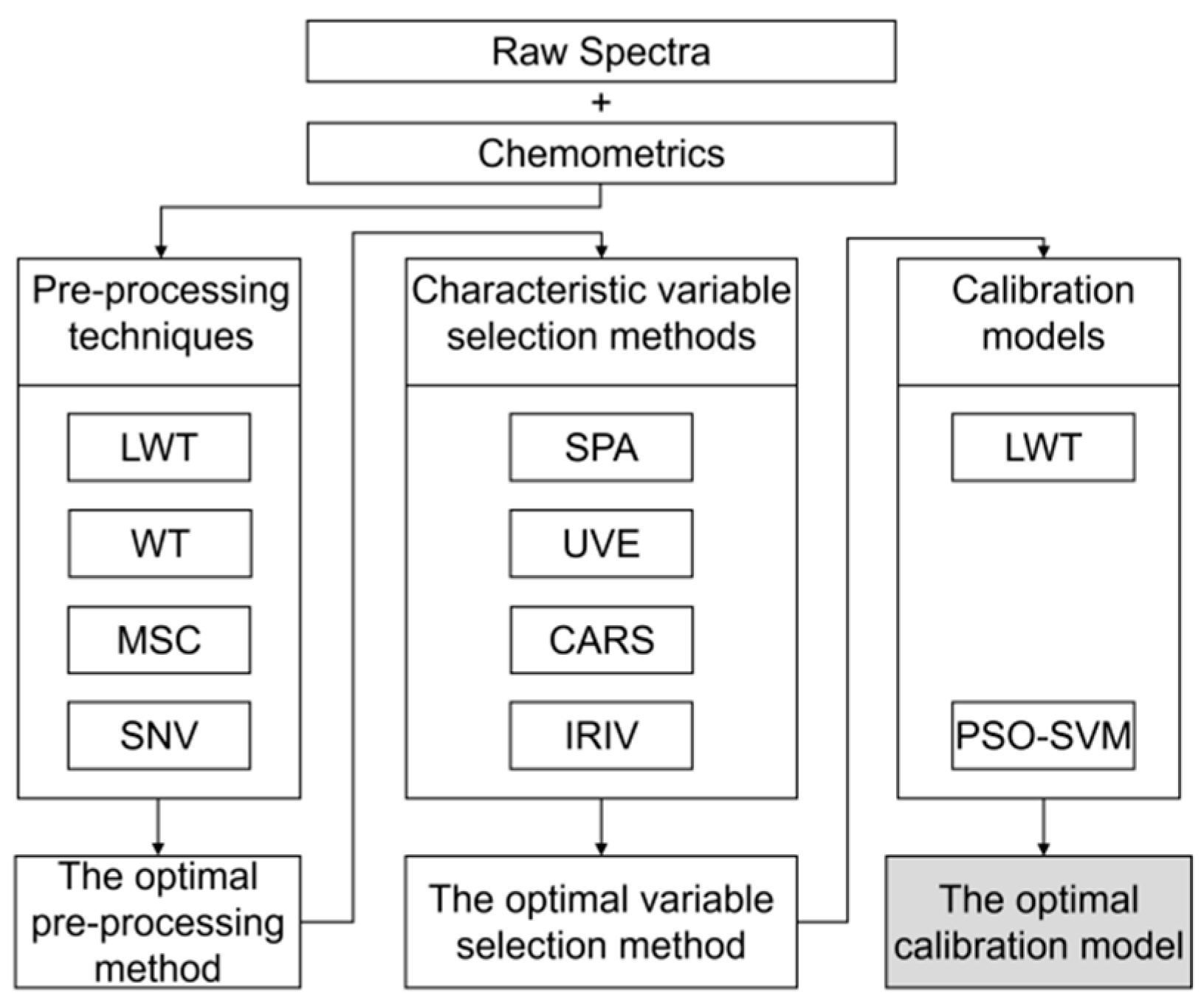
2.3. Spectral Data Analysis
2.3.1. Pre-Processing
2.3.2. Characteristic Wavelengths Selection
2.3.3. Establishment of Vis-NIR Calibration Models
2.4. Overview of Optimization of the Wood Density Model
3. Results
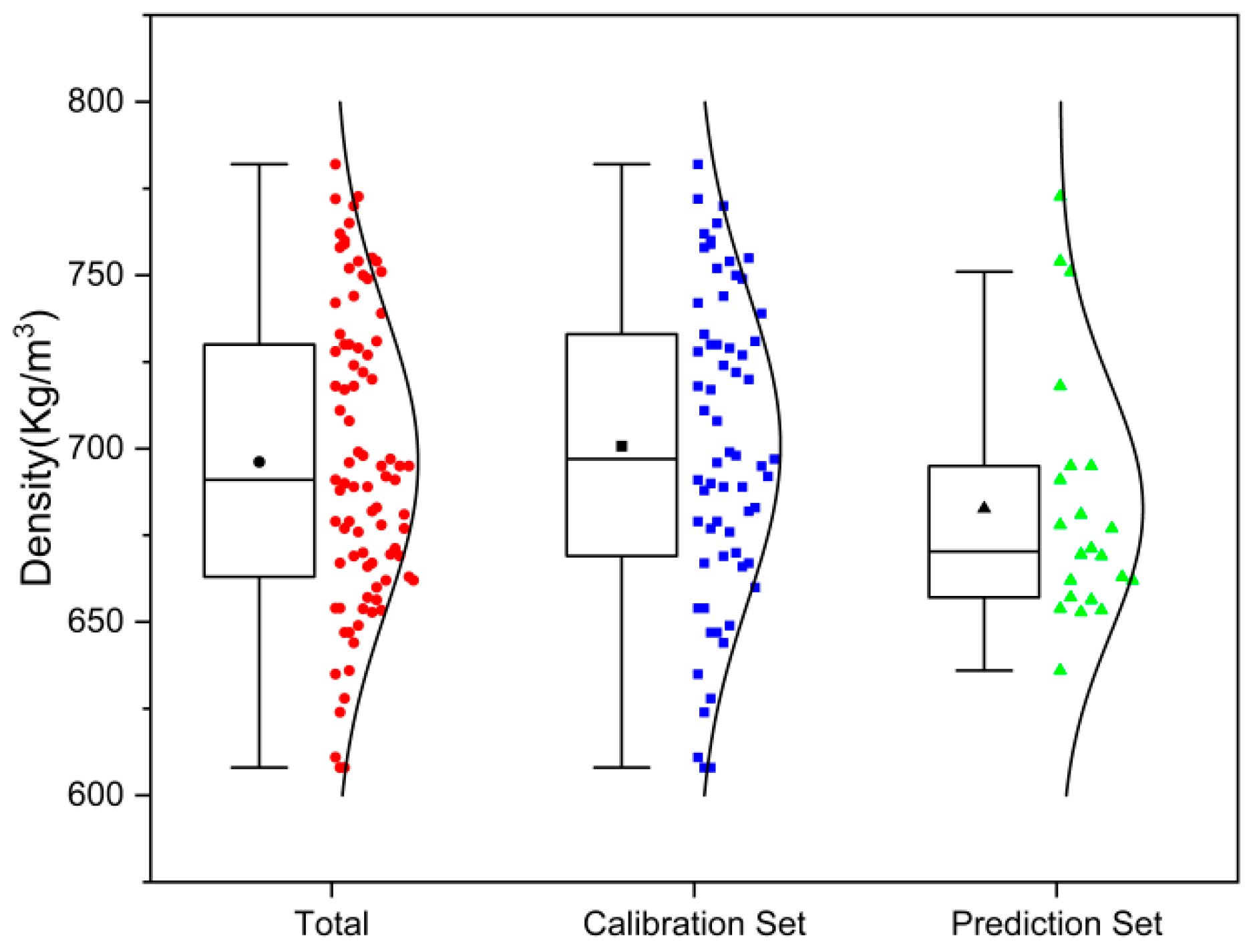
3.1. Descriptive Statistics of Wood Density
3.2. Comparison of Various Pre-Processing Methods
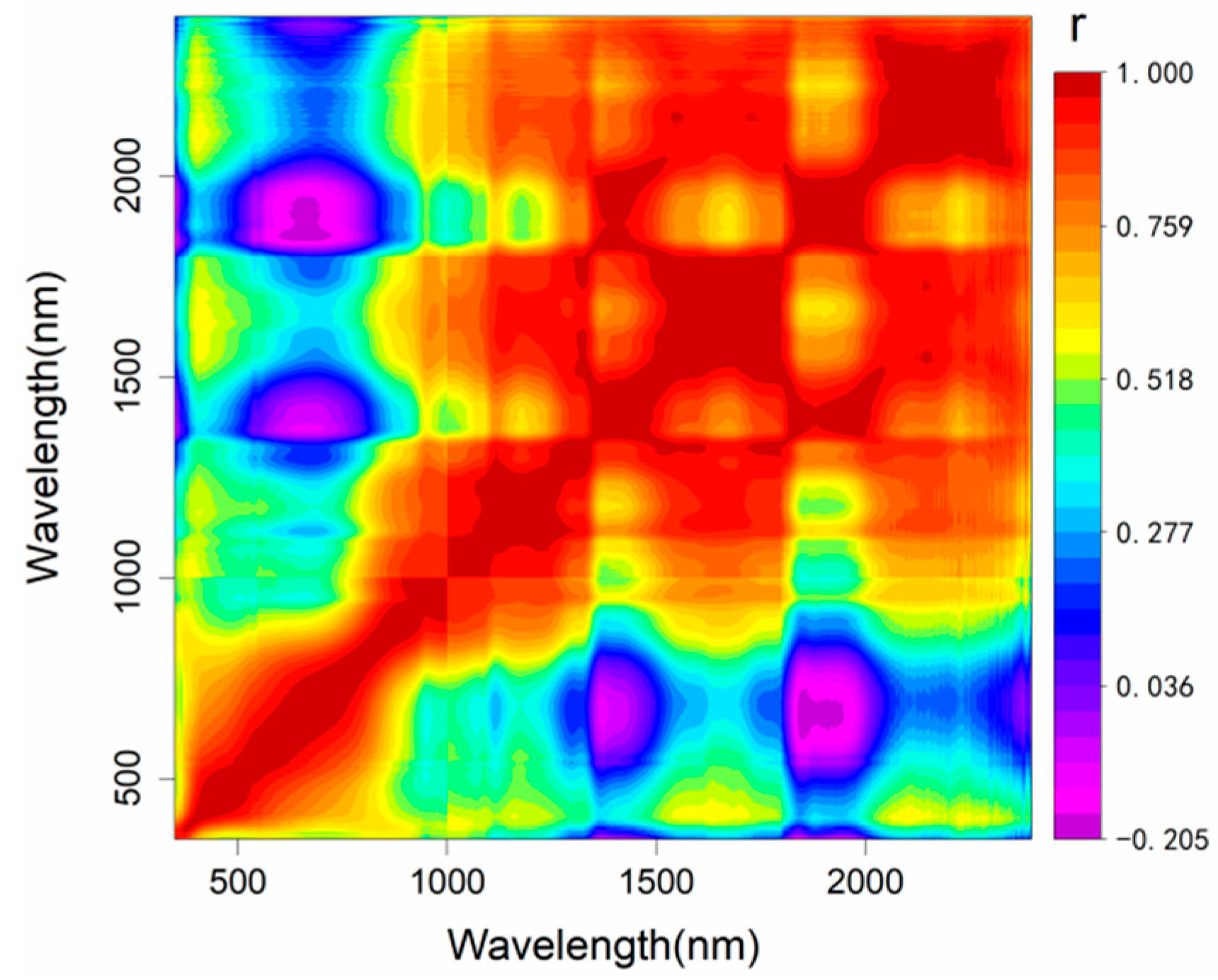
3.3. Characteristic Wavelengths for Predicting Density
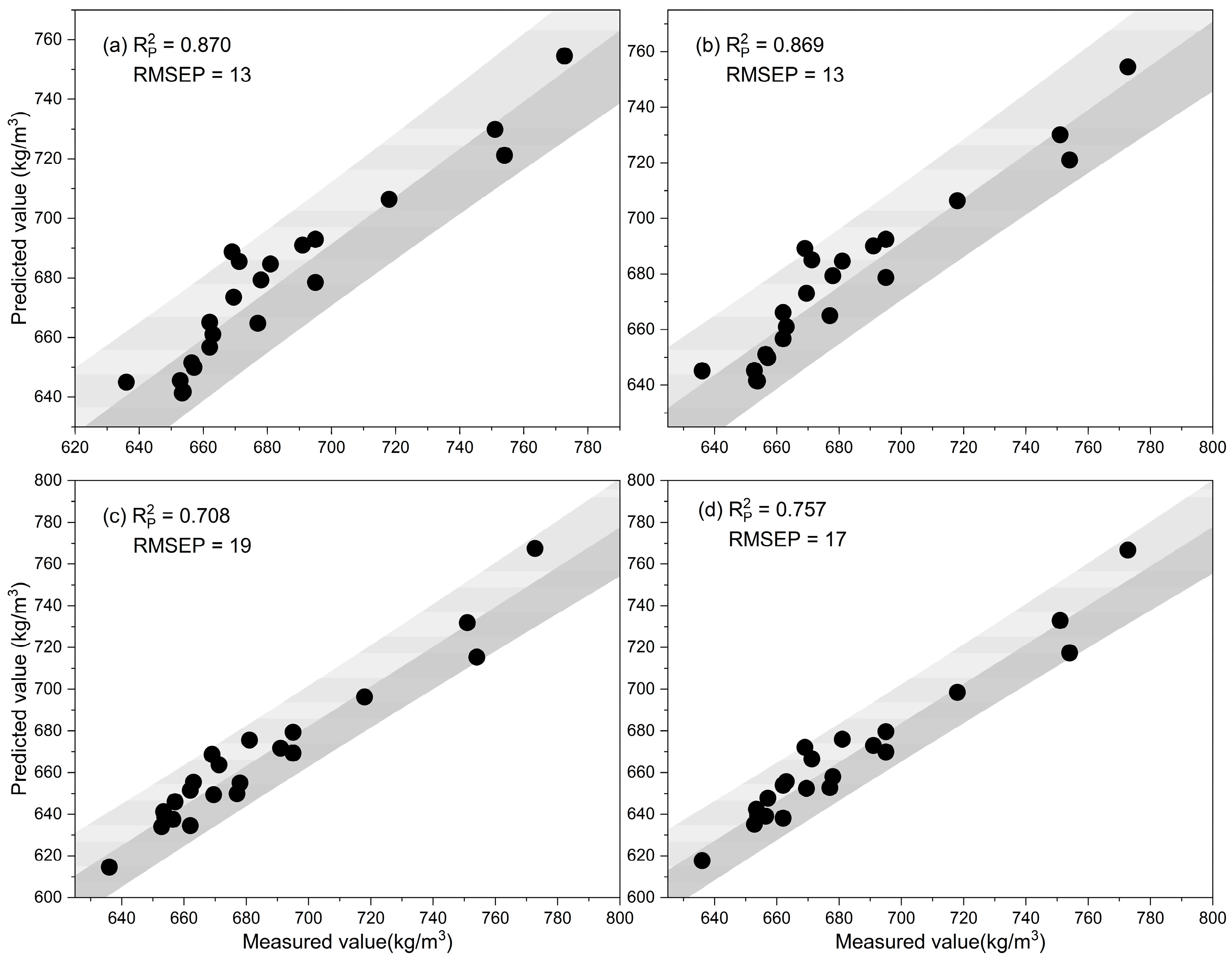
3.4. Prediction Accuracy of Non-Linear Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Filková, V.; Kolár, T.; Rybníček, M.; Gryc, V.; Vavrčík, H.; Jurčík, J. Historical utilization of wood in southeastern Moravia (Czech Republic). iForest 2015, 8, 101–107. [Google Scholar] [CrossRef] [Green Version]
- Fang, S.Z.; Liu, Y.; Yue, J.; Tian, Y.; Xu, X.Z. Assessments of growth performance, crown structure, stem form and wood property of introduced poplar clones: Results from a long-term field experiment at a lowland site. For. Ecol. Manag. 2021, 479, 118586. [Google Scholar] [CrossRef]
- Waldron, K.; Auty, D.; Tong, T.; Ward, C.; Pothier, D.; Torquato, L.P.; Achim, A. Fire as a driver of wood mechanical traits in the boreal forest. For. Ecol. Manag. 2020, 476, 118460. [Google Scholar] [CrossRef]
- Schimleck, L.; Antony, F.; Mora, C.; Dahlen, J. Comparison of whole-tree wood property maps for 13- and 22-year-old loblolly pine. Forests 2018, 9, 287. [Google Scholar] [CrossRef] [Green Version]
- Henry, M.; Besnard, A.; Asante, W.A.; Eshun, J.; Adu-Bredu, S.; Valentini, R.; Bernoux, M.; Saint-André, L. Wood density, phytomass variations within and among trees, and allometric equations in a tropical rainforest of Africa. For. Ecol. Manag. 2010, 260, 1375–1388. [Google Scholar] [CrossRef]
- Schimleck, L.; Dahlen, J.; Apiolaza, L.A.; Downes, G.; Emms, G.; Evans, R.; Moore, J.; Pâques, L.; Bulcke, J.V.; Wang, X.P. Non-destructive evaluation techniques and what they tell us about wood property variation. Forests 2019, 10, 728. [Google Scholar] [CrossRef] [Green Version]
- Tsuchikawa, S.; Kobori, H. A review of recent application of near infrared spectroscopy to wood science and technology. J. Wood Sci. 2015, 61, 213–220. [Google Scholar] [CrossRef] [Green Version]
- Sergent, A.S.; Segura, V.; Charpentier, J.P.; Dalla-Salda, G.; Fernández, M.E.; Rozenberg, P.; Martinez-Meier, A. Assessment of resistance to xylem cavitation in cordilleran cypress using near-infrared spectroscopy. For. Ecol. Manag. 2020, 462, 117943. [Google Scholar] [CrossRef]
- Paul, A.; Harrington, P.B. Chemometric applications in metabolomic studies using chromatography-mass spectrometry. TrAC Trends Anal. Chem. 2021, 135, 116165. [Google Scholar] [CrossRef]
- Chu, X.L. Molecular Spectroscopy Analytical Technology Combined with Chemometrics and Its Applications; Chemical Industry Press: Beijing, China, 2011; pp. 231–249. [Google Scholar]
- Song, X.; Huang, Y.; Tian, K.; Min, S. Near infrared spectral variable optimization by final complexity adapted models combined with uninformative variables elimination-A validation study. Optik 2019, 203, 164019. [Google Scholar] [CrossRef]
- Lu, B.; Liu, N.H.; Li, H.L.; Yang, K.F.; Hu, C.; Wang, X.F.; Li, Z.X.; Shen, Z.X.; Tang, X.Y. Quantitative determination and characteristic wavelength selection of available nitrogen in coco-peat by NIR spectroscopy. Soil Tillage Res. 2019, 191, 266–274. [Google Scholar] [CrossRef]
- Xu, S.; Zhao, Y.; Wang, M.; Shi, X. Determination of rice root density from Vis–NIR spectroscopy by support vector machine regression and spectral variable selection techniques. Catena 2017, 157, 12–23. [Google Scholar] [CrossRef]
- Hu, F.; Zhou, M.; Yan, P.; Li, D.; Lai, W.; Zhu, S.; Wang, Y. Selection of characteristic wavelengths using SPA for laser induced fluorescence spectroscopy of mine water inrush. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2019, 219, 367–374. [Google Scholar] [CrossRef]
- Virginia dos Santos Pereira, E.; Douglas de Sousa Fernandes, D.; Ugulino de Araújo, M.C.; Gonçalves Dias Diniz, P.H.; Sucupira Maciel, M.I. Simultaneous determination of goat milk adulteration with cow milk and their fat and protein contents using NIR spectroscopy and PLS algorithms. LWT 2020, 127, 109427. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, M.; Wei, G.; Hu, R.; Luo, Z.; Li, G. Improved PLS regression based on SVM classification for rapid analysis of coal properties by near-infrared reflectance spectroscopy. Sens. Actuators B Chem. 2014, 193, 723–729. [Google Scholar] [CrossRef]
- Chen, J.; Li, G. Prediction of moisture content of wood using modified random frog and Vis-NIR hyperspectral imaging. Infrared Phys. Technol. 2020, 105, 103225. [Google Scholar] [CrossRef]
- Liang, L.; Wei, L.; Fang, G.; Xu, F.; Deng, Y.; Shen, K.; Tian, Q.W.; Wu, T.; Zhu, B. Prediction of holocellulose and lignin content of pulp wood feedstock using near infrared spectroscopy and variable selection. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2019, 225, 117515. [Google Scholar] [CrossRef]
- Chang, C.W.; Laird, D.A.; Mausbach, M.J.; Hurburg, C.R.J. Near-infrared reflectance spectroscopy-principal component regression analysis of soil properties. Soil Sci. Soc. Am. J. 2001, 65, 480–490. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.N. Preliminary Investigation of Wood Identification by Near Infrared Spectroscopy. Master’s Thesis, Chinese Academy of Forestry, Beijing, China, 2014. [Google Scholar]
- Rinnan, Å.; Berg, F.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. TrAC Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Geladi, P.; MacDougall, D.; Martens, H. Linearization and scatter-correction for near-infrared reflectance spectra of meat. Appl. Spectrosc. 1985, 39, 491–500. [Google Scholar] [CrossRef]
- Titterington, D.M. Statistical challenges of high-dimensional data. Phil. Trans. R. Soc. A 2009, 367, 4235–4470. [Google Scholar]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Williams, P.C.; Norris, K. Implementation of Near-Infrared Technology. In Near-Infrared Technology in the Agricultural and Food Industries; AACC: St. Paul, MN, USA, 2001; pp. 145–171. [Google Scholar]
- Zhang, X.C.; Wu, J.Z.; Xu, Y. Near Infrared Spectroscopy Technique and Applications in Modern Agriculture; Publishing House of Electronics Industry: Beijing, China, 2012; pp. 48–49. [Google Scholar]
- Huang, H.P.; Hu, X.J.; Tian, J.P.; Jiang, X.N.; Sun, T.; Luo, H.B.; Huang, D. Rapid and nondestructive prediction of amylose and amylopectin contents in sorghum based on hyperspectral imaging. Food Chem. 2021, 359, 129954. [Google Scholar] [CrossRef]
- Shenk, J.S.; Workman, J.J.; Westerhaus, M.O. Handbook of Near-Infrared Analysis; Burns, D.A., Ciurczak, E.W., Eds.; Marcel Dekker Inc.: New York, NY, USA, 2001; pp. 7–21. [Google Scholar]
- Watanabe, A.; Morita, S.; Ozaki, Y. Temperature-dependent structural changes in hydrogen bonds in microcrystalline cellulose studied by infrared and near-infrared spectroscopy with perturbation-correlation moving-window two-dimensional correlation analysis. Appl. Spectrosc. 2006, 60, 611–618. [Google Scholar] [CrossRef]
- Li, Y.; Via, B.; Li, Y.X. Lifting wavelet transform for Vis-NIR spectral data optimization to predict wood density. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 240, 118566. [Google Scholar] [CrossRef] [PubMed]
- Schwanninger, M.; Hinterstoisser, B.; Gradinger, C.; Messner, K.; Fackler, K. Examination of spruce wood biodegraded by Ceriporiopsis subvermispora using near and mid infrared spectroscopy. J. Near Infrared Spectrosc. 2004, 12, 397. [Google Scholar] [CrossRef]
- Workman, J.; Weyer, L. Practical Guide to Interpretive Near-Infrared Spectroscopy, 1st ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Hein, P.R.G.; Campos, A.C.M.; Mendes, R.F.; Mendes, L.M.; Chaix, G. Estimation of physical and mechanical properties of agro-based particleboards by near infrared spectroscopy. Eur. J. Wood Prod. 2011, 69, 431. [Google Scholar] [CrossRef] [Green Version]


| Pre-Processing Methods | LVs Number | Calibration Set | Cross-Validation | ||
|---|---|---|---|---|---|
| R2 | RMSE (Kg/m3) | R2 | RMSE (Kg/m3) | ||
| Raw spectra | 3 | 0.749 | 22 | 0.715 | 24 |
| LWT | 6 | 0.809 | 19 | 0.720 | 24 |
| WT | 3 | 0.748 | 22 | 0.721 | 24 |
| MSC | 4 | 0.646 | 26 | 0.522 | 32 |
| SNV | 4 | 0.654 | 26 | 0.540 | 31 |
| Methods | Variable Numbers | Percentage Decrease | Calibration Set | Cross-Validation Set | ||
|---|---|---|---|---|---|---|
| R2 | RMSE (Kg/m3) | R2 | RMSE (Kg/m3) | |||
| Full spectra | 2048 | 0 | 0.749 | 22 | 0.715 | 24 |
| SPA | 64 | 96.88% | 0.765 | 22 | 0.682 | 26 |
| UVE | 410 | 79.98% | 0.679 | 26 | 0.667 | 26 |
| CARS | 23 | 98.88% | 0.783 | 21 | 0.767 | 22 |
| IRIV | 16 | 99.22% | 0.755 | 22 | 0.697 | 25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, G.; Guo, G.; Li, Y.; Via, B.K.; Pei, Z. Spectral Pre-Processing and Multivariate Calibration Methods for the Prediction of Wood Density in Chinese White Poplar by Visible and Near Infrared Spectroscopy. Forests 2022, 13, 62. https://doi.org/10.3390/f13010062
Li Y, Wang G, Guo G, Li Y, Via BK, Pei Z. Spectral Pre-Processing and Multivariate Calibration Methods for the Prediction of Wood Density in Chinese White Poplar by Visible and Near Infrared Spectroscopy. Forests. 2022; 13(1):62. https://doi.org/10.3390/f13010062
Chicago/Turabian StyleLi, Ying, Guozhong Wang, Gensheng Guo, Yaoxiang Li, Brian K. Via, and Zhiyong Pei. 2022. "Spectral Pre-Processing and Multivariate Calibration Methods for the Prediction of Wood Density in Chinese White Poplar by Visible and Near Infrared Spectroscopy" Forests 13, no. 1: 62. https://doi.org/10.3390/f13010062
APA StyleLi, Y., Wang, G., Guo, G., Li, Y., Via, B. K., & Pei, Z. (2022). Spectral Pre-Processing and Multivariate Calibration Methods for the Prediction of Wood Density in Chinese White Poplar by Visible and Near Infrared Spectroscopy. Forests, 13(1), 62. https://doi.org/10.3390/f13010062





