Dynamic Top Height Growth Models for Eight Native Tree Species in a Cool-Temperate Region in Northeast China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Ecological Characteristics of the Tree Species
2.2. Characteristics of the Study Site
2.3. Characteristics of the Sample Trees for Height Growth Analysis
2.4. Field and Laboratory Measurements
2.5. Statistical Analysis Methods
2.5.1. Model Development
2.5.2. Model Calibration and Evaluation
- (1)
- Estimation of the global parameters
- (2)
- Estimation of the site-specific parameter using the estimates of the global parameters in step (1)
- (3)
- Re-estimation of the global parameters using the site-specific parameter estimates in step (2)
- (4)
- Iteration of the steps (2) and (3) until the residual sums of squares from successive iterations stabilizes.
3. Results
4. Discussion
4.1. Development of Top Height Growth Models
4.2. Limitations of the Developed Top Height Growth Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Skovsgaard, J.P.; Vanclay, J.K. Forest site productivity: A review of the evolution of dendrometric concepts for even-aged stands. Forestry 2008, 81, 12–31. [Google Scholar] [CrossRef] [Green Version]
- Pretzsch, H. Grundlagen der Waldwachstumsforschung; Springer: Berlin/Heidelberg, Germany, 2017; p. 664. ISBN 978-3-662-58155-1. [Google Scholar] [CrossRef]
- Pretzsch, H. Modellierung des Waldwachstums; Parey: Singhofen, Germany, 2003; p. 341. ISBN 978-3-8001-4555-3. [Google Scholar]
- Dai, L.; Wang, Y.; Su, D.; Zhou, L.; Yu, D.; Lewis, B.J.; Qi, L. Major forest types and the evolution of sustainable forestry in China. Environ. Manag. 2011, 48, 1066–1078. [Google Scholar] [CrossRef]
- Xu, H.; Sun, Y.; Wang, X.; Fu, Y.; Dong, Y.; Li, Y. Nonlinear Mixed-Effects (NLME) Diameter Growth Models for Individual China-Fir (Cunnighamia lanceolata) Trees in Southeast China. PLoS ONE 2014, 9, e104012. [Google Scholar] [CrossRef]
- Bachmann, P. Skript Waldwachstum. Professur für Forsteinrichtung und Waldwachstum ETH Zürich. 2008. Available online: https://www.wsl.ch/forest/waldman/vorlesung/ww_tk62.ehtml (accessed on 20 January 2021).
- Assmann, E.; Franz, F. Vorläufige Fichtenertragstafeln für Bayern. In Hilfstafeln für die Forsteinrichtung, Auflage 1990; Institut für Ertragskunde der Forstlichen Forschungsanstalt: München, Germany, 1963; pp. 52–63. [Google Scholar]
- Kindermann, G. Methoden zur Erstellung von Oberhöhenfächern. In Tagungsbericht 2015 der Sektion Ertragskunde (DVFFA), Deutscher Verband Forstlicher Forschungsanstalten, Kohnle, U.; Klädtke, J., Ed.; Sektion Ertragskunde der Forstlichen Versuchs- und Forschungsanstalt Baden-Württemberg: Freiburg, Germany, 2015; pp. 143–152. [Google Scholar]
- Wiedemann, E. Ertragstafeln der Wichtigen Holzarten bei Verschiedener Durchforstung Sowie Einiger Mischbestandsformen; M. & H. Schaper: Hannover, Germany, 1949; 100p. [Google Scholar]
- von Gadow, K. Waldstruktur und Wachstum; Universitätsverlag: Göttingen, Germany, 2003; p. 254. ISBN 3-930457-32-6. [Google Scholar]
- Sánchez-González, M.; Stiti, B.; Chaar, H.; Cañellas, I. Dynamic dominant height growth model for Spanish and Tunisian cork oak (Quercus suber L.) forest. For. Syst. 2010, 19, 285–298. [Google Scholar] [CrossRef]
- Krumland, B.; Eng, H. Site index systems for major young-growth forest and woodland species in northern California. California Department of Forestry and Fire Protection, Sacramento, CA. Calif. For. Rep. 2005, 4, 1–219. [Google Scholar]
- Cieszewski, C.J.; Strub, M.; Zasada, M. New dynamic site equation that fits best the Schwappach data for Scots pine (Pinus sylvestris L.) in Central Europe. For. Ecol. Manag. 2007, 243, 83–93. [Google Scholar] [CrossRef]
- Bailey, R.L.; Clutter, J.L. Base-age invariant polymorphic site curves. For. Sci. 1974, 20, 155–159. [Google Scholar] [CrossRef]
- Cieszewski, C.J.; Bailey, R.L. generalized algebraic difference approach: Theory Based Derivation of Dynamic Site Equations with Polymorphism and Variable Asymptotes. For. Sci. 2000, 46, 116–126. [Google Scholar]
- Manso, R.; McLean, J.P.; Arcangeli, C.; Matthews, R. Dynamic top height models for several major forest tree species in Great Britain. Forestry 2021, 94, 181–192. [Google Scholar] [CrossRef]
- Sharma, R.P.; Brunner, A.; Eid, T.; Oyen, B.-H. Modelling dominant height growth from national forest inventory individual tree data with short time series and large age errors. For. Ecol. Manag. 2011, 262, 2162–2175. [Google Scholar] [CrossRef]
- Ercanli, I.; Kahriman, A.; Yavuz, H. Dynamic base-age invariant site index models based on generalized algebraic difference approach for mixed Scots pine (Pinus sylvestris L.) and Oriental beech (Fagus orientalis Lipsky) stands. Turk J. Agric. For. 2014, 38, 134–147. [Google Scholar] [CrossRef]
- Akbas, U.; Senyurt, M. Site quality estimations based on the generalized algebraic difference approach: A case study in Cankiri forests. Rev. Arvore 2018, 42, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Cieszewski, C.J. Three methods of deriving advanced dynamic site equations demonstrated on inland Douglas-fir site curves. Can. J. For. Res. 2001, 31, 165–173. [Google Scholar] [CrossRef]
- Cieszewski, C.J. Comparing Fixed- and Variable-Base-Age Site Equations Having Single Versus Multiple Asymptotes. For. Sci. 2002, 48, 7–23. [Google Scholar]
- Nord-Larsen, T. Developing dynamic site index curves for European beech (Fagus sylvatica L.) in Denmark. For. Sci. 2006, 52, 173–181. [Google Scholar]
- Farjon, A. Pinus tabuliformis. In The IUCN Red List of Threatened Species; IUCN Red List: Gland, Switzerland, 2013; p. e.T42419A2978916. [Google Scholar] [CrossRef]
- Liu, B.; Bussmann, R.W. Pinus sylvestris L. var. mongolica Litv. Pinaceae. In Ethnobotany of the Mountain Regions of Central Asia and Altai; Batsatsashvili, K., Kikvidze, Z., Bussmann, R., Ethnobotany of Mountain Regions, Eds.; Springer: Cham, Germany, 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Farjon, A. Larix gmelinii var. Principis-rupprechtii. In The IUCN Red List of Threatened Species; IUCN Red List: Gland, Switzerland, 2013; p. e.T191616A1991224. [Google Scholar] [CrossRef]
- Carter, G.; Farjon, A. Picea asperata. In The IUCN Red List of Threatened Species; IUCN Red List: Gland, Switzerland, 2013; p. e.T42320A2972242. [Google Scholar] [CrossRef]
- Barstow, M. Quercus mongolica. In The IUCN Red List of Threatened Species; IUCN Red List: Gland, Switzerland, 2018; p. e.T194200A2303793. [Google Scholar] [CrossRef]
- Gradel, A.; Haensch, C.; Batsaikhan, G.; Batdorj, D.; Ochirragchaa, N.; Günther, B. Response of white birch (Betula platyphylla Sukaczev) to temperature and precipitation in the mountain forest steppe and taiga of northern Mongolia. Dendrochronologia 2017, 41, 24–33. [Google Scholar] [CrossRef]
- Hua, H. Betula dahurica Pal. In Flora of China; Science Press: Beijing, China, 2002; Volume 4, p. 312. [Google Scholar]
- Hou, Z.; Li, A.; Zhang, J. Genetic architecture, demographic history, and genomic differentiation of Populus davidiana revealed by whole-genome resequencing. Evol. Appl. 2020, 13, 2582–2596. [Google Scholar] [CrossRef]
- Ni, J.; Zhang, X.-S.; Scurlock, J.M.O. Synthesis and analysis of biomass and net primary productivity in Chinese forests. Ann. For. Sci. 2001, 58, 351–384. [Google Scholar] [CrossRef]
- Hu, X.; (Chinese Academy of Forestry, Beijing, China). Personal communication, 2014.
- Kraft, G. Beiträge zur Lehre von den Durchforstungen, Schlagstellungen und Lichtungshieben; Klindworth: Hannover, Germany, 1884; p. 147. [Google Scholar]
- West, P.W. Tree and Forest Measurement, 3rd ed.; Springer International Publishing: Basel, Switzerland, 2015; p. 214. [Google Scholar]
- Van Laar, A.; Akca, A. Forest Mensuration; Springer: Heidelberg, Germany, 2007; p. 390. ISBN 13-978-1-4020-5991-9. [Google Scholar]
- Kramer, H.; Akca, A. Leitfaden zur Waldmesslehre; J.D. Sauerländer’s Verlag: Frankfurt, Germany, 2008; p. 226. ISBN 978-3-7939-0880-7. [Google Scholar]
- Roloff, A. Kronenentwicklung und Vitalitätsbeurteilung Ausgewählter Baumarten der Gemäßigten Breiten; J.D. Sauerländer’s Verlag: Frankfurt, Germany, 1994; p. 258. ISBN 978-3793950936. [Google Scholar]
- Huixun, Z.; Chuankuan, W.; Binhui, L. Growth of Mongolian Oak. J. Northeast For. Univ. 1994, 5, 10–17. [Google Scholar]
- WinDendroTM. Manual for Tree-Ring Analysis; Instruments Regent Inc.: Quebec, CA, USA, 2014; Available online: http://www.regentinstruments.com (accessed on 3 September 2020).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- RStudio Team. RStudio: Integrated Development Environment for R; RStudio, Inc.: Boston, MA, USA, 2019. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 2nd ed.; Monash University: Melbourne, Australia, 2018. [Google Scholar]
- Available online: https://cran.r-project.org/web/packages/nlmrt/nlmrt.pdf (accessed on 28 June 2021).
- Goelz, J.C.G.; Burk, T.E. Development of a well-behaved site index equation: Jack pine in north central Ontario. Can. J. For. Res. 1992, 22, 776–784. [Google Scholar] [CrossRef]
- Richards, F.J. A Flexible Growth Function for Empirical Use. J. Exp. Bot. 1959, 10, 290–300. [Google Scholar] [CrossRef]
- Hossfeld, J.W. Mathematik für Forstmänner, Ökonomen und Cameralisten. Gotha 1822, 4, 310. [Google Scholar]
- Anta, M.B.; Dorado, F.C.; Dieguez-Aranda, U.; Gonzalez, J.G.A.; Parresol, B.R.; Soalleiro, R.R. Development of a basal area growth system for maritime pine in northwestern Spain using the generalized algebraic difference approach. Can. J. For. Res. 2006, 36, 1461–1474. [Google Scholar] [CrossRef] [Green Version]
- Sloboda, B. Zur Darstellung von Wachstumsprozessen mit Hilfe von Differentialgleichungen erster Ordnung. In Mitteilungen der Forstlichen Versuchs- und Forschungsanstalt Baden-Württemberg; Forstliche Versuchs- und Forschungsanstalt Baden-Württemberg: Freiburg, Germany, 1971; Volume 32, p. 109. [Google Scholar]
- Anta, M.B.; Dieguez-Aranda, U. Site quality of pedunculate oak (Quercus robur L.) stands in Galicia (northwest Spain). Eur. J. For. Res. 2005, 124, 19–28. [Google Scholar] [CrossRef]
- Korf, V. Pøíspìvek k matematické definici vzrùstového zákona lesních porostù. Lesnická Práce 1939, 18, 339–356. [Google Scholar]
- Liziniewicz, M.; Nilsson, U.; Agestam, E.; Ekö, P.M.; Elfving, B. A site index model for lodgepole pine (Pinus contorta Dougl. var. latifolia) in northern Sweden. Scand. J. For. Res. 2016, 31, 583–591. [Google Scholar] [CrossRef]
- Cieszewski, C.J. Developing a well-behaved dynamic site equation using a modified Hossfeld IV function Y−3 = (ax(m))/(c + x(m − 1)), a simplified mixed-model and scant subalpine fir data. For. Sci. 2003, 494, 539–554. [Google Scholar]
- Zeide, B. Analysis of growth equations. For. Sci. 1993, 39, 594–616. [Google Scholar] [CrossRef]
- Dieguez-Aranda, U.; Burkhart, H.E.; Rodriguez-Soalleiro, R. Modeling dominant height growth of radiata pine (Pinus radiata D. Don) plantations in north-western Spain. For. Ecol. Manag. 2005, 215, 271–284. [Google Scholar] [CrossRef]
- Hägglund, B.; Lundmark, J.E. Site estimation by means of site properties: Scots pine and Norway spruce in Sweden. Stud. For. Suec. 1977, 138, 1–38. [Google Scholar]
- Spiecker, H. Overview of recent growth trends in European forests. Water Air Soil Poll. 1999, 116, 33–46. [Google Scholar] [CrossRef]
- Spiecker, H.; Mielikäinen, K.; Köhl, M.; Skovsgaard, J.P. Growth Trends in European Forests; Springer: Berlin/Heidelberg, Germany, 1996; p. 372. ISBN 978-3-642-61178-0. [Google Scholar] [CrossRef]
- Körner, M. Erfassung und Modellierung des Wachstums der Karibischen Kiefer (Pinus caribaea var. hondurensis) in der Dominikanischen Republik. In Tagungsbericht 2013 der Sektion Ertragskunde (DVFFA), Deutscher Verband Forstlicher Forschungsanstalten; Kohnle, U., Klädtke, J., Eds.; Sektion Ertragskunde der Forstlichen Versuchs- und Forschungsanstalt Baden-Württemberg: Freiburg, Germany, 2013; pp. 146–153. [Google Scholar]
- Carmean, W.H. Site Index Curves For Black, White, Scarlet, and Chestnut Oaks in The Central States. North Central Forest Experiment Station, U.S. Department of Agriculture. (USDA) For. Serv. Res. Paper NC 1971, 62, 1–8. [Google Scholar]
- Méndez, M.G.; Cobos, F.C.; Barraza, G.Q.; Larreta, B.V.; Luna, J.A.N. Dominant height growth model for Pinus pseudostrobus Lindl. in Guerrero state. Rev. Mex. De Cienc. For. 2016, 7, 7–20. [Google Scholar]
- Mann, S. Forest Protection and Sustainable Forest Management in Germany and the P.R. China—A Comparative Assessment; Federal Agency for Nature Conservation: Bonn, Germany, 2012; p. 120. [Google Scholar]
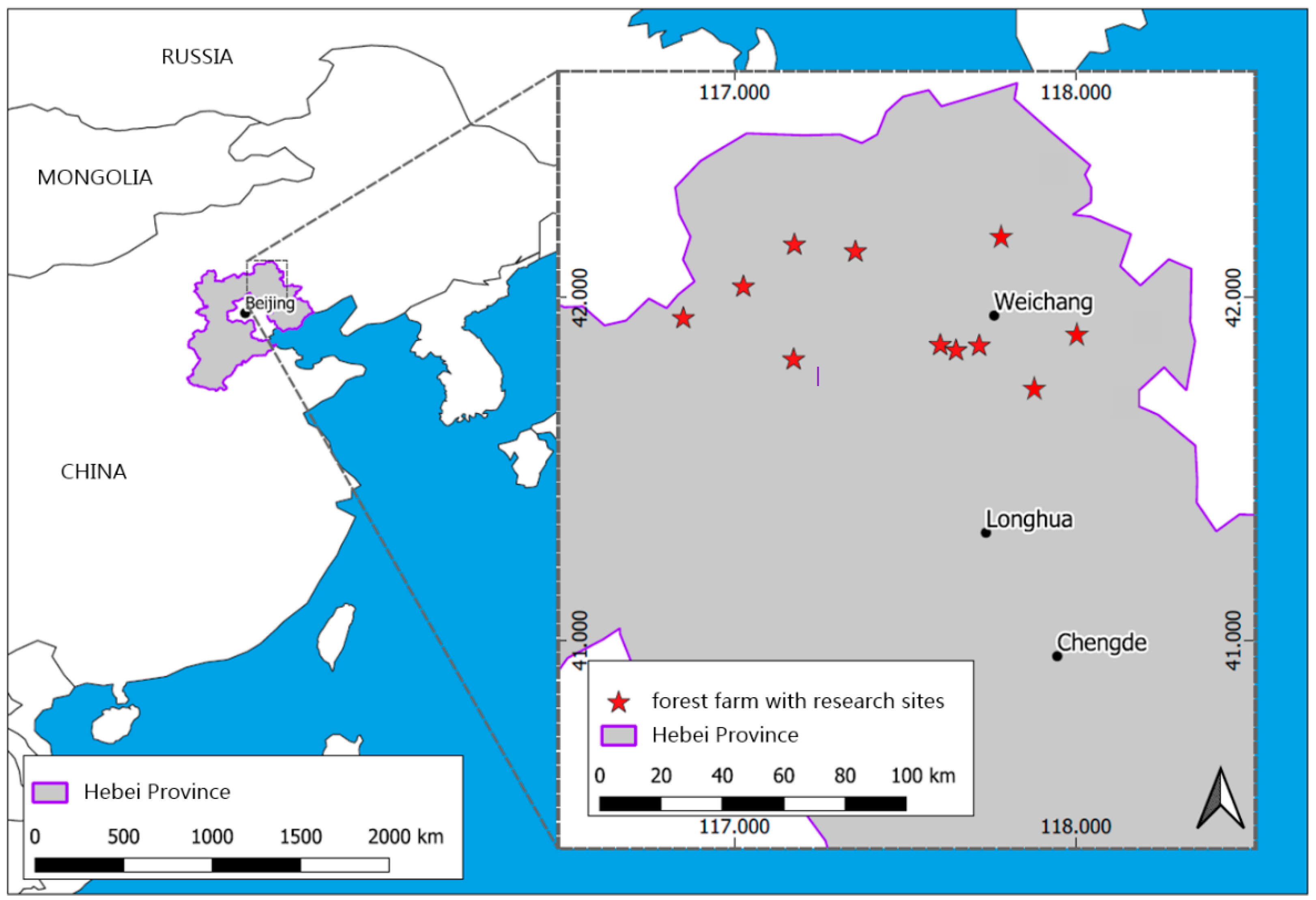
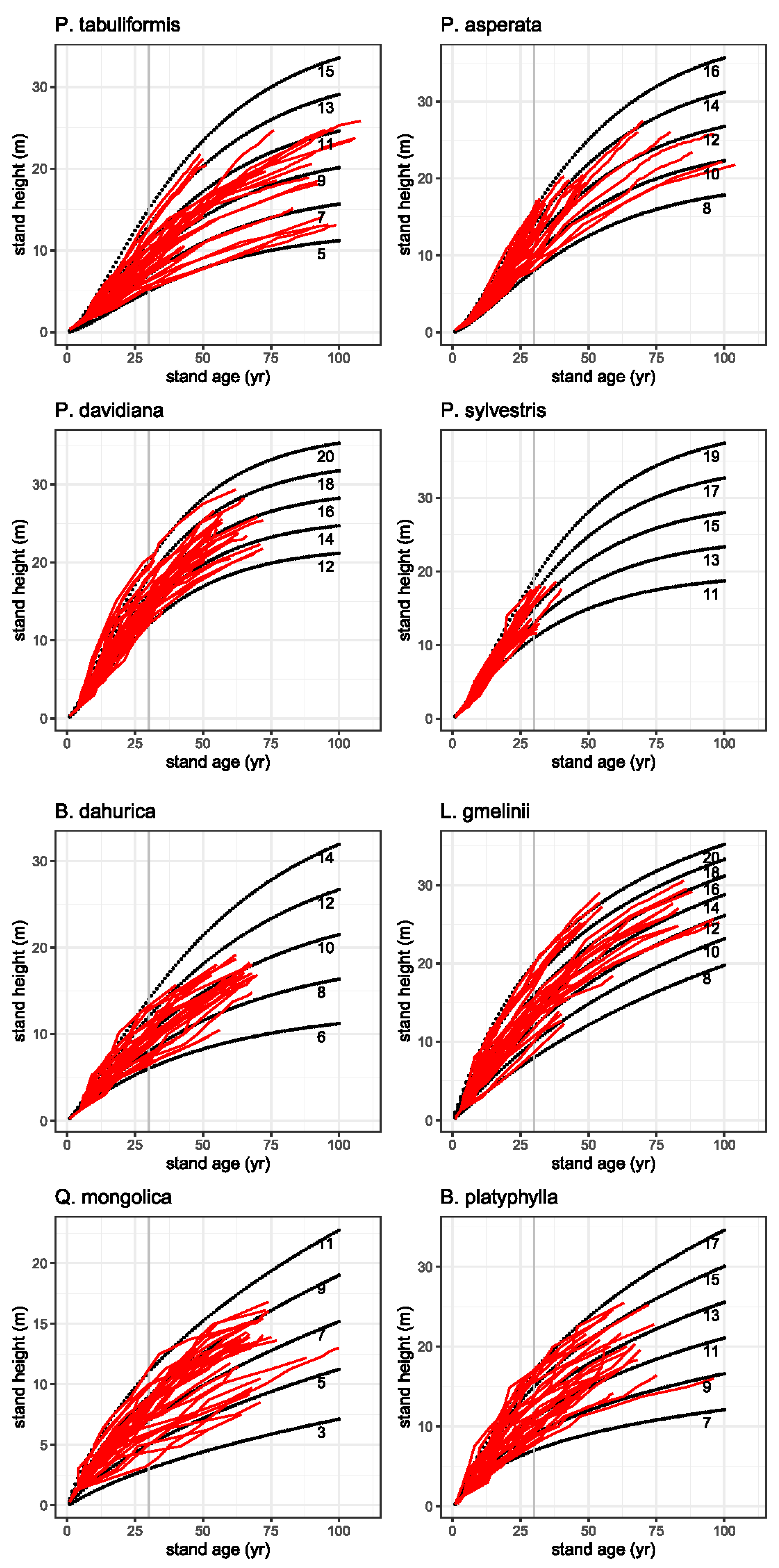
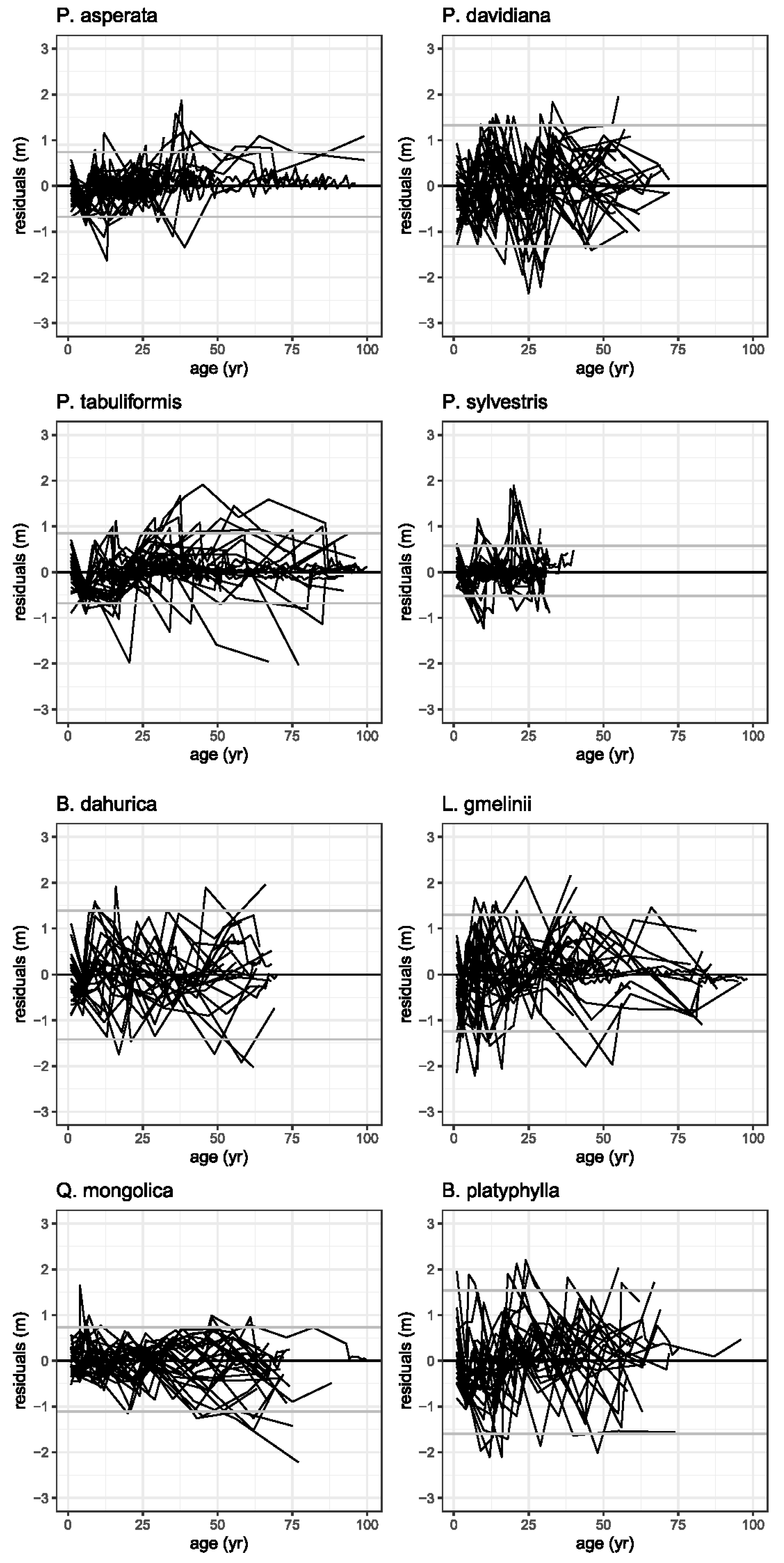
| Forest Type | Tree Species | Elevation a.s.l. (m) | T (°C) | P (mm) | Tree Height (m) | Lifespan (yr) |
|---|---|---|---|---|---|---|
| Cold-temperate & temperate mountain coniferous forest | Larix gmelinii | 450–2900 | −2 to −5 | 350–550 | 10–30 | 150 |
| Pinus sylvestris | 300–900 | 0 to −5 | 400–550 | 20–40 | 150–300 | |
| Picea asperata | 1100–4300 | 0–8 | 600–1000 | 20–40 | 150–300 | |
| Temperateconiferous forest | Pinus tabuliformis | 1200–1800 | <14 | <900 | 20–30 | 300 |
| Temperate deciduous broad-leavedforest | Quercus mongolica | <1500 | 9–14 | 500–900 | 20–30 | 300 |
| Betula platyphylla | 400–1300 | <8 | 400–800 | 20–30 | 120–140 | |
| Betula dahurica | 400–1300 | <8 | 400–800 | 20 | 120–140 | |
| Populus davidiana | 100–3800 | <8 | 400–800 | 25 | 120 |
| Tree Species | Stands | Trees | Stem Discs | Annual Shoot Length Measurements | Tree Age | Tree Height | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Range | Mean | SD | Range | Mean | SD | |||||
| L. gmelinii | 9 | 30 | 232 | 1308 | 39–98 | 69 | 20.6 | 12.7–30.6 | 21.7 | 7.2 |
| P. tabuliformis | 9 | 30 | 215 | 1529 | 41–108 | 75 | 22.4 | 10.3–24.7 | 17.5 | 4.9 |
| P. sylvestris | 9 | 27 | 184 | 725 | 24–40 | 32 | 3.5 | 11.6–18.6 | 15.1 | 2.5 |
| P. asperata | 9 | 30 | 235 | 1007 | 28–104 | 66 | 26.2 | 10.8–27.7 | 19.3 | 5.1 |
| Q. mongolica | 9 | 30 | 313 | 30 | 38–100 | 69 | 9.9 | 7.4–16.8 | 12.1 | 2.7 |
| B. platyphylla | 9 | 29 | 310 | 1308 | 38–96 | 67 | 14.7 | 11.9–25.5 | 18.7 | 4.2 |
| B. dahurica | 9 | 27 | 206 | 1529 | 39–70 | 55 | 8.1 | 9.1–19.2 | 14.2 | 2.6 |
| P. davidiana | 9 | 30 | 339 | 725 | 32–72 | 52 | 13.5 | 19.4–29.3 | 24.4 | 2.6 |
| Base Model | Site-Specific Parameters | Solution for Variable X with Initial Values | GADA Model Form | Tree Species | |
|---|---|---|---|---|---|
| Chapman–Richards [45]: | = X | = | Krumland and Eng [12] in Sharma [17]: | P. asperata P. davidiana | [I] |
| = with = ln and | Krumland and Eng [12] in Sharma [17]: = | P. tabuliformis P. sylvestris B. dahurica | [II] | ||
| Hossfeld [46]: | = X | = | Anta et al. [47] in Sharma [17]: = | L. gmelinii | [III] |
| Sloboda [48]: h = | = X | = | Anta and Dieguez-Aranda [49] in Sharma [17]: | Q. mongolica | [IV] |
| Korf [50]: | = with | Anta et al. [47] in Sharma [17]: | B. platyphylla | [V] |
| Parameter Estimates | Fit Statistics | |||||||
|---|---|---|---|---|---|---|---|---|
| Tree Species | Parameter | Estimate | SE | t-Value | Pr (>|t|) | RMSE | AAB | |
| L. gmelinii | b1 | 51.772 | 3.0440 | 17.01 | <0.001 | 0.5979 | 0.9956 | 0.3883 |
| b3 | 1.0118 | 0.0266 | 38.06 | <0.001 | ||||
| P. tabuliformis | b1 | 0.0139 | 0.0002 | 92.83 | <0.001 | 0.3792 | 0.9966 | 0.1928 |
| b2 | 1.9426 | 0.0368 | 52.73 | <0.001 | ||||
| b3 | −2.7807 | 0.1179 | −23.58 | <0.001 | ||||
| P. sylvestris | b1 | 0.0306 | 0.0004 | 83.33 | <0.001 | 0.3024 | 0.9960 | 0.1685 |
| b2 | 2.8043 | 0.1584 | 17.71 | <0.001 | ||||
| b3 | −4.9288 | 0.5274 | −9.35 | <0.001 | ||||
| P. asperata | b1 | 0.0273 | 0.0004 | 66.93 | <0.001 | 0.3337 | 0.9979 | 0.2322 |
| b2 | 1.5622 | 0.0274 | 57.03 | <0.001 | ||||
| Q. mongolica | b1 | 9.2465 | 0.3937 | 23.49 | <0.001 | 0.4748 | 0.9889 | 0.3541 |
| b2 | 0.1204 | 0.0069 | 17.25 | <0.001 | ||||
| b3 | 1.0644 | 0.0049 | 213.90 | <0.001 | ||||
| B. platyphylla | b1 | 10.4131 | 0.5222 | 19.94 | <0.001 | 0.7628 | 0.9866 | 0.5737 |
| b2 | −20.2949 | 2.3630 | −8.59 | <0.001 | ||||
| b3 | 0.2994 | 0.0031 | 98.13 | <0.001 | ||||
| B. dahurica | b1 | 0.0190 | 0.0004 | 43.30 | <0.001 | 0.6877 | 0.9858 | 0.4996 |
| b2 | 1.9289 | 0.1149 | 16.79 | <0.001 | ||||
| b3 | −2.5615 | 0.3602 | −7.11 | <0.001 | ||||
| P. davidiana | b1 | 0.0356 | 0.0008 | 43.82 | <0.001 | 0.6925 | 0.9921 | 0.5267 |
| b2 | 1.4489 | 0.0389 | 37.19 | <0.001 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hipler, S.-M.; Spiecker, H.; Wu, S. Dynamic Top Height Growth Models for Eight Native Tree Species in a Cool-Temperate Region in Northeast China. Forests 2021, 12, 965. https://doi.org/10.3390/f12080965
Hipler S-M, Spiecker H, Wu S. Dynamic Top Height Growth Models for Eight Native Tree Species in a Cool-Temperate Region in Northeast China. Forests. 2021; 12(8):965. https://doi.org/10.3390/f12080965
Chicago/Turabian StyleHipler, Sandra-Maria, Heinrich Spiecker, and Shuirong Wu. 2021. "Dynamic Top Height Growth Models for Eight Native Tree Species in a Cool-Temperate Region in Northeast China" Forests 12, no. 8: 965. https://doi.org/10.3390/f12080965
APA StyleHipler, S.-M., Spiecker, H., & Wu, S. (2021). Dynamic Top Height Growth Models for Eight Native Tree Species in a Cool-Temperate Region in Northeast China. Forests, 12(8), 965. https://doi.org/10.3390/f12080965






