Next Article in Journal
Applying Machine Strength Grading System to Round Timber Used in Hydraulic Engineering Works
Next Article in Special Issue
Machine Learning Modeling of Forest Road Construction Costs
Previous Article in Journal
Can Payments for Watershed Services Help Advance Restoration of Longleaf Pine? A Critically Engaged Research Approach
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 12
Issue 3
10.3390/f12030280
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Heuristic Optimization of Thinning Individual Douglas-Fir

by
Todd West
,
John Sessions
and
Bogdan M. Strimbu
*
Department of Forest Engineering and Resource Management, Oregon State University, Corvallis, OR 97331, USA
*
Author to whom correspondence should be addressed.
Forests 2021, 12(3), 280; https://doi.org/10.3390/f12030280
Submission received: 27 January 2021 / Revised: 20 February 2021 / Accepted: 23 February 2021 / Published: 28 February 2021
(This article belongs to the Special Issue Natural Resources Management in Tropical, Temperate and Boreal Forests)
Browse Figures
Versions Notes

Abstract

:
Research Highlights: (1) Optimizing mid-rotation thinning increased modeled land expectation values by as much as 5.1–10.1% over a representative reference prescription on plots planted at 2.7 and 3.7 m square spacings. (2) Eight heuristics, five of which were newly applied to selecting individual trees for thinning, produced thinning prescriptions of near identical quality. (3) Based on heuristic sampling properties, we introduced a variant of the hero heuristic with a 5.3–20% greater computational efficiency. Background and Objectives: Thinning, which is arguably the most subjective human intervention in the life of a stand, is commonly executed with limited decision support in tree selection. This study evaluated heuristics’ ability to support tree selection in a factorial experiment that considered the thinning method, tree density, thinning age, and rotation length. Materials and Methods: The Organon growth model was used for the financial optimization of even age Douglas-fir (Pseudotsuga menziesii (Mirb.) Franco) harvest rotations consisting of a single thinning followed by clearcutting on a high-productivity site. We evaluated two versions of the hero heuristic, four Monte Carlo heuristics (simulated annealing, record-to-record travel, threshold accepting, and great deluge), a genetic algorithm, and tabu search for their efficiency in maximizing land expectation value. Results: With 50–75 years rotations and a 4% discount rate, heuristic tree selection always increased land expectation values over other thinning methods. The two hero heuristics were the most computationally efficient methods. The four Monte Carlo heuristics required 2.8–3.4 times more computation than hero. The genetic algorithm and the tabu search required 4.2–8.4 and 21–52 times, respectively, more computation than hero. Conclusions: The accuracy of the resulting thinning prescriptions was limited by the quality of stand measurement, and the accuracy of the growth and yield models was linked to the heuristics rather than to the choice of heuristic. However, heuristic performance may be sensitive to the chosen models.

1. Introduction

While tree harvest scheduling has been studied since the late 1600s [1], it remains a topic of current interest due to its complexity. Given a planning unit containing thousands of trees, one form of forest scheduling seeks to determine which, if any, silvicultural interventions on the unit produce the most desirable outcomes. Most desirable has often been defined as producing the greatest amount of revenue from harvesting the trees [2]. Previous studies have shown revenue varies with the species composition of the trees, their current density and sizes, the future growth rates anticipated on the site, the present and anticipated pricing of the wood products made from harvested trees, the number and frequency of harvests, and how many trees of which types are removed in each harvest (e.g., [3,4,5,6,7,8,9,10]). This broad range of parameters has motivated the ongoing demand for techniques that can identify the most desirable management choices, ideally at the level of individual trees.
Forest planning abilities are closely associated with tree measurement capabilities, forest models predicting the effects of silvicultural actions, mathematical optimization techniques, and available computing power. When a unit is thinned by removing some of its trees, optimization seeks to identify the best set of trees to cut and the best harvest timing under a given set of planning objectives. These decisions also determine the trees retained for later harvest and other purposes. Recent works on thinning (Table 1) have therefore included laser scanning to identify individual trees, the projection of individual trees’ growth, the estimation of timber assortments provided by harvest, and the use of 16 different optimization methods.
This study expanded the range of heuristic optimization techniques that have been evaluated for developing thinning prescriptions based on selecting individual trees for harvest. While Pascual [3 and Vaukhonen et al. 8] selected individual trees and Xue et al. [7] used heuristics, Fransson et al. [5] conducted the only other study we are aware of which combines the two approaches. More commonly, thinning prescriptions are optimized by dividing trees into 2–10 size classes and determining the proportion of trees that should be cut within each size class [11]. While size class-based approaches may produce good prescriptions, their accuracy is restricted by the granularity of the used size classes. The use of size classes also reduces the amount of decision support provided because the optimization method typically does not identify specific trees to cut. Given a harvest unit containing N trees, harvesting staff must then identify the best implementation among the 2N possible tree selections. This is a challenging task [12] but it can be supported by heuristic optimization of individual trees’ selections using a combination of onsite computing, mobile computing, and greater offsite computing power. Unfortunately, heuristics are not guaranteed to find the best possible solution and may instead converge to a good solution that is a local, rather than global, optimum.
Because it is desirable to optimize each unit on a managed landscape, the amount of time a heuristic requires to determine a good tree selection is important. For a given amount of computing power and planning time, a more computationally efficient heuristic can be run more times. These additional runs can be allocated to increasing the range of growth, harvest, and pricing combinations available to inform management decisions. Runs can also be used to replicate the optimization of scenarios of interest, increasing the probability of finding the global optimum and mitigating the risk of reaching only a relatively undesirable local optimum. While a range of techniques have been developed to increase the efficiency of subsequent heuristic runs by making of use of information from prior runs [13], this study was devoted to properties of initial heuristic runs.
A second concern is the characterization of optimal thinning prescriptions for Douglas-fir. Because tree selections depend upon species- and site-specific responses, prescriptions do not necessarily transfer between studies [4]. Douglas-fir is a major commercial species in the south-central portion of the Pacific Temperate Rainforest along the west coast of North America and a worldwide plantation species [14]. Within our study area of western Oregon and Washington, investigations of Douglas-fir thinning in the past 30 years have emphasized ecosystem services [15]. Comparatively little research attention has been given to linking developments in growth models, numerical optimization methods, and computing power in the support of selecting individual Douglas-fir trees.
Our objectives were therefore to (1) determine how the choice of heuristic affected tree selection quality, (2) quantify differences in computational efficiency among heuristics, (3) re-examine thinning prescriptions for Douglas-fir in the context of selecting individual trees, and (4) identify areas for further investigation when integrating heuristic tree selection into the planning and execution of thinning sales. The following sections summarize how heuristics were used to perform tree selection, present corresponding results for thinning three Douglas-fir densities, discuss the limitations of the methods used in this study, and conclude with recommendations for improved modeling.

2. Materials and Methods

2.1. The Financially Optimal Thinning Problem

A common objective when optimizing thinning prescriptions is to maximize the financial return from a timber harvest unit. Often, the maximization is done under the assumption of an infinite sequence of identical harvests, in which case the financial return is the land expectation value (LEV, also referred to as the bare land value or the soil expectation value) defined by the Faustmann formula (e.g., [4,5,7,9]). In the case of an infinite sequence of tree planting, growth followed by one thinning, continued growth, and then clearcutting at a rotation length of R years, Faustmann’s formula is:
L E V p r e s c r i p t i o n , i = ( 1 + r ) R ( 1 + r ) R − 1 ( N P V r e f o r e s t a t i o n + N P V t h i n , i + N P V f i n a l , i ) + C a n n u a l r
where r is the annual discount rate; Cannual is the annual management cost for holding the land; and NPVreforestation, NPVthin,i, and NPVfinal,i are the net present values (NPVs) of the planting, thinning, and final harvest at the end of the rotation, respectively (Table 2). Here, the NPVs associated with thinning prescription i are calculated from the real mean appreciated prices P ¯ (•) for the wood volume harvested, the volumes (Vj) of individual trees, and the timber sale administration, harvest, and haul costs Cvariable and Cfixed.
N P V t h i n , i = 1 ( 1 + r ) T ( ( P ¯ ( T ) ( 1 + a ) T − C t h i n , v a r i a b l e ) ( ∑ j = 1 N u i ( j ) V t h i n , j ) − C t h i n , f i x e d )
N P V f i n a l , i = 1 ( 1 + r ) R ( ( P ¯ ( R ) ( 1 + a ) R − C f i n a l , v a r i a b l e ) ( ∑ j = 1 N ¬ u i ( j ) V f i n a l , i , j ) − C f i n a l , f i x e d )
where T is the age of thinning, a is the real appreciation rate for Douglas-fir sawtimber, and N is again the number of trees representing the stand. The tree selection made by a heuristic at thinning is ui, with ui(j) taking the value 1 if tree j is thinned and 0 if it is retained until final harvest. At final harvest, the logical complement of ui(j), ¬ui(j), takes the value 0 if the tree was previously removed at thinning and is 1 if the tree is removed at final harvest. Unlike its volume when retained to final harvest, Vfinal,i,j, a tree’s volume at the time of thinning, Vthin,j, is independent of prescription i because the stand has not yet been silviculturally modified.
We obtained the individual tree volumes, Vthin,j and Vfinal,i,j, required by Equations (2) and (3) from the individual tree growth model Organon [16] and the Scribner board-foot volume regressions of Brackett [17]. Since this study emphasized Douglas-fir in western Oregon and Washington, we present results from Organon’s northwest Oregon variant as it applies to the middle of the study region (Figure 1). We initialized Organon from height and diameter at breast height measurements of individual trees on three Douglas-fir plots of differing densities (Figure 1 and Table 3; University of British Columbia [18] with additional information in Reukema [19]).
After initializing Organon, LEV maximization proceeded by simulating the plot’s growth to a specified thinning age, removing the trees indicated by ui, and continuing simulation to the final harvest age. The resulting LEV was then calculated, the heuristic generated a new ui, and the process repeated from the tree removal step until the heuristic ceased generating new ui values to investigate.

2.2. Adaptation of Heuristics to Select Individual Trees

Because growth and yield calculations are computationally expensive, we sought heuristics that could quickly find a desirable choice of u. Since most heuristics incorporate randomness into their search process, a computationally efficient heuristic is one that produces high LEVs at low variance while requiring the smallest number of growth simulations. For this study, we elected to compare the efficiency of eight different heuristics (Table 4). Seven of these heuristics have been demonstrated in other forest scheduling problems (e.g. [22,23]). Simulated annealing and threshold accepting have been used for selecting individual trees with non-financial objectives [24,25] and Fransson et al. [5] used a genetic algorithm for the financial optimization of individual tree selection.
To our knowledge, this study was the first to investigate use of hero, the four Monte Carlo heuristics (simulated annealing, record-to-record travel, threshold accepting, and great deluge), and tabu search for financial optimization by selecting individual trees for thinning. As originally described, hero sequentially evaluates the elements of u. We introduce a variation of hero which randomizes the order of evaluation. For clarity, we refer to this new variant as hero stochastic and the original version of hero as hero sequential. Because of limited prior use and because we made adjustments for computational efficiency in individual tree selection, we describe implementation details and provide pseudocode for all eight heuristics in the Supplementary Material.
For the six heuristics with parameters, we sought combinations of parameters that resulted in good performance across all 69 available combinations of the three plots, four thinning ages, and six rotation lengths. Since LEV depends on these three variables, we made many heuristic parameters relative to a heuristic’s internal working values of LEV. Most other parameters were made relative to the number of trees on each plot. This approach allowed for a single parameterization of each heuristic to run across all combinations, avoiding the tuning of parameters for different factor levels. We identified parameter values by running a heuristic 100 or more times at each of several parameter levels, evaluating the resulting LEV distributions, and selecting the most effective combination of observed parameters. The resulting default parameters are provided in the Supplementary Material (Listings S1–S8). After selecting a heuristic’s parameterization, we evaluated its empirical LEV distribution by running it 1000 times on each combination of plot and harvest timing. The one exception was tabu search which, due to its computational cost, was run only 100 times per combination of thinning age and rotation length on the Nelder plot.
As controls on heuristic performance, we included a reference prescription representative of common silvicultural practices used in commercial thinning of Douglas-fir [32], as well as an optimized conventional prescription. The reference prescription primarily thinned from below (preferentially removing the smallest diameter trees) to a basal area retention of 27.5 m2 ha−1 and was intended to provide mid-rotation cashflow from units planted at spacings around 3.2 × 3.2 m square (1000 trees per hectare). It did not apply to the Nelder plot due to the plot’s variable planting density, and it is typically used in circumstances most similar to thinning the 2.7 and 3.7 m plots in this study by age 30. We therefore did not consider use of the reference prescription on the plots at later thinning ages. The reference prescription is also not intended for long intervals between thinning and final harvest, so we excluded its use with rotations beyond 60 years. While the prescription’s intent is to thin from below, other trees will likely be removed due to defects or to maintain spacing. We approximated defect or spacing constraints as a proportional removal (equal thinning of trees across the diameter range) of 10% of the trees in each plot. This created reference thinning intensities of 37% from below plus 10% proportional intensities, thus equaling 47% of trees on the 2.7 m plot and 44% plus 10% equaling 54% on the 3.7 m plot.
To produce optimized conventional prescriptions, we considered 1% steps in the intensity of thinning from below, proportional thinning, and thinning from above (preferential removal of the largest diameter trees) for a total of 8.61 million prescriptions. Each combination of plot, thinning age, and rotation length resulted in 124,807 prescriptions that removed 30–90% of trees from a plot. We selected the prescription with the highest LEV among these as the optimized conventional prescription.

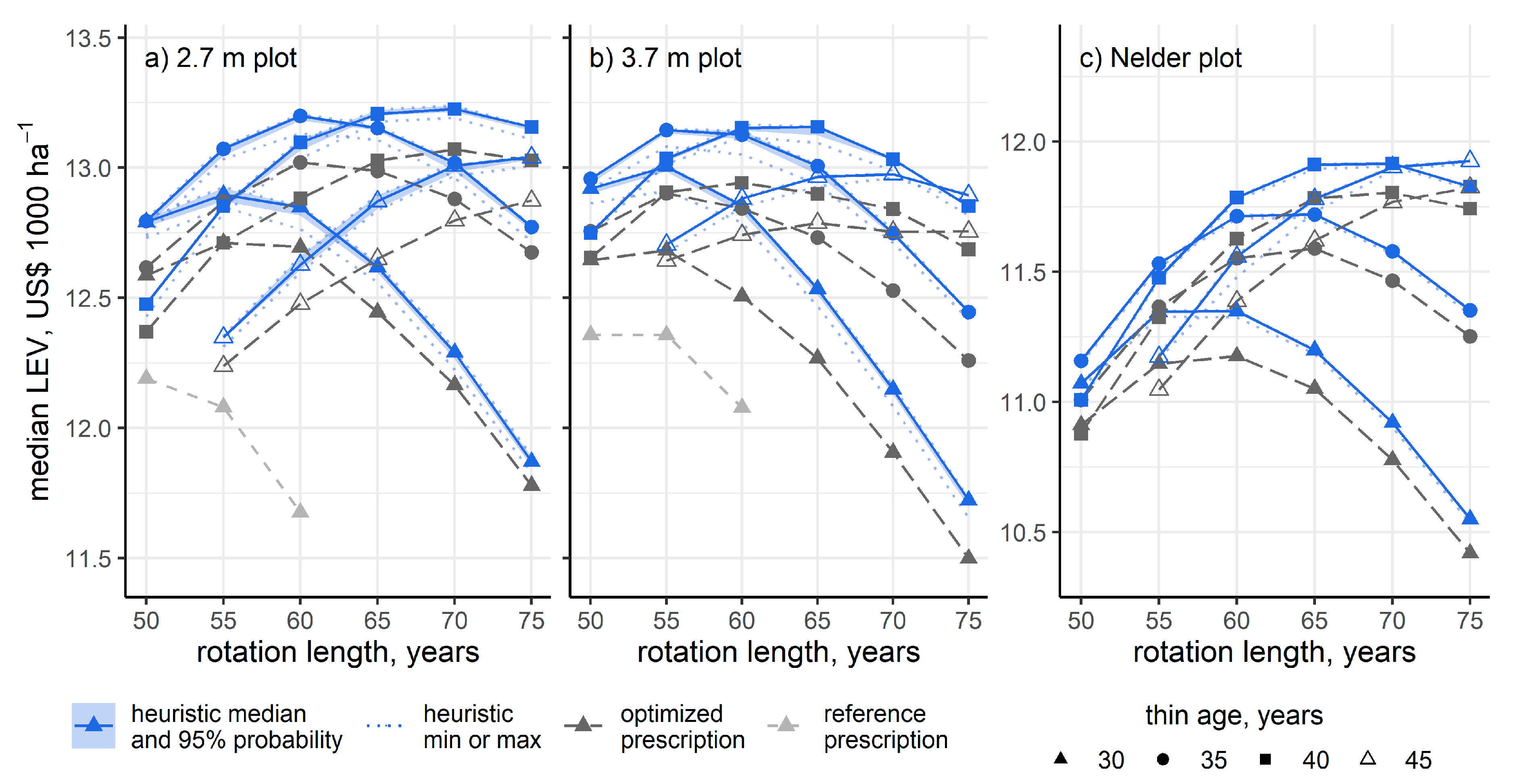
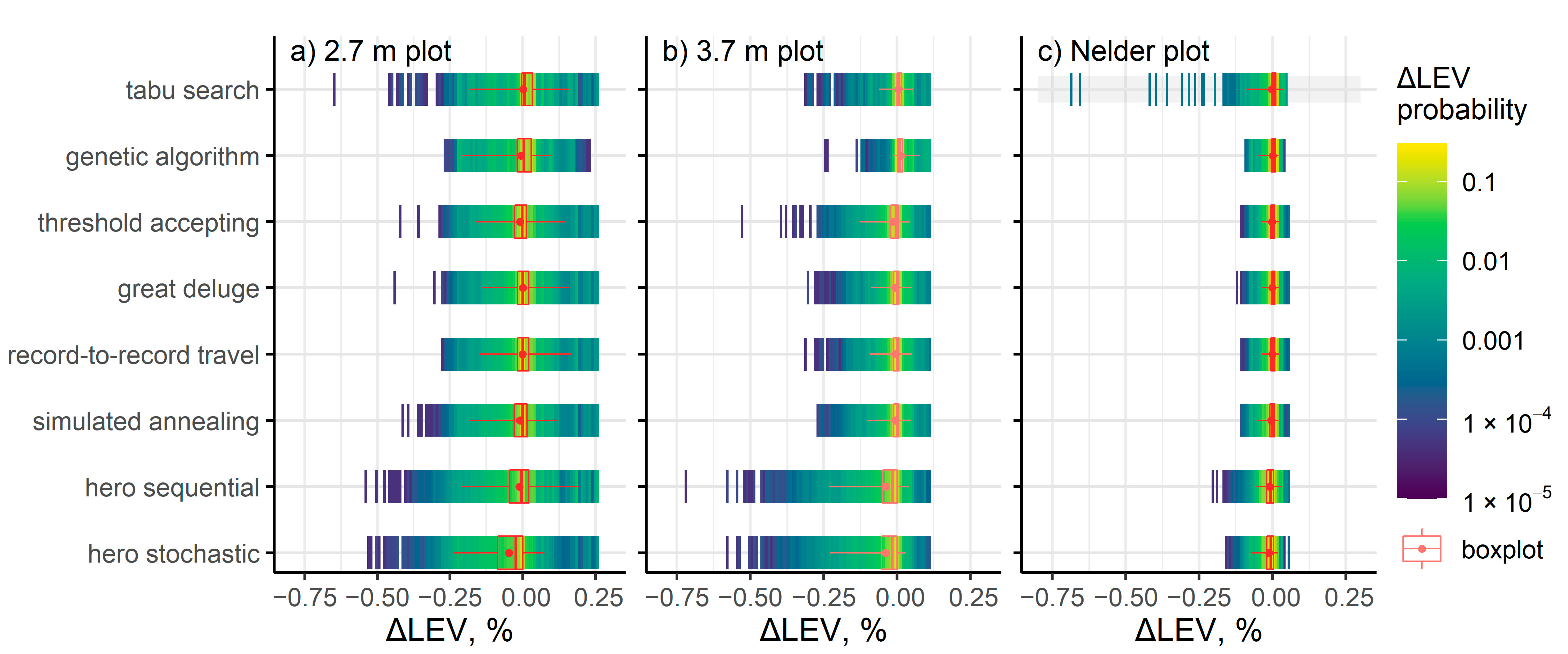
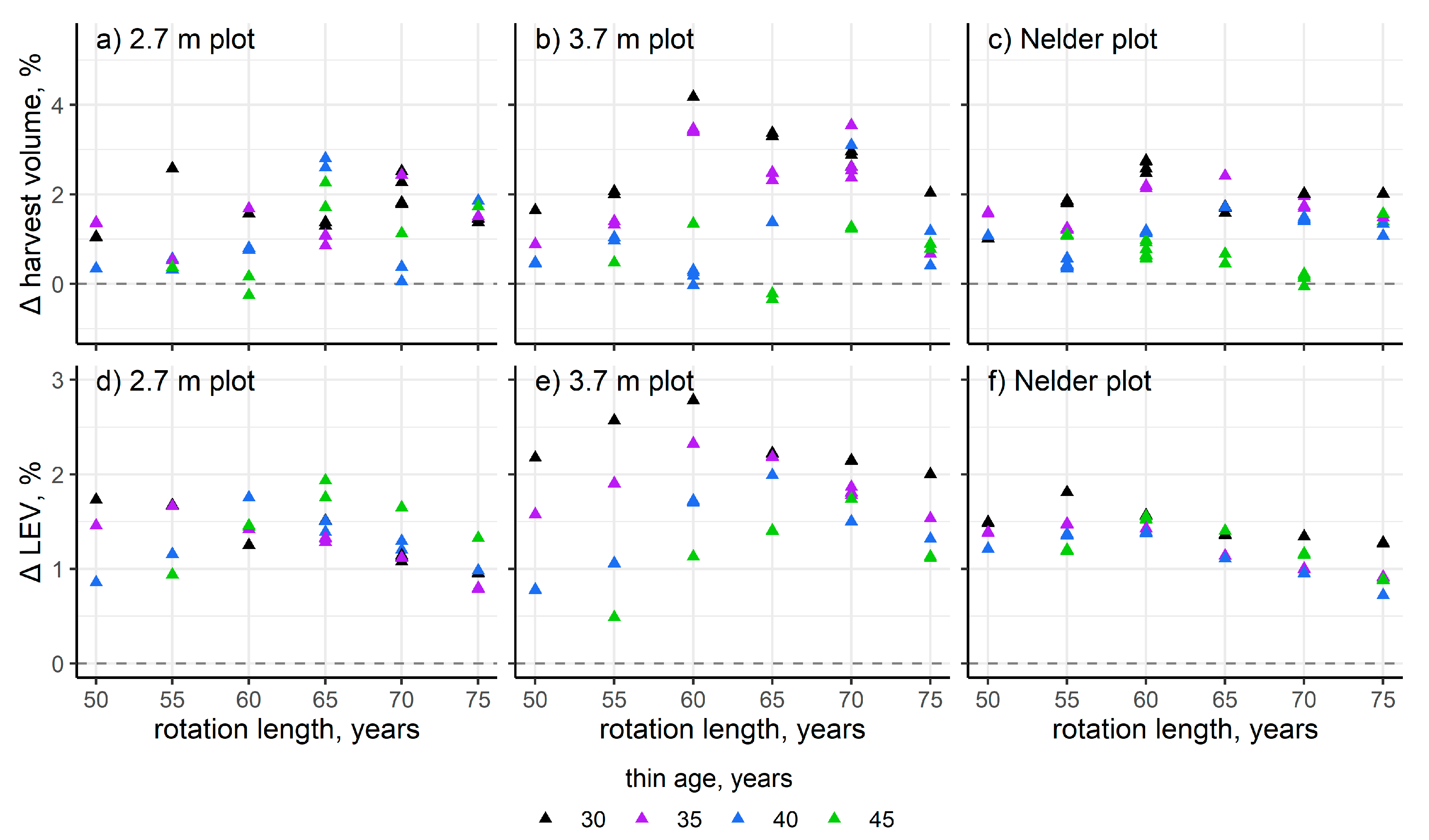
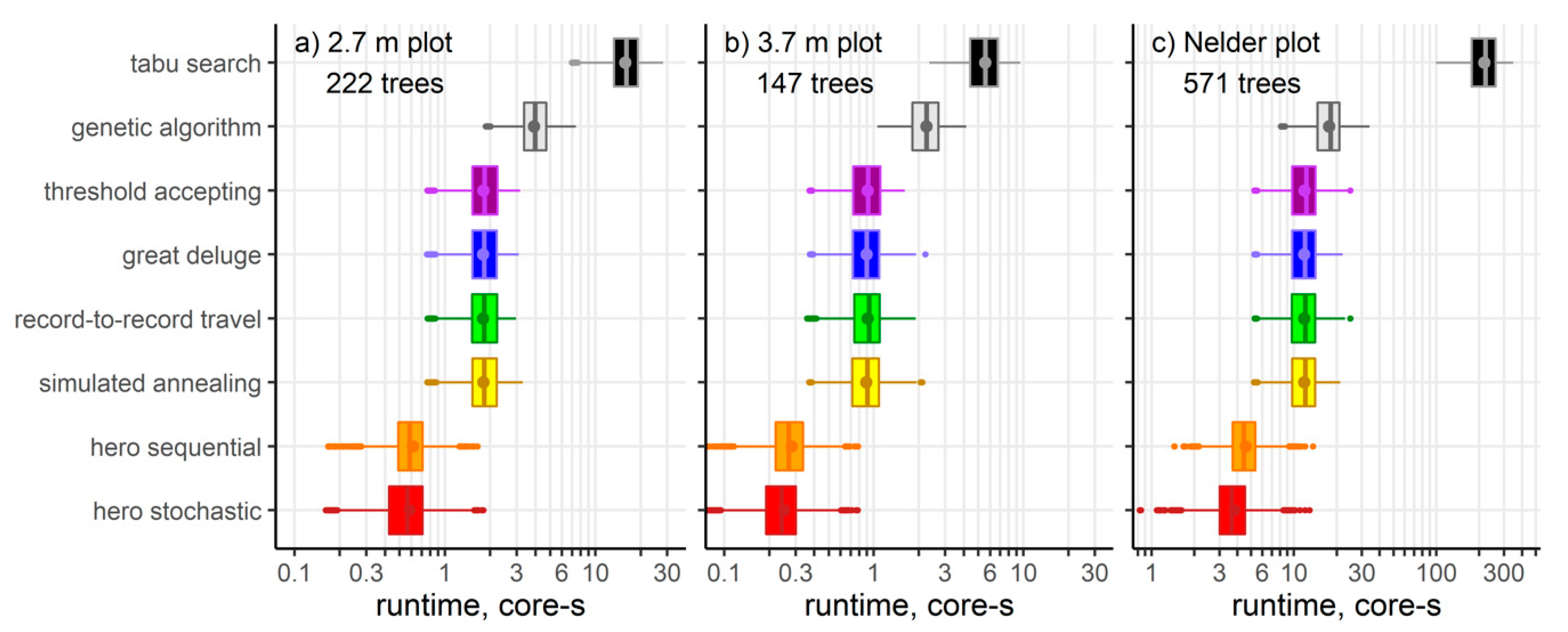
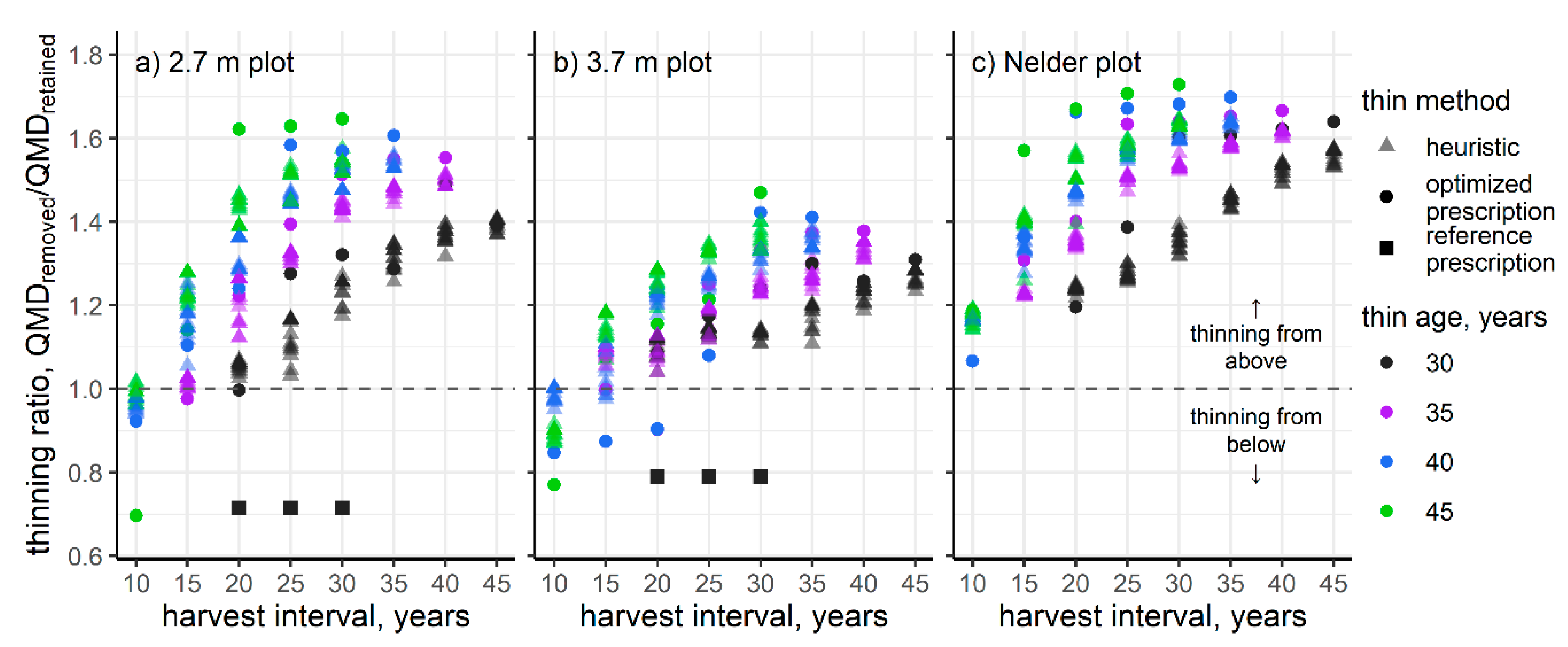
3. Results

For all combinations of plot, thinning age, and rotation length, every run of all eight heuristics resulted in a thinning prescription with a higher LEV than available from conventional prescription optimization (Figure 2 and Figure 3). Conventional prescription optimization always resulted in higher LEVs than the reference prescription (Figure 2). Heuristic prescriptions increased LEV by 0.5–2.8% over optimized conventional prescriptions. In most cases, heuristics increased LEV by increasing total volume growth, but the relationship between volume and LEV lacked a clear pattern across plots, thinning ages, and rotation lengths (Figure 4). LEV increases on the 2.7 and 3.7 m plots were 5.1–10.1% relative to the reference prescription (Table 5).
Because the choice of heuristic had little effect on LEV (Figure 3), the primary criteria for selecting a heuristic is likely to be its computational cost (Figure 5). While hero did not guarantee an O(N2 log N) runtime and exhibited median LEVs of 0.004–0.024% below the overall median, its N2 log N behavior made hero one-to-two orders more computationally efficient than tabu search’s O(N3/log N). Tabu search’s O(N3) behavior resulted from evaluating N growth simulations in order to choose the next ui, a computationally intensive process that increased the median LEV over by at most 0.003% and decreased the median LEV by 0.003% on the 3.7 m plot. The genetic algorithm’s expected runtimes were 2.5–12 times shorter than tabu search, with the greatest reduction occurring on the Nelder plot.
The four Monte Carlo heuristics all performed interchangeably (Figure 3, Figure 4 and Figure 5). During parameterization, we found their implementations converged to functional equivalence and that varying computational effort by ±20% had little effect on solution quality. However, the Monte Carlo heuristics required at least 1.5–2 times more computation to reach solutions of quality comparable to the hero variants (Figures S1–S3). Because the heuristics were configured to operate in an otherwise identical fashion during their initial LEV maximization phase (Supplementary Material, S1.3), hero’s greater efficiency was attributable to its more systematic assessment of each tree’s cut decision rather than performing random sampling with replacement as the Monte Carlo heuristics did.
Additionally, hero stochastic often converged to a solution more quickly than hero sequential, decreasing the expected runtime by 5.0–17% (Figure 5). Because the only difference between the two variants was hero’s stochastic iterative evaluation of all of a plot’s trees using sampling without replacement rather than in a fixed order, this increase in efficiency was attributable to hero’s stochastic randomization. Hero sequential lacked this feature, repeatedly evaluating trees in the order in which they appeared in the plot data (Supplementary Material, S1.2). The Monte Carlo heuristics and genetic algorithm also randomized against tree order, and tabu search’s steepest ascent approach rendered it independent of ordering as well.
The LEV increases of heuristic prescriptions over the reference prescription were due to increasing use of thinning from above, with later thinning ages and longer intervals between thinning and final harvest lengthened (Figure 6 and Figure 7). Fransson et al. reported optimal thinning ratios of 1.25–1.33 for selecting individual Norway spruce trees (Picea abies L.) with thinning ages of 40–48 years, a final harvest at 65 or 75 years, and plots with age 30 densities in the vicinity of 2000–2200 TPH (trees per hectare) ([5]; see Table 1 and Table 3). Matching Fransson et al.’s use of arithmetic means, we found thinning ratios of 1.20–1.50 for ages of 40 and 45 years and the same rotation lengths on the 3.7 m plot. Since the 3.7 m plot had an age 30 density of 596 TPH (Table 3), we interpreted these higher Douglas-fir thinning ratios at lower density as supporting the non-transferability of the results between species and sites asserted by Halbritter [4].
While Organon neglected the Nelder plot’s spatial density variation, it did consider a tree’s social position. The resulting prescriptions removed some of the small trees in dense areas of the plot and favored higher thinning ratios than on the 2.7 or 3.7 m plots, increasing removal of large trees in less dense areas of the plot (Figure 1, Figure 6, and Figure 7). This pattern was consistent with the prescriptions obtained for the more homogenous 2.7 and 3.7 m plots, and the Nelder plot’s comparatively smaller ΔLEV range (Figure 3) provided no evidence of heuristic optimization difficulty.

4. Discussion

We found the maximum LEV difference among heuristic runs to be less than 1%, an order of magnitude smaller than uncertainties in stand measurement [33,34], and LEV differences could be reduced below 0.1% by selecting the best result from multiple heuristic runs. It is also unlikely growth, yield, and financial models maintain a better-than-1% accuracy, both when preparing a thinning sale in the near term and when predicting a final harvest 20–40 years in the future. Therefore, the accuracy of a thinning prescription is most likely limited by the stand models used and not by choice of heuristic. However, realizing the LEV increase offered by heuristic tree selection is likely to be difficult due to the complexity of translating a prescription based on a few hundred trees, as was the case here, to a production harvest unit containing perhaps 10,000–40,000 trees.
Given sufficient computational resources, scanning a harvest unit with LiDAR (light detection and ranging) or SfM (structure from motion photogrammetry) and applying a spatially explicit growth model would allow for a heuristic to automate tree selection across the entire unit. Because scanning a harvest unit georeferences the trees within it and because a heuristic selects specific trees, thinning could then be performed by georeferenced harvest equipment [35], thus implementing the heuristic’s cut list. While Fransson et al. [5] implement elements of this approach in Norway spruce, a spatial model calibrated for Douglas-fir is needed. Extrapolation from the runtimes observed here also suggests the optimization of an entire harvest unit would require heuristic runs lasting several hours to a few days. Because scanning errors will likely be encountered during thinning and cutting errors may additionally occur, a need for an investigation into the rapid re-optimization of a thinning prescription is apparent, as is the desirability of performing initial optimizations more quickly.
Certain silvicultural concerns specific to our study area were not modeled in this study due to the use of an LEV formulation and Organon being a regression-based model without a carbon cycle. A common management objective is the restoration of large, structurally complex Douglas-firs and their eventual conversion to snags and down wood [15]. Because such trees continue to grow over multiple harvest rotations, the Faustmann assumption of an infinite series of identical rotations no longer holds. A constant climate is also implicit in the Faustmann assumption and, while Organon accepts site productivity in the form a site index, it is unclear whether Organon remains accurate if the site index changes under future climate scenarios. This suggests combining a physiological process-based model, the consideration of stand structural objectives over periods of 100–500 years or longer, and more flexible financial accounting [10] could provide both more desirable and more accurate thinning prescriptions.
Because heuristic performance can be problem-specific [36], changes in the used models may alter heuristics’ optimization success. This study’s finding of near equal LEVs across heuristics does not appear to be unique, as Xue et al. [7] obtained LEVs matched within 0.82% on five of seven Scots pine (Pinus sylvestris L.) stands across five heuristics and 10 diameter classes. However, we are not aware of any thinning optimization study that has evaluated a given heuristic across multiple growth, yield, or economic models. Our results suggest regression-based growth and yield models provide a smooth enough optimization surface the cost of carrying a population of solutions, as a genetic algorithm does, and that this not offset by a population’s greater resilience to local minima [37]. It follows single-solution, hill-climbing heuristics such as hero and Monte Carlo methods are more computationally efficient than the genetic algorithm in the current case. This property may not hold when models include weather, episodic disturbance, timber price fluctuations, or other effects creating more complexity in how trees are valued over time.
The thinning prescriptions obtained in this study may also be affected by four sources of bias or error. First, Organon relies on stand-level multipliers to increase diameter growth and reduce height growth after thinning, thus leading to overestimation of post-thinning growth in small diameter classes ([38] and personal communication [39]). Second, thinning may damage retained trees and increase their exposure. Greater retention may therefore be required to mitigate injury or windthrow risks on some sites. Third, in our study area, logs with scaling diameters near 55 cm or larger often incur higher costs and lower mill-delivered prices, which may favor thinning from above to remove trees before they exceed this size. Fourth, while the simple linear regressions used for P ¯ (•) captured nearly all variation in log assortment prices (Table 2; R2 > 0.997 and p < 0.001), they did so under the idealized assumptions of perfectly predictable pricing and tree taper. Providing heuristics with a refined growth model, information about disturbance and fluctuating price risks, or log values obtained from individual trees’ taper when a harvest unit is scanned would very likely alter the optimum tree selection.
However, despite these uncertainties, it appears use of proportional thinning or thinning from above could increase financial returns compared to thinning primarily from below. Emmingham et al. [32] evaluated thinning from above versus below in Douglas-fir experimental plots within our study area. Their 10-year results appear broadly consistent with the prescriptions obtained here but do suggest heuristic tree selection could be improved by considering crown ratios or other metrics of tree vigor available when stands are scanned.

5. Conclusions

We found selection of individual trees using heuristics consistently increased the modeled LEV over prescriptions employing combinations of thinning from above, proportional thinning, and thinning from below. While the LEV of tree selections varied between heuristic runs, differences among heuristic prescriptions were an order of magnitude smaller than typical volume prediction and valuation uncertainties. The eight heuristics also differed by up to two orders of magnitude in the computation required to find the prescriptions. The choice of heuristic was therefore of limited importance to the quality of thinning prescriptions but had large effects on the speed at which solutions could be obtained. We introduced a stochastic variant of hero that required less computation per run than hero’s sequential form or the other six heuristics considered.
It appears this study’s primary limitation was the growth, yield, and economic models used. Repetition of this study or conducting similar studies with a process-based spatial growth model, more detailed yield estimation, and a more flexible economic formulation is therefore desirable to verify the observed LEV increases. While the heuristic optimization methods employed in this study will likely improve in the future, changing the models used may also require changing the heuristics to maintain performance. Further work is also recommended to incorporate non-monetary values such as large tree recruitment and retention, snag creation, understory development, wildfire fuel loads and geometry, and resilience to other ecological risks. Over the past few decades, forest policy in our study area has sought to balance financial returns with other ecosystem services and we caution against applying this study’s optimization techniques without considering them within this broader context.

Supplementary Materials

The following are available online at https://www.mdpi.com/1999-4907/12/3/280/s1, Listings S1–S9: heuristic and enumeration pseudocode; Figure S1: heuristic convergence on the 2.7 m plot; Figure S2: heuristic convergence on the 3.7 m plot; Figure S3: heuristic convergence on the Nelder plot; Figure S4: LEV optimization of the 2.7 and 3.7 m plots combined; Section S3: soft-ware and regression imputation used. References [40,41,42,43,44,45,46,47,48] are cited in the supplementary materi-als.

Author Contributions

Conceptualization, B.M.S.; methodology, J.S.; software, T.W.; validation, T.W.; formal analysis, T.W.; investigation, T.W.; resources, B.M.S.; data curation, T.W.; writing—original draft preparation, T.W.; writing—review and editing, T.W., J.S. and B.M.S.; visualization, T.W.; supervision, B.M.S.; project administration, B.M.S.; funding acquisition, J.S. and B.M.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Oregon State University Graduate School and U.S. Department of Agriculture, grant number 2019-67019-29462.

Data Availability Statement

Data was obtained from [18] and is available from https://www.mkrf.forestry.ubc.ca/research/research-projects-database/ with the permission of the University of British Columbia.

Acknowledgments

The tree measurements used to initialize plot simulations were provided by the University of British Columbia’s Malcolm Knapp Research Forest and the British Columbia’s Ministry of Forests under BC Research Forests Project 2020-02. We thank Doug Maguire for his comments on Organon and suggestion of [32].

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Viitala, E.-J. The Discovery of the Faustmann Formula in Natural Resource Economics. Hist. Political Econ. 2013, 45, 523–548. [Google Scholar] [CrossRef]
  2. Çağlayan, İ.; Yeşil, A.; Çınar, D.; Cieszewski, C. Taxonomy for the optimization in forest management: A review and assessment. Forestist 2018, 68, 122–135. [Google Scholar] [CrossRef]
  3. Pascual, A. Multi-objective forest planning at tree-level combining mixed integer programming and airborne laser scanning. For. Ecol. Manag. 2020, 118714. [Google Scholar] [CrossRef]
  4. Halbritter, A. An economic analysis of thinning intensity and thinning type of a two-tiered even-aged Forest stand. For. Policy Econ. 2020, 111, 102054. [Google Scholar] [CrossRef]
  5. Fransson, P.; Franklin, O.; Lindroos, O.; Nilsson, U.; Brännström, Å. A simulation-based approach to a near-optimal thinning strategy: Allowing harvesting times to be determined for individual trees. Can. J. For. Res. 2019, 320–331. [Google Scholar] [CrossRef]
  6. Jin, X.; Pukkala, T.; Li, F. A new approach to the development of management instructions for tree plantations. For. Int. J. For. Res. 2019, 92, 196–205. [Google Scholar] [CrossRef]
  7. Xue, H.; Mäkelä, A.; Valsta, L.; Vanclay, J.K.; Cao, T. Comparison of population-based algorithms for optimizing thinnings and rotation using a process-based growth model. Scand. J. For. Res. 2019, 34, 458–468. [Google Scholar] [CrossRef] [Green Version]
  8. Vauhkonen, J.; Pukkala, T. Selecting the trees to be harvested based on the relative value growth of the remaining trees. Eur. J. For. Res. 2016, 135, 581–592. [Google Scholar] [CrossRef]
  9. Messerer, K.; Kacprowski, T.; Kolo, H.; Baumbach, J.; Knoke, T. Importance of considering the growth response after partial harvesting and economic risk of discounted net revenues when optimizing uneven-aged forest management. Can. J. For. Res. 2020, 50, 487–499. [Google Scholar] [CrossRef]
  10. Chang, S.J. Twenty one years after the publication of the generalized Faustmann formula. For. Policy Econ. 2020, 118, 102238. [Google Scholar] [CrossRef]
  11. Yoshimoto, A.; Asante, P.; Konoshima, M. Stand-Level Forest Management Planning Approaches. Curr. For. Rep. 2016, 2, 163–176. [Google Scholar] [CrossRef] [Green Version]
  12. Maher, C.T.; Oja, E.; Marshall, A.; Cunningham, M.; Townsend, L.; Worley-Hood, G.; Robinson, L.R.; Margot, T.; Lyons, D.; Fety, S.; et al. Real-Time Monitoring with a Tablet App Improves Implementation of Treatments to Enhance Forest Structural Diversity. J. For. 2019, 117, 280–292. [Google Scholar] [CrossRef]
  13. Martí, R.; Pardalos, P.M.; Resende, M.G.C. (Eds.) Handbook of Heuristics; Springer International Publishing: Cham, Switzerland, 2018; ISBN 978-3-319-07123-7. [Google Scholar]
  14. Lavender, D.P.; Hermann, R.K. Douglas-Fir: The Genus Pseudotsuga; College of Forestry, Oregon State University: Corvallis, OR, USA, 2014. [Google Scholar]
  15. Puettmann, K.; Ares, A.; Burton, J.; Dodson, E. Forest Restoration Using Variable Density Thinning: Lessons from Douglas-Fir Stands in Western Oregon. Forests 2016, 7, 310. [Google Scholar] [CrossRef] [Green Version]
  16. Weiskittel, A.R.; Hann, D.W.; Kershaw, J.A.; Vanclay, J.K. Forest Growth and Yield Modeling; Wiley-Blackwell: Chichester, UK, 2011; ISBN 978-0-470-66500-8. [Google Scholar]
  17. Brackett, M. Notes on Tarif Tree Computation. Resource Management Report No. 24, Department of Natural Resources, State of Washington. 1977. Available online: https://www.fs.fed.us/forestmanagement/products/measurement/volume/nvel/index.php (accessed on 26 February 2021).
  18. University of British Columbia [Dataset] RP 1957-05 Influence of Spacing on Growth of Douglas-fir, Western Hemlock, and Western Red Cedar in Plantations. Malcolm Knapp Research Forest, University of British Columbia, Canada. 2007. Available online: https://www.mkrf.forestry.ubc.ca/research/research-projects-database/ (accessed on 26 February 2021).
  19. Reukema, D.L.; Smith, H.G. Development over 25 Years of Douglas-Fir, Western Hemlock, and Western Redcedar Planted at Various Spacings on A Very Good Site in British Columbia; Research Paper PNW-RP-381; Pacific Northwest Research Station: Olympia, WA, USA; U.S. Forest Service: Olympia, WA, USA, 1987. [Google Scholar] [CrossRef]
  20. Mathys, A.; Coops, N.C.; Waring, R.H. Soil water availability effects on the distribution of 20 tree species in western North America. For. Ecol. Manag. 2014, 313, 144–152. [Google Scholar] [CrossRef]
  21. Wolf, E.C.; Mitchell, A.P.; Schoonmaker, P.K. The Rain Forests of Home: An Atlas of People and Place. Part 1: Natural Forests and Native Languages of the Coastal Temperate Rainforest. Available online: https://ecotrust.org/wp-content/uploads/Rainforests_of_Home.pdf (accessed on 26 February 2021).
  22. Bettinger, P.; Graetz, D.; Boston, K.; Sessions, J.; Chung, W. Eight heuristic planning techniques applied to three increasingly difficult wildlife planning problems. Silva Fenn. 2002, 36. [Google Scholar] [CrossRef] [Green Version]
  23. Pukkala, T.; Kurttila, M. Examining the performance of six heuristic optimisation techniques in different forest planning problems. Silva Fenn. 2005, 39. [Google Scholar] [CrossRef] [Green Version]
  24. Martín-Fernández, S.; García-Abril, A. Optimisation of spatial allocation of forestry activities within a forest stand. Comput. Electron. Agric. 2005, 49, 159–174. [Google Scholar] [CrossRef]
  25. Bettinger, P.; Tang, M. Tree-Level Harvest Optimization for Structure-Based Forest Management Based on the Species Mingling Index. Forests 2015, 6, 1121–1144. [Google Scholar] [CrossRef]
  26. Pukkala, T.; Kangas, J. A Heuristic Optimization Method for Forest Planning and Decision Making. Scand. J. For. Res. 1993, 8, 560–570. [Google Scholar] [CrossRef]
  27. Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1984, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
  28. Dueck, G. New Optimization Heuristics: The Great Deluge Algorithm and the Record-to-Record Travel. J. Comput. Phys. 1993, 104, 86–92. [Google Scholar] [CrossRef]
  29. Dueck, G.; Scheuer, T. Threshold Accepting: A General Purpose Optimization Algorithm Appearing Superior to Simulated Annealing. J. Comput. Phys. 1990, 90, 161–175. [Google Scholar] [CrossRef]
  30. Lozano, M.; Herrera, F.; Cano, J.R. Replacement strategies to preserve useful diversity in steady-state genetic algorithms. Inf. Sci. 2008, 178, 4421–4433. [Google Scholar] [CrossRef]
  31. Glover, F. Tabu search—Part I. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
  32. Emmingham, W.; Fletcher, R.; Fitzgerald, S.; Bennett, M. Comparing Tree and Stand Volume Growth Response to Low and Crown Thinning in Young Natural Douglas-fir Stands. West. J. Appl. For. 2007, 22, 124–133. [Google Scholar] [CrossRef] [Green Version]
  33. Lu, Y.; Coops, N.C.; Bolton, D.K.; Wang, T.; Wang, G. Comparing Stem Volume Predictions of Coastal Douglas-Fir Stands in British Columbia Using a Simple Physiological Model and LiDAR Remote Sensing. For. Sci. 2015, 61, 586–596. [Google Scholar] [CrossRef] [Green Version]
  34. Holopainen, M.; Vastaranta, M.; Rasinmäki, J.; Kalliovirta, J.; Mäkinen, A.; Haapanen, R.; Melkas, T.; Yu, X.; Hyyppä, J. Uncertainty in timber assortment estimates predicted from forest inventory data. Eur. J. For. Res. 2010, 129, 1131–1142. [Google Scholar] [CrossRef]
  35. Saukkola, A.; Melkas, T.; Riekki, K.; Sirparanta, S.; Peuhkurinen, J.; Holopainen, M.; Hyyppä, J.; Vastaranta, M. Predicting Forest Inventory Attributes Using Airborne Laser Scanning, Aerial Imagery, and Harvester Data. Remote Sens. 2019, 11, 797. [Google Scholar] [CrossRef] [Green Version]
  36. Adam, S.P.; Alexandropoulos, S.-A.N.; Pardalos, P.M.; Vrahatis, M.N. No Free Lunch Theorem: A Review. In Approximation and Optimization; Demetriou, I.C., Pardalos, P.M., Eds.; Springer Optimization and Its Applications; Springer International Publishing: Cham, Switzerland, 2019; Volume 145, pp. 57–82. ISBN 978-3-030-12766-4. [Google Scholar]
  37. Prügel-Bennett, A. Benefits of a Population: Five Mechanisms That Advantage Population-Based Algorithms. IEEE Trans. Evol. Comput. 2010, 14, 500–517. [Google Scholar] [CrossRef] [Green Version]
  38. Hann, D.W.; Marshall, D.D.; Hanus, M.L. Equations for Predicting Height-to-crown-base, 5-year Diameter-Growth Rate, 5-Year height-Growth Rate, 5-year Mortality Rate, and Maximum Size-Density Trajectory for Douglas-Fir and Western Hemlock in the Coastal Region of the Pacific Northwest. Research Contribution 40, Forest Research Laboratory, Oregon State University. 2003. Available online: https://ir.library.oregonstate.edu/concern/technical_reports/jd472x893 (accessed on 26 February 2021).
  39. Maguire, D. Personal Communication on Organon Model Bias; Oregon State University, Center for Intensive Planted-Forest Silviculture: Corvallis, OR, USA, 2020. [Google Scholar]
  40. Henderson, D.; Jacobson, S.H.; Johnson, A.W. Theory and Practice of Simulated Annealing. In Handbook of Metaheuristics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003. [Google Scholar]
  41. Battiti, R.; Brunato, M.; Mascia, F. Reactive Search and Intelligent Optimization; Springer Science+Business Media: New York, NY, USA, 2009. [Google Scholar]
  42. Goh, S.L.; Kendall, G.; Sabar, N.R. Simulated annealing with improved reheating and learning for the post enrolment course timetabling problem. J. Oper. Res. Soc. 2019, 70, 872–888. [Google Scholar] [CrossRef]
  43. McMullan, P. An Extended Implementation of the Great Deluge Algorithm for Course Timetabling. In Computational Science—ICCS 2007; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4487. [Google Scholar]
  44. Hu, T.C.; Kahng, A.B.; Tsao, C.-W.A. Old Bachelor Acceptance: A New Class of Non-Monotone Threshold Accepting Methods. ORSA J. Comput. 1995, 7, 417–425. [Google Scholar] [CrossRef] [Green Version]
  45. Kramer, O. Genetic Algorithm Essentials; Springer: Cham, Switzerland, 2017. [Google Scholar]
  46. Thompson, M.P.; Hamann, J.D.; Sessions, J. Selection and Penalty Strategies for Genetic Algorithms Designed to Solve Spatial Forest Planning Problems. Int. J. For. Res. 2009, 2009, 527392. [Google Scholar] [CrossRef]
  47. Črepinšek, M.; Liu, S.-H.; Mernik, M. Exploration and Exploitation in Evolutionary Algorithms: A Survey. ACM Comput. Surv. (CSUR) 2013, 43, 35. [Google Scholar] [CrossRef]
  48. Nelder, J.A. New Kinds of Systematic Designs for Spacing Experiments. Biometrics 1962, 18, 283–307. [Google Scholar] [CrossRef]
Forests 12 00280 g001 550
Figure 1. (a) Location of study area [20,21] and (b–d) stem maps of live trees on the 2.7 m, 3.7 m, and Nelder spacing trial plots, respectively, used for model initialization as of their measurement at age 30 years. Plots are shown to scale, but their placement relative to each other is not shown. Spacing in the Nelder plot varies from 0.91 to 4.94 m.
Figure 1. (a) Location of study area [20,21] and (b–d) stem maps of live trees on the 2.7 m, 3.7 m, and Nelder spacing trial plots, respectively, used for model initialization as of their measurement at age 30 years. Plots are shown to scale, but their placement relative to each other is not shown. Spacing in the Nelder plot varies from 0.91 to 4.94 m.
Forests 12 00280 g001
Forests 12 00280 g002 550
Figure 2. Land expectation values (LEVs) obtained from thinning the three Douglas-fir plots in this study as a function of the method used to create a thinning prescription, a plot’s stand age at the time of thinning, and length of the even age rotation. For heuristics, the median LEV was taken across all eight heuristics to integrate with Figure 3.
Figure 2. Land expectation values (LEVs) obtained from thinning the three Douglas-fir plots in this study as a function of the method used to create a thinning prescription, a plot’s stand age at the time of thinning, and length of the even age rotation. For heuristics, the median LEV was taken across all eight heuristics to integrate with Figure 3.
Forests 12 00280 g002
Forests 12 00280 g003 550
Figure 3. Empirical distributions of the differences (ΔLEV) between a plot’s median LEV and the LEVs obtained from 531,300 individual heuristic runs. Each heuristic was run 23,000 times on each plot, except for tabu search on the Nelder plot, which was limited to 2300 runs due to its computational cost (light grey shading); 98.8% of the runs converged within ±0.2% of the median LEV. The largest differences of −0.65%, −0.72%, and −0.69% were outliers on the 2.7 m, 3.7 m, and Nelder plots, respectively.
Figure 3. Empirical distributions of the differences (ΔLEV) between a plot’s median LEV and the LEVs obtained from 531,300 individual heuristic runs. Each heuristic was run 23,000 times on each plot, except for tabu search on the Nelder plot, which was limited to 2300 runs due to its computational cost (light grey shading); 98.8% of the runs converged within ±0.2% of the median LEV. The largest differences of −0.65%, −0.72%, and −0.69% were outliers on the 2.7 m, 3.7 m, and Nelder plots, respectively.
Forests 12 00280 g003
Forests 12 00280 g004 550
Figure 4. Changes in total merchantable volume harvested (thinned plus final harvest) and increases in LEV over optimized conventional prescriptions due to use of heuristic tree selection by plot, rotation length, and thinning age. Correlations between harvest volume and LEV were 0.08, 0.71, and 0.08 for the 2.7 m, 3.7 m, and Nelder plots, respectively.
Figure 4. Changes in total merchantable volume harvested (thinned plus final harvest) and increases in LEV over optimized conventional prescriptions due to use of heuristic tree selection by plot, rotation length, and thinning age. Correlations between harvest volume and LEV were 0.08, 0.71, and 0.08 for the 2.7 m, 3.7 m, and Nelder plots, respectively.
Forests 12 00280 g004
Forests 12 00280 g005 550
Figure 5. Boxplots of the elapsed time required to run each of the eight heuristics on each plot using an Intel i7-3300 quad-core processor with a 3.3 GHz base clock. One core-second represents the use of one processor core for one second. Since all heuristics obtained similar LEVs, heuristics with shorter runtimes would typically be preferred.
Figure 5. Boxplots of the elapsed time required to run each of the eight heuristics on each plot using an Intel i7-3300 quad-core processor with a 3.3 GHz base clock. One core-second represents the use of one processor core for one second. Since all heuristics obtained similar LEVs, heuristics with shorter runtimes would typically be preferred.
Forests 12 00280 g005
Forests 12 00280 g006 550
Figure 6. Retention of trees on each plot, by diameter class, resulting from heuristic optimization across all combinations of thinning age and rotation length. While the reference prescription thinned from below, heuristic tree selection typically identified complex prescriptions thinning predominantly from above.
Figure 6. Retention of trees on each plot, by diameter class, resulting from heuristic optimization across all combinations of thinning age and rotation length. While the reference prescription thinned from below, heuristic tree selection typically identified complex prescriptions thinning predominantly from above.
Forests 12 00280 g006
Forests 12 00280 g007 550
Figure 7. Thinning ratios obtained on each plot as a function of thinning method, a plot’s stand age at time of thinning, and the length of the even age rotation (the harvest interval was the number of years between thinning and end of rotation). Thinning ratios greater than 1.0 (dashed line) indicate thinning from above, and ratios below 1.0 indicate thinning from below.
Figure 7. Thinning ratios obtained on each plot as a function of thinning method, a plot’s stand age at time of thinning, and the length of the even age rotation (the harvest interval was the number of years between thinning and end of rotation). Thinning ratios greater than 1.0 (dashed line) indicate thinning from above, and ratios below 1.0 indicate thinning from below.
Forests 12 00280 g007
Table
Table 1. Comparison of this study to other recent investigations of thinning optimization. The authors of Çağlayan et al. and Yoshimoto et al. [2,11] non-exhaustively surveyed an additional 182 studies of optimal management from 2016 and earlier.
Table 1. Comparison of this study to other recent investigations of thinning optimization. The authors of Çağlayan et al. and Yoshimoto et al. [2,11] non-exhaustively surveyed an additional 182 studies of optimal management from 2016 and earlier.
StudyYearTree SpeciesObjectivesOptimization Methods
this study2020Douglas-firLEVEight heuristics
Pascual [3]2020Stone pineValue increment and spacingMixed integer programming
Halbritter [4]2020AnyLEVAnalytic
Fransson et al. [5]2019Norway spruceLEVGenetic algorithm (heuristic)
Jin et al. [6]2019Changbai larchNPVParticle swarm (heuristic)
Xue et al. [7]2019Scots pineLEVFive population heuristics
Vaukhonen and Pukkala [8]2016≥95% Norway spruceValue incrementIterative
LEV: land expectation value; NPV: net present value; value increment: tree growth in the first model time step after thinning. Tree species are Douglas-fir (Pseudotsuga menziesii (Mirb.) Franco), stone pine (Pinus pinea L.), Norway spruce (Picea abies L.), Changbai larch (Larix olgensis A. Henry) and Scots pine (Pinus sylvestris L.).
Table
Table 2. Economic parameters used in calculating per hectare land expectation value (LEV). Timber volumes in thousands of board feet (MBF) are measured using the Scribner Decimal C long log scale.
Table 2. Economic parameters used in calculating per hectare land expectation value (LEV). Timber volumes in thousands of board feet (MBF) are measured using the Scribner Decimal C long log scale.
ParameterValue
Reforestation cost, NPVreforestationUS$ 813 ha−1 + US$0.50 seedling ha−1
Discount rate, r4% year−1
Thinning age, T30–45 years in 5-year increments
Rotation length, R50–75 years in 5-year increments
Selection vector of individual trees, uicontrolled by heuristic
Volume of Douglas-fir j at thinning, Vthin,jMBF ha−1 from growth and yield models
Mean Douglas-fir pond value at thinning, P ¯ (T)US$453.67 + 2.776T MBF−1, 7.3 m logs
Douglas-fir real appreciation rate, a1% year−1 within rotation
Fixed thinning cost, Cthin,fixedUS$148 ha−1
Variable thinning cost, Cthin,variableUS$275 MBF−1
Volume of Douglas-fir j at final harvest, Vfinal,i,jMBF ha−1 from growth and yield models
Mean Douglas-fir pond value at final harvest, P ¯ (R)US$567.56 + 0.365R MBF−1, 12.2 m logs
Fixed final harvest cost, Cfinal,fixedUS$247 ha−1
Variable final harvest cost, Cfinal,variableUS$250 MBF−1
Annual management cost, CannualUS$18.50 ha−1
Table
Table 3. Summary of the three Douglas-fir spacing trial plots used for growth model initialization, as measured at age 30. All three plots are located in the Malcolm Knapp Research Forest in southwestern British Columbia, Canada (Figure 1) and have 50 years Douglas-fir site indices of 39.5 ± 0.5 m.
Table 3. Summary of the three Douglas-fir spacing trial plots used for growth model initialization, as measured at age 30. All three plots are located in the Malcolm Knapp Research Forest in southwestern British Columbia, Canada (Figure 1) and have 50 years Douglas-fir site indices of 39.5 ± 0.5 m.
Plot
Spacing		Area
(ha)		Live
Trees		Mean Density
(TPH)		QMD
(cm)		H100
(m)		Mean Planting Density (TPH)Tree Heights
Imputed
2.7 m square0.2522299629.527.012780
3.7 m square0.2214759623.328.37300
Nelder radial0.7557175724.128.610354
TPH: trees per hectare; QMD: quadratic mean diameter; H100: average height of the tallest 100 trees ha−1 measured. The regression for imputing Nelder plot heights is provided in Section S3 of the Supplementary Materials.
Table
Table 4. Comparison of heuristics evaluated in this study in order of increasing computational cost. Details of heuristic implementations and optimization mechanisms are provided in the Supplementary Material.
Table 4. Comparison of heuristics evaluated in this study in order of increasing computational cost. Details of heuristic implementations and optimization mechanisms are provided in the Supplementary Material.
HeuristicCost Including
Growth Model		Optimization MechanismsParameters
hero stochastic [this study]~O(N2 log N)sampling without replacement0
hero sequential [26]sequential iteration0
Simulated annealing [27]~O(19N2)sampling with replacement, reheating6
Record-to-record travel [28]4
Threshold accepting [29]1 or 4+
Great deluge [28]5
Steady state genetic algorithm [30]~O(60N2.6)parent selection, uniform crossover, mutation, replacement4
Tabu search [31]~O(N3/log N)steepest ascent, tenure1–2
O(•): empirically observed cost expressed in Landau notation; N: number of trees used to describe stand.
Table
Table 5. Changes in merchantable volume harvested and increases of median LEVs relative to the reference prescription from use of heuristic tree selection on the 2.7 and 3.7 m plots. The reference prescription was not valid for the Nelder plot, other rotation lengths, or other thinning ages.
Table 5. Changes in merchantable volume harvested and increases of median LEVs relative to the reference prescription from use of heuristic tree selection on the 2.7 and 3.7 m plots. The reference prescription was not valid for the Nelder plot, other rotation lengths, or other thinning ages.
Rotation Length
(Years)		2.7 m Plot Increase in3.7 m Plot Increase in
Volume (%)LEV (%)Volume (%)LEV (%)
502.375.053.264.55
551.027.002.665.27
600.5910.12.206.42
Minimum and maximum values across both plots are indicated in bold.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

West, T.; Sessions, J.; Strimbu, B.M. Heuristic Optimization of Thinning Individual Douglas-Fir. Forests 2021, 12, 280. https://doi.org/10.3390/f12030280

AMA Style

West T, Sessions J, Strimbu BM. Heuristic Optimization of Thinning Individual Douglas-Fir. Forests. 2021; 12(3):280. https://doi.org/10.3390/f12030280

Chicago/Turabian Style

West, Todd, John Sessions, and Bogdan M. Strimbu. 2021. "Heuristic Optimization of Thinning Individual Douglas-Fir" Forests 12, no. 3: 280. https://doi.org/10.3390/f12030280

APA Style

West, T., Sessions, J., & Strimbu, B. M. (2021). Heuristic Optimization of Thinning Individual Douglas-Fir. Forests, 12(3), 280. https://doi.org/10.3390/f12030280

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop