Next Article in Journal
Dynamics of Carbon Storage and Its Drivers in Guangdong Province from 1979 to 2012
Next Article in Special Issue
Optimizing Operational-Level Forest Biomass Logistic Costs for Storage, Chipping and Transportation through Roadside Drying
Previous Article in Journal
Calorific Value and Ash Content of Extracted Birch Bark
Previous Article in Special Issue
Effects of Spatial Boreal Forest Harvesting Practices on Efficiency through a Benchmarking Approach in Eastern Canada
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 12
Issue 11
10.3390/f12111481
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Compromise Programming Application to Support Forest Industrial Plantation Decision-Makers

by
Silvana Ribeiro Nobre
1,*,
Luis Diaz-Balteiro
2 and
Luiz Carlos Estraviz Rodriguez
3
1
Department of Administration, Economics and Sociology, Luiz de Queiroz College of Agriculture, University of Sao Paulo, Av Padua Dias 11, Piracicaba 13418-900, SP, Brazil
2
E.T.S. de Ingeniería de Montes, Forestal y del Medio Natural, Universidad Politécnica de Madrid, 28040 Madrid, Spain
3
Department of Forest Science, Luiz de Queiroz College of Agriculture, University of Sao Paulo, Av Padua Dias 11, Piracicaba 13418-900, SP, Brazil
*
Author to whom correspondence should be addressed.
Forests 2021, 12(11), 1481; https://doi.org/10.3390/f12111481
Submission received: 8 September 2021 / Revised: 4 October 2021 / Accepted: 15 October 2021 / Published: 28 October 2021
(This article belongs to the Special Issue Operations Research and Optimisation Techniques in Forest Management and Operations)
Browse Figures
Versions Notes

Abstract

:
The conflicts that arise between natural resources consumption and the desire to preserve them make the multicriteria decision theory necessary. Brazil, one of the 10 largest timber producers globally, uses optimization models that represent the growth of forests integrated with decision support systems. Brazilian forest plantation managers often face conflicts when continuously seeking efficiency gains (higher productivity at lower costs) and efficacy (higher profits with minimum social and environmental impacts). Managers of leading producing countries on timber, pulp, and fiberboard constantly interact to fine-tune industry processing demands vis-a-vis the demands of highly productive fast-growing forest plantations. The decision process in such cases seeks a compromise that accommodates short-term industry productivity optimization and long-term forestry production capacity. This paper aims to apply a forest management decision support system (FMDSS) to a case study that represents the challenges that industrial plantations in Brazil usually face. A vertically integrated pulp company situation was simulated to provide a real scenario. In this scenario, forest managers tend to shorten the rotations due to Brazil’s usually high-interest rates; meanwhile, industrial managers tend to ask for longer ones due to the positive correlation between age and wood density. Romero®, a Forest Management Decision Support System, developed by following the multi-criteria decision theory, was used to process the case study. Expressly, the hypothesis that mill managers initially have, that older ages rotation could improve mill production, was not confirmed. Moreover, mill managers lean towards changes in the short term, while the case study shows that changes in rotation size and genetic material take time, and decisions have to be made involving both interests: forest and mill managers.

1. Introduction

Forest management science encompasses the challenge of working with the forests that produce required benefits now without compromising future benefits [1]. Due to the need for disruption with business-as-usual approaches and the adoption of sustainable production patterns [2] (p. 13), there is an increasing trend for participation and transparency to improve planning processes [3,4] (p. 58; p. 217).
Environmental concerns, including sustainable production, bring challenges and opportunities to the forest industry. South America has continued expanding pulpwood production with an increasing number of new mills being built in Brazil, Chile, and Uruguay. These countries in 2016 accounted for 15% of global pulpwood production and 33% of exports. Pulp and paper demand are expected to grow by 2.7% annually, reaching 747 million tons by 2030 [5]. Following this trend, the Brazilian pulp industry has increased by 5.9% a year in the last 15 years, guaranteeing its position in the international scenario [6] (p. 41). Meanwhile, eucalyptus timber became expensive; sectoral inflation was 1.5 times higher than average Brazilian inflation over the last 10 years [6] (p. 18).
Since the 1970s, the Brazilian pulp industry has invested in plantations quality, such as photosynthetic capacity and higher wood density. These efforts resulted in the availability of a variety of suitable genetic materials for plantations. Genetic variability may now contribute to further productivity growth [7,8,9].
However, Eucalyptus clones that respond well in nurseries are not necessarily the best options to perform well during the first years after establishment [10]. Additionally, genetic material prepared to perform excellently in the fields is often not the best alternative for industry processing [11,12,13,14].
In this scenario, forest managers want to maximize their profits through operational efficiency and more productive genetic materials [15]. Otherwise, industry managers want to receive a regular and suitable mix of wood-density materials to maximize their pulp productivity [13]. Therefore, forest management may optimize the use of forest resources considering pulp tons per ha per year.
Optimized forest management began in the 1960s in North America and Europe and in the 1980s in Brazil [16]. It has expanded its scope to address new needs from preliminary harvest scheduling models over the last five decades [17]. Furthermore, a growing number of papers after 2000 show the widening application of Multicriteria Decision Making (MCDM) techniques to forest optimization models [18,19]. The literature agrees on the suitability of the MCDM to address increasing conflicts arising from environmental issues and production sustainability [20,21,22].
MCDM techniques might be applied to achieve sustainable forest resources through conflict resolution support [23,24,25]. Belavenutti et al. [18] analyzed 203 articles, from 1986 to 2016, on operations research applications into forest management. In total, 76 (37%) are related to industrial forest plantations (IFP) and were published in this century. A total of 25 (12%) are about IFP in Brazil and were published after 2000, most using classic optimization techniques. Furthermore, among those 76 on IFP, only 10 articles mention group decision-making (GDM) techniques, and none were among Brazilian case studies.
According to Acosta and Corral [19], the more participatory the process is, the better the decision-making process will be. Therefore, the application of interactive GDM has increased in the last decade [26]. Thus, this research work embedded models and methods in an FMDSS, allowing the interaction among decision-makers. They promote conveying, debating opinions, and committing to the impacts of the decisions.
In this context, given the state-of-the-art (Figure 1), this paper presents a case study of a Brazilian pulp industry situation where forest managers have pushed for high volumes of wood, prescribing six to seven-year-old rotations, with mean annual increment (MAI) generally reaching its peak. Due to the positive correlation between age and wood density, low wood density logs are usually delivered to the mill. Mill managers complain about low densities, as they typically lead to a lower content of cellulose fibers per ton of dry wood. Moreover, forest managers tend to shorten the rotations due to the usually high market interest rates.
This conflict scenario is represented by a multiple objective linear programming (MOLP) model used to calculate trade-off curves among conflicting criteria, commonly called the Pareto frontier. On top of those Pareto efficient solutions, this research uses compromise programming to reveal the best compromise interval between the main groups of stakeholders: forest managers and industrial managers.
This paper aims to demonstrate a decision process involving an industrial forest plantation case supported by an FMDSS that allows interactions among stakeholders with divergent interests. Specifically, this paper intends to present (i) the principles of the MOLP model that represents an industrial forest plantation case, (ii) the decision process from the preliminary results until the compromise solution, and (iii) a reasonable compromise between industrial and forest managers involving wood density and forest genetic material.

2. Material and Methods

2.1. Case Study

In Brazil, the yearly production of pulp mills ranges from 200,000 to 2 million tons of pulp per mill. In 2019, Brazil produced 19.7 million tons, 16.9 of short fiber, 100% from Eucalyptus planted in 2 million hectares, where MAI varies from 30 to 50 m3/ha-year, averaging 35.3 m3/ha-year [27].
In 2016, Brazil produced 69 million m3 of non-coniferous pulpwood [28]. The industrial short fiber average consumption was 4.34 m3 of wood to produce one ton of pulp. The literature mentions productivities from 3.5 to 5.1 m3 per ton of dry pulp [13]. To sustain their high level of productivity, Brazilian pulp mills’ main concerns regarding wood quality are (i) wood density [13], (ii) size uniformity of the chips [29], and (iii) chemical composition [30].
The case study refers to a hypothetical pulp mill that replicates actual conditions in Brazilian pulp mills. The main aspects of the plantation supplying wood to the mill are presented in Table 1. Due to the short rotation plantation being around six years, the length of the planning horizon was set to 19 years to guarantee the completion of at least three entire rotations [31].
The total area is 21,400 hectares distributed in 18 management units. The smallest unit has 550 hectares, and the largest one has 1900 hectares. Each management unit is homogeneous in terms of region, species, cycle, and age. The silvicultural costs are R$9500/ha over the years to complete one entire Eucalyptus plantation cycle, the pulpwood price is R$50/m3, and the annual nominal interest rate is 7% [32].
Wood density was used to classify clones into three groups. Group GenMat3 is the lower density class (average 420 kg/m3). The other two GenMat2 and GenMat1 classify clones into mid-density (500 kg/m3) and high density (580 kg/m3), respectively. The productivity varies from 42 to 52 m3/ha-year at seven years old. In the business-as-usual scenario, harvesting ages are limited to only two alternatives: six and seven years old.
Lopes and Garcia [14] isolated the effect of age into the density of some species of eucalyptus. Foekel [33] also found a good correlation between wood density and pulp production efficiency. The hypothetical curves for wood density as a function of age shown in Figure 2 and Figure 3 were created, fixing the slope coefficient and varying the intercept. Figure 3 presents the efficiency after the pulp digester; the efficiency was measured considering two moments in the process: (i) how many m3 of wood had entered into the mill, and (ii) how much pulp had been produced in dry tons of pulp.
The GenMat3 group is equivalent to the Eucalyptus grandis average wood density [14]. The GenMat2 (500 kg/m3) group and GenMat1 (580 kg/m3) density are equivalent to E. grandis × E. urophilla hybrids and E.urophilla, respectively. These species are widely used in genetic improvement programs in Brazil to boost volume productivity [34,35].
The after-digester efficiency has a positive correlation with wood density and a negative with the size regularity of the chips [33]. The chip size regularity does not correlate with any forest management variables. Therefore, for simplicity, the same average regularity was used for all groups. Average wood density values per age of the GenMat1, GenMat2, and GenMat3 groups were used to build the curves shown in Figure 3.
The initial situation of the plantation, in hectares per age class and GenMat groups, reflects the characteristics of the three groups of genetic material (Figure 4). GenMat1, the most desirable group by mill managers due to its high density, is less represented in each age class. Group GenMat3, which has a higher volume productive clone but lower wood density, prevails in most age classes.

2.2. Brief Description of Romero®

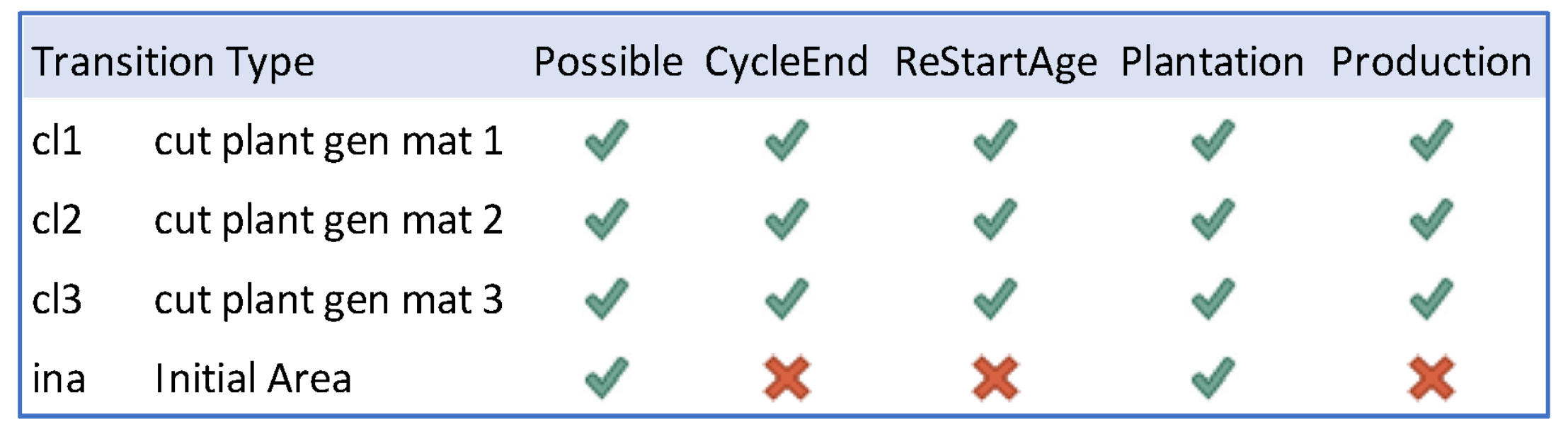
2.2.1. Forest Harvest Schedule Formulation

Since the beginning of the 1960s, forest researchers have been using mathematical programming to address forest planning. The harvest schedule is one of the most appropriate models used for long-term strategic forest planning worldwide [17,36,37,38,39,40,41,42,43,44]. This model consists of looking for the best alternative to intervene in forest growth. Decision variables are related to when, where, and how interventions would be made to maximize profits, ecosystem services, or production [45]. In those models, interventions are often linked to several types of forest establishments, restoration, silvicultural treatments, cuts, thinning, and non-wood product pickups.
Johnson and Scheurman [46] offered three alternatives for linear programming formulations to address a harvest scheduling model. From those three formulations, two have been often used to formulate a harvest schedule since then.
In the Model I formulation, the decision variable Xur is an area of a unit u managed according to a prescription r, where prescription refers to a sequence of interventions that can happen within the planning horizon. In the Model II formulation, the decision variable is an area of a unit u where one complete forest cycle occurs. Romero® encompasses an extension of Model II formulation where the decision variable is an area of a unit u in which a management intervention changes the previous course of the forest [47]. The formulation proposed by Nobre [47] is described in Appendix A.

2.2.2. Multicriteria Concepts Embedded in Romero®

Essential multicriteria concepts, described by Ballestero and Romero [48], are the foundation of Romero®’s model formulation. They are implemented according to the following descriptions.
(a)
Attributes. These values are calculated independently from any stakeholder’s choice. In our case study, a “Production” accounting variable could be written using the expression, ∑ i = 1 I ∑ u = 1 U ∑ k = 1 K V i u p k X i u p k which is the total production within the horizon. It is called xTotalProd.
(b)
Objectives. They are all available to be selected by the user. If the user selects the attribute xTotalProd to form a maximization objective, then the model creates statements as follows:
M a x     Z     =     ∑ p = 1 P x T o t a l P r o d p s u b j e c t   t o :                       I n i t i a l   A r e a ) ...                       C o n s e r v a t i o n     o f   A r e a ) ...                     P r o d u c t i o n )   ∑ i = 1 I ∑ u = 1 U ∑ k = 1 K V i u p k X i u p k     −     x T o t a l P r o d p     =       0           ∀   p   ,   p   =   1 , 2 , .... P
(c)
Targets and Goals. In statement (1), in the line “Goal”, the value vMinp is a target; decisionmakers want at least vMinp of production in period p. In Romero®’s implementation, targets are parameters that are saved in a database and ready to be updated.
P r o d u c t i o n )             ∑ i = 1 I ∑ u = 1 U ∑ k = 1 K V i u p k X i u p k         −         x T o t a l P r o d p     =   0                                   ∀   p   ,   p   =   1 , 2 , .... P G o a l )                                     x T o t a l P r o d p                                                                                                           ≥     v M i n p         ∀   p   ,   p   =   1 , 2 , .... P
Moreover, deviation variables can be included in the “Goal” line. The objective function should be modified to minimize the sum of the deviation variables to turn the model into a Goal-programming model, which is not the case when compromise programming is the selected multicriteria technique. In this case study, Romero® calculates the deviations but does not minimize them.
(d)
Criteria. In statements (1) and (2) the Production criterion means that the attribute xTotalProd is used to calculate the objective MaxTotalProd.
Romero® controls attributes, objectives, targets, and goals. It always calculates many other attributes like in the Production line of the statement (2). Depending on the decision-makers choices, the attributes will be used in goals or objectives.
The acceptable technique for considering multiple objectives is multiobjective mathematical programming (MOLP). The MOLP notation proposed by Romero [49] states that the model seeks a set of efficient solutions that satisfy the objective functions f1, f2, …, fn, and they are subject to a set of constraints represented by a vector of functions Q(x) (statement (3)).
E f f     f ( x ) =     [ f 1 ( x ) ,   f 2 ( x )   ,   .... ,   f n ( x ) ] s u b j e c t   t o :                                          Q ( x )
In this case study, f1and f2 of statement (3) are the mill production and the forest profits, respectively. The function Q(x) will be the entire Model formulation proposed by Nobre [47]. To do so, Romero® implements the two following steps.
The first step of a MOLP consists of (i) optimizing one criterion at a time, using the same scenario, and (ii) calculating all attributes related to the other criteria (the ones that are not being optimized). After calculations, a payoff matrix shows the level of conflicts among the objectives. The second step is to figure out what happens among the extreme points presented in the payoff matrix, which are optimal for each criterion using the Pareto optimality concept. Figure 5 summarizes the Romero® calculation process.
The most common methodology for calculating Pareto-optimal solutions [48,49] is the constraint method because it has the lowest computational cost. This method consists of optimizing one of the objectives while the others are placed as parametric equality constraints. We generate one Pareto-optimal solution for each vector of values to be used as a right-hand side in the parametric constraints.
Romero® shows the payoff matrix and the Pareto frontier as described above and saves the entire MOLP solution of each point along the curve; however, the decision process needs to go further. The next phase is to select a small set of solutions that could best fit a specific group of decision-makers along the Pareto frontier. One of the most productive ways to accomplish this task was proposed in 1973 by Yu and Zeleny under the name of Compromising Programming [48,49].

2.2.3. Compromise Programming (CP)

The ideal point is the point where all criteria have their best level, which is never achievable because all criteria cannot assume the best level at the same time in a conflict context. The fundamental concept of CP, the Zeleny axioma, says that efficient solutions closer to the ideal point would be preferred to those farther. Moreover, a rational choice is as close as possible to the ideal point [49,50,51].
Therefore, we need to calculate the distance to the ideal point [52] and deal with the decision-maker’s preferences regarding staying closer to one best attribute level than to another. Additionally, to avoid meaningless comparisons between attribute values due to their different measurement units, the attribute values must be normalized [52]. Distance, normalization, and preference concepts [49,50] are described in Appendix B.
According to Ballestero and Romero [48], the optimum choice for the decision-maker is given by the feasible solution where the utility function reaches its maximum value, i.e., the Lagrangian maximum tangency between the Pareto frontier and the family of iso-utility curves. CP defines a compromise set as the portion of the Pareto frontier where the tangency with the iso-utility curves will occur; that is, something like a landing area of the utility curve. The limits of the compromise set are Min(L1) and Min(L∞), which are also described in Appendix B.
Therefore, Romero® calculates both distances to the ideal point, with a minimum of L1 and a minimum of L∞ [53]. That is to say, the compromise set is a closed interval of the Pareto frontier, and Romero® shows the distances Min(L1) and Min(L∞) along the Pareto frontier, later shown graphically in the results section.
As all attribute values of each efficient solution are saved in a database, there is no need to build and run the linear models of the statements (A10) and (A11) described in Appendix B. To find the two points Min(L1) and Min(L∞) along the Pareto frontier, Romero® implemented the following sequence of steps:
  • The user inputs how many points he wants to calculate in the Pareto-efficient set. The user should set as many points as possible depending on the time each run (to obtain one point) takes.
  • Romero®
    o
    distributes those points between the best and worst values of each attribute,
    o
    runs the MOLP model to calculate the efficient point using the constraint methodology,
    o
    saves the results (attribute values, decision variables, and deviation variables) of all points into the database.
  • The user updates the decision-makers’ weights for each criterion according to their preferences.
  • Romero®:
    o
    calculates L1 and L∞ for each efficient point,
    o
    finds the minimum L1 and minimum L∞ using as SQL to implement and find a proxy of the linear programming models of the statements (A8) and (A9) in Appendix B.

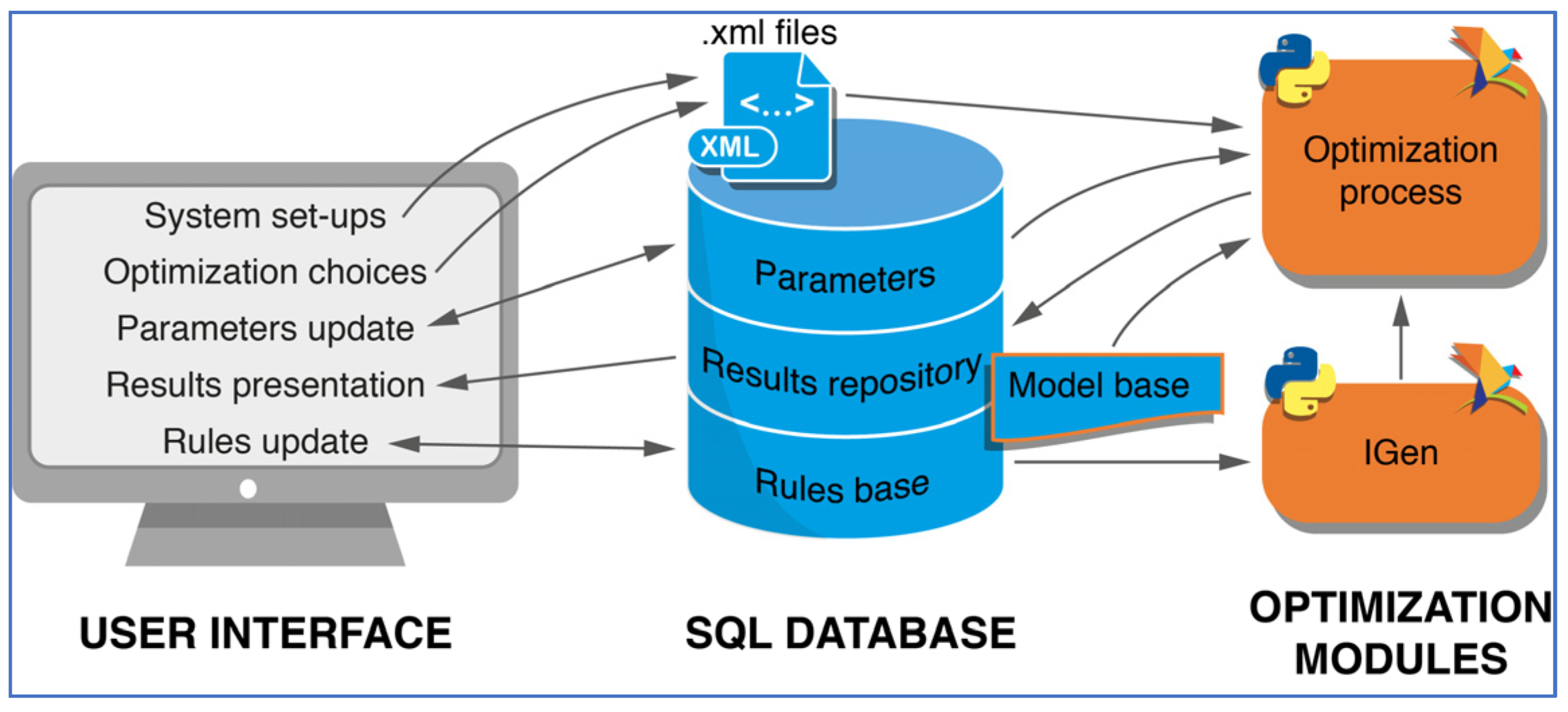
2.2.4. Romero® Architecture

This section describes Romero®architecture and embedded mathematical programming. Most importantly, this section focuses on how the system guarantees the interactive MCDM principles.
According to Kanojiya and Nagori [54] guidelines, a DSS, and any other type of model-driven system, should include, at least, these general components: (i) a user interface, (ii) a database, knowledgebase, or data repository to handle with inputs and outputs (iii) model base, and (iv) a rule engine. To follow the literature guidelines, Romero® comprises the general components shown in Figure 6.
The first component, the database, deals with many types of information. A SQL Database Management System controls information such as parameters, results, and rules. The user’s optimization process and set-up information choices are stored in XML files. The model is saved in Pyomo© source files. The second component, the user interface, comprises a set of screens to communicate with users. The third component includes the optimization modules written in Pyomo©, Python©, and its libraries to read parameters, generate forest interventions, run the model, and save results. Finally, the fourth component, the inference engine named iGen, covers the generation of the possible forest interventions.
In the optimization modules, while optimization for each criterion is running, Romero® prepares the results to calculate the payoff matrix and automatically sets the parameters to the Pareto frontier. Two steps are needed to use the constraint method: (1) get the range from minimum and maximum values of all attributes and (2) use these range values as constraints. Romero® can recreate a solution when decision-makers choose any point along the Pareto frontier because it saves all decision variable results. To calculate the two points Min(L1) and Min(L∞), Romero®runs a minimization SQL query from results stored in the database.
The main objective of the inference engine iGen is to generate the indexes i (interventions) of the model described in Appendix A. The initial area information and rules regarding changes in a specific forest project feed the engine. iGen’s first step is to create a structure according to the initial area. The possible transitions are generated based on the rules and the initial situation of the forest. The last step schedules the possible transitions along the horizon using the information about periods and ages. Scheduled transitions get the name of intervention.

2.3. Romero’s® Application to the Case Study

Due to the high productivity in volume, and general low wood densities, the case study considers that pulp mill managers require higher densities and want to evaluate the hypothesis that longer rotations would increase mill productivity. Romero® was configured to evaluate the consequences of harvesting the eucalyptus plantations at older ages.
The case study demands older ages of alternative prescriptions. New rules were set to iGen, allowing genetic material changes after clear-cuts, as shown in Figure 7. The transition types cl1, cl2, and cl3, represent clear-cuts; the cl1 clear-cuts and re-establishes the plantation with GenMat1, cl2 with GenMat2, and cl3 with GenMat3. After a cl1 intervention, it will be alternatively possible to have interventions of all three types (cl1, cl2, and cl3). Figure 7 shows the ina transition type, which represents the initial forest status. After an intervention of the ina type, interventions cl1, cl2, or cl3 may follow; ina does not change the value of any forest attribute.
Figure 8 shows that the transition types cl1, cl2, and cl3 are possible in this scenario. They all end a forest cycle, reset the age to zero, renew plantations, and define the productive transition according to the corresponding production parameter. All transition types (cl1, cl2, and cl3) trigger changes in the values of attributes c, r, and sp for the forest plantation (Figure 7). Attribute u (management unit) remains the same u. However, attribute c (cycle) turns into c + 1, attribute r (rotation) turns to 1, and attribute sp (species) turns to cl1, cl2, or cl3, depending on the transition type.
Furthermore, cl1, cl2, and cl3 interventions may be repeated for a set of possible harvesting ages. This case study considers three scenarios for a distinct set of ages described (Table 2).
iGen uses rules to generate alternative forest prescriptions that can potentially meet mill requirements regarding higher wood density. Besides wood quality, the mill also imposes further requirements such as:
  • regulated wood flow,
  • genetic diversification to mitigate risk exposure to plagues and diseases, and
  • production sustainability.
From period two onwards, wood delivery cannot decrease above 10% or decrease above 25%. The planted area should simultaneously have (i) less than 60% covered by one single genetic material and (ii) at least 20% of each of the three genetic materials to avoid plagues and diseases.
Regarding production sustainability, the age class constraints were included in the model to guarantee a reasonably well-regulated plantation forest. Therefore, one age class can have up to 10% more or less area than the following age class. Table 3 summarizes the mill requirements.
The initial situation, the forest managers’ demands, and the mill requirements were applied by setting Romero’s® parameters and constraints. After setting the parameters and acceptable prescriptions for future management, it is possible to define the prime conflicts accurately.
MaxNPV (maximize Net Present Value), listed among available criteria in Romero®© (Table 4), was chosen to represent forest managers’ aspirations. At the same time, mill managers’ aspirations are represented by MaxMillPrd (Maximize Mill Production). MaxNPV and MaxMillPrd are determined using accounting xTotalNPV and xTotalMillPrd.
Additionally, one more criterion represents the environmental concerns since environmental issues pressure both sides. MaxStck (Maximize Final Stock) can represent the environmental concern; MaxStck expresses wood stock at the end of the planning horizon employing the accounting variable xTotalStock.
The objective functions built to calculate the three objectives (MaxNPV, MaxMillPrd, MaxStck) depend on decision variables xi, which refers to the area in which the intervention i will occur. Romero® was used to set up the parameters, handle parameter combinations, run different scenarios, and report the results.
Finally, upon the definitions mentioned in previous paragraphs, it is possible to summarize the model that represents the case study. Statement (4) is a brief schema of the resulting formulation, which shows a multiobjective linear programming (MOLP) model designed to address the described case study.
The first sentence in the statement (4) states that this model seeks efficient solutions using variable xi. Likewise, the following list of the constraints defines the feasibility, which depends on the same decision variables xi.
E f f       f ( x i , ) =         [ M a x N P V ( x i ) ,                                                 M a x M i l l P r d ( x i ) ,                                                 M a x S t c k ( x i ) ] S u b j e c t   t o :                             I n i t i a l   A r e a                             C o n s e r v a t i o n     o f   A r e a                             ...                             C a l c     o f   a c c o u n t i n g   v a r i a b l e s                                                 p r o d u c t i o n                                                 a l l   M u l t i c r i t e r i a     a t t r i b u t e       v a r i a b l e s                             ...

3. Results

This section initially presents a subset of three scenarios created by iGen combining different ages (Table 2), limiting the choice of ages considering only short, medium, or long rotations as forest management prescriptions. For each scenario, the corresponding multiobjective linear programming (MOLP) problem optimized all three criteria, one at a time. Table 5 shows the main results of the three scenarios.
Due to the conflicting nature of these two criteria, as mill production increases, the forest net present value (NPV) decreases. Table 5 shows the differences observed between the highest and lowest NPV as Forest NPV Reduction. The differences observed between the highest and the lowest pulp production are reported as Pulp Production Reduction.
The results demonstrate how conflicting interests expressed by forest managers and industrial managers can create fairly different outcomes. Consequently, the multi-criteria approach is adequate to evaluate the case study. Additionally, Romero® could support the multi-stakeholders simulated teams, starting by defining the minimum and maximum ages that foresters would be allowed to harvest.
Considering the three scenarios presented in Table 5, and as described in Section 2, the simulation would start by confirming the parameter and asking Romero® to run. The simulation finishes when Romero® shows the results window. Table 6 summarizes the running information of Romero® after each scenario.
Table 6 shows the data processing as time-consuming; the more variables and constraints Romero® had to deal with, the more time-consuming the data processing became. The most time-consuming step is the concrete model building routine when Pyomo builds an abstract model. Naturally, the larger the model, the longer it took to build it.
As observed in Table 6, the short-rotation scenario took 21 min to build, while the smallest one took only three minutes. It is worth noting that although lengthy, this is not relevant when it gets to the phase when stakeholders seek a consensus. At that point, with the model built, Romero® will cycle through solving, changing the values of a few parameters defining the next objective, and solving again. These latter steps run faster than the model building steps (6–7 s for the smallest problem and 18–19 s for the biggest problem).
Scenario number 217 illustrates the analysis provided by Romero® to facilitate the search for consensus between stakeholders. The third criterion, maximize final stock, was included to add more substance to the analysis. It considers the consequences of regulating the annual pulpwood demand and maximizing the standing wood stock at the end of the planning horizon. NPV and pulp parameters were only calculated and left unconstrained.
A payoff matrix was built to evaluate the scenario and to allow us to see in detail the conflicting results in terms of NPV (MaxNPV), pulp production (MaxMillPrd), and final wood stock (MaxStck). Table 7 shows the resulting payoff matrix. The test was done using the midrange rotations scenario, considered a good starting point due to its conciliatory nature of not tending to either of the two extremes (very short or very large rotations). It allows for harvests to happen in 6-, 7-, and 8-year-old stands.
The first column of Table 7, “Clear-cut area”, refers to a summation of all areas harvested during the planning horizon. Additionally, the “Production” column reports the total volume produced in these cuts. From these two pieces of information, it is possible to get average productivity along with the horizon.
It is assumed that foresters and mill managers agree on how far they would like to be from the final stock constraint. Therefore, from this point on, for simplicity, the results are shown considering only the two original groups of stakeholders.
Figure 9 shows the annual flow of pulpwood when each criterion is maximized. It is worth noting the striking differences in how the plantations evolve along the planning horizon in terms of the area of GenMat groups distributed annually. Visibly, the MaxNPV criterion conducts the management units to the more extensive sharing of GenMat3 (the lower density group). On the other hand, the MaxMillPrd strategy gradually replaces GenMat3 with GenMat1 and manages the plantations to more significant sharing of GenMat1 in the future.
Figure 10 shows the quality of the pulpwood in terms of the age classes at which the logs were harvested. Conversion rates were higher, though density increases with age, and the use of logs from longer rotations would be more significant. More substantial participation of logs from older trees seems to be a trend in the future but is not so evident at the beginning and middle of the horizon. Nevertheless, maximizing pulp changes the annual composition of logs in terms of age classes.
An agreement would not be on extreme points; therefore, the two stakeholder groups might be willing to verify the trade-offs between the two criteria. Twenty points were calculated between the two extremes to create the Pareto frontier between the two criteria (Figure 11).
The Pareto frontier can give further support to negotiation. It visually expresses the tendency of the consensus solution toward one stakeholder or the other. It may also help as a tool during the discussion to mitigate eventual tendencies of one part becoming more influential than the other.
In this analysis stage, compromise programming (CP) can lead one step closer toward the consensus. Figure 12 shows the compromise set, considering that the relative importance between forest and industrial managers is even. Table 8 demonstrates how the distances were calculated.
NPV and pulp production assume the higher values in the theoretical optimum point, reported as “Optimum”, in Figure 12, R$266,445,003 and 5,022,290, respectively. The distance function calculates the distance from any point over the Pareto frontier to this theoretical optimum point.
Line segments a and c (Figure 12) are the distances from points L∞ and L1 to the industrial managers’ best value. Likewise, b and d are the distances from L∞ and L1 to forest managers’ best value. The sum of the distances from point L∞ to the Optimum point is a + b. The sum of the distances from point L1 to the Optimum point is c + d. Herein, these distances (a, b, c, and d) from the Optimum point are called losses.
L1 is the point where the sum of both losses is at its minimum along the Pareto frontier (line segments c + d). In other words, L1 is the point where stakeholders lose less together. On the other hand, L∞ is the minimum of the max between them, which corresponds to line segment a in Figure 12. At L∞, there are no noteworthy losses for any of the stakeholders.
Table 8 shows details of only three points of the Pareto frontier. The 9th point is the L∞, and the 11th point is the L1. The columns “Best Value” and “Worst Value” repeat the optimum point’s values. The “Interval” column refers to the difference between the best and the worse values. The Distance column presents the distances between the point on the Pareto front and the line that crosses the optimum point. These distances are calculated according to statement (A2).
According to CP concepts, the utility curve touches the Pareto frontier between L∞ and L1. Point 10 of Table 8, which is located between L∞ and L1 (Figure 12) can be considered a good compromise in this case study. Even if the decision-makers agree to select point 10, they might need a more in-depth understanding of this particular solution. Therefore, point 10 should be examined to determine if it meets the needs of the decision-maker.
The graphs shown in Figure 9 and Figure 10 are rebuilt using data from the solution of the Pareto frontier point 10. While previous figures show the extreme solutions, in Figure 13 and Figure 14, it is possible to see a balanced solution that might be taken as a compromise.
In this particular point, the solution strategy emphasizes the adoption of GenMat2, which is the intermediate group of genetic material in terms of forest productivity in volume, wood density, and industry efficiency. Gradually, the plantations with GenMat3 and GenMat1 were replaced with GenMat2 until it reached the maximum possible for each group, 60%.
Meanwhile, the other two groups, GenMat1 and GenMat2, achieve the lowest level for each group with 20%. The solution strategy leads to younger ages at the beginning of the planning horizon and, gradually, guides to 100% of the median age.

4. Discussion

Among the scenarios presented in the previous section, the differences between the best and worst outcomes, from the forest managers’ perspective, cause losses in NPV, ranging from 14.51% to 16.97%. On the opposite side, from the mill managers’ perspective, the differences between the best and worst outcomes cause decreases in pulp production, ranging from 6.29% to 7.85%.
Table 5 presents interesting and unexpected results. The first is the most significant reduction in NPV, which occurs in the shorter-rotations scenario 216, precisely what prevails in Brazil. Another impressive result is that the value of total NPV increases in the midrange and more extended rotation scenarios. That seems counterintuitive to the current preferences for shorter rotations expressed by Brazilian forest managers; leverage for mill managers favors optimizing pulp production.
Contrary to mill managers’ expectations, the best mill performance does not come from longer rotations but from the possibility of cutting at five years old at the beginning of the horizon and replacing the genetic material as soon as possible. Scenario 217 shows this effect clearly (Figure 10). It is assumed that, in scenario 216, this effect was more intense because the model allowed cutting at five years old.
These results indicate that five-year-old cuts are good, paradoxically, only for the mill due to the opportunity to replace GenMat3. An in-depth analysis of forest yield curves might show that the maximum MAI is closer to seven years old than five years old.
It is worth mentioning that no improvements happen when age nine is added to alternative cut ages (Table 5). One of the reasons might also be the need for MatGen3’s replacement. However, there is one more significant reason in this context. Figure 4 shows that there is 2000 ha of age five and 2000 ha of age six. At the beginning of the planning horizon, it would not be possible to cut at ages eight or nine to achieve the required flow production. Cuts in older ages can only be possible from the fourth period on (Figure 10).
Therefore, results demonstrate more gains in changing the genetic material than in cutting at older ages, given the industrial efficiency curves (Figure 3). Both extreme solutions show that the model conducts replacing genetic material according to the criterion that is being maximized. Even in the compromise solution, the model led to the maximum possible, a 60% area of the intermediate genetic material group.
The results illustrate how CP embedded in an FMDSS with the characteristics of Romero® can support large-scale multi stakeholders’ decision processes. Any harvest-schedule-based problem involving diverse objectives can be addressed by the approach when parties involved in the negotiation are willing to seek consensus interactively driven by the compromise programming principle.
Romero® can guide to a compromise solution where stakeholders assume responsibilities regarding the decisions’ impact as prescribed by Bruña-García and Marey-Pérez [4] and other authors [20,21].
Forest monitoring information and knowledge usually indicate improvements in how the forest is managed [55]. The presented case study gave an example of this kind of dynamics through the age rotation analysis when stakeholders ask for a new forest management shape; not to mention that the attributes calculated under the multicriteria conceptual framework provide the stakeholders with the means to test their hypotheses and achieve their aims.
Despite the literature recommendation [4,19,56,57,58], only a few FMDSS implemented MCDM, including interactive participatory planning [17,59]. Regarding the application of MCDM techniques, CP concepts embedded in Romero® contribute to filling the gap on the use of MCDM techniques into FMDSS capable of supporting participatory processes.

5. Conclusions

From this discussion, we conclude that the initial hypothesis that cutting in older ages could improve mill production was not confirmed. Secondly, changes in rotation size and genetic material take time, and decisions should be made involving both long-term interests: forest and mill. Thirdly, Romero®’s support was essential to consider and inspect all aspects of the solution; it was an information-based decision-making process as preconized by literature.
Romero® and its embedded models and methods, when applied to an industrial forest plantation case involving interactions among groups with diverse interests, demonstrated that incorporating MDCM techniques in a participatory process could improve the decision-making process and the quality of the decisions. Expressly, the hypothesis proposed in the study case that longer rotations could improve mill production, as expected by the mill managers, could not be confirmed. Nevertheless, Romero® led the compromise to an unexpected point where the possibility of harvesting in younger ages allowed an earlier replacement of less efficient genetic material.
Additionally, a specific MOLP integrated into an MCDM framework can produce the necessary elements for a comprehensive multicriteria analysis, such as efficiently reporting (i) pay-off matrices, (ii) the efficient solutions of the Pareto frontier, and (iii) the compromise set. Therefore, the Compromise programming approach proved suitable for dealing with cases in which different stakeholders have conflicting views on managing production forests. Furthermore, Romero® was shown capable of promoting interaction among stakeholders while seeking consensual decisions.
The Romero® approach can be packed as applying rigorous multicriteria principles to a MOLP harvest schedule formulation. It employed an interface that promotes compromise and consensual planning. Furthermore, Romero® demonstrated through the case study application that strategic scenario analysis is still an essential tool to evaluate future impacts of short-term decisions.
This case study model demands an empiric correlation between after-digester productivity and wood ages or other wood attributes. Further and more specific case studies should be conducted to increase the integration between pulp mill requirements and forest management, which will undoubtedly contribute to the effective use of the natural resources dedicated to pulp production.

Author Contributions

Conceptualization, S.R.N. and L.D.-B.; methodology, S.R.N.; software, S.R.N.; validation, S.R.N., L.C.E.R. and L.D.-B.; formal analysis, S.R.N.; investigation, S.R.N.; resources, L.C.E.R. and L.D.-B.; data curation, S.R.N.; writing—original draft preparation, S.R.N.; writing—review and editing, S.R.N., L.C.E.R. and L.D.-B.; supervision, L.D.-B. and L.C.E.R.; project administration, L.D.-B.; funding acquisition, L.D.-B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: romeromulticriteria.com/RomeroThesis.db; romeromulticriteria.com/RomeroThesis-Results.xlsx; romeromulticriteria.com/RomeroThesis.zip. The database is an SQLite file; it can be open using the free software SQLite Studio (RomeroThesis.db) and the spreadsheet is an Excel file that contains the analysis of the result (RomeroThesis-Results.xlsx).

Acknowledgments

The first author gratefully acknowledges the support of CNPq–Brazilian National Research Council—scholarship 202017/2015-0. Additionally, this research was partially funded by the European Union’s H2020 research and innovation program under the Marie Sklodowska-Curie grant agreement No 691149–SuFoRun and grant agreement No 101007950—DecisionES. Moreover, Luis Diaz-Balteiro was funded by the Ministry of Economic and Competitiveness of Spain under project AGL2015-68657.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A. Model Formulation

   M a x       Q     =       ∑ i = 1 I ∑ u = 1 U ∑ p = 1 P ∑ k = j + n K E i u p k X i u p k        s u b j e c t     t o : I n i t i a l   A r e a )                                 ∑ i = 1 I ∑ p = 1 P X i u p k                                                                     =           A u             ∀   u     ,     u   =   1 , 2 , ... , U                                                                                                                                                                                                                               w h e r e   k = 0   C o n s e r v a t i o n   o f   A r e a ) ∑ i = 1 I ∑ j = p + n J X i u j p           −           ∑ i = 1 I ∑ k   =   1 K X i u p k           =           0                   ∀   p   ,   p   =   1 , 2 , ..... ,   P                                                                                                                                           ∀ u ,     u   =   1 , 2 , ..... , U P r o d u c t i o n )                                     ∑ i = 1 I ∑ u = 1 U ∑ k = 1 K V i u p k X i u p k   −     T o t a l P r o d p =       0                       ∀   p   ,   p   =   1 , 2 , .... P W h e r e   :                   X i u p k     i s   t h e   a r e a   ( h a )   o f   t h e   u n i t   u ,   i n   w h i c h   i n t e r v e n t i o n   i   h a s                                                                         o c c u r r e d   i n   p e r i o d   p , l i n k e d   t o   t h e   l a s t   i n t e r v e n t i o n   ( i k )                                                                           t h a t   h a p p e n e d   i n   p e r i o d   k                                               E i u p k       i s   a   p e r − h a   N P V   o f   a l l   c o s t s   a n d   i n c o m e s   a s s o c i a t e d   t o                                                                         t h e   i n t e r v e n t i o n   i   t h a t   h a s   o c c u r r e d   i n   p e r i o d   p   l i n k e d   t o                                                                         t h e   l a s t   i n t e r v e n t i o n   ( i k )   h a p p e n e d   i n   p e r i o d   k                                               A u               i s   t h e   s i z e   ( h a )   o f   t h e   u n i t   u                                                 V i u p k       i s   a   p e r − h a   o u t c o m e   o b t a i n e d   f r o m   u n i t   u                                                                         i n   w h i c h   i n t e r v e n t i o n   i   h a s   o c c u r r e d   i n   p e r i o d   p                                                                       l i n k e d   t o   t h e   l a s t   i n t e r v e n t i o n   ( i k )   h a p p e n e d   i n   p e r i o d   k                                                 n                   i s   t h e   n u m b e r   o f   p e r i o d s   b e t w e e n   i n t e r v e n t i o n s   i   a n d   ( i k ) ,                                                                       n   a s s u m e s   d i f f e r e n t   v a l u e s   d e p e n d i n g   o n   t h e   t y p e   o f   i                                               K   a n d   J   a s s u m e   d i f f e r e n t   v a l u e s   d e p e n d i n g   o n   t h e   t y p e   o f   i                                               I   c a n   a s s u m e   d i f f e r e n t   v a l u e s   d e p e n d i n g   o n   u                                               P   w i l l   b e   t h e   h i g h e r   v a l u e   o f   p   f o r   e a c h   u n i t   u , t h a t   i s , w h e n i t                                                         t h e   l a t e s t   a l t e r n a t i v e   i n t e r v e n t i o n      

Appendix B. Compromise Programming Definitions

The Ideal point is the point where all criteria have their best level, and this point is never achievable because all criteria cannot assume the best level at the same time in a context of conflict. Efficient solutions closer to the ideal point would be better than those that are farther, precisely the Zeleny axioma content and the fundamental concept of compromise programming. Moreover, to be as close as possible to the ideal point is the rationale of human choice [49,50].
Therefore, to go further in defining a compromise, there are questions to answer, such as (a) how to calculate the distance to the ideal point [52], and (b) what if the decision-makers have preferences regarding staying closer to one attribute best level than to another. Additionally, to avoid meaningless comparisons between attribute values due to their different measurement units, the attribute values must be normalized [52].
N o r m a l i z e d   D i s t a n c e =   | ( B e s t V a l u e     −     V a l u e ) ( B e s t V a l u e   −   W o r s t V a l u e ) |    
The normalized distance from an efficient point along the Pareto frontier to the ideal point can be determined as follows:
N a ( x )   =     | f a *     −     f a ( x ) | | f a *     −     f * a | w h e r e :     N a ( x )         a   n o r m a l i z e d   d i s t a n c e     o f   t h e   a t t r i b u t e   a       f a *                       t h e   b e s t   v a l u e   o f   t h e   a t t r i b u t e   a   w h e n   t h e   o b j e c t i v e   a     i s   o p t i m i z e d     f * a                     t h e   w o r s e   v a l u e     o f   t h e   a t t r i b u t e   a   w h e n   o t h e r   o b j e c t i v e s   a r e   o p t i m i z e d     f a ( x )           t h e   a t t r i b u t e   a   v a l u e     i n   a   s p e c i f i c   P a r e t o − e f f i c i e n t   p o i n t  
The set of techniques to measure this distance, inside the CP context, is called “a family of distance functions” Lp. This text does not intend to go deep into the Lp definitions; however, it is crucial to have a clear understanding of the distance concepts [49] to sanction the use of the two limits of the compromise set: Min(L1) and Min(L∞).
The starting point is the geometric distance defined by Pythagoras theorem that is the minimum distance between two points in two-dimensional space named “Euclidean distance”. It is easy to generalize the “Euclidean distance” to an n-dimensional space where the distance between two points x 1 =     ( x 1 1   ,   x 2 2   ,   ...   ,   x n 1   )   and x 2     =     ( x 1 2   ,   x 2 2   ,   ...   ,   x n 2   ) can be written as follows:
d   =     ∑ j = 1 n ( x j 1   −   x j 2 ) 2  
However, the most acceptable generalization of the n-dimensional “Euclidean distance” [49] is given by the following expression:
L 1   =     ∑ j = 1 n | x j 1   −     x j 2 |  
where Lp represents the family of distance functions. For each value of p, there is a different distance value Lp for the same pair of points x1 and x2. A particular case Lp is for p = 2 when the two-dimensional “Euclidean distance” is obtained. A second particular case of Lp is for p = 1, called “Manhattan distance”, which, in a two-dimensional space, is the sum of the cathetus lengths. Therefore, L1 is the largest distance between x1 and x2, while L2 is the shortest one according to Pythagoras theorem.
L 1   =   ∑ j = 1 n | x j 1   −   x j 2 |  
when the metrics p tends to ∞, L∞ is called “Chebysev distance” and tends to the value that can be calculated as follows:
L ∞   =       M a x j = 1 n   ( | x 1 1   −     x 1 2 | ,   | x 2 1   −     x 2 2 | ,   ... ,   | x n 1   −     x n 2 | )
The statement (A7) means that the L∞ is given by only one deviation of the set of n deviations: the larger one. If L1 and L∞ are calculated for each point along the Pareto frontier, it is possible to determine two shorter distances, the Min(L1) and Min(L∞).
The Yu theorem, presented in the literature in 1974 [49] demonstrated that for a two-criterion problem, the compromise solutions calculated with Lp (statement (A5)) are contained in a “compromise set”, which is a subset of the efficient solutions set (Pareto frontier). In addition, the limits of this subset are given by L1 and L∞ (statements (A6) and (A7)). Two years later, Freimer and Yu demonstrated similar conditions to a more than two-criterion problem. Moreover, according to the traditional economic analysis and the theorems of Yu, the utility functions intercept a Pareto frontier in one of the points of the “compromise set”.
L1 is a summation of the deviations between each attribute value from this ideal value (statement (A6)). The minimum L1 is the maximum efficiency point, where the best point is achieved considering the value of the attributes. However, this point may be unbalanced, that is to say, in that point; one attribute can have much more value than others. Moreover, if the decision-makers have different preferences that can be translated into weights (from 0 to 1), L1 could be mathematically represented as follows using previous definitions of statements (A3) and (A6):
L 1   =     ∑ a = 1 A w a     N a ( x ) w h e r e :       w a       i s   t h e   w h e i g h t   o f   t h e   a t t r i b u t e   a       N a ( x )       i s   t h e   n o r m a l i z e d   d i s t a n c e  
On the other hand, to obtain L∞, it is necessary to select the maximum deviation between attribute individual deviations. That is, only the largest deviation of each attribute from its best value is considered. Considering all previous definitions, L∞ could be mathematically represented as follows:
L ∞     =       M a x a ( w a     N a ( x ) )                  
A linear programming model to calculate Min(L1) is presented by Romero (1993) and can be written as follows, based on statements (A3) and (A8).
M i n   L 1   =     ∑ a = 1 A w a     ( | f a *     −     f a ( x ) | | f a *     −     f * a | ) S u b j e c t   t o :                           x     ∈     F
Additionally, to calculate Min(L∞) a linear programming model can be written as follows:
M i n   L ∞   =     d S u b j e c t   t o :                     x     ∈ F                   w a     ( | f a *     −     f a ( x ) | | f a *     −     f * a | )         ≤       d                   ∀ a

References

  1. Wang, S. One hundred faces of sustainable forest management. For. Policy Econ. 2004, 6, 205–213. [Google Scholar] [CrossRef]
  2. UNDP Human Development Indices and Indicators. 2018 Statistical Update. Rev. Mal. Respir. 2018, 27, 123.
  3. Secco, L.; Da Re, R.; Pettenella, D.M.; Gatto, P. Why and how to measure forest governance at local level: A set of indicators. For. Policy Econ. 2014, 49, 57–71. [Google Scholar] [CrossRef]
  4. Bruña-García, X.; Marey-Pérez, M.F. Public participation: A need of forest planning. IForest 2014, 7, 57–71. [Google Scholar] [CrossRef] [Green Version]
  5. FAO. Global Forest Products 2016: Facts and Figures; FAO: Rome, Italy, 2017. [Google Scholar]
  6. IBÁ. Relatório 2017. Available online: https://www.iba.org/images/shared/Biblioteca/IBA_RelatorioAnual2017.pdf (accessed on 26 September 2021).
  7. De Morais, P.H.D.; Longue Júnior, D.; Colodette, J.L.; Morais, E.H.D.C.; Jardim, C.M. Influência da idade de corte de clones de Eucalyptus grandis e híbridos de Eucalyptus grandis × Eucalyptus urophylla na composição química da madeira e polpação kraft. Cienc. Florest. 2017, 27, 237–248. [Google Scholar] [CrossRef] [Green Version]
  8. Gomide, J.L.; Colodette, J.L.; de Oliveira, R.C.; Silva, C.M. Caracterização tecnológica, para produção de celulose, da nova geração de clones de Eucalyptus do Brasil. Rev. Árvore 2006, 29, 129–137. [Google Scholar] [CrossRef]
  9. Queiroz, S.C.S.; Gomide, J.L.; Colodette, J.L.; Oliveira, R.C. de Influência da densidade básica da madeira na qualidade da polpa kraft de clones hibrídos de Eucalyptus grandis W. Hill ex Maiden X Eucalyptus urophylla S. T. Blake. Rev. Árvore 2004, 28, 901–909. [Google Scholar] [CrossRef]
  10. Nobre, S.R.; Rodriguez, L.C.E. Integrating Nursery and Planting Activities. In The Management of Forest Plantations; Borges, G.J., Diaz-Balteiro, L., McDill, E.M., Rodriguez, C.E.L., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 347–371. ISBN 978-94-017-8899-1. [Google Scholar]
  11. Kelty, M.J. The role of species mixtures in plantation forestry. For. Ecol. Manag. 2006, 233, 195–204. [Google Scholar] [CrossRef]
  12. Kavaliauskas, D.; Fussi, B.; Westergren, M.; Aravanopoulos, F.; Finzgar, D.; Baier, R.; Alizoti, P.; Bozic, G.; Avramidou, E.; Konnert, M.; et al. The Interplay between Forest Management Practices, Genetic Monitoring, and Other Long-Term Monitoring Systems. Forests 2018, 9, 133. [Google Scholar] [CrossRef] [Green Version]
  13. Mokfienski, A.; Colodette, J.L.; Gomide, J.L.; Carvalho, A.M.M.L. Relative Importance of Wood Density and Carbohydrate Content on Pulping. Cienc. Florest. 2008, 18, 401–413. [Google Scholar] [CrossRef] [Green Version]
  14. Lopes, G.A.; Garcia, J.N. Basic density and natural moisture content of Eucalyptus saligna Smith, from Itatinga, associated to the population bark patterns. Sci. For. 2002, 1, 13–23. [Google Scholar]
  15. Gomide, J.L.; Fantuzzi Neto, H.; Regazzi, A.J. Análise de critérios de qualidade da madeira de eucalipto para produção de celulose kraft. Rev. Árvore 2010, 34, 339–344. [Google Scholar] [CrossRef]
  16. Rodriguez, L.C.E. Programa Cooperativo em Planejamento Florestal—Relatório Final; IPEF-Instituto de Pesquisas e Estudos Florestais: Piracicaba, Brazil, 1988. [Google Scholar]
  17. Eriksson, L.O.; Garcia-Gonzalo, J.; Trasobares, A.; Hujala, T.; Nordström, E.M.; Borges, J.G. Computerized decision support tools to address forest management planning problems: History and approach for assessing the state of art world-wide. In Computer-Based Tools for Supporting Forest Management: The Experience and the Expertise World-Wide; Borges, J., Nordström, E.-M., Garcia Gonzalo, J., Hujala, T., Eds.; SLU: Umea, Sweden, 2014; pp. 3–25. [Google Scholar]
  18. Belavenutti, P.; Romero, C.; Diaz-Balteiro, L. A critical survey of optimization methods in industrial forest plantations management. Sci. Agric. 2018, 75, 239–245. [Google Scholar] [CrossRef] [Green Version]
  19. Acosta, M.; Corral, S. Multicriteria decision analysis and participatory decision support systems in forest management. Forests 2017, 8, 116. [Google Scholar] [CrossRef]
  20. Esmail, B.A.; Geneletti, D. Multi-criteria decision analysis for nature conservation: A review of 20 years of applications. Methods Ecol. Evol. 2018, 9, 42–53. [Google Scholar] [CrossRef] [Green Version]
  21. De Castro, M.; Urios, V. A critical review of multi-criteria decision making in protected areas. Econ. Agrar. Y Recur. Nat. Agric. Resour. Econ. 2016, 16, 89–109. [Google Scholar] [CrossRef] [Green Version]
  22. Diaz-Balteiro, L.; González-Pachón, J.; Romero, C. Goal programming in forest management: Customising models for the decision-maker’s preferences. Scand. J. For. Res. 2013, 28, 166–173. [Google Scholar] [CrossRef]
  23. Diaz-Balteiro, L.; Romero, C. Making forestry decisions with multiple criteria: A review and an assessment. For. Ecol. Manag. 2008, 255, 3222–3241. [Google Scholar] [CrossRef]
  24. Ananda, J.; Herath, G. A critical review of multi-criteria decision making methods with special reference to forest management and planning. Ecol. Econ. 2009, 68, 2535–2548. [Google Scholar] [CrossRef]
  25. Giménez, J.C.; Bertomeu, M.; Diaz-Balteiro, L.; Romero, C. Optimal harvest scheduling in Eucalyptus plantations under a sustainability perspective. For. Ecol. Manag. 2013, 291, 367–376. [Google Scholar] [CrossRef]
  26. Ortiz-Urbina, E.; González-Pachón, J.; Diaz-Balteiro, L. Decision-Making in Forestry: A Review of the Hybridisation of Multiple Criteria and Group Decision-Making Methods. Forests 2019, 10, 375. [Google Scholar] [CrossRef] [Green Version]
  27. IBÁ Anuário Estatístico do IBÁ. Ano Base 2019. Available online: https://iba.org/datafiles/publicacoes/relatorios/relatorio-iba-2020.pdf (accessed on 26 September 2021).
  28. FAO FAOSTAT. Available online: http://www.fao.org/faostat/en/#data/FO (accessed on 22 June 2019).
  29. Camargo, S.A.C.; José, T.; Moura, D. De Influência da dimensão e qualidade dos cavacos na polpação. Influence the size and quality of chips in the pulping. 1 Introdução Revisão Bibliográfica. Rev. Eletrônica Em Gest. Educ. E Tecnol. Ambient. 2015, 19, 813–820. [Google Scholar]
  30. Alves, I.C.N.; Gomide, J.L.; Colodette, J.L.; Silva, H.D. Caracterização TEcnológica da Madeira de Eucalyptus para produção de Celulose Kraft. Cienc. Florest. 2011, 21, 167–174. [Google Scholar] [CrossRef] [Green Version]
  31. Clutter, J.L.; Forston, J.C.; Pienaar, L.V.; Brister, G.H.; Bailey, R.L. Timber Management, A Quantitative Approach, 1st ed.; John Wiley & Sons: New York, NY, USA, 1983; ISBN 0-471-02961-0. [Google Scholar]
  32. Brasil Ministerio da Economia Taxa de Juros Selic. Available online: http://receita.economia.gov.br/orientacao/tributaria/pagamentos-e-parcelamentos/taxa-de-juros-selic (accessed on 23 June 2019).
  33. Foekel, C.E.B. Rendimentos em celulose sulfato de Eucalyptus spp em função do grau de deslignificação e da densidade da madeira. IPEF Piracicaba 1974, 9, 61–77. [Google Scholar]
  34. Stape, J.L.; Binkley, D.; Ryan, M.G.; Fonseca, S.; Loos, R.A.; Takahashi, E.N.; Silva, C.R.; Silva, S.R.; Hakamada, R.E.; de Ferreira, J.M.A.; et al. The Brazil Eucalyptus Potential Productivity Project: Influence of water, nutrients and stand uniformity on wood production. For. Ecol. Manag. 2010, 259, 1684–1694. [Google Scholar] [CrossRef]
  35. Binkley, D.; Campoe, O.C.; Alvares, C.; Carneiro, R.L.; Cegatta, Í.; Stape, J.L. The interactions of climate, spacing and genetics on clonal Eucalyptus plantations across Brazil and Uruguay. For. Ecol. Manag. 2017, 405, 271–283. [Google Scholar] [CrossRef] [Green Version]
  36. Garcia-Gonzalo, J.; Bushenkov, V.; McDill, M.; Borges, J.G. A decision support system for assessing trade-offs between ecosystem management goals: An application in portugal. Forests 2015, 6, 65–87. [Google Scholar] [CrossRef] [Green Version]
  37. Garcia-Gonzalo, J.; Borges, J.G.; Palma, J.H.N.; Zubizarreta-Gerendiain, A. A decision support system for management planning of Eucalyptus plantations facing climate change. Ann. For. Sci. 2014, 71, 187–199. [Google Scholar] [CrossRef]
  38. Borges, J.G.; Diaz-Balteiro, L.; Rodriguez, L.C.E.; McDill, M. The Management of Industrial Forest Plantations, 1st ed.; Borges, J.G., Diaz-Balteiro, L., Rodriguez, L.C.E., Mcdill, M., Eds.; Springer: London, UK, 2014; Volume 33, ISBN 978-94-017-8898-4. [Google Scholar]
  39. Garcia-Gonzalo, J.; Palma, J.H.N.; Freire, J.P.A.; Tome, M.; Mateus, R.; Rodriguez, L.C.E.; Bushenkov, V. A decision support system for a multi stakeholder’s decision process in a Portuguese National Forest. For. Syst. 2013, 22, 359–373. [Google Scholar] [CrossRef] [Green Version]
  40. Borges, J.G.; Marques, S.; Garcia-Gonzalo, J.; Rahman, A.U.; Bushenkov, V.; Sottomayor, M.; Carvalho, P.O.; Nordström, E.M. A multiple criteria approach for negotiating ecosystem services supply targets and forest owners’ programs. For. Sci. 2017, 63, 49–61. [Google Scholar] [CrossRef]
  41. McDill, M. An Overview of Forest Management Planning and Information Management. In The Management of Industrial Forest Plantations; Borges, G.J., Diaz-Balteiro, L., McDill, E.M., Rodriguez, C.E.L., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 27–59. ISBN 978-94-017-8899-1. [Google Scholar]
  42. Borges, J.G.; Nordström, E.M.; Garcia-Gonzalo, J.; Hujala, T.; Trasobares, A. Computer-Based Tools for Supporting Forest Management. The Experience and the Expertise World-Wide, 1st ed.; Department of Forest Resource Management, Swedish University of Agricultural Sciences: Umea, Sweden, 2014. [Google Scholar]
  43. McDill, M.E.; Toth, S.F.; St:John, R.; Braze, J.; Rebaine, S.A. Comparing Model I and Model II Formulations of Spatially Explicit Harvest Scheduling Models with Adjacency Constraints. For. Sci. 2016, 62, 28–37. [Google Scholar] [CrossRef]
  44. Garcia-Gonzalo, J.; Pais, C.; Bachmatiuk, J.; Barreiro, S.; Weintraub, A. A progressive hedging approach to solve harvest scheduling problem under climate change. Forests 2020, 11, 224. [Google Scholar] [CrossRef] [Green Version]
  45. Ware, G.O.; Clutter, J.L. Mathematical Programming System for Management of Industrial Forests. For. Sci. 1971, 17, 428–445. [Google Scholar]
  46. Johnson, K.N.; Scheurman, H.L. Tequiniques for precribing optimal timber harvest and investment under different objectives—Discussion and synthesis. For. Sci. 1977, 23, a0001–z0001. [Google Scholar]
  47. Nobre, S.R. Forest Management Decision Support System for Forest Plantation in Brazil: A Multicriteria Apporach. Ph.D. Thesis, Univesidad Politécnica de Madrid, Madrid, Spain, 2019. [Google Scholar]
  48. Ballestero, E.; Romero, C. Multiple Criteria Decision Making and Its Applications to Economic Problems, 1st ed.; Kluwer Academic Publishers: Boston, MA, USA, 1998; ISBN 0-7923-8238-2. [Google Scholar]
  49. Romero, C. Teoría de la Decisión Multicriterio, 1st ed.; Alianza Universidad Textos: Madrid, Spain, 1993; ISBN 84-206-8144-X. [Google Scholar]
  50. Steuer, R.E. Multiple Criteria Optimization—Theory, Computation, and Application, 1st ed.; John Willey & Sons: New York, NY, USA, 1986; ISBN 0271-6232. [Google Scholar]
  51. Ballestero, E.; Romero, C. A theorem connecting utility function optimization and compromise programming. Oper. Res. Lett. 1991, 10, 421–427. [Google Scholar] [CrossRef]
  52. Diaz-Balteiro, L.; Belavenutti, P.; Ezquerro, M.; González-Pachón, J.; Nobre, S.R.; Romero, C. Measuring the sustainability of a natural system by using multi-criteria distance function methods: Some critical issues. J. Environ. Manag. 2018, 214, 197–203. [Google Scholar] [CrossRef] [PubMed]
  53. Beula, T.M.N.; Prasad, G.E. Multiple Criteria Decision Making with Compromise Programming. Int. J. Eng. Sci. Technol. 2012, 4, 4083–4086. [Google Scholar]
  54. Kanojiya, A.; Nagori, V. Analysis of Architecture and Forms of Outputs of Decision Support Systems Implemented for Different Domains. In Proceedings of the 2018 Second International Conference on Inventive Communication and Computational Technologies (ICICCT), Coimbatore, India, 20–21 April 2018; pp. 346–350. [Google Scholar]
  55. Reynolds, J.H.; Knutson, M.G.; Newman, K.B.; Silverman, E.D.; Thompson, W.L. A road map for designing and implementing a biological monitoring program. Environ. Monit. Assess. 2016, 188, 399. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  56. Ezquerro, M.; Pardos, M.; Diaz-Balteiro, L. Operational research techniques used for addressing biodiversity objectives into forest management: An overview. Forests 2016, 7, 299. [Google Scholar] [CrossRef] [Green Version]
  57. Segura, M.; Maroto, C.; Belton, V.; Ginestar, C. A New Collaborative Methodology for Assessment and Management of Ecosystem Services. Forests 2015, 6, 1696–1720. [Google Scholar] [CrossRef] [Green Version]
  58. Diaz-Balteiro, L.; González-Pachón, J.; Romero, C. Measuring systems sustainability with multi-criteria methods: A critical review. Eur. J. Oper. Res. 2016, 258, 607–616. [Google Scholar] [CrossRef]
  59. Rodriguez, L.C.E.; Nobre, S.R. The Use of Forest Decision support System in Brazil. In Computer-Based Tools for Supporting Forest Management. The Experience World-Wide; Borges, J.G., Eriksson, L.O., Nordström, E.M., Garcia-Gonzalo, J., Eds.; Department of Forest Resource Management, Swedish University of Agricultural Sciences: Uppsala, Sweden, 2014; pp. 33–47. [Google Scholar]
Forests 12 01481 g001 550
Figure 1. State of the art.
Figure 1. State of the art.
Forests 12 01481 g001
Forests 12 01481 g002 550
Figure 2. Wood density.
Figure 2. Wood density.
Forests 12 01481 g002
Forests 12 01481 g003 550
Figure 3. Industrial efficiency.
Figure 3. Industrial efficiency.
Forests 12 01481 g003
Forests 12 01481 g004 550
Figure 4. Initial area.
Figure 4. Initial area.
Forests 12 01481 g004
Forests 12 01481 g005 550
Figure 5. Romero® calculation process.
Figure 5. Romero® calculation process.
Forests 12 01481 g005
Forests 12 01481 g006 550
Figure 6. Romero® components.
Figure 6. Romero® components.
Forests 12 01481 g006
Forests 12 01481 g007 550
Figure 7. Intervention rules.
Figure 7. Intervention rules.
Forests 12 01481 g007
Forests 12 01481 g008 550
Figure 8. Transition types.
Figure 8. Transition types.
Forests 12 01481 g008
Forests 12 01481 g009 550
Figure 9. Pulpwood supply per genetic material.
Figure 9. Pulpwood supply per genetic material.
Forests 12 01481 g009
Forests 12 01481 g010 550
Figure 10. Pulpwood supply per age.
Figure 10. Pulpwood supply per age.
Forests 12 01481 g010
Forests 12 01481 g011 550
Figure 11. Pareto frontier.
Figure 11. Pareto frontier.
Forests 12 01481 g011
Forests 12 01481 g012 550
Figure 12. Compromising programming.
Figure 12. Compromising programming.
Forests 12 01481 g012
Forests 12 01481 g013 550
Figure 13. Genetic material distribution.
Figure 13. Genetic material distribution.
Forests 12 01481 g013
Forests 12 01481 g014 550
Figure 14. Clear-cut ages distribution.
Figure 14. Clear-cut ages distribution.
Forests 12 01481 g014
Table
Table 1. Plantation case study.
Table 1. Plantation case study.
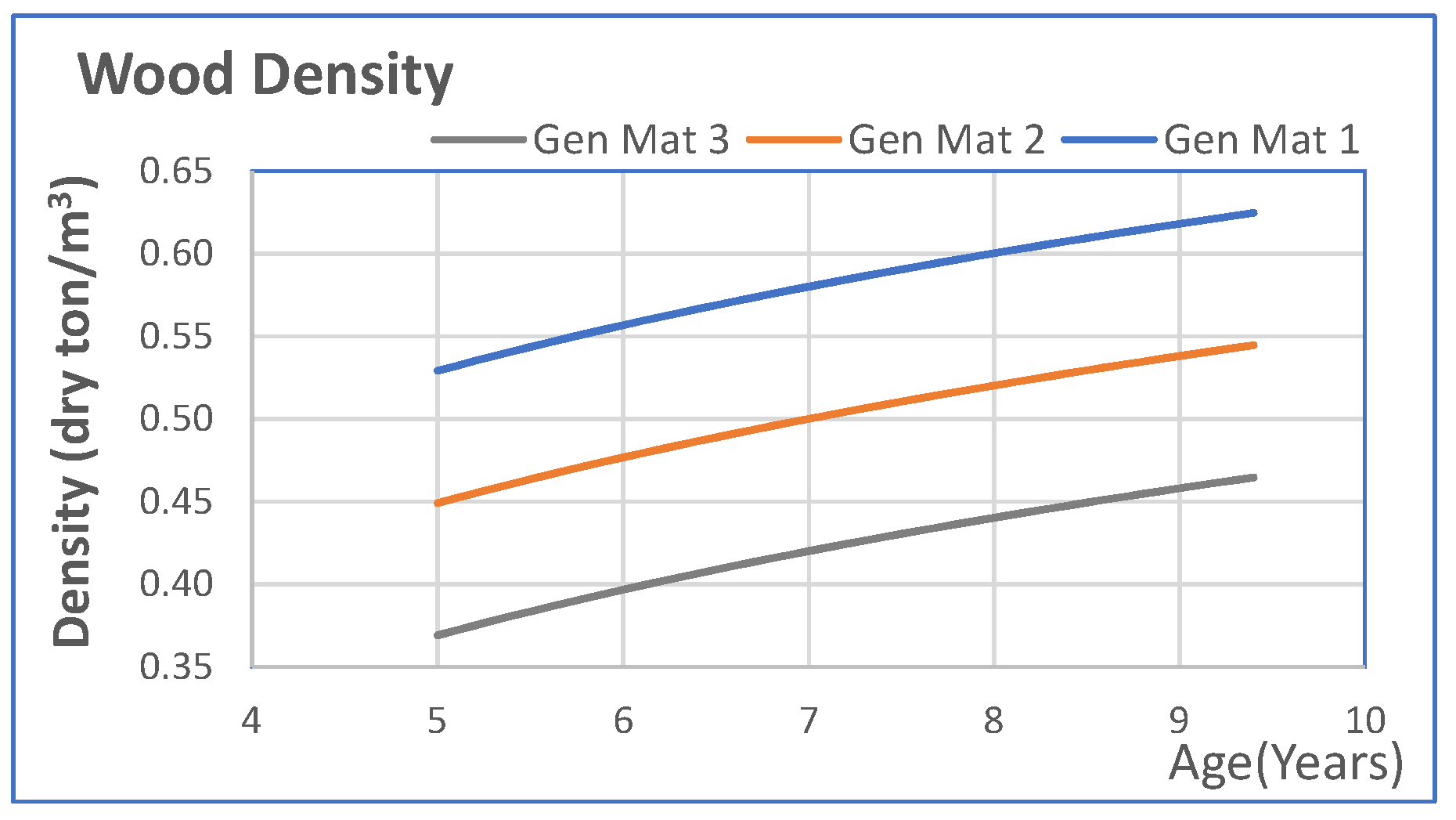
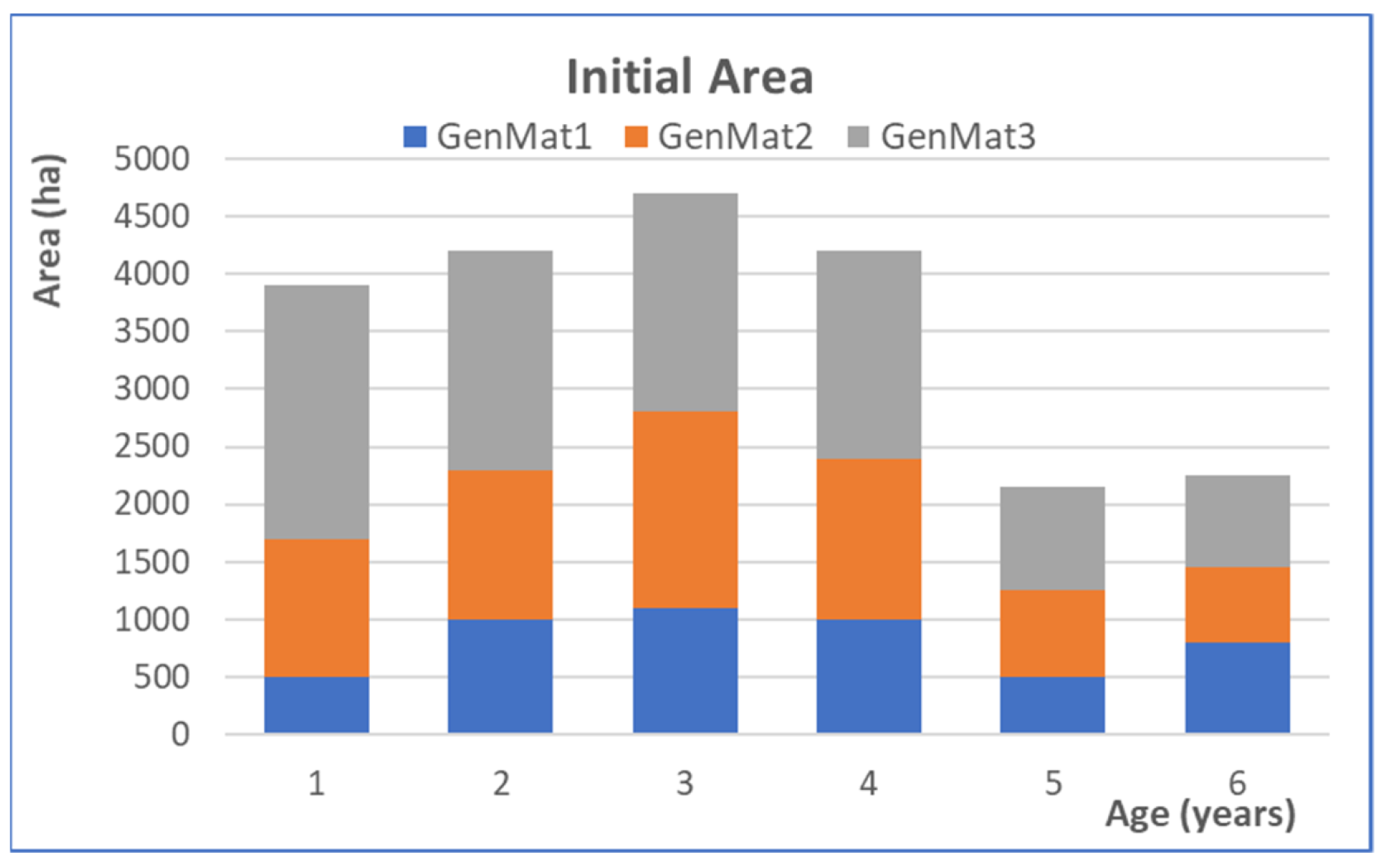
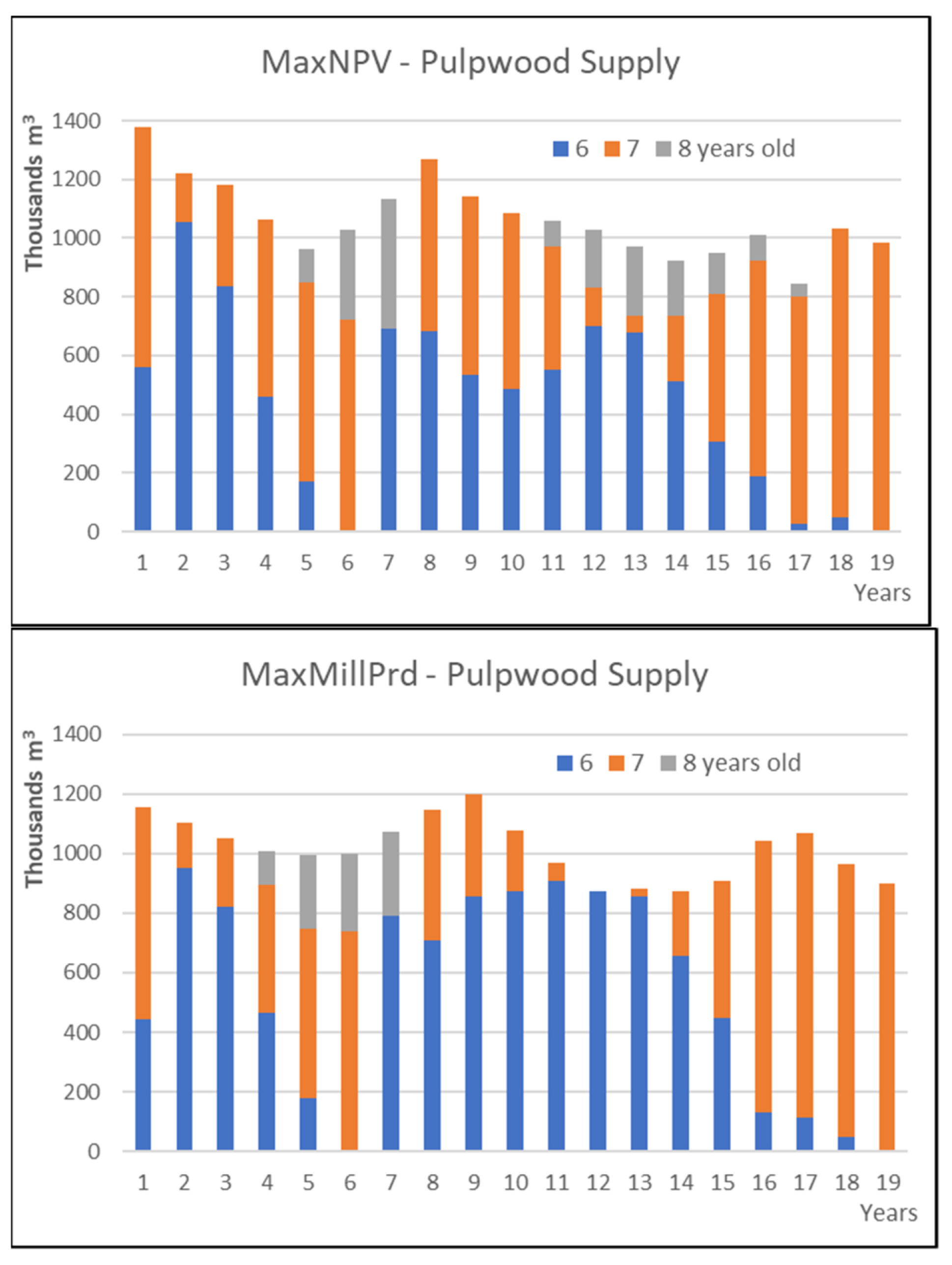
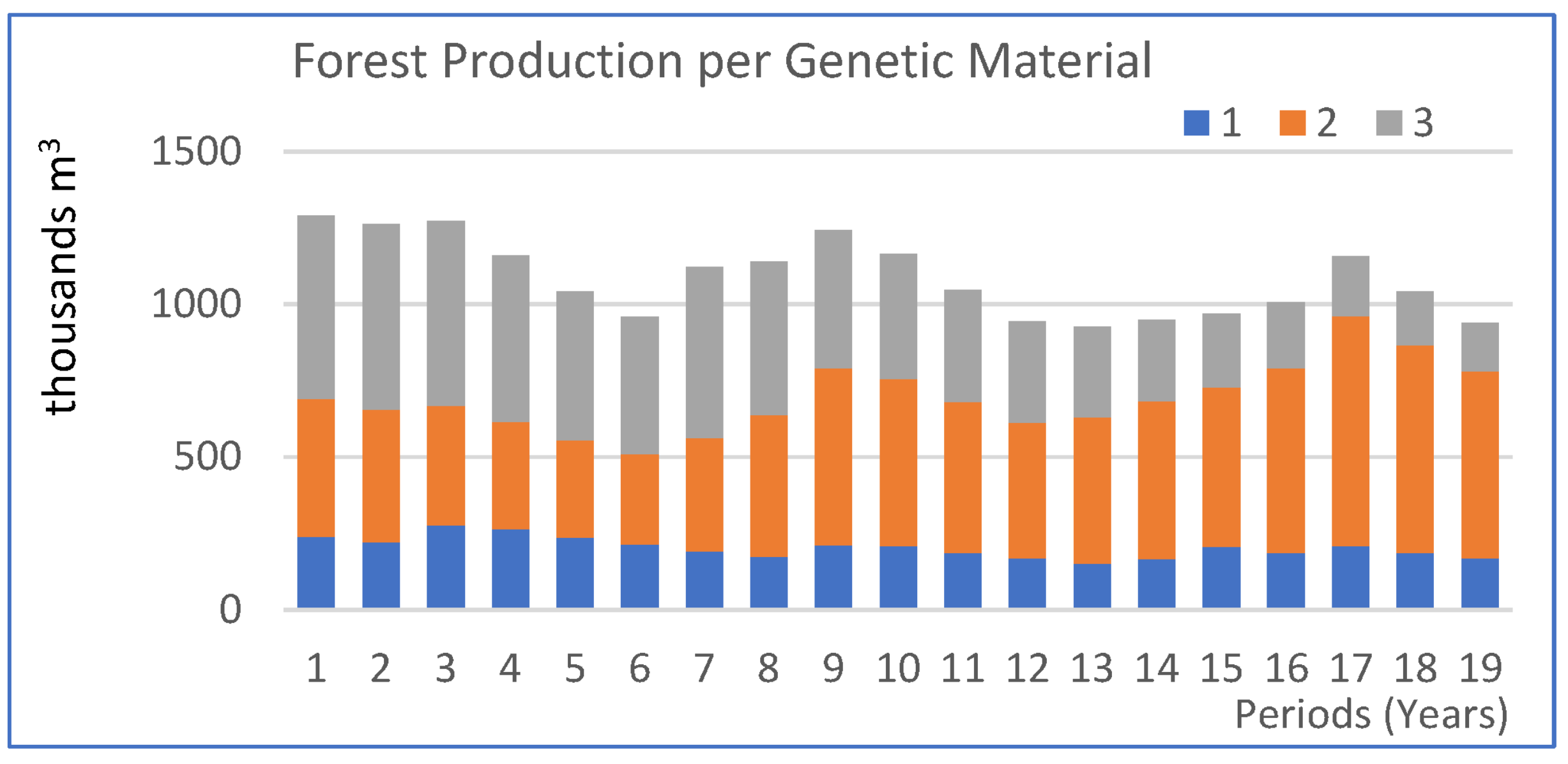
Area21,400 ha
Management units18
Area of each unitFrom 500 to 1900 ha
Allowable harvest ages6 and 7 years old
Silvicultural costsR$9500.00/ha
Pulpwood priceR$50/m3
Discount rate7%
GroupsAverage Productivity
(m3/ha.year at 7 years old)		Average Wood Density
(kg/m3 at 7 years old)
Species
Eucalyptus spp.		GenMat142580
GenMat248500
GenMat352420
Table
Table 2. Allowable harvesting ages.
Table 2. Allowable harvesting ages.
ScenariosAllowable Ages
2165, 6, 7
2176, 7, 8
2186, 7, 8, 9
Table
Table 3. Mill requirements.
Table 3. Mill requirements.
Mill RequirementsImplementation
Regulated wood flow From period 2 onwards
No decrease above 10%
No increase above 25%
Genetic material safety 60% maximum area for any GenMat type
20% minimum area for any GenMat type
Production sustainabilityAge class control
10% flexibility
Table
Table 4. Available Criteria.
Table 4. Available Criteria.
ObjectivesObjective DescriptionAttribute (Accounting Variable)
MaxNPVMaximize Net Present ValuexTotalNPV
MaxMillPrdMaximize Mill ProductionxTotalMillPrd
MaxStckMaximize Final StockxTotalStock
Table
Table 5. Case study main results.
Table 5. Case study main results.
ScenarioAges (Years)Highest NPV (M R$)Lowest NPV (M R$)Forest NPV ReductionHighest Pulp Production (K t)Lowest Pulp Production (K t)Mill Production Reduction
2165, 6, 7262,293 224,24616.97%5149 4845 6.29%
2176, 7, 8266,445 232,677 14.51%5022 4671 7.51%
2186, 7, 8, 9266,612 232,677 14.58%5022 4656 7.85%
Table
Table 6. Romero® running information.
Table 6. Romero® running information.
Scenarios
216217218
number of constraints 53,30423,28038,049
number of variables 76,58833,14555,096
time consumption (min:s)
iGen 00:01.000:01.000:02.0
Mem structure optimization 00:01.000:00.000:00.0
Building abstract model 00:01.000:00.000:00.0
Building concrete model 21:21.003:44.012:33.0
Solving 1st criteria and save resultsMaxNPV00:19.000:07.000:11.0
Solving 2nd criteria and save resultsMaxStck00:18.000:06.000:12.0
Solving 3rd criteria and save resultsMaxMillPrd00:19.000:07.000:12.0
Table
Table 7. Scenario 217 payoff matrix.
Table 7. Scenario 217 payoff matrix.
CriteriaClear-Cut Area (ha)Production (K m3)Productivity (m3/ha)%Max Stock Forest NPV (M R$)Pulp Production (K t)Final Stock (K m3)
MaxNPV82,99219,708 23788.42%266,445 4671 624
MaxMillPrd84,62218,856 22391.79%232,677 5022648
MaxStck81,69518,335 224 239,414 4801 706
Table
Table 8. Compromise programming.
Table 8. Compromise programming.
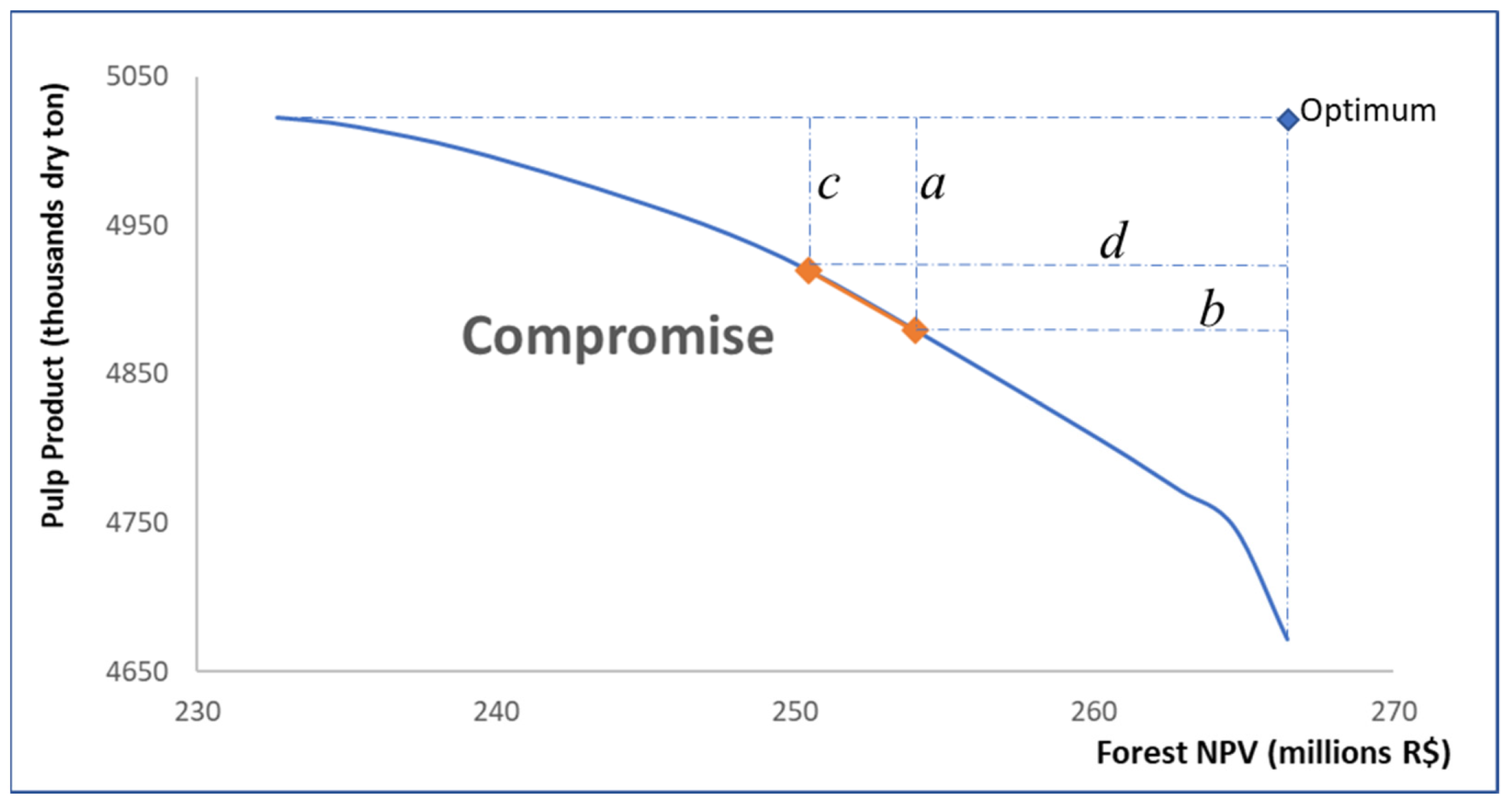
PointCriterionValueBest ValueWorst ValueInterval Distance SumMax
(M R$)
9MaxMillPrd4879 5022 4671 350 a 0.4071
9MaxNPV254,004 266,445 232,677 33,767 b 0.3684 0.7755 0.4071 L∞
10MaxMillPrd4900 5022 4671 350 0.3479
10MaxNPV252,227 266,445 232,677 33,767 0.4210 0.7690 0.4210
11MaxMillPrd4919 5,022 4671 350 c 0.2929
11MaxNPV250,449 266,445 232,677 33,767 d 0.4736 0.7666 0.4736 L1
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Nobre, S.R.; Diaz-Balteiro, L.; Rodriguez, L.C.E. A Compromise Programming Application to Support Forest Industrial Plantation Decision-Makers. Forests 2021, 12, 1481. https://doi.org/10.3390/f12111481

AMA Style

Nobre SR, Diaz-Balteiro L, Rodriguez LCE. A Compromise Programming Application to Support Forest Industrial Plantation Decision-Makers. Forests. 2021; 12(11):1481. https://doi.org/10.3390/f12111481

Chicago/Turabian Style

Nobre, Silvana Ribeiro, Luis Diaz-Balteiro, and Luiz Carlos Estraviz Rodriguez. 2021. "A Compromise Programming Application to Support Forest Industrial Plantation Decision-Makers" Forests 12, no. 11: 1481. https://doi.org/10.3390/f12111481

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop