Scots Pine and Norway Spruce Wood Properties at Sites with Different Stand Densities
Abstract
1. Introduction
2. Material and Methods
2.1. Study Site
2.2. Study Plots and Field Measurements
2.3. Sampling and Analysis of Wood Properties
2.4. Data Analysis
3. Results
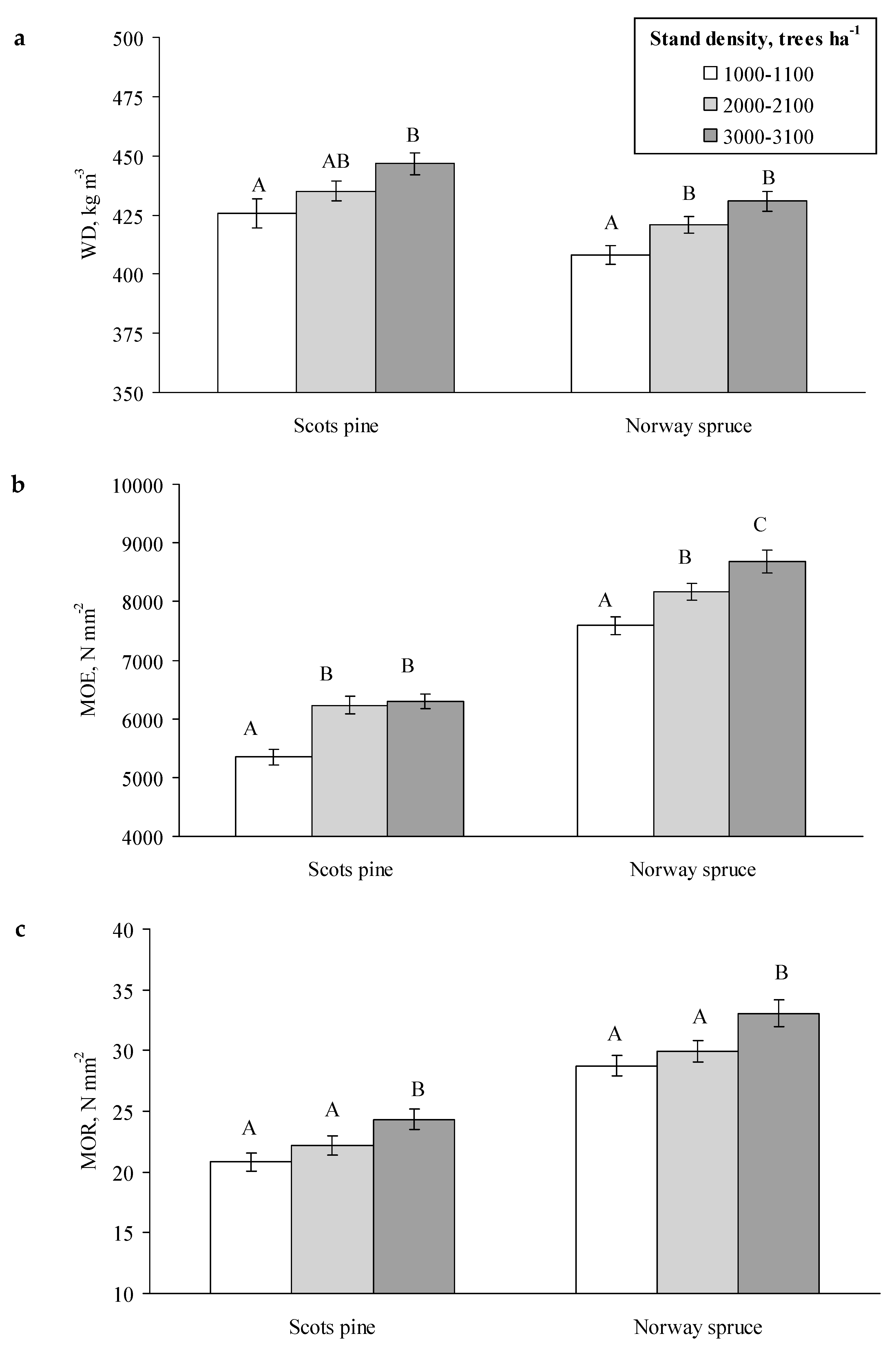
3.1. Wood Properties at the Sites of Different Stand Densities
3.2. Relationships of Stand and Tree Characteristics with Wood Quality Parameters
3.3. Modeling Wood Quality Parameters in Relation to Stand and Tree Characteristics
4. Discussion
4.1. Effects of Stand Density on Wood Quality Characteristics
4.2. Relationships Between Tree Characteristics and Wood Quality Parameters
4.3. Modeling Wood Quality Parameters in Relation to Tree Characteristics
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zobel, B. Silvicultural effects on wood properties. IPEF International. 1992, 2, 31–38. [Google Scholar]
- Wang, X.; Ross, R.J.; McClellan, M.; Barbour, R.J.; Erickson, J.R.; Forsman, J.W.; McGinnis, G.D. Strength and Stiffness Assessment of Standing Trees Using a Nondestructive Stress Wave Technique; Res. Pap. FPL–RP–585; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2000. [Google Scholar]
- Beets, P.N.; Kimberley, M.O.; McKinley, R.B. Predicting wood density of Pinus radiata annual growth increments. N. Z. J. For. Sci. 2007, 37, 241–266. [Google Scholar]
- Brand, D.G.; Magnussen, S. Asymetric, two-sided competition in even-aged monocultures of red pine. Can. J. Forest Res. 1988, 18, 901–910. [Google Scholar] [CrossRef]
- Barron-Gafford, G.A.; Will, R.E.; Burkes, E.C.; Shiver, B.; Teskey, R.O. Nutrient concentrations and contents, and their relation to stem growth, of intensively managed Pinus teada and Pinus elliottii stands of different planting densities. For. Sci. 2003, 49, 291–300. [Google Scholar]
- Zhu, J.; Scott, C.T.; Scallon, K.L.; Myers, G.C. Effects of plantation density on wood density and anatomical properties of red pine (Pinus resinosa ait.). Wood Fiber Sci. 2007, 39, 502–512. [Google Scholar]
- Will, R.; Hennessey, T.; Lynch, T.; Holeman, R.; Heinemann, R. Effects of planting density and seed source on loblolly pine stands in southeastern Oklahoma. For. Sci. 2010, 56, 437–443. [Google Scholar]
- Akers, M.K.; Kane, M.; Zhao, D.; Teskey, R.O.; Daniels, R.F. Effects of planting density and cultural intensity on stand and crown attributes of mid-rotation loblolly pine plantations. For. Ecol. Manag. 2013, 310, 468–475. [Google Scholar] [CrossRef]
- Machado, J.S.; Louzada, J.L.; Santos, A.J.A.; Nunes, L.; Anjos, O.; Rodrigues, J.; Simões, R.M.S.; Pereira, H. Variation of wood density and mechanical properties of blackwood (Acacia Melanoxylon R. Br.). Mater. Des. 2014, 56, 975–980. [Google Scholar] [CrossRef]
- Moreno-Fernández, D.; Hevia, A.; Majada, J.; Cañellas, I. Do Common Silvicultural Treatments Affect Wood Density of Mediterranean Montane Pines? Forests 2018, 9, 80. [Google Scholar] [CrossRef]
- Peltola, H.; Kilpeläinen, A.; Sauvala, K.; Räisänen, T.; Ikonen, V. Effects of early thinning regime and tree status on the radial growth and wood density of Scots pine. Silva Fenn. 2007, 41, 489–505. [Google Scholar] [CrossRef]
- Mäkinen, H.; Hynynen, J. Wood density and tracheid properties of Scots pine: Responses to repeated fertilization and timing of the first commercial thinning. Forestry 2014, 87, 437–447. [Google Scholar] [CrossRef]
- Mäkinen, H.; Hynynen, J.; Penttilä, T. Effect of thinning on wood density and tracheid properties of Scots pine on drained peatland stands. Forestry 2015, 88, 359–367. [Google Scholar] [CrossRef]
- Jaakkola, T.; Mäkinen, H.; Saranpää, P. Wood density in Norway spruce: Changes with thinning intensity and tree age. Can. J. For. Res. 2005, 35, 1767–1778. [Google Scholar] [CrossRef]
- Jaakkola, T.; Mäkinen, H.; Saranpää, P. Wood density of Norway spruce: Responses to timing and intensity of first commercial thinning and fertilisation. For. Ecol. Manag. 2006, 237, 513–521. [Google Scholar] [CrossRef]
- Linkevičius, E.; Kuliešis, A.; Rohle, H.; Schroder, J.; Aleinikovas, M. The Impact of Competition for Growing Space on Diameter, Basal Area and Height Growth in Pine treles. Balt For. 2014, 20, 301–313. [Google Scholar]
- Hébert, F.; Krause, C.; Plourde, P.; Achim, A.; Prégent, G.; Ménétrier, J. Effect of Tree Spacing on Tree Level Volume Growth, Morphology, and Wood Properties in a 25-Year-Old Pinus banksiana Plantation in the Boreal Forest of Quebec. Forests 2016, 7, 276. [Google Scholar] [CrossRef]
- Høibø, O.; Vestøl, G.I.; Fischer, C.; Fjeld, L.; Øvrum, A. Bending properties and strength grading of Norway spruce: Variation within and between stands. Can. J. Forest Res. 2014, 44, 128–135. [Google Scholar] [CrossRef]
- Ruso, D.; Marziliano, P.A.; Macri, G.; Proto, A.R.; Zimbalatti, G.; Lombardi, F. Does Thinning Intensity Affect Wood Quality? An Analysis of Calabrian Pine in Southern Italy Using a Non-Destructive Acoustic Method. Forests 2019, 10, 303. [Google Scholar] [CrossRef]
- Hautamäki, S.; Kilpeläinen, H.; Verkasalo, E. Factors and Model for Bending Properties of Sawn Timber from Finland and North-Western Russia. Part I: Norway Spruce. Balt For. 2013, 19, 106–119. [Google Scholar]
- Hautamäki, S.; Kilpeläinen, H.; Verkasalo, E. Factors and Model for Bending Properties of Sawn Timber from Finland and North-Western Russia. Part II: Scots Pine. Balt For. 2014, 20, 142–156. [Google Scholar]
- Verkasalo, E.; Leban, J.M. MOE and MOR in static bending of small clear specimens of Scots pine, Norway spurce and European fir from Finland and France and their prediction for the comparison of wood quality. Pap. Puu-Pap Tim. 2002, 84, 332–340. [Google Scholar]
- Jiang, Z.; Wang, X.; Fei, B.; Ren, H.; Liu, X. Effect of stand and tree attributes on growth and wood quality characteristics from a spacing trial with Populus xiaohei. Ann. For. Sci. 2007, 64, 807–814. [Google Scholar] [CrossRef]
- Johansson, K. Influence of initial spacing and tree class on the basic density of Picea abies. Scand. J. For. Res. 1993, 8, 18–27. [Google Scholar] [CrossRef]
- Lassere, J.P.; Mason, E.G.; Watt, M.S. Influence of genotype and spacing on Pinus radiata [D. Don] corewood stiffness in an 11-year old experiment. For. Ecol. Manag. 2005, 205, 375–383. [Google Scholar] [CrossRef]
- Rais, A.; Poschenrieder, W.; Pretzsch, H.; van de Kuilen, J.-W.G. Influence of initial plant density on sawn timber properties for Douglas-fir (Pseudotsuga menziesii (Mirb.) Franco). Ann. For. Sci. 2014, 71, 617–626. [Google Scholar] [CrossRef]
- Simic, K.; Gendvilas, V.; O’Reilly, C.; Nieuwenhuis, M.; Harte, A.M. The Influence of Planting Density on Modulus of Elasticity of Structural Timber from Irish-Grown Sitka Spruce. Int. J. Des. Nat. Ecodyn. 2017, 12, 438–447. [Google Scholar] [CrossRef]
- Stöd, R.; Verkasalo, E.; Heinonen, J. Quality and Bending Properties of Sawn Timber from Commercial Thinnings of Scots Pine (Pinus sylvestris L.). Balt. For. 2016, 22, 148–162. [Google Scholar]
- Baltrušaitis, A.; Mišeikytė, S. Strength and Stiffness Properties of the Lithuanian Grown Scots Pine (Pinus Sylvestris): Non-destructive Testing Methods vs. Static Bending. Wood Res. 2011, 56, 157–168. [Google Scholar]
- Baltrušaitis, A.; Aleinikovas, M. Early-stage Prediction and Modelling Strength Properties Lithuanian-Grown Scots Pine (Pinus sylvestris L.). Balt. For. 2012, 18, 327–333. [Google Scholar]
- Lithuanian Hydrometeorological Service under the Ministry of Environment. Climate Atlas of Lithuania; Petro ofsetas: Vilnius, Lithuania, 2013.
- Ministry of Environment, State Forest Service. Lithuanian Statistical Yearbook of Forestry; Butkus, A., Dumčienė, V., Eigirdas, M., Kuliešis, A., Vižlenskas, D., Eds.; Lututė: Kaunas, Lithuania, 2017.
- Kuliešis, A.; Saladis, J. The effect of early thinning on the growth of pine and spruce stands. Balt. For. 1998, 1, 8–16. [Google Scholar]
- Vaičys, M.; Karazija, S.; Kuliešis, A.; Rutkauskas, A. Miškų Augavietės [Forest Sites]; Lututė: Kaunas, Lithuania, 2006; p. 95. (In Lithuanian) [Google Scholar]
- World Reference Base for Soil Resources. International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; World Soil Resources Reports No. 106; FAO: Rome, Italy, 2014. [Google Scholar]
- Hegyi, F. A simulation model for managing Jack-pine stands. In Growth Models for Tree and Stand Simulation; Fries, J., Ed.; Research Note No. 30; Royal College of Forestry, Department of Forest Yield Research: Stockholm, Sweden, 1974; pp. 74–90. [Google Scholar]
- EN 408:2006. Timber Structures. Structural Timber and Glued Laminated Timber—Determination of some Physical and Mechanical Properties; European Committee for Standardization: Brussels, Belgium, 2006. [Google Scholar]
- EN 384:2016. Structural timber. Determination of Characteristic Values of Mechanical Properties and Density; European Committee for Standardization: Brussels, Belgium, 2016. [Google Scholar]
- EN 13183-1. Moisture Content of a Piece of Sawn Timber. Part 1: Determination by Oven Dry Method; European Committee of Standardization: Brussels, Belgium, 2002. [Google Scholar]
- EN 338:2009. Structural Timber. Strength Classes; European Committee for Standardization: Brussels, Belgium, 2009. [Google Scholar]
- Zobel, B.J.; Buijtenen, J.P. Wood Variation-its Cause and Control; Springer: Berlin/Heidelberg, Germany; New York, NY, USA; London, UK; Paris, French; Tokyo, Japan, 1989. [Google Scholar]
- Krajnc, L.; Farrelly, N.; Harte, A.M. The effect of thinning on mechanical properties of Douglas fir, Norway spruce, and Sitka spruce. Ann. For. Sci. 2019, 76, 25–37. [Google Scholar] [CrossRef]
- Vincent, M.; Krause, C.; Koubaa, A. Variation in black spruce (Picea mariana (Mill.) BSP) wood quality after thinning. Ann. For. Sci. 2011, 68, 1115–1125. [Google Scholar] [CrossRef]
- Moore, J.R.; Lyon, A.J.; Searles, G.J.; Lehneke, S.A.; Ridley-Ellis, D.J. Within-and between-stand variation in selected properties of Sitka spruce sawn timber in the UK: Implications for segregation and grade recovery. Ann. For. Sci. 2013, 70, 403–415. [Google Scholar] [CrossRef]
- Aslezaeim, N. Effect of Cultural Intensity and Planting Density on Wood Properties of Loblolly Pine (Pinus taeda L.). Ph.D Thesis, Mississippi State University, Starkville, MS, USA, 2016. [Google Scholar]
- Lowell, E.C.; Todoroki, C.L.; Dykstra, D.P.; Briggs, D.G. Linking acoustic velocity of standing Douglas-fir trees to veneer stiffness: A tree-log-product study across thinning treatments. N. Z. J. For. Sci. 2014, 44, 1. [Google Scholar] [CrossRef]
- Gil-Moreno, D.; Ridley-Ellis, D.; Harte, A.M. Timber grading potential of Douglas fir in the Republic of Ireland and the UK. Int. Wood Prod. J. 2019, 10, 64–69. [Google Scholar] [CrossRef]
- Lei, Y.C.; Zhang, S.Y.; Jiang, Z.H. Models for predicting lumber bending MOR and MOE based on tree and stand characteristics in black spruce. Wood Sci. Technol. 2005, 39, 37–47. [Google Scholar]
- Faust, T.D.; McAlister, R.H.; Zarnoch, S.J. Strength and stiffness properties of sweetgum and yellow-poplar structural lumber. For. Prod. J. 1991, 40, 58–64. [Google Scholar]
- Castéra, P.; Faye, C.; Ouadrani, A.E. Prevision of the bending strength of timber with a multivariate statistical approach. Ann. For. Sci. 1996, 53, 885–898. [Google Scholar]
- Liu, C.; Zhang, S.Y.; Cloutier, A.; Rycabel, T. Modeling lumber bending stiffness and strength in natural black spruce stands using stand and tree characteristics. For. Ecol. Manag. 2007, 242, 648–655. [Google Scholar] [CrossRef]
- Yang, K.C.; Hazenberg, G. Impact of spacing on tracheid lenght, relative density, and growth rate of juvenile wood and mature wood in Picea mariana. Can. J. Forest Res. 1994, 24, 996–1007. [Google Scholar] [CrossRef]
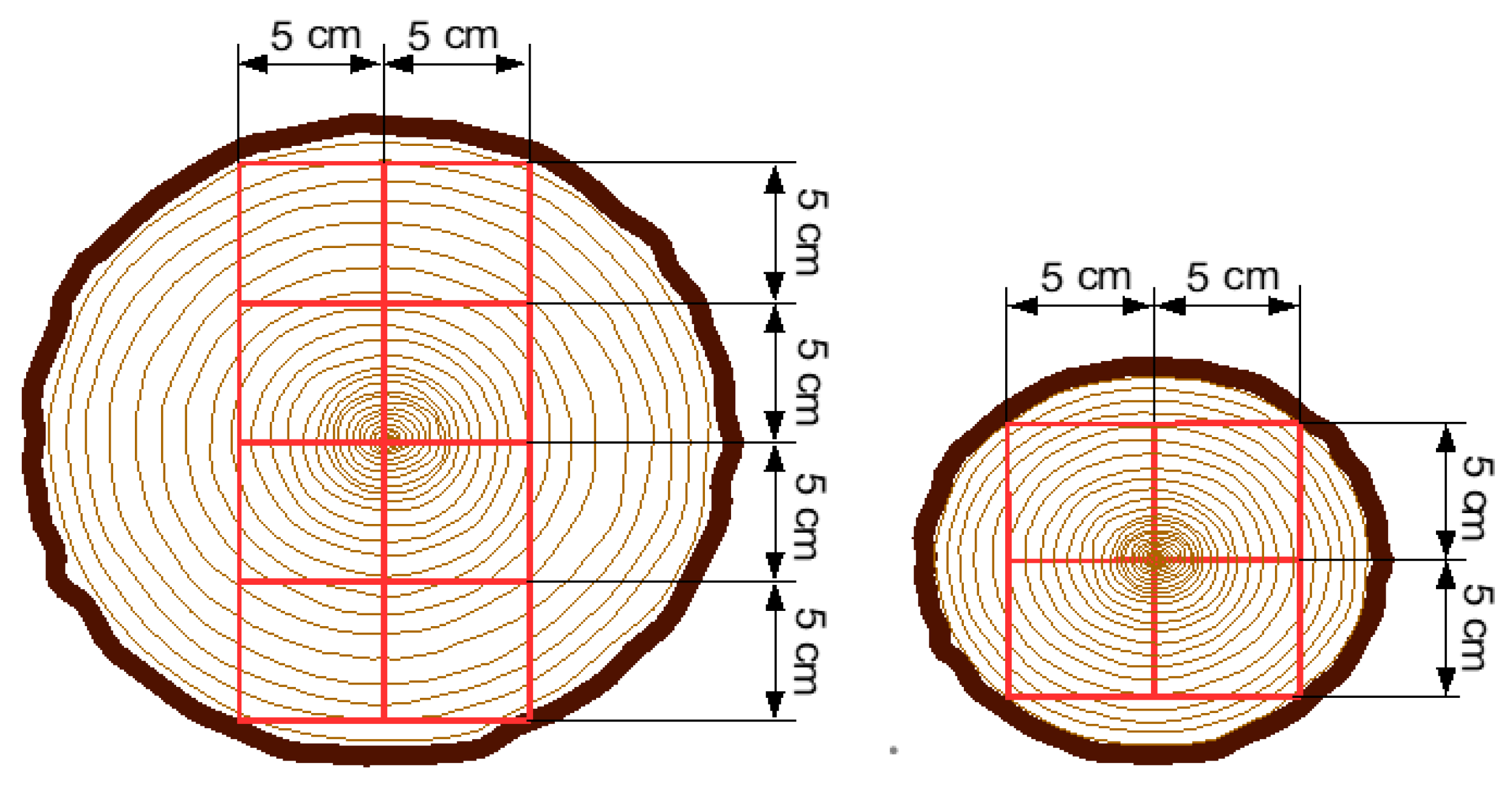
| Tree Species | Stand Age a, Years | Stand Density b, Trees ha−1 | Stand Age, Years | Stand Density, Trees ha−1 | Stand Age, Years | Stand Density, Trees ha−1 | Stand Age, Years | Stand Density, Trees ha−1 | Stand Age, Years | Stand Density, Trees ha−1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1st Thinning | 2nd Thinning | 3rd Thinning | 4th Thinning | 5th Thinning | ||||||
| Scots pine | 8 | 3000 | 15 | 1900 | 21 | 1200 | 35 | 900 | 50 | 650 |
| 8 | 2000 | 15 | 1200 | - | - | 35 | 900 | 50 | 650 | |
| 8 | 1000 | - | - | - | - | 35 | 800 | 50 | 650 | |
| Norway spruce | 9 | 3100 | 15 | 1900 | 21 | 1200 | 35 | 1000 | 50 | 650 |
| 9 | 2100 | 15 | 1200 | - | - | 35 | 900 | 50 | 650 | |
| 9 | 1100 | - | - | - | - | 35 | 900 | 50 | 650 | |
| Stand Density, Trees ha−1 | Variable | Mean | Std Dev | Std Error | Minimum | Maximum |
|---|---|---|---|---|---|---|
| Scots pine | ||||||
| 1000 | DBH, cm | 18.18 | 0.91 | 0.1 | 16.7 | 19.6 |
| CI | 1.28 | 0.36 | 0.04 | 0.28 | 1.87 | |
| K, mm | 18.93 | 8.71 | 1.18 | 6 | 40 | |
| WD, kg m−3 | 425.7 | 55.3 | 6.03 | 284.29 | 676.77 | |
| MOE, N mm−2 | 5352.28 | 1219.97 | 133.11 | 2308.25 | 8540.63 | |
| MOR, N mm−2 | 20.81 | 6.99 | 0.76 | 8.79 | 40.28 | |
| 2000 | DBH, cm | 19.51 | 3.11 | 0.31 | 15.1 | 25.7 |
| CI | 1.15 | 0.54 | 0.05 | 0.32 | 2.07 | |
| K, mm | 21.68 | 8.4 | 0.95 | 7 | 43 | |
| WD, kg m−3 | 435.1 | 41.57 | 4.16 | 363.21 | 558.01 | |
| MOE, N mm−2 | 6232.88 | 1530.02 | 153 | 3853.42 | 10,877.55 | |
| MOR, N mm−2 | 22.16 | 8.23 | 0.82 | 7.4 | 48.32 | |
| 3000 | DBH, cm | 17.87 | 1.42 | 0.15 | 15.2 | 20.6 |
| CI | 1.19 | 0.46 | 0.05 | 0.63 | 1.98 | |
| K, mm | 17.66 | 7.53 | 0.96 | 4 | 38 | |
| WD, kg m−3 | 446.62 | 45.48 | 4.77 | 355.4 | 554.49 | |
| MOE, N mm−2 | 6300.82 | 1208.11 | 126.64 | 3425.82 | 9933.33 | |
| MOR, N mm−2 | 24.33 | 8.12 | 0.85 | 11.21 | 48.9 | |
| Norway spruce | ||||||
| 1100 | DBH, cm | 18.95 | 1.91 | 0.18 | 16.7 | 23 |
| CI | 1.07 | 0.46 | 0.04 | 0.43 | 2.16 | |
| K, mm | 14.27 | 4 | 0.41 | 4 | 34 | |
| WD, kg m−3 | 408.04 | 41.77 | 3.88 | 315.12 | 541.99 | |
| MOE, N mm−2 | 7592.13 | 1630.79 | 151.41 | 4387.81 | 14,136.29 | |
| MOR, N mm−2 | 28.75 | 8.92 | 0.83 | 10.81 | 55.66 | |
| 2100 | DBH, cm | 17.86 | 0.85 | 0.09 | 16.50 | 19.70 |
| CI | 1.47 | 0.52 | 0.05 | 0.69 | 2.19 | |
| K, mm | 13.77 | 5.19 | 0.57 | 2.00 | 41 | |
| WD, kg m−3 | 420.76 | 35.73 | 3.65 | 299.57 | 523.02 | |
| MOE, N mm−2 | 8170.18 | 1410.01 | 143.91 | 5350.82 | 11,903.09 | |
| MOR, N mm−2 | 29.92 | 8.43 | 0.86 | 11.73 | 54.85 | |
| 3100 | DBH, cm | 17.98 | 0.96 | 0.1 | 16.4 | 19.6 |
| CI | 1.33 | 0.39 | 0.04 | 0.75 | 2.12 | |
| K, mm | 12.78 | 3.74 | 0.39 | 4 | 21 | |
| WD, kg m−3 | 430.78 | 39.94 | 4.03 | 357.63 | 530.34 | |
| MOE, N mm−2 | 8682.9 | 1882.47 | 190.16 | 4993.7 | 13,355.48 | |
| MOR, N mm−2 | 33.06 | 10.91 | 1.1 | 15.09 | 59.13 | |
| Species | Stand Density, Trees ha−1 | MOE, N mm−2 | MOR 5%, N mm−2 | WD 5%, kg m−3 | Strength Class | Samples Rejected for C14, % |
|---|---|---|---|---|---|---|
| Scots Pine | 3000 | 6418.7 | 12.9 | 372.8 | R * | 72.3% |
| 2000 | 6147.4 | 11.5 | 372.7 | R | 78.7% | |
| 1000 | 5352.3 | 11.6 | 358 | R | 89.3% | |
| Norway Spruce | 3100 | 8682.9 | 16.7 | 373.5 | C16 | - |
| 2100 | 8170.2 | 18 | 368.7 | C16 | - | |
| 1100 | 7592.1 | 13.8 | 345.8 | R | 5.2% |
| SD * | LH | CI | DBH | K | WD | MOE | MOR | |
|---|---|---|---|---|---|---|---|---|
| SD | 0.016 | −0.079 | −0.063 | −0.067 | 0.174 | 0.268 | 0.177 | |
| 10.79 | 0.19 | 0.30 | 0.35 | <0.05 | <0.0001 | <0.05 | ||
| LH | 0.016 | −0.0003 | 0.053 | 0.108 | −0.177 | 0.133 | −0.114 | |
| 0.79 | 0.99 | 0.38 | 0.13 | <0.05 | <0.05 | 0.06 | ||
| CI | −0.079 | −0.0003 | −0.350 | −0.169 | 0.017 | 0.108 | 0.075 | |
| 0.19 | 0.99 | <0.0001 | <0.05 | 0.78 | 0.07 | 0.21 | ||
| DBH | −0.063 | 0.053 | −0.350 | 0.316 | −0.094 | −0.092 | −0.168 | |
| 0.30 | 0.38 | <0.0001 | <0.0001 | 0.12 | 0.13 | <0.05 | ||
| K | −0.067 | 0.108 | −0.169 | 0.316 | 0.016 | −0.172 | −0.447 | |
| 0.35 | 0.13 | <0.05 | <0.0001 | 0.82 | <0.05 | <0.0001 | ||
| WD | 0.174 | −0.177 | 0.017 | −0.094 | 0.016 | 0.182 | 0.207 | |
| <0.05 | <0.05 | 0.78 | 0.12 | 0.82 | <0.05 | <0.05 | ||
| MOE | 0.268 | 0.133 | 0.108 | −0.092 | −0.172 | 0.182 | 0.716 | |
| <0.0001 | <0.05 | 0.07 | 0.13 | <0.05 | <0.05 | <0.0001 | ||
| MOR | 0.177 | −0.114 | 0.075 | −0.168 | −0.447 | 0.207 | 0.716 | |
| <0.05 | 0.06 | 0.21 | <0.05 | <0.0001 | <0.05 | <0.0001 |
| SD * | LH | CI | DBH | K | WD | MOE | MOR | |
|---|---|---|---|---|---|---|---|---|
| SD | −0.0009 | 0.234 | −0.287 | −0.142 | 0.234 | 0.265 | 0.184 | |
| 0.99 | <0.0001 | <0.0001 | <0.05 | <0.0001 | <0.0001 | <0.05 | ||
| LH | −0.0009 | 0.016 | −0.011 | 0.113 | 0.103 | 0.329 | 0.222 | |
| 0.99 | 0.79 | 0.85 | 0.07 | 0.07 | <0.0001 | <0.0001 | ||
| CI | 0.234 | 0.0155 | −0.214 | −0.029 | −0.087 | 0.004 | 0.031 | |
| <0.0001 | 0.79 | <0.05 | 0.64 | 0.13 | 0.94 | 0.59 | ||
| DBH | −0.287 | −0.011 | −0.214 | −0.014 | −0.233 | −0.225 | −0.18 | |
| <0.0001 | 0.85 | <0.05 | 0.82 | <0.0001 | <0.0001 | <0.05 | ||
| K | −0.142 | 0.113 | −0.029 | −0.014 | 0.03 | −0.229 | −0.381 | |
| <0.05 | 0.07 | 0.64 | 0.82 | 0.62 | 0.0001 | <0.0001 | ||
| WD | 0.234 | 0.103 | −0.087 | −0.233 | 0.03 | 0.402 | 0.271 | |
| <0.0001 | 0.07 | 0.13 | <0.0001 | 0.62 | <0.0001 | <0.0001 | ||
| MOE | 0.265 | 0.329 | 0.004 | −0.225 | −0.229 | 0.402 | 0.769 | |
| <0.0001 | <0.0001 | 0.94 | <0.0001 | 0.0001 | <0.0001 | <0.0001 | ||
| MOR | 0.184 | 0.222 | 0.031 | −0.179 | −0.381 | 0.271 | 0.769 | |
| <0.05 | <0.0001 | 0.59 | <0.05 | <0.0001 | <0.0001 | <0.0001 |
| Model | R2 | R2 Ajusted | RMSE | Coeficient of Variation | |
|---|---|---|---|---|---|
| Scots pine | |||||
| 1 | MOE = 1817.33 + 0.40SD + 763.61LH + 20.74DBH + 219.73CI − 31.83K + 4.73WD + ε | 0.18 | 0.15 | 1309.95 | 22.33 |
| 2 * | MOE = 2501.66 + 0.38SD + 771.52LH − 32.37K + 4.75WD + ε | 0.17 | 0.16 | 1306.51 | 22.27 |
| 3 | MOR = 9.14 − 0.0001SD − 2.17LH − 0.12DBH − 0.38CI − 0.27K + 0.007WD + 0.003MOE + ε | 0.62 | 0.61 | 4.57 | 21.78 |
| 4 * | MOR = 9.23 − 2.32LH − 0.27K + 0.004MOE + ε | 0.62 | 0.62 | 4.54 | 21.65 |
| Norway spruce | |||||
| 5 | MOE = 4500.43 + 0.26SD + 967.78LH − 168.35DBH − 6.95CI − 99.96K + 14.32WD + ε | 0.38 | 0.37 | 1354.13 | 16.82 |
| 6 * | MOE = 4479.62 + 0.26SD + 967.42LH − 167.93DBH − 99.97K + 14.34WD + ε | 0.38 | 0.37 | 1351.56 | 16.79 |
| 7 | MOR* = 8.41 − 0.0002SD − 0.43LH − 0.24DBH + 0.05CI − 0.47K + 0.001WD + 0.004MOE + ε | 0.65 | 0.64 | 5.69 | 19.13 |
| 8 * | MOR = 3.52 - 0.46K + 0,004MOE + ε | 0.65 | 0.64 | 5.65 | 19 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šilinskas, B.; Varnagirytė-Kabašinskienė, I.; Aleinikovas, M.; Beniušienė, L.; Aleinikovienė, J.; Škėma, M. Scots Pine and Norway Spruce Wood Properties at Sites with Different Stand Densities. Forests 2020, 11, 587. https://doi.org/10.3390/f11050587
Šilinskas B, Varnagirytė-Kabašinskienė I, Aleinikovas M, Beniušienė L, Aleinikovienė J, Škėma M. Scots Pine and Norway Spruce Wood Properties at Sites with Different Stand Densities. Forests. 2020; 11(5):587. https://doi.org/10.3390/f11050587
Chicago/Turabian StyleŠilinskas, Benas, Iveta Varnagirytė-Kabašinskienė, Marius Aleinikovas, Lina Beniušienė, Jūratė Aleinikovienė, and Mindaugas Škėma. 2020. "Scots Pine and Norway Spruce Wood Properties at Sites with Different Stand Densities" Forests 11, no. 5: 587. https://doi.org/10.3390/f11050587
APA StyleŠilinskas, B., Varnagirytė-Kabašinskienė, I., Aleinikovas, M., Beniušienė, L., Aleinikovienė, J., & Škėma, M. (2020). Scots Pine and Norway Spruce Wood Properties at Sites with Different Stand Densities. Forests, 11(5), 587. https://doi.org/10.3390/f11050587





