Mean Annual Wood Density Variations of Larix gmelinii (Rupr.), Quercus mongolica Fisch. ex Ledeb., and Pinus tabulaeformis Carr. at Two Different Stem Heights
Abstract
1. Introduction
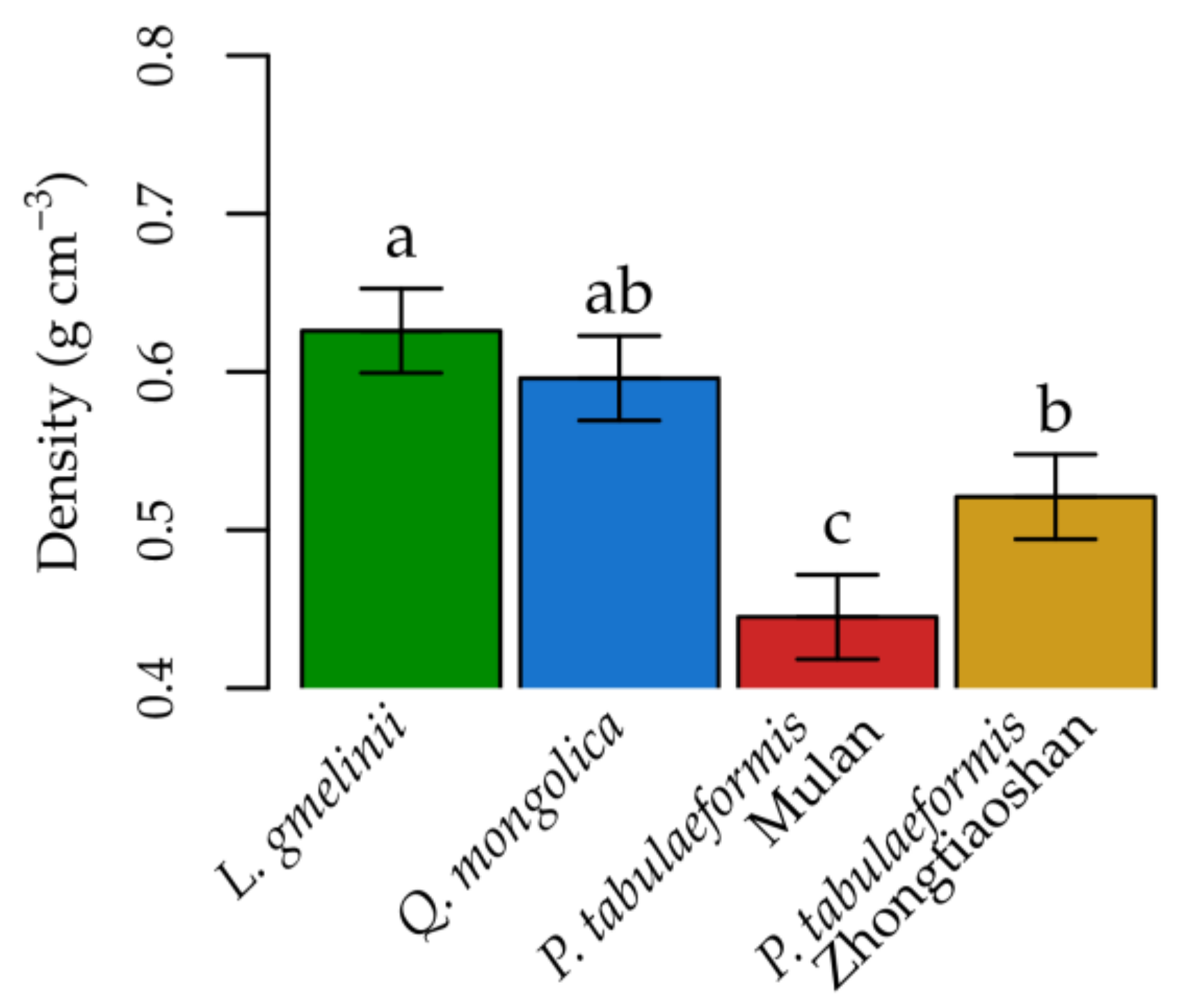
- Averaged over both stem heights and all observed CA, was highest for Q. mongolica and lowest for P. tabulaeformis.
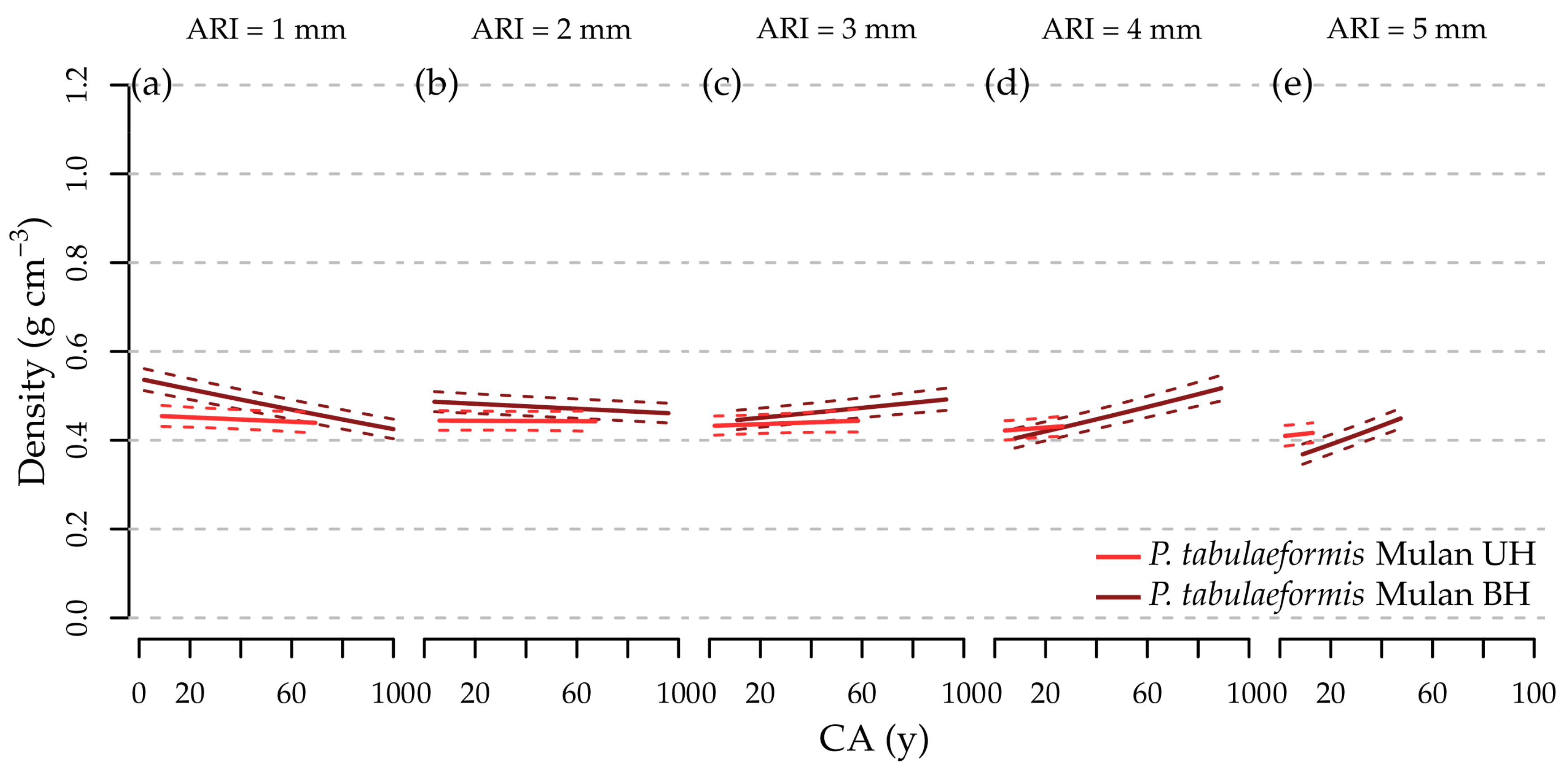
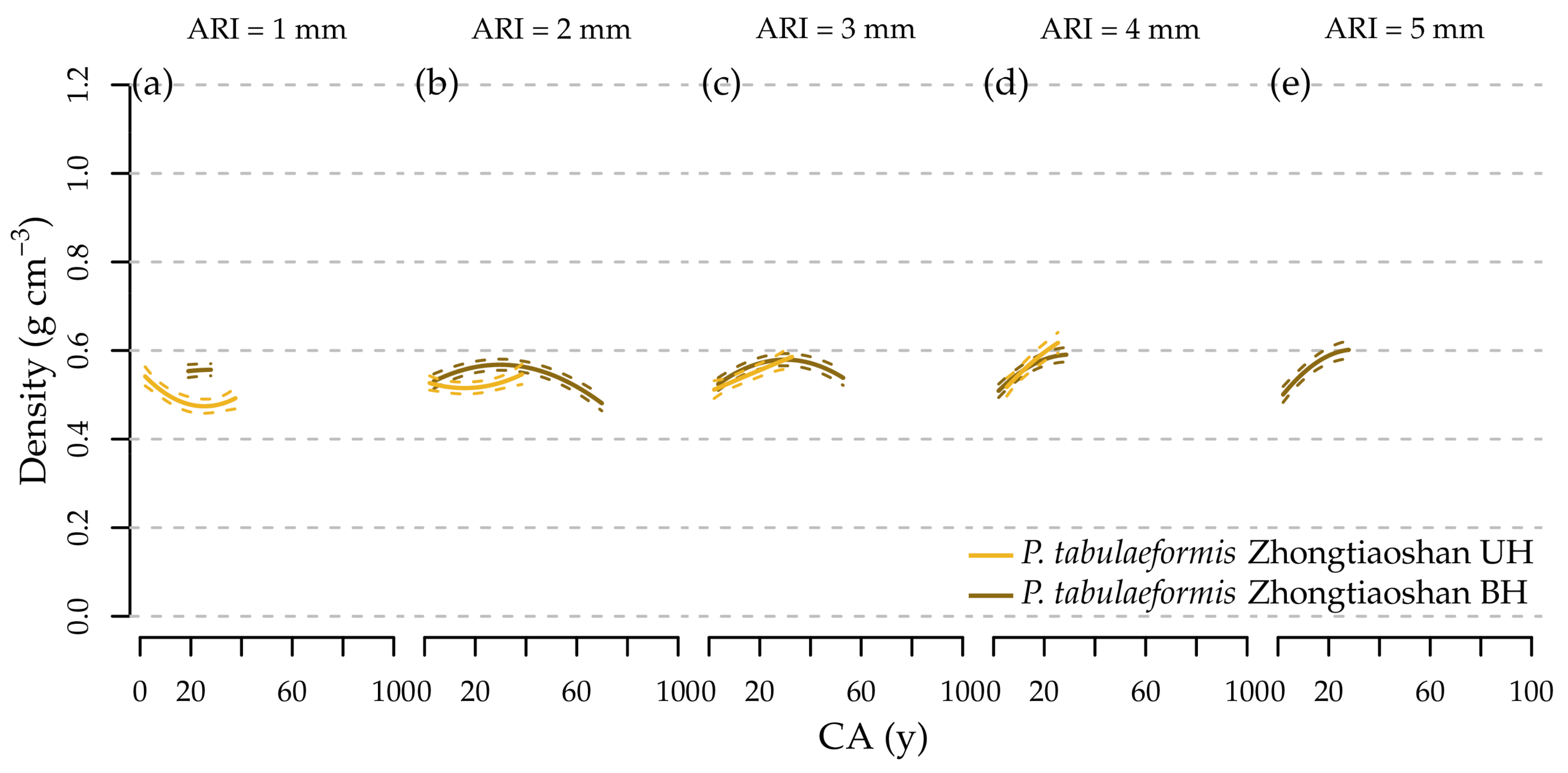
- For P. tabulaeformis, had no significant difference between the two different climatic regions.
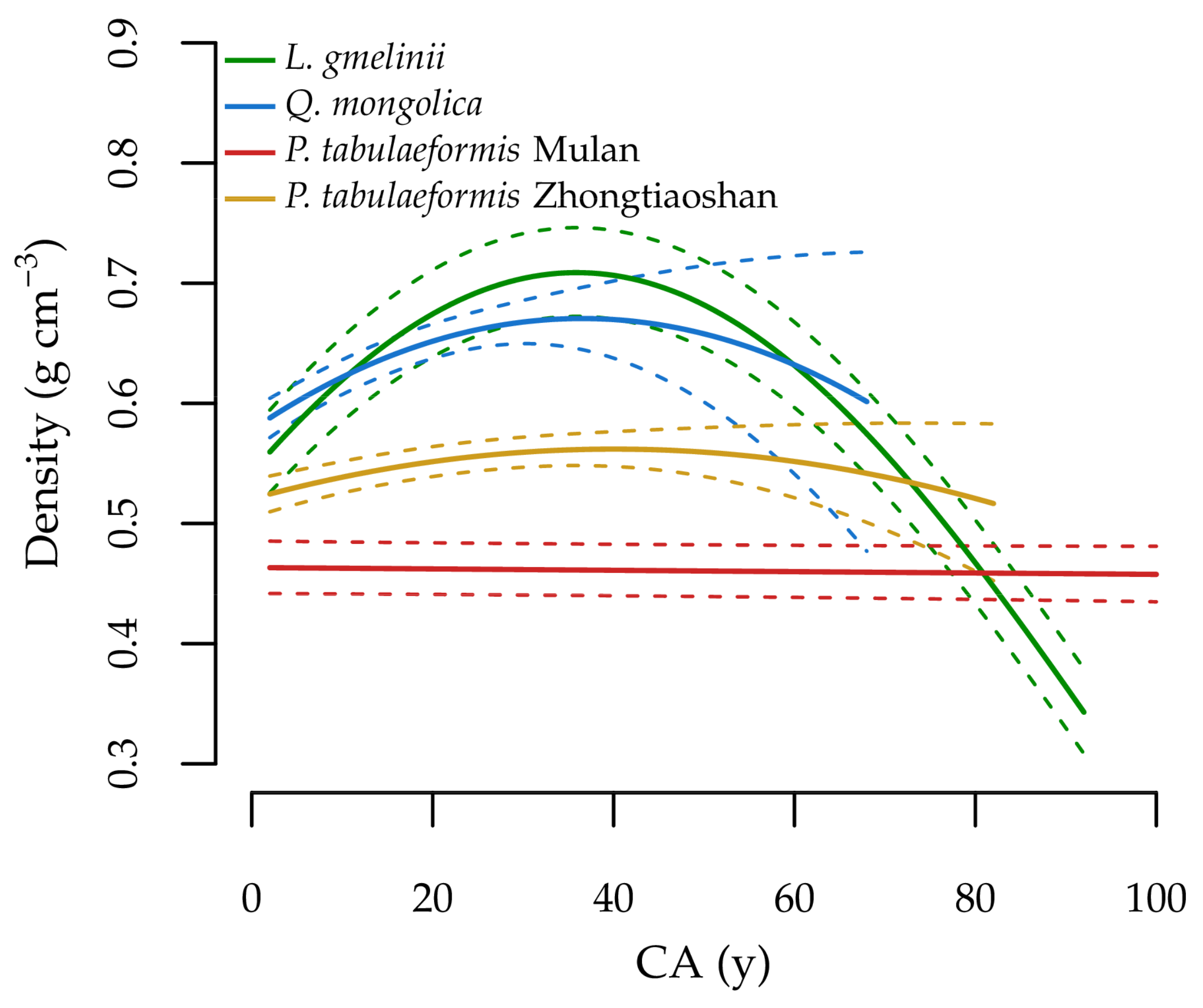
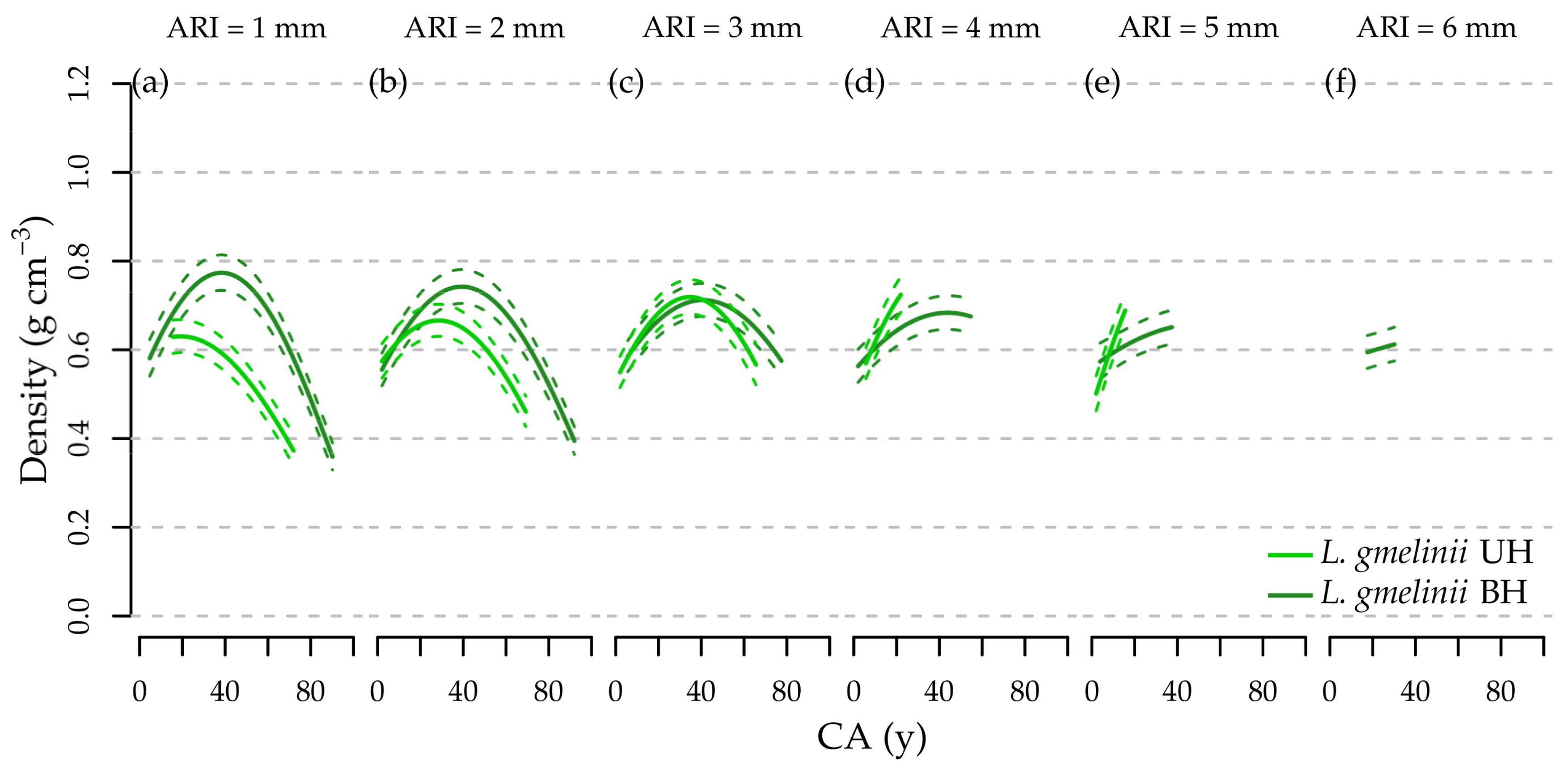
- With increasing CA, increased for the two coniferous tree species L. gmelinii and P. tabulaeformis.
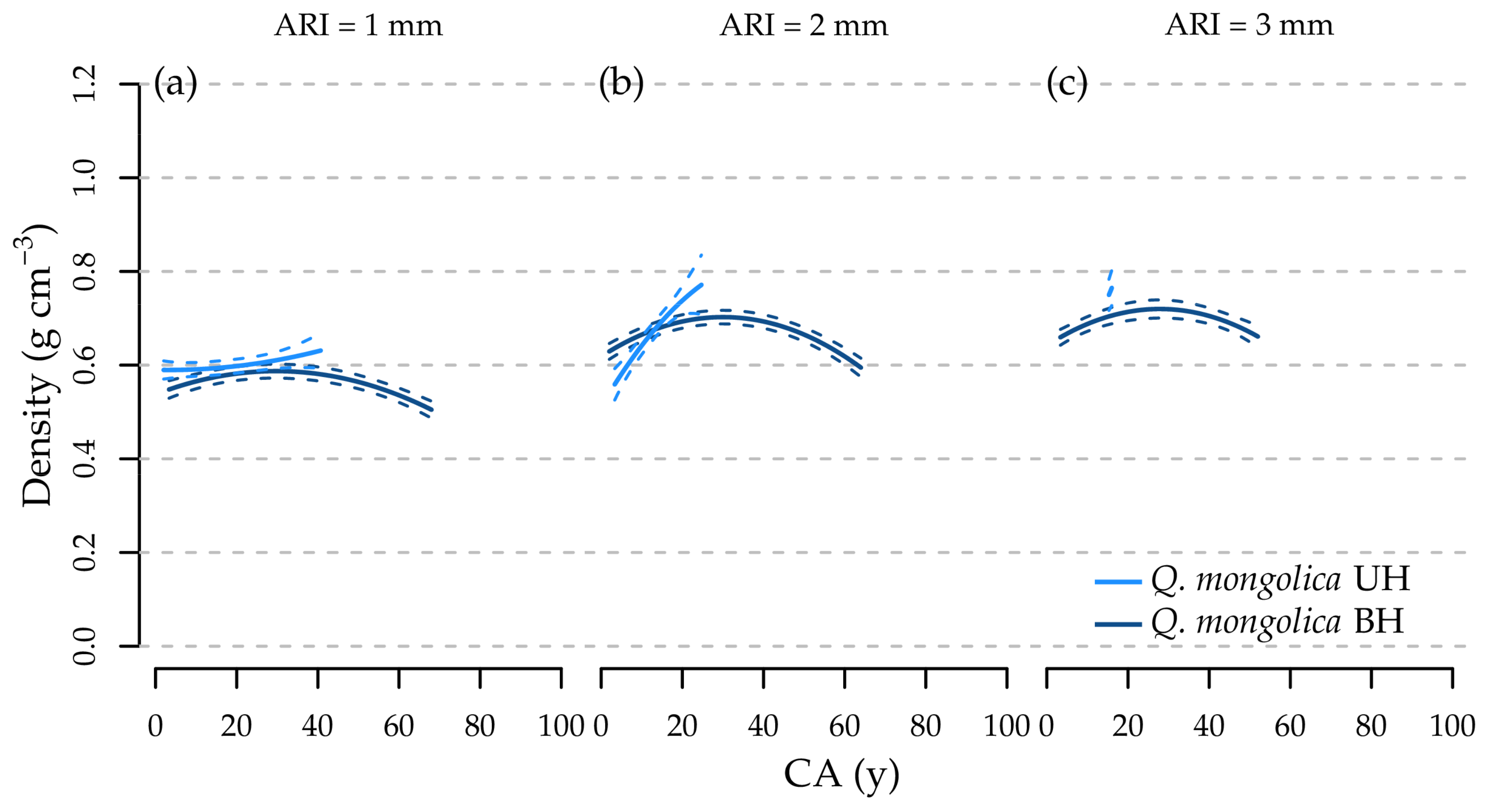
- For Q. mongolica, we expected to decrease with increasing CA.
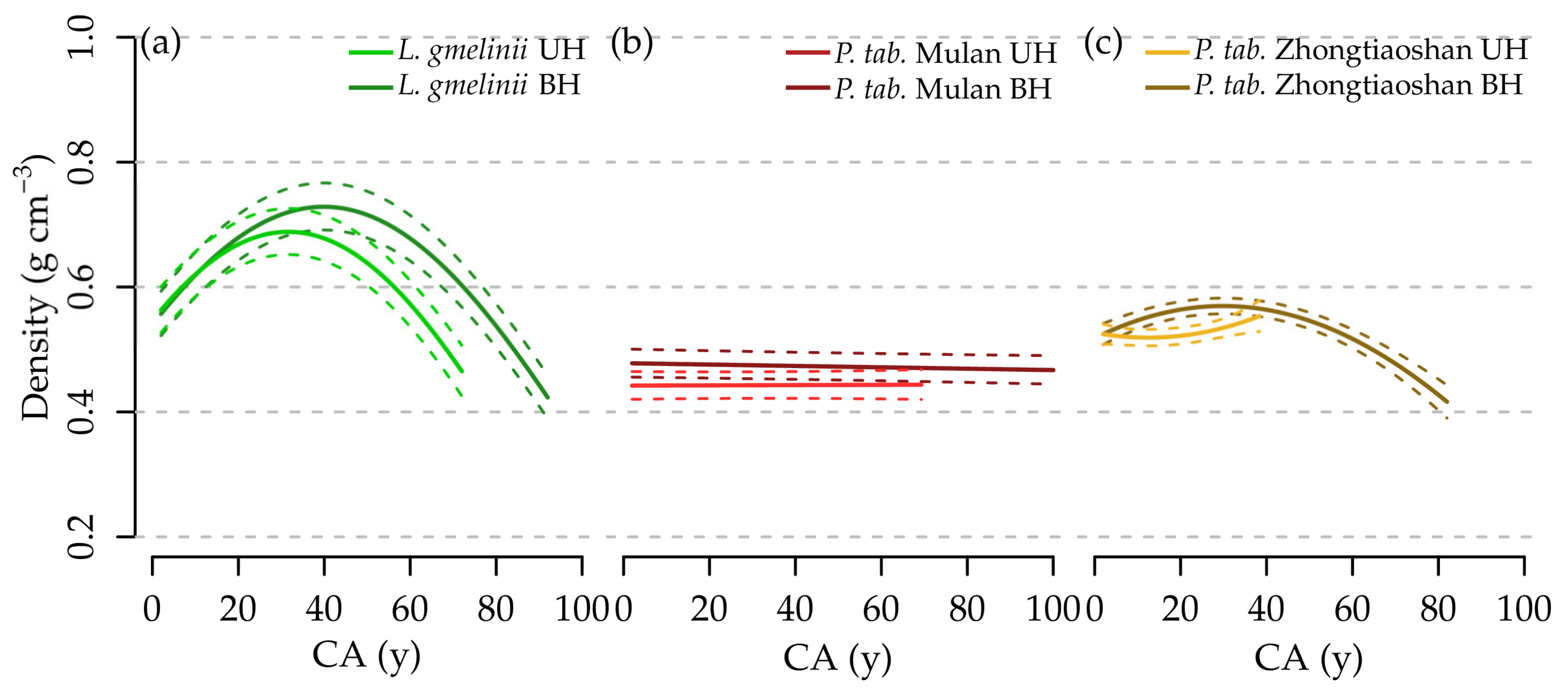
- For the effect of SH, we expected to observe significantly higher at BH compared to at UH at the same CA for Q. mongolica and significantly lower for the coniferous tree species.
2. Materials and Methods
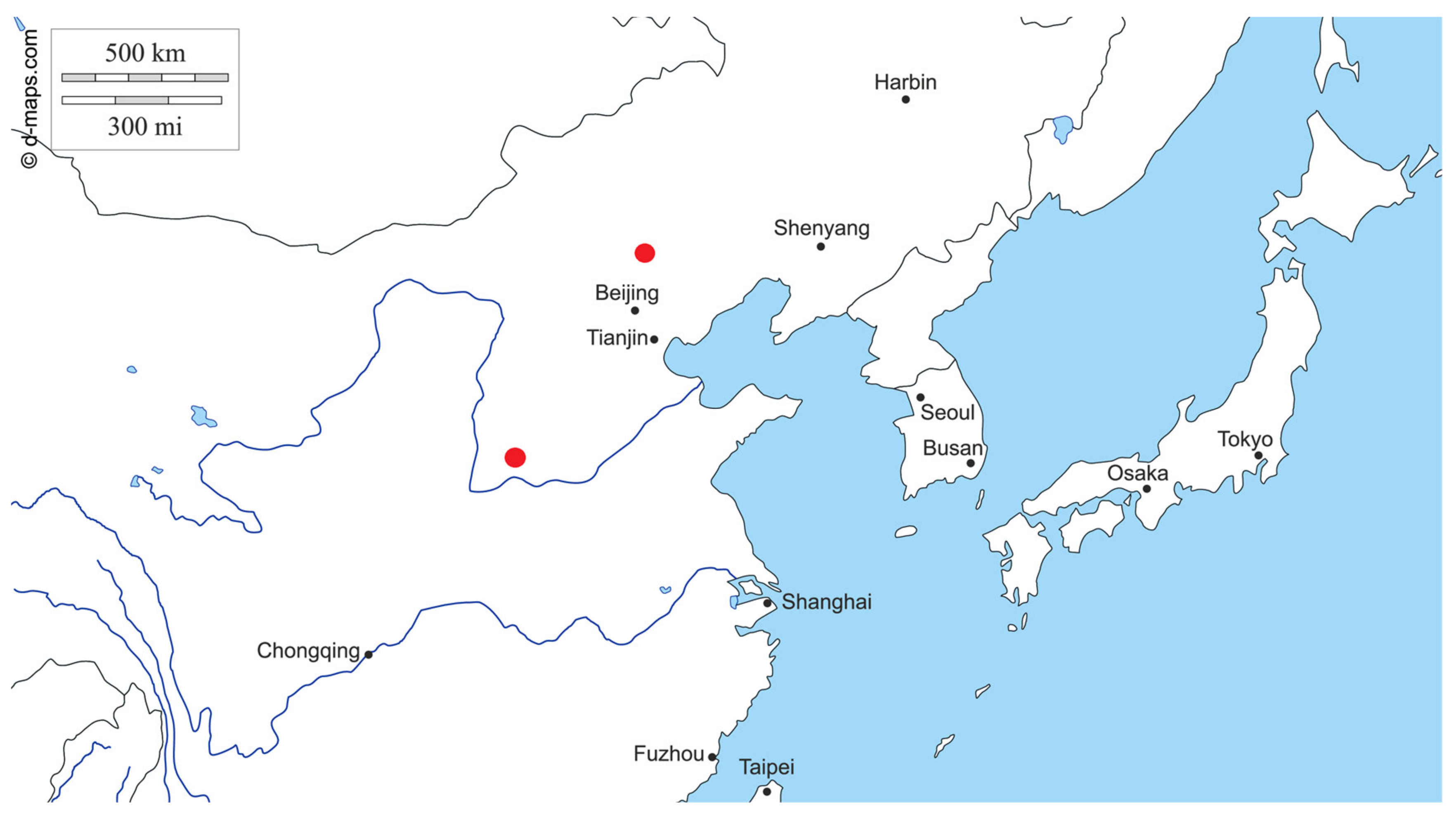
2.1. Research Area
2.2. Collection of Cross-Sections
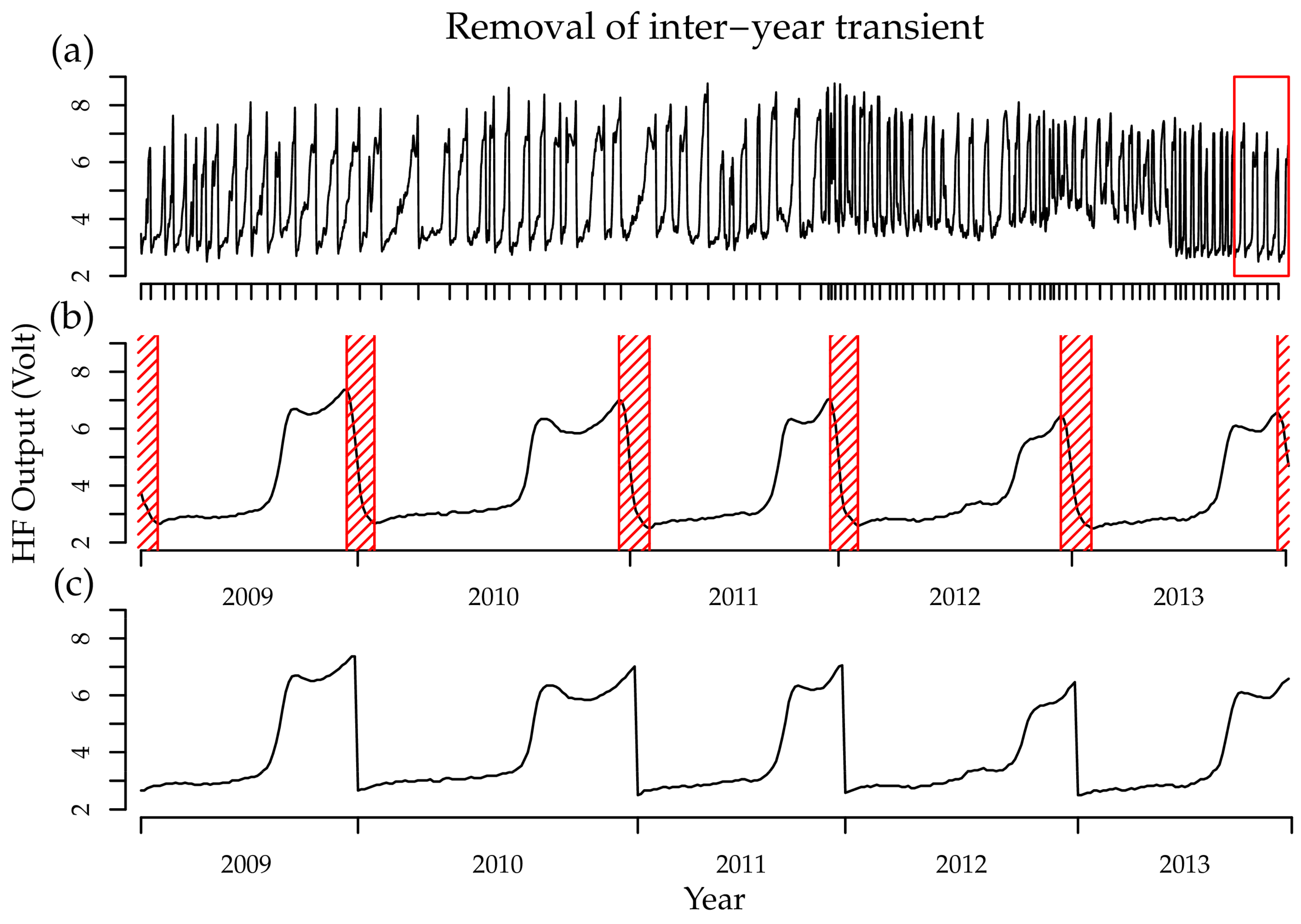
2.3. Density Measurement
2.4. Data Processing
2.5. Data Analysis
3. Results
3.1. Effect of Tree Species
3.2. Effect of Stem Height
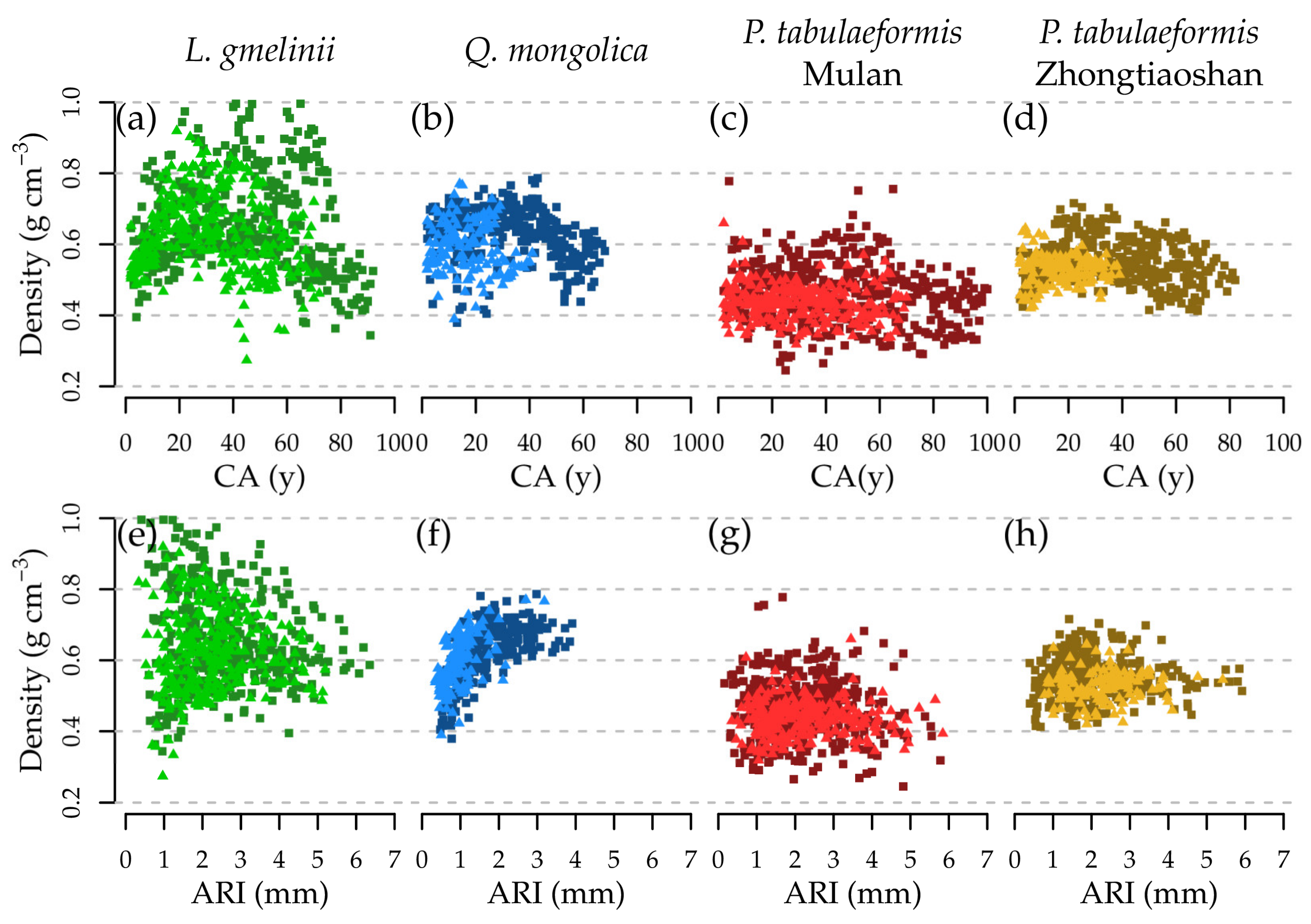
3.3. Effect of Cambial Age
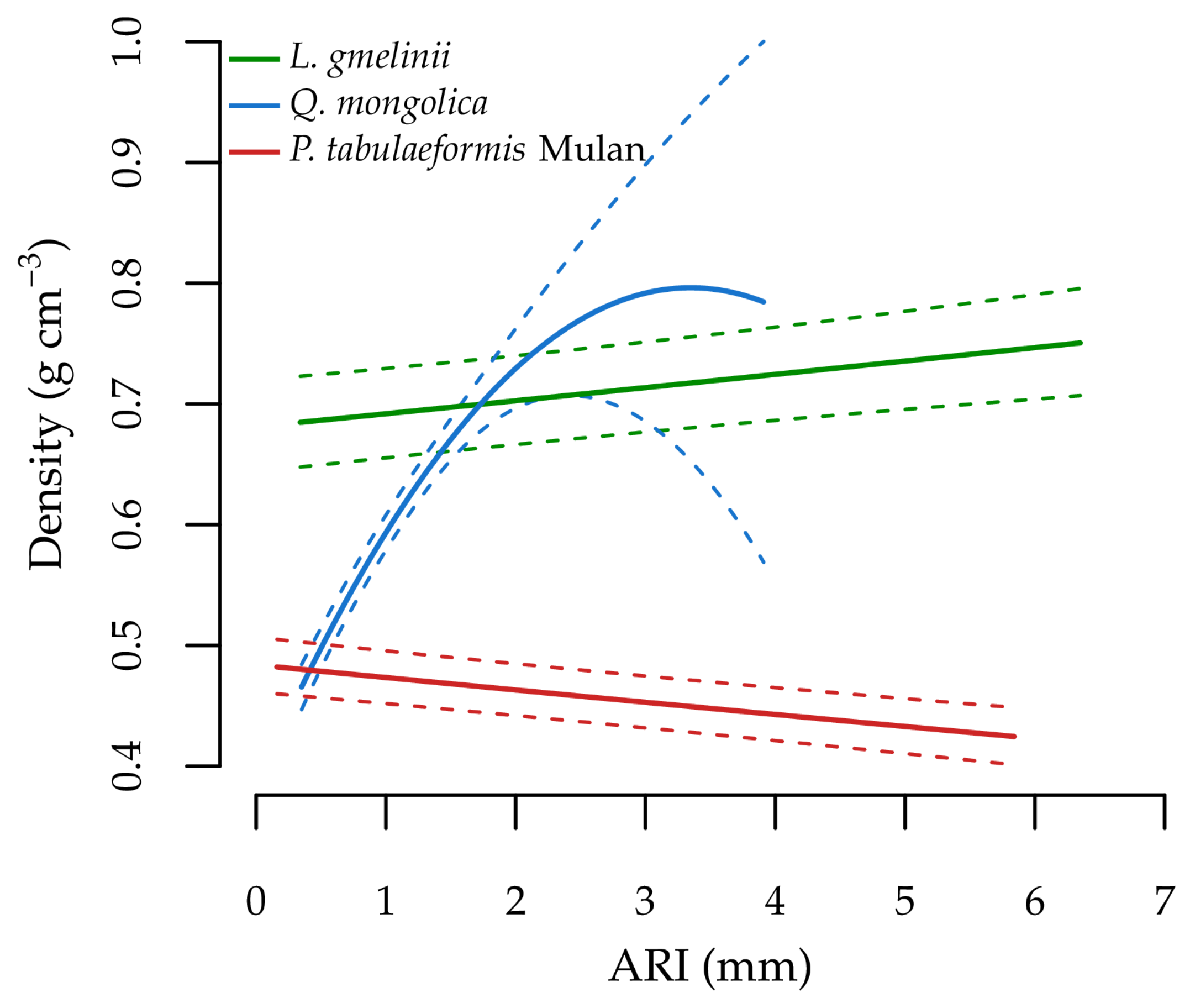
3.4. Effect of Annual Radial Increment
3.5. Effect of Cambial Age, Annual Radial Increment, and Stem Height
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
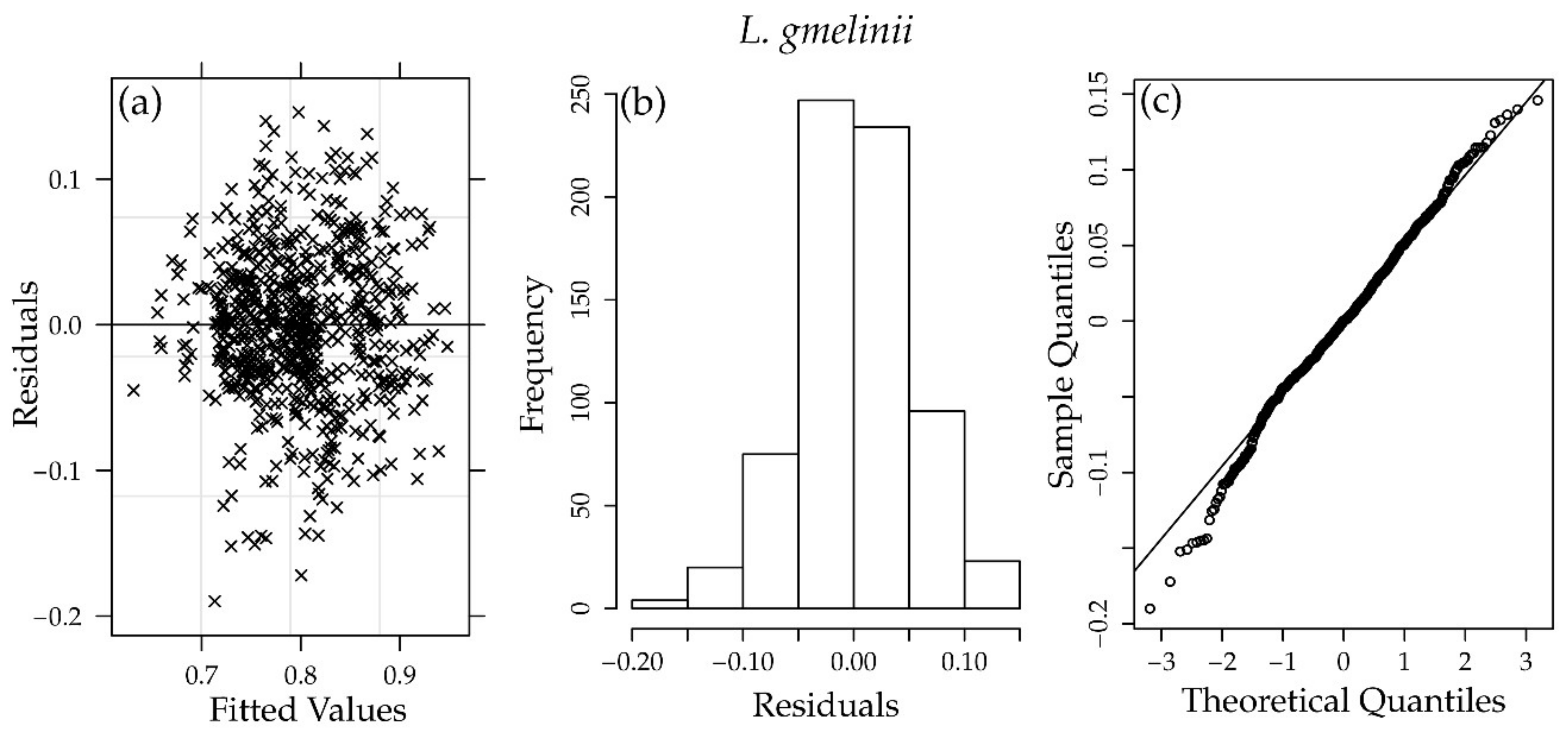
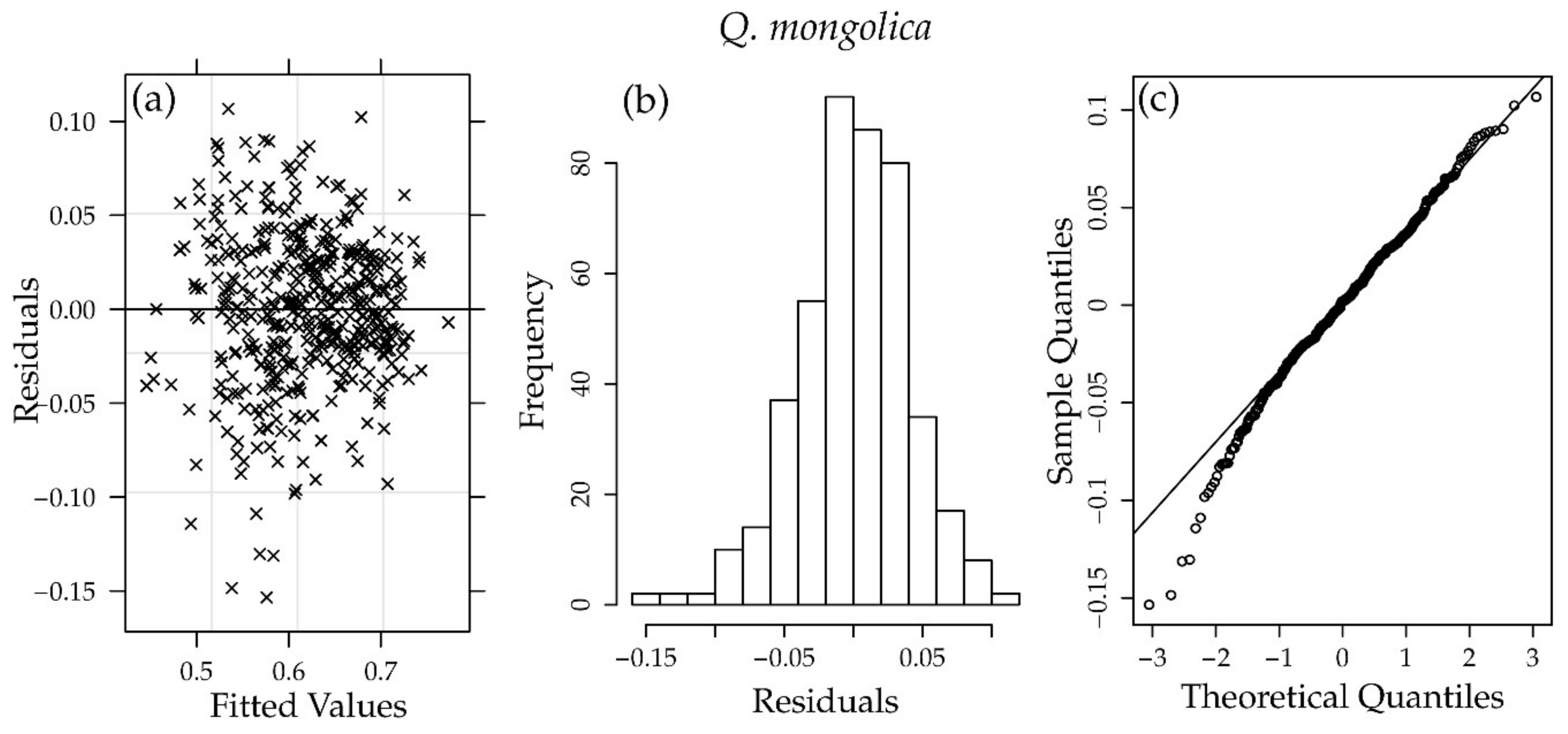
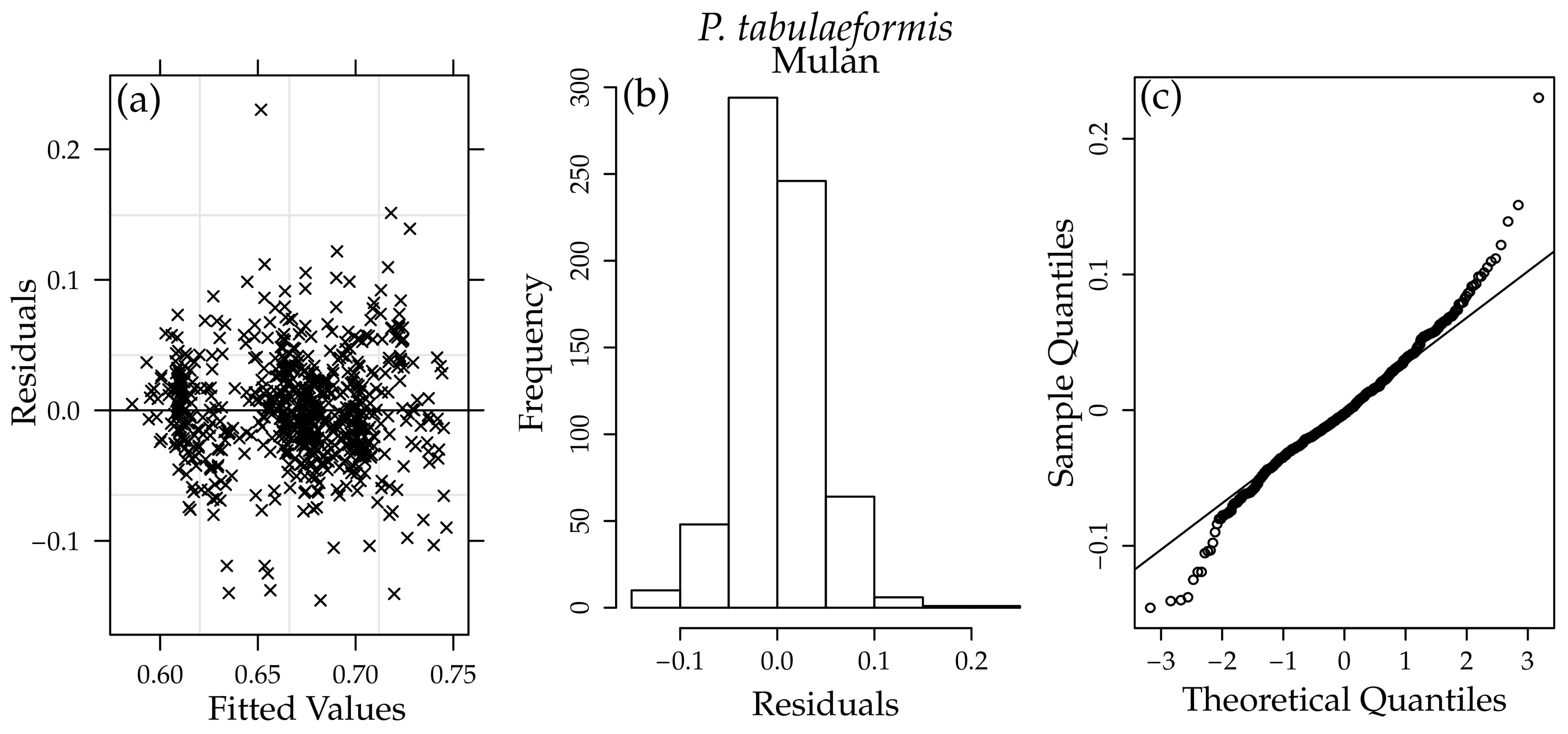
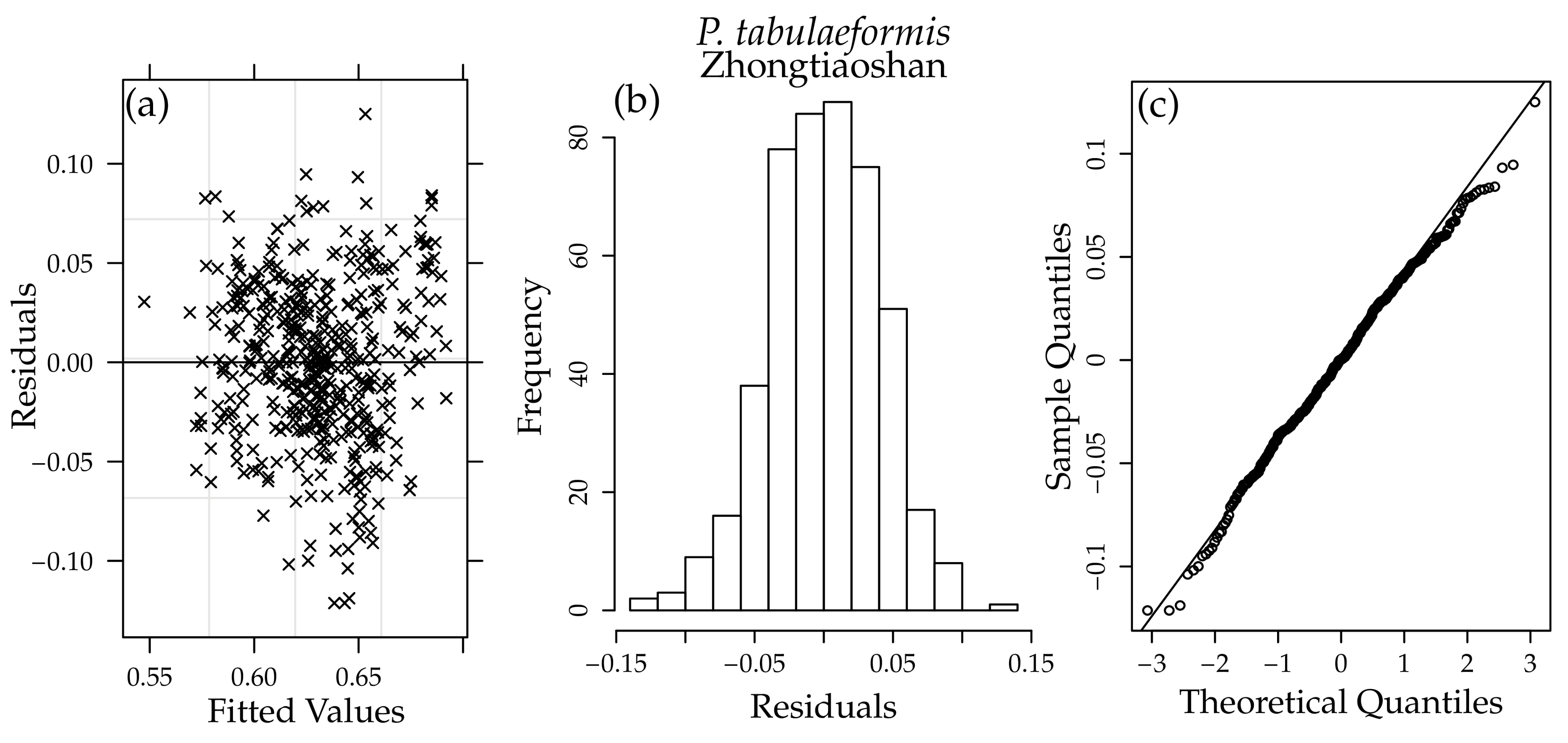
Appendix B
References
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Canadell, J.G.; Raupach, M.R. Managing Forests for Climate Change Mitigation. Science 2008, 320, 1456–1457. [Google Scholar] [CrossRef] [PubMed]
- Fahey, T.J.; Woodbury, P.B.; Battles, J.J.; Goodale, C.L.; Hamburg, S.P.; Ollinger, S.V.; Woodall, C.W. Forest carbon storage: Ecology, management, and policy. Front. Ecol. Environ. 2010, 8, 245–252. [Google Scholar] [CrossRef]
- Sathre, R.; O’Connor, J. Meta-analysis of greenhouse gas displacement factors of wood product substitution. Environ. Sci. Policy 2010, 13, 104–114. [Google Scholar] [CrossRef]
- Sathre, R.; Gustavsson, L. Energy and carbon balances of wood cascade chains. Resour. Conserv. Recycl. 2006, 47, 332–355. [Google Scholar] [CrossRef]
- Zanne, A.E.; Lopez-Gonzalez, G.; Coomes, D.A.; Ilic, J.; Jansen, S.; Lewis, S.L.; Miller, R.B.; Swenson, N.G.; Wiemann, M.C.; Chave, J. Data from: Towards a worldwide wood economics spectrum. Dry. Digit. Repos. 2009. [Google Scholar] [CrossRef]
- Niklas, K.J.; Spatz, H.-C. Worldwide correlations of mechanical properties and green wood density. Am. J. Bot. 2010, 97, 1587–1594. [Google Scholar] [CrossRef]
- Hacke, U.G.; Sperry, J.S.; Pockman, W.T.; Davis, S.D.; McCulloh, K.A. Trends in wood density and structure are linked to prevention of xylem implosion by negative pressure. Oecologia 2001, 126, 457–461. [Google Scholar] [CrossRef]
- Briffa, K.R.; Osborn, T.J.; Schweingruber, F.H.; Jones, P.D.; Shiyatov, S.G.; Vaganov, E.A. Tree-ring width and density data around the Northern Hemisphere: Part 1, local and regional climate signals. Holocene 2002, 12, 737–757. [Google Scholar] [CrossRef]
- Hannrup, B.; Cahalan, C.; Chantre, G.; Grabner, M.; Karlsson, B.; Bayon, I.L.; Jones, G.L.; Müller, U.; Pereira, H.; Rodrigues, J.C.; et al. Genetic parameters of growth and wood quality traits in Picea abies. Scand. J. For. Res. 2004, 19, 14–29. [Google Scholar] [CrossRef]
- Bouriaud, O.; Bréda, N.; Le Moguédec, G.; Nepveu, G. Modelling variability of wood density in beech as affected by ring age, radial growth and climate. Trees 2004, 18, 264–276. [Google Scholar] [CrossRef]
- Jyske, T.; Mäkinen, H.; Saranpää, P. Wood density within Norway spruce stems. Silva Fenn. 2008, 42, 439–455. [Google Scholar] [CrossRef]
- Ivković, M.; Gapare, W.; Wu, H.; Espinoza, S.; Rozenberg, P. Influence of cambial age and climate on ring width and wood density in Pinus radiata families. Ann. For. Sci. 2013, 70, 525–534. [Google Scholar] [CrossRef]
- DeBell, D.S.; Singleton, R.; Gartner, B.L.; Marshall, D.D. Wood density of young-growth western hemlock: Relation to ring age, radial growth, stand density, and site quality. Can. J. For. Res. 2004, 34, 2433–2442. [Google Scholar] [CrossRef]
- Hu, D.; Ruan, Z.; Qian, Z.; Huang, Y.; Huang, X.; Chen, Z. The Genetics and Variation of Wood Density in Chinese Fir Clones and Its Interaction to the Growth Characters. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFD2004&filename=ZNLB200405006&v=MTY4MzkxRnJDVVI3cWZZK1p1Rnlqa1ZyL0xQeVBIYkxHNEh0WE1xbzlGWW9SOGVYMUx1eFlTN0RoMVQzcVRyV00 (accessed on 11 March 2020).
- Liu, Q.; Zhang, R.; Jin, G.; Chu, D.; Zhou, Z. Variation of Ring Width and Wood Basic Density and Early Selection of Pinus massoniana Provenances. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFD2010&filename=LYKE201005010&v=MTYzMTdyM1BLVFRBYTdHNEg5SE1xbzlFWklSOGVYMUx1eFlTN0RoMVQzcVRyV00xRnJDVVI3cWZZK1p1RnlqbFU (accessed on 11 March 2020).
- Hong, P. Pinus tabulaeformis. In Enzyklopädie der Holzgewächse: Handbuch und Atlas der Dendrologie; Wiley-VCH: Weinheim, Germany, 2004; ISBN 978-3-527-32141-4. [Google Scholar]
- Yin, M.; Yang, L.; Yin, W.; Lei, Q.; Tan, X.; Zhang, Y.; Li, Z. Dynamic changes of carbon storage in trunk volume of Pinus tabulaeformis, Robinia pseudoacacia and Populus euramericana. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFD2011&filename=BJLY201105013&v=MjczNzhSOGVYMUx1eFlTN0RoMVQzcVRyV00xRnJDVVI3cWZZK1p1RnlqbFU3L0FKeWZIZDdHNEg5RE1xbzlFWjQ (accessed on 11 March 2020).
- Xu, Y. Specific Gravity Variation in Pinus Tabulaeformis. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFD9093&filename=HZNY199103011&v=MzAyMzc3dkJMVGZGZDdLeEY5RE1ySTlFWllSOGVYMUx1eFlTN0RoMVQzcVRyV00xRnJDVVI3cWZZK1p1RnlqbFU (accessed on 11 March 2020).
- Debreczy, Z.; Rácz, I.; Musial, K. Conifers around the World: Conifers of the Temperate Zones and Adjacent Regions. Vol. 1; DendroPress: Budapest, Hungary, 2011; ISBN 978-963-219-063-1. [Google Scholar]
- Huang, P.; Zhuo, L.; Li, G.; Wei, C.; Zhou, W.; Li, Y.; Chen, T.; Wu, J. Studies on Physical and Mechanical Properties of Dahurian Larch-Wood of Two Wood Colours. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFD9495&filename=DBLY403.003&v=MjAxMDU3ZTRIYy9NcjR3cUY1NE9mZ2c1emhBVTRqaDRPWDZUckgwM2ViQ1VSYjZmWnVkdUZ5dmdWUT09SVMvSGQ (accessed on 11 March 2020).
- Jiang, L.; Liu, M.; Liu, Y. Variation of Wood Basic Density and Early Selection of Dahurian Larch and Mongolian Pine. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFD2013&filename=BJLY201301003&v=MjY0ODV4WVM3RGgxVDNxVHJXTTFGckNVUjdxZlkrWnVGeWpsVWIzT0p5ZkhkN0c0SDlMTXJvOUZaNFI4ZVgxTHU (accessed on 11 March 2020).
- Farjon, A. Pinaceae: Drawings and Descriptions of the Genera Abies, Cedrus, Pseudolarix, Keteleeria, Nothotsuga, Tsuga, Cathaya, Pseudotsuga, Larix and Picea; Regnum vegetabile; Koeltz: Königstein, Germany, 1990; ISBN 978-3-87429-298-6. [Google Scholar]
- Puhua, H. Quercus mongolica. In Enzyklopädie der Holzgewächse: Handbuch und Atlas der Dendrologie; Wiley-VCH: Weinheim, Germany, 2004; ISBN 978-3-527-32141-4. [Google Scholar]
- Schweingruber, F.H.; Fritts, H.C.; Bräker, O.U.; Drew, L.G.; Schär, E. The X-Ray Technique as Applied to Dendroclimatology. Tree-Ring Bul. 1978, 38, 61–91. [Google Scholar]
- Park, W.-K.; Telewski, F.W. Measuring maximum latewood density by image analysis at the cellular level. Wood Fibre Sci. 2007, 25, 326–332. [Google Scholar]
- Hoffmeyer, P.; Pedersen, J.G. Evaluation of density and strength of Norway spruce wood by near infrared reflectance spectroscopy. Holz Roh- Werkst. 1995, 53, 165–170. [Google Scholar] [CrossRef]
- Sheppard, P.R.; Graumlich, L.J.; Conkey, L.E. Reflected-light image analysis of conifer tree rings for reconstructing climate. Holocene 1996, 6, 62–68. [Google Scholar] [CrossRef]
- Koch, M.; Hunsche, S.; Schumacher, P.; Nuss, M.C.; Feldmann, J.; Fromm, J. THz-imaging: A new method for density mapping of wood. Wood Sci. Technol. 1998, 32, 421–427. [Google Scholar] [CrossRef]
- McCarroll, D.; Pettigrew, E.; Luckman, A.; Guibal, F.; Edouard, J.-L. Blue Reflectance Provides a Surrogate for Latewood Density of High-latitude Pine Tree Rings. Arct. Antarct. Alp. Res. 2002, 34, 450–453. [Google Scholar] [CrossRef]
- Rinn, F.; Schweingruber, F.-H.; Schär, E. RESISTOGRAPH and X-Ray Density Charts of Wood. Comparative Evaluation of Drill Resistance Profiles and X-ray Density Charts of Different Wood Species. Holzforschung 1996, 50, 303–311. [Google Scholar] [CrossRef]
- Schinker, M.G.; Hansen, N.; Spiecker, H. High-Frequency Densitometry-A New Method for the Rapid Evaluation of Wood Density Variations. IAWA J. 2003, 24, 231–239. [Google Scholar] [CrossRef]
- Johansson, J.; Hagman, O.; Fjellner, B.-A. Predicting moisture content and density distribution of Scots pine by microwave scanning of sawn timber. J. Wood Sci. 2003, 49, 312–316. [Google Scholar] [CrossRef]
- Mannes, D.; Lehmann, E.; Cherubini, P.; Niemz, P. Neutron imaging versus standard X-ray densitometry as method to measure tree-ring wood density. Trees 2007, 21, 605–612. [Google Scholar] [CrossRef]
- Franceschini, T.; Bontemps, J.-D.; Gelhaye, P.; Rittie, D.; Herve, J.-C.; Gegout, J.-C.; Leban, J.-M. Decreasing trend and fluctuations in the mean ring density of Norway spruce through the twentieth century. Ann. For. Sci. 2010, 67, 816. [Google Scholar] [CrossRef][Green Version]
- Boden, S.; Schinker, M.G.; Duncker, P.; Spiecker, H. Resolution abilities and measuring depth of High-Frequency densitometry on wood samples. Measurement 2012, 45, 1913–1921. [Google Scholar] [CrossRef]
- Wassenberg, M.; Montwé, D.; Kahle, H.-P.; Spiecker, H. Exploring high frequency densitometry calibration functions for different tree species. Dendrochronologia 2014, 32, 273–281. [Google Scholar] [CrossRef]
- East Asia Free Map, Free Blank Map, Free Outline Map, Free Base Map Hydrography, States, Main Cities, Names. Available online: https://d-maps.com/carte.php?num_car=28780&lang=en (accessed on 23 January 2020).
- Li, Q.; Liu, Y.; Song, H.; Cai, Q.; Yang, Y. Long-term variation of temperature over North China and its links with large-scale atmospheric circulation. Quat. Int. 2013, 283, 11–20. [Google Scholar] [CrossRef]
- Köppen, W. Klassifikation der Klimate nach Temperatur, Niederschlag und Jahreslauf. Pet. Mitt. 1918, 64, 193–203. [Google Scholar]
- Kraft, G. Beiträge zur Lehre von den Durchforstungen, Schlagstellungen und Lichtungshieben; Klindworth: Hannover, Germany, 1884. [Google Scholar]
- Spiecker, H.; Schinker, M.G.; Hansen, J.; Park, Y.-I.; Ebding, T.; Döll, W. Cell structure in tree rings: Novel methods for preparation and image analysis of large cross sections. IAWA J. 2000, 21, 361–373. [Google Scholar] [CrossRef]
- Wassenberg, M.; Schinker, M.; Spiecker, H. Technical aspects of applying high frequency densitometry: Probe-sample contact, sample surface preparation and integration width of different dielectric probes. Dendrochronologia 2015, 34, 10–18. [Google Scholar] [CrossRef]
- Torgovnikov, G.I. Dielectric Properties of Wood and Wood-Based Materials; Springer: Berlin, Germany, 2012; ISBN 978-3-642-77455-3. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- RStudio Team. RStudio: Integrated Development Environment for R; RStudio, Inc.: Boston, MA, USA, 2019. [Google Scholar]
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Kuznetsova, A.; Brockhoff, P.B.; Christensen, R.H.B. lmerTest Package: Tests in Linear Mixed Effects Models. J. Stat. Softw. 2017, 82, 1–26. [Google Scholar] [CrossRef]
- Lenth, R. emmeans: Estimated Marginal Means, aka Least-Squares Means. Available online: https://CRAN.R-project.org/package=emmeans (accessed on 29 May 2019).
- Fox, J.; Weisberg, S. An R Companion to Applied Regression, 3rd ed.; SAGE: Los Angeles, CA, USA, 2019; ISBN 978-1-5443-3647-3. [Google Scholar]
- Liu, M.Y.; Liu, Y.B.; Jiang, L.C. Variation of Wood Density in Larch in Northeast of China. Adv. Mater. Res. 2012, 487, 38–42. [Google Scholar] [CrossRef]
- Wassenberg, M.; Chiu, H.-S.; Guo, W.; Spiecker, H. Analysis of wood density profiles of tree stems: Incorporating vertical variations to optimize wood sampling strategies for density and biomass estimations. Trees 2015, 29, 551–561. [Google Scholar] [CrossRef]
- Gindl, W.; Grabner, M.; Wimmer, R. The influence of temperature on latewood lignin content in treeline Norway spruce compared with maximum density and ring width. Trees 2000, 14, 409–414. [Google Scholar] [CrossRef]
- Rossi, S.; Deslauriers, A.; Anfodillo, T.; Morin, H.; Saracino, A.; Motta, R.; Borghetti, M. Conifers in cold environments synchronize maximum growth rate of tree-ring formation with day length. New Phytol. 2006, 170, 301–310. [Google Scholar] [CrossRef]
- Larson, P.R. Effect of Environment on the Percentage of Summerwood and Specific Gravity of Slash Pine; Yale School of Forestry & Environmental Studies Bulletin Series; Yale University: New Haven, CT, USA, 1957. [Google Scholar]
- Fritts, H.C. Tree Rings and Climate; Academic Press: London, UK, 1976; ISBN 978-0-12-268450-0. [Google Scholar]
- Knapic, S.; Louzada, J.L.; Leal, S.; Pereira, H. Radial variation of wood density components and ring width in cork oak trees. Ann. For. Sci. 2007, 64, 211–218. [Google Scholar] [CrossRef]
- Bergès, L.; Dupouey, J.-L.; Franc, A. Long-term changes in wood density and radial growth of Quercus petraea Liebl. in northern France since the middle of the nineteenth century. Trees 2000, 14, 398–408. [Google Scholar] [CrossRef]
- Zhang, S.-Y.; Owoundi, R.E.; Nepveu, G.; Mothe, F.; Dhôte, J.-F. Modelling wood density in European oak (Quercus petraea and Quercus robur) and simulating the silvicultural influence. Can. J. For. Res. 1993, 23, 2587–2593. [Google Scholar] [CrossRef]
- Zhang, S.-Y.; Zhong, Y. Effect of growth rate on specific gravity of East-Liaoning oak (Quercus liaotungensis) wood. Can. J. For. Res. 1991, 21, 255–260. [Google Scholar] [CrossRef]
- Bouriaud, O.; Bréda, N.; Dupouey, J.-L.; Granier, A. Is ring width a reliable proxy for stem-biomass increment? A case study in European beech. Can. J. For. Res. 2005, 35, 2920–2933. [Google Scholar] [CrossRef]
- Sprengel, L.; Stangler, D.F.; Sheppard, J.; Morhart, C.; Spiecker, H. Comparative Analysis of the Effects of Stem Height and Artificial Pruning on Seasonal Radial Growth Dynamics of Wild Cherry (Prunus avium L.) and Sycamore (Acer pseudoplatanus L.) in a Widely Spaced System. Forests 2018, 9, 174. [Google Scholar] [CrossRef]
- van der Maaten-Theunissen, M.; Bouriaud, O. Climate–growth relationships at different stem heights in silver fir and Norway spruce. Can. J. For. Res. 2012, 42, 958–969. [Google Scholar] [CrossRef]
- Repola, J. Models for vertical wood density of Scots pine, Norway spruce and birch stems, and their application to determine average wood density. Silva Fenn. 2006, 40. [Google Scholar] [CrossRef]
- Liang, D.; Jin, Y.; Zhao, G.; Dong, Y.; Leng, W.; Chen, C.; Wang, H.; Zhao, X. Variance Analyses of Growth and Wood Characteristics of 50 Pinus Koraiensis Clones. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFDLAST2016&filename=BJLY201606007&v=MTc4ODRkN0c0SDlmTXFZOUZZNFI4ZVgxTHV4WVM3RGgxVDNxVHJXTTFGckNVUjdxZlkrWnVGeWpsVnIzQkp5Zkg (accessed on 11 March 2020).
- Molteberg, D.; Høibø, O. Development and variation of wood density, kraft pulp yield and fibre dimensions in young Norway spruce (Picea abies). Wood Sci. Technol. 2006, 40, 173–189. [Google Scholar] [CrossRef]
- Petty, J.A.; Macmillan, D.C.; Steward, C.M. Variation of Density and Growth Ring Width in Stems of Sitka and Norway Spruce. Forestry 1990, 63, 39–49. [Google Scholar] [CrossRef]
| Tree No. | Species Location | Age at 1.3 m Stem Height (y) | Tree Height (m) | DBH (cm) | Elevation (m) | Exposition |
|---|---|---|---|---|---|---|
| LM1 | L. gmelinii Mulan | 80 | 27.00 | 53.0 | 1450 | NW |
| LM2 | 79 | 27.16 | 58.0 | 1430 | NW | |
| LM3 | 80 | 27.64 | 48.8 | 1430 | NW | |
| LM4 | 94 | 25.65 | 52.4 | 1293 | NE | |
| LM5 | 93 | 25.30 | 52.7 | 1338 | E | |
| QM1 | Q. mongolica Mulan | 55 | 11.75 | 27.5 | 1352 | NA |
| QM2 | 66 | 15.30 | 28.6 | 1130 | W | |
| QM3 | 66 | 15.42 | 28.6 | 1352 | S | |
| QM4 | 66 | 14.06 | 29.2 | 1347 | S | |
| QM5 | 70 | 13.65 | 28.2 | 1185 | N | |
| PM1 | P. tabulaeformis Mulan | 67 | 19.85 | 42.8 | 1162 | NW |
| PM2 | 70 | 24.60 | 41.5 | 954 | NE | |
| PM3 | 101 | 25.80 | 50.6 | 961 | NE | |
| PM4 | 98 | 24.70 | 42.2 | 1020 | NW | |
| PM5 | 100 | 23.74 | 46.8 | 1013 | NW | |
| PZ1 | P. tabulaeformis Zhongtiaoshan | 71 | 11.98 | 21.2 | 1223 | NW |
| PZ2 | 87 | 15.40 | 34.5 | 1190 | NE | |
| PZ3 | 75 | 16.14 | 41.4 | 1614 | NW | |
| PZ4 | 72 | 16.50 | 63.0 | 1211 | NW | |
| PZ5 | 55 | 17.90 | 34.5 | 1578 | N |
| Fixed-Effect(s) | Subset | F-Value | p-Value | Subset | F-Value | p-Value |
|---|---|---|---|---|---|---|
| L. gmelinii | 29.69 | <0.001 | P. tabulaeformis Mulan | 19.39 | <0.001 | |
| 11.14 | <0.001 | 56.26 | <0.001 | |||
| 87.36 | <0.001 | 26.17 | <0.001 | |||
| 6.35 | 0.002 | 17.80 | <0.001 | |||
| 16.28 | <0.001 | 7.56 | 0.006 | |||
| 34.29 | <0.001 | 20.52 | <0.001 | |||
| 14.25 | <0.001 | 5.95 | 0.015 | |||
| Q. mongolica | 12.38 | <0.001 | P. tabulaeformis Zhongtiaoshan | 4.50 | 0.012 | |
| 12.08 | <0.001 | 0.61 | 0.436 | |||
| 0.22 | 0.642 | 0.40 | 0.529 | |||
| 7.71 | <0.001 | 10.62 | <0.001 | |||
| 1.96 | 0.142 | 4.59 | 0.011 | |||
| 0.02 | 0.978 | 0.49 | 0.482 | |||
| 3.26 | 0.012 | 3.05 | 0.048 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sprengel, L.; Cheng, Z.; Hipler, S.-M.; Wu, S.; Spiecker, H. Mean Annual Wood Density Variations of Larix gmelinii (Rupr.), Quercus mongolica Fisch. ex Ledeb., and Pinus tabulaeformis Carr. at Two Different Stem Heights. Forests 2020, 11, 394. https://doi.org/10.3390/f11040394
Sprengel L, Cheng Z, Hipler S-M, Wu S, Spiecker H. Mean Annual Wood Density Variations of Larix gmelinii (Rupr.), Quercus mongolica Fisch. ex Ledeb., and Pinus tabulaeformis Carr. at Two Different Stem Heights. Forests. 2020; 11(4):394. https://doi.org/10.3390/f11040394
Chicago/Turabian StyleSprengel, Lars, Zhongqian Cheng, Sandra-Maria Hipler, Shuirong Wu, and Heinrich Spiecker. 2020. "Mean Annual Wood Density Variations of Larix gmelinii (Rupr.), Quercus mongolica Fisch. ex Ledeb., and Pinus tabulaeformis Carr. at Two Different Stem Heights" Forests 11, no. 4: 394. https://doi.org/10.3390/f11040394
APA StyleSprengel, L., Cheng, Z., Hipler, S.-M., Wu, S., & Spiecker, H. (2020). Mean Annual Wood Density Variations of Larix gmelinii (Rupr.), Quercus mongolica Fisch. ex Ledeb., and Pinus tabulaeformis Carr. at Two Different Stem Heights. Forests, 11(4), 394. https://doi.org/10.3390/f11040394






