From Dendrochronology to Allometry
Abstract
1. Introduction
2. What Is Wrong with This Picture?
3. Simple Mathematical Relationships
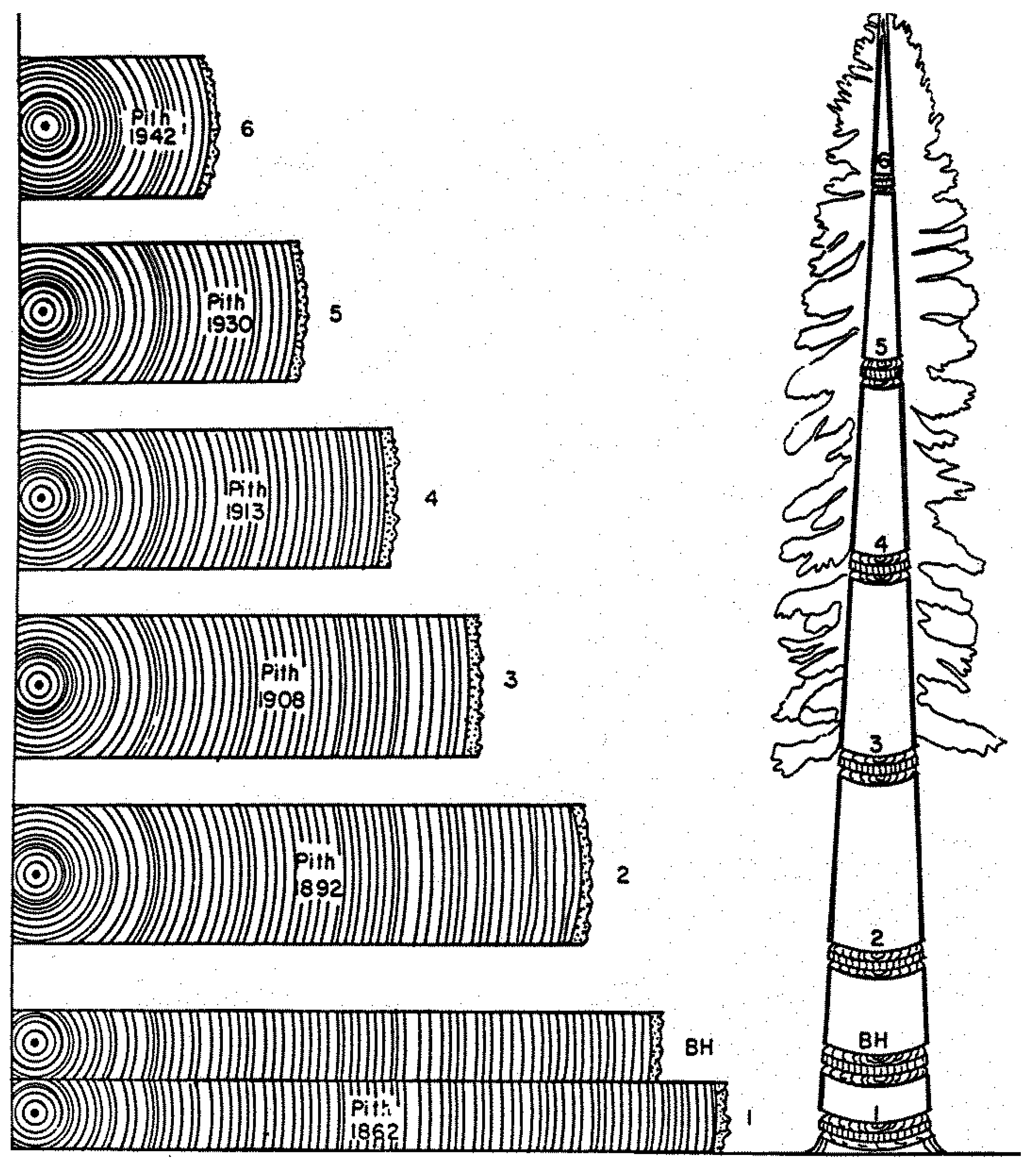
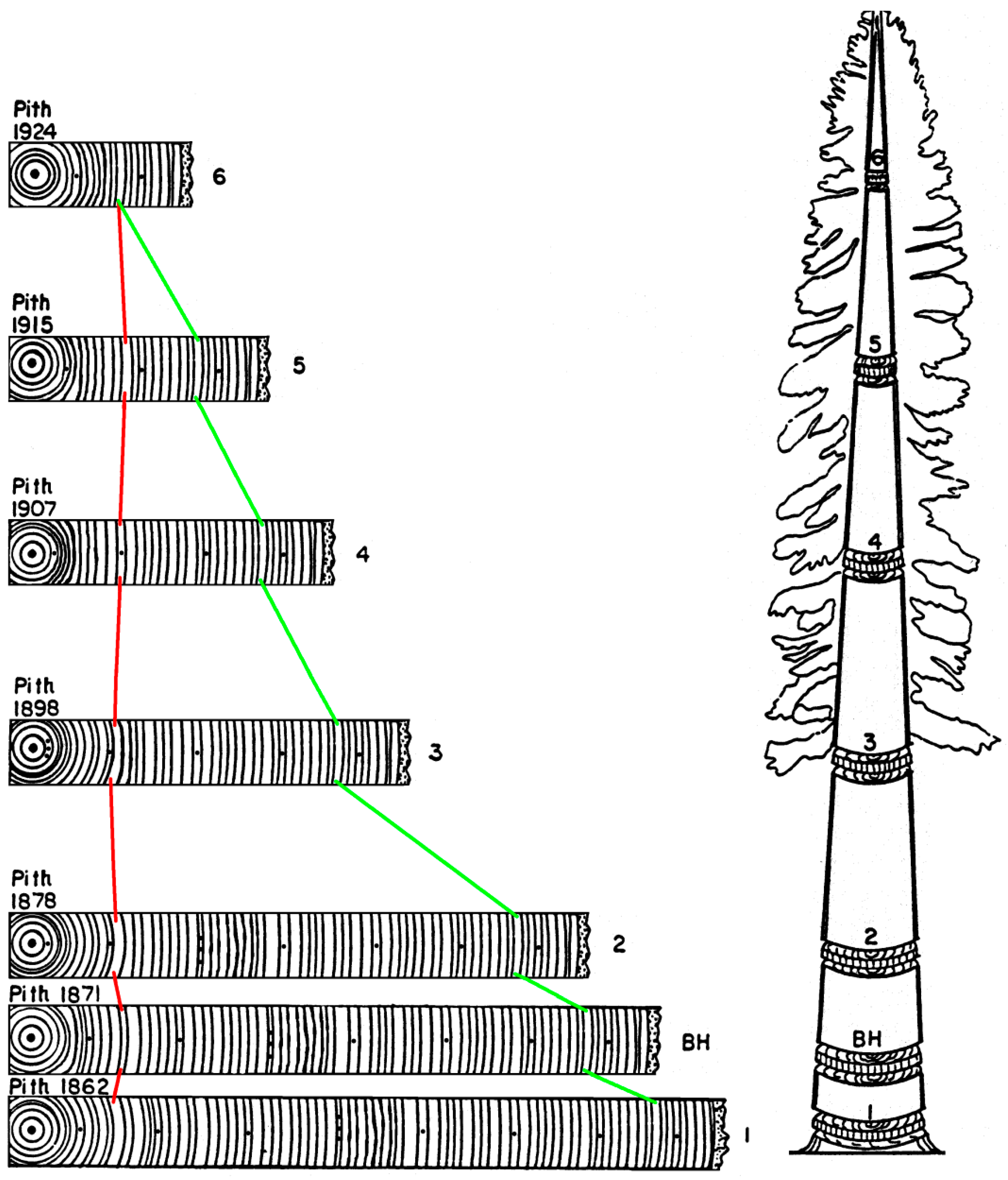
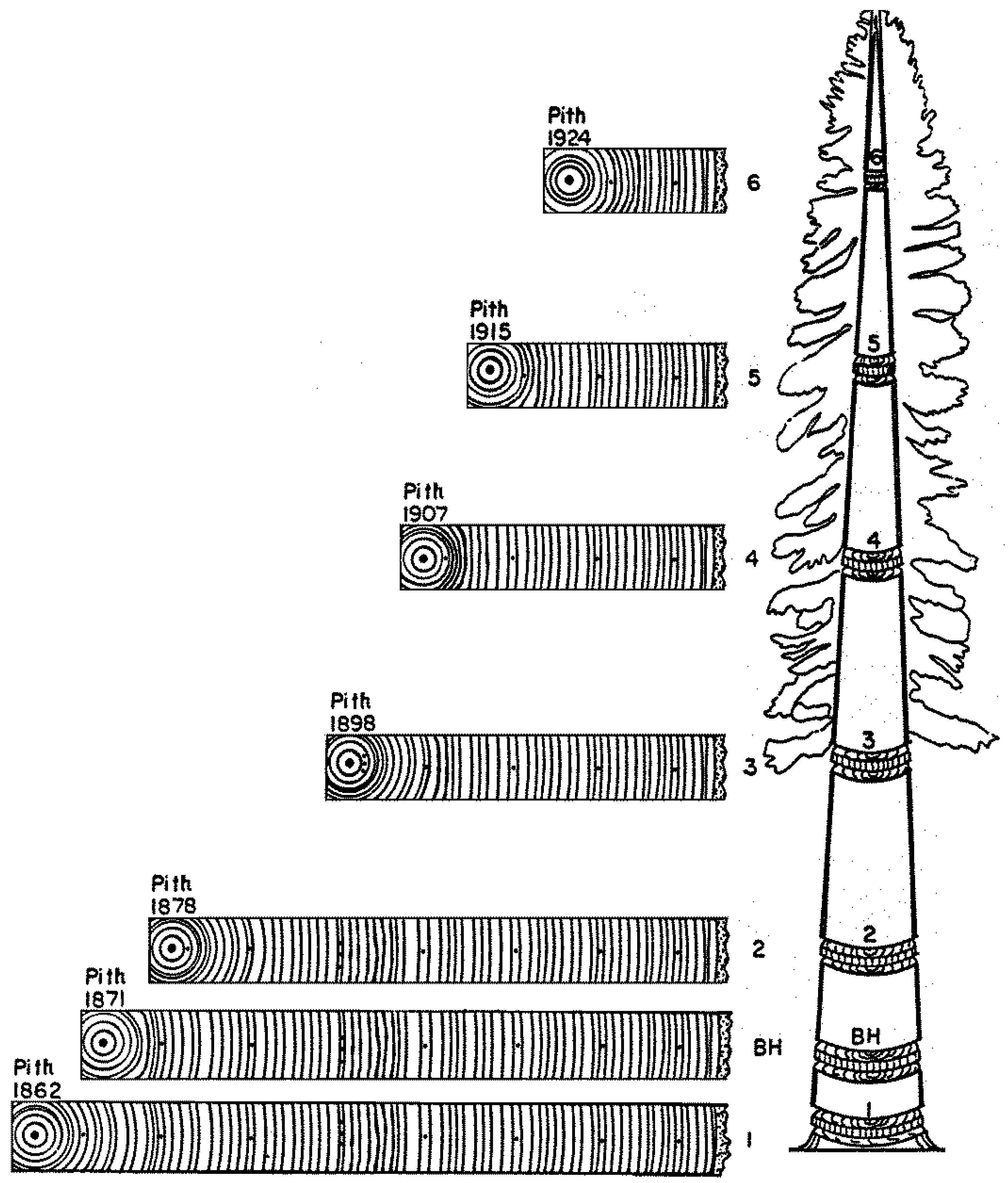
4. A Visual Example of Tree-Ring Data
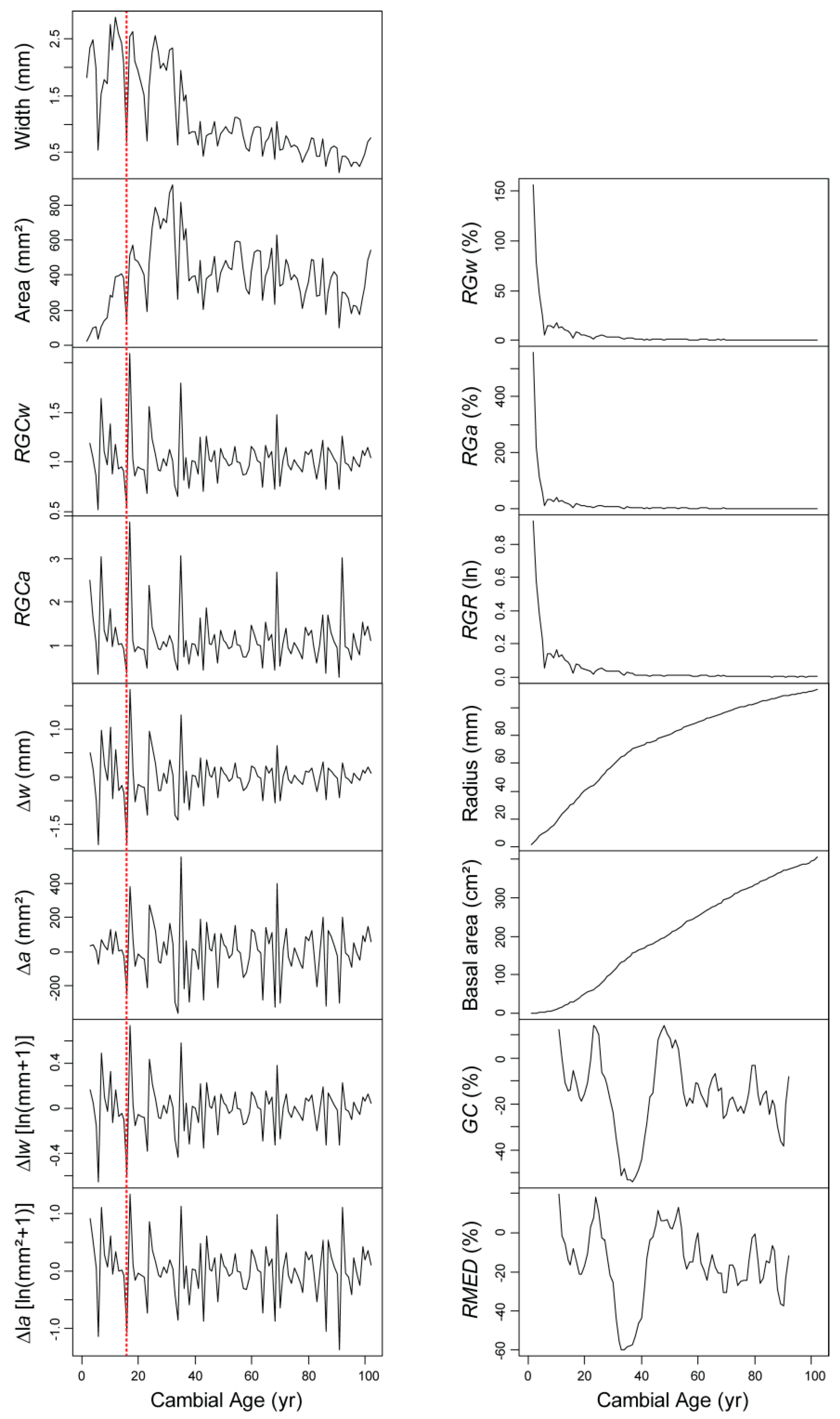
5. From Dendrochronology to Allometry
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Dobbertin, M.K.; Grissino-Mayer, H.D. The bibliography of dendrochronology and the glossary of dendrochronology: Two new online tools for tree-ring research. Tree-Ring Res. 2004, 60, 101–104. [Google Scholar]
- Stokes, M.A.; Smiley, T.L. An Introduction to Tree-Ring Dating; Reprint of the 1968 Edition; University of Arizona Press: Tucson, AZ, USA, 1996; p. 73. [Google Scholar]
- Douglass, A.E. Crossdating in dendrochronology. J. For. 1941, 39, 825–831. [Google Scholar]
- Fritts, H.C.; Swetnam, T.W. Dendroecology: A Tool for Evaluating Variations in Past and Present Forest Environments. In Advances in Ecological Research; Begon, M., Fitter, A.H., Ford, E.D., MacFadyen, A., Eds.; Academic Press: San Diego, CA, USA, 1989; Volume 19, pp. 111–188. [Google Scholar]
- Nash, S.E. Time, Trees, and Prehistory: Tree-Ring Dating and the Development of North American Archaeology, 1914–1950; The University of Utah Press: Salt Lake City, UT, USA, 1999; p. 294. [Google Scholar]
- Webb, G.E. Tree Rings and Telescopes: The Scientific Career of A.E. Douglass; The University of Arizona Press: Tucson, AZ, USA, 1983; p. 242. [Google Scholar]
- Studhalter, R.A. Early history of crossdating. Tree-Ring Bull. 1956, 1956, 31–35. [Google Scholar]
- Wimmer, R. Arthur Freiherr von Seckendorff-Gudent and the early history of tree-ring crossdating. Dendrochronologia 2001, 19, 153–158. [Google Scholar]
- Peñuelas, J.; Munné-Bosch, S. Potentially immortal? New Phytol. 2010, 187, 564–567. [Google Scholar] [CrossRef] [PubMed]
- Shmulsky, R.; Jones, P.D. Forest Products and Wood Science: An Introduction, 6th ed.; Wiley-Blackwell: New York, NY, USA, 2011; p. 477. [Google Scholar]
- Husch, B.; Beers, T.W.; Kershaw, J.A., Jr. Forest Mensuration; John Wiley & Sons: Hoboken, NJ, USA, 2003; p. 443. [Google Scholar]
- LeBlanc, D.C. Temporal and spatial variation of oak growth–climate relationships along a pollution gradient in the midwestern United States. Can. J. For. Res. 1993, 23, 772–782. [Google Scholar] [CrossRef]
- Bakker, J.D. A new, proportional method for reconstructing historical tree diameters. Can. J. For. Res. 2005, 35, 2515–2520. [Google Scholar] [CrossRef]
- Bunn, A.G.; Biondi, F. Dendrochronology in R with the dplR library. In Abstracts of WorldDendro2010, The 8th International Conference on Dendrochronology; Mielikäinen, K., Mäkinen, H., Timonen, M., Eds.; METLA: Rovaniemi, Finland, 2010; p. 274. [Google Scholar]
- R Core Team. R: A language and Environment for Statistical Computing, version 3.0.2; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- Van Deusen, P.C. A dynamic program for cross-dating tree rings. Can. J. For. Res. 1990, 20, 200–205. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Revised ed.; Holden-Day: Oakland, CA, USA, 1976. [Google Scholar]
- Valentine, H.T.; Mäkelä, A. Bridging process-based and empirical approaches to modeling tree growth. Tree Physiol. 2005, 25, 769–779. [Google Scholar] [CrossRef]
- Van Laar, A.; Akça, A. Forest Mensuration; Springer: Dordrecht, The Netherlands, 2007; Volume 13. [Google Scholar]
- Schlesinger, W.H. Biogeochemistry: An Analysis of Global Change, 2nd ed.; Academic Press: San Diego, CA, USA, 1997. [Google Scholar]
- Paine, C.E.T.; Marthews, T.R.; Vogt, D.R.; Purves, D.; Rees, M.; Hector, A.; Turnbull, L.A. How to fit nonlinear plant growth models and calculate growth rates: An update for ecologists. Methods Ecol. Evol. 2012, 3, 245–256. [Google Scholar] [CrossRef]
- Harper, J.L. Population Biology of Plants; Academic Press: London, UK, 1977; p. 892. [Google Scholar]
- Fritts, H.C. Tree Rings and Climate; Academic Press: London, UK, 1976; p. 567. [Google Scholar]
- Nowacki, G.J.; Abrams, M.D. Radial-growth averaging criteria for reconstructing disturbance histories from presettlement-origin oaks. Ecol. Monogr. 1997, 67, 225–249. [Google Scholar] [CrossRef]
- Rubino, D.L.; McCarthy, B.C. Comparative analysis of dendroecological methods used to assess disturbance events. Dendrochronologia 2004, 21, 97–115. [Google Scholar] [CrossRef]
- Sokal, R.R.; Rohlf, F.J. Biometry, 4th ed.; W.H. Freeman and Co.: New York, NY, USA, 2012; p. 937. [Google Scholar]
- Douglass, A.E. The secret of the Southwest solved by talkative tree rings. Natl. Geogr. Mag. 1929, 736–770. [Google Scholar]
- Nash, S.E. Archaeological tree-ring dating at the millennium. J. Archaeol. Res. 2002, 10, 243–275. [Google Scholar] [CrossRef]
- Biondi, F.; Qeadan, F. A theory-driven approach to tree-ring standardization: Defining the biological trend from expected basal area increment. Tree-Ring Res. 2008, 64, 81–96. [Google Scholar] [CrossRef]
- Helama, S.; Lindholm, M.; Timonen, M.; Eronen, M. Detection of climate signal in dendrochronological data analysis: A comparison of tree-ring standardization methods. Theor. Appl. Climatol. 2004, 79, 239–254. [Google Scholar] [CrossRef]
- Meko, D.M.; Friedman, J.M.; Touchan, R.; Edmondson, J.R.; Griffin, E.R.; Scott, J.A. Alternative standardization approaches to improving streamflow reconstructions with ring-width indices of riparian trees. Holocene 2015, 25, 1093–1101. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J.; Liu, X.; Chen, Z. Improved EEMD-based standardization method for developing long tree-ring chronologies. J. For. Res. 2019. [Google Scholar] [CrossRef]
- Biondi, F. Dendrochronology, Volcanic Eruptions. In Encyclopedia of Scientific Dating Methods; Rink, W.J., Thompson, J.W., Eds.; Springer: Dordrecht, The Netherlands, 2015; pp. 1–11. [Google Scholar] [CrossRef]
- Schweingruber, F.H.; Eckstein, D.; Serre-Bachet, F.; Bräker, O.U. Identification, presentation and interpretation of event years and pointer years in dendrochronology. Dendrochronologia 1990, 8, 9–38. [Google Scholar]
- Baillie, M.G.L. Dendrochronology raises questions about the nature of the AD 536 dust-veil event. Holocene 1994, 4, 212–217. [Google Scholar] [CrossRef]
- Baillie, M.G.L. Tree-ring chronologies present us with independent records of past natural events which, strangely, or perhaps not so strangely, seem to link with some stories from myth. In Kalendarische, Chronologische und Astronomische Aspekte der Vergangenheit; Krojer, F., Starke, R., Eds.; Differenz-Verlag: München, Germany, 2012; pp. 109–129. [Google Scholar]
- Speer, J.H. Fundamentals of Tree-Ring Research; University of Arizona Press: Tuscon, AZ, USA, 2010; p. 333. [Google Scholar]
- Kelly, P.M.; Munro, M.A.R.; Hughes, M.K.; Goodess, C.M. Climate and signature years in west European oaks. Nature 1989, 340, 57–60. [Google Scholar] [CrossRef]
- Minot, C.S. The Problem of Age, Growth, and Death; G.P. Putnam’s Sons, The Knickerbocker Press: New York, NY, USA, 1908; p. 280. [Google Scholar]
- Mallows, C.L. Some theory of nonlinear smoothers. Ann. Stat. 1980, 8, 695–715. [Google Scholar] [CrossRef]
- Slutzky, E. The summation of random causes as the source of cyclic processes. Econometrica 1937, 5, 105–146. [Google Scholar] [CrossRef]
- Owens, A.J. On detrending and smoothing random data. J. Geophys. Res. Space Phys. 1978, 83, 221–224. [Google Scholar] [CrossRef]
- MacCurdy, E. The Notebooks of Leonardo da Vinci; George Braziller: New York, NY, USA, 1955; p. 1247. [Google Scholar]
- Shinozaki, K.; Yoda, K.; Hozumi, K.; Kira, T. A quantitative analysis of plant form: The pipe model theory. I. Basic analyses. Jpn. J. Ecol. 1964, 14, 97–105. [Google Scholar]
- Valentine, H.T. Tree-growth models: Derivations employing the pipe-model theory. J. Theor. Biol. 1985, 117, 579–585. [Google Scholar] [CrossRef]
- Larson, P.R. Stem form development of forest trees. For. Sci. 1963, 9, 1–42. [Google Scholar] [CrossRef]
- LeBlanc, D.C.; Raynal, D.J.; White, E.H. Acidic deposition and tree growth: 1. The use of stem analysis to study historical growth patterns. J. Environ. Qual. 1987, 16, 325–333. [Google Scholar] [CrossRef]
- Speer, J.H.; Holmes, R.L. Effects of pandora moth outbreaks on ponderosa pine wood volume. Tree-Ring Res. 2004, 60, 69–76. [Google Scholar] [CrossRef]
- Vaganov, E.A.; Hughes, M.K.; Shashkin, A.V. Growth Dynamics of Conifer Tree Rings: Images of Past and Future Environments; Springer: New York, NY, USA, 2006; Volume 183, p. 354. [Google Scholar]
- Biondi, F.; Fessenden, J.E. Radiocarbon analysis of Pinus lagunae tree rings: Implications for tropical dendrochronology. Radiocarbon 1999, 41, 241–249. [Google Scholar] [CrossRef]
- Duff, G.H.; Nolan, N.J. Growth and morphogenesis in the Canadian forest species: I. The controls of cambial and apical activity in Pinus resinosa Ait. Can. J. Bot. 1953, 31, 471–513. [Google Scholar] [CrossRef]
- Bevilacqua, E.; Puttock, D.; Blake, T.J.; Burgess, D. Long-term differential stem growth responses in mature eastern white pine following release from competition. Can. J. For. Res. 2005, 35, 511–520. [Google Scholar] [CrossRef]
- Arbaugh, M.J.; Peterson, D.L. Stemwood Production Patterns in Ponderosa Pine: Effects of Stand Dynamics and Other Factors; PSW-RP-217; Pacific Southwest Research Station: Albany, CA, USA, 1993; p. 11.
- Cortini, F.; Groot, A.; Filipescu, C.N. Models of the longitudinal distribution of ring area as a function of tree and stand attributes for four major Canadian conifers. Ann. For. Sci. 2013, 70, 637–648. [Google Scholar] [CrossRef]
- Kershaw, A.; Maguire, A. Influence of vertical foliage structure on the distribution of stem cross-sectional area increment in western hemlock and balsam fir. For. Sci. 2000, 46, 86–94. [Google Scholar]
- Jenkins, J.C.; Chojnacky, D.C.; Heath, L.S.; Birdsey, R.A. National-scale biomass estimators for United States tree species. For. Sci. 2003, 49, 12–35. [Google Scholar]
- Jenkins, J.C.; Chojnacky, D.C.; Heath, L.S.; Birdsey, R.A. Comprehensive Database of Diameter-Based Biomass Regressions for North American Tree Species; Gen. Tech. Rep. NE-319; Northeastern Research Station: Newtown Square, PA, USA, 2004; p. 45. [Google Scholar]
- Zianis, D.; Muukkonen, P.; Mäkipää, R.; Mencuccini, M. Biomass and Stem Volume Equations for Tree Species in Europe; Finnish Society of Forest Science: Helsinki, Finland, 2005; p. 63. [Google Scholar]
- Niklas, K.J. Plant Allometry: The Scaling of Form and Process; The University of Chicago Press: Chicago, IL, USA, 1994; p. 395. [Google Scholar]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric scaling laws in biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef] [PubMed]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the structure and allometry of plant vascular systems. Nature 1999, 400, 664–667. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. The Fourth Dimension of Life: Fractal Geometry and Allometric Scaling of Organisms. Science 1999, 284, 1677–1679. [Google Scholar] [CrossRef]
- Niklas, K.J. Plant allometry: Is there a grand unifying theory? Biol. Rev. 2004, 79, 871–889. [Google Scholar] [CrossRef]
- Zimmermann, M.H. Xylem Structure and the Ascent of Sap; Springer: Berlin, Germany, 1983. [Google Scholar]
- Olano, J.M.; Eugenio, M.; García-Cervigón, A.I.; Folch, M.; Rozas, V. Quantitative tracheid anatomy reveals a complex environmental control of wood structure in continental Mediterranean climate. Int. J. Plant Sci. 2012, 173, 137–149. [Google Scholar] [CrossRef]
- Ziaco, E.; Biondi, F. Wood cellular dendroclimatology: A pilot study on bristlecone pine in the southwest US. In Proceedings of the Fall Meeting of the American Geophysical Union, San Francisco, CA, USA, 14–18 December 2015. Abstract GC33B-1276. [Google Scholar]
- Sperry, J.S.; Nichols, K.L.; Sullivan, J.E.M.; Eastlack, S.E. Xylem embolism in ring-porous, diffuse-porous, and coniferous trees of northern Utah and interior Alaska. Ecology 1994, 75, 1736–1752. [Google Scholar] [CrossRef]
- Tyree, M.T.; Ewers, F.W. The hydraulic architecture of trees and other woody plants. New Phytol. 1991, 119, 345–360. [Google Scholar] [CrossRef]
- Anfodillo, T.; Carraro, V.; Carrer, M.; Fior, C.; Rossi, S. Convergent tapering of xylem conduits in different woody species. New Phytol. 2006, 169, 279–290. [Google Scholar] [CrossRef] [PubMed]
- Tyree, M.T.; Zimmermann, M.H. Xylem Structure and the Ascent of Sap, 2nd ed.; Springer: Berlin, Germany, 2002; p. 283. [Google Scholar]
- Rudinsky, J.A.; Vité, J.P. Certain ecological and phylogenetic aspects of the pattern of water conduction in conifers. For. Sci. 1959, 5, 259–266. [Google Scholar]
- Schlenz, M.A.; Flaherty, D. A Day in the Ancient Bristlecone Pine Forest; Companion Press: Bishop, CA, USA, 2008; p. 64. [Google Scholar]
- DeRosa, E.W. Lightning and trees. J. Arboric. 1983, 9, 51–53. [Google Scholar]
- Harris, J.M. Spiral Grain and Wave Phenomena in Wood Formation; Springer: Berlin/Heidelberg, Germany, 1989; p. 214. [Google Scholar]
- Enquist, B.J. Universal scaling in tree and vascular plant allometry: Toward a general quantitative theory linking plant form and function from cells to ecosystems. Tree Physiol. 2002, 22, 1045–1064. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H. The origin of allometric scaling laws in biology from genomes to ecosystems: Towards a quantitative unifying theory of biological structure and organization. J. Exp. Biol. 2005, 208, 1575–1592. [Google Scholar] [CrossRef]
- Brown, J.H.; West, G.B.; Enquist, B.J. Yes, West, Brown and Enquist”s model of allometric scaling is both mathematically correct and biologically relevant. Funct. Ecol. 2005, 19, 735–738. [Google Scholar] [CrossRef]
- Enquist, B.J.; Allen, A.P.; Brown, J.H.; Gillooly, J.F.; Kerkhoff, A.J.; Niklas, K.J.; Price, C.A.; West, G.B. Biological scaling: Does the exception prove the rule? Nature 2007, 445, E9–E10. [Google Scholar] [CrossRef]
- Eloy, C. Leonardo’s rule, self-similarity, and wind-induced stresses in trees. Phys. Rev. Lett. 2011, 107, 258101. [Google Scholar] [CrossRef]
- Brown, J.H.; Gillooly, J.F.; Allen, A.P.; Savage, V.M.; West, G.B. Toward a metabolic theory of ecology. Ecology 2004, 85, 1771–1789. [Google Scholar] [CrossRef]
- Price, C.A.; Gilooly, J.F.; Allen, A.P.; Weitz, J.S.; Niklas, K.J. The metabolic theory of ecology: Prospects and challenges for plant biology. New Phytol. 2010, 188, 696–710. [Google Scholar] [CrossRef] [PubMed]
- Whitfield, J. Ecology’s big, hot idea. PLoS Biol. 2004, 2, e440. [Google Scholar] [CrossRef] [PubMed]
- Kozłowski, J.; Konarzewski, M. West, Brown and Enquist’s model of allometric scaling again: The same questions remain. Funct. Ecol. 2005, 19, 739–743. [Google Scholar] [CrossRef]
- Reich, P.B.; Tjoelker, M.G.; Machado, J.-L.; Oleksyn, J. Universal scaling of respiratory metabolism, size and nitrogen in plants. Nature 2006, 439, 457–461. [Google Scholar] [CrossRef] [PubMed]
- Bejan, A.; Lorente, S. The constructal law of design and evolution in nature. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2010, 365, 1335–1347. [Google Scholar] [CrossRef]
- Enquist, B.J.; West, G.B.; Charnov, E.L.; Brown, J.H. Allometric scaling of production and life-history variation in vascular plants. Nature 1999, 401, 907–911. [Google Scholar] [CrossRef]
- Niklas, K.J.; Spatz, H.-C. Growth and hydraulic (not mechanical) constraints govern the scaling of tree height and mass. Proc. Nat. Acad. Sci. USA 2004, 101, 15661–15663. [Google Scholar] [CrossRef]
- Enquist, B.J.; Niklas, K.J. Invariant scaling relations across tree-dominated communities. Nature 2001, 410, 655–660. [Google Scholar] [CrossRef]
- Price, C.A.; Weitz, J.S.; Savage, V.M.; Stegen, J.; Clarke, A.; Coomes, D.A.; Dodds, P.S.; Etienne, R.S.; Kerkhoff, A.J.; McCulloh, K.A.; et al. Testing the metabolic theory of ecology. Ecol. Lett. 2012, 15, 1465–1474. [Google Scholar] [CrossRef]
- Baillie, M.G.L.; Hillam, J.; Briffa, K.R.; Brown, D.M. Re-dating the English art-historical tree-ring chronologies. Nature 1985, 315, 317–319. [Google Scholar] [CrossRef]

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biondi, F. From Dendrochronology to Allometry. Forests 2020, 11, 146. https://doi.org/10.3390/f11020146
Biondi F. From Dendrochronology to Allometry. Forests. 2020; 11(2):146. https://doi.org/10.3390/f11020146
Chicago/Turabian StyleBiondi, Franco. 2020. "From Dendrochronology to Allometry" Forests 11, no. 2: 146. https://doi.org/10.3390/f11020146
APA StyleBiondi, F. (2020). From Dendrochronology to Allometry. Forests, 11(2), 146. https://doi.org/10.3390/f11020146




