Allometric Biomass Models for European Beech and Silver Fir: Testing Approaches to Minimize the Demand for Site-Specific Biomass Observations
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Study Site
2.1.2. Biomass Datasets
Dataset #1
Dataset #2
Dataset #3
Dataset #4
2.1.3. Inventory Plot
2.2. Development of Allometric Biomass Models
2.2.1. Linear Regression Model on Log-Transformed Data (LM)
2.2.2. Random Intercept Models (RIM)
2.2.3. Bayesian Models
2.3. Evaluation of Calibration Approaches
- (1)
- For the kth replication (K = 5000, K is the total number of replications), a set of allometric model parameters and residuals were sampled from a multivariate normal distribution and a univariate normal distribution, respectively.
- (a)
- Sampling a residual value from a normal distribution with the mean zero and standard deviation equal to residual standard error of the allometric model;
- (b)
- Sampling a set of model parameter values from a bivariate normal distribution (for models using only D as predictor of AGB) or a trivariate normal distribution (for models based on both D and H to predict AGB);
- (c)
- Calculate the predicted ln(AGB) for each tree within the 1 ha inventory plot (Section 2.1.3), based on the model parameters sampled at step 1.b and the residual sampled at step 1.a;
- (d)
- Back transform the predicted ln(AGB), using a correction factor (CF) calculated as in Section 2.2.1;
- (e)
- Calculate the total plot AGB by addition of individual tree predictions;
- (2)
- Steps (1.a) to (1.e) were repeated for a number of K = 5000 times to calculate:
- (a)
- Mean predicted plot biomass, as the mean of values obtained at step 1.e;
- (b)
- Standard error of the mean (values at step 1.e), which, because of using a single plot, equals the standard deviation of the sample mean.
2.4. Data Processing
3. Results
3.1. Allometric Biomass Models
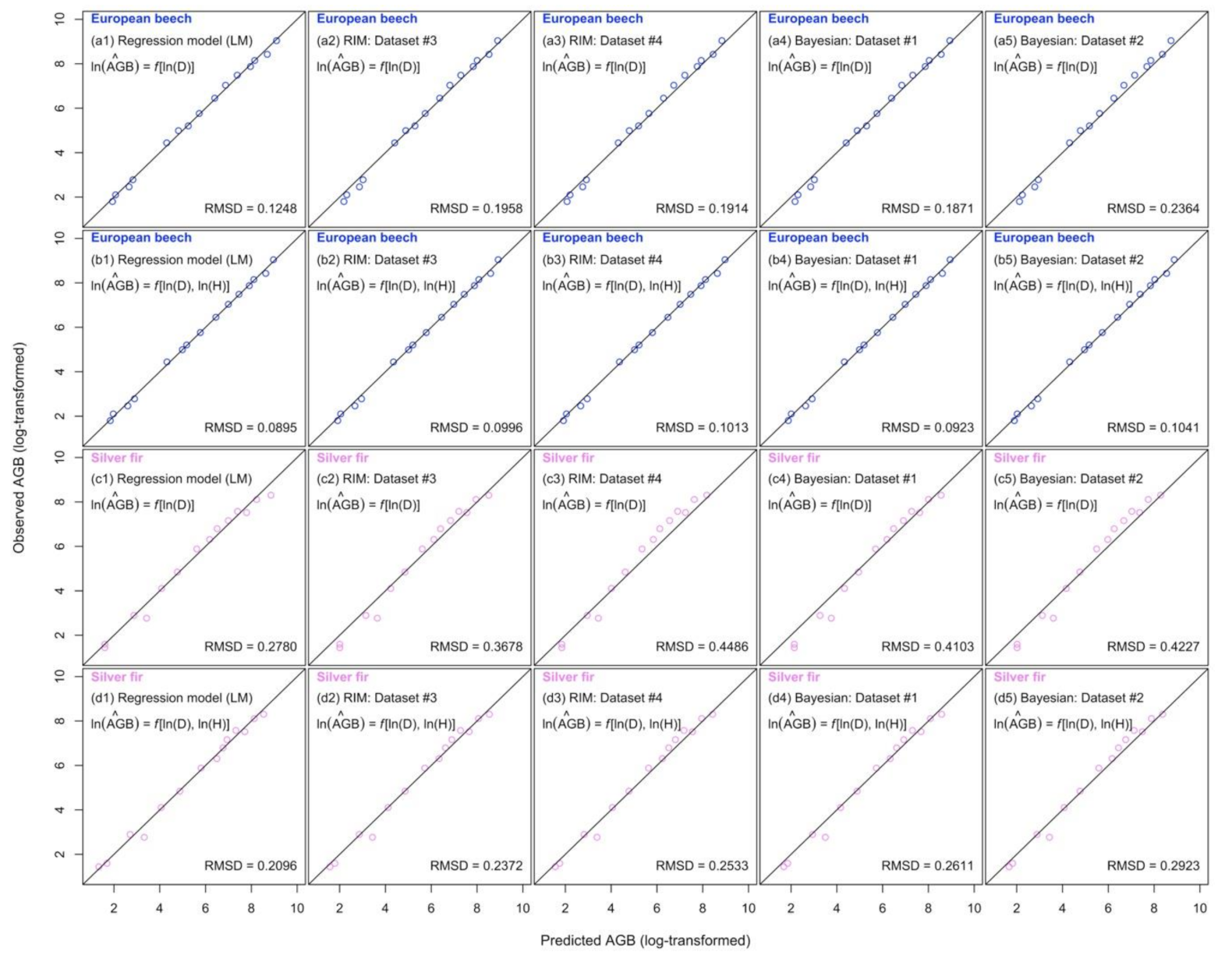
3.2. Comparison of Biomass Estimates on 1 ha Sample Plot
4. Discussion
- (a)
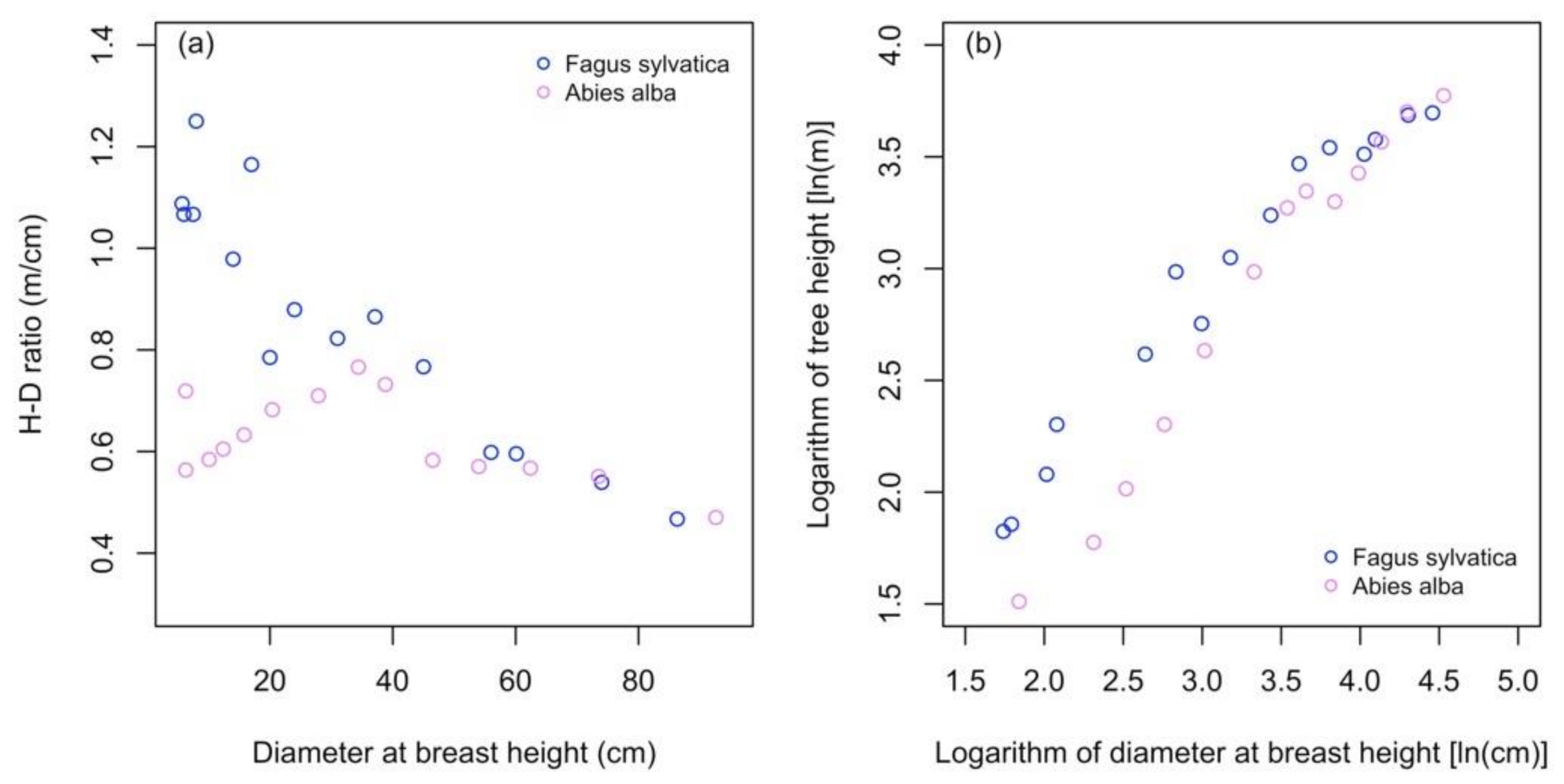
- The H-D ratio, which should be checked in advance. As we observed in our analysis with silver fir trees, the H-D ratio can affect the parameter estimates, which affect further the performance of small trees sample approach. Therefore, the user should check whether the H-D ratio decreases relatively linearly with the increase in tree size.
- (b)
- Either a random intercept model or a Bayesian model can be used with the reduced sample approach. Preference to one of the methods can be decided based on the raw data availability. Nevertheless, access to raw observations should not be an issue given the increasing trend in publication of biomass datasets, e.g., [44,55,56,57,58].
- (c)
- The generic biomass sample should contain as many species-specific observations as possible, including very large trees (D-range should match that of the local population for which the models are developed).
- (d)
- The reduced sample of small trees should contain a large enough number of trees to calibrate mainly the intercept; at least 6–7 trees should be used (the greater the number, the better the result). It is recommended that trees with D < 5 cm should not be used with the reduced sample approach, since the allometry of very small trees can be affected by the competition with herbaceous plants.
- (e)
- Using the reduced sample approach should always be performed using no less than D and H as predictors; other additional predictors can be used, because using both variables, the biomass estimates were more precise.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Luyssaert, S.; Marie, G.; Valade, A.; Chen, Y.-Y.; Djomo, S.N.; Ryder, J.; Otto, J.; Naudts, K.; Lansø, A.S.; Ghattas, J.; et al. Trade-offs in using European forests to meet climate objectives. Nature 2018, 562, 259–262. [Google Scholar] [CrossRef] [PubMed]
- Grassi, G.; House, J.; Dentener, F.; Federici, S.; den Elzen, M.; Penman, J. The key role of forests in meeting climate targets requires science for credible mitigation. Nat. Clim. Chang. 2017, 7, 220–226. [Google Scholar] [CrossRef]
- Canadell, J.G.; Raupach, M.R. Managing forests for climate change mitigation. Science 2008, 320, 1456–1457. [Google Scholar] [CrossRef] [PubMed]
- Le Quéré, C.; Andrew, R.M.; Friedlingstein, P.; Sitch, S.; Pongratz, J.; Manning, A.C.; Korsbakken, J.I.; Peters, G.P.; Canadell, J.G.; Jackson, R.B.; et al. Global carbon budget 2017. Earth Syst. Sci. Data 2018, 10, 405–448. [Google Scholar]
- Ketterings, Q.M.; Coe, R.; van Noordwijk, M.; Ambagau’, Y.; Palm, C.A. Reducing uncertainty in the use of allometric biomass equations for predicting above-ground tree biomass in mixed secondary forests. For. Ecol. Manag. 2001, 146, 199–209. [Google Scholar] [CrossRef]
- Gregoire, T.G.; Næsset, E.; McRoberts, R.E.; Ståhl, G.; Andersen, H.-E.; Gobakken, T.; Ene, L.; Nelson, R. Statistical rigor in LiDAR-assisted estimation of aboveground forest biomass. Remote Sens. Environ. 2016, 173, 98–108. [Google Scholar] [CrossRef]
- Klingenberg, C.P. Evolution and development of shape: Integrating quantitative approaches. Nat. Rev. Genet. 2010, 11, 623–635. [Google Scholar] [CrossRef]
- Xia, J.; Yuan, W.; Lienert, S.; Joos, F.; Ciais, P.; Viovy, N.; Wang, Y.; Wang, X.; Zhang, H.; Chen, Y.; et al. Global patterns in net primary production allocation regulated by environmental conditions and forest stand age: A model-data comparison. J. Geophys. Res. Biogeosci. 2019, 124, 2039–2059. [Google Scholar] [CrossRef]
- Dutcă, I.; Mather, R.; Ioraş, F. Tree biomass allometry during the early growth of Norway spruce (Picea abies) varies between pure stands and mixtures with European beech (Fagus sylvatica). Can. J. For. Res. 2018, 48, 77–84. [Google Scholar] [CrossRef]
- Dutcă, I.; Mather, R.; Blujdea, V.N.B.; Ioraș, F.; Olari, M.; Abrudan, I.V. Site-effects on biomass allometric models for early growth plantations of Norway spruce (Picea abies (L.) Karst.). Biomass Bioenergy 2018, 116, 8–17. [Google Scholar] [CrossRef]
- Dutcă, I. The variation driven by differences between species and between sites in allometric biomass models. Forests 2019, 10, 976. [Google Scholar] [CrossRef]
- Pretzsch, H. Species-specific allometric scaling under self-thinning: Evidence from long-term plots in forest stands. Oecologia 2006, 146, 572–583. [Google Scholar] [CrossRef] [PubMed]
- Ngomanda, A.; Obiang, N.L.E.; Lebamba, J.; Mavouroulou, Q.M.; Gomat, H.; Mankou, G.S.; Loumeto, J.; Iponga, D.M.; Ditsouga, F.K.; Koumba, R.Z.; et al. Site-specific versus pantropical allometric equations: Which option to estimate the biomass of a moist central African forest? For. Ecol. Manag. 2014, 312, 1–9. [Google Scholar] [CrossRef]
- Xiang, W.; Zhou, J.; Ouyang, S.; Zhang, S.; Lei, P.; Li, J.; Deng, X.; Fang, X.; Forrester, D.I. Species-specific and general allometric equations for estimating tree biomass components of subtropical forests in southern China. Eur. J. For. Res. 2016, 135, 963–979. [Google Scholar] [CrossRef]
- Fayolle, A.; Doucet, J.-L.; Gillet, J.-F.; Bourland, N.; Lejeune, P. Tree allometry in Central Africa: Testing the validity of pantropical multi-species allometric equations for estimating biomass and carbon stocks. For. Ecol. Manag. 2013, 305, 29–37. [Google Scholar] [CrossRef]
- Bouriaud, L.; Nichiforel, L.; Weiss, G.; Bajraktari, A.; Curovic, M.; Dobsinska, Z.; Glavonjic, P.; Jarský, V.; Sarvasova, Z.; Teder, M.; et al. Governance of private forests in Eastern and Central Europe: An analysis of forest harvesting and management rights. Ann. For. Res. 2013, 56, 199–215. [Google Scholar]
- Duncanson, L.; Rourke, O.; Dubayah, R.; Schilz, M.H.; Palm, C.A. Small sample sizes yield biased allometric equations in temperate forests. Sci. Rep. 2015, 5, 17153. [Google Scholar] [CrossRef]
- Dutcă, I.; Stăncioiu, P.T.; Abrudan, I.V.; Ioraș, F. Using clustered data to develop biomass allometric models: The consequences of ignoring the clustered data structure. PLoS ONE 2018, 13, e0200123. [Google Scholar] [CrossRef]
- Kilmer, J.T.; Rodríguez, R.L. Ordinary least squares regression is indicated for studies of allometry. J. Evol. Biol. 2017, 30, 4–12. [Google Scholar] [CrossRef]
- Al-Wathiqui, N.; Rodríguez, R.L. Allometric slopes not underestimated by ordinary least squares regression: A case study with Enchenopa treehoppers (Hemiptera: Membracidae). Ann. Entomol. Soc. Am. 2011, 104, 562–566. [Google Scholar] [CrossRef]
- Temesgen, H.; Affleck, D.; Poudel, K.; Gray, A.; Sessions, J. A review of the challenges and opportunities in estimating above ground forest biomass using tree-level models. Scand. J. For. Res. 2015, 1–10. [Google Scholar] [CrossRef]
- Dutcă, I.; Mather, R.; Ioraș, F. Sampling trees to develop allometric biomass models: How does tree selection affect model prediction accuracy and precision? Ecol. Indic. 2020, 117, 106553. [Google Scholar] [CrossRef]
- Zianis, D.; Mencuccini, M. On simplifying allometric analyses of forest biomass. For. Ecol. Manag. 2004, 187, 311–332. [Google Scholar] [CrossRef]
- Dietze, M.C.; Wolosin, M.S.; Clark, J.S. Capturing diversity and interspecific variability in allometries: A hierarchical approach. For. Ecol. Manag. 2008, 256, 1939–1948. [Google Scholar] [CrossRef]
- Bouriaud, O.; Stefan, G.; Saint-André, L. Comparing local calibration using random effects estimation and Bayesian calibrations: A case study with a mixed effect stem profile model. Ann. For. Sci. 2019, 76, 65. [Google Scholar] [CrossRef]
- Zianis, D.; Pantera, A.; Papadopoulos, A.; Losada, M.R.M. Bayesian and classical biomass allometries for open grown valonian oaks (Q. ithaburensis subs. macrolepis L.) in a silvopastoral system. Agrofor. Syst. 2017, 93, 1–13. [Google Scholar] [CrossRef]
- Petritan, I.C.; Commarmot, B.; Hobi, M.L.; Petritan, A.M.; Bigler, C.; Abrudan, I.V.; Rigling, A. Structural patterns of beech and silver fir suggest stability and resilience of the virgin forest Sinca in the Southern Carpathians, Romania. For. Ecol. Manag. 2015, 356, 184–195. [Google Scholar] [CrossRef]
- Hobi, M.L.; Commarmot, B.; Bugmann, H. Pattern and process in the largest primeval beech forest of Europe (Ukrainian Carpathians). J. Veg. Sci. 2015, 26, 323–336. [Google Scholar] [CrossRef]
- Višnjić, Ć.; Solaković, S.; Mekić, F.; Balić, B.; Vojniković, S.; Dautbašić, M.; Gurda, S.; Ioras, F.; Ratnasingam, J.; Abrudan, I.V. Comparison of structure, regeneration and dead wood in virgin forest remnant and managed forest on Grmeč Mountain in Western Bosnia. Plant Biosyst. Int. J. Deal. All Asp. Plant Biol. 2013, 147, 913–922. [Google Scholar] [CrossRef][Green Version]
- Glatthorn, J.; Feldmann, E.; Pichler, V.; Hauck, M.; Leuschner, C. Biomass stock and productivity of primeval and production beech forests: Greater canopy structural diversity promotes productivity. Ecosystems 2018, 21, 704–722. [Google Scholar] [CrossRef]
- Geßler, A.; Keitel, C.; Kreuzwieser, J.; Matyssek, R.; Seiler, W.; Rennenberg, H. Potential risks for European beech (Fagus sylvatica L.) in a changing climate. Trees 2006, 21, 1–11. [Google Scholar] [CrossRef]
- Bouriaud, O.; Don, A.; Janssens, I.A.; Marin, G.; Schulze, E.-D. Effects of forest management on biomass stocks in Romanian beech forests. For. Ecosyst. 2019, 6, 19. [Google Scholar] [CrossRef]
- Vejpustková, M.; Zahradník, D.; Čihák, T.; Šrámek, V. Models for predicting aboveground biomass of European beech (Fagus sylvatica L.) in the Czech Republic. J. For. Sci. 2015, 61, 45–54. [Google Scholar]
- Bartelink, H. Allometric relationships for biomass and leaf area of beech (Fagus sylvatica L.). Ann. Sci. For. 1997, 54, 39–50. [Google Scholar] [CrossRef]
- Zianis, D.; Muukkonen, P.; Mäkipää, R.; Mencuccini, M. Biomass and Stem Volume Equations for Tree Species in Europe; Finnish Society of Forest Science, Finnish Forest Research Institute: Tampere, Finland, 2005. [Google Scholar]
- Jagodziński, A.M.; Dyderski, M.K.; Horodecki, P. Differences in biomass production and carbon sequestration between highland and lowland stands of Picea abies (L.) H. Karst. and Fagus sylvatica L. For. Ecol. Manag. 2020, 474, 118329. [Google Scholar] [CrossRef]
- Genet, A.; Wernsdörfer, H.; Jonard, M.; Pretzsch, H.; Rauch, M.; Ponette, Q.; Nys, C.; Legout, A.; Ranger, J.; Vallet, P.; et al. Ontogeny partly explains the apparent heterogeneity of published biomass equations for Fagus sylvatica in central Europe. For. Ecol. Manag. 2011, 261, 1188–1202. [Google Scholar] [CrossRef]
- Forrester, D.I.; Tachauer, I.H.H.; Annighoefer, P.; Barbeito, I.; Pretzsch, H.; Ruiz-Peinado, R.; Stark, H.; Vacchiano, G.; Zlatanov, T.; Chakraborty, T.; et al. Generalized biomass and leaf area allometric equations for European tree species incorporating stand structure, tree age and climate. For. Ecol. Manag. 2017, 396, 160–175. [Google Scholar] [CrossRef]
- Wutzler, T.; Wirth, C.; Schumacher, J. Generic biomass functions for Common beech (Fagus sylvatica) in Central Europe: Predictions and components of uncertainty. Can. J. For. Res. 2008, 38, 1661–1675. [Google Scholar] [CrossRef]
- Jagodziński, A.M.; Dyderski, M.K.; Gęsikiewicz, K.; Horodecki, P. Tree and stand level estimations of Abies alba Mill. aboveground biomass. Ann. For. Sci. 2019, 76, 56. [Google Scholar] [CrossRef]
- Tabacchi, G.; Di Cosmo, L.; Gasparini, P. Aboveground tree volume and phytomass prediction equations for forest species in Italy. Eur. J. For. Res. 2011, 130, 911–934. [Google Scholar] [CrossRef]
- Petritan, I.C.; Mihăilă, V.V.; Bragă, C.I.; Boura, M.; Vasile, D.; Petritan, A.M. Litterfall production and leaf area index in a virgin european beech (Fagus sylvatica L.)–Silver fir (abies alba mill.) forest. Dendrobiology 2020, 83, 75–84. [Google Scholar] [CrossRef]
- Bouriaud, O.; Ştefan, G.; Flocea, M. Predictive models of forest logging residues in Romanian spruce and beech forests. Biomass Bioenergy 2013, 54, 59–66. [Google Scholar] [CrossRef]
- Schepaschenko, D.; Shvidenko, A.; Usoltsev, V.; Lakyda, P.; Luo, Y.; Vasylyshyn, R.; Lakyda, I.; Myklush, Y.; See, L.; McCallum, I.; et al. A dataset of forest biomass structure for Eurasia. Sci. Data 2017, 4, 170070. [Google Scholar] [CrossRef]
- Baskerville, G.L. Use of logarithmic regression in the estimation of plant biomass. Can. J. For. Res. 1972, 2, 49–53. [Google Scholar] [CrossRef]
- Sprugel, D.G. Correcting for bias in log-transformed allometric equations. Ecology 1983, 64, 209–210. [Google Scholar] [CrossRef]
- Su, Y.-S.; Yajima, M. Using R to Run “JAGS”; R Core Team: Vienna, Austria, 2020. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Plummer, M. JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling. In Proceedings of the 3rd International Workshop on Distributed Statistical Computing, Vienna, Austria, 20–22 March 2003; p. 8. [Google Scholar]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; Authors, E.; Siem, H.; Van Willigen, B. Linear and Nonlinear Mixed Effects Models; R Core Team: Vienna, Austria, 2020. [Google Scholar]
- Cole, T.J.; Altman, D.G. Statistics notes: Percentage differences, symmetry, and natural logarithms. BMJ 2017, 358, j3683. [Google Scholar] [CrossRef]
- Zianis, D.; Mencuccini, M. Aboveground biomass relationships for beech (Fagus moesiaca Cz.) trees in Vermio Mountain, Northern Greece, and generalised equations for Fagus sp. Ann. For. Sci 2003, 60, 439–448. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric scaling laws in biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef] [PubMed]
- Dutcă, I.; McRoberts, R.E.; Næsset, E.; Blujdea, V.N.B. A practical measure for determining if diameter (D) and height (H) should be combined into D2H in allometric biomass models. Forestry 2019, 92, 627–634. [Google Scholar]
- Ung, C.H.; Lambert, M.C.; Raulier, F.; Guo, X.J.; Bernier, P.Y. Biomass of Trees Sampled across Canada as Part of the Energy from the Forest Biomass (ENFOR) Program; Natural Resources Canada: Hamilton, ON, Canada, 2017. [Google Scholar]
- Falster, D.S.; Duursma, R.A.; Ishihara, M.I.; Barneche, D.R.; FitzJohn, R.G.; Vårhammar, A.; Aiba, M.; Ando, M.; Anten, N.; Aspinwall, M.J.; et al. BAAD: A biomass and allometry database for woody plants. Ecology 2015, 96, 1445. [Google Scholar] [CrossRef]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.C.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Chang. Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef] [PubMed]
- Dutcă, I. Biomass data for young, planted Norway spruce (Picea abies (L.) Karst.) trees in Eastern Carpathians of Romania. Data Br. 2018, 19, 2384–2392. [Google Scholar] [CrossRef] [PubMed]

| Characteristic | European Beech | Silver Fir |
|---|---|---|
| Sample size | 15 | 14 |
| D range (cm) | 5.7–86.3 | 6.3–92.6 |
| D mean (standard deviation) (cm) | 32.8 (26.1) | 35.8 (27.0) |
| H range (m) | 6.2–40.3 | 3.5–43.5 |
| H mean (standard deviation) (cm) | 22.8 (12.5) | 21.2 (13.8) |
| AGB range (kg) | 6.0–8447.1 | 4.2–4042.9 |
| AGB mean (standard deviation) (kg) | 1561.4 (2382.7) | 1034.6 (1316.9) |
| Characteristic | European Beech | Silver Fir |
|---|---|---|
| Sample size | 7 | 7 |
| D range (cm) | 5.7–20.0 | 6.3–27.9 |
| D mean (standard deviation) (cm) | 11.1 (5.8) | 14.2 (7.9) |
| H range (m) | 6.2–19.8 | 3.5–19.8 |
| H mean (standard deviation) (m) | 11.4 (5.2) | 9.3 (5.8) |
| AGB range (kg) | 6.0–182.2 | 4.2–358.9 |
| AGB mean (standard deviation) (kg) | 65.1 (73.9) | 84.2 (128.8) |
| Characteristic | Generic Dataset | Dataset #3 | ||
|---|---|---|---|---|
| European Beech | Silver Fir | European Beech | Silver Fir | |
| Sample size | 144 | 102 | 159 | 116 |
| D range (cm) | 5.2–62.1 | 5.1–64.0 | 5.2–86.3 | 5.1–92.6 |
| H range (m) | 9.2–33.0 | 4.1–28.9 | 6.2–40.3 | 3.5–43.5 |
| AGB range (kg) | 6.6–3116.2 | 7.0–1652.3 | 6.0–8447.1 | 4.2–4042.9 |
| Number of sites | 10 | 10 | 11 | 11 |
| References | [35,44] | [35,44] and this study | ||
| Characteristic | European Beech | Silver Fir |
|---|---|---|
| Sample size | 151 (i.e., 144 + 7) | 109 (i.e., 102 + 7) |
| D range (cm) | 5.2–62.1 | 5.1–64.0 |
| H range (m) | 6.2–33.0 | 3.5–28.9 |
| AGB range (kg) | 6.0–3116.2 | 4.2–358.9 |
| Number of sites | 11 | 11 |
| Fitting Approach | Dataset | Predictors | Model Form | RSE | CF | |||
|---|---|---|---|---|---|---|---|---|
| European Beech | ||||||||
| LM | #1 | ln(D) | Equation (2) | −2.6634 (0.1254) | 2.6368 (0.0384) | N.A. | 0.1337 | 1.0089 |
| ln(D), ln(H) | Equation (3) | −3.1632 (0.1761) | 2.1468 (0.1489) | 0.6909 (0.2060) | 0.1000 | 1.0050 | ||
| RIM | #3 | ln(D) | Equation (2) | −2.1312 (0.0901) | 2.4714 (0.0253) | N.A. | 0.1712 | 1.0148 |
| ln(D), ln(H) | Equation (3) | −3.0039 (0.1389) | 2.1151 (0.0495) | 0.6733 (0.0845) | 0.1450 | 1.0106 | ||
| #4 | ln(D) | Equation (2) | −2.1625 (0.0997) | 2.4368 (0.0284) | N.A. | 0.1683 | 1.0143 | |
| ln(D), ln(H) | Equation (3) | −2.9793 (0.1593) | 2.1191 (0.0511) | 0.6512 (0.0916) | 0.1474 | 1.0109 | ||
| Bayesian model | #1 | ln(D) | Equation (2) | −2.1768 (0.1148) | 2.4884 (0.0345) | N.A. | 0.2042 | 1.0211 |
| ln(D), ln(H) | Equation (3) | −3.0637 (0.1076) | 2.1497 (0.0445) | 0.6553 (0.0605) | 0.1091 | 1.0060 | ||
| #2 | ln(D) | Equation (2) | −2.1456 (0.1115) | 2.4349 (0.0398) | N.A. | 0.2363 | 1.0283 | |
| ln(D), ln(H) | Equation (3) | −2.9856 (0.1508) | 2.1347 (0.0525) | 0.6324 (0.0680) | 0.1475 | 1.0109 | ||
| Silver Fir | ||||||||
| LM | #1 | ln(D) | Equation (2) | −3.4141 (0.3106) | 2.6997 (0.0922) | N.A. | 0.2965 | 1.0449 |
| ln(D), ln(H) | Equation (3) | −2.9687 (0.2907) | 1.3301 (0.4839) | 1.4460 (0.5051) | 0.2344 | 1.0278 | ||
| RIM | #3 | ln(D) | Equation (2) | −2.4756 (0.1106) | 2.4219 (0.0346) | N.A. | 0.2033 | 1.0209 |
| ln(D), ln(H) | Equation (3) | −2.8079 (0.0984) | 1.7737 (0.0708) | 0.8745 (0.0920) | 0.1624 | 1.0133 | ||
| #4 | ln(D) | Equation (2) | −2.5086 (0.1205) | 2.3561 (0.0375) | N.A. | 0.1824 | 1.0168 | |
| ln(D), ln(H) | Equation (3) | −2.7987 (0.1126) | 1.8076 (0.0751) | 0.8040 (0.0992) | 0.1548 | 1.0121 | ||
| Bayesian model | #1 | ln(D) | Equation (2) | −2.3284 (0.1598) | 2.3859 (0.0471) | N.A. | 0.3965 | 1.0818 |
| ln(D), ln(H) | Equation (3) | −2.7679 (0.1609) | 1.9264 (0.0771) | 0.6847 (0.0897) | 0.2788 | 1.0396 | ||
| #2 | ln(D) | Equation (2) | −2.3553 (0.1591) | 2.3316 (0.0552) | N.A. | 0.4064 | 1.0861 | |
| ln(D), ln(H) | Equation (3) | −2.6917 (0.1707) | 1.9063 (0.0810) | 0.6305 (0.0969) | 0.3192 | 1.0523 | ||
| Fitting Approach | Biomass Dataset | Model Type | Both Species | European Beech | Silver Fir | |||
|---|---|---|---|---|---|---|---|---|
| Mean (kg/ha) | SE (kg/ha) | Mean (kg/ha) | SE (kg/ha) | Mean (kg/ha) | SE (kg/ha) | |||
| LM | #1 | Equation (2) | 542,758 | 71,118 | 410,860 | 57,906 | 131,881 | 41,260 |
| Equation (3) | 505,277 | 49,181 | 378,396 | 39,159 | 126,881 | 29,754 | ||
| RIM | #3 | Equation (2) | 455,408 | 68,745 | 350,901 | 64,759 | 104,514 | 23,054 |
| Equation (3) | 484,465 | 59,552 | 368,402 | 56,126 | 115,934 | 19,398 | ||
| #4 | Equation (2) | 370,296 | 55,126 | 293,328 | 52,952 | 76,972 | 15,297 | |
| Equation (3) | 459,387 | 57,947 | 354,853 | 55,409 | 104,537 | 16,992 | ||
| Bayesian | #1 | Equation (2) | 487,053 | 100,743 | 364,564 | 77,672 | 122,523 | 64,197 |
| Equation (3) | 497,354 | 76,448 | 376,447 | 68,229 | 120,921 | 34,488 | ||
| #2 | Equation (2) | 438,556 | 175,137 | 318,630 | 129,117 | 119,831 | 118,287 | |
| Equation (3) | 460,279 | 76,274 | 352,865 | 61,428 | 107,410 | 45,214 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dutcă, I.; Zianis, D.; Petrițan, I.C.; Bragă, C.I.; Ștefan, G.; Yuste, J.C.; Petrițan, A.M. Allometric Biomass Models for European Beech and Silver Fir: Testing Approaches to Minimize the Demand for Site-Specific Biomass Observations. Forests 2020, 11, 1136. https://doi.org/10.3390/f11111136
Dutcă I, Zianis D, Petrițan IC, Bragă CI, Ștefan G, Yuste JC, Petrițan AM. Allometric Biomass Models for European Beech and Silver Fir: Testing Approaches to Minimize the Demand for Site-Specific Biomass Observations. Forests. 2020; 11(11):1136. https://doi.org/10.3390/f11111136
Chicago/Turabian StyleDutcă, Ioan, Dimitris Zianis, Ion Cătălin Petrițan, Cosmin Ion Bragă, Gheorghe Ștefan, Jorge Curiel Yuste, and Any Mary Petrițan. 2020. "Allometric Biomass Models for European Beech and Silver Fir: Testing Approaches to Minimize the Demand for Site-Specific Biomass Observations" Forests 11, no. 11: 1136. https://doi.org/10.3390/f11111136
APA StyleDutcă, I., Zianis, D., Petrițan, I. C., Bragă, C. I., Ștefan, G., Yuste, J. C., & Petrițan, A. M. (2020). Allometric Biomass Models for European Beech and Silver Fir: Testing Approaches to Minimize the Demand for Site-Specific Biomass Observations. Forests, 11(11), 1136. https://doi.org/10.3390/f11111136





