The ranges and averages (± standard deviation) of the predictor variables for 205 shrubs and 106 trees are provided in
Supplementary Material 1, Tables S1 and S2, respectively. Regression coefficients, correction factors, and standard errors are presented in
Supplementary Material 2, Tables S3–S5, and can be input into Equations (2)–(7). For all allometric models, regression coefficients were positive, indicating increasing biomass with increasing predictor variable for total AGB, as was found by Lambert et al. [
14].
The applicability of multispecies models to predict total AGB for single genus and species has been shown for shrubs by He et al. [
16]. Similarly, the differences between our modeled means of total AGB via the multispecies equations and the genus/species-specific modeled means were not significant (
p > 0.05). Furthermore, the difference between the modeled means of shrub and tree biomass in previously burned sites and the unburned sites was not significant (
p > 0.05). Species-specific coefficients for input into the allometric Equations (2)–(7) are provided in
Supplementary Material 2, Table S3, using volume as the predictor and
Supplementary Material 2, Table S4, using cross-sectional area as the predictor.
3.1. Comparison of 1D, 2D, and 3D Variables for Shrub Total AGB Prediction
For the genus/species-specific 1D-based models using max stem length or max basal diameter as input into each of the three allometric models (LLR, LLRC, and NLS),
Betula spp.,
Dasiphora fruticosa, and
Salix spp. had lower
R2 (0.005 ≤
R2 ≤ 0.325) compared to
Shepherdia canadensis (0.433 ≤
R2 ≤ 0.809,
Table S6). In addition,
Dasiphora fruticosa was the only species where stem length was not significantly related (
p > 0.05) to the dependent variable of measured total AGB. For the multispecies shrub models (pooled for all shrub genera and species), the use of 1D predictor variables yielded the lowest model fits (RMSE) ranging from 262 (NLS) to 318 (LLRC) g for max stem length and 252 (NLS) to 388 (LRC) g for max basal diameter (
Table 2). These results are in contrast with previous allometric models for boreal [
11,
16,
17] or subtropical [
27] shrubs, where the 1D variable basal diameter of the longest stem had provided the most accurate prediction of total AGB. However, 1D field variables, although related to the dependent variable (
p < 0.001) (with the exception of max stem length of
Dasiphora fruticosa), did not explain total AGB variability when considering all stems of the entire plant (0.228 ≤
R2 ≤ 0.335,
Table 2,
Figure 3a,b). This was true for each genus/species model as well as the multispecies equation, with the exception of
Sheperdia canadensis. For this species, max basal diameter was a similarly good predictor variable (
R2 = 0.809) to cross-sectional area (
R2 = 0.738) and volume (
R2 = 0.765,
Table S6). The performance of total AGB models increased for all other genera and species as well as for all genera and species combined using the 3D predictor variable of volume, with
R2 ranging between 0.684 (
Betula spp. and
Dasiphora fruticosa) and 0.882 (
Alnus spp.). The RMSEs for the multispecies models ranged from 141 (NLS) to 144 (LLR and LLRC) g with
R2 of ~0.790 using any of the three models (LLR, LLRC, and NLS;
Table 2).
Figure 3a–d shows the relationship between the three models for 1D, 2D, and 3D variables for the multispecies shrub AGB.
Of the three model forms tested, the 3D volume predictor produced the most consistent shrub AGB results (
Figure 3,
Table 3), suggesting the choice of model form is less critical when using a 3D predictor. As expected, the exponent
was greater for 1D models and close to unity for the 3D models. This suggests that a simple linear model would result in similar model fits compared to the LLRC or NLS models when using a 3D predictor. However, after testing this (results not shown), the model results achieved slightly less goodness of fit (
R2 = 0.769, RMSE 148.6 g) compared to LLRC or NLS (
Table 2). Decreasing exponents (holding all else equal) can be explained by the nature of allometric scaling between 1D, 2D, and 3D measurements of a plant to its mass (a 3D attribute) via a power function. Assuming no change in the multiplier (
β) (which might be considered analogous to a density attribute), scaling from a 1D measurement to a 3D property requires a higher exponent (α) compared to scaling from a 2D or 3D measurement (
Table 3). Therefore, predictions that are extrapolated from lower to higher dimensions contain more inherent model-based uncertainty than predictions requiring no dimensional extrapolation. However, field volume observations consisted of three single measurements and therefore might contain a high overall measurement uncertainty compared to a single 1D measurement. The exact quantity of model vs. field measurement error propagation is unknown, but the net outcome of the tests performed shows that 3D volume produced the highest AGB model accuracies, followed by 2D and then 1D models.
Better model performance and linearity via the 3D predictor variable of volume may also be explained by the structural variability of multi-stemmed shrubs. For example, shrub stems can grow comparably long while being simultaneously thinner rather than being shorter but thicker, so the total dry weight of the shrub with the longer stems may be lower than the dry weight of a shrub that has shorter but thicker stems. This variability is represented in the scatterplots of
Figure 3a,b and illustrates that shrub structural variability cannot be sufficiently explained using a measurement from one single perspective alone. The structural heterogeneity of shrubs is a function of site conditions, such as nutrient, water, and light availability. To capture structural heterogeneity, a measurement is needed that describes the shrub structure from three different perspectives. For example, a taller shrub with a single stem will be narrower in width and cover than a shrub with many stems extending in multiple directions. If we assume that the shrub with many stems has a larger width, then it is also likely that the shrub with many stems will have more biomass (dry weight). We demonstrated that neither max stem length nor max basal diameter could be used to predict the dry weight of multi-stemmed shrubs. Volume, however, captured the shrub extent and directional growth and therefore predicted total AGB with less total model uncertainty. The exception of better model performance using max basal diameter for
Shepherdia canadensis can be explained by the comparably low number of stems for each harvested individual (<12 stems per plant) and the observed uniform growth of this species in the areas sampled.
A second alternative to volume is the measurement of basal diameters for all stems per plant, converted to cross-sectional area and summed. This is because (a) stem count is represented and (b) shrubs with larger stem counts usually have greater extents (width and line-intercept cover) and dry weight compared to shrubs with lower stem counts. To improve the accuracy of AGB predictions for northern boreal shrubs, measurements to determine volume (max height, line-intercept cover, and width) are recommended. These can be measured rapidly in the field. 1D measures may take slightly less time for shrub individuals that have developed a low number of stems. However, 1D measurements result in both over- and underestimation of AGB depending on the regression form used, especially for shrubs with a high number of stems. 2D cross-sectional area provides the second-best predictions of shrub AGB, although it is slightly more time intensive to measure the basal diameter of each stem per shrub individual. Here, the time required increases with number of stems.
3.2. Comparison of Regression Models for Shrub Total AGB Prediction
With regard to model comparisons (LLR, LLRC, and NLS), NLS produced the best model fits for each shrub genus and species (
Supplementary Material 3, Table S6) as well as for the multispecies data (
Table 2). Here, we found significant differences using 1D vs. 3D models. RMSE varied between 251.68 (NLS, using max basal diameter) and 317.95 (LLRC, using max stem length) g and were greatly reduced with volume as the input variable (RMSE between 141.04 (NLS) and 144.12 (LLRC) g). For the multispecies data, NLS and LLRC overestimated total AGB for all 1D, 2D, and 3D models, while LLR continuously underestimated total AGB (
Table 2). NLS produced the best model fit, independent of the variable used, while the 3D models of all regression forms resulted in the best AGB predictions (RMSE = 141.04 g,
R2 = 0.790 (NLS), RMSE 144.08 g,
R2 = 0.788 (LLR), RMSE = 144.12 g,
R2 = 0.788 (LLRC);
Table 2). However, although NLS produces slightly better model fits, nonlinear models require an even variance of errors across the domain of the predictor variable in order to perform valid comparisons of model uncertainties and regression coefficients amongst datasets (e.g., [
23]). Residual analysis of our models showed that errors were free of heteroscedasticity. However, when models are transferred to different areas and data, we recommend using the LLRC-based models. This is because biomass data can contain natural heteroscedastic variation. Heteroscedasticity needs to be accounted for in the model development to ensure that model results do not contain bias [
25]. For example, Mascaro et al. [
25] reported a bias of ~100% overestimation when extending predicted small tree (diameter at breast height (DBH) range 2–12 cm) aboveground biomass to stand level biomass using NLS. For model transfer purposes, we have provided regression coefficients and error statistics not only for our best models based on NLS but also for our LLRC models (
Supplementary Material 2, Table S3).
3.3. Comparison of 1D and 2D Variables for Tree Total AGB Prediction
For the short-stature tree AGB equations, diameter measured at 0.3 m stem length resulted in better model fits compared to stem length for each genus and species (
Supplementary Material 3, Table S7). For the multispecies data, total AGB prediction using stem length (1D variable) provided the lowest goodness of fit (highest RMSE and lowest
R2,
Table 4,
Figure 4), while inclusion of stem diameter at 0.3 m, alternatively cross-sectional area at 0.3 m, improved predictions by 87% using LLRC or NLS (
Table 4).
For multispecies tree total AGB prediction, the exponent
was greater for the 1D model based on stem length and close to unity for the 1D model diameter at 0.3 m, alternatively 2D model cross-sectional area at 0.3 m (
Table 5). The 2D cross-sectional area model produced equivalent results compared to the 1D diameter model but allowed to effectively reconcile tree with shrub AGB predictions. The combined prediction of shrub and tree AGB has not been developed for this study region yet, but would allow the prediction of AGB for boreal short-stature shrubs and trees (<4.5 m) as well as tall-stature trees (>4.5 m) in just a few steps (see
Section 3.5). When transferring these allometric models to different areas within the region, we recommend measuring the diameter at 0.3 m stem length.
3.4. Comparison of Regression Models for Tree Total AGB Prediction
For the prediction of tree total AGB per genus/species and all genera/species combined, NLS achieved the lowest RMSE, highest
R2, and lowest total percentage error compared to measured biomass (<−5%–4%), while the dependent and independent variables were significantly related (
p < 0.001,
Table 4 and
Table S7). LLR predictions resulted in the highest RMSE, similar
R2, and highest total percentage error relative to the measured biomass compared to LLRC and NLS for each genus/species and for all data combined. The single exception was for predicting total AGB for
Picea spp. based on stem length (
Table S7). Using LLR, the prediction based on stem length resulted in an underestimation of total AGB of −51% and an underestimation of −20% when using diameter or cross-sectional area, respectively, as input variable for the multispecies models. LLRC had comparably lower RMSE, similar
R2, and underestimated total multispecies AGB by −6% (stem length) to <−10% (diameter at 0.3 m, cross-sectional area at 0.3 m). In order to address potential heteroscedasticity effects, we have provided the regression coefficients for both NLS and LLRC models with cross-sectional area (measured at 0.3 m stem length) as predictor variable (
Supplementary Material 2, Table S4).
3.5. Comparison of Regression Models for General Shrub and Tree Total AGB Prediction
The prediction of total AGB for shrubs and trees combined resulted in similar predictive capability to multispecies shrub and multispecies short-stature trees (
R2 ≥ 0.770,
p < 0.001). This was determined using the 2D independent variable of cross-sectional area, measured at the base for shrubs and at 0.3 m stem length for trees (
Table 6,
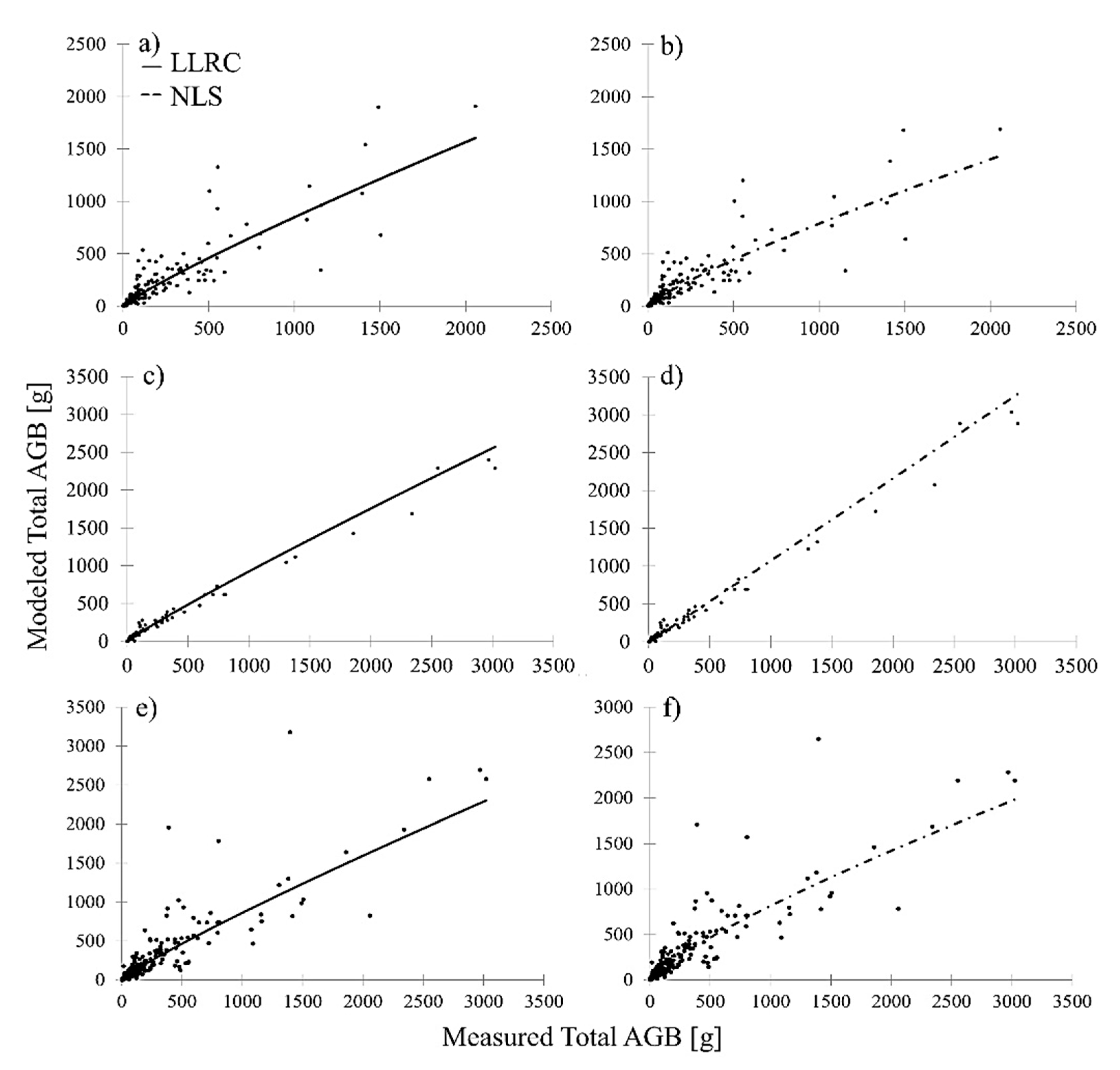
Figure 5). Relating modeled total AGB to measured total AGB showed no evident bias in the 2D-based prediction of combined shrub and tree AGB in comparison to 3D multispecies shrub and 2D multispecies tree AGB models. This is depicted in
Figure 6, which shows modeled AGB in relation to measured AGB of the 2D general shrub and tree AGB model (
Figure 6e,f) in comparison to the 3D multispecies shrub (
Figure 6a,b) and 2D multispecies tree (
Figure 6b,c) AGB models. Similar to the multispecies shrub models, NLS achieved the lowest RMSE and highest
R2 (RMSE = 94.80 g,
R2 = 0.776). The RMSE of model LLR increased by 53% (RMSE = 202.17 g,
R2 = 0.770) and by 54% for the LLRC model (RMSE = 206.37 g,
R2 = 0.770). Compared to Ali et al. [
27], who derived best model fits for combined shrub and tree AGB prediction using diameter of the longest stem and total plant height combined, our model results show that AGB of boreal plants can be predicted with a simpler one-variable model using cross-sectional area. For our AGB models based on cross-sectional area, the exponent
was greater for the 1D model based on stem length and close to unity for the 2D model cross-sectional area at 0.3 m (
Table 7). However, stem length of shrubs and trees was also weakly related to measured total AGB (
p < 0.001,
Table 6) and thus represents an alternative to cross-sectional area, which has potential for use in rapid field measurement or non-invasive observation situations (e.g., remote sensing via airborne lidar) where it may be acceptable to trade accuracy at the individual sample-level for greater overall population representation. For model transfer purposes, we recommend the use of LLRC regression coefficients and correction factor in order to address heteroscedasticity.