Correlation of Field-Measured and Remotely Sensed Plant Water Status as a Tool to Monitor the Risk of Drought-Induced Forest Decline

Abstract

Increased frequency of tree mortality and forest decline due to anomalous drought events calls for the adoption of effective monitoring of tree water status over large spatial and temporal scales. We correlated field-measured and remotely sensed plant water status parameters, to test the possibility of monitoring the risk of drought-induced dehydration and hydraulic failure using satellite images calibrated on reliable physiological indicators of tree hydraulics. The study was conducted during summer 2019 in the Karst plateau (NE Italy) in a woodland dominated by Fraxinus ornus L.; Sentinel-2 images were acquired on a seasonal scale on the same dates when absolute water content (AbWC), relative water content (RWC), and minimum water potential (Ψ_min) were measured in the field. Plant water status parameters were correlated with normalized difference vegetation index (NDVI and NDVI 8A), normalized difference water index (NDWI), and soil-adjusted vegetation index (SAVI). Significant Pearson and Spearman linear correlations (α < 0.05) emerged between all tree-level measured variables and NDWI, while for NDVI, NDVI 8A, and SAVI no correlation was found. Our results suggest the possibility of using the NDWI as a proxy of tree water content and water potential.

1. Introduction

Forests cover roughly 30% of the world’s land surface [1], and account for a large share of global net primary production. Forests also provide essential services for ecosystems and humankind, including carbon sequestration, biodiversity conservation, timber production, and hydrological cycle regulation [2,3,4]. In the last decades, anomalous tree mortality events have been recorded in many forests worldwide, frequently coupled to anomalous drought and heat waves [5,6,7,8,9,10]. Despite the variability of future climate change projections, most scenarios foresee an increase in global mean temperature with more frequent, severe, and prolonged heat waves and dry periods [11]. These changes may exacerbate tree mortality and forest die-off events [12,13].

In this light, the development of an effective monitoring system of forest health status would be fundamental to assess the drought-induced mortality risk at a landscape scale [14,15]. Despite the complexity of the mechanisms involved, the cause leading to drought-induced mortality is ultimately thought to be hydraulic failure [16]. Therefore, the most adequate predictor of mortality risk should be a proxy of plant water status calibrated against critical thresholds related to hydraulic failure, as previously suggested by Martinez Vilalta et al. [17]. The gold standard parameter to assess plant water status is the water potential, a measure of the free energy of water in plant tissues. As soil water availability decreases and atmospheric evaporative demand increases, the plant water potential drops and the likelihood of embolism formation in xylem conduits increases [18,19]. Another commonly used parameter is the leaf water content, expressed as the amount of water in the leaf tissues as an absolute value, or relative to the fully hydrated status [20,21]. Usually expressed as relative water content (RWC), this is a common estimate of plant water status [17,22,23]. Recently, Martinez Vilalta et al. [17] have proposed to use the RWC as an indicator of mortality risks of trees and forests at a landscape level, as it is closely related to plant water status, it is scalable from plant organ to the ecosystem, it has consistent thresholds relative to the loss of hydraulic functions (e.g., RWC at turgor loss point) and it is easy to measure.

Widespread and frequent measurements of RWC or plant water potential at field level are challenging. However, remotely sensed satellite data may be a useful tool to provide information on broad and remote areas from most regions of the world, provided that such measurements can be correlated to functionally meaningful parameters at the plant level. This workflow strategy has been indeed implemented, and an increasing number of studies have focused on the assessment of a set of remotely sensed metrics related to water content and to the loss of hydraulic function, in order to predict drought-induced tree mortality at landscape scale (e.g., [24,25,26]). Specifically, it has been suggested that remote sensing vegetation indices may be used as proxies of parameters such as the water potential and the RWC.

The normalized difference vegetation index (NDVI) is one of the most commonly used vegetation indices in ecosystem monitoring [27,28]. NDVI is a proxy of vegetation productivity based on the estimation of absorbed photosynthetically active radiation [29], but it is also used to estimate other features such as leaf area index, vegetation biomass, and water availability [30,31,32]. NDVI is calculated as:

$$NDVI= \frac{{\rho }_{NIR}-{\rho }_{red}}{{\rho }_{NIR}+{\rho }_{red}}$$

(1)

where ρ_NIR is the near-infrared reflectance (~0.83 μm), sensible to cell structures of leaves, and ρ_red is the red reflectance (~0.65 μm) [27]

Despite the common use of NDVI, its utility is limited because of oversaturation of red light in areas having leaf area index > 3, and NIR radiation reflectance by soil [33,34]. For these reasons, Huete [35] proposed a soil-adjusted vegetation index (SAVI), calculated as:

$$SAVI= \frac{\left(1+L\right)({\rho }_{NIR}-{\rho }_{red})}{\left({\rho }_{NIR}+{\rho }_{red}+L\right)}$$

(2)

where L is the canopy background adjustment factor which reduces soil brightness variations [35].

Gao [36] introduced the normalized difference water index (NDWI), where the red channel is replaced by an infrared channel, located in the water absorption region between 0.9 and 2.5 μm [36]. NDWI is calculated as:

$$NDWI= \frac{{\rho }_{NIR}-{\rho }_{SWIR}}{{\rho }_{NIR}+{\rho }_{SWIR}}$$

(3)

where ρ_SWIR is the short-wave-infrared reflectance (~1.24 μm), sensible to water content and weakly affected by other features [33].

Remote sensing data have been regularly used for ecophysiological studies, sometimes coupled with forest structure data measured in the field (e.g., diameter at breast height, tree density, dead tree density), to model biophysical features of vegetation (e.g., [25,37,38,39]). Majasalmi and Rautiainen [38] used satellite data, coupled with field measures of tree basal area, density, diameter, height, and crown length, to model the canopy biophysical properties in boreal forests in Finland. Nevertheless, studies correlating satellite remote sensed data with physiological parameters connected to plant water status are scarce and mainly focused on crops (e.g., [40,41,42,43]). Sun et al. [44] have used a field spectrometer in wheat farmlands, coupled to field measurements of leaf and plant water content, in order to assess possible relations between remote sensing indices and spectral bands and field-measured parameters. Their results showed good correlations between water status parameters and vegetation indices, highlighting the possibility to predict water stress in wheat by using canopy reflectance data.

In this study, we report measurements of tree water status (minimum leaf water potential, relative and absolute water content) during seasonal progression of drought in two sites dominated by Fraxinus ornus, but characterized by contrasting substrate properties and hydrology. Measurements were taken on the same dates of satellite data acquisitions. The objective of the study was to test correlations between the most used vegetation indices and field measured parameters, in order to provide a first insight on the possibility to monitor tree water content and forest health status by remote devices operating at large spatial scales, with high temporal and spatial resolution.

2. Materials and Methods

2.1. Study Area

The study area was located near the village of Sgonico (North-Eastern Italy, 45° 44′ 12.1′′ N–13° 44′′ 56.4′′ E), in a woodland in the Karst Plateau, a limestone-dominated region on the border between Slovenia and Italy. The climate in the area is sub-Mediterranean with warm summers (average temperature in July of 22.7 °C), while winters are cold (average temperature in January of 3.9 °C). Mean annual rainfall exceeds 1200 mm, mostly occurring in spring and autumn (data from ARPA-OSMER https://www.meteo.fvg.it/clima/clima_fvg, reference period 1992–2019). The vegetation is composed by coniferous forests dominated by Pinus nigra that have suffered extensive dieback following anomalous summer droughts [45], inter-mixed with deciduous woodlands dominated by Quercus pubescens, Fraxinus ornus, and Ostrya carpinifolia.

A 30 m resolution digital elevation model of the study area was processed using the function “r.slope.aspect” of the Geographic Resources Analysis Support System (GRASS [46], v7.8) software, in order to generate a slope and an exposure map. Two sites of 20,000 m² each, south exposed, with similar slope (between 10% and 20%) hosting vegetation dominated by F. ornus with different health status (one site with healthy individuals, H site, and one site with some individuals showing die-back symptoms, D site) were then selected within the study area (Figure 1) [47].

In each site, six healthy individuals of Fraxinus ornus with comparable age and height (trunk diameter at breast height ~5 cm) were selected and the parameters listed below were measured in the field during the progression of summer drought. This species was selected because of its water use strategy characterized by a substantial degree of anisohydry [48,49], which can induce large variations in plant water status on a seasonal time scale. Hence, this species was considered as an optimal bio-monitor of vegetation water status.

Two sampling areas (one per site) for remote sensing analyses were designed using the QGIS software, version 3.4.5 [50]. A grid was overlapped to the field sampling sites using the “Create Grid Layer” tool and vectorial polygon shapefiles for sampling areas were designed as rectangles (80 × 250 m), in order to include the sampled individuals.

2.2. Physiological Parameters

Field sampling was performed between 12:30 and 1:00 p.m., on 16 May, 27 June, 25 July, and 12 August in 2019 (Figure 2). Two sun-exposed pairs of leaves were sampled from each tree, on the upper and outer part of the canopy. Leaves were wrapped in plastic film and stored in a plastic bag with humid paper inside, maintained in a refrigerated bag until measurements (~1 h after sampling).

In the laboratory, the minimum water potential (Ψ_min, MPa) was measured on one leaf for each pair using a pressure chamber (mod. 1505D, PMS Instrument Company, Albany, OR, USA). Preliminary experiments had shown that this procedure produces results consistent with those obtained by measuring Ψ_min directly in the field. The second leaf of each pair was used to measure the fresh weight (FW, g) using an analytical balance (model SPU123, Ohaus Scout ProBalance, Parsippany, NJ, USA) and were rehydrated overnight in order to measure the leaf turgid weight (TW, g). After that, they were dried for 24 h at 70 °C in an oven to obtain their dry weight (DW, g).

Relative water content (RWC, g/g) and absolute water content (AbWC, g/g) were calculated as:

$$RWC= \frac{FW-DW}{TW-DW}$$

(4)

$$AbWC= \frac{FW-DW}{FW}$$

(5)

2.3. Remote Sensing Data

The Sentinel-2 mission was developed by the European Space Agency as part of the Copernicus European initiative, which aims to provide operational monitoring information for environment and security applications relying on multispectral high spatial resolution optical observations over global terrestrial surface, also providing a narrow-NIR band (0.865 μm) scarcely contaminated by atmospheric water vapor and representing the NIR plateau for vegetation [51,52]. It comprises a constellation of two near-polar-orbiting satellites placed in the same sun-synchronous orbit, phased at 180° to each other, granting a revisit time from five days at the equator to 2–3 days at mid-latitudes [52].

Sentinel-2A/-2B level 2A images (bottom of atmosphere product) with tile 33TUL were retrieved on the Copernicus Open Access Hub (https://scihub.copernicus.eu/). We downloaded four multispectral images from 16 May to 12 August, matching field sampling dates. We selected only cloud-free dates every 2/3 weeks during the growing season. Vegetation indices were calculated using optical spectral bands of red (B04, 665 nm), near-infrared (B08, 833 nm), narrow near-infrared (B8A, 864 nm), and short-wave-infrared (B11, 1610 nm), with the “r.mapcalc” function in GRASS, setting the geographic regions boundaries for the sampling areas with the “g.region” and “r.mask” functions.

Indices were calculated as:

$$NDVI= \frac{B08-B04}{B08+B04};$$

(6)

$$NDVI 8A=\frac{B8A-B04}{B8A+B04};$$

(7)

$$NDWI= \frac{B08-B11}{B08+B11};$$

(8)

$$SAVI= \frac{\left(1+L\right)\left(B08-B04\right)}{\left(B08+B04+L\right)},$$

(9)

where L is the canopy background adjustment factor, conventionally set at 0.5.

2.4. Statistical Analyses

Mean values and associated standard deviation of the physiological parameters and the remote sensing indices were calculated for each sampling and acquisition date for each sampling site using the R software [53]. Generalized linear mixed models (GLMMs) were used to test whether physiological parameters and remote sensing indices were different between the two sampling sites per each date, using “glmer” function in “lme4” package [54]. Specifically, a Gaussian model with a log link function (see equations below) was calculated for each physiological parameter and remote sensing indices (dependent variables), while site (healthy or H, die-back or D), sampling/acquisition date and their interaction were the fixed covariates. To incorporate the temporal dependency among observations, we used the sampling/acquisition date as a random intercept. Pseudo R² of each model was calculated using “r2beta” function in “MuMIn” package [55]. The structure of each model was as follows:

• Physiological parameter/remote sensing indexs_ij = Gaussian (μ_ij).
• E(Physiological parameter/remote sensing index) = μ_ij.
• log(Physiological parameter/remote sensing index) = site_ij × sampling/acquisition date.
• Sampling/acquisition date ~ N (0, σ²).

where physiological parameter/remote sensing index_ij is the jth observation in sampling/acquisition date i, and i = 1,…, 4, and sampling/acquisition date is the random intercept, which is assumed to be normally distributed with mean 0 and variance σ². Correlations between mean values of physiological parameters and vegetation indices were calculated using the Pearson r correlation coefficient or the Spearman’s ρ correlation coefficient when normality assumption was violated, with the “cor.test” function in the “stats” package. Data normality was checked with the Shapiro-Wilcoxon test using “shapiro.test” function in “stats” package.

3. Results

Mean values and associated standard deviation of physiological parameters and remote sensing indices are listed in

Table 1. Means and standard deviations of physiological parameters measured on F. ornus in H and D sites and corresponding remote sensing indices. Abbreviations are as follows: Absolute water content (AbWC), relative water content (RWC), minimum water potential (Ψ_min), normalized difference vegetation index (NDVI), NDVI calculated using the narrow-near-infrared band (NDVI 8A), normalized difference water index (NDWI), soil-adjusted vegetation index (SAVI).

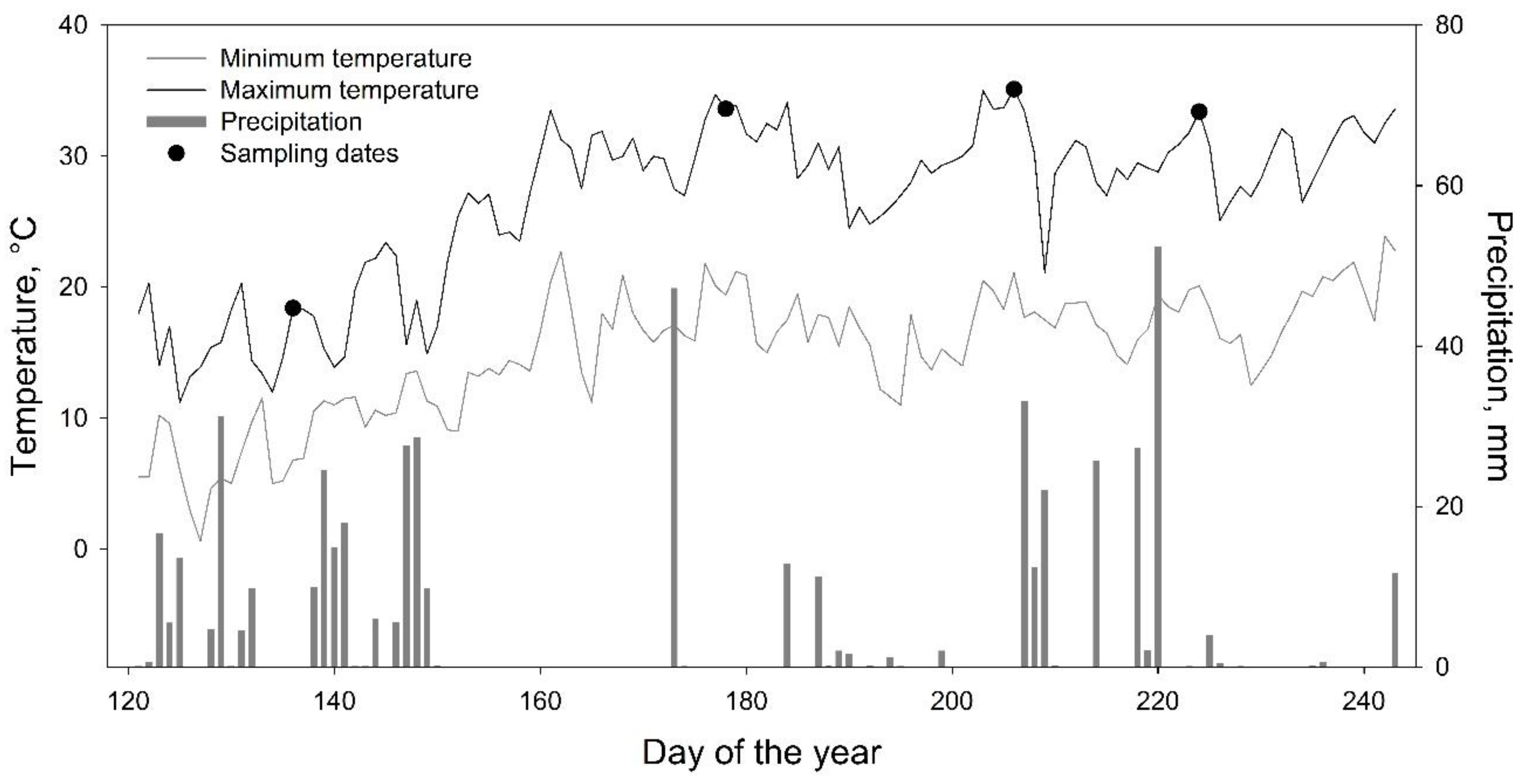
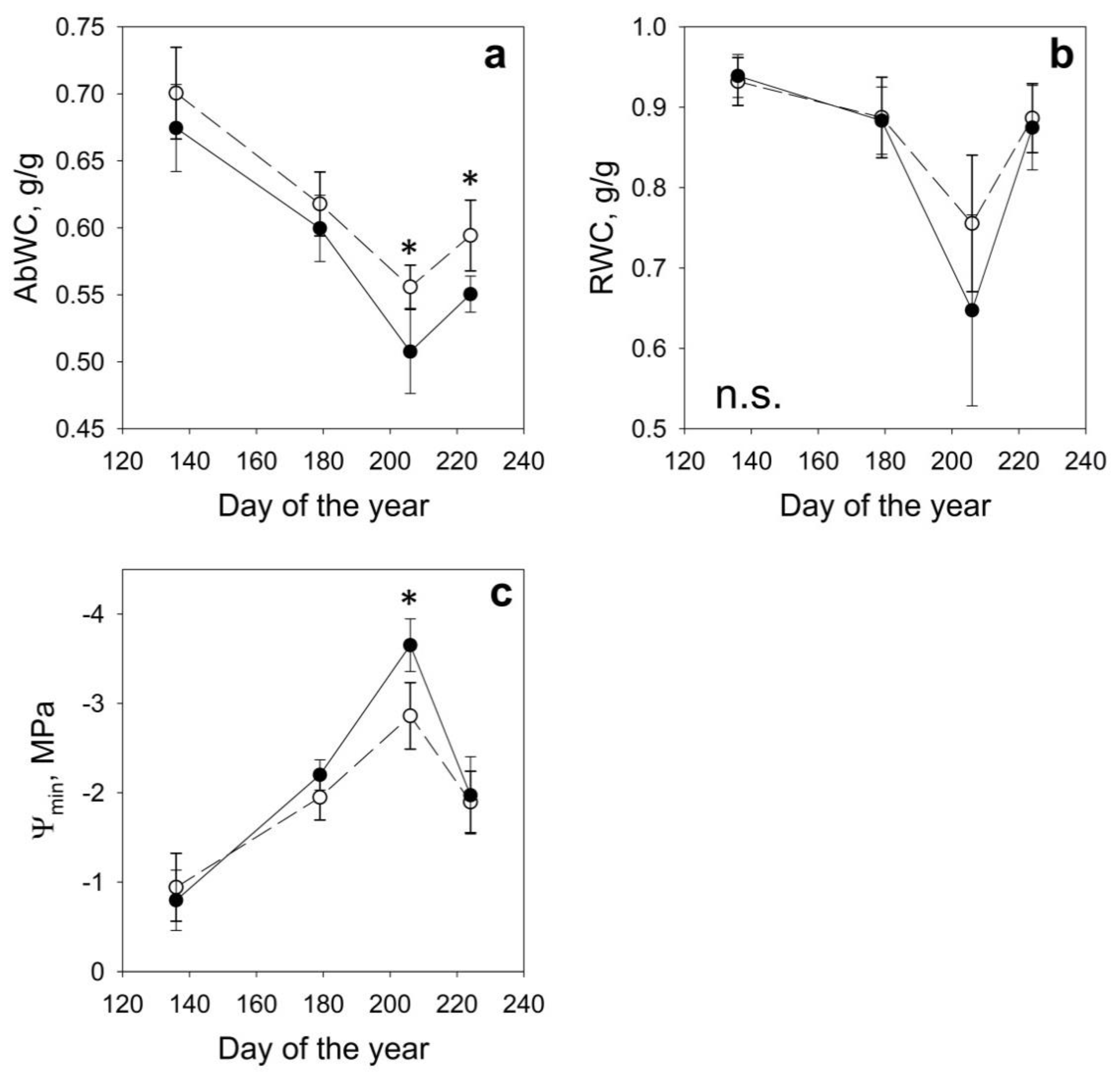
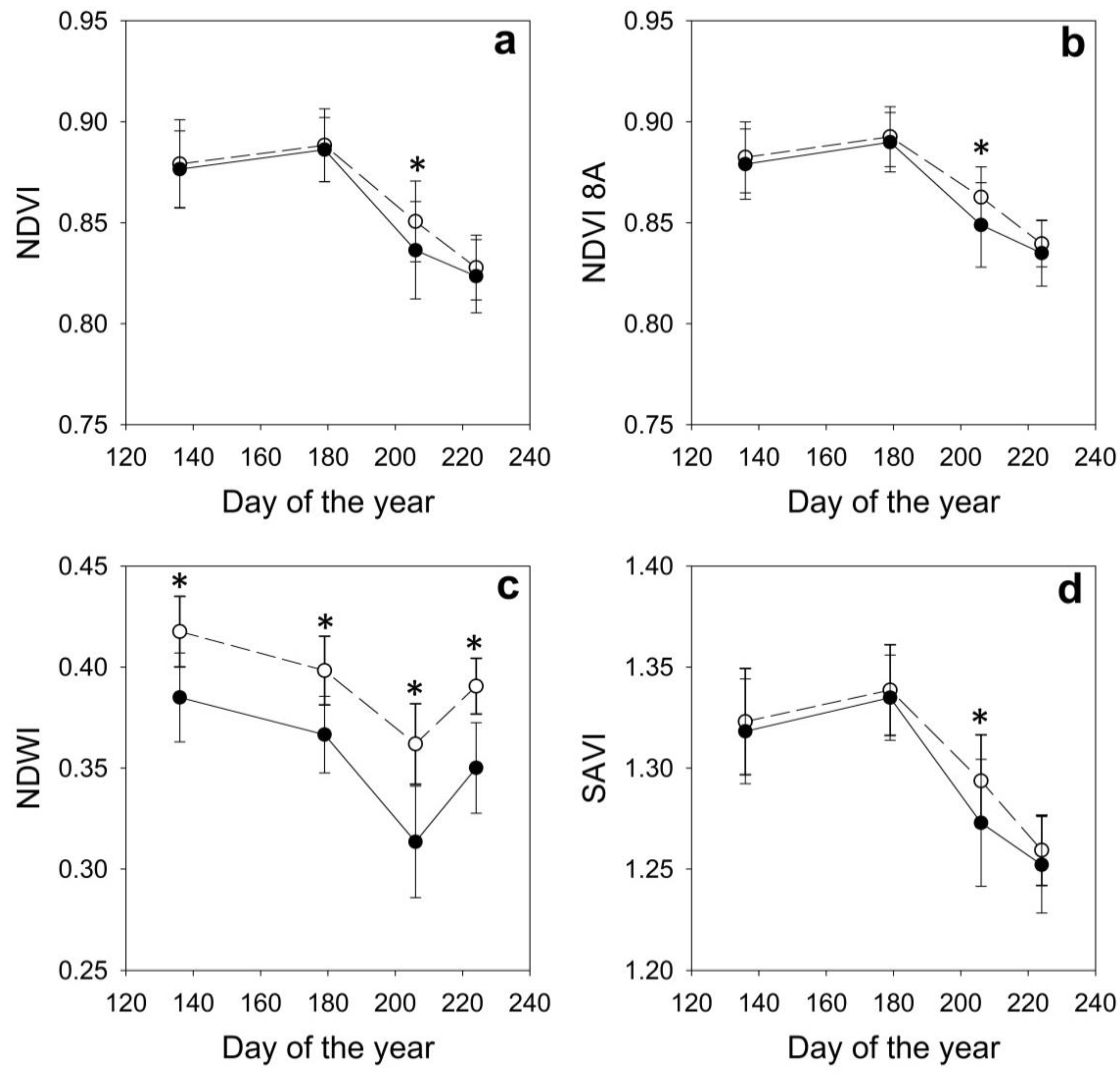
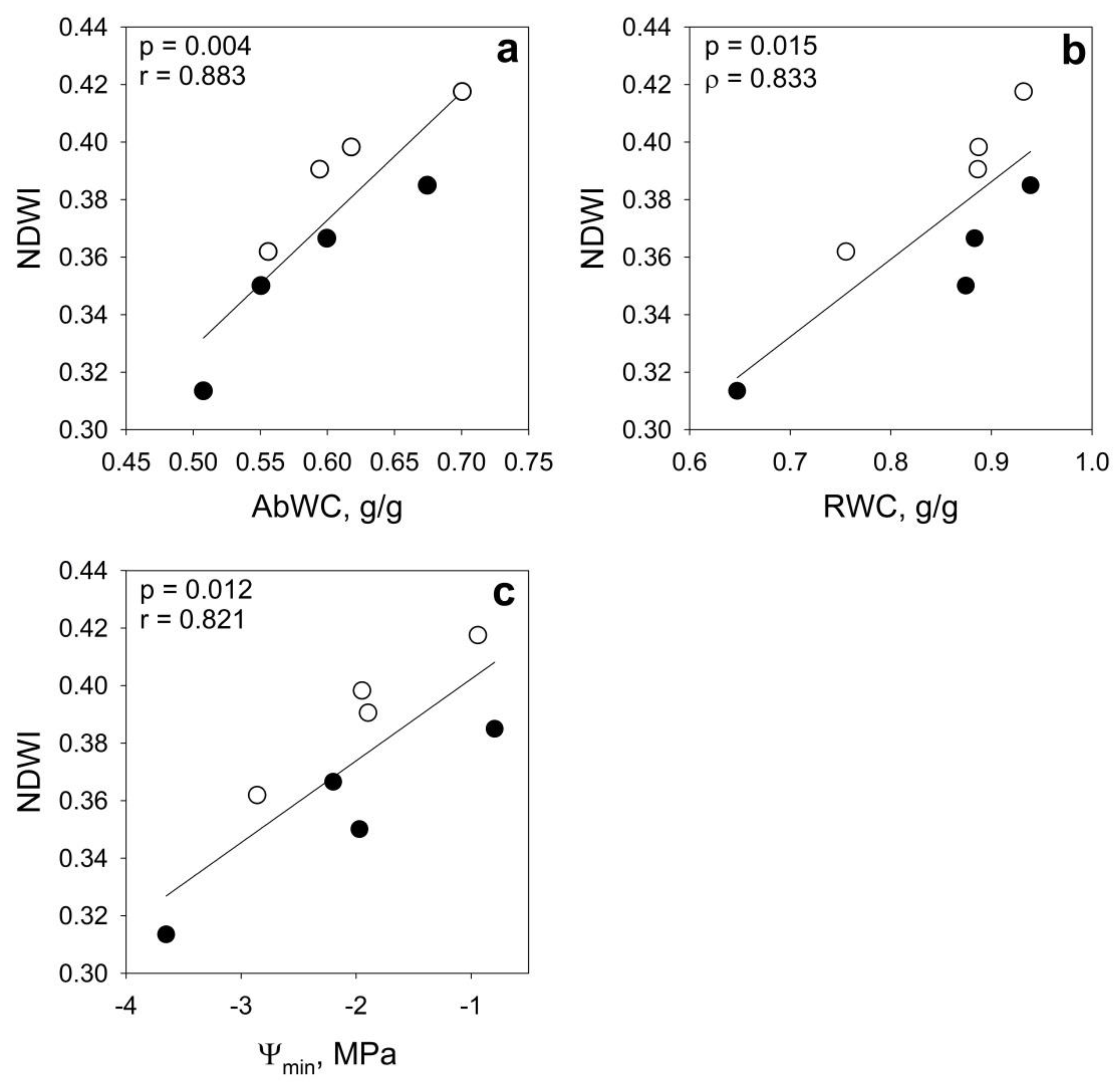
DOY	Date	Site	AbWc g/g	RWC g/g	Ψmin MPa	NDVI	NDVI 8A	NDWI	SAVI
136	May 16th	H	0.70 ± 0.03	0.93 ± 0.03	−0.94 ± 0.38	0.886 ± 0.012	0.889 ± 0.011	0.428 ± 0.016	1.333 ± 0.016
		D	0.67 ± 0.03	0.94 ± 0.03	−0.80 ± 0.34	0.870 ± 0.021	0.873 ± 0.020	0.380 ± 0.026	1.309 ± 0.029
179	June 28th	H	0.62 ± 0.02	0.89 ± 0.05	−1.95 ± 0.25	0.902 ± 0.013	0.905 ± 0.011	0.410 ± 0.013	1.358 ± 0.017
		D	0.60 ± 0.02	0.89 ± 0.04	−2.20 ± 0.17	0.880 ± 0.016	0.884 ± 0.014	0.359 ± 0.022	1.326 ± 0.022
206	July 25th	H	0.56 ± 0.02	0.76 ± 0.08	−2.86 ± 0.37	0.859 ± 0.013	0.870 ± 0.011	0.362 ± 0.018	1.305 ± 0.016
		D	0.51 ± 0.03	0.65 ± 0.12	−3.65 ± 0.29	0.826 ± 0.027	0.839 ± 0.024	0.308 ± 0.031	1.259 ± 0.036
224	August 12th	H	0.59 ± 0.03	0.89 ± 0.04	−1.90 ± 0.34	0.837 ± 0.013	0.848 ± 0.011	0.392 ± 0.019	1.272 ± 0.016
		D	0.55 ± 0.01	0.87 ± 0.05	−1.97 ± 0.43	0.816 ± 0.017	0.827 ± 0.015	0.353 ± 0.022	1.241 ± 0.022

. The most favorable plant water status was measured at the beginning of the summer season at day 136 (16 May), while minimum values of water potential and water content were measured at day 206 (25 July) (Table 1, Figure 3). The individuals growing in the H site generally had higher AbWC and Ψ_min than those growing in the D site, while RWC was not statistically different between the two sites (Figure 2). Specifically, values of AbWC were higher in the H site at days 206 and 224, while values of Ψ_min were higher only on day 206 (Figure 3).

Maximum values of NDVI, NDVI 8A, and SAVI were measured on day 178 (27 June), while minimum values were recorded at the end of the summer season (day 224, 12 August) (Table 1, Figure 4). Maximum values of NDWI were reached at the beginning of the summer season at day 136, while minimum values were reached at day 206.

Values of NDVI, NDVI_8A, and SAVI were significantly higher in the H site only on 26 July, whereas NDWI values were significantly higher in H than in D on each sampling date (Figure 4).

Pearson and Spearman correlation coefficients (r/ρ) and associated p-values (p) between the physiological parameters and remote sensing vegetation indices are listed in

Table 2. Pearson and Spearman correlation coefficients (r/ρ) for tested correlations between physiological parameters and calculated vegetation indices. * = p < 0.05; ** = p < 0.01.

		NDVI	NDVI 8A	NDWI	SAVI
AbWC	r	0.676	0.630	0.883 **	0.628
RWC	ρ	0.476	0.476	0.833 *	0.476
Ψmin	r	0.446	0.382	0.821 *	0.381

. Statistically significant correlations were only found between the NDWI and all the physiological parameters (Figure 5).

4. Discussion

Physiological parameters measured in the field and NDWI followed the same seasonal trend, reaching maximum values on 16 May and the minimum on 26 July. On the contrary, NDVI, NDVI 8A, and SAVI values followed a different pattern, with a maximum at the end of June followed by a progressive decrease (Figure 3 and Figure 4).

The absence of statistical differences between sites in terms of NDVI, NDVI 8A, and SAVI, suggests that the use of the narrow-NIR band does not improve the quality of NDVI output for the purpose of monitoring vegetation water status. Moreover, despite generally high NDVI values, this index did not saturate and the use of SAVI did not provide any additional information. On the contrary, significant differences emerged between H and D sites in terms of the NDWI trend, consistent with field-measured changes in plant water status.

Differences in terms of AbWC and Ψ_min in H and D trees did not emerge until the end of July, while RWC was always statistically similar between the two sites. The leaf turgor loss point (Ψ_tlp) of F. ornus has been reported to range between −2.0 and −3.5 MPa on a seasonal scale, with most negative values recorded at the peak of summer drought [48]. The most negative Ψ_min values recorded in this study were −2.86 and −3.65 MPa in H and D trees, respectively. Hence, our study plants experienced a severe water stress during summer 2019, but H trees remained in the positive turgor range, while D trees actually reached or even surpassed Ψ_tlp.

Significant and strong correlations were recorded between all these physiological parameters and the NDWI (Figure 5). A similar result was reported by Dennison et al. [56], which correlated NDVI and NDWI measured with moderate resolution imaging spectroradiometer (MODIS) data, with the live fuel moisture on six shrub species in 12 sites in California (USA). Their results also suggested that NDWI represents the best index for monitoring vegetation water content, as it is not affected by pigments’ absorption as in the case of NDVI.

Despite the common use of NDVI to assess water stress, based on the relation between water availability and primary production [57], the variation in water content and energetic status due to water stress cannot be highlighted using only the ρ_red and the ρ_NIR. Due to higher sensitivity to leaf water content, the use of the ρ_SWIR to calculate NDWI seems to be more relevant to assess water stress and predict drought-related impacts on vegetation physiological water status, highlighting the reliability of this index for forest monitoring in the context of increased risks of drought-induced tree die-back and mortality. According to Carter [57], since water in leaves is mainly held in the palisade and epidermal tissues, the water-absorption effect is more relevant in outlying the leaf spectral profile than the leaf structure, increasing the absorption in the 400–2500 nm wavelength range. Since variations in the visible region reflectance spectrum are driven both by leaf water content and photosynthetic pigments abundance [58], drought-stress monitoring should focus on the 1300–2500 nm region, where the absorption is mainly driven by leaf water content [57]. This supports our results, suggesting the suitability of NDWI in wide-scale drought-stress monitoring, when calibrated against field-measured physiological traits.

The better correlation of NDWI with AbWC (r = 0.883) than with RWC (ρ = 0.833) could arise by the use of TW to calculate the latter parameter. In fact, this measurement might be biased for at least two reasons: (i) The forced leaf rehydration could induce over-hydration with flooding of intercellular leaf air spaces, leading to incorrect estimation of TW; (ii) the physical interactions involved in absorbance and reflection of electromagnetic radiation are influenced by the amount of existing water, and the potential maximum water content might have no relevance at all in this specific context. Similar results have been reported by Maki et al. [59], which successfully correlated the NDWI with two drought-related variables: fuel moisture content (calculated as AbWC) and equivalent water thickness, using three deciduous woody species selected for their different drought-resistance.

Interestingly, NDWI was also strongly correlated to Ψ_min (r = 0.821). Considering that recent vegetation dynamics models have incorporated plant hydraulics as a predictor of gas exchange, primary productivity and mortality risk under drought [24,25], the possibility to detect by remote the time when plants reach critical species—specific Ψ_leaf values leading to stomatal closure or xylem embolism represents a very promising opportunity to setup forest monitoring protocols with increased physiological meaning and with great spatial and temporal resolution.

Our results provide useful insights into the possibility of monitoring forest health status on a wide scale with high temporal and spatial resolution, via calibration and conversion of poorly-defined scales of remotely sensed vegetation indices to reliable and mechanistic drought-related physiological parameters. However, caution is needed, as our correlations are based on a relatively limited number of field measurements and needs to be further validated, ideally focusing on a larger set of drought-related parameters measured on multiple species’ assemblages, also including a higher diversity of environments and forest types.

5. Conclusions

This paper provides one of the few examples of correlation between drought-stress related physiological parameters measured in the field, and satellite remotely sensed data in a forest ecosystem.

Due to the strong correlation with field-measured parameters, the normalized difference water index emerged as the best remote sensing vegetation index for monitoring vegetation water status, while the normalized difference vegetation index and the soil-adjusted vegetation index did not correlate with any physiological parameter. These results are encouraging in the view of developing a wide-scale monitoring system, especially relying on the Sentinel-2 mission, allowing free access to data with high spatial and temporal resolution from most regions of the world.