Abstract
Forest road aggregate changes due to traffic. The physical processes that cause these aggregate changes need to be understood for more effective road management that can help reduce maintenance costs and efforts, and negative environmental impacts of forest roads. This study modeled three processes that could change the particle size distribution (PSD) of forest road aggregate: crushing (breaking down the surfacing material), subgrade mixing (moving upward of fine-grained, roadbed sediment), and sweeping (migration of loose aggregate particles to the shoulder and roadside by tire action). There are two types of sweeping: sweeping-out (dislodging large-size particles from tire tracks) and sweeping-in (accumulating large-size particles near the roadside and shoulder). Our study modeled the expected traffic-induced processes based on theoretical concepts and literature to examine how these processes change forest road aggregate PSD. Then the modeled results were compared with the observed PSDs from cross-sectional locations where traffic-induced processes likely occurred. Based on these comparisons, we enhanced the modeling and inferred how much the crushing, subgrade mixing, and sweeping-in processes changed the PSDs, but could not infer the sweeping-out process due to the difficulty in separating the sweeping-out from crushing. This study demonstrates that the traffic-induced processes could be modeled and quantified using the following assumptions: crushing was estimated by assuming a half logarithmic normal distribution with a mean of the crushed particle diameter and higher crushing rates for large-size particles; subgrade mixing was estimated by assuming the move-in of fine-grained subgrade soils from the road bed; and sweeping-in was estimated by assuming the move-in of large-size particles with a logarithmic normal distribution. Our modeling approach can offer insights on how traffic-induced processes affect road aggregate under various road and traffic conditions. This information can be useful in developing cost-effective road maintenance strategies and implementation plans.
1. Introduction
Forest roads are essential for forest management, providing access for timber harvesting and recreation. Most forest roads are unpaved and are constructed with either aggregate or native soil surface [1,2,3,4]. Aggregate is a broad category of coarse- to medium-grained material used in road construction [5]. It is used for surfacing low-volume forest roads to lessen wheel load stress delivered to the subgrade below, reduce maintenance costs, and improve driving comfort, as compared to native surface roads [6]. Aggregate surface roads have higher hydraulic conductivity than native surface roads, thus helping to reduce soil erosion from forest roads [7,8,9]. However, the road aggregate layer deteriorates due to traffic and weather, and, therefore, requires regular maintenance [10]. Additional road maintenance is needed when aggregate material is lost from the road running surface or when the road is deformed (e.g., forming a rut or pothole) due to vehicle traffic. A better understanding of the processes by which traffic changes aggregate properties can help develop preventive and cost-effective road maintenance strategies.
There are several physical processes associated with vehicle traffic that ultimately change forest road aggregate conditions. Rhee et al. [11] reviewed and classified three such traffic-induced processes. The first process is “crushing” [12,13,14] which is defined as the “breakdown of the surfacing material” [7,15], “powdering by traffic”, “particle attrition”, “abrasion” [5,14,16], and “the mechanical degradation of surface aggregate under traffic loading” [17]. The second process is “subgrade mixing” [17] defined as the “forcing upward of fine-grained sediment from the roadbed as traffic pushes the surfacing gravels into the bed” [7,15], “piping” (enabling roadbed soil to pipe through the road prism) [9], “pressing larger particles down through a matrix of fine sediment” [12], “churning” [13], “fine materials move through the pore spaces to the surface” [18], and “pumping of fine particles onto the surface” [16]. The third process is “sweeping”. This process migrates loose aggregate particles to the shoulder of the road and roadside through tire action [11,19]. There are two types of sweeping: sweeping-out (dislodging large-size particles from tire tracks) and sweeping-in (accumulating large-size particles near the roadside and shoulder) [11].
Traffic-induced processes that affect road aggregates are difficult to investigate directly because they can be affected by many factors, such as aggregate strength and particle size [17,20,21], tire pressure [22,23], road slope [9,16,24], road type [9], road conditions [14,19,24], traffic use [9,14,15], and nearby tree root systems [25]. Instead, Rhee et al. [11] used the particle size distribution (PSD) of road aggregate to infer the traffic-induced processes. Particle size distribution is an important engineering property of road aggregates and mineral soil, and is frequently used to assess the appropriateness of the aggregate or soil as a road construction material. A PSD is composed of particle size fractions (PSFs) and is represented as a cumulative frequency diagram that has the logarithmic scale of particle size on the x-axis and percent passing on the y-axis.
In-depth knowledge of the three traffic-induced processes can help to better understand how traffic changes forest road aggregate. Previous work by Rhee et al. [11] compared the PSDs of forest road aggregate from different cross-sectional locations and traffic uses in the Clearwater National Forest in Idaho, USA, and inferred where and how crushing, subgrade mixing, and sweeping occurred. However, there have been no studies that model and quantify the traffic-induced processes, and assess their effects on forest road aggregate.
This study aimed at understanding how traffic changes the physical properties of forest road aggregate. More specifically, the objectives were to (1) model and quantify the traffic-induced processes of crushing, subgrade mixing, and sweeping and (2) infer how much each process changes forest road aggregate PSDs by comparing modeled PSDs with field observations from the previous study by Rhee et al. [11].
2. Materials and Methods
We used three steps to understand traffic-induced processes that alter forest road aggregate PSDs (Figure 1). First, we modeled the expected traffic-induced processes by considering a control volume of forest road aggregate and how each process changes its PSD. Since these processes were not well documented or investigated, we used rock strength and failure behavior from the literature and assumed parameter values for the model development. Second, we compared the modeled results (i.e., expected observation) with PSDs measured from forest road aggregate samples collected from different cross-sectional locations where the traffic-induced processes were likely to have occurred. Third, we inferred how the modeled processes changed the PSDs based on the comparisons made in the second step.
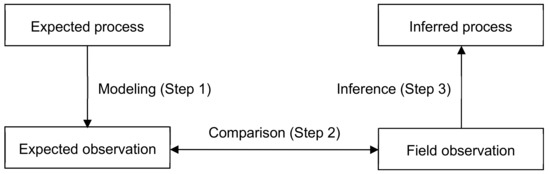
Figure 1.
Diagram of inferring traffic-induced processes from field observations.
Observed PSDs from the forest road aggregate samples that were collected from nine cross-sectional locations on three different roads were used in the model [11]. The nine cross-sectional locations were composed of three vertical layers (upper (U), middle (M), and bottom (B)) and three horizontal locations (tire track (T), shoulder (S), and in-between (I; a half-way point between the tire track and the shoulder)) (Figure 2). After the three roads were constructed, they had different traffic uses: no (N; only administrative traffic), light (L; no log-haul), and heavy (H; log-haul from June to September). The no traffic road received about 20 passes/year of occasional administrative traffic. The light traffic road received recreational traffic by trucks and automobiles, in addition to the occasional administrative traffic, and was seasonally closed. The heavy traffic road received about 375 round trips of a standard logging truck and a round trip of logging equipment, such as tracked linkbelt yarder, high track caterpillar, and excavator, in addition to about 40 passes/week of administrative traffic (pickup trucks). We used the abbreviations of the vertical layer, horizontal location, and traffic use to specify the cross-sectional location and traffic use where the forest road aggregate samples were collected for the observed PSDs.
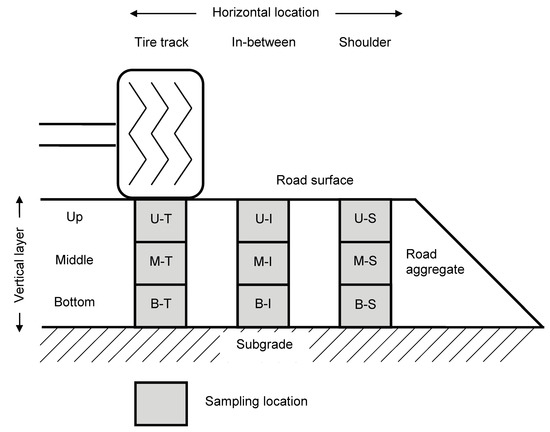
Figure 2.
Forest road cross-sectional locations of observed particle size distributions (PSDs). The abbreviations indicate vertical and horizontal locations of observed PSDs. U: Upper; M: Middle; B: Bottom; T: Tire track; S: Shoulder; I: In-between [11].
This study compared the modeled results with the observed PSDs of the forest road aggregate as changed by the traffic-induced processes and with the original PSD obtained from undisturbed aggregate samples from the quarry [11]. For this current effort to model traffic-induced processes, we used the PSD of 12 aggregate samples taken from the previous quarry samples at the time of road construction. The quarry PSD was analyzed by the Palouse Ranger District, Clearwater National Forest, USDA Forest Service. Their analysis used seven sieves for PSD (38.1 mm (1.5 inch), 19.0 mm (3/4 inch), 12.7 mm (1/2 inch), 4.76 mm (US standard sieve No. 4), 2.38 mm (No. 8), 0.595 mm (No. 30), and 0.074 mm (No. 200)). The same seven sieves were used for modeled PSDs. However, 13 sieve sizes were used to determine the observed PSDs (25.4 mm (1 inch), 19.0 mm, 12.7 mm, 9.51 mm (3/8 inch), 6.35 mm (1/4 inch), 4.76 mm, 3.36 mm (No. 6), 2.00 mm (No. 10), 1.00 mm (No. 18), 0.420 mm (No. 40), 0.250 mm (No. 60), 0.149 mm (No. 100), and 0.074 mm). We conducted point-to-point comparisons of the modeled and observed values for the four sieve sizes in common between the two analyses (19.0 mm, 12.7 mm, 4.76 mm, and 0.074 mm). For comparisons of the values for the sieve sizes not in common, linear interpolation was used to estimate the observed PSDs for the sieves 2.38 mm (interpolated from 3.36 mm and 2.00 mm sieves) and 0.595 mm (interpolated from 1.00 mm and 0.420 mm sieves) that were used for the modeled PSDs, but not used for the observed PSDs. The linear interpolations were conducted in logarithmic scale (x-axis) and percent passing (y-axis). Finally, we compared the observed and interpolated values with the modeled ones. In addition, the 38.1 mm sieve was used for modeled PSDs, but not for the observed PSDs. There were no particles greater than 38.1 mm in the aggregate samples from the quarry, and therefore it was used for both the modeled and observed PSDs. Each PSD consisted of PSFs from each particle size class. Therefore, we compared the PSFs of the modeled and observed PSDs. Since seven sieves were used for the modeled PSDs, we compared eight PSFs (the seven sieve size classes and <0.074 mm) of the modeled and observed PSDs.
Our initial models, in comparison with the observed PSDs, focused on understanding the trend in the effects of the traffic-induced processes on a forest road aggregate PSD, rather than matching the modeled PSDs to the observed PSDs. After understanding the trend from our initial models, we modified the models to fit the observed PSDs. The optimized fit for the modified model was obtained by minimizing the sum of the differences between the modeled and observed PSF values for individual sieve sizes, while adjusting model parameter values; i.e., minimizing the following objective function modified from Foltz et al. [26]:
where Objsim is the objective function for the model, n is the total number of sieve size classes used for PSD (i.e., n = 8), PSFobs(i) is the observed PSF for the ith sieve, and PSFsim(i) is the modeled PSF for the ith sieve. For this task, we used an optimization tool called What’s Best! [27]. Modified models with the optimized model fits were used to infer the actual processes that occurred on the forest road aggregate PSDs from Rhee et al. [11].
3. Results and Discussion
3.1. Modeling the Traffic-Induced Processes
3.1.1. Crushing
In a control volume of forest road aggregate, there is no material-in or material-out and the only aggregate breakdown occurs within the control volume in the process of crushing (Table 1). Modeling the crushing process consists of crushing the initial PSFs and generating crushed fragments. Since rock (aggregate) strength decreases with increasing particle size [28,29,30], we assumed that large-size particles were more likely crushed than small-size particles (≤2.38 mm). Therefore, we used arbitrary crushing rates of −0.80, −0.40, and −0.20 for the large-size particles (19.0, 12.7, and 4.76 mm diameters) for the model, resulting in a change of 22 percentage points by crushing the initial PSFs (hereafter called “the 22% crushing”). For the crushed fragments, we assumed the fragment size distribution could be described by a truncated logarithmic normal distribution by mass [31,32,33].

Table 1.
Modeling traffic-induced processes and their effects on forest road aggregate particle size distributions.
A truncated logarithmic normal distribution is described using three parameters: the mean (µ), standard deviation (σ), and truncated point (t). Then, the rate of the crushed fragments in mass, of which particle sizes were between j and k, from larger particles with sieve size class t (Rcf(µ, σ, t, j, k)) was found:
Model parameters for crushing were crushing rates (Rcf), µ, σ, and t. For the truncated logarithmic normal distribution, we used arbitrary parameter values; i.e., a half-logarithmic normal distribution with a mean of the crushed particle diameter (µ = t) and a standard deviation of 10.0 mm. Then, the denominator in Equation (2) became 0.5. This truncated logarithmic normal distribution was used for the crushed fragment size distribution and applied to all particle size diameters. This assumed all the aggregate material had the same properties, since it was from the same quarry. Based on these assumptions, crushing changed the PSD from the quarry to a finer PSD (Figure 3A). Details on modeling the 22% crushing are shown in Table S1. When crushing occurred, the portions of small-size particles (≤2.38 mm) increased, but most of the changes in PSD occurred in the medium-size particles (2.38 to 12.7 mm), causing the PSD curve to shift toward the upper right-hand corner (Table 1; Figure 3A). Since stress on the road aggregate is from vehicle tires, crushing is more likely to occur first within the tire track on the surface, than down in the aggregate (Table 1).
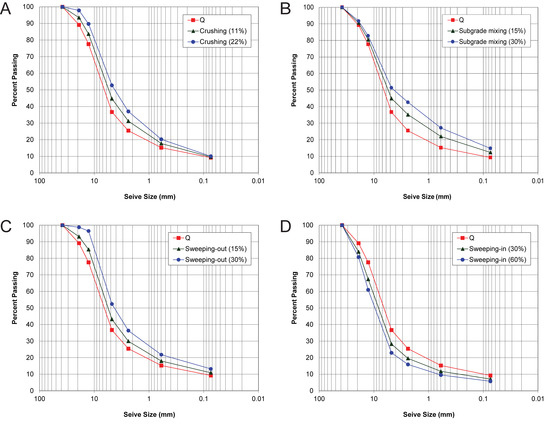
Figure 3.
Initial models of how the traffic-induced processes change the particle size distribution from the quarry (Q): (A) Crushing, (B) subgrade mixing, (C) sweeping-out, and (D) sweeping-in. Details on the modeled particle size distributions are shown in Tables S1–S3. A set of the models that used a half of the model parameter values are also plotted.
3.1.2. Subgrade Mixing
Using a control volume of forest road aggregate, there is no breakdown of material or no material-out within the control volume, but fine-grained road bed material moves into the control volume by subgrade mixing (Table 1). For the move-in of fine-grained road bed material, we assumed that the subgrade mixing process added an arbitrary 10 percentage points to the three smallest particle-size classes (0.595, 0.074, and less than 0.074 mm sieve sizes), resulting in an increase of 30 percentage points in this material (hereafter called “the 30% subgrade mixing”).
Model parameters for subgrade mixing were percentage points for addition to small particle size classes. Since fine-grained particles moved in, subgrade mixing changed the PSD from the quarry to a finer PSD (Figure 3B). Details on modeling the 30% subgrade mixing are shown in Table S2. When subgrade mixing occurred, the portions of small-size particles increased; most of the changes in the PSD occurred in the medium and small-size sieves (0.595 to 4.76 mm); and the PSD curve shifted toward the upper right-hand corner (Table 1; Figure 3B). Subgrade mixing occurs first at the boundary between the aggregate and road bed (subgrade) material, then in the upper aggregate (Table 1).
3.1.3. Sweeping
As noted earlier, there are two types of the sweeping: sweeping-out and sweeping-in. Sweeping-out occurs near the tire track where vehicle tires dislodge loose, large-size particles toward the outside of a road. In a control volume of forest road aggregate, there is no breakdown of material or no material-in, but large-size particles are removed from the control volume (Table 1). For the removal of large-size particles, we assumed that the sweeping-out process subtracted an arbitrary 10 percentage points from the three largest particle-size classes (19.0, 12.7, and 4.76 mm sieve sizes), resulting in a decrease of 30 percentage points from the large particle-size classes (hereafter called “the 30% sweeping-out”). Therefore, the model parameters for sweeping-out were percentage points for subtraction from large particle-size classes. Due to the loss of large-size particles, sweeping-out changed the PSD from the quarry to a finer PSD (Figure 3C). Details on modeling the 30% sweeping-out are shown in Table S3. When sweeping-out occurred, the portions of large-size particles decreased, with most PSD changes occurring in the large and medium-size sieves (2.38 to 19.0 mm). The PSD curve shifted toward the upper right-hand corner (Table 1; Figure 3C).
Unlike sweeping-out, sweeping-in occurs near the shoulder, where the dislodged loose, large-size particles accumulate. In a control volume of forest road aggregate, there is no breakdown of material or no material-out within the control volume, but large-size particles are moved into the control volume (Table 1). For this model, we assumed that sweeping-in added an arbitrary 20 percentage points to each of the three largest particle-size classes (19.0, 12.7, and 4.76 mm sieve sizes), resulting in an increase of 60 percentage points in these particle-size classes (hereafter called “the 60% sweeping-in”). Model parameters for sweeping-in were percentage points for addition to large particle-size classes. Due to the addition of the large-size particles, the sweeping-in process changed the PSD from the quarry to a coarser PSD (Figure 3D). Details on modeling the 60% sweeping-in are shown in Table S3. When sweeping-in occurred, the proportion of large-size particles increased, predominantly in the medium-size sieves (2.38 to 12.7 mm). In this model, the PSD curve shifted toward the bottom left-hand corner, with more changes in medium-size sieves and less changes in large and small-size sieves (Table 1; Figure 3D). The sweeping-in process is not likely to occur simultaneously with crushing or subgrade mixing process, because sweeping-in occurs outside the tire track, whereas crushing or subgrade mixing occurs at the tire track. If sweeping-in occurs, there is also likely sweeping-out, and vice versa. Since both crushing and sweeping-out can occur at the tire track, sweeping can be determined largely by the existence of sweeping-in at the shoulder.
3.2. Comparison of the Model Results with Observed Particle Size Distributions
Our study compared crushing, subgrade mixing, and sweeping-in model results with observed PDSs. Sweeping-out and crushing can occur at the tire track at the same time, and result in a similar PSD curve. Modeling crushing at a change of 11% (Figure 3A) and sweeping-out at a change of 15% (Figure 3C) are difficult to separate. Therefore, we did not compare the sweeping-out model results with observed PSDs.
Furthermore, we assumed that crushing was the dominant process occurring on the road surface. Abrasion may be one other process that changes PSD, but we were unable to quantify it. However, if abrasion changed the PSD curve differently from crushing on the observed forest road, we would have found different PSDs at U–H (from the road surface to 33.3 mm depth) compared to the PSDs at M–H, B–T–H, and B–I–H (below 33.3 mm depth) where only crushing occurred, as reported by Rhee et al. [11]. Therefore, this indicates that either abrasion changes the PSD curve in a similar manner to crushing or that crushing is the dominant process. However, abrasion may be the dominant process on native surface roads where no large-size particles (aggregate) are available. On native surfaces, stress from traffic (the torque at the contact area between the tire and road surface) [14] likely abrades or detaches fine sediment, because much less energy is needed for abrasion or detachment than for crushing of fine-grained soil particles.
3.2.1. Comparison Using Initial Models
We compared the model results of the 22% crushing with the PSD at U–I–H. Some differences were found for modeled PSFs in the sieve sizes of 4.76 mm and equal to or less than 0.595 mm, resulting in an objective function value of 17.95 (Table S1). The PSD is plotted as a cumulative frequency, and some individual PSF differences might be offset in a PSD curve. Therefore, differences in PSFs are not necessarily found in the PSD curve. We found small differences, mainly in the medium-size sieves (<12.7 mm and >0.595 mm) in which PSD from modeling the 22% crushing was finer than the observed PSD (Figure 4A).
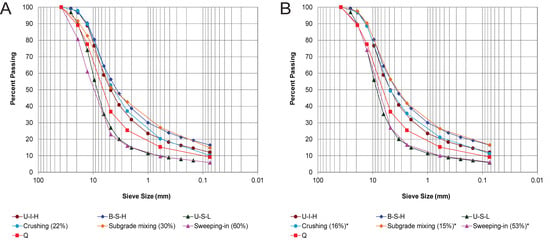
Figure 4.
Comparison of the observed particle-size distributions from Rhee et al. [11] with the models of the traffic-induced processes using (A) the selected particle size distributions from Figure 4 that are from the initial models and (B) the particle size distributions from the modified models to fit the observed particle size distributions. The particle size distributions at U–I–H (up vertical layer, in-between horizontal location, and heavy traffic use), B–S–H (bottom vertical layer, shoulder horizontal location, and heavy traffic use), and U–S–L (up vertical layer, shoulder horizontal location, and light traffic use) were caused by crushing, subgrade mixing, and sweeping-in processes. The particle size distribution from the quarry (Q) is also plotted. The asterisk (*) indicates the modified models to fit the observed particle size distributions. Details on the particle size distributions for the modified models are shown in Tables S4–S6.
When we compared the model results of the 30% subgrade mixing with the PSD at B–S–H, large differences were found in the modeled PSFs in the sieve sizes of 19.0 and 2.38 mm, which resulted in an objective function value of 83.52 (Table S2). We also found large differences in large-size sieves and some differences in medium-size sieves of the modeled PSD (Figure 4A). The modeled PSD of the 30% subgrade mixing was coarser than the observed PSD in sieves greater than 2.38 mm and equal to or less than 0.074 mm. However, it was finer than the observed PSD in the sieves equal to or less than 2.38 mm and greater than 0.074 mm.
Comparison of the model results of the 60% sweeping-in with the PSD at U–S–L indicated large differences for the modeled PSFs in the sieve sizes of 19.0 and 4.76 mm, and some differences in the sieve sizes of 12.7 and 2.38 mm. This resulted in an objective function value of 191.70 (Table S3). We detected large differences in large-size sieves (≥12.7 mm), some differences in medium-size sieves (<12.7 mm and >2.38 mm), and no differences in small-size sieves (≤2.38 mm) of the modeled PSD (Figure 4A). Modeled PSD of the 60% sweeping-in was coarser than observed PSD.
3.2.2. Modified Models to Fit Observed Particle Size Distributions
Initial model results showed that the 22% crushing made the PSD finer than the observed PSD. Therefore, a value of less than 22% crushing should be used for the model. Modified crushing rates should increase as particle size increases, because large-size particles are more likely to break [28,29,30,34]. We used the same assumption for the modified model as for the initial model; small-size particles (≤2.38 mm) were not crushed. For our initial model we assumed the truncated logarithmic normal distribution by mass for the crushed fragments [31,32,33], and used the arbitrary parameter values: µ = t and σ = 10.0 mm. Assuming the same half-logarithmic normal distribution with a mean of the crushed particle diameter (µ = t), we found a modified model to fit the observed PSD, which had crushing rates of −0.73, −0.33, and −0.11 for the sieve size of 19.0, 12.7, and 4.76 mm, resulting in a total of 16 percentage points by crushing with a standard deviation of 25.6 mm for the logarithmic normal distribution (Table S4). The value of the objective function (Equation (1)) was 4.20. This change resulted in the modeled PSD more closely matching the observed PSD (Figure 4B).
The initial model assumed that the 30% subgrade mixing added 10 percentage points to each of 0.595, 0.074, and less than 0.074 mm sieve sizes. For the modified model we included another model parameter (percentage points for addition) for the sieve size of 2.38 mm to model a more accurate subgrade mixing process. The initial simulation of the 30% subgrade mixing changed the PSD from the quarry to a complicated PSD (i.e., making the modeled PSD coarser and finer than the observed PSD depending on sieve size class). This made us consider another factor other than adding percentage points for the small-size sieves (≤2.38 mm) for the modified model. Rhee et al. [11] observed that the PSDs at all cross-sectional locations on H were uniform due to the crushing, except for the PSD at B–S–H where subgrade mixing occurred. Therefore, it was reasonable to assume that both crushing and subgrade mixing occurred at B–S–H. If this reasoning is correct, then the PSD where crushing already occurred (U–I–H), not the PSD from the quarry, should have been used to model subgrade mixing. We modified the subgrade mixing models using both PSDs at U–I–H and from the quarry and found the parameter values (the percentage points for addition) for the sieve sizes of 2.38, 0.595, 0.074, and less than 0.074 mm minimized the differences between the modeled and observed PSF values (Table S5). When using the PSD from the quarry aggregate, we could not modify the model to result in a reasonable fit to the observed PSD, especially considering that the best objective function value was 44.55. However, using the PSD at U–I–H resulted in a good fit of the modified model (Figure 4B), and had a function value of 1.48. This modified model indicated that both crushing and subgrade mixing occurred at B–S–H.
The initial model assumed that the 60% sweeping-in would add 20 percentage points to each of 19.0, 12.7, and 4.76 mm sieve sizes. Our initial model used only the three largest sieves to make the sweeping-in process simple. For the modified model we included another model parameter (percentage points for addition) for the sieve size of 2.38 mm to model a more accurate sweeping-in process. Initially, we determined that the 60% sweeping-in made the PSD coarser than the observed PSD. Therefore, a value of less than 60% sweeping-in should be used for the model. The modified model, which used sieve sizes of 19.0, 12.7, 4.76, and 2.38 mm, minimized the differences between the modeled and observed PSF values (Table S6). If we convert the percentage points added for this model to percent values, they reasonably matched the logarithmic normal distribution with a mean of 10.0 mm and a standard deviation of 1.70 mm (Table S7). The objective function value between the percent values and the logarithmic normal distribution was 10.11. It is not clear how to explain the matching of the parameter values with the logarithmic normal distribution.
3.3. Soil Rheological Models with Traffic-Induced Processes
Soil rheological models (Figure 5) [35,36] can be used to explain traffic-induced processes. For example, crushing near the tire track and road surface (U–T and U–I) on light traffic use (L), and at all cross-sectional locations on heavy traffic use (H) has been inferred [11]. They also inferred subgrade mixing at B–S–H and sweeping-in at U–S–L. In addition, Rhee et al. [11] also found a certain PSD limit (i.e., maximum crushing capacity), close to the PSD curve at U–I–H, where the traffic induced stress cannot crush road aggregate any more. This PSD limit can be considered as the optimum compaction by crushing under a given aggregate property and road condition. When the aggregate reaches this limit, stress from traffic does not change the PSD anymore and is delivered down to the aggregate or subgrade, thus enabling more crushing or subgrade mixing to continue.
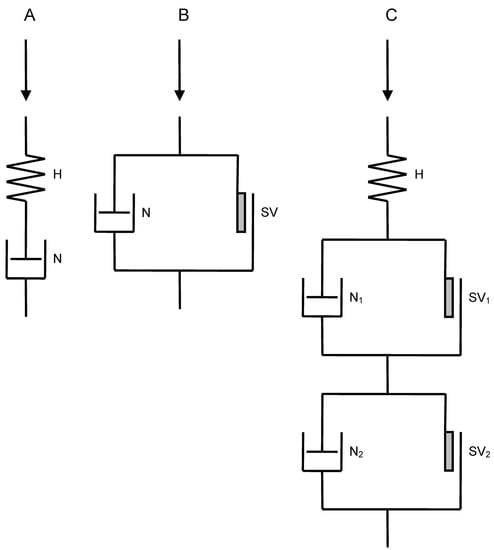
Figure 5.
The structural rheological models: (A) The Maxwell’s body that consists of the Hookean spring (H) and the Newtonian dashpot (N), connected in series; (B) the Bingham’s body that consists of the friction block (i.e., Saint-Venant’s body (SV)) and the Newtonian dashpot, connected in parallel; and (C) a combination of the Hookean spring and two Bingham’s bodies, connected in series [35,36]. The arrows indicate pressure.
The PSD limit can also be explained using soil rheological models that consist of different elements, such as the Hookean spring, Newtonian dashpot, and friction block (Saint-Venant body; SV) that are connected in series or parallel (Figure 5) [35,36]. The Hookean spring represents elasticity; the Newtonian dashpot (i.e., a piston moving in a cylinder containing viscous liquid) represents viscosity, and the friction block represents plasticity, allowing no motion until stress exceeds a certain resistance [35,36]. The crushing process can be modeled using a simple visco-elastic body, such as Maxwell’s body that consists of the Hookean spring and the Newtonian dashpot elements connected in series (Figure 5A). In this model, we consider that some traffic stress altered the PSDs by crushing up to maximum capacity (completely pushed dashpot) [11]. The subgrade mixing process can be modeled using a visco-plastic body, such as the Bingham’s body, by using the Newtonian dashpot and the friction block elements connected in parallel (Figure 5B). This models stress from light traffic that does not exceed the resistance of the friction block and, therefore, cannot change PSDs by subgrade mixing. Stress from heavy traffic is enough to exceed the frictional resistance and changes the PSD by crushing. Soil rheological models that explain both crushing and subgrade mixing processes are more complex and have more elements connected in series and parallel. For example, a model that consists of the Hookean spring and two Bingham’s bodies connected in series (Figure 5C) can be used to examine forest road aggregate and subgrade. In this model, the spring element represents elasticity in the aggregate and subgrade. In the first Bingham’s body the PSD changes by crushing, and in the second it changes by subgrade mixing. Ultimately, this model can explain both crushing and subgrade mixing processes found in Rhee et al. [11]. When light traffic passes, it provides stress greater than the frictional resistance of SV1, but less than SV2. Light traffic only causes crushing and changes the PSDs up to a certain limit (completely pushed dashpot), but does not cause subgrade mixing. When heavy traffic passes, it provides stress greater than frictional resistance of both SV1 and SV2. Heavy traffic causes crushing first, then changes the PSDs to the limit because the frictional resistance of SV1 is less than SV2. Finally, it changes the PSDs by subgrade mixing. The rheological elements in the model are likely affected by many factors, such as the aggregate and subgrade physical properties (depth, particle size, shape, and strength) and road conditions (moisture content and compaction). For example, soft, weak subgrade, and saturated (wet) conditions during traffic can result in mixing subgrade with the aggregate particles more easily. Subsequently, the saturated and softened subgrade soils will be pumped upward [37,38]. In such a case, the frictional resistance of SV1 is greater than SV2 in the model, and the subgrade mixing can occur before crushing.
3.4. Sediment Production from the Traffic-Induced Processes
Both crushing and subgrade mixing resulted in more fine material in the PSD, but in different shapes. Changes in PSD do not necessarily increase sediment production from forest roads and sediment delivery to streams. The fine particle size classes of sediment eroded from forest road aggregate are measured as: <0.02 mm [39], <0.063 mm [40], and suspended sediment [14,41]. Particle size of sediment delivered to stream is considered very fine (<0.004 mm) [9,42]. In this study, PSF less than 0.074 mm sieve size was crucial to understanding sediment production from forest roads. Comparing the observed PSFs less than 0.074 mm sieve size shows that 2.76% of fine sediment (<0.074 mm) was increased after the crushing (Table S4) and 4.52% was increased after the subgrade mixing (Table S5). Even if fine-grained sediment from the road bed did not reach the road surface, the subgrade mixing can potentially produce 63.8% more fine sediment than crushing based on observations from Rhee et al. [11].
4. Conclusions
This study contributes to understanding traffic-induced processes that change the physical properties of forest road aggregate. We modeled and quantified crushing, subgrade mixing, and sweeping-in processes, and inferred how much they changed PSDs of forest road aggregate. We could not infer how much the sweeping-out process changed PSD due to the difficulty in separating sweeping-out from crushing. This study shows that process modeling could be useful for understanding traffic effects on the physical properties of forest road aggregate.
After the initial model development, we modified the models to fit the observed PSDs and found the assumptions and model parameter values for an optimized fit. Our study demonstrates that traffic-induced processes could be modeled using appropriate assumptions and modeling approaches. Crushing can be modeled by assuming a half-logarithmic normal distribution with a mean of the crushed particle diameter and higher crushing rates for large-size particles. Subgrade mixing can be modeled by assuming the move-in of fine-grained subgrade soils from the road bed. Sweeping-in can be modeled by assuming the move-in of large-size particles with a logarithmic normal distribution. Future study is needed to further investigate why the swept-in, large-size particles had a logarithmic normal distribution.
This approach can be used to understand and infer processes in other regions with different geology, aggregate, subgrade properties, traffic, and road conditions. Our modeling approach can offer insights on how traffic-induced processes affect aggregate changes under various road and traffic conditions. This information can be certainly useful in developing cost-effective road maintenance strategies and implementation plans. For example, by understanding how road aggregate from a given quarry will change with road use, forest managers would be able to know if they should strengthen the surface material (e.g., surface stabilization) to reduce crushing, strengthen the subgrade (e.g., geotextile reinforcement) to minimize subgrade mixing, or recycle large aggregate material on the shoulder and roadside for road resurfacing to move aggregate that has been swept out. In addition, the ability to predict aggregate changes and its causes in a spatial context provide opportunity for precise prescription of treatments and mitigation of negative environmental impacts of forest roads, such as sediment production.
Supplementary Materials
The following are available online at https://www.mdpi.com/1999-4907/10/9/769/s1; Table S1: Details on an example of the particle size fractions modeled for crushing process; Table S2: Details on an example of the particle size fractions modeled for subgrade mixing process; Table S3: Details on an example of the particle size fractions modeled for sweeping process; Table S4: Details on the particle size fractions that are fitted to the particle size distribution result for crushing process; Table S5: Details on the particle size fractions that are fitted to the particle size distribution results for subgrade mixing process; Table S6: Details on the particle size fractions that are fitted to the particle size distribution results for sweeping-in process; and Table S7: Comparison of the modified model parameter values and the logarithmic normal distribution for sweeping-in process.
Author Contributions
H.R. and J.F. conceived and designed the modeling approach; H.R. performed the modeling and quantifying the processes; H.R. and W.C. analyzed the data; and H.R. and D.P.-D. wrote the paper.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank Randy Foltz (retired) at the Rocky Mountain Research Station, USDA Forest Service for his guidance in conceiving and designing the modeling approach.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Coghlan, G.; Sowa, R. National Forest Road System and Use; US Department of Agriculture, Forest Service, Engineering Staff: Washington, DC, USA, 1998.
- USDA Forest Service Road Management Website. Available online: https://www.fs.fed.us/eng/road_mgt/index.shtml (accessed on 1 July 2019).
- Bolander, P.; Marocco, D.; Kennedy, R. Earth and Aggregate Surfacing Design Guide for Low Volume Roads; Engineering Staff EM-7170-16; US Department of Agriculture, Forest Service: Washington, DC, USA, 1996; p. 24.
- Turner, S.K.; Hutchinson, K. Forest Service Specifications for Construction of Roads and Bridges, revised ed.; Engineering Staff EM-7720-100; US Department of Agriculture, Forest Service: Washington, DC, USA, 1996; pp. 495–513.
- Wikipedia. Construction Aggregate. Available online: https://en.wikipedia.org/wiki/Construction_aggregate (accessed on 1 July 2019).
- Thompson, M.; Sessions, J. Optimal policies for aggregate recycling from decommissioned forest roads. Environ. Manag. 2008, 42, 297–309. [Google Scholar] [CrossRef] [PubMed]
- Swift, L.W. Gravel and grass surfacing reduces soil loss from mountain roads. For. Sci. 1984, 30, 657–670. [Google Scholar]
- Kochenderfer, J.N.; Helvey, J.D. Using gravel to reduce soil losses from minimum-standard forest roads. J. Soil Water Conserv. 1987, 42, 46–50. [Google Scholar]
- Bilby, R.E.; Sullivan, K.; Duncan, S.H. The generation and fate of road-surface sediment in forested watershed in southwestern Washington. For. Sci. 1989, 35, 453–468. [Google Scholar]
- Larcombe, G. Forest Roading Manual; Liro Forestry Solutions: Rotorua, New Zealand, 1999; pp. 168–173, 284. [Google Scholar]
- Rhee, H.; Fridley, J.L.; Page-Dumroese, D.S. Traffic-induced changes and processes in forest road aggregate particle-size distributions. Forests 2018, 9, 181. [Google Scholar] [CrossRef]
- Luce, C.H.; Black, T.A. Effects of traffic and ditch maintenance on forest road sediment production. In Proceedings of the Seventh Federal Interagency Sedimentation Conference, Reno, NV, USA, 25–29 March 2001; Subcommittee on Sedimentation: Washington, DC, USA, 2001; pp. V67–V74. [Google Scholar]
- Ziegler, A.D.; Sutherland, R.A.; Giambelluca, T.W. Interstorm surface preparation and sediment detachment by vehicle traffic on unpaved mountain roads. Earth Surf. Proc. Landf. 2001, 26, 235–250. [Google Scholar] [CrossRef]
- Sheridan, G.J.; Noske, P.J.; Whipp, R.K.; Wijesinghe, N. The effect of truck traffic and road water content on sediment delivery from unpaved forest roads. Hydrol. Process. 2006, 20, 1683–1699. [Google Scholar] [CrossRef]
- Reid, L.M.; Dunne, T. Sediment production from forest road surfaces. Water Resour. Res. 1984, 20, 1753–1761. [Google Scholar] [CrossRef]
- Ramos-Scharrón, C.E.; MacDonald, L.H. Measurement and prediction of sediment production from unpaved roads, St John, US Virgin Islands. Earth Surf. Proc. Landf. 2005, 30, 1283–1304. [Google Scholar] [CrossRef]
- Toman, E.M.; Skaugset, A.E. Reducing sediment production from forest roads during wet-weather hauling. Transp. Res. Rec. 2011, 2203, 13–19. [Google Scholar] [CrossRef]
- Foltz, R.B. Environmental impacts of forest roads: An overview of the state of the knowledge. In Proceedings of the Second International Forest Engineering Conference, Växjö, Sweden, 12–15 May 2003; Wide, M.I., Baryd, B., Eds.; Skogforsk: Uppsala, Sweden, 2003; pp. 121–128. [Google Scholar]
- Foltz, R.B.; Evans, G.L.; Truebe, M. Relationship of forest road aggregate test properties to sediment production. In Proceedings of the Conference on Watershed Management and Operation Management 2000, Fort Collins, CO, USA, 20–24 June 2000; Flug, M., Donald, F., Watkins, D.W., Eds.; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2000. [Google Scholar]
- Foltz, R.B.; Truebe, M. Effect of aggregate quality on sediment production from a forest road. In Proceedings of the Sixth International Conference on Low-Volume Roads, Minneapolis, MN, USA, 25–29 June 1995; National Academy Press: Washington, DC, USA, 1995; pp. 49–57. [Google Scholar]
- Foltz, R.B.; Truebe, M. Locally available aggregate and sediment production. Transp. Res. Rec. 2003, 1819, 185–193. [Google Scholar] [CrossRef]
- Foltz, R.B.; Burroughs, E.R. A test of normal tire pressure and reduced tire pressure on forest roads: Sedimentation effects. In Forestry and Environment Engineering Solutions, Proceedings of 1991 Conference, New Orleans, LA, USA, 5–6 June 1991; Stokes, B.J., Rawlins, C.L., Eds.; American Society of Agricultural Engineers (ASAE) Publication: St. Joseph, MI, USA, 1991; pp. 103–112. [Google Scholar]
- Foltz, R.B.; Elliot, W.J. Effect of lowered tire pressures on road erosion. Transp. Res. Rec. 1997, 1589, 19–25. [Google Scholar] [CrossRef]
- Parsakhoo, A.; Lotfalian, M.; Kavian, A.; Hosseini, S.A. Assessment of soil erodibility and aggregate stability for different parts of a forest road. J. For. Res. 2014, 25, 193–200. [Google Scholar] [CrossRef]
- Giuliani, F.; Autelitano, F.; Degiovanni, E.; Montepara, A. DEM modelling analysis of tree root growth in street pavements. Int. J. Pavement Eng. 2017, 18, 1–10. [Google Scholar] [CrossRef]
- Foltz, R.B.; Rhee, H.; Yanosek, K.A. Infiltration, erosion, and vegetation recovery following road obliteration. Trans. ASABE 2007, 50, 1937–1943. [Google Scholar] [CrossRef][Green Version]
- LINDO Systems Inc. What’s Best! LINDO Systems Inc.: Chicago, IL, USA, 2014; Available online: http://www.lindo.com (accessed on 11 March 2014).
- Weibull, W. A statistical theory of the strength of materials. Proc. R. Swed. Inst. Eng. Res. 1939, 151, 1–45. [Google Scholar]
- Lundborg, N. The strength-size relation of granite. Int. J. Rock Mech. Min. Sci. 1967, 4, 269–272. [Google Scholar] [CrossRef]
- Tang, C.A.; Tham, L.G.; Lee, P.K.K.; Tsui, Y.; Liu, H. Numerical studies of the influence of microstructure on rock failure in uniaxial compression—Part II: Constraint, slenderness and size effect. Int. J. Rock Mech. Min. Sci. 2000, 37, 571–583. [Google Scholar] [CrossRef]
- Schönert, K. The influence of particle bed configurations and confinements on particle breakage. Int. J. Miner. Process. 1996, 44–45, 1–16. [Google Scholar] [CrossRef]
- Tomas, J.; Schreier, M.; Gröger, T.; Ehlers, S. Impact crushing of concrete for liberation and recycling. Powder Technol. 1999, 105, 39–51. [Google Scholar] [CrossRef]
- Unland, G.; Szczelina, P. Coarse crushing of brittle rocks by compression. Int. J. Miner. Process. 2004, 74, S209–S217. [Google Scholar] [CrossRef]
- Lundborg, N. Strength of rock-like materials. Int. J. Rock Mech. Min. Sci. 1968, 5, 427–454. [Google Scholar] [CrossRef]
- Šuklje, L. Rheological Aspects of Soil Mechanics; Wiley-Interscience: London, UK, 1969; pp. 24–41. ISBN 0471835501. [Google Scholar]
- Vyalov, S.S. Rheological Fundamentals of Soil Mechanics; Elsevier: New York, USA, 1986; pp. 221–229. ISBN 0444422234. [Google Scholar]
- Giummarra, G.; McRobert, J.; Robinson, P. Unsealed Roads Manual: Guidelines to Good Practice, revised ed.; ARRB Transport Research Ltd.: Vermont South, VIC, Australia, 2000. [Google Scholar]
- Skorseth, K.; Selim, A.A. Gravel Roads: Maintenance and Design Manual; South Dakota Transportation Assistance Program (SD LTAP); US Department of Transportation, Federal Highway Administration: Washington, DC, USA, 2000; pp. 30–32. Available online: https://www.epa.gov/sites/production/files/2015-10/documents/2003_07_24_nps_gravelroads_gravelroads.pdf (accessed on 1 July 2019).
- Costantini, A.; Loch, R.J.; Connolly, R.D.; Garthe, R. Sediment generation from forest roads: Bed and eroded size distributions, and runoff management strategies. Aust. J. Soil Res. 1999, 37, 947–964. [Google Scholar] [CrossRef]
- Croke, J.; Mockler, S.; Hairsine, P.; Fogarty, P. Relative contributions of runoff and sediment from sources within a road prism and implications for total sediment delivery. Earth Surf. Proc. Landf. 2006, 31, 457–468. [Google Scholar] [CrossRef]
- Sheridan, G.J.; Noske, P.J. A quantitative study of sediment delivery and stream pollution from different forest road types. Hydrol. Process. 2007, 21, 387–398. [Google Scholar] [CrossRef]
- Bilby, R.E. Contributions of road surface sediment to a western Washington stream. For. Sci. 1985, 31, 827–838. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).