Mobile Terrestrial Photogrammetry for Street Tree Mapping and Measurements
Abstract
1. Introduction
2. Materials and Methods
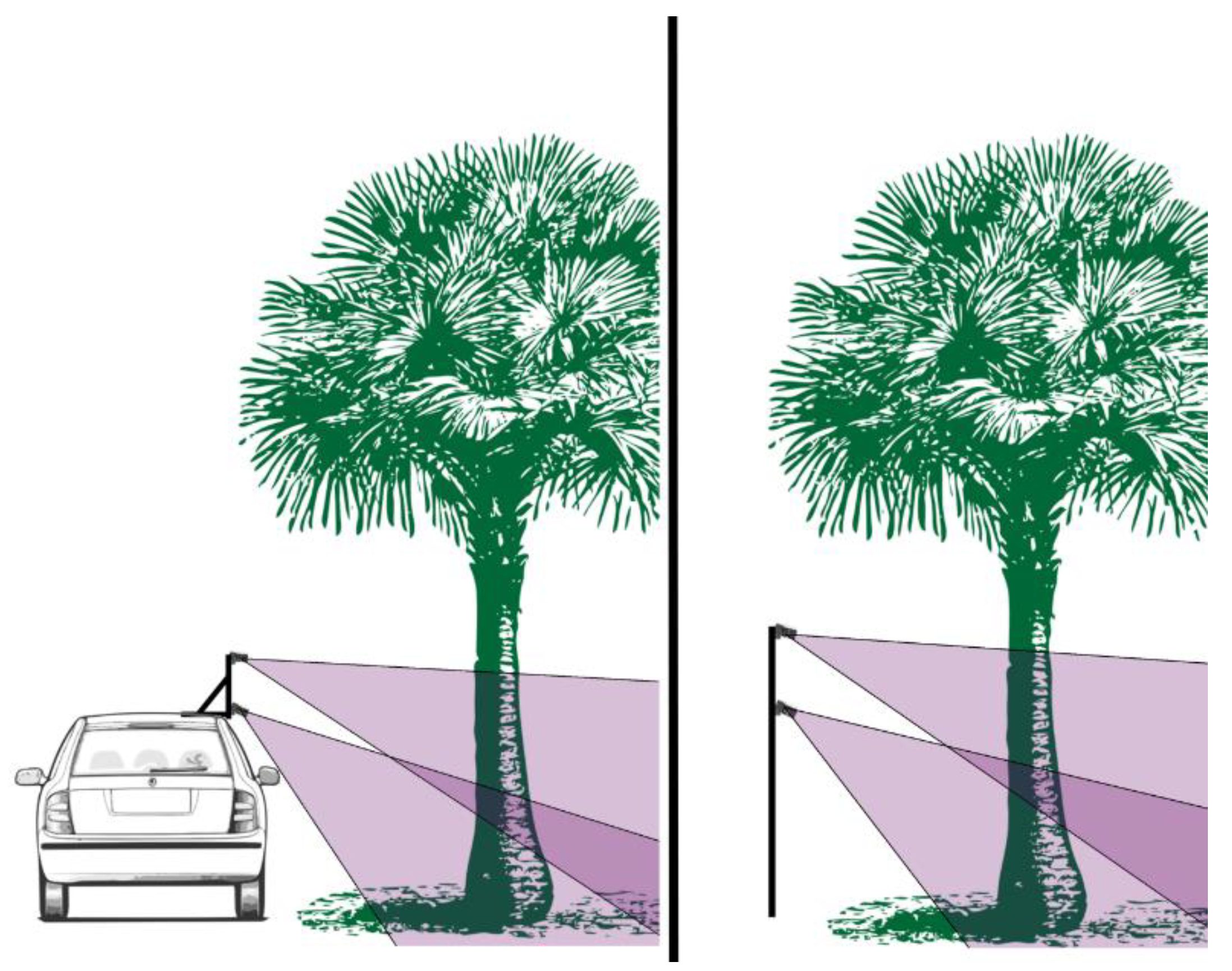
2.1. Study Site and Field Methods
2.2. Model Processing and Measurements
2.3. Data Analysis
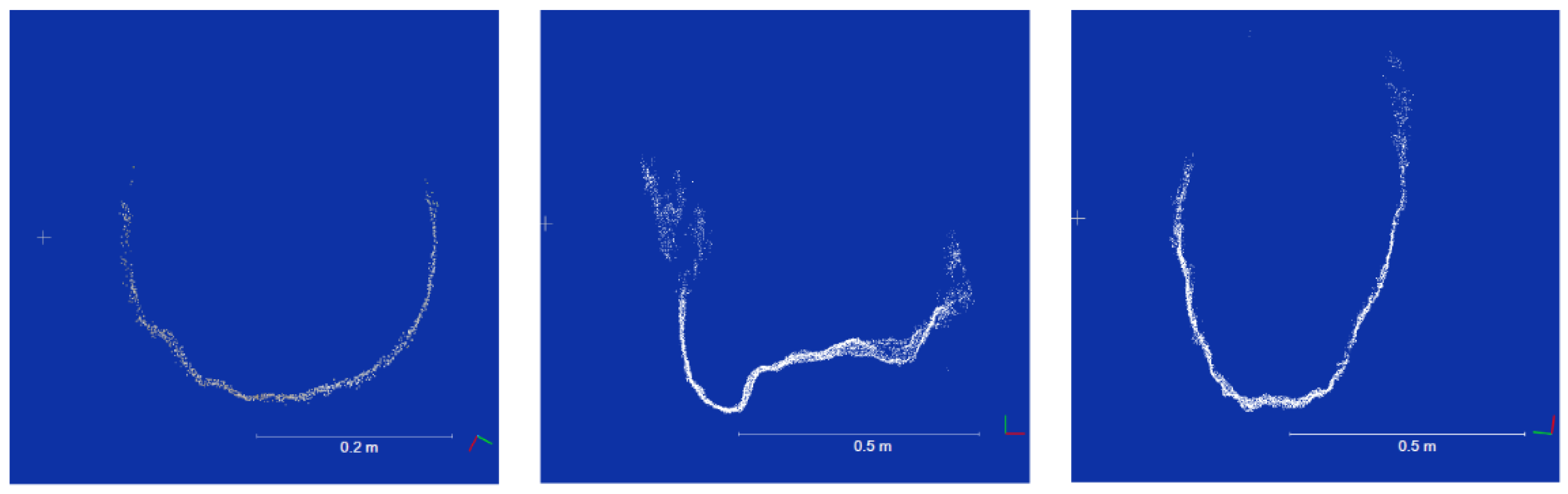
3. Results
3.1. General Site and Point Cloud Observations
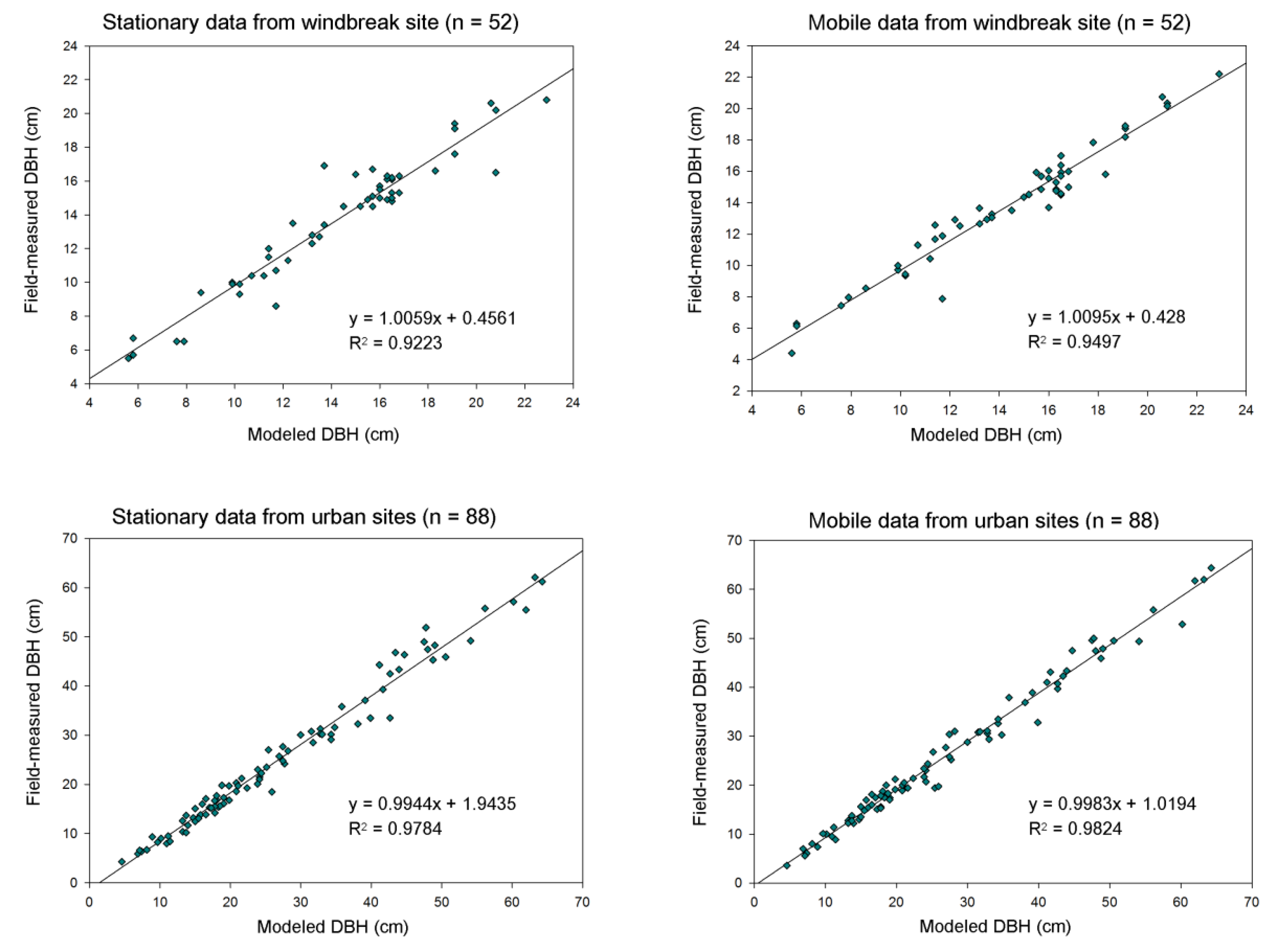
3.2. Mobile vs. Stationary
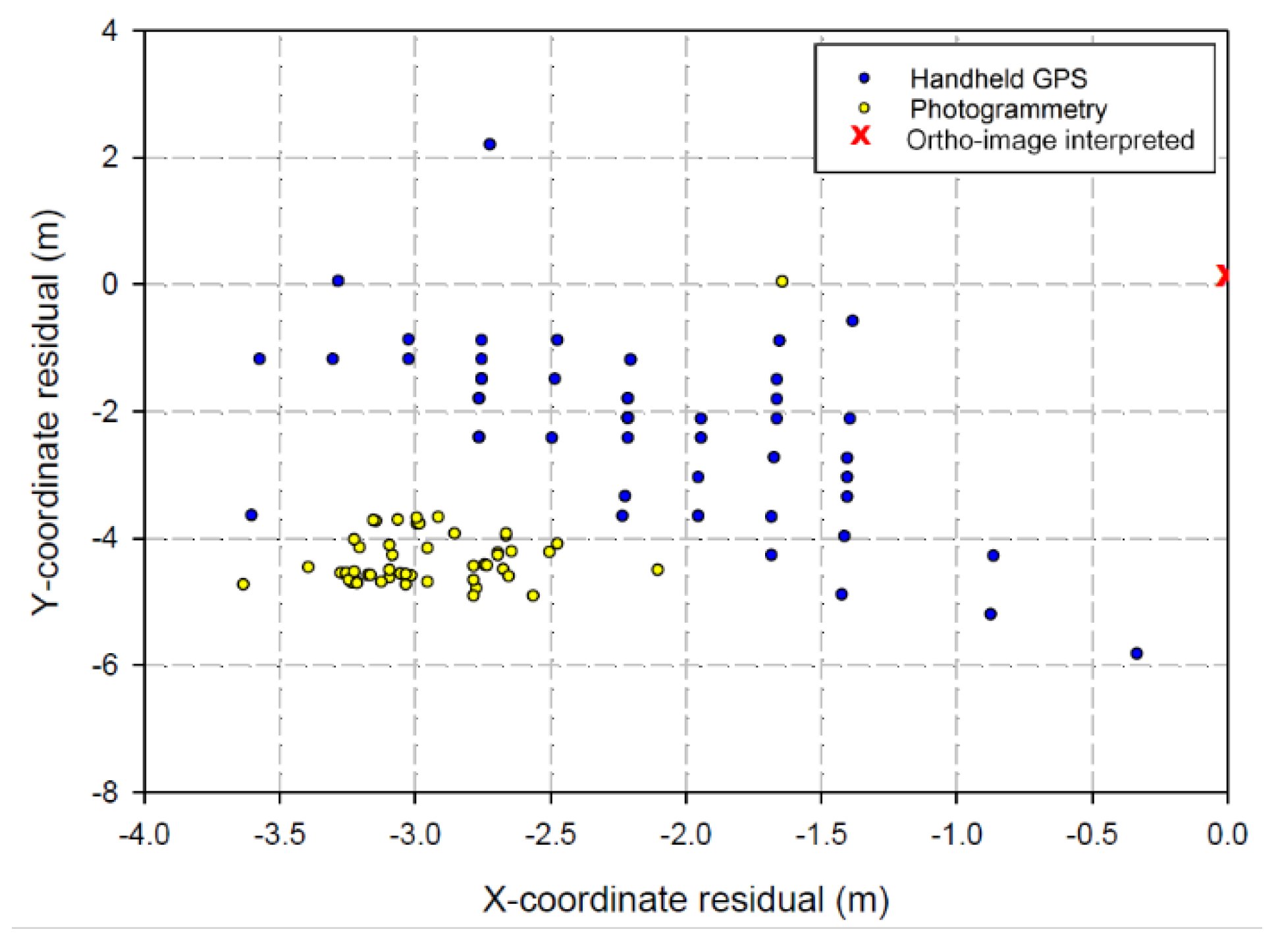
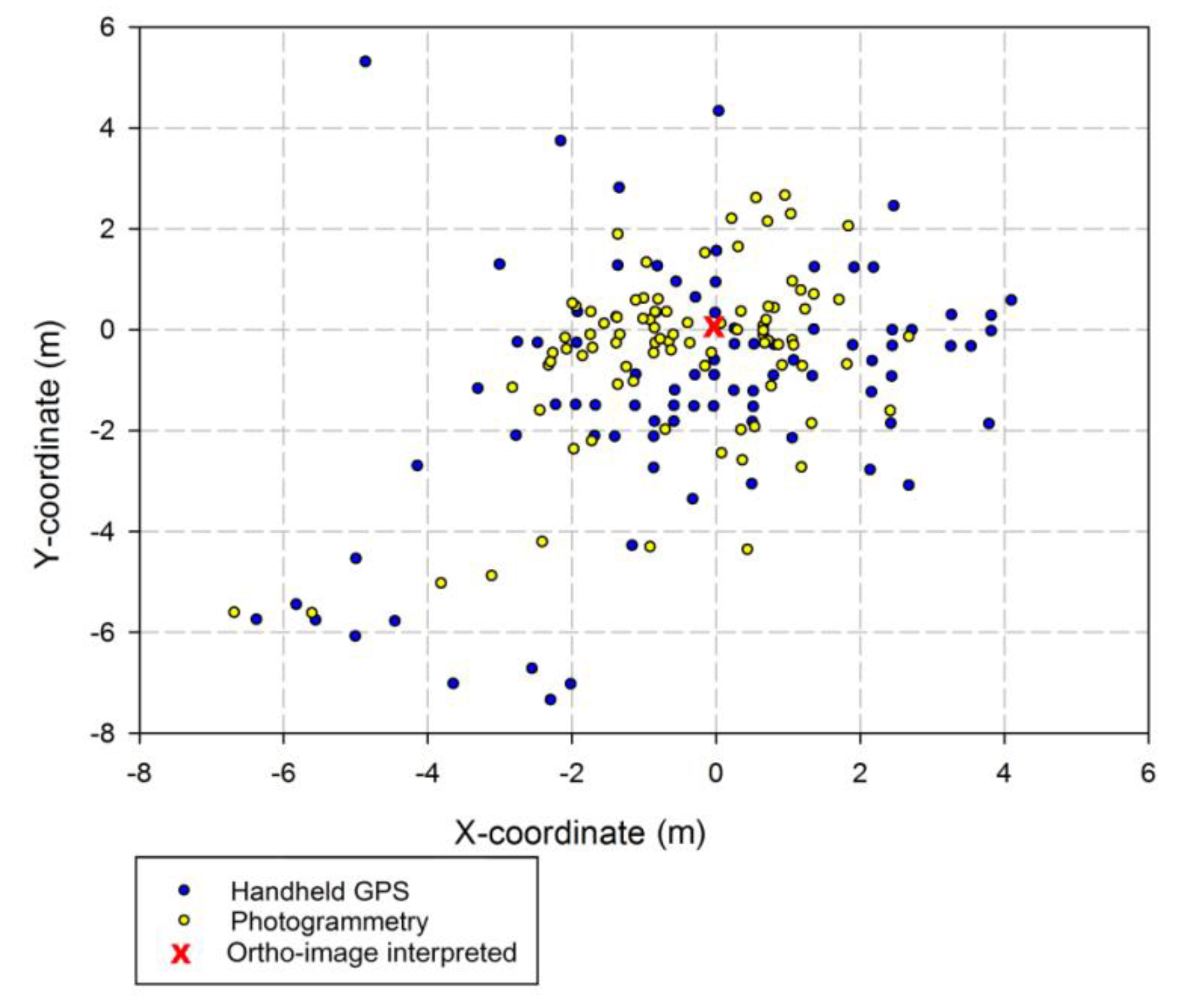
3.3. Stem Positions
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Roy, S.; Byrne, J.; Pickering, C. A systematic quantitative review of urban tree benefits, costs, and assessment methods across cities in different climatic zones. Urban For. Urban Green. 2012, 11, 351–363. [Google Scholar] [CrossRef]
- Seamans, G.S. Mainstreaming the environmental benefits of street trees. Urban For. Urban Green. 2013, 12, 2–11. [Google Scholar] [CrossRef]
- Nowak, D.; Crane, D.; Stevens, J.; Hoehn, R.; Walton, T.; Bond, J. A ground-based method of assessing urban forest structure and ecosystem services. Arboric. Urban For. 2008, 34, 347–358. [Google Scholar]
- Hauer, R.; Vogt, J.; Fischer, B. The cost of not maintaining the urban forest. Arborist News. 2015, 24, 12–19. [Google Scholar]
- Vogt, J.; Hauer, R.; Fischer, B. The Costs of Maintaining and Not Maintaining the Urban Forest: A Review of the Urban Forestry and Arboriculture Literature. Arboric. Urban For. 2015, 41, 293–323. [Google Scholar]
- Keller, J.; Konijnendijk, C. Short communication: A comparative analysis of municipal urban tree inventories of selected major cities in North America and Europe. Arboric. Urban For. 2012, 38, 24–30. [Google Scholar]
- Roman, L.; McPherson, E.; Scharenbroch, B.; Bartens, J. Identifying common practices and challenges for local urban tree monitoring programs across the United States. Arboric. Urban For. 2013, 39, 292–299. [Google Scholar]
- Bond, J. Tree Inventories; International Society of Arboriculture: Atlanta, GA, USA, 2013. [Google Scholar]
- Östberg, J.; Delshammar, T.; Wiström, B.; Nielsen, A. Grading of parameters for urban tree inventories by city officials, arborists, and academics using the Delphi method. Environ. Manag. 2013, 51, 694–708. [Google Scholar] [CrossRef]
- Maco, S.; McPherson, E. A practical approach to assessing structure, function, and value of street tree populations in small communities. J. Arboric. 2003, 29, 84–97. [Google Scholar]
- Koeser, A.K.; Hauer, R.J.; Miesbauer, J.W.; Peterson, W. Municipal tree risk assessment in the United States: Findings from a comprehensive survey of urban forest management. Arboric. J. 2016, 38, 1–12. [Google Scholar] [CrossRef]
- Ward, K.T.; Johnson, G.R. Geospatial methods provide timely and comprehensive urban forest information. Urban For. Urban Green. 2007, 6, 15–22. [Google Scholar] [CrossRef]
- Dwyer, M.; Miller, R. Using GIS to assess urban tree canopy benefits and surrounding greenspace distributions. J. Arboric. 1999, 25, 102–107. [Google Scholar]
- Walton, J.; Nowak, J.; Greenfield, J. Assessing urban forest canopy cover using airborne or satellite imagery. Arboric. Urban For. 2008, 34, 334–340. [Google Scholar]
- Sander, H.; Polasky, S.; Haight, R.G. The value of urban tree cover: A hedonic property price model in Ramsey and Dakota Counties, Minnesota, USA. Ecol. Econ. 2010, 69, 1646–1656. [Google Scholar] [CrossRef]
- Wu, C.; Xiao, Q.; McPherson, E.G. A method for locating potential tree-planting sites in urban areas: A case study of Los Angeles, USA. Urban For. Urban Green. 2008, 7, 65–76. [Google Scholar] [CrossRef]
- Locke, D.; Grove, J.; Lu, J.; Troy, A.; O’Neil-Dunne, J.; Beck, B. Prioritizing preferable locations for increasing urban tree canopy in New York City. Cities Environ. CATE 2011, 3, 4. [Google Scholar]
- Abd-Elrahman, A.H.; Thornhill, M.E.; Andreu, M.G.; Escobedo, F. A community-based urban forest inventory using online mapping services and consumer-grade digital images. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 249–260. [Google Scholar] [CrossRef]
- Pu, R.; Landry, S. A comparative analysis of high spatial resolution IKONOS and WorldView-2 imagery for mapping urban tree species. Remote Sens. Environ. 2012, 124, 516–533. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A.; Clark, D.B. Hyperspectral discrimination of tropical rain forest tree species at leaf to crown scales. Remote Sens. Environ. 2005, 96, 375–398. [Google Scholar] [CrossRef]
- Bunting, P.; Lucas, R. The delineation of tree crowns in Australian mixed species forests using hyperspectral Compact Airborne Spectrographic Imager (CASI) data. Remote Sens. Environ. 2006, 101, 230–248. [Google Scholar] [CrossRef]
- Koch, B.; Heyder, U.; Weinacker, H. Detection of individual tree crowns in airborne LiDAR data. Photogramm. Eng. Remote Sens. 2006, 72, 357–363. [Google Scholar] [CrossRef]
- Lee, A.C.; Lucas, R.M. A LiDAR-derived canopy density model for tree stem and crown mapping in Australian forests. Remote Sens. Environ. 2007, 111, 493–518. [Google Scholar] [CrossRef]
- Tanhuanpää, T.; Vastaranta, M.; Kankare, V.; Holopainen, M.; Hyyppä, J.; Hyyppä, H.; Alho, P.; Raisio, J. Mapping of urban roadside trees—A case study in the tree register update process in Helsinki City. Urban For. Urban Green. 2014, 13, 562–570. [Google Scholar] [CrossRef]
- Zhang, C.; Qiu, F. Mapping individual tree species in an urban forest using airborne LiDAR data and hyperspectral imagery. Photogramm. Eng. Remote Sens. 2012, 78, 1079–1087. [Google Scholar] [CrossRef]
- Alonzo, M.; Bookhagen, B.; Roberts, D. Urban tree species mapping using hyperspectral and LiDAR data fusion. Remote Sens. Environ. 2014, 148, 70–83. [Google Scholar] [CrossRef]
- Lee, J.H.; Ko, Y.; McPherson, E.G. The feasibility of remotely sensed data to estimate urban tree dimensions and biomass. Urban For. Urban Green. 2016, 16, 208–220. [Google Scholar] [CrossRef]
- Alonzo, M.; McFadden, J.; Nowak, D.; Roberts, D. Mapping urban forest structure and function using hyperspectral imagery and LiDAR data. Urban For. Urban Green. 2016, 17, 135–147. [Google Scholar] [CrossRef]
- Nielsen, A.; Östberg, J.; Delshammar, T. Review of Urban Tree Inventory Methods Used to Collect Data at Single-Tree Level. Arboric. Urban For. 2014, 40, 96–111. [Google Scholar]
- Wu, J.; Yao, W.; Polewski, P. Mapping Individual Tree Species and Vitality along Urban Road Corridors with LiDAR and Imaging Sensors: Point Density versus View Perspective. Remote Sens. 2018, 10, 1403. [Google Scholar] [CrossRef]
- Singh, K.; Gagné, S.; Meentemeyer, R. Comprehensive Remote Sensing, Chapter: 9.22. In Urban Forests and Human Well-Being; Liang, S.L., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 287–305. [Google Scholar] [CrossRef]
- Fröhlich, C.; Mettenleiter, M. Terrestrial laser scanning—New perspectives in 3D surveying. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, W2. [Google Scholar]
- Watt, P.J.; Donoghue, D.N.M. Measuring forest structure with terrestrial laser scanning. Int. J. Remote Sens. 2005, 26, 1437–1446. [Google Scholar] [CrossRef]
- Abellan, A.; Vilaplana, J.; Martinez, J. Application of a long-range Terrestrial Laser Scanner to a detailed rockfall study at Vall de Núria (Eastern Pyrenees, Spain). Eng. Geol. 2006, 88, 136–148. [Google Scholar] [CrossRef]
- Lerma, J.L.; Navarro, S.; Cabrelles, M.; Villaverde, V. Terrestrial laser scanning and close range photogrammetry for 3D archaeological documentation: The Upper Palaeolithic Cave of Parpalló as a case study. J. Archaeol. Sci. 2010, 37, 499–507. [Google Scholar] [CrossRef]
- Van Leeuwen, M.; Nieuwenhuis, M. Retrieval of forest structural parameters using LiDAR remote sensing. Eur. J. For. Res. 2010, 129, 749–770. [Google Scholar] [CrossRef]
- Moskal, L.M.; Zheng, G. Retrieving Forest Inventory Variables with Terrestrial Laser Scanning (TLS) in Urban Heterogeneous Forest. Remote Sens. 2011, 4, 1–20. [Google Scholar] [CrossRef]
- Yao, W.; Krzystek, P.; Heurich, M. Tree species classification and estimation of stem volume and DBH based on single tree extraction by exploiting airborne full-waveform LiDAR data. Remote Sens. Environ. 2012, 123, 368–380. [Google Scholar] [CrossRef]
- Henning, J.; Radtke, P. Detailed stem measurements of standing trees from ground-based scanning LiDAR. For. Sci. 2006, 52, 67–80. [Google Scholar] [CrossRef]
- Williams, K.; Olsen, M.; Roe, G.; Glennie, C. Synthesis of transportation applications of mobile LiDAR. Remote Sens. 2013, 5, 4652–4692. [Google Scholar] [CrossRef]
- Holopainen, M.; Kankare, V.; Vastaranta, M.; Liang, X.; Lin, Y.; Vaaja, M.; Yu, X.; Hyyppä, J.; Hyyppä, H.; Kaartinen, H.; et al. Tree mapping using airborne, terrestrial and mobile laser scanning—A case study in a heterogeneous urban forest. Urban For. Urban Green. 2013, 12, 546–553. [Google Scholar] [CrossRef]
- Dandois, J.P.; Ellis, E.C. High spatial resolution three-dimensional mapping of vegetation spectral dynamics using computer vision. Remote Sens. Environ. 2013, 136, 259–276. [Google Scholar] [CrossRef]
- Lisein, J.; Pierrot-Deseilligny, M.; Bonnet, S.; Lejeune, P. A Photogrammetric Workflow for the Creation of a Forest Canopy Height Model from Small Unmanned Aerial System Imagery. Forests 2013, 4, 922–944. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Diaz-Varela, R.; Angileri, V.; Loudjani, P. Tree height quantification using very high resolution imagery acquired from an unmanned aerial vehicle (UAV) and automatic 3D photo-reconstruction methods. Eur. J. Agron. 2014, 55, 89–99. [Google Scholar] [CrossRef]
- Morgenroth, J.; Gomez, C. Assessment of tree structure using a 3D image analysis technique—A proof of concept. Urban For. Urban Green. 2014, 13, 198–203. [Google Scholar] [CrossRef]
- Miller, J.; Morgenroth, J.; Gomez, C. 3D modelling of individual trees using a handheld camera: Accuracy of height, diameter and volume estimates. Urban For. Urban Green. 2015, 14, 932–940. [Google Scholar] [CrossRef]
- Bauwens, S.; Foyelle, A.; Gourlet-Fleury, S.; Ndjele, L.; Mengal, C.; Lejeune, P. Terrestrial photogrammetry: A non-destructive method for modelling irregularly shaped tropical tree trunks. Methods Ecol. Evol. 2017, 8, 460–471. [Google Scholar] [CrossRef]
- Liang, X.; Jaakkola, A.; Wang, Y.; Hyyppa, J.; Honkavaara, E.; Liu, J.; Kaartinen, H. The Use of a Hand-Held Camera for Individual Tree 3D Mapping in Forest Sample Plots. Remote Sens. 2014, 6, 6587–6603. [Google Scholar] [CrossRef]
- Surový, P.; Yoshimoto, A.; Panagiotidis, D. Accuracy of Reconstruction of the Tree Stem Surface Using Terrestrial Close-Range Photogrammetry. Remote Sens. 2016, 8, 123. [Google Scholar] [CrossRef]
- Mikita, T.; Janata, P.; Surový, P. Forest Stand Inventory Based on Combined Aerial and Terrestrial Close-Range Photogrammetry. Forests 2016, 7, 165. [Google Scholar] [CrossRef]
- Mokroš, M.; Liang, X.; Surový, P.; Valent, P.; Čerňava, J.; Chudý, F.; Tunák, D.; Saloň, Š.; Merganič, J. Evaluation of close-range photogrammetry image collection methods for estimating tree diameters. ISPRS Int. J. Geo Inf. 2018, 7, 93. [Google Scholar] [CrossRef]
- Mokroš, M.; Výbošťok, J.; Tomaštík, J.; Grznárová, A.; Valent, P.; Slavik, M.; Merganič, J. High precision individual tree diameter and precision estimation from close-range photogrammetry. Forests 2018, 9, 696. [Google Scholar] [CrossRef]
- Koeser, A.K.; Roberts, J.W.; Miesbauer, J.W.; Lopes, A.B.; Kling, G.J.; Lo, M.; Morgenroth, J. Testing the accuracy of imaging software for measuring tree root volumes. Urban For. Urban Green. 2016, 18, 95–99. [Google Scholar] [CrossRef]
- Roberts, J.W.; Koeser, A.K.; Abd-Elrahman, A.H.; Hansen, G.; Landry, S.M.; Wilkinson, B.E. Terrestrial photogrammetric stem mensuration for street trees. Urban For. Urban Green. 2018, 35, 66–71. [Google Scholar] [CrossRef]
- Abd-Elrahman, A.; Pande-Chhetri, R.; Vallad, G. Design and Development of a Multi-Purpose Low-Cost Hyperspectral Imaging System. Remote Sens. 2011, 3, 570–586. [Google Scholar] [CrossRef]
- Abd-Elrahman, A.; Sassi, N.; Wilkinson, B.; DeWitt, B. Georeferencing of mobile ground-based hyperspectral digital single-lens reflex imagery. J. Appl. Remote Sens. 2016, 10, 14002. [Google Scholar] [CrossRef]
- Microsoft Corporation. Microsoft Excel 2010 (V14.0); Microsoft Corporation: Redmond, WA, USA, 2010. [Google Scholar]
- Kitahara, F.; Mizoue, N.; Yoshida, S. Effects of training for inexperienced surveyors on data quality of tree diameter and height measurements. Silva Fenn. 2010, 44, 657–667. [Google Scholar] [CrossRef]
- Luoma, V.; Saarinen, N.; Wulder, M.A.; White, J.C.; Vastaranta, M.; Holopainen, M.; Hyyppä, J. Assessing Precision in Conventional Field Measurements of Individual Tree Attributes. Forests 2017, 8, 38. [Google Scholar] [CrossRef]
- Liang, X.; Wang, Y.; Jaakkola, A.; Kukko, A.; Kaartinen, H.; Hyyppä, J.; Honkavaara, E.; Liu, J. Forest Data Collection Using Terrestrial Image-Based Point Clouds from a Handheld Camera Compared to Terrestrial and Personal Laser Scanning. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1–16. [Google Scholar] [CrossRef]
- Daneshmand, M.; Helmi, A.; Avots, E.; Noroozi, F.; Alisinanoglu, F.; Sait Arslan, H.; Gorbova, J.; Haamer, R.; Ozcinar, C.; Anbarjafari, G. 3D scanning: A comprehensive survey. Scand. J. For. Res. 2018, 30, 73–86. [Google Scholar]
- Bertin, S.; Friedrich, H.; Delmas, H.; Chan, E.; Gimel’farb, G. Digital stereo photogrammetry for grain-scale monitoring of fluvial surfaces: Error evaluation and workflow optimization. ISPRS J. Photogramm. Remote Sens. 2015, 101, 193–208. [Google Scholar] [CrossRef]
- Omasa, K.; Hosoi, F.; Uenishi, T.; Shimizu, Y.; Akiyama, Y. Three-dimensional modeling of an urban park and trees by combined airborne and portable on-ground scanning LIDAR remote sensing. Environ. Modeling Assess. 2008, 13, 473–481. [Google Scholar] [CrossRef]
- Lassiter, H.; Wilkinson, B. Comparison of terrestrial 3D mapping methods for urban forest parameters. In Proceedings of the International LiDAR Mapping Forum, Denver, CO, USA, 22–24 February 2016. [Google Scholar]
- Gatziolis, D.; Lienard, J.F.; Vogs, A.; Strigul, N.S. 3D Tree Dimensionality Assessment Using Photogrammetry and Small Unmanned Aerial Vehicles. PLoS ONE 2015, 10, e0137765. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote Sensing Technologies for Enhancing Forest Inventories: A Review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Puente, I.; González-Jorge, H.; Martínez-Sánchez, J.; Arias, P. Review of mobile mapping and surveying technologies. Measurement 2013, 46, 2127–2145. [Google Scholar] [CrossRef]
- Fritz, A.; Kattenborn, T.; Koch, B. Uav-Based Photogrammetric Point Clouds—Tree Stem Mapping in Open Stands in Comparison to Terrestrial Laser Scanner Point Clouds. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 40, 141–146. [Google Scholar] [CrossRef]
- Li, X.J.; Zhang, C.; Li, W.; Ricard, R.; Meng, Q.; Zhang, W. Assessing street-level urban greenery using Google Street View and a modified green view index. Urban For. Urban Green. 2015, 14, 675–685. [Google Scholar] [CrossRef]
- Berland, A.; Lange, D.A. Google Street View shows promise for virtual street tree surveys. Urban For. Urban Green. 2017, 21, 11–15. [Google Scholar] [CrossRef]
- Wegner, J.; Branson, S.; Hall, D.; Schindler, K.; Perona, P. Cataloging public objects using aerial and street level images—Urban trees. In Proceedings of the the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 6014–6023. [Google Scholar]
- Alvarez, I.; Gallo, B.; Garçon, E.; Oshiro, O. Street tree inventory of Campinas, Brazil: An instrument for urban forestry management and planning. Arboric. Urban For. 2015, 41, 233–244. [Google Scholar]
- Branson, S.; Wegner, J.D.; Hall, D.; Lang, N.; Schindler, K.; Perona, P. From Google Maps to a fine-grained catalog of street trees. ISPRS J. Photogramm. Remote Sens. 2018, 135, 13–30. [Google Scholar] [CrossRef]



| Study | Feature | RMSE (%) | RMSE in Units | Accuracy |
|---|---|---|---|---|
| Bauwens et al. (2017) | stem diameter | 4.5–4.6 | 5.8–5.9 cm | - |
| Koeser et al. (2016) | root system volume | 12.3 | 40.37 cm3 | - |
| Liang et al. (2014) | DBH | 6.6 | 2.39 cm | - |
| tree detection rate | - | - | 88% | |
| Mikita et al. (2016) | tree positional accuracy | - | - | 0.071—0.951 m |
| DBH | - | 0.911–1.797 cm | - | |
| stem volume | - | 0.082–0.180 m3 | - | |
| Miller et al. (2015) | DBH | 9.6 | 0.99 mm | - |
| height | 3.74 | 5.15 cm | - | |
| crown spread | 14.76 | 4.1 cm | - | |
| crown depth | 11.93 | 2.53 cm | - | |
| stem volume | 12.33 | 115.45 cm3 | - | |
| branch volume | 47.53 | 138.59 cm3 | - | |
| total volume | 18.53 | 266.79 cm3 | - | |
| Mokroš et al. (2018) | tree detection rate | - | - | 80.60% |
| Mokroš et al. (2018) | stem diameter | 0.9–1.85 | - | - |
| stem perimeter | 0.21–0.99 | - | - | |
| Morgenroth and Gomez (2014) | DBH | 3.7 | 3 cm | - |
| height | 2.59 | 9 cm | - | |
| Roberts et al. (2018) | DBH | 7.04–12.35 | 0.97–3.10 cm | - |
| Surový et al. (2016) | DBH | NA | 0.59 cm | - |
| Site | Data | Meanfield-measured (cm) | Meanmodeled (cm) | RMSE (cm) | RMSE (%) | Bias (cm) | Bias (%) |
|---|---|---|---|---|---|---|---|
| Urban (n = 88) | Stationary | 27.13 | 25.32 | 2.81 | 10.37 | −1.80 | −6.64 |
| Mobile | 27.13 | 26.15 | 2.18 | 8.02 | −0.98 | −3.60 | |
| Windbreak (n = 52) | Stationary | 14.21 | 13.68 | 1.24 | 8.70 | −0.54 | −3.78 |
| Mobile | 14.21 | 13.65 | 1.06 | 7.43 | −0.56 | −3.93 |
| Site | Data | Mean Residual (m) | Standard Deviation (m) | Min. (m) | Max. (m) |
|---|---|---|---|---|---|
| Urban (n = 88) | HH-GPS Y | −1.17 (0.25) * | 2.38 | −7.36 | 5.29 |
| Photo. Y | −0.49 (0.18) * | 1.70 | −5.64 | 2.64 | |
| Windbreak (n = 52) | HH-GPS Y | −2.23 (0.20) * | 1.42 | −5.84 | 2.18 |
| Photo. Y | −4.38 (0.05) * | 0.35 | −4.93 | −3.69 |
| Site | Data | Mean Residual (m) | Standard Deviation (m) | Min. (m) | Max. (m) |
|---|---|---|---|---|---|
| Urban | HH-GPS X | −0.30 (0.25) * | 2.36 | −6.36 | 4.11 |
| Photo. X | −0.48 (0.17) * | 1.59 | −6.67 | 2.69 | |
| Windbreak | HH-GPS X | −2.15 (0.09) * | 0.70 | −3.6 | −0.33 |
| Photo. X | −2.95 (0.05) * | 0.33 | −3.63 | −1.64 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roberts, J.; Koeser, A.; Abd-Elrahman, A.; Wilkinson, B.; Hansen, G.; Landry, S.; Perez, A. Mobile Terrestrial Photogrammetry for Street Tree Mapping and Measurements. Forests 2019, 10, 701. https://doi.org/10.3390/f10080701
Roberts J, Koeser A, Abd-Elrahman A, Wilkinson B, Hansen G, Landry S, Perez A. Mobile Terrestrial Photogrammetry for Street Tree Mapping and Measurements. Forests. 2019; 10(8):701. https://doi.org/10.3390/f10080701
Chicago/Turabian StyleRoberts, John, Andrew Koeser, Amr Abd-Elrahman, Benjamin Wilkinson, Gail Hansen, Shawn Landry, and Ali Perez. 2019. "Mobile Terrestrial Photogrammetry for Street Tree Mapping and Measurements" Forests 10, no. 8: 701. https://doi.org/10.3390/f10080701
APA StyleRoberts, J., Koeser, A., Abd-Elrahman, A., Wilkinson, B., Hansen, G., Landry, S., & Perez, A. (2019). Mobile Terrestrial Photogrammetry for Street Tree Mapping and Measurements. Forests, 10(8), 701. https://doi.org/10.3390/f10080701







