Estimation of Pinus massoniana Leaf Area Using Terrestrial Laser Scanning
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Characteristics
2.2. Specific Leaf Area Acquisition
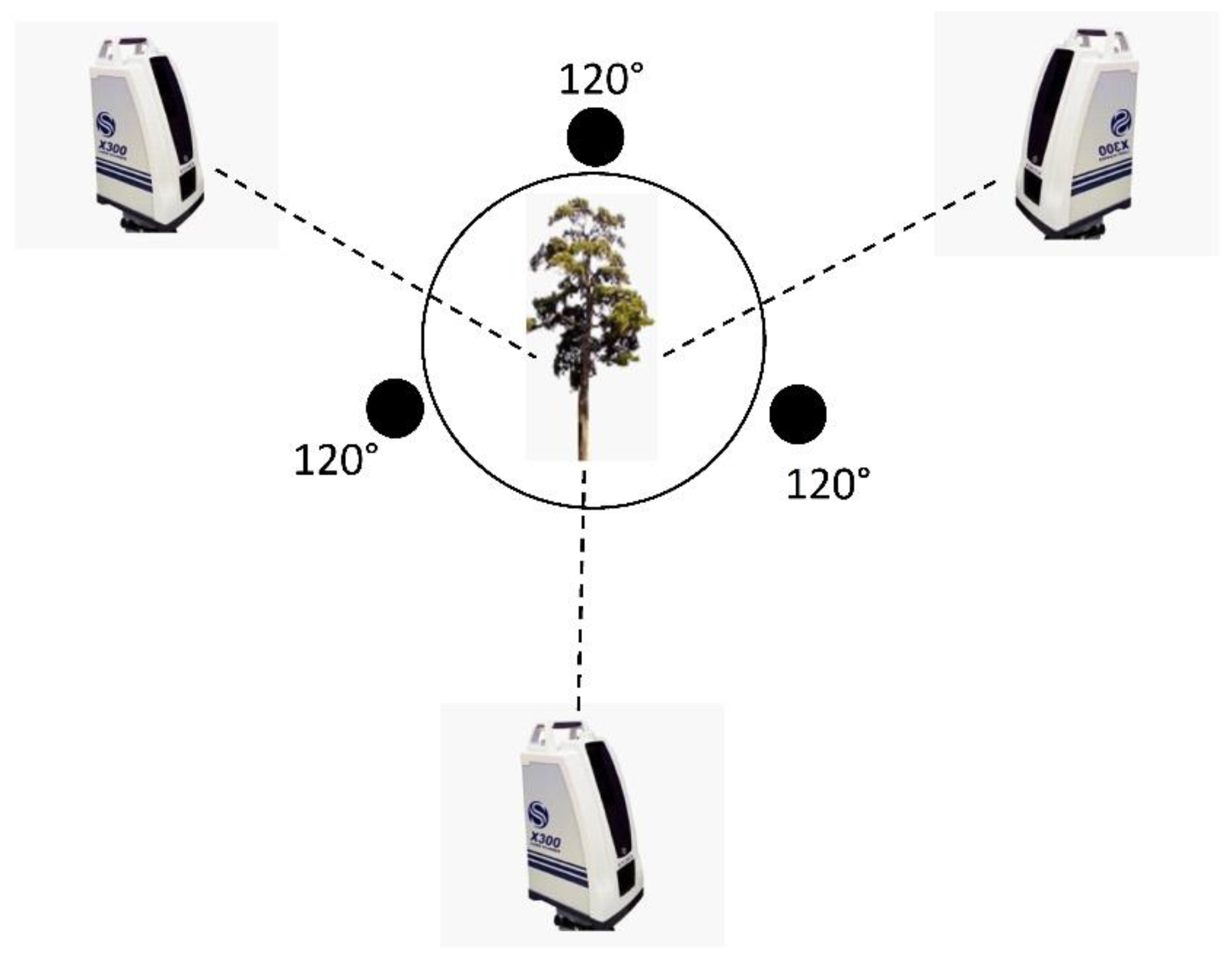
2.3. Point Cloud Data Acquisition
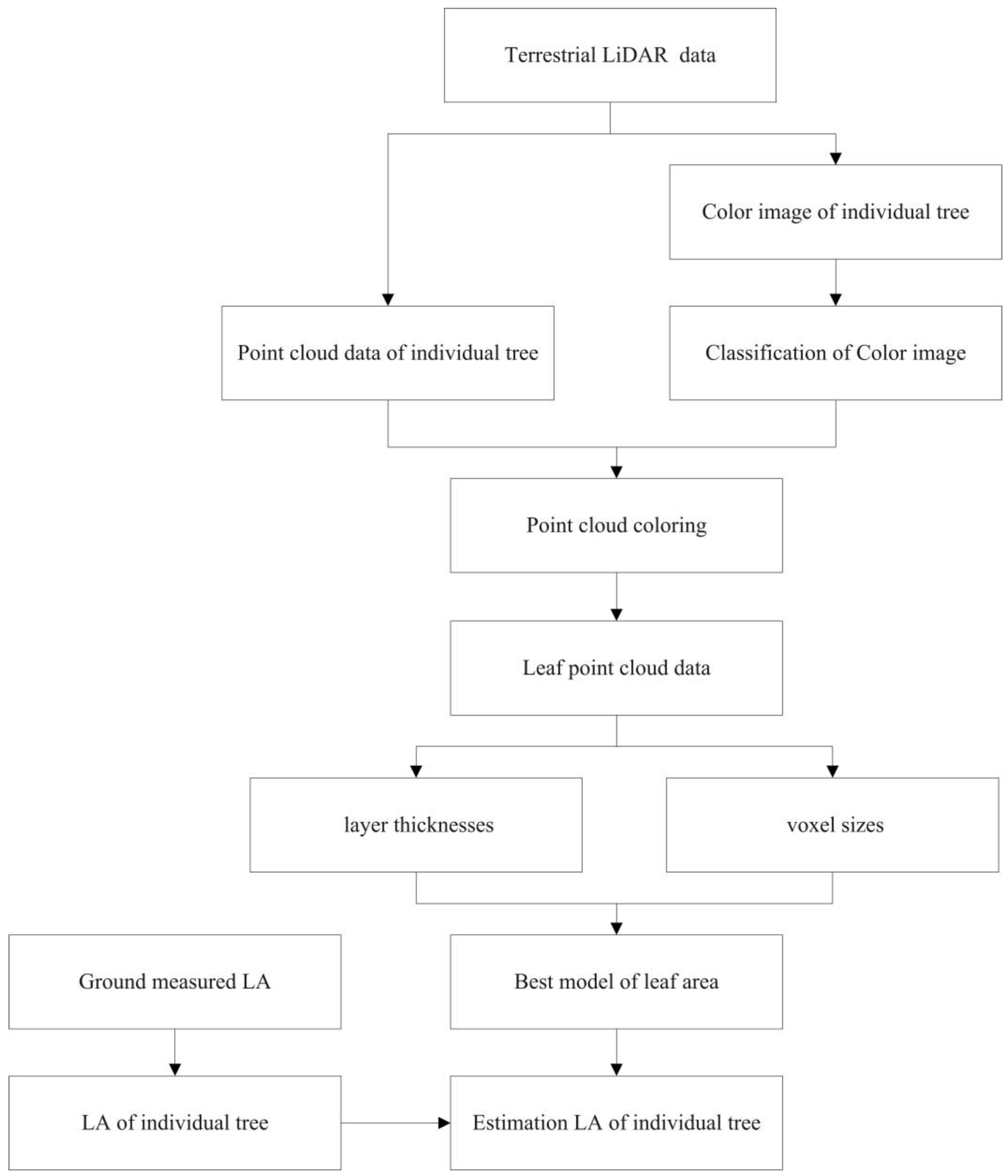
2.4. Point Cloud Data Processing
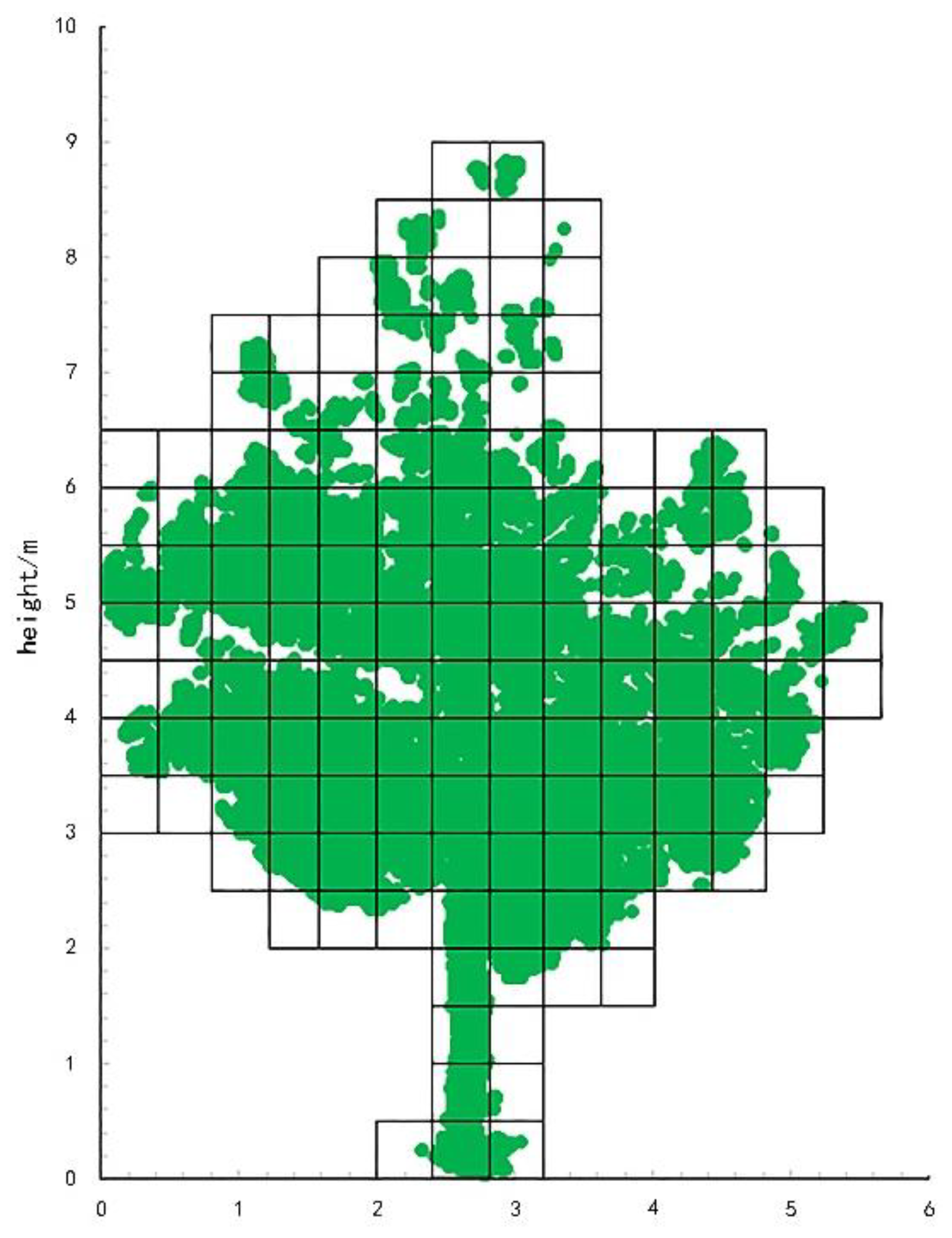
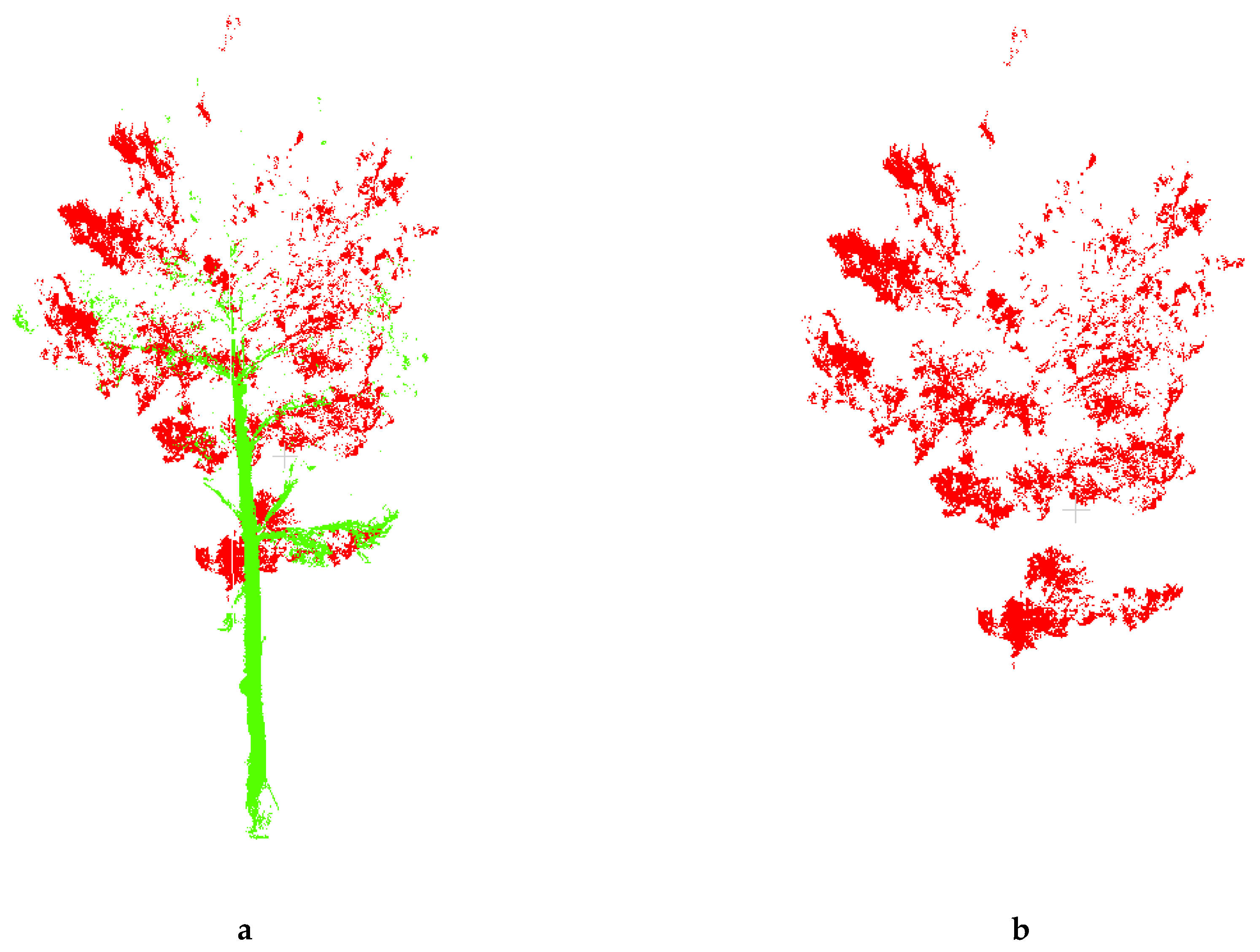
2.5. Point Cloud Data Extraction
2.6. Model Validation
3. Results
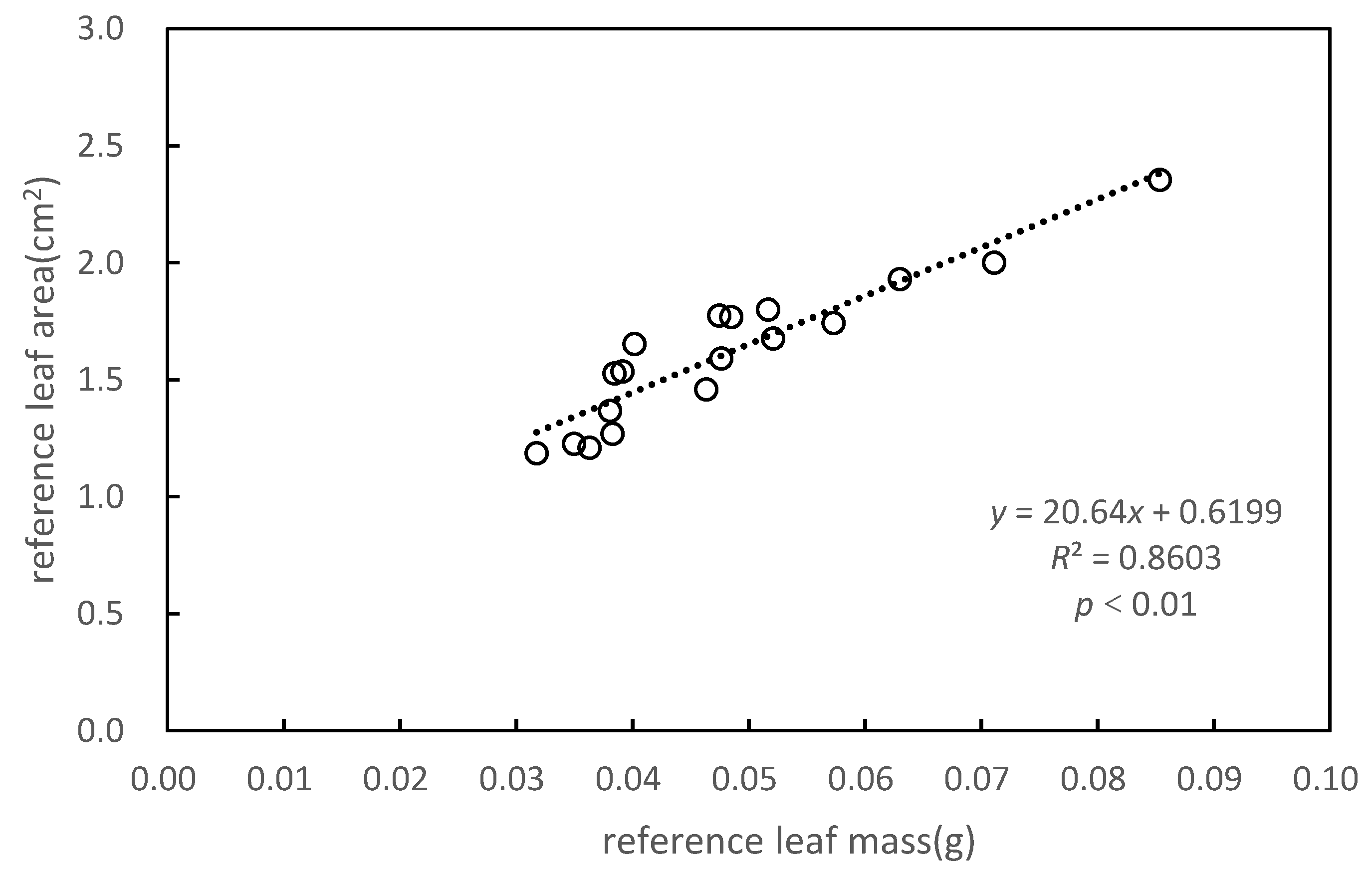
3.1. Specific Leaf Area of Pinus massoniana
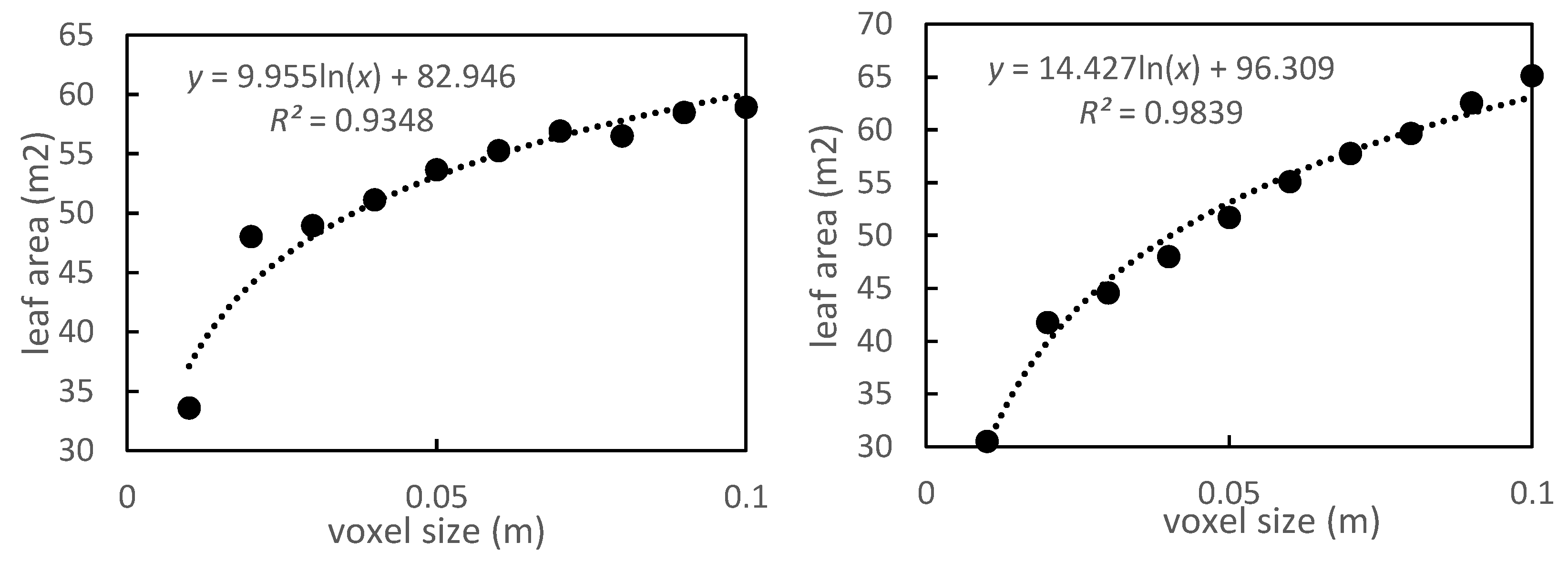
3.2. Leaf Area Estimation at Different Scales
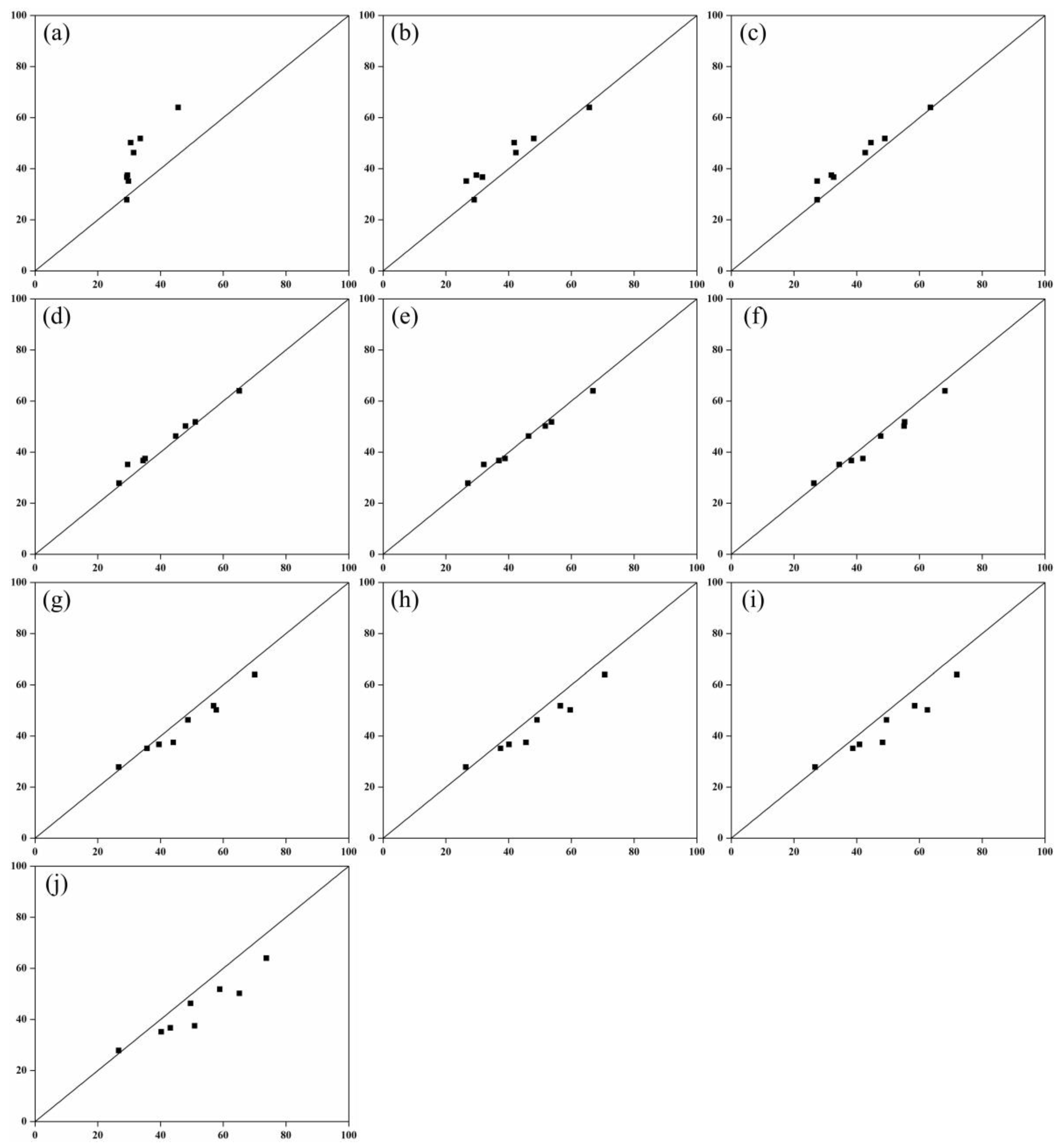
3.3. Model Validation
4. Discussion
4.1. Measurement of Specific Leaf Area
4.2. Effects of Different Voxel Sizes
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, J.M.; Leblanc, S.G. A Four-scale bidirectional reflectance model based on canopy architecture. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1316–1337. [Google Scholar] [CrossRef]
- Sepaskhah, A.R.; Amini-Nejad, M.; Kamgar-Haghighi, A.A. Developing a dynamic yield and growth model for saffron under different irrigation regimes. Int. J. Plant Prod. 2013, 7, 473–504. [Google Scholar]
- Shabani, A.; Sepaskhah, A.R.; Kamkar-Haghighi, A.A. A model to predict the dry matter and yield of rapeseed under salinity and deficit irrigation. Arch. Agron. Soil Sci. 2014, 61, 525–542. [Google Scholar] [CrossRef]
- Diao, J.; Guo, H.; Lu, J.; Lei, X.D.; Tang, S.Z. Leaf area estimation model and specific leaf area of Chinese pine. For. Res. 2013, 26, 174–180. (In Chinese) [Google Scholar]
- Baker, S.C.; Halpern, C.B.; Wardlaw, T.J.; Crawford, R.L.; Bigley, R.E.; Edgar, G.J.; Evans, S.A.; Franklin, J.F.; Jordan, G.J.; Karpievitch, Y.; et al. Short- and long-term benefits for forest biodiversity of retaining unlogged patches in harvested areas. For. Ecol. Manag. 2015, 353, 187–195. [Google Scholar] [CrossRef]
- Weraduwage, S.M.; Chen, J.; Anozie, F.C.; Morales, A.; Weise, S.E.; Sharkey, T.D. The relationship between leaf area growth and biomass accumulation in Arabidopsis thaliana. Front. Plant Sci. 2015, 6, 167. [Google Scholar] [CrossRef] [PubMed]
- Alton, P.B. The sensitivity of models of gross primary productivity to meteorological and leaf area forcing: A comparison between a Penman–Monteith ecophysiological approach and the MODIS Light-Use Efficiency algorithm. Agric. For. Meteorol. 2016, 218, 11–24. [Google Scholar] [CrossRef]
- Landsberg, J.; Gower, S. Canopy Architecture and Microclimate. Appl. Physiol. Ecol. For. Manag. 1997, 51–88. [Google Scholar]
- Sepaskhah, A.R. Estimation of individual and total leaf area of safflowers. Agron. J. 1977, 69, 783–785. [Google Scholar] [CrossRef]
- Shabani, A.; Sepaskhah, A.R.; Kamkar-Haghighi, A.A. Growth and physiologic response of rapeseed (Brassica Napus L.) to deficit irrigation, water salinity and planting method. Int. J. Plant Prod. 2013, 7, 569–596. [Google Scholar]
- Montero, F.; De Juan, J.; Cuesta, A.; Brasa, A. Nondestructive Methods to Estimate Leaf Area in (Vitis vinifera) L. HortScience 2000, 35, 696–698. [Google Scholar] [CrossRef]
- Peksen, E. Non-destructive leaf area estimation model for faba bean (Vicia Faba L.). Sci. Hortic. 2007, 113, 322–328. [Google Scholar] [CrossRef]
- Kandiannan, K.; Parthasarathy, U.; Krishnamurthy, K.S.; Thankamani, C.K.; Srinivasan, V. Modeling individual leaf area of ginger (Zingiber Officinale Roscoe) using leaf length and width. Sci. Hortic. 2009, 120, 532–537. [Google Scholar] [CrossRef]
- Chen, J.M.; Black, T.A. Defining leaf area index for non-flat leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Salazar, J.C.S.; Melgarejo, L.M.; Bautista, E.H.D.; Di Rienzo, J.A.; Casanoves, F. Non-destructive estimation of the leaf weight and leaf area in cacao (Theobroma Cacao L.). Sci. Hortic. 2018, 229, 19–24. [Google Scholar] [CrossRef]
- Wehr, A.; Lohr, U. Airborne laser scanning—An introduction and overview. ISPRS J. Photogramm. Remote Sens. 1999, 54, 68–82. [Google Scholar] [CrossRef]
- Hese, S.; Lucht, W.; Schmullius, C.; Barnsley, M.J.; Dubayah, R.C.; Knorr, D.; Neumann, K.; Riedel, T.; Schroeter, K. Global biomass mapping for an improved understanding of the CO2 balance-the earth observation mission carbon-3D. Remote Sens. Env. 2005, 94, 94–104. [Google Scholar] [CrossRef]
- Bouvier, M.; Durrieu, S.; Fournier, R.A.; Renaud, J.P. Generalizing predictive models of forest inventory attributes using an area-based approach with airborne LiDAR data. Remote Sens. Environ. 2015, 156, 322–334. [Google Scholar] [CrossRef]
- Li, X.R.; Liu, Q.C.; Cai, Z. Specific leaf area and leaf area index of conifer plantations in Qianyanzhou station of subtropical china. J. Plant Ecol. 2007, 31, 93–101. (In Chinese) [Google Scholar]
- Zhili, L.; Yu, Z.; Fengri, L.; Guangze, J. Non-destructively predicting leaf area, leaf mass and specific leaf area based on a linear mixed-effect model for broadleaf species. Ecol. Indic. 2017, 78, 340–350. [Google Scholar] [CrossRef]
- Roberts, S.D.; Dean, T.J.; Evans, D.L.; McCombs, J.W.; Harrington, R.L.; Glass, P.A. Estimating individual tree leaf area in loblolly pine plantations using LiDAR-derived measurements of height and crown dimensions. For. Ecol. Manag. 2005, 213, 54–70. [Google Scholar] [CrossRef]
- Bao, Y.; Ni, W.; Wang, D.; Yue, C.; He, H.; Verbeeck, H. Effects of Tree Trunks on Estimation of Clumping Index and LAI from HemiView and Terrestrial LiDAR. Forests 2018, 9, 144. [Google Scholar] [CrossRef]
- Hosoi, F.; Omasa, K. Voxel-based 3-D modeling of individual trees for estimating leaf area density using high-resolution portable scanning LiDAR. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3610–3618. [Google Scholar] [CrossRef]
- Béland, M.; Baldocchi, D.D.; Widlowski, J.L.; Fournier, R.A.; Verstraete, M.M. On seeing the wood from the leaves and the role of voxel size in determining leaf area distribution of forests with terrestrial LiDAR. Agric. For. Meteorol. 2014, 184, 82–97. [Google Scholar] [CrossRef]
- Yao, X.; Yu, K.; Deng, Y.; Zeng, Q.; Lai, Z.; Liu, J. Spatial distribution of soil organic carbon stocks in Masson pine (Pinus Massoniana) forests in subtropical China. Catena 2019, 178, 189–198. [Google Scholar] [CrossRef]
- Ma, Z.; Hartmann, H.; Wang, H.; Li, Q.; Wang, Y.; Li, S. Carbon dynamics and stability between native Masson pine and exotic slash pine plantations in subtropical China. Eur. J. For. Res. 2014, 133, 307–321. [Google Scholar] [CrossRef]
- Schaffer, B.; Schaffer, B.; Whiley, A.W.; Wolstenholme, B.N. The Avocado Botany, Production and Uses, 2nd ed.; Schaffer, B.A., Wolstenholme, B.N., Whiley, A.W., Eds.; CABI: Wallingford, UK, 2013. [Google Scholar]
- Ghoreishi, M.; Hossini, Y.; Maftoon, M. Simple models for predicting leaf area of mango (Mangifera indica L.). J. Biol. Earth Sci. 2012, 2, 9. [Google Scholar]
- McFadyen, L.M.; Morris, S.G.; Oldham, M.A.; Huett, D.O.; Meyers, N.M.; Wood, J.; McConchie, C.A.; Morris, S. The relationship between orchard crowding, light interception, and productivity in macadamia. Aust. J. Agric. Res. 2004, 55, 1029. [Google Scholar] [CrossRef]
- Yu, K.; Yao, X.; Deng, Y.; Lai, Z.; Lin, L.; Liu, J. Effects of stand age on soil respiration in Pinus massoniana plantations in the hilly red soil region of Southern China. Catena 2019, 178, 313–321. [Google Scholar] [CrossRef]
- Liu, J.; Gu, Z.; Shao, H.; Zhou, F.; Peng, S. N–P stoichiometry in soil and leaves of Pinus massoniana, forest at different stand ages in the subtropical soil erosion area of China. Environ. Earth Sci. 2016, 75, 1091. [Google Scholar] [CrossRef]
- Fascella, G.; Darwich, S.; Rouphael, Y. Validation of a leaf area prediction model proposed for rose. Chil. J. Agric. Res. 2013, 73, 73–76. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Dai, L.; Wang, H.; Wang, Y.; He, Z.; Lin, S. Estimating Leaf Area Density of Individual Trees Using the Point Cloud Segmentation of Terrestrial LiDAR Data and a Voxel-Based Model. Remote Sens. 2017, 9, 1202. [Google Scholar] [CrossRef]
- Guarato, A.Z.; Quinsat, Y.; Mehdi-Souzani, C.; Lartigue, C.; Sura, E. Conversion of 3D scanned point cloud into a voxel-based representation for crankshaft mass balancing. Int. J. Adv. Manuf. Technol. 2018, 95, 1315–1324. [Google Scholar] [CrossRef]
- Nourian, P.; Gonçalves, R.; Zlatanova, S.; Ohori, K.A.; Vu Vo, A. Voxelization algorithms for geospatial applications: Computational methods for voxelating spatial datasets of 3D city models containing 3D surface, curve and point data models. Methods 2016, 3, 69–86. [Google Scholar] [CrossRef]
- Dionne, O.; De Lasa, M. Voxelization Techniques. U.S. Patent Application No. 14/252,399, 1 October 2015. [Google Scholar]
- Keramatlou, I.; Sharifani, M.; Sabouri, H.; Alizadeh, M.; Kamkar, B. A simple linear model for leaf area estimation in Persian walnut (Juglans Regia L.). Sci. Hortic. 2015, 184, 36–39. [Google Scholar] [CrossRef]
- Tondjo, K.; Brancheriau, L.; Sabatier, S.A.; Kokutsè, A.D.; Akossou, A.Y.J.; Kokou, K.; Fourcaud, T. Non-destructive measurement of leaf area and dry biomass in Tectona grandis. Trees 2015, 29, 1625–1631. [Google Scholar] [CrossRef]
- Wang, Y.J.; Jin, G.Z.; Liu, Z.L. Construction of empirical models for leaf area and leaf dry mass of two broadleaf species in Xiaoxing’an Mountains, China. Chin. J. Appl. Ecol. 2018, 29, 1745–1752, (In English abstract). [Google Scholar]
- Poux, F.; Billen, R. Voxel-based 3D point cloud semantic segmentation: unsupervised geometric and relationship featuring vs deep learning methods. ISPRS Int. J. Geo-Inf. 2019, 8, 213. [Google Scholar] [CrossRef]
- Cai, H.Y.; Di, X.Y.; Jin, G.Z. Allometric models for leaf area and leaf mass predictionsacross different growing periods of elm tree (Ulmus japonica). J. For. Res. 2017, 28, 975–982. [Google Scholar] [CrossRef]
- Shipley, B.; Almeida-Cortez, J. Interspecific consistency and intraspecific variability of specific leaf area with respect to irradiance and nutrient availability. Écoscience 2003, 10, 74–79. [Google Scholar] [CrossRef]
- Pompelli, M.; Antunes, W.; Ferreira, D.; Cavalcante, P.; Wanderley-Filho, H.; Endres, L. Allometric models for non-destructive leaf area estimation of Jatropha curcas. Biomass Bioenergy 2012, 36, 77–85. [Google Scholar] [CrossRef]
- Graham, L. Mobile mapping systems overview. Photogramm. Eng. Remote Sens. 2010, 76, 222–228. [Google Scholar]
- Su, W.; Guo, H.; Zhao, D.L.; Zhang, M.Z.; Zhang, L.; Wu, D.Y. Estimation of actual leaf area of maize based on terrestrial laser scanning. Chin. Soc. Agric. Mach. 2016, 7, 345–353. [Google Scholar]
- Cifuentes, R.; Van Der Zande, D.; Farifteh, J.; Salas, C.; Coppin, P. Effects of voxel size and sampling setup on the estimation of forest canopy gap fraction from terrestrial laser scanning data. Agric. For. Meteorol. 2014, 194, 230–240. [Google Scholar] [CrossRef]
| Model | STONEX X300 |
|---|---|
| Measuring range | 2–300 m (100% Reflectivity) |
| Visual range | Level 360° (Panoramic view) vertical 90° (−25° to +65°) |
| Accuracy | <6 mm (50 m) <40 mm (300 m) |
| Scanning speed | >40,000 points/s |
| Scan resolution | 0.37 mrad |
| Data storage | 32 GB |
| Sample Number | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1-1 | 1-2 | 1-3 | 1-4 | 1-5 | 1-6 | 1-7 | 1-8 | 1-9 | |
| Reference leaf mass (g) | 0.038 | 0.057 | 0.032 | 0.071 | 0.038 | 0.046 | 0.048 | 0.038 | 0.052 |
| Reference leaf area (cm2) | 1.528 | 1.743 | 1.187 | 2.002 | 1.269 | 1.459 | 1.592 | 1.367 | 1.800 |
| SLA (cm2/g) | 39.705 | 30.397 | 37.390 | 28.142 | 33.130 | 31.463 | 33.394 | 35.891 | 34.810 |
| 2-1 | 2-2 | 2-3 | 2-4 | 2-5 | 2-6 | 2-7 | 2-8 | 2-9 | |
| Reference leaf mass (g) | 0.049 | 0.035 | 0.039 | 0.085 | 0.063 | 0.040 | 0.052 | 0.036 | 0.047 |
| Reference leaf area (cm2) | 1.769 | 1.226 | 1.535 | 2.354 | 1.930 | 1.653 | 1.677 | 1.209 | 1.774 |
| SLA (cm2/g) | 36.464 | 35.035 | 39.196 | 27.570 | 30.623 | 41.159 | 32.169 | 33.268 | 37.365 |
| R2 of Different Scales of LA Estimation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Layers (m) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
| 0.01 (m) | ||||||||||
| L | 0.532 | 0.575 | 0.59 | 0.594 | 0.603 | 0.603 | 0.606 | 0.609 | 0.61 | 0.63 |
| E | 0.4 | 0.428 | 0.44 | 0.444 | 0.454 | 0.452 | 0.457 | 0.459 | 0.459 | 0.481 |
| Q | 0.649 | 0.654 | 0.659 | 0.659 | 0.661 | 0.662 | 0.661 | 0.663 | 0.662 | 0.673 |
| 0.02 (m) | ||||||||||
| L | 0.652 | 0.686 | 0.707 | 0.71 | 0.717 | 0.72 | 0.723 | 0.727 | 0.729 | 0.753 |
| E | 0.497 | 0.528 | 0.548 | 0.551 | 0.561 | 0.561 | 0.569 | 0.57 | 0.571 | 0.599 |
| Q | 0.69 | 0.71 | 0.725 | 0.728 | 0.732 | 0.735 | 0.736 | 0.74 | 0.74 | 0.761 |
| 0.03 (m) | ||||||||||
| L | 0.708 | 0.746 | 0.765 | 0.768 | 0.773 | 0.777 | 0.781 | 0.782 | 0.786 | 0.809 |
| E | 0.548 | 0.586 | 0.606 | 0.61 | 0.62 | 0.622 | 0.631 | 0.629 | 0.631 | 0.662 |
| Q | 0.729 | 0.757 | 0.773 | 0.776 | 0.781 | 0.785 | 0.787 | 0.788 | 0.791 | 0.812 |
| 0.04 (m) | ||||||||||
| L | 0.749 | 0.785 | 0.804 | 0.806 | 0.611 | 0.817 | 0.821 | 0.817 | 0.823 | 0.844 |
| E | 0.587 | 0.625 | 0.646 | 0.652 | 0.662 | 0.665 | 0.676 | 0.67 | 0.673 | 0.703 |
| Q | 0.76 | 0.79 | 0.807 | 0.809 | 0.815 | 0.82 | 0.824 | 0.82 | 0.825 | 0.845 |
| 0.05 (m) | ||||||||||
| L | 0.755 | 0.793 | 0.81 | 0.812 | 0.832 | 0.838 | 0.841 | 0.836 | 0.844 | 0.847 |
| E | 0.583 | 0.624 | 0.645 | 0.647 | 0.691 | 0.693 | 0.704 | 0.698 | 0.701 | 0.715 |
| Q | 0.767 | 0.798 | 0.813 | 0.814 | 0.835 | 0.84 | 0.843 | 0.839 | 0.845 | 0.849 |
| 0.06 (m) | ||||||||||
| L | 0.8 | 0.831 | 0.844 | 0.844 | 0.847 | 0.854 | 0.847 | 0.845 | 0.859 | 0.871 |
| E | 0.641 | 0.68 | 0.7 | 0.702 | 0.712 | 0.716 | 0.705 | 0.706 | 0.723 | 0.749 |
| Q | 0.804 | 0.833 | 0.846 | 0.846 | 0.849 | 0.856 | 0.848 | 0.847 | 0.86 | 0.87 |
| 0.07 (m) | ||||||||||
| L | 0.815 | 0.845 | 0.857 | 0.856 | 0.857 | 0.862 | 0.865 | 0.858 | 0.865 | 0.877 |
| E | 0.659 | 0.698 | 0.715 | 0.718 | 0.728 | 0.732 | 0.742 | 0.733 | 0.735 | 0.763 |
| Q | 0.819 | 0.847 | 0.858 | 0.857 | 0.858 | 0.864 | 0.866 | 0.86 | 0.866 | 0.878 |
| 0.08 (m) | ||||||||||
| L | 0.834 | 0.851 | 0.869 | 0.865 | 0.868 | 0.873 | 0.876 | 0.869 | 0.877 | 0.886 |
| E | 0.681 | 0.706 | 0.732 | 0.732 | 0.747 | 0.749 | 0.762 | 0.75 | 0.75 | 0.779 |
| Q | 0.837 | 0.852 | 0.87 | 0.866 | 0.869 | 0.875 | 0.877 | 0.871 | 0.878 | 0.886 |
| 0.09 (m) | ||||||||||
| L | 0.82 | 0.862 | 0.871 | 0.868 | 0.868 | 0.873 | 0.873 | 0.868 | 0.876 | 0.878 |
| E | 0.689 | 0.722 | 0.741 | 0.74 | 0.75 | 0.755 | 0.764 | 0.755 | 0.757 | 0.778 |
| Q | 0.829 | 0.863 | 0.872 | 0.869 | 0.869 | 0.875 | 0.874 | 0.869 | 0.877 | 0.878 |
| 0.1 (m) | ||||||||||
| L | 0.859 | 0.87 | 0.875 | 0.873 | 0.873 | 0.881 | 0.878 | 0.829 | 0.879 | 0.881 |
| E | 0.71 | 0.738 | 0.761 | 0.755 | 0.764 | 0.768 | 0.775 | 0.739 | 0.764 | 0.788 |
| Q | 0.861 | 0.871 | 0.877 | 0.874 | 0.873 | 0.882 | 0.879 | 0.835 | 0.88 | 0.882 |
| Voxel | Model | R2 |
|---|---|---|
| 0.01 | 0.673 | |
| 0.02 | 0.761 | |
| 0.03 | 0.812 | |
| 0.04 | 0.845 | |
| 0.05 | 0.849 | |
| 0.06 | y = 0.0088x + 2.8488 | 0.871 |
| 0.07 | 0.878 | |
| 0.08 | 0.886 | |
| 0.09 | 0.878 | |
| 0.1 | 0.882 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Y.; Yu, K.; Yao, X.; Xie, Q.; Hsieh, Y.; Liu, J. Estimation of Pinus massoniana Leaf Area Using Terrestrial Laser Scanning. Forests 2019, 10, 660. https://doi.org/10.3390/f10080660
Deng Y, Yu K, Yao X, Xie Q, Hsieh Y, Liu J. Estimation of Pinus massoniana Leaf Area Using Terrestrial Laser Scanning. Forests. 2019; 10(8):660. https://doi.org/10.3390/f10080660
Chicago/Turabian StyleDeng, Yangbo, Kunyong Yu, Xiong Yao, Qiaoya Xie, Yita Hsieh, and Jian Liu. 2019. "Estimation of Pinus massoniana Leaf Area Using Terrestrial Laser Scanning" Forests 10, no. 8: 660. https://doi.org/10.3390/f10080660
APA StyleDeng, Y., Yu, K., Yao, X., Xie, Q., Hsieh, Y., & Liu, J. (2019). Estimation of Pinus massoniana Leaf Area Using Terrestrial Laser Scanning. Forests, 10(8), 660. https://doi.org/10.3390/f10080660





