Next Article in Journal
Reasons for the Extremely Small Population of putative hybrid Sonneratia × hainanensis W.C. Ko (Lythraceae)
Next Article in Special Issue
Analysis of Economic Feasibility of Ash and Maple Lamella Production for Glued Laminated Timber
Previous Article in Journal
Drivers of Wildfire Occurrence Patterns in the Inland Riverine Environment of New South Wales, Australia
Previous Article in Special Issue
Orthotropic Tension Behavior of Two Typical Chinese Plantation Woods at Wide Relative Humidity Range
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 10
Issue 6
10.3390/f10060525
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Construction of Wood-Based Lamella for Increased Load on Seating Furniture

by
Nadežda Langová
,
Roman Réh
,
Rastislav Igaz
,
Ľuboš Krišťák
*,
Miloš Hitka
and
Pavol Joščák
Faculty of Wood Sciences and Technology, Technical University in Zvolen, 960 01 Zvolen, Slovakia
*
Author to whom correspondence should be addressed.
Forests 2019, 10(6), 525; https://doi.org/10.3390/f10060525
Submission received: 9 May 2019 / Revised: 6 June 2019 / Accepted: 18 June 2019 / Published: 25 June 2019
(This article belongs to the Special Issue Wood Properties and Processing)
Browse Figures
Versions Notes

Abstract

:
The research on population shows that the count of overweight people has been constantly growing. Therefore, designing and modifying utility items, e.g., furniture should be brought into focus. Indeed, furniture function and safety is associated with the weight of a user. Current processes and standards dealing with the design of seating furniture do not meet the requirements of overweight users. The research is aimed at designing flexible chairs consisting of lamellae using the finite element method (FEM). Three types of glued lamellae based on wood with different number of layers and thickness were made and subsequently, their mechanical properties were tested. Values for modulus of elasticity and modulus of rupture were used to determine stress and deformation applying the FEM method for modelling flexible chairs. In this research, the methodology for evaluating the ultimate state of flexible chairs used to analyse deformation and stability was defined. The analysis confirms that several designed constructions meet the requirements of actual standards (valid for the weight of a user up to 110 kg) but fail to meet the requirements for weight gain of a population.

1. Introduction

Requirements of the construction design of furniture for sitting arise from the needs to ensure that healthy sitting provides physical, mental and social comfort for users. Promoting correct posture with high quality lumbar support (total surface pressure is reduced as much as possible) and the ability to change positions while sitting are two ways to make users feel comfortable over long periods of usage. Correct sitting positions may prevent permanent spinal deformity or lower quality of life physiology, such as breathing, digestion, etc. [1]. Several requirements must be taken into consideration while designing seating furniture, but two of them are considered essential: Various measurements of the human body (especially height), and different weight and human body shapes must be taken into account.
Determining the appropriate single weight for all users is a difficult process as weight gain has recently been reported all over the world. In many countries, population weight gain is seen as part of the global obesity epidemic [2,3,4,5,6,7,8]. Data from 591 local and 369 national research studies were used by the author [9]. Another study based on 450 national studies determined the trends in weight gain from 1990 to 2020 [10]. The data mentioned in both research studies, as well as in many others, have showed overall weight gain in recent decades [11,12,13]. Regional and national studies in European countries (Figure 1) show that the situation is very similar all over Europe [14,15,16,17]. In 2002, the 95th, 98th and 99th percentiles for the body weight of men in the US were 114.6 kg, 131.61 kg and 141.17 kg [18].
Similar increase in average weight of users has been observed in the Slovak population as well. In 2017, the weight of more than 5% Slovak men was 110 kg (Figure 2). Moreover, the weight of 11% of these men was more than 130 kg. Based on BMI data in Slovakia, in 2017, 400,000 men in Slovakia suffered from obesity and 90,000 men suffered from severe obesity [19,20,21,22,23].
Various industrial sectors, such as automation, aviation, furniture manufacturing, footwear, and clothing industries have been affected by the current trend in human dimensions, especially steady weight gain and an increase in human height over the last few years [24,25,26]. In the case of furniture, these trends have been applied in some countries in the world recently, e.g., in the US, the standard BIFMA X6.1 (2012), as a new safety and performance standard for educational seating was accepted by the National Standards Institute (ANSI). Three sizes of school chairs were defined in the standard: A (seat height of less than 352 mm, user weight of 35 kg—it corresponds with the 95th percentile for boys aged 6), B (352 mm to 425 mm, 75 kg—it corresponds with the 95th percentile for girls aged 12), and C (more than 425 mm, 115 kg—it corresponds with 95% for adult male population) [27,28]. The standard resulted from long-term research that aimed at the importance of designing appropriate classroom furniture for schoolchildren [29,30,31,32,33]. Furniture for users with weight from 253 lb (115 kg) up to 400 lb (181 kg), which corresponds with the 99.5th percentile for men in the US, is specified in another accepted standard BIFMA X5.11 (2015) [34]. Similar standards were also accepted in Australia, e.g., the standard AFRDI 142 (2012) focused on four categories of users of “heavy duty” office chairs: 135 kg for a single shift (8 h), 135 kg for multiple shifts, 160 kg for single/multiple shifts [35]. Another Australian standard AFRDI 151 (2014) deals with chairs for home, designed for users with weight more than 100 kg (four options—135kg, 160 kg, 185 kg and chairs for bariatric patients with the weight more than 300 kg) [36]. In Europe, there is the standard BS 5459-2 focused on static and dynamic load of office pedestal chairs for persons with weight up to 225 kg [37]. This standard was designed by the company Satra, furniture testing facility in the UK (ISO 17025:2017) [38,39].
There are not many research studies dealing with furniture dimensions and construction in connection with overweight population or persons with disabilities [40]. References [41,42,43,44] suggest using anthropometric measurements in the process of designing furniture. The research of the authors [45,46] is focused on static analysis and testing the chairs in connection with the weight of users. In Slovakia, the effect of body weight on the size of chair joints was analysed in the study [46]. At the same time, the effect of a secular trend on functional dimensions of furniture was studied [47]. Czech authors [48] dealt with the use of anthropometric data in connection with seating and bed furniture as well. The authors [49] discussed the use of wider beds by healthcare providers in the case of patients with weight of more than 159 kg. The use of specific bed size for users with weight more than 147 kg or BMI score greater than 55 is suggested in another study [50]. Oversized beds for patients with BMI greater than 45 are recommended in the study [51].
Native wood and wood composites, besides plastics, and metals, are the most used materials in the manufacturing process of seating furniture. Fixed and flexible seating arrangement can be recognised in terms of constructing and joining structural elements of seating furniture. Stiffness required, especially in the case of dining chairs, is a typical feature of fixed seating arrangement made out of solid timber [52]. Flexible seating arrangement is especially used in manufacturing chairs designed for relaxation or as office chairs [53]. Wood is modified or wood-based composite materials are made of it in order to increase wood flexibility (as well as wood strength). Laminated furniture panels—lamellae and plywood—are widely used in furniture manufacturing. Properties of lamellae and plywood used in furniture projects depend on many various factors, such as moisture content of veneers, temperature, pressure and pressing time [54,55,56,57,58]. Adhesive properties, its viscosity, thickness of adhesive layer, quality of adhesive application, mechanical properties of veneers, treatment quality or removal of small elements from the surface (saw dust) are other factors affecting the bending strength [59,60,61,62,63]. Due to high bending strength of lamellae during dynamic loading, laminated wood is preferred in furniture manufacturing, especially chairs and beds [64].
At present, there are two directions in the research into chair anatomy. The first direction is focused on experimental testing of furniture construction. Experimental measurements and calculations are focused mainly on the weakest point—the joint—during static and dynamic loading and on the effect of tenon size on the ratio of dynamic to static loading rate [65,66,67,68,69,70,71,72]. The second direction deals with furniture design and construction using numerical and analytical methods. The finite element method (FEM) used to estimate or determine the load capacity of individual joint dimensions is the most often used method [73,74,75,76,77,78].
FEM allows manufacturers to optimise the shape and size of chairs. The developed models establish procedures to perform virtual testing on laminated bamboo chair to reduce product design and testing time [79]. This virtual testing results in design improvement and development of the laminated bamboo chair. The research study [80] is focused on classification of chairs according to their performance. Three hundred and fifteen chairs were tested and following the test results, acceptable light, medium and heavy design loads were determined for wood chair performance. Moreover, these values are in compliance with the allowable design loads.
Current European Standards associated with seating furniture (EN 1728:2012, EN 12520:2015, EN 1022:2018) are based on users with body weights of up to 110 kg [81,82,83]. Based on results of weight gain all around the world, the aim of the research is to determine the effect of the human weight on the load-carrying capacity and the dimensions of flexible chair consisting of lamellae. Mentioned data are required to a large extent by chair manufacturers.
The aim of this paper was to analyse the effect of laminated furniture panels with various thicknesses on the function of chair frame construction. Suggested minimum lamella thickness meeting the requirements of chairs for users with weight up to 110 kg and 150 kg resulted from the conducted research. For the ultimate load-carrying capacity and ability to use lamellae in flexible chairs, three thicknesses of lamellae were studied. Other thicknesses of lamellae, required to ensure overweight users feel safe, were tested. The methodology for evaluating the ultimate limit state of flexible chairs used based on ergonomics and chair safety can be considered for further research; normal and shear strength must be evaluated as well.

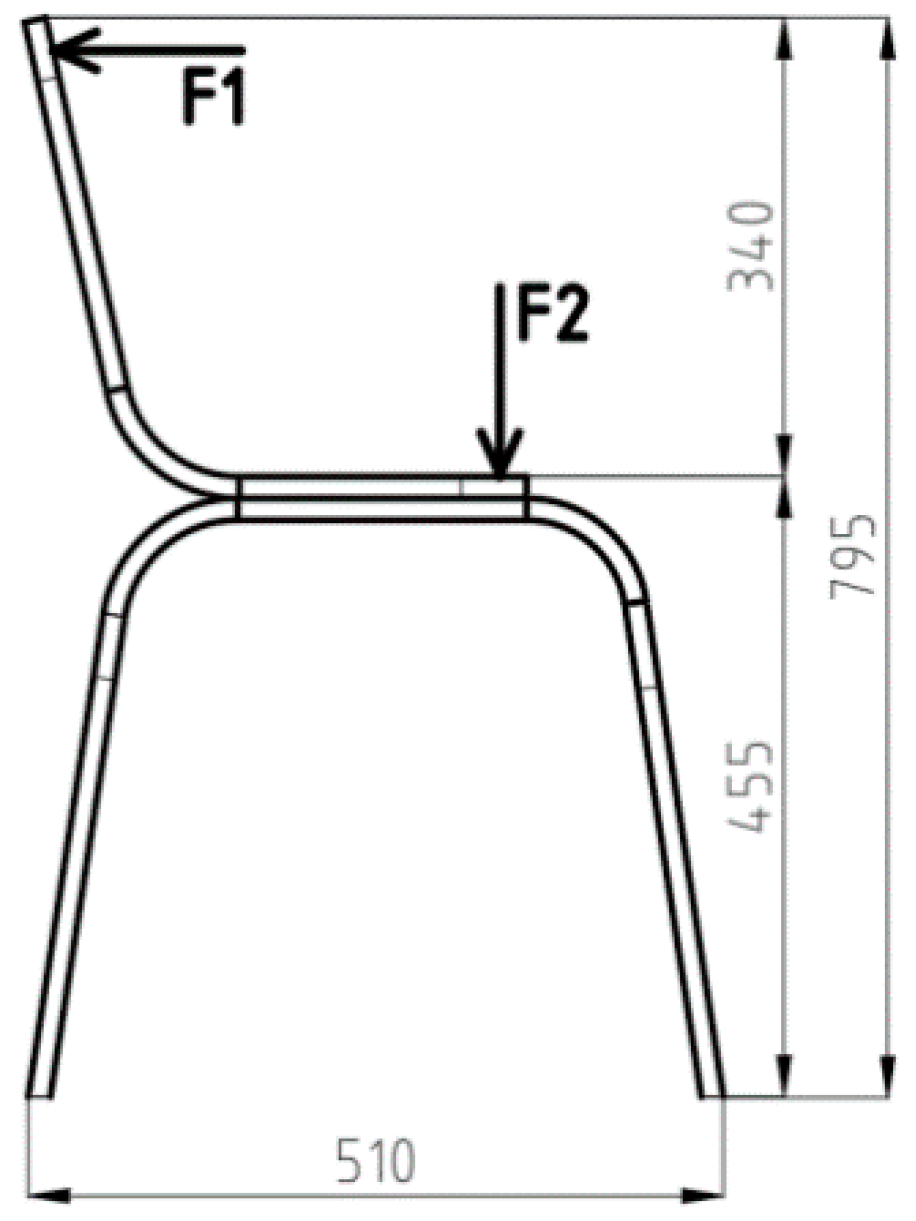
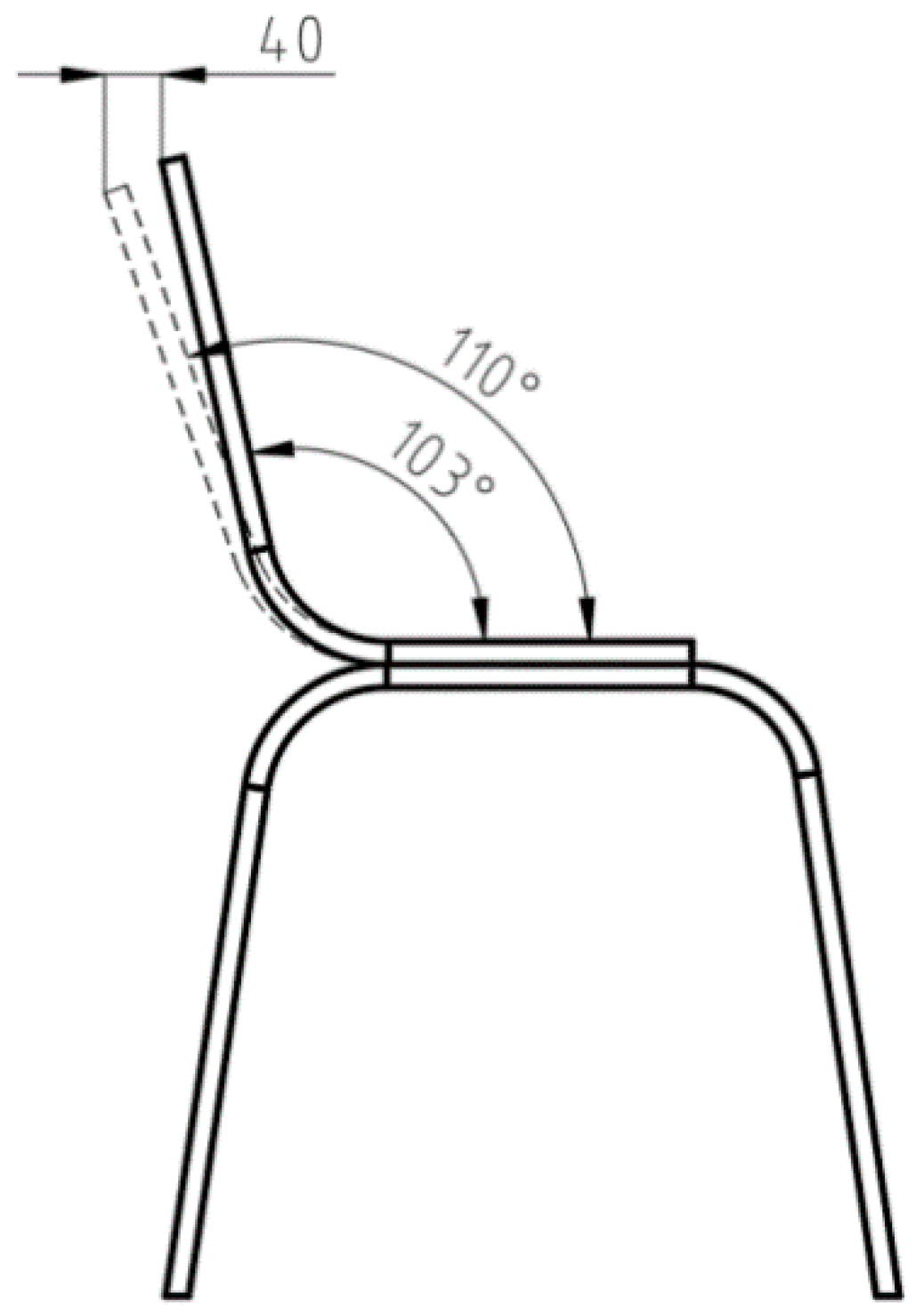
2. Materials and Methods

Three types of lamellae with various numbers of layers and total thickness were examined in the research on mechanical properties. Individual types of lamellae consisted of 9, 11 or 13 veneer layers created the final thickness of lamellae of 11.0 mm (type A), 13.5 mm (type B) or 16.0 mm (type C).
The lamellae were made of veneers of European beech wood (Fagus sylvatica L.) without defects by rotary peeling process using a 4-foot lathe (Královopolská strojírna, Brno, Czech Republic) at the Technical University in Zvolen, Slovakia from plasticized round wood. Beech wood is the most used wood species in furniture manufacturing in Slovakia. Its mechanical properties make it ideal for veneer production. The average thickness of veneers after drying to the moisture content of 6 ± 1% was 1.23 mm. Direction of wood grain in all veneers in lamella set was the same. PVAC dispersion Rakoll E WB 0301 (H. B. Fuller, Minnesota, USA) was used for gluing. The viscosity of the adhesive mixture was 5.500 mPa·s and pH value was 3.5 at the time of gluing. Adhesive was applied to the second veneer on both sides using a glue spreader with two rollers and an adhesive layer formed was 220 g·m−2.
Veneer set pressing was carried out in a hydraulic press using a press mold to form the final lamella shape. Forasmuch as the molds were under stress, the pressure during pressing process was 0.8 N·mm−2, at a temperature of 20 °C for 30 min. The total dimension of pressed semi-finished products was as follows: length of 600 mm and width of 280 mm. The angle between the two adjacent lamella sides was 103° with radius of curvature of 80 mm. After stabilizing (120 h in standard climatic conditions), the semi-finished product was cut into final lamellae with width of 50 mm. Subsequently, individual lamellae were smoothed with 80-, 120- and 150-grit sandpaper to improve final surface quality.
Afterwards, test specimens were formed from lamellae in order to determine mechanical properties. Thirty test specimens of each type (A, B and C) with dimension of 250 × 50 mm were formed from the straight part of the lamellae. From the mold lamella part, 30 mold test specimens for each type (A, B and C) were formed. Subsequently, test specimens were air-conditioned at a temperature of 20 ± 2 °C and air humidity of 65 ± 5%. The moisture content (EMC) of specimens after air-conditioning was 12 ± 1%.
Flat common specimens were tested using the standard methodology of the three-point bend test according to the standard EN 310: 1993. Mold unconventional specimens were tested by modified methodology created for the needs of this research. Mechanical testing of mold specimens was carried out using the modified three-point bend test. The load was spread evenly and the specimen was broken after 60 ± 30 s.
Wood is a material whose properties possess orthogonal anisotropy, i.e., its physical and mechanical properties differ in three principal planes [84]. Three symmetry planes are differentiated in wood: cross-section perpendicular to the grain direction, longitudinal-radial and longitudinal-tangential, which are parallel with the wood grain direction and at the same time are mutually perpendicular. Due to its structural organization, lamella can be considered to be an anisotropy material in the plane perpendicular to the grain direction. The mechanical properties of lamella in both planes perpendicular to the grain direction are almost identical. Therefore, wood-based lamellae can be defined as transverse-axial anisotropic material. In the presented research, lamellae were formed as an orthogonal anisotropic material. Anisotropy must be taken into account in the modeling with the finite element method. The physical and mechanical properties of lamellae used in the modelling are summarized in Table 1.
In the research on seating construction, a chair consisting of two frames was created. Base chair frame consisted of two U-shaped profiles were joined with transverse rails. The frame of seat and back was flexible and joined with transverse elements. Glued joints were used for chair construction because in comparison to other mechanical joining components, their stiffness was higher and they transferred the load better. Anthropometric measurements of users were taken into account for dimensions, construction and shape of the chair. Basic dimensions of designed chair are mentioned in Figure 3. Lamella dimensions and shape used in the project corresponded with those made and tested experimentally. While creating a chair model, three types of tested lamellae were used one after another (type A, B and C).
The methodology for testing the chairs, especially loading, was based on the standard EN 1728: 2012. The users’ weight of 110 kg was regarded as maximum weight in the standard, while horizontal force acting on the back was F1 = 450 N and the vertical force acting on the seat was F2 = 1300 N. In the case of users with weight more than 110 kg, acting forces were not defined. However, statistics dealing with the weight of adult population showed the fact that designing the furniture for users with weight of up to 110 kg did not meet the actual requirements. Therefore, the forces resulting from the load caused by the overweight users had to be defined. 150 kg was the maximum user’s weight set and the forces were determined using multiple linear regression. Acting forces of F1 = 613 N and F2 = 1775 N and user’s weight of 150 kg were used in the process of creating a chair model. Direction and the point at which the force was applied are defined in Figure 3.
The loading analysis of the tested chair was conducted using the program ANSYS. In the software environment, a 3D volume model taking into consideration the orthotropic properties of wood-based lamellae was created. A coordinate system used was as follows: Y-axis was in the grain direction, X-axis was perpendicular to the grain in the radial direction and Z-axis was perpendicular to the grain in tangential direction. When mold lamellae were created—base, seat and chair back—the properties of lamellae were changed in relation to the lamella shape. Chair base lamella was created from three parts. Properties in individual planes were changed in relation to grain orientation. In the mold parts of lamella, the values of loading perpendicular to the grain were defined. Material constants are defined in Table 1. Every element had to be assigned to a particular material. 3D element Solid 95 with 20 nodes was an element type. Boundary conditions were according to the standard EN 1728:2012. Supports of the back legs of a chair were regarded as fixed (fixed supports) in order to ensure that the loading was evenly transferred to the construction. Displacement supports were used in the front legs of the chair, movement in the y-axis direction was available. All joints in chair construction were considered fixed (bonded).
In terms of dimensioning the structural elements, limit state design requires the construction to meet two principal criteria: the ultimate limit state (ULS) used to evaluate the strength of construction, i.e., design strength and the serviceability limit state (SLS) used to evaluate the construction deformation.
The serviceability limit state, i.e., maximum deformation of flexible chair frame is defined neither in scientific journals nor in standards. It can result from an ergonomic chair design, suggested dimensions and seat-to-back angle. The angle recommended for designing a relaxed chair ranges from 103° to 110°. When 110° was the maximum value of an angle that could not be exceeded during loading, then the maximum displacement of a chair back was 40 mm backwards (Figure 4). This value of displacement was considered the maximum value for evaluating the serviceability limit state.
When determining the serviceability limit state for flexible chairs, maximum limit displacement of the chair back in the highest point could be umax = 40 mm. It resulted from the suggested seat-to-back angle of 110° (Figure 4). Reliability of the designed displacement ud (determined by the FEM calculation) is:
u d ≤ u m a x
However, in terms of safety, a chair with mentioned limit displacement of back must be safe and stable, i.e., backward overturning must not occur (chair must not tip over). Calculation of stability is mentioned in the standard EN 1022:2018. Loading is shown in Figure 5. Considering the flexibility, the studied lamella chair was a chair with variable geometry. According to the mentioned standard, the chair was considered stable when it does not tip after applying a load of m = 110 kg. When the seat-to-back angle was 110°, the centre of gravity of the load could not be positioned behind the tipping point of a chair, i.e., the point when the back leg is in contact with the floor. The position of the centre of gravity of the load can be defined using the graphical method (Figure 5).
The serviceability limit state boundary conditions resulting from the lamella stiffness determined experimentally was defined specifically in the chair construction. Following the results of the FEM analysis, normal and shear stresses were determined. When structural elements were dimensionised, normal and shear stresses were considered to be a design stress. In the process of dimensioning the chair components according to the serviceability limit state, requirements for reliable molding had to be met:
σ 0 , d ≤ f b , 0 , d
where: σ0,d—design stress in the beech lamella mold (MPa),
 fb,0,d—design strength in the beech lamella mold (MPa).
The value of characteristic strength had to be determined in order to calculate the design strength of lamella. Mean value of the bending strength ( σ ¯ ) of tested lamellae achieved experimentally at a temperature of t = 20 °C and φ = 65% was an essential condition to determine the characteristic strength. Characteristic bending strength is a value corresponding with α quantile of assumed statistical division of evaluated strength. When α = 5%, the formula is:
f b , 0 , k = σ ¯ · ( 1 − t 95 · ϑ x )
where:  f b , 0 , k —characteristic bending strength of glued lamella (MPa),
  σ ¯ —mean value of bending strength (MPa),
  t 95 —quantile of Student’s t-distribution (one-side test), when t95 = 1.64,
  ϑ x —coefficient of variation (absolute value) (MPa).
When the characteristic bending strength is known, design strength f b , 0 , d is determined using the formula:
f b , 0 , d = k m o d · f b , 0 , k γ M
where:  f b , 0 , k —characteristic strength of beech lamella in mold (MPa),
  γ M —partial safety factor (-), for wood-based materials γM = 1.3,
  k m o d —modification coefficient (-) (takes into account the effect of loading time and moisture content on the characteristic strength of material) for the action/load with the shortest design situation kmod = 1.10.

3. Results and Discussion

Values of bending strength were determined experimentally using the specimens made of lamellae described in methodology. Bending strength was defined individually for flat and mold parts of lamellae. Mean values of bending strength, characteristic values, as well as design values for flat and mold lamella parts determined experimentally are summarised in the following tables (Table 2 and Table 3). The values in Table 3 highlighted in bold (fb,0,d) were used for evaluation of the ultimate limit state.

3.1. Ultimate Limit State Assessment

With dependence on the type of chair construction, the joint between the side rail and back leg or the seat-back joint is the most stressed joint [86,87,88]. This fact was confirmed in the process of lamella chair construction with the stress concentrated especially in the mold of seat frame. In terms of anisotropy, lamella mold is stressed in a direction perpendicular to the grain. Due to the direction of chair loading and according to the theory of simple bending, the inner mold part is affected by the compression parallel to the grain direction; on the other hand, outer mold part is affected by tension parallel to the grain direction. Bending strength of wood perpendicular to the grain direction is greater than the compression strength parallel to the grain direction and lower than the tensile strength parallel to the grain direction. Therefore, when evaluating the ultimate limit state, design bending strength of lamella fb,0,d (gathered experimentally) is compared to maximum normal stress (in tension σt,0,d or on compression σc,0,d) gathered using FEM. Design stress determined by FEM cannot exceed the value of design bending strength of lamella resulting from specimen testing in order to meet the conditions associated with the ultimate limit state. Due to the fact that the most significant effect of stresses is in lamella mold, values determined in mold lamellae were used for comparison. Maximum values of normal stress achieved using the FEM for chairs made of lamellae (type A, B and C) and for loading of 110 kg and 150 kg are mentioned in Table 4. FEM visual outputs of stresses are shown in Figure 6. Values highlighted in red colour are not suitable in terms of ultimate limit state.
Following the analysis of data gathered by comparing design values of bending strength determined experimentally and the values of design bending strength resulting from the use of FEM, the fact that ultimate limit state conditions were met can be stated. The values in Table 4 show that lamella with thickness of 11 mm (type A) met the requirements for use for a user with weight of 110 kg, only in the case of tensile stress. The value of compression stress was exceeded by 25.57 MPa. When the customer’s weight was 150 kg, design tensile stress was exceeded by 20.08 MPa and design compression stress by 70.40 MPa. Following the results, the fact that this type of lamella cannot be used in chair construction for overweight users can be stated.
Lamella with thickness of 13.5 mm (type B) met the requirements of the ultimate limit state when the user’s weight was 110 kg. In the case of a user with weight of 150 kg, design values of tensile stress were exceeded by 4.40 MPa and design compression stress by 64.62 MPa. Therefore, the lamella cannot be used when the chair is loaded with 150 kg.
The thickness of the last tested lamella was 16 mm (type C). It met the ultimate limit state conditions when the weight of a user is 110 kg. However, in the case of weight of 150 kg, it only met conditions in terms of tensile stress. Design value of compression stress was exceeded by 20.70 MPa. It means that lamella C cannot be used for chair construction for a user with weight of 150 kg as well.

3.2. Serviceability Limit State Assessment

Maximum values of the displacement of the upper edge of the seat u (mm) with loading of 110 kg and 150 kg and corresponding values of the distance of the centre of gravity of the load from the tipping point b (mm) in the direction of x-axis are mentioned in Table 5. FEM visual outputs to analyze the displacement of the back are shown in Figure 7. The values of displacement highlighted in red color are not satisfactory in terms of the serviceability limit state.
Analyzing the data summarized in Table 5, the serviceability limit state conditions can be evaluated. According to the requirements, seat-to-back angle must not exceed 110° (meeting the conditions results from the displacement of the upper edge of the seat). At the same time, the position of the centre of gravity must not be behind the tipping point and b value must not be negative in the direction of the x-axis. Tipping point is defined in the position of the back edge of the back leg.
Following the values determined by FEM for the lamella-type A, it is clear that the lamella did not meet defined conditions in the case of the loading of neither 110 kg nor 150 kg. In both loadings, allowable value of the displacement of the upper edge of the chair back was exceeded, and the value describing the position of the centre of gravity was negative in the direction of x-axis. Support provided by this lamella in the chair back was not adequate. Therefore, there was a danger of tipping over.
The lamella-type B did not meet the requirements for allowable back deformation for user weight of 110 kg and 150 kg. In terms of the position of the centre of gravity, the requirement is met only in case of loading of 110 kg. When user weight is 150 kg, there is a danger of tipping over because the centre of gravity was positioned behind the back leg of the chair.
The lamella-type C met the requirements for the position of the centre of gravity in the case of both weights of users. In spite of these findings, its use was not accepted due to the deformation of the chair back. Its value exceeded the allowable value for user weight of 110 kg or 150 kg.
The mentioned findings associated with meeting the requirements of the ultimate limit state as well as the serviceability limit state and the use of lamellae implied that no lamella type can be used in any tested cases of chair construction. Albeit the lamella-type C met the requirement for the ultimate limit state for the user with weight of 110 kg, the requirements for the serviceability limit state were not met.

3.3. Lamella construction meeting the requirements of ultimate states

Following the mentioned findings, the fact that lamella used in given chair construction should consist of a higher number of layers, thus, with greater thickness can be stated. Therefore, the group of specimens of lamella (type D) with 17 layers with total thickness of 21 mm was formed. Following the testing, design value of bending strength σ ¯ = 35.83 MPa with the coefficient of variation of ϑ = 5.3% was determined. Consequently, FEM analysis was carried out to determine the values of design stresses and deformation of the chair back. Calculated values are summarized in Table 6. FEM visual outputs of the stresses and displacement of the chair back are shown in Figure 8.
Comparing the values of design bending strength and design values of stresses and values of the displacement of the upper edge of chair back achieved by the FEM analysis, it is clear that the lamella-type D with thickness of 21 mm would meet the requirements for both ultimate states in the case of loading of 150 kg. Due to the fact that in the research only a small sample size of this lamella type was made, testing lamella type D will offer an excellent opportunity for further research focused on dynamic loading.
Comparing the results to other studies dealing with chair modeling using FEM is quite difficult because of the evaluation stress according to von Mises mentioned by most authors. Wood is a material whose properties possess orthogonal anisotropy with nonlinear performance in elastic and plastic deformation. According to our opinion, two mentioned facts are key factors not allowing researchers to evaluate the stresses in wood-based material according to von Mises. The von Mises stress criterion is weighing the different oriented stresses to one “mixed” stress, which is not suitable to be compared to a scalar failure value for wood [89].

4. Conclusions

Various areas of economy, including furniture design and construction, have been affected by weight gain trends across populations in the last years. In Slovakia, the average weight of the population has increased by almost 10 kg over the last 25 years. A similar trend is observed globally. Almost 6% of the Slovak population is men with weight more than 110 kg. Therefore, the current standards must be re-evaluated. Valid legislation dealing with furniture design takes into account users’ weight of 110 kg. However, according to anthropometric studies, 150 kg is the weight of users that should be taken into account in the future.
  • The research presented was focused on the assessment of two ultimate states of flexible chair construction. Minimum thickness requirements for lamellae needed for chairs for users with weight up to 110 kg and 150 kg resulted from the research.
  • Following the mechanical properties of laminated veneer lamellae and the assessment of ultimate limit state and serviceability limit state, as well as the use of lamella in flexible chairs, four thicknesses of lamellae were examined.
  • Requirements for the strength of structural elements were evaluated by the ultimate limit state and allowable deformation of chair construction and the position of the centre of gravity during the loading were evaluated by the serviceability limit state. Following the results of the research, the fact that three types of tested lamellae (thickness 11 mm, 13.5 mm and 16 mm) did not meet the requirements of the both ultimate states. Lamella with thickness of 21 mm met the requirements for both ultimate states in the case of loading of 110 kg and 150 kg.
  • The methodology to evaluate the serviceability limit state of flexible chairs based on ergonomy and chair safety can be considered as another contribution of the research.
Weight gain is a global problem affecting the industrial goods sector. In the case of research, the cooperation of professionals in anthropology, ergonomics, construction, design and health is needed, in order to modify the size and function of furniture. Designing wooden furniture should be connected with a sustainable strategy of economy aimed at efficient use of local renewable resources. Only a complex approach can contribute to meeting the goals of sustainability of the furniture industry leading to sustainability of standards and timeliness.

Author Contributions

Conceptualization, N.L., M.H., P.J. and R.I.; Data curation, N.L., R.R. and M.H.; Visualization, R.R., Ľ.K., R.I.; Writing-original draft, N.L., R.R., Ľ.K. and R.I.

Acknowledgments

This research was supported by the Slovak Research and Development Agency under Contract No. APVV-16-0297, Contract No. APVV-14-0506, Contract No. APVV-17-0583, VEGA 1/0717/19, VEGA 1/0556/19 and KEGA 012TU Z-4/2017.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Joščák, P.; Dudas, J.; Gáborík, J.; Gaff, M.; Langová, N.; Navrátil, V.; Slabejová, G. Wood and Wood-Based Furniture Constructions; Technická univerzita vo Zvolene: Zvolen, Slovakia, 2014. [Google Scholar]
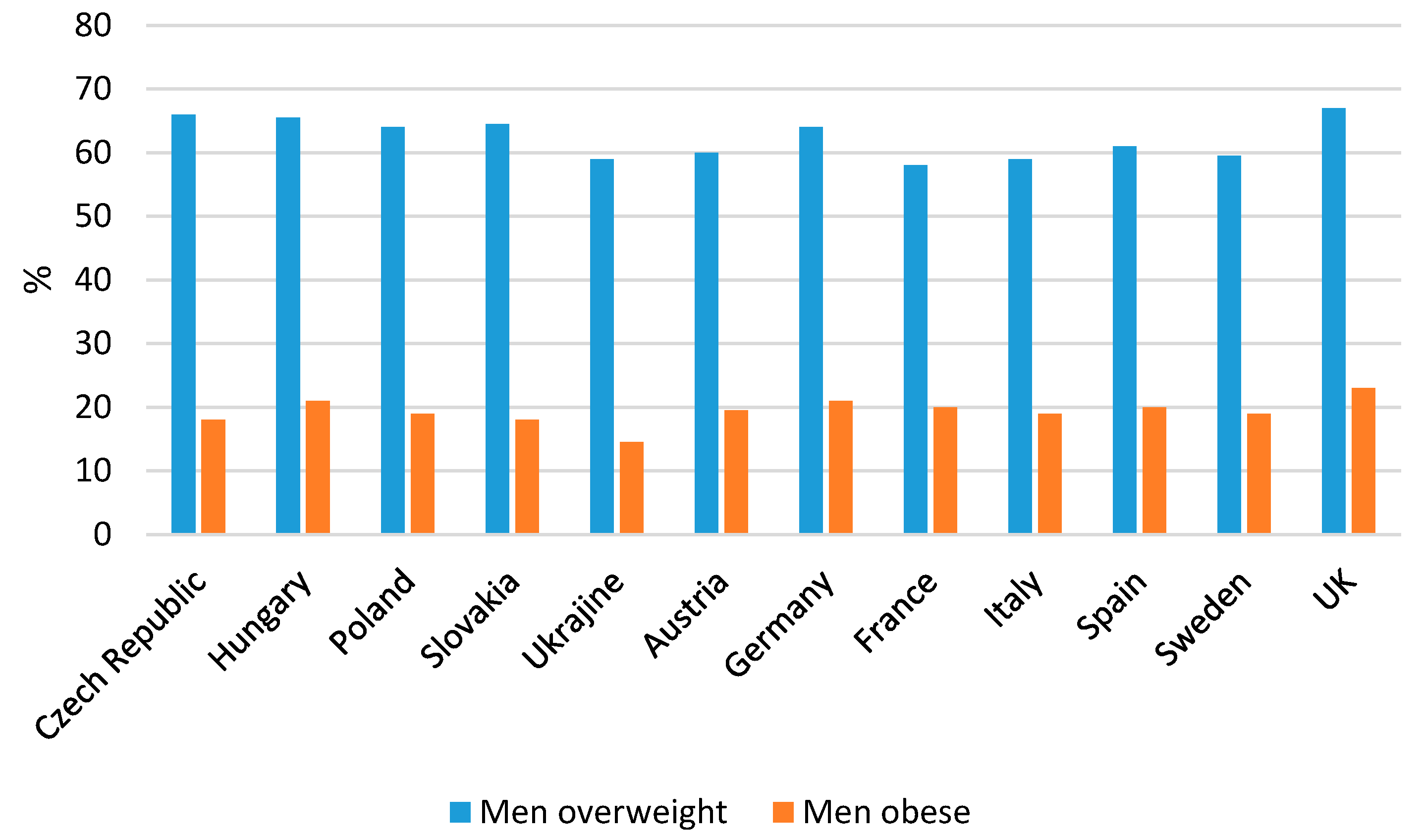
  2. Wang, Y.; Beydoun, M.A. The obesity epidemic in the United States—Gender, age, socioeconomic, racial/ethnic, and geographic characteristics: A systematic review and meta-regression analysis. Epidemiol. Rev. 2007, 29, 6–28. [Google Scholar] [CrossRef] [PubMed]
  3. Stevens, G.A.; Singh, G.M.; Lu, Y.; Danaei, G.; Lin, J.K.; Finucane, M.M.; Bahalim, A.N.; McIntire, R.K.; Gutierrez, H.R.; Cowman, M.; et al. National, regional, and global trends in adult overweight and obesity prevalences. Popul. Health Metr. 2012, 10, 22. [Google Scholar] [CrossRef] [PubMed]
  4. Tremmel, M.; Gerdtham, U.G.; Nilsson, P.M.; Saha, S. Economic Burden of Obesity: A Systematic Literature Review. Int. J. Environ. Res. Public Health 2017, 14, 435. [Google Scholar] [CrossRef] [PubMed]
  5. González-Rodríguez, L.G.; Perea Sánchez, J.M.; Aranceta-Bartrina, J.; Gil, Á.; González-Gross, M.; Serra-Majem, L.; Varela-Moreiras, G.; Ortega, R.M. Intake and Dietary Food Sources of Fibre in Spain: Differences with Regard to the Prevalence of Excess Body Weight and Abdominal Obesity in Adults of the ANIBES Study. Nutrients 2017, 9, 326. [Google Scholar] [CrossRef] [PubMed]
  6. Burke, N.L.; Shomaker, L.B.; Brady, S.; Reynolds, J.C.; Young, J.F.; Wilfley, D.E.; Sbrocco, T.; Stephens, M.; Olsen, C.H.; Yanovski, J.A.; et al. Impact of Age and Race on Outcomes of a Program to Prevent Excess Weight Gain and Disordered Eating in Adolescent Girls. Nutrients 2017, 9, 947. [Google Scholar] [CrossRef] [PubMed]
  7. Chan, R.S.; Woo, J. Prevention of Overweight and Obesity: How Effective is the Current Public Health Approach. Int. J. Environ. Res. Public Health 2010, 7, 765–783. [Google Scholar] [CrossRef] [Green Version]
  8. Peltzer, K.; Pengpid, S.; Samuels, T.A.; Özcan, N.K.; Mantilla, C.; Rahamefy, O.H.; Wong, M.L.; Gasparishvili, A. Prevalence of Overweight/Obesity and Its Associated Factors among University Students from 22 Countries. Int. J. Environ. Res. Public Health 2014, 11, 7425–7441. [Google Scholar] [CrossRef] [Green Version]
  9. Finucane, M.M.; Stevens, G.A.; Cowan, M.J.; Danaei, G.; Lin, J.K.; Paciorek, C.J.; Singh, G.M.; Gutierrey, H.R.; Lu, Y.; Bahalim, A.N. Global burden of metabolic risk factors of chronic diseases collaborating group body mass index. Lancet 2011, 377, 557–567. [Google Scholar] [CrossRef]
  10. De Onis, M.; Blössner, M.; Borghi, E. Global prevalence and trends of overweight and obesity among preschool children. Am. J. Clin. Nutr. 2010, 92, 1257–1264. [Google Scholar] [CrossRef] [Green Version]
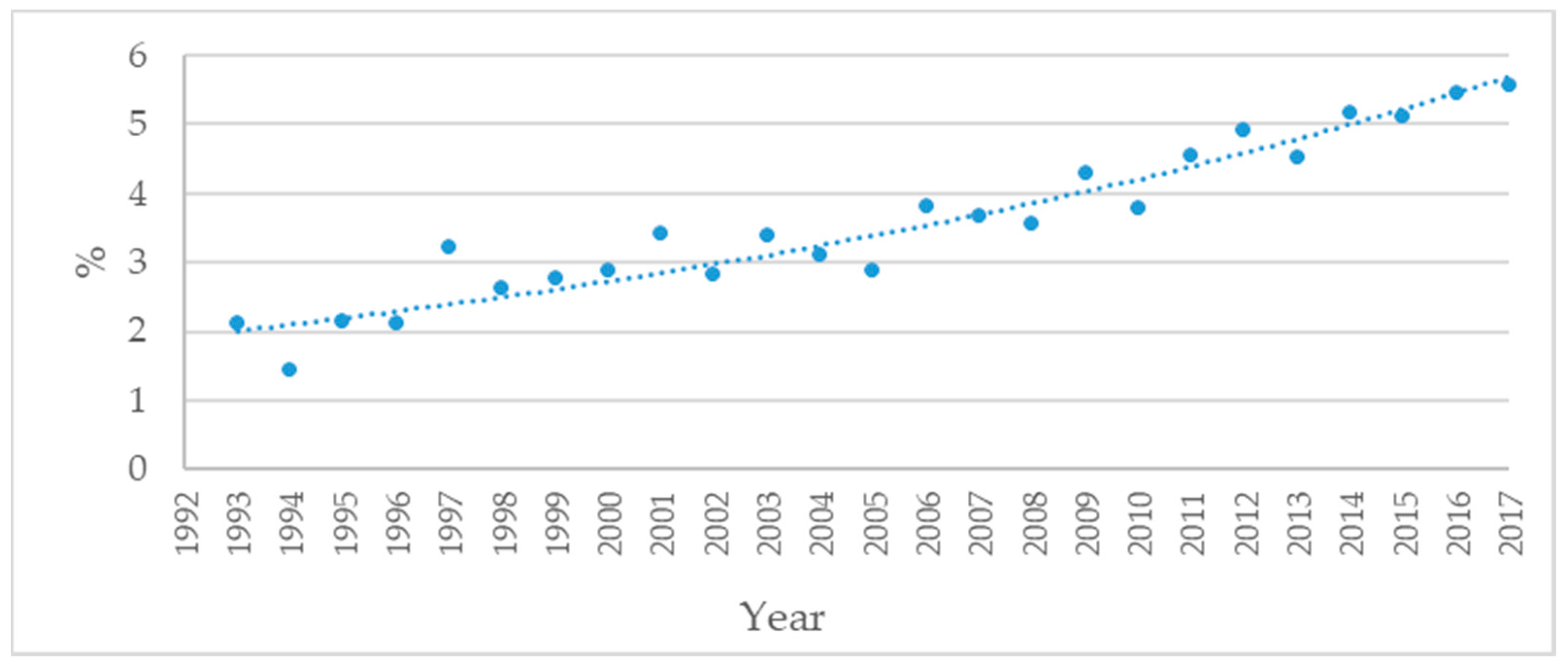
  11. Rockholm, B.; Baker, J.L.; Sorensen, T.I.A. The levelling off of the obesity epidemic since the year 1999- A review of evidence and perspectives. Obes. Rev. 2010, 11, 835–846. [Google Scholar] [CrossRef]
  12. Odunitan-Wayas, F.; Okop, K.; Dover, R.; Alaba, O.; Micklesfield, L.; Puoane, T.; Uys, M.; Tsolekile, L.; Levitt, N.; Battersby, J.; et al. Food Purchasing Characteristics and Perceptions of Neighborhood Food Environment of South Africans Living in Low-, Middle- and High-Socioeconomic Neighborhoods. Sustainability 2018, 10, 4801. [Google Scholar] [CrossRef]
  13. Manzano, S.; Doblaré, M.; Hamdy Doweidar, M. Altered Mechano-Electrochemical Behavior of Articular Cartilage in Populations with Obesity. Appl. Sci. 2016, 6, 186. [Google Scholar] [CrossRef]
  14. Ng, M.; Fleming, T.; Robinson, M.; Tomson, B.; Graetz, N.; Margono, C.; Mullany, E.C.; Biryukov, S.; Abbafati, C.; Abera, S.F.; et al. Global, regional, and national prevalence of overweight and obesity in children and adults during 1980-2013: A systematic analysis for the Global Burden of Disease Study 2013. Lancet 2014, 384, 766–781. [Google Scholar] [CrossRef]
  15. Di Cesare, M.; Bentham, J.; Stevens, G.A.; Zhou, B.; Danaei, G.; Lu, Y.; Bixby, H.; Cowan, M.J.; Riley, L.M.R.; Hajifathalian, K.; et al. Trends in adult body-mass index in 200 countries from 1975 to 2014: A pooled analysis of 1698 population-based measurement studies with 19.2 million participants. Lancet 2016, 387, 1377–1396. [Google Scholar]
  16. Hitka, M.; Hajduková, A. Antropometrická optimalizácia rozmerov lôžkového nábytku. Acta Facultatis Xylologiae Zvolen 2013, 55, 101–109. [Google Scholar]
  17. Čuta, M.; Kukla, L.; Novák, L. Modelling the development of body height (length) in children using parental height data. Československá Pediatrie 2010, 65, 159–166. [Google Scholar]
  18. Harrison, C.R.; Robinette, K.M. CAESAR > Summarz Statistics for the Adult Population (Ages 18–65) of the United States of America; United States Air Force Research Laboratorz: Wright-Patterson AFB, OH, USA, 2002.
  19. Réh, R.; Krišťák, Ľ.; Hitka, M.; Langová, N.; Joščák, P.; Čambál, M. Analysis to Improve the Strength of Beds Due to the Excess Weight of Users in Slovakia. Sustainability 2019, 11, 624. [Google Scholar] [CrossRef]
  20. Ministry of Health of the Slovak Republic. Report on Health Status in Slovakia. Health 2016. Available online: http://health.gov.sk (accessed on 31 September 2018).
  21. Public Health Authority of the Slovak Republic. Annual Report on the Activities of the Public Health Office for 2017. Available online: http://uvzsr.sk/docs/vs/vyrocna_sprava_2017.pdf (accessed on 31 September 2018).
  22. Statistical Office of the Slovak Republic. View of Health Status of the Slovak Population and Its Determinants (Results of EHIS 2016). Available online: http://slovak.statistics.sk (accessed on 31 September 2018).
  23. World Health Organization Regional Office for Europe. The Health Systems in Transition (HiT). Available online: http://euro.whoint/en/countries/slovakia (accessed on 31 September 2018).
  24. Porta, J.; Saco-Ledo, G.; Cabanas, M.D. The ergonomics of airplane seats: The problem with economy class. Int. J. Ind. Ergon. 2019, 69, 90–95. [Google Scholar] [CrossRef]
  25. Quigley, C.; Southall, D.; Freer, M.; Moody, A.; Porter, M. Anthropometric Study to Update Minimum Aircraft Seating Standards. Available online: https://dspace.lboro.ac.uk/2134/701 (accessed on 18 January 2019).
  26. Roggla, G.; Moser, B.; Roggla, M. Seat space on airlines. Lancet 1999, 353, 1532. [Google Scholar] [CrossRef]
  27. BIFMA X6.1. Educational Seating. American National Standard for Office Furnishings (Revised in 2018); BIFMA: Grand Rapids, MI, USA, 2018. [Google Scholar]
  28. Bellingar, T.A.; Benden, M.E. New ANSI/BIFMA standard for testing of educational seating. Ergon. Des. Q. Hum. Factors Appl. 2015, 23, 23–27. [Google Scholar] [CrossRef]
  29. Parcells, C.; Stommel, M.; Hubbard, R.P. Mischmatch of classroom furniture and student body dimensions: Empirical findings and health implications. J. Adolesc. Health 1999, 24, 265–273. [Google Scholar] [CrossRef]
  30. Panagiotopoulou, G.; Christoulas, K.; Papanckolaou, A.; Mandroukas, K. Classroom furniture dimensions and anthropometric measures in primary school. Appl. Ergon. 2004, 35, 121–128. [Google Scholar] [CrossRef] [PubMed]
  31. Mohamed-Thariq, M.G.; Munasinghe, H.P.; Abeysekara, J.D. Designing chairs with mounted desktop for university students Ergonomics and comfort. Int. J. Ind. Ergon. 2010, 40, 8–18. [Google Scholar] [CrossRef]
  32. Oyewole, S.A.; Haight, J.M.; Freivalds, A. The ergonomic design of classroom furniture/computer work station for first graders in the elementary school. Int. J. Ind. Ergon. 2010, 40, 437–447. [Google Scholar] [CrossRef]
  33. Agha, S.R.; Alnahhal, M.J. Neural network and multiple linear regression to predict school children dimensions for ergonomic school furniture design. Appl. Ergon. 2012, 43, 979–984. [Google Scholar] [CrossRef] [PubMed]
  34. BIFMA X5.11. Large Occupant Office Chair Standard. American National Standard for Office Furnishings; BIFMA: Grand Rapids, MI, USA, 2015. [Google Scholar]
  35. AFRDI 142. Certification for Heavy Duty Office Chairs; Australian Furnishings Research and Development Institute: Launceston, Australia, 2012. [Google Scholar]
  36. AFRDI 151. Rated Load Standard for Fixed Height Chairs; Australian Furnishings Research and Development Institute: Launceston, Australia, 2014. [Google Scholar]
  37. BS 5459-2:2000 and A2:2008. Specification for Performance Requirements and Tests for Office Furniture; British Standards Institutions: London, UK, 2000. [Google Scholar]
  38. ISO 17025. General Requirements for the Competence of Testing and Calibration Laboratories; International Organization for Standardization: Geneva, Switzerland, 2017. [Google Scholar]
  39. SATRA. Satra Technology—International Product Research, Testing and Supply Chain Quality. Available online: http://satra.com (accessed on 31 September 2018).
  40. Bonenberg, A.; Branowski, B.; Kurcyewski, P.; Lewandowska, A.; Sydor, M.; Torzynski, D.; Zablocki, M. Designing for human use: Examples of kitchen interiors for person with disability and elderly people. Hum. Factors Ergon. Manuf. 2019, 29, 177–186. [Google Scholar] [CrossRef]
  41. Mehrparvar, A.H.; Mirmohammadi, S.J.; Hafezi, R.; Mostaghaci, M.; Davari, M.H. Static anthropometric dimensions in a population of Iranian high school students: Considering ethnic differences. Hum. Factors J. Hum. Factors Ergon. Soc. 2015, 57, 447–460. [Google Scholar] [CrossRef]
  42. Qutubuddin, S.M.; Hebbal, S.S.; Kumar, C.S. Anthropometric consideration for designing students desks in engineering colleges. Int. J. Curr. Eng. Technol. 2013, 3, 1179–1185. [Google Scholar]
  43. Shin, D.; Kim, J.Y.; Hallbeck, M.S.; Haight, J.M.; Jung, M.C. Ergonomic hand tool and desk and chair development process. Int. J. Occup. Saf. Ergon. 2008, 14, 247–252. [Google Scholar] [CrossRef]
  44. Masson, A.E.; Hignett, S.; Gyi, D.E. Anthropometric Study to Understand Body Size and Shape for Plus Size People at Work. Procedia Manuf. 2015, 3, 5647–5654. [Google Scholar] [CrossRef] [Green Version]
  45. Smardzewski, J. Furniture Design; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
  46. Hitka, M.; Joščák, P.; Langová, N.; Krišťák, L.; Blašková, S. Load-Carrying Capacity and the Size of Chair Joints D etermined for Users with a Higher Body Weight. Bioresources 2018, 13, 6428–6443. [Google Scholar]
  47. Hitka, M.; Sedmák, R.; Joščák, P.; Ližbetinová, L. Positive Secular Trend in Slovak Population Urges on Updates of Functional Dimensions of Furniture. Sustainability 2018, 10, 3474. [Google Scholar] [CrossRef]
  48. Dvouletá, K.; Káňová, D. Utilization of anthropometry in the sphere of sitting and bed furniture. Acta Univ. Agric. Silvic. Mendel. Brun. 2014, 62, 81–90. [Google Scholar] [CrossRef]
  49. Muir, M.; Archer-Heese, G. Essentials of a bariatric patient handling program. OJIN Online J. Issues Nurs. 2009, 14, 5. [Google Scholar]
  50. Gourash, W.; Rogula, T.; Schauer, P.R. Essential Bariatric Equipment: Making Your Facility More Accommodating to Bariatric Surgical Patients; Springer: New York, NY, USA, 2007. [Google Scholar]
  51. Wiggermann, N.; Smith, K.; Kumpar, D. What bed size does a patient need? The relationship between body mass index and space required to turn in bed. Nurs. Res. 2017, 66, 483–489. [Google Scholar] [CrossRef] [PubMed]
  52. Ko, Y.C.; Lo, C.H.; Chen, C.C. Influence of Personality Traits on Consumer Preferences: The Case of Office Chair Selection by Attractiveness. Sustainability 2018, 10, 4183. [Google Scholar] [CrossRef]
  53. Nüesch, C.; Kreppke, J.N.; Mündermann, A.; Donath, L. Effects of a Dynamic Chair on Chair Seat Motion and Trunk Muscle Activity during Office Tasks and Task Transitions. Int. J. Environ. Res. Public Health 2018, 15, 2723. [Google Scholar] [CrossRef]
  54. Borůvka, V.; Dudík, R.; Zeidler, A.; Holeček, T. Influence of Site Conditions and Quality of Birch Wood on Its Properties and Utilization after Heat Treatment. Part I—Elastic and Strength Properties, Relationship to Water and Dimensional Stability. Forests 2019, 10, 189. [Google Scholar] [CrossRef]
  55. Wei, P.; Rao, X.; Yang, J.; Guo, Y.; Chen, H.; Zhang, Y.; Chen, S.; Deng, X.; Wang, Z. Hot pressing of wood-based composites: A review. For. Prod. J. 2016, 66, 419–427. [Google Scholar] [CrossRef]
  56. Derikvand, M.; Kotlarewski, N.; Lee, M.; Jiao, H.; Nolan, G. Characterisation of Physical and Mechanical Properties of Unthinned and Unpruned Plantation-Grown Eucalyptus nitens H. Deane & Maiden Lumber. Forests 2019, 10, 194. [Google Scholar]
  57. Šubic, B.; Fajdiga, G.; Lopatič, J. Bending Stiffness, Load-Bearing Capacity and Flexural Rigidity of Slender Hybrid Wood-Based Beams. Forests 2018, 9, 703. [Google Scholar] [CrossRef]
  58. Réh, R.; Igaz, R.; Krišťák, Ľ.; Ružiak, I.; Gajtanska, M.; Božíková, M.; Kučerka, M. Functionality of beech bark in adhesive mixtures used in plywood and its effect on the stability associated with material systems. Materials 2019, 12, 1298. [Google Scholar] [CrossRef] [PubMed]
  59. Morales, G.A. Potential of Gmelina arborea for solid wood products. New For. 2004, 28, 331–337. [Google Scholar] [CrossRef]
  60. Sikora, A.; Svoboda, T.; Záborský, V.; Gaffová, Z. Effect of selected factors on the bending deflection at the limit of proportionality and at the modulus of rupture in laminated veneer lumber. Forests 2019, 10, 401. [Google Scholar] [CrossRef]
  61. Zhang, X.; Zhu, Y.; Yu, Y.; Song, J. Improve Performance of Soy Flour-Based Adhesive with a Lignin-Based Resin. Polymers 2017, 9, 261. [Google Scholar] [CrossRef] [PubMed]
  62. Gejdoš, M.; Tončíková, Z.; Němec, M.; Chovan, M.; Gergeľ, T. Balcony cultivator: New biomimicry design approach in the sustainable device. Futures 2018, 98, 32–40. [Google Scholar] [CrossRef]
  63. Bekhta, P.; Hiziroglu, S.; Potapova, O.; Sedliačik, J. Shear Strength of Exterior Plywood Panels Pressed at Low Temperature. Materials 2009, 2, 876–882. [Google Scholar] [CrossRef]
  64. Erdil, Y.Z.; Zhang, J.; Eckelman, C.A. Withdrawal and bending strength of dowel-nuts in plywood and oriented strandboard. For. Prod. J. 2003, 53, 54–57. [Google Scholar]
  65. Prekrat, S.; Smardzewski, J. Effect of gluline shape on strength of mortise and tenon joint. Drv. Ind. 2010, 61, 223–228. [Google Scholar]
  66. Kilic, H.; Kasal, A.; Kuskun, T.; Acar, M.; Erdil, Y.Z. Effect of Tenon Size on Static Front to Back Loading Performance of Wooden Chairs in Comparison with Acceptable Design Loads. Bioresources 2018, 13, 256–271. [Google Scholar]
  67. Kuskun, T.; Kasal, A.; Haviarova, E.; Kilic, H.; Uysal, M.; Erdil, Y.Z. Relationship between static and cyclic front to back load capacity of wooden chairs, and evaluation of the strength values according to acceptable design values. Wood Fiber Sci. 2018, 50, 1–9. [Google Scholar] [CrossRef]
  68. Oktaee, J.; Ebrahimi, G.; Layeghi, M.; Ghofrani, M.; Eckelman, C.A. Bending moment capacity of simple and haunched mortise and tenon furniture joints under tension and compression loads. Turk. J. Agric. For. 2014, 38, 291–297. [Google Scholar] [CrossRef]
  69. Likos, E.; Haviarova, E.; Eckelmna, C.A.; Erdil, Y.Z.; Ozcifci, A. Technical note: Static versus cyclic load capacity of side chairs constructed with mortise and tenon joints. Wood Fiber Sci. 2013, 45, 223–227. [Google Scholar]
  70. Gaff, M.; Gašparík, M.; Boruvka, V.; Haviarová, E. Stress simulation in layered wood-based materials under mechanical loading. Mater. Des. 2015, 87, 1065–1071. [Google Scholar] [CrossRef]
  71. Grič, M.; Joščák, P.; Tarvainen, I.; Ryonankoski, H.; Lagaňa, R.; Langová, N.; Andor, T. Mechanical properties of furniture self-locking frame joints. Bioresources 2017, 12, 5525–5538. [Google Scholar] [CrossRef]
  72. Branowski, B.; Zablocki, M.; Sydor, M. Experimental analysis of new furniture joints. Bioresources 2018, 13, 370–382. [Google Scholar] [CrossRef]
  73. Hajdarevič, S.; Busuladžič, I. Stiffness Analysis of Wood Chair Frame. Procedia Eng. 2015, 100, 746–755. [Google Scholar] [CrossRef] [Green Version]
  74. Staneva, N.; Genchev, Y.; Hristodorova, D. Approach to designing an upolstered furniture frame by the finite element method. Acta Fac. Xylologiae 2018, 60, 61–70. [Google Scholar]
  75. Hu, W.G.; Guan, H.Y. Research on withdrawal strength of mortise and tenon joint by numerical and analytic methods. Wood Res. 2017, 62, 575–586. [Google Scholar]
  76. Derikvand, M.; Ebrahimi, G. Finite element analysis of stress and strain distributions in mortise and loose tenon furniture joints. J. For. Res. 2014, 25, 677–681. [Google Scholar] [CrossRef]
  77. Hu, W.G. Study of finite element analysis of node in solid wood structure furniture based on ANSYS. Furnit. Inter. Des. 2015, 46, 65–67. [Google Scholar]
  78. Kasal, A.; Eckelman, C.A.; Haviarova, E.; Yalcin, I. Bending moment capacities of L-shaped mortise and tenon joints under compression and tension loadings. Bioresources 2016, 1, 6836–6853. [Google Scholar] [CrossRef]
  79. Diler, H.; Efe, H.; Erdil, Y.Z.; Kuskun, T.; Kasal, A. Determination of allowable design loads for wood chairs. In Proceedings of the XXVIII International Conference Research for Furniture Industry, Poznan, Poland, 21–22 September 2017. [Google Scholar]
  80. Laemlaksakul, V. Innovative Design of Laminated Bamboo Furniture Using Finite Element Method. Int. J. Math. Comput. Simul. 2008, 3, 274–284. [Google Scholar]
  81. EN 1728. Furniture. Seating. Test Methods for the Determination of Strength and Durability; BSI: London, UK, 2012. [Google Scholar]
  82. EN 12520. Furniture—Strength, Durability and Safety—Requirements for Domestic Seating; BSI: London, UK, 2015. [Google Scholar]
  83. EN 1022. Domestic Furniture. Seating. Determination of Stability; BSI: London, UK, 2018. [Google Scholar]
  84. Sydor, M.; Wieloch, G. Construction properties of wood taken into consideration in engenering practice. Drewno 2009, 52, 63–73. [Google Scholar]
  85. Požgaj, A.; Chovanec, D.; Kurjatko, S.; Babiak, M. Štruktúra a Vlastnosti Dreva; Príroda a.s.: Bratislava, Slovakia, 1993. [Google Scholar]
  86. Sedlecký, M.; Kvietková, M.S.; Kminiak, R. Medium-density fiberboard (MDF) and Edge-glued Panels (EGP) after edge milling—Surface roughness after machining with different parameters. Bioresources 2018, 13, 2005–2021. [Google Scholar] [CrossRef]
  87. Němec, M.; Kminiak, R.; Danihelová, A.; Gergel, T.; Ondrejka, V. Vibrations and workpiece surface quality at changing feed speed of CNC machine. Akustika 2017, 28, 117–124. [Google Scholar]
  88. Ke, Q.; Zhang, F.; Zhang, Y. Optimisation design of pine backrest chair based on Taguchi method. Int. Wood Prod. J. 2017, 8, 18–25. [Google Scholar] [CrossRef]
  89. Szalai, J. Festigkeitstheorien von anisotropen Stoffen mit sprodem bruchverhalten. Acta Silv. Lign. Hung. 2008, 4, 61–79. [Google Scholar]
Forests 10 00525 g001 550
Figure 1. Overweight and obese men in European countries in 2016 [19].
Figure 1. Overweight and obese men in European countries in 2016 [19].
Forests 10 00525 g001
Forests 10 00525 g002 550
Figure 2. Percentage of Slovak men with weight more than 110 kg.
Figure 2. Percentage of Slovak men with weight more than 110 kg.
Forests 10 00525 g002
Forests 10 00525 g003 550
Figure 3. Static loading of the chair according to the standard EN 1728:2012 + dimensions of the designed chair.
Figure 3. Static loading of the chair according to the standard EN 1728:2012 + dimensions of the designed chair.
Forests 10 00525 g003
Forests 10 00525 g004 550
Figure 4. Deformation of the flexible chair.
Figure 4. Deformation of the flexible chair.
Forests 10 00525 g004
Forests 10 00525 g005 550
Figure 5. Defining the maximum possible deformation of the flexible chair.
Figure 5. Defining the maximum possible deformation of the flexible chair.
Forests 10 00525 g005
Forests 10 00525 g006 550
Figure 6. FEM visual outputs and stress concentration in tension and compression parts of lumbar curve of chair. Left for 110 kg tension (max. 47.18 MPa) and compression (max. 65.14 MPa) design stress and right for 150 kg tension (max. 64.25 MPa) and compression (max. 88.98 MPa).
Figure 6. FEM visual outputs and stress concentration in tension and compression parts of lumbar curve of chair. Left for 110 kg tension (max. 47.18 MPa) and compression (max. 65.14 MPa) design stress and right for 150 kg tension (max. 64.25 MPa) and compression (max. 88.98 MPa).
Forests 10 00525 g006
Forests 10 00525 g007 550
Figure 7. FEM visual outputs of deformation and displacement of the back while the load is applied. Left figure for 110 kg and right figure for 150 kg.
Figure 7. FEM visual outputs of deformation and displacement of the back while the load is applied. Left figure for 110 kg and right figure for 150 kg.
Forests 10 00525 g007
Forests 10 00525 g008 550
Figure 8. FEM visual outputs of stresses and displacement of the chair back with thickness of 21 mm when loading is 150 kg. Left: Values of design compression (23,781 MPa) and tensile stresses (28,157 MPa), right: value of the backward displacement of the chair back (37,413 mm).
Figure 8. FEM visual outputs of stresses and displacement of the chair back with thickness of 21 mm when loading is 150 kg. Left: Values of design compression (23,781 MPa) and tensile stresses (28,157 MPa), right: value of the backward displacement of the chair back (37,413 mm).
Forests 10 00525 g008
Table
Table 1. Material constants for laminated beech lamellae, y direction is along the grain [85].
Table 1. Material constants for laminated beech lamellae, y direction is along the grain [85].
Young’s Modulus (MPa)Poisson’s Ratio (-)Shear Modulus (MPa)
ExEyEzµxyµyzµxzGxyGyzGxz
1130.016670.0630.00.0440.330.0271200.0190.0930.0
Table
Table 2. Calculated values of flat lamella.
Table 2. Calculated values of flat lamella.
Type of LamellaMean Value
σ ¯ (MPa)		Coefficient of Variation
ϑ (%)		Characteristic Bending Strength
fb,0,k (MPa)		Design Bending Strength
fb,0,d (MPa)
A111.854.96102.7686.86
B104.646.5793.3779.01
C93.806.1184.4171.42
Table
Table 3. Calculated values of mold lamella.
Table 3. Calculated values of mold lamella.
Type of LamellaMean Value
σ ¯ (MPa)		Coefficient of Variation
ϑ (%)		Characteristic Bending Strength
fb,0,k (MPa)		Design Bending Strength
fb,0,d (MPa)
A123.854.55114.6196.98
B98.133.5992.3578.15
C89.485.9780.7068.28
Table
Table 4. Maximum values of normal stress for the pitch seat-to-back angle of 103°.
Table 4. Maximum values of normal stress for the pitch seat-to-back angle of 103°.
Type of LamellaLoading of 110 kgLoading of 150 kg
Design Stress FEM (MPa)Design Stress FEM (MPa)
In Tension σt,0,dIn Compression σc,0,dIn Tension σt,0,dIn Compression σc,0,d
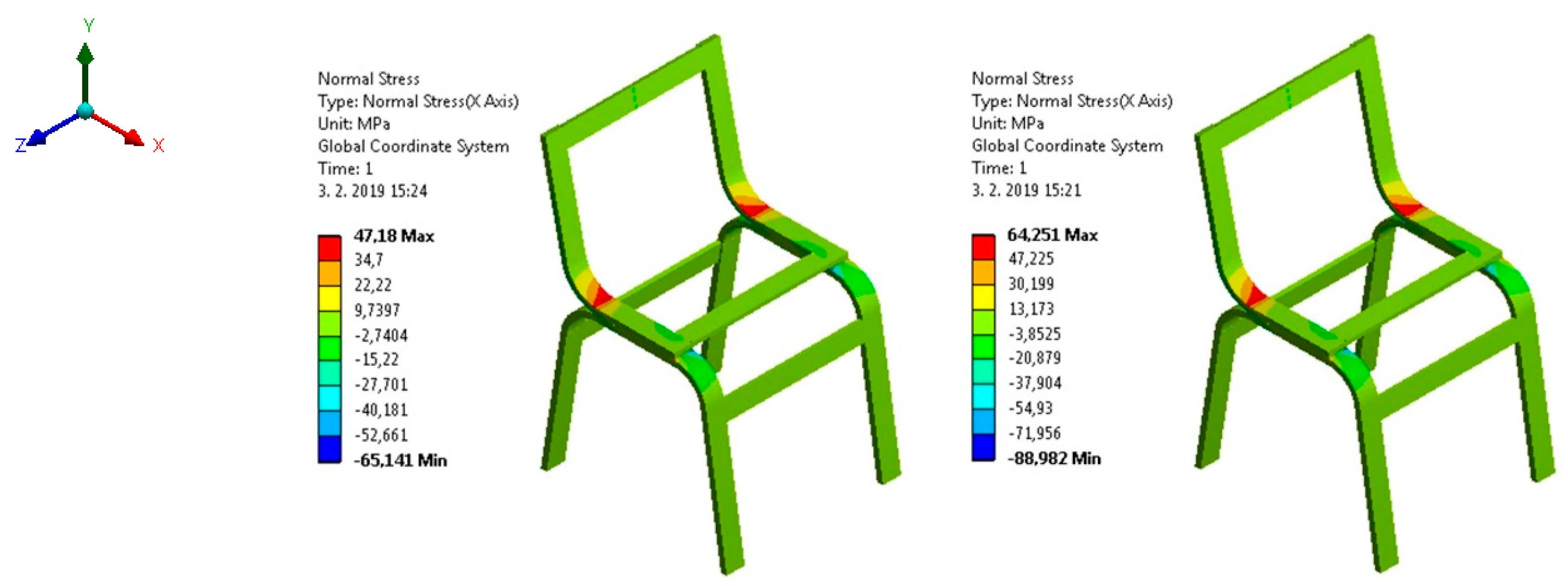
A85.90122.55117.06167.38
B69.04104.5282.55142.77
C47.1865.1464.2588.98
Table
Table 5. Maximum values of the backward displacement of the back u (mm) and values of the distance of the centre of gravity of the load from the tipping b (mm) in the direction of x-axis.
Table 5. Maximum values of the backward displacement of the back u (mm) and values of the distance of the centre of gravity of the load from the tipping b (mm) in the direction of x-axis.
Type of Lamella.Loading of 110 kgLoading of 150 kg
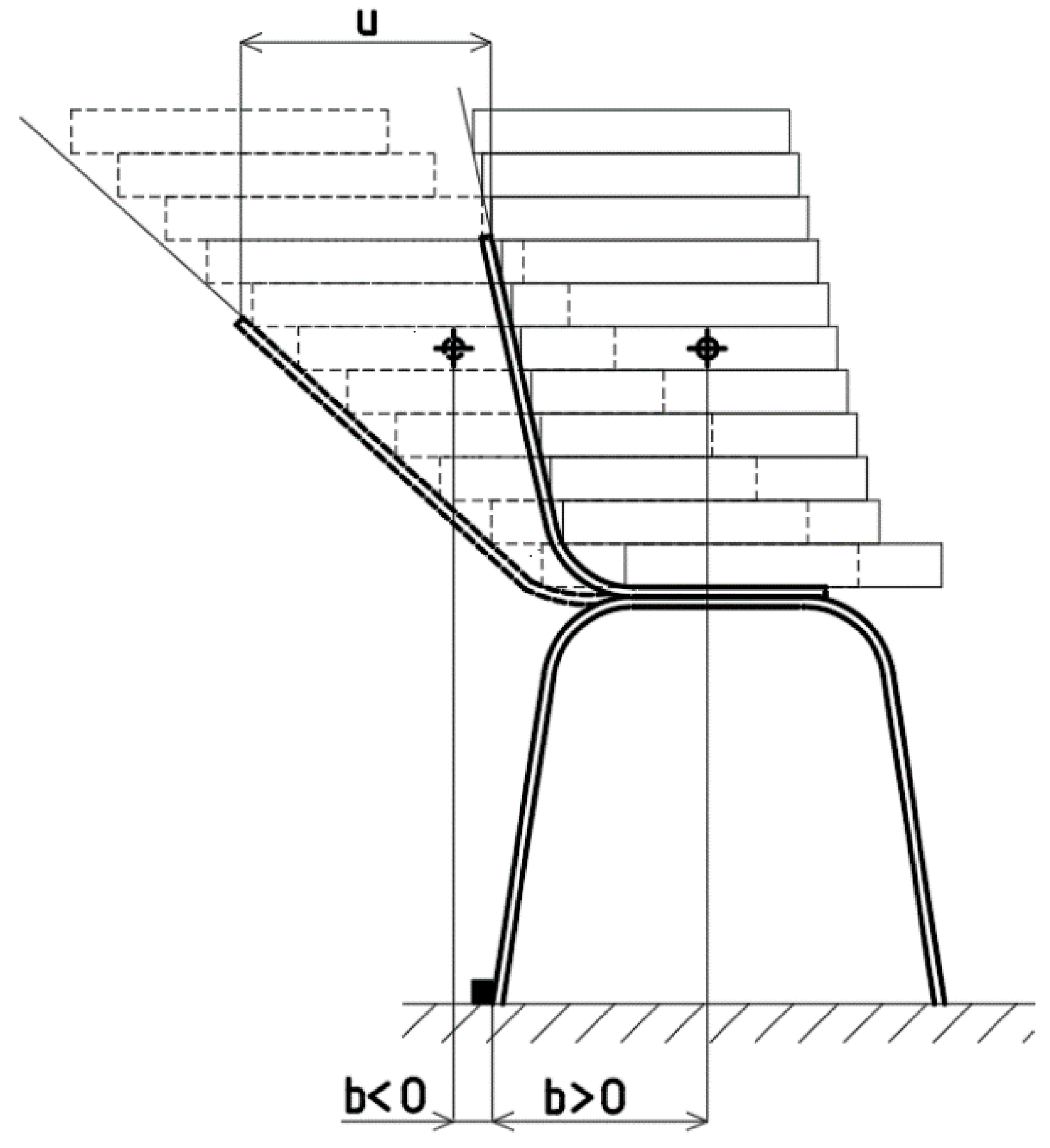
u (mm)b (mm)u (mm)b (mm)
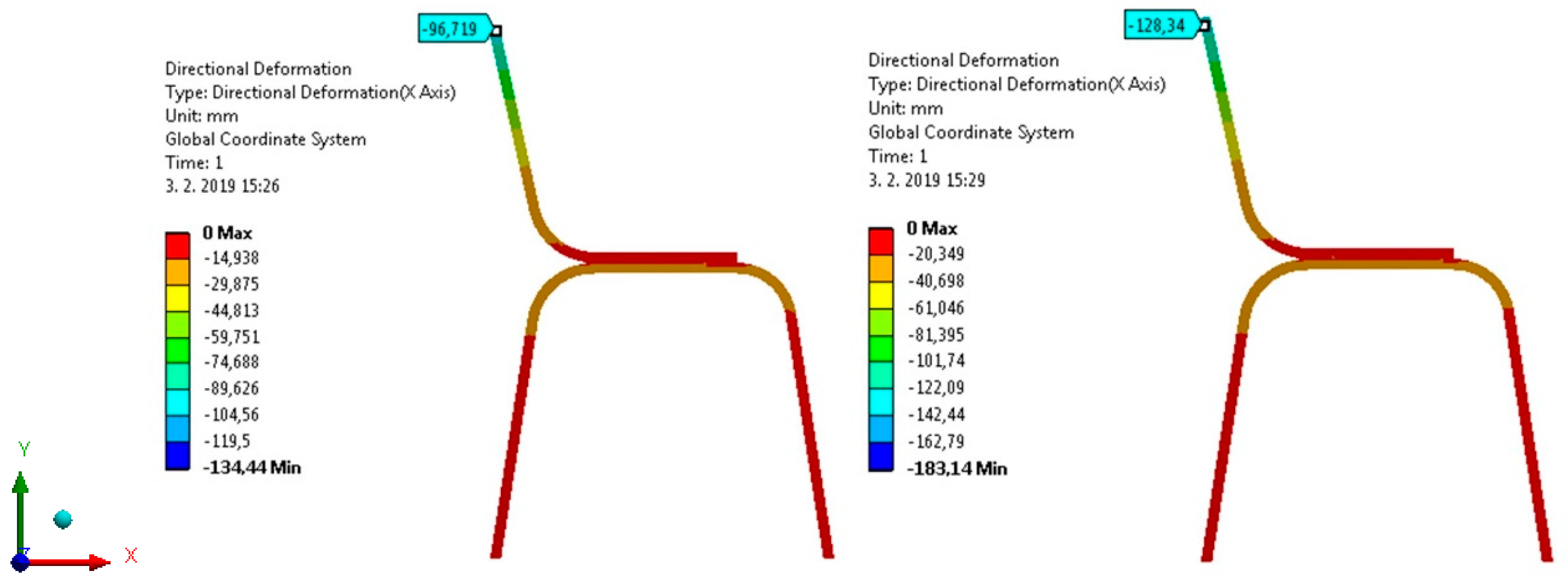
A289.15−63.5343.15−140.1
B189.13+33.7256.16−54.6
C96.72+157.4128.34+74.2
Note: In case the back is not loaded, the distance between the centre of gravity of the load and the back leg is b = +237.2 mm in the direction of x-axis.
Table
Table 6. Values of design compression and tensile stresses and values of the backward displacement of the chair back u (mm) in the case of the lamella type D when loading is 150 kg.
Table 6. Values of design compression and tensile stresses and values of the backward displacement of the chair back u (mm) in the case of the lamella type D when loading is 150 kg.
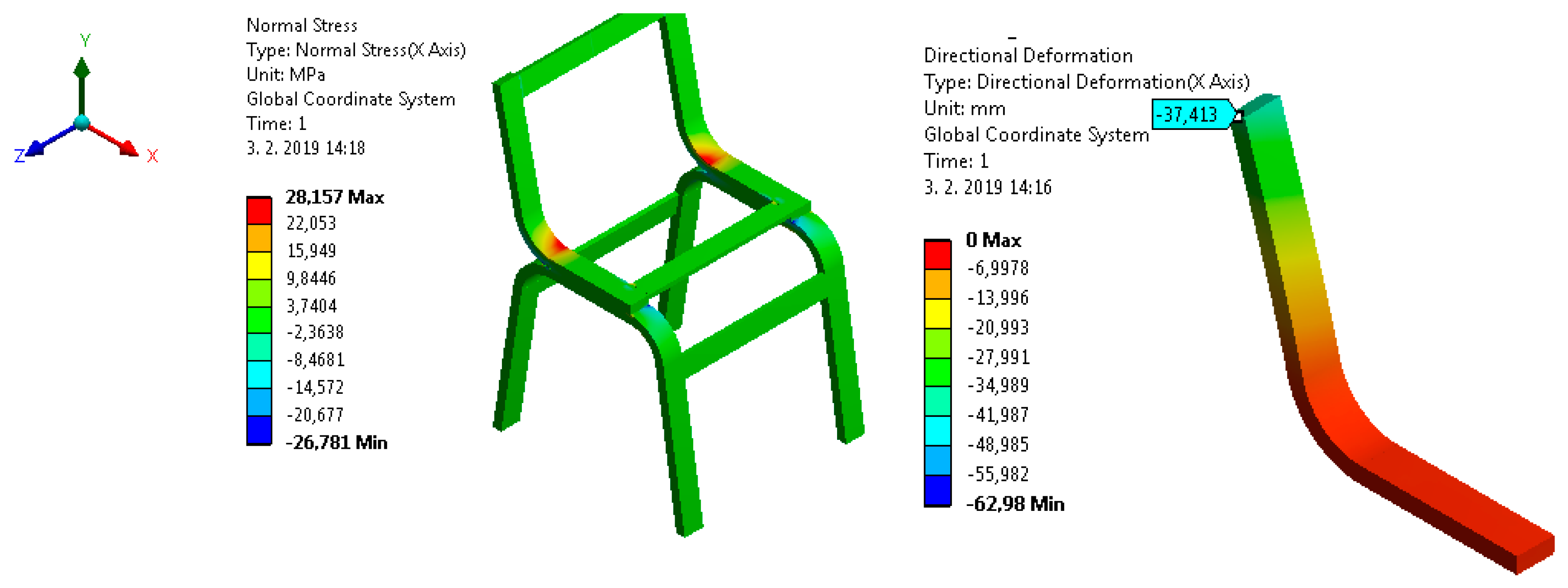
Type of LamellaDesign Stress-FEM (MPa)Displacement of the Chair Back
in Tensionin Compressionu (mm)
D28.1626.7837.41

Share and Cite

MDPI and ACS Style

Langová, N.; Réh, R.; Igaz, R.; Krišťák, Ľ.; Hitka, M.; Joščák, P. Construction of Wood-Based Lamella for Increased Load on Seating Furniture. Forests 2019, 10, 525. https://doi.org/10.3390/f10060525

AMA Style

Langová N, Réh R, Igaz R, Krišťák Ľ, Hitka M, Joščák P. Construction of Wood-Based Lamella for Increased Load on Seating Furniture. Forests. 2019; 10(6):525. https://doi.org/10.3390/f10060525

Chicago/Turabian Style

Langová, Nadežda, Roman Réh, Rastislav Igaz, Ľuboš Krišťák, Miloš Hitka, and Pavol Joščák. 2019. "Construction of Wood-Based Lamella for Increased Load on Seating Furniture" Forests 10, no. 6: 525. https://doi.org/10.3390/f10060525

APA Style

Langová, N., Réh, R., Igaz, R., Krišťák, Ľ., Hitka, M., & Joščák, P. (2019). Construction of Wood-Based Lamella for Increased Load on Seating Furniture. Forests, 10(6), 525. https://doi.org/10.3390/f10060525

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop