Modeling Dynamics of Structural Components of Forest Stands Based on Trivariate Stochastic Differential Equation
Abstract
1. Introduction
2. Materials and Methods
2.1. Stochastic Differential Equation Model
2.2. Marginal and Conditional Distributions
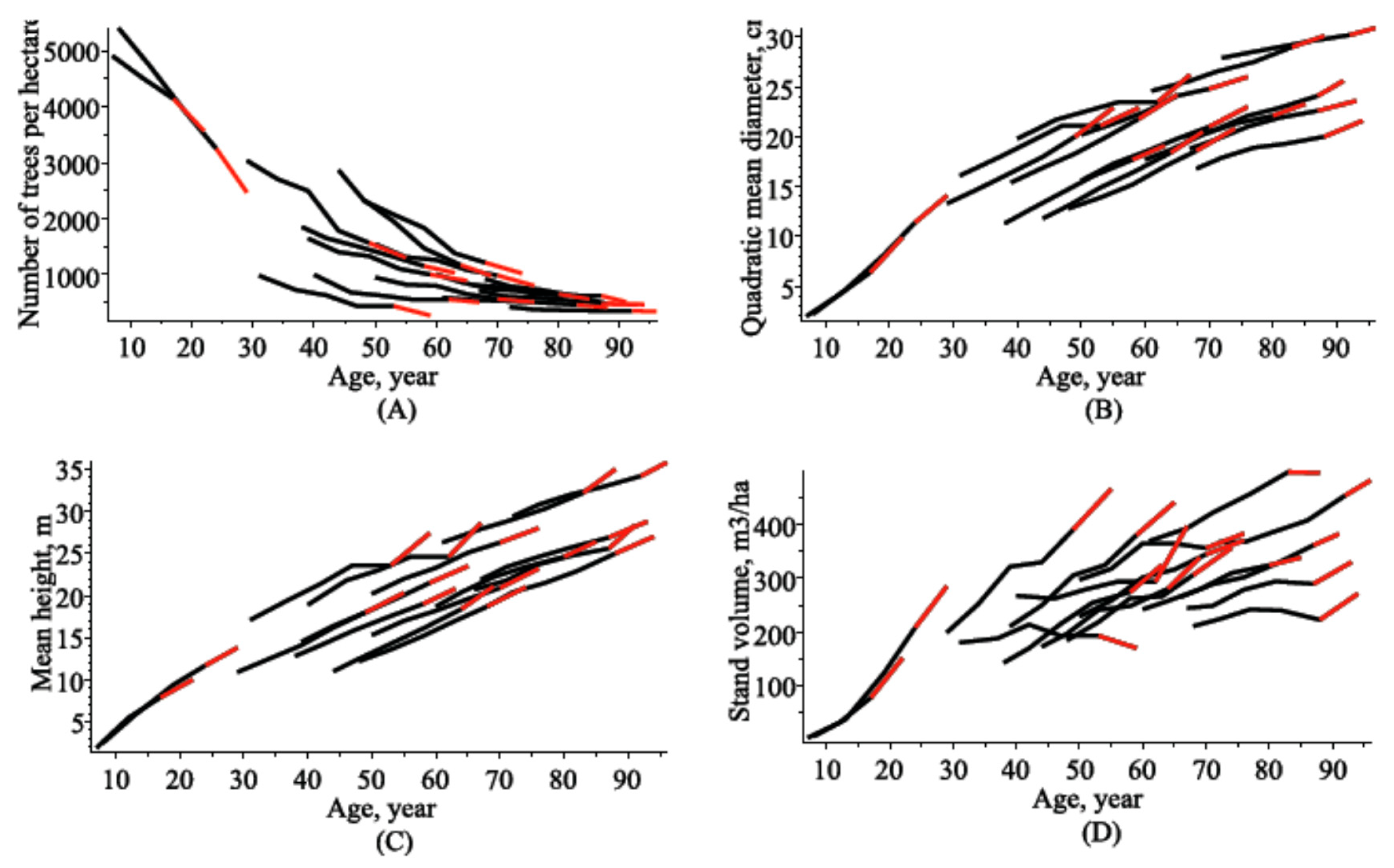
2.3. Data
2.4. Estimating Results
3. Results
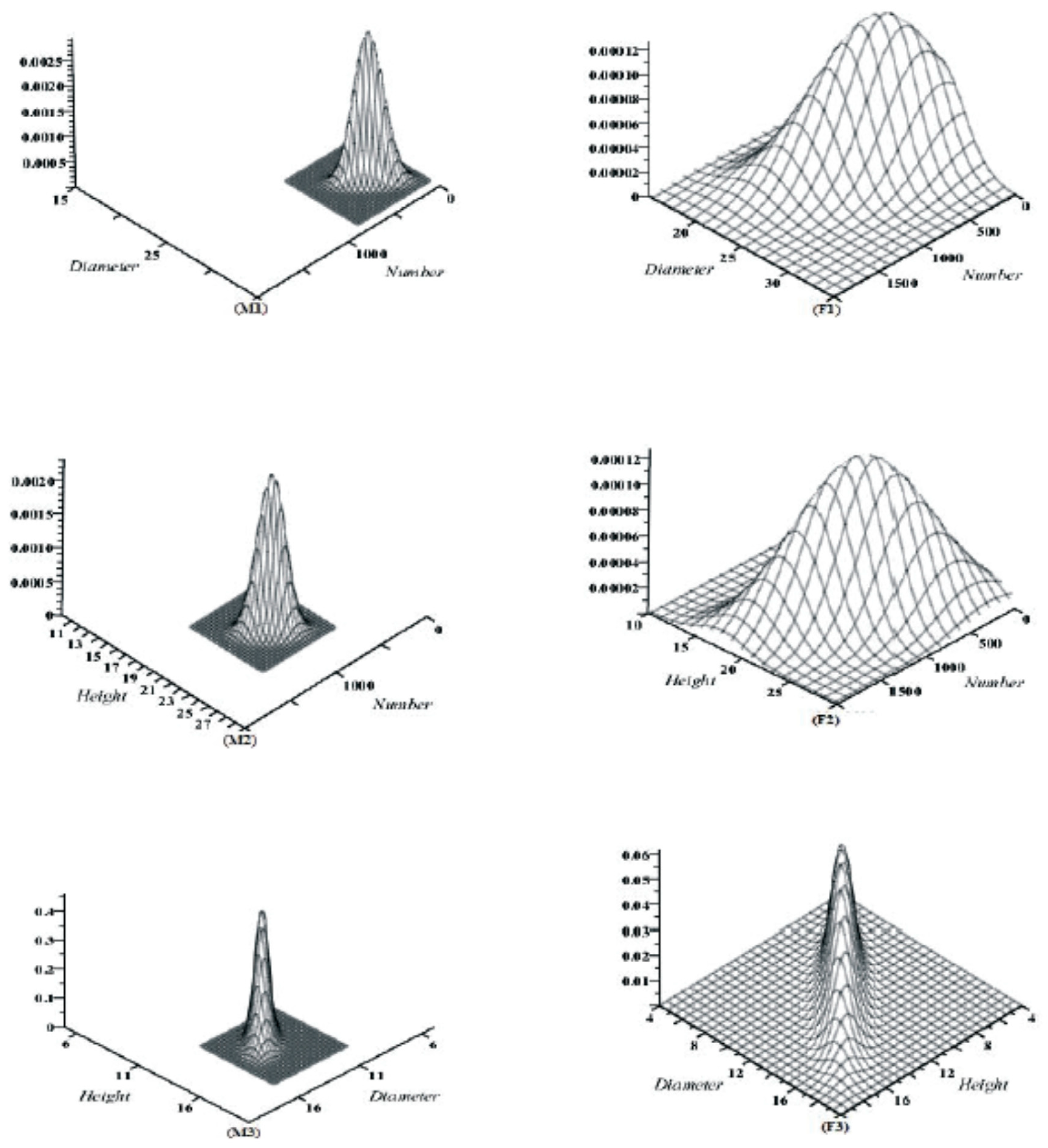
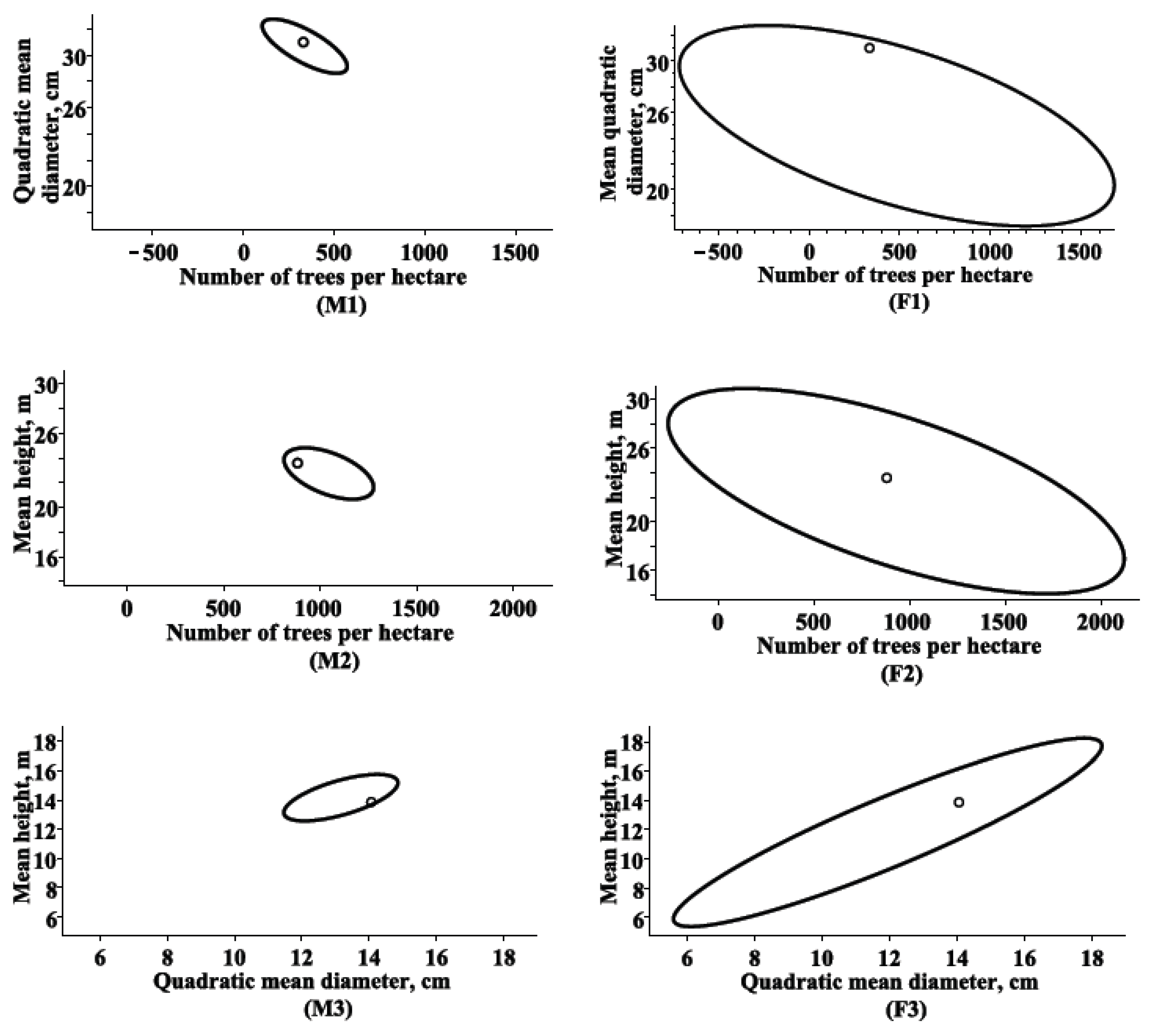
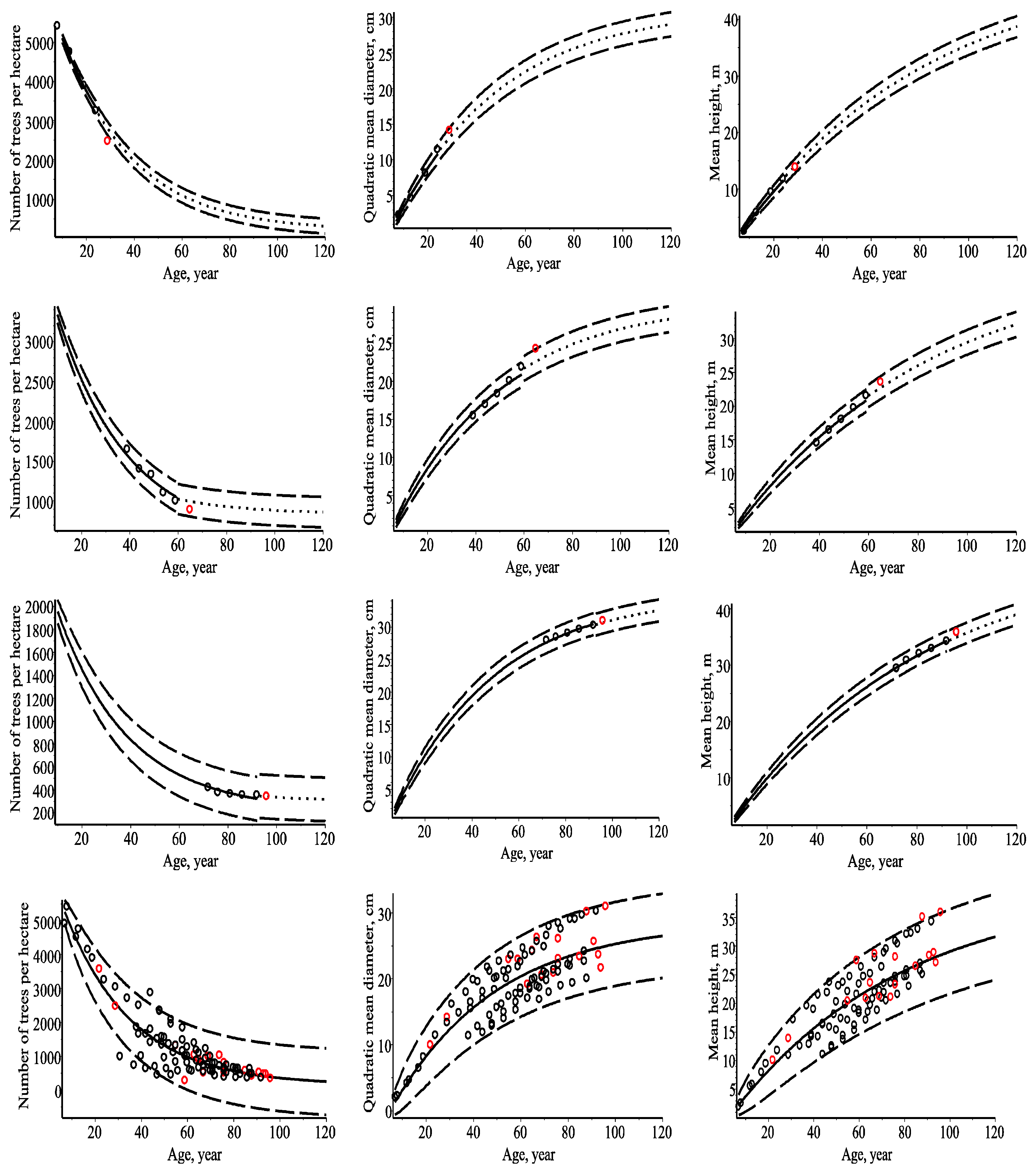
3.1. Marginal Bivariate Distributions
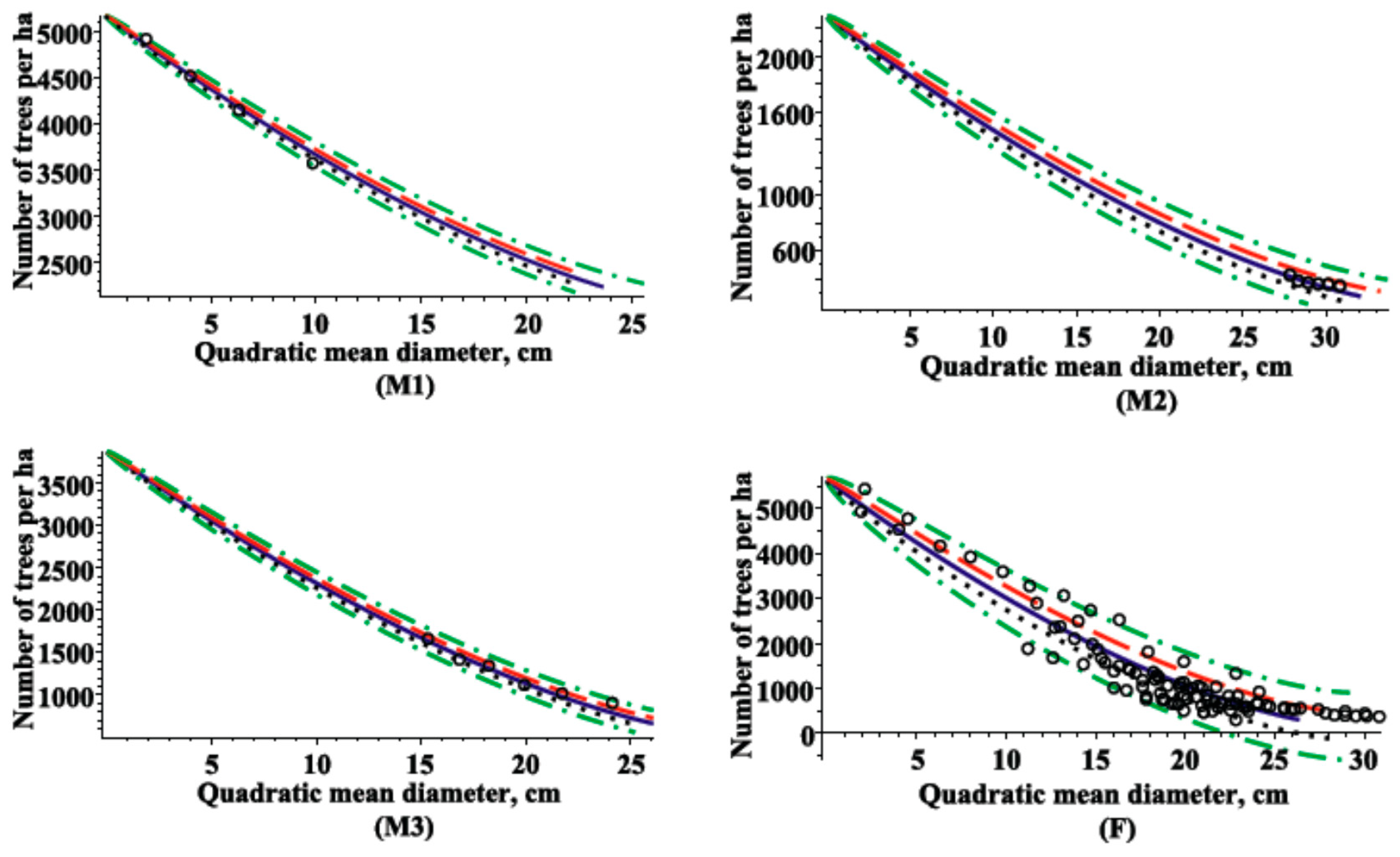
3.2. Maximum Density-Size Relationships
- 1)
- , lower quartile of stand density over quadratic mean diameter;
- 2)
- , upper quartile of stand density over quadratic mean diameter;
- 3)
- , mean of stand density over quadratic mean diameter;
- 4)
- , 95% percentile of stand density over quadratic mean diameter;
- 5)
- , 5% percentile of stand density over quadratic mean diameter.
4. Discussion
4.1. Models of the Number of Trees per Hectare, Quadratic Mean Diameter and Mean Height
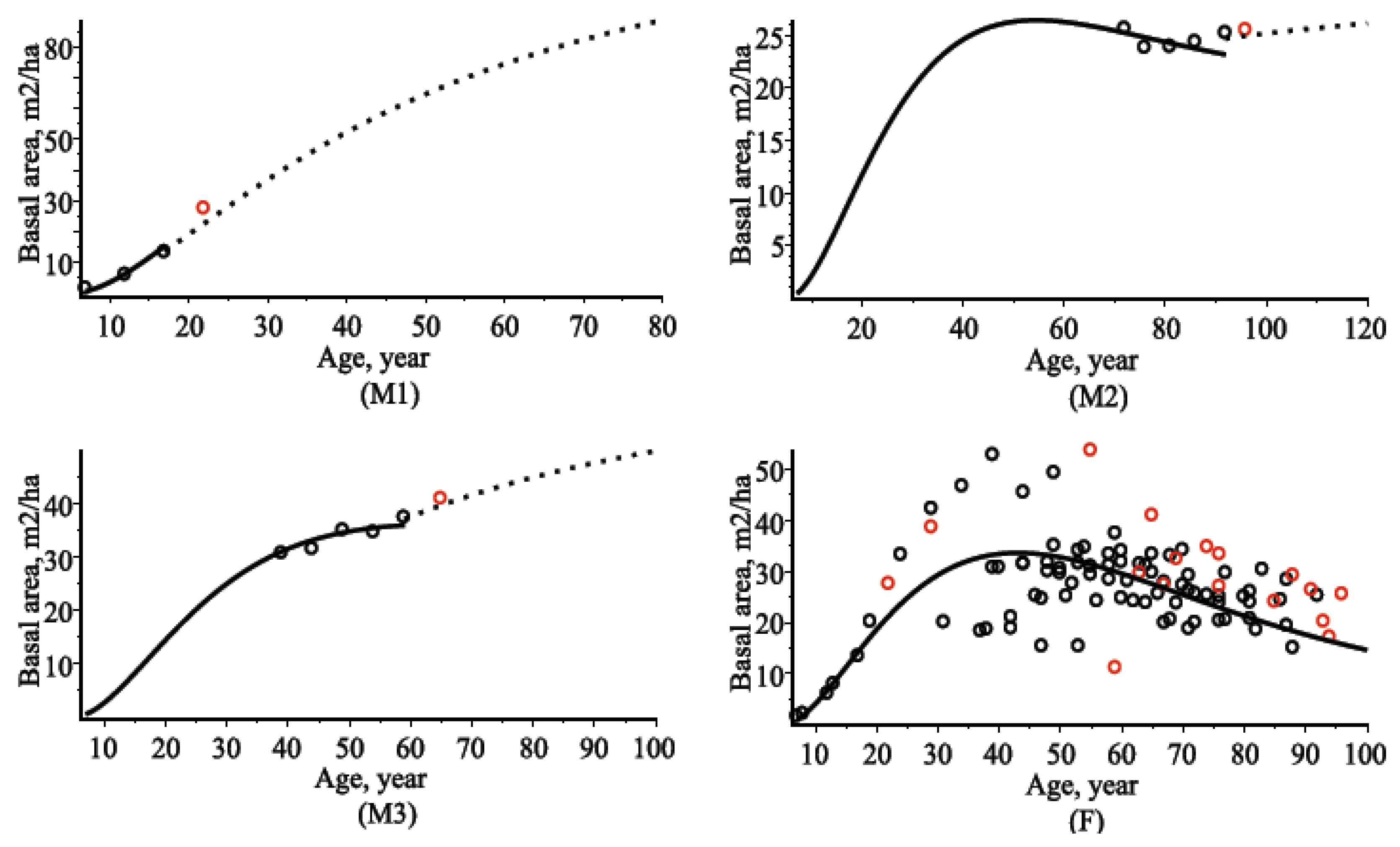
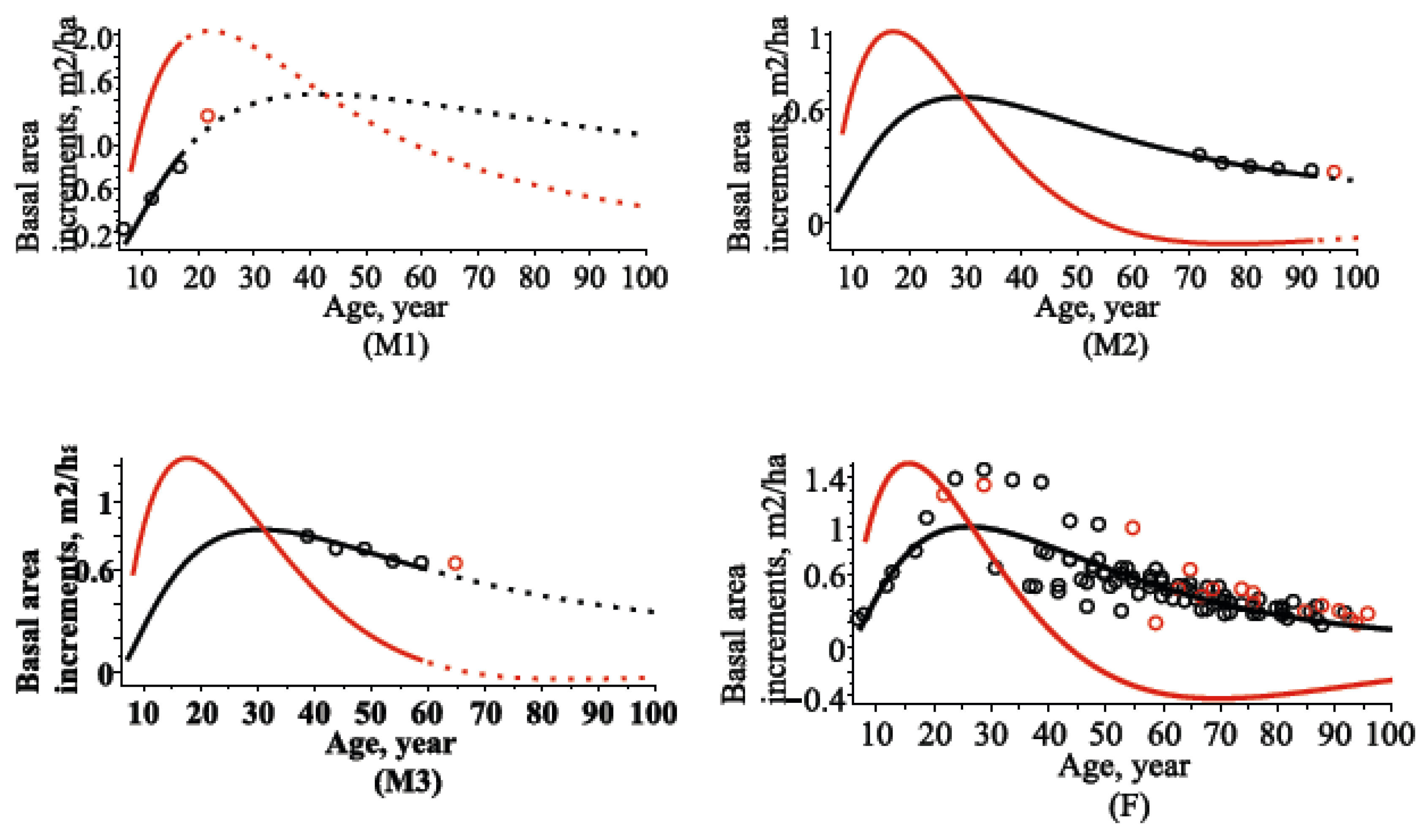
4.2. Stand Basal Area Models
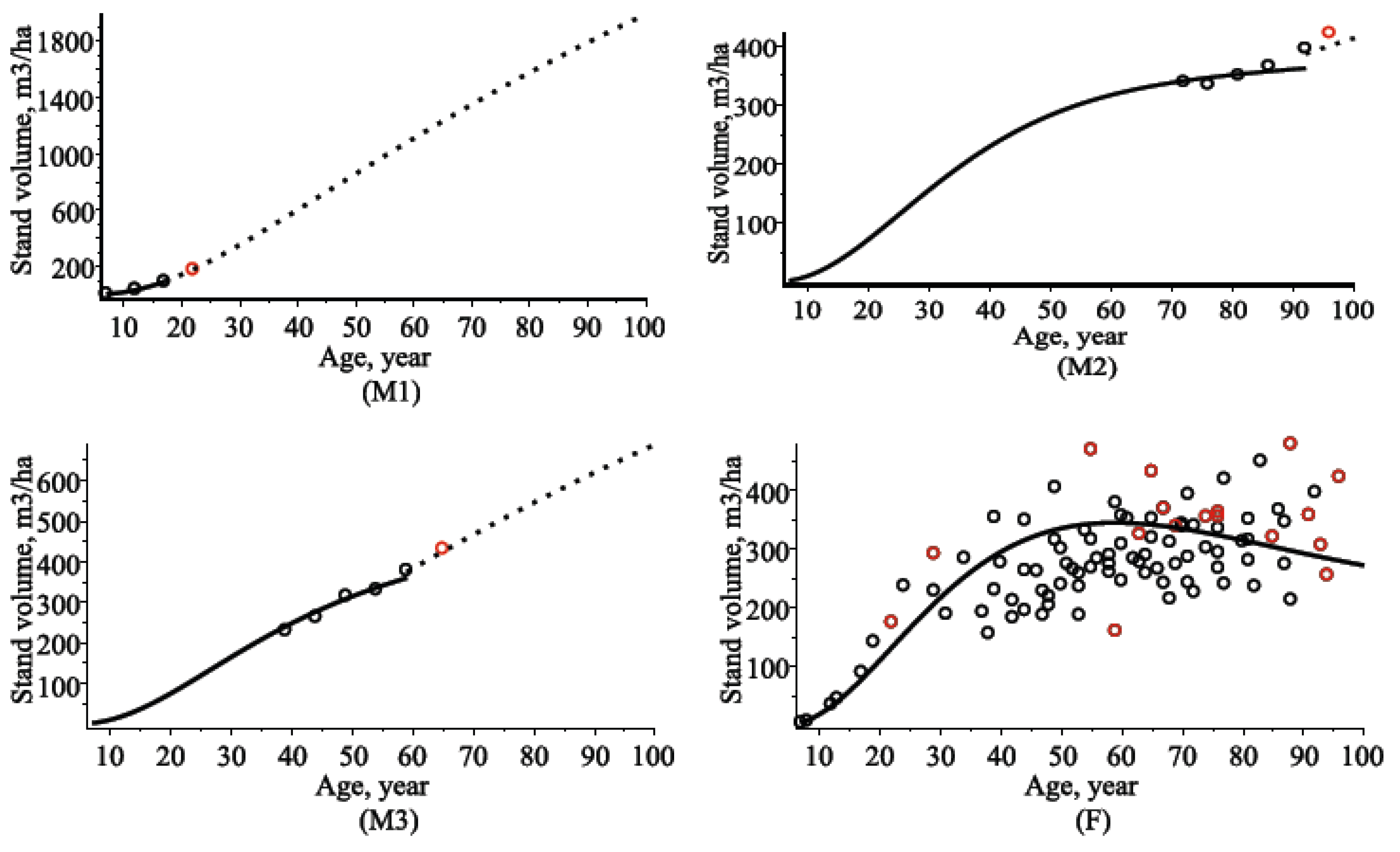
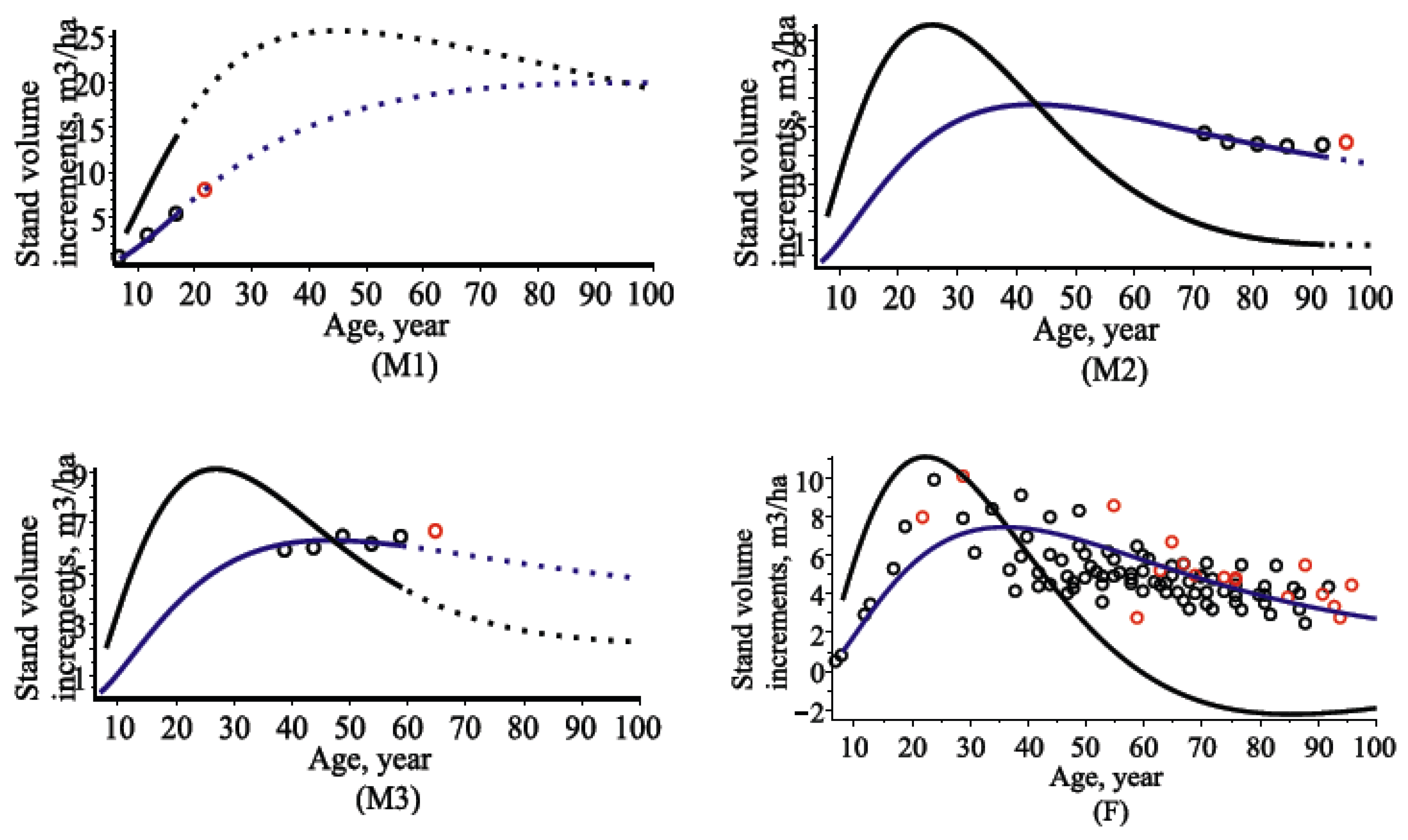
4.3. Stand Volume Models
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Maximum Likelihood Estimates
References
- Burkhart, H.E.; Tomé, M. Modeling Forest Trees and Stands; Springer Science+Business Media: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Hara, T. A stochastic model and the moment dynamics of the growth and size distribution in plant populations. J. Theor. Biol. 1984, 109, 173–190. [Google Scholar] [CrossRef]
- Vanclay, J.K. Tree diameter, height and stocking in even-aged forests. Ann. For. Sci. 2009, 66, 702. [Google Scholar] [CrossRef]
- Schwappach, A. Wachstum und Ertrag Normaler Fichtenbestände; Springer: Berlin, Germany, 1890. [Google Scholar]
- Guttenberg, A. Wachstum und Ertrag der Fichte im Hochgebirger; Wien: Leipzig, Germany, 1915. [Google Scholar]
- Assmann, E.; Franz, F. Vorläufige Fichten-Ertragstafel für Bayern. Forstwiss. Cent. 1965, 84, 13–43. [Google Scholar] [CrossRef]
- Curtis, R.O.; Marshall, D.D. Why quadratic mean diameter? West J. Appl. For. 2000, 15, 137–139. [Google Scholar]
- Newton, P. Stand density management diagrams: Review of their development and utility in stand–level management planning. For. Ecol. Manag. 1997, 98, 251–265. [Google Scholar] [CrossRef]
- Castedo-Dorado, F.; Crecente-Campo, F.; Álvarez-Álvarez, P.; Anta, M.B. Development of a stand density management diagram for radiata pine stands including assessment of stand stability. Forestry 2009, 82, 1–16. [Google Scholar] [CrossRef]
- Tewari, V.P.; Álvarez-Gonz, G. Development of a stand density management diagram for teak forests in southern India. J. For. Environ. Sci. 2018, 30, 259–266. [Google Scholar] [CrossRef]
- Garciá, O. Cohort aggregation modelling for complex forest stands: Spruce–aspen mixtures in British Columbia. Ecol. Model. 2017, 343, 109–122. [Google Scholar] [CrossRef]
- Cieszewski, C.J.; Balley, R.L. Generalized algebraic difference approach: Theory based derivation of dynamic site equations with polymorphism and variable asymptotes. For. Sci. 2000, 46, 116–126. [Google Scholar]
- Reineke, L.H. Perfecting a stand-density index for evenaged forests. J. Agric. Res. 1933, 46, 627–638. [Google Scholar]
- Lonsdale, W.M. The self–thinning rule: Dead or alive? Ecology 1990, 71, 1373–1388. [Google Scholar] [CrossRef]
- Pretzsch, H.; Biber, P. A re–evaluation of Reineke’s rule and stand density index. For. Sci. 2005, 51, 304–320. [Google Scholar]
- Vospernik, S.; Sterba, H. Do competition–density rule and selfthinning rule agree? Ann. For. Sci. 2014, 72, 379–390. [Google Scholar] [CrossRef]
- Yoda, K.; Kira, T.; Ogawa, H.; Hozumi, K. Self–thinning in overcrowded pure stands pure stands under cultivated and natural conditions. J. Biol. Osaka City Univ. 1963, 14, 107–129. [Google Scholar]
- Zeide, B. Analysis of the 3/2 power law of self-thinning. For. Sci. 1987, 33, 517–537. [Google Scholar]
- Ogawa, K.; Hagihara, A. Self–thinning and size variation in a sugi (Cryptomeria japonica D. Don) plantation. For. Ecol. Manag. 2003, 174, 413–421. [Google Scholar] [CrossRef]
- Clutter, J.L.; Bennett, F.A. Diameter Distributions in Old–Field Slash Pine Plantations; Georgia Forest Research Council: Atlanta, GA, USA, 1965.
- Cai, W.; Pan, J. Stochastic differential equation models for the price of European CO2 emissions allowances. Sustainability 2017, 9, 207. [Google Scholar] [CrossRef]
- Román-Román, P.; Serrano-Pérez, J.J.; Torres-Ruiz, F. Some notes about inference for the lognormal diffusion process with exogenous factors. Mathematics 2018, 6, 85. [Google Scholar] [CrossRef]
- Suzuki, T. Forest transition as a stochastic process. Mitt. Forstl. Bundesversuchsanstalt Wien 1971, 91, 69–86. [Google Scholar]
- Sloboda, B. Kolmogorow–Suzuki und die stochastische Differentialgleichung als Beschreibungsmittel der Bestandesevolution. Mitt. Forstl. Bundes-Versuchsanst. Wien 1977, 120, 71–82. [Google Scholar]
- Rupšys, P.; Petrauskas, E. Analysis of height curves by stochastic differential equations. Int. J. Biomath. 2012, 5, 1250045. [Google Scholar] [CrossRef]
- Rupšys, P. New insights into tree height distribution based on mixed effects univariate diffusion processes. PLoS ONE 2016, 11, e0168507. [Google Scholar] [CrossRef] [PubMed]
- Rupšys, P.; Petrauskas, E. A new paradigm in modelling the evolution of a stand via the distribution of tree sizes. Sci. Rep. 2017, 7, 15875. [Google Scholar] [CrossRef] [PubMed]
- Rupšys, P.; Petrauskas, E. A Linkage among tree diameter, height, crown base height, and crown width 4–variate distribution and their growth models: A 4–variate diffusion process approach. Forests 2017, 8, 479. [Google Scholar] [CrossRef]
- Rupšys, P.; Petrauskas, E. Evolution of bivariate tree diameter and height distribution via stand age: Von Bertalanffy bivariate diffusion process approach. J. For. Res. 2019, 24, 16–26. [Google Scholar] [CrossRef]
- Vasicek, O. An equilibrium characterization of the term structure. J. Financ. Econ. 1977, 5, 177–188. [Google Scholar] [CrossRef]
- Itô, K. On stochastic processes. Jpn. J. Math. 1942, 18, 261–301. [Google Scholar] [CrossRef]
- Tong, Y.L. The Multivariate Normal Distribution; Springer: New York, NY, USA, 1990. [Google Scholar]
- Linkevičius, E. Single Tree Level Simulator for Lithuanian Pine Forests. Ph.D. Thesis, Technische Universität Dresden, Tharandt, Germany, 2014. [Google Scholar]
- Monagan, M.B.; Geddes, K.O.; Heal, K.M.; Labahn, G.; Vorkoetter, S.M.; Mccarron, J. Maple Advanced Programming Guide; Maplesoft: Waterloo, ON, Canada, 2007. [Google Scholar]
- Ge, F.; Zeng, W.; Ma, W.; Meng, J. Does the slope of the self-thinning line remain a constant value across different site qualities?—An implication for plantation density management. Forests 2017, 8, 355. [Google Scholar] [CrossRef]
- Quiñonez-Barraza, G.; Ramírez-Maldonado, H. Can an exponential function be applied to the asymptotic density–size relationship? Two new stand-density indices in mixed–species forests. Forests 2019, 10, 9. [Google Scholar] [CrossRef]
- Mehtätalo, L.; Gregoire, T.G.; Burkhart, H.E. Comparing strategies for modeling tree diameter percentiles from remeasured plots. Environmetrics 2008, 19, 529–548. [Google Scholar] [CrossRef]
- Garciá, O. Reverse causality in size–dependent growth. Int. J. Math. Comput. For. Nat.-Resour. Sci. 2018, 10, 1–5. [Google Scholar]
- Ogana, F.N.; Osho, J.S.A.; Gorgoso-Varela, J.J. An approach to modeling the joint distribution of tree diameter and height data. J. Sustain. For. 2018, 37, 475–488. [Google Scholar] [CrossRef]
- Mulverhill, C.; Coops, N.C.; White, J.C.; Tompalski, P.; Marshall, P.L.; Bailey, T. Enhancing the estimation of stem–size distributions for unimodal and bimodal stands in a boreal mixedwood forest with airborne laser scanning data. Forests 2018, 9, 95. [Google Scholar] [CrossRef]
- McTague, J.P.; Weiskittel, A.R. Individual–tree competition indices and improved compatibility with stand–level estimates of stem density and long-term production. Forests 2016, 7, 238. [Google Scholar] [CrossRef]
- Humagain, K.; Portillo-Quintero, C.; Cox, R.D.; Cain, J.W. Mapping tree density in forests of the southwestern USA using landsat 8 data. Forests 2017, 8, 287. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Dodge, Y. The Concise Encyclopedia of Statistics; Springer: New York, NY, USA, 2008; pp. 234–235. [Google Scholar]
- Stankova, T.V. A dynamic whole-stand growth model, derived from allometric relationships. Silva Fenn. 2016, 50, 1406. [Google Scholar] [CrossRef]
- Tewari, V.P.; Álvarez-González, J.G.; García, O. Developing a dynamic growth model for teak plantations in India. For. Ecosyst. 2014, 1, 9. [Google Scholar] [CrossRef]
- Zhang, X.; Lei, Y. A linkage among whole–stand model, individual tree model and diameter–distribution model. J. For. Sci. 2010, 56, 600–608. [Google Scholar] [CrossRef]
- Fu, L.; Sharma, R.P.; Zhu, G.; Li, H.; Hong, L.; Guo, H.; Duan, G.; Shen, C.; Lei, Y.; Li, Y.; et al. A basal area increment–based approach of site productivity evaluation for multi–aged and mixed forests. Forests 2017, 8, 119. [Google Scholar] [CrossRef]
- Yue, C.; Kohnle, U.; Hein, S. Combining tree and stand level models: A new approach to growth prediction. For. Sci. 2008, 54, 553–566. [Google Scholar]
- Cao, Q.V. Linking individual–tree and whole–stand models for forest growth and yield prediction. For. Ecosyst. 2014, 1, 1–8. [Google Scholar] [CrossRef]
- Petrauskas, E.; Bartkevičius, E.; Rupšys, P.; Memgaudas, R. The use of stochastic differential equations to describe stem taper and volume. Balt. For. 2013, 19, 43–151. [Google Scholar]
- Zianis, D.; Muukkonen, P.; Mäkipää, R.; Mencuccini, M. Biomass and stem volume equations for tree species in Europe. Silva Fenn. 2005, 4, 1–63. [Google Scholar]
- He, A.; McDermid, G.J.; Rahman, M.M.; Strack, M.; Saraswati, S.; Xu, B. Developing allometric equations for estimating shrub biomass in a Boreal Fen. Forests 2018, 9, 569. [Google Scholar] [CrossRef]
- McCullagh, A.; Black, K.; Nieuwenhuis, M. Evaluation of tree and stand–level growth models using national forest inventory data. Eur. J. For. Res. 2017, 136, 251–258. [Google Scholar] [CrossRef]
- Tompalski, P.; Coops, N.; White, J.; Wulder, M. Enhancing forest growth and yield predictions with airborne laser scanning data: Increasing spatial detail and optimizing yield curve selection through template matching. Forests 2016, 7, 255. [Google Scholar] [CrossRef]
- Picchini, U.; Ditlevsen, S.; De Gaetano, A. Practical estimation of high dimensional stochastic differential mixed–effects models. Comput. Stat. Data Anal. 2011, 55, 1426–1444. [Google Scholar] [CrossRef]
| Scenario | Parameters of drift term | |||||||||
| α1 | β1 | α2 | β2 | α3 | β3 | δ | ||||
| Fixed | 278.6 | 0.0378 | 28.53 | 0.0228 | 39.40 | 0.0136 | 5705.0 | |||
| Mixed | 330.9 | 0.0343 | 28.59 | 0.0227 | 41.03 | 0.0128 | 5496.4 | |||
| Scenario | Parameters of diffusion term | |||||||||
| σ11 | ρ12 | ρ13 | σ22 | ρ23 | σ33 | σ1 | σ2 | σ3 | σ3 | |
| Fixed | 12,765.0 | −0.5447 | −0.6327 | 0.4189 | 0.9104 | 0.3473 | - | - | - | - |
| Mixed | 625.3 | −0.7589 | −0.5572 | 0.0330 | 0.6412 | 0.0237 | 435.7 | 4.249 | 7.047 | 1837.9 |
| (Equation): (Predictors) | Estimation Dataset (Prediction) | Validation Dataset (Forecast) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| B (%B) | PR | AB (%AB) | R2 | SW p T p | B (%B) | PR | AB (%AB) | R2 | SW p T p | |
| Number of trees per hectare | ||||||||||
| (4): (t) | 1.753 (–0.62) | 75.91 | 57.20 (5.45) | 0.996 | 0.090 0.989 | −67.10 (–3.80) | 132.03 | 102.06 (11.68) | 0.982 | 0.650 0.750 |
| (10): (d,h,t) | 0.352 (–0.06) | 45.18 | 32.31 (3.33) | 0.998 | 0.002 0.998 | 23.98 (8.05) | 107.77 | 73.09 (10.04) | 0.985 | 0.650 0.909 |
| (13): (d,t) | 0.455 (−0.09) | 46.02 | 32.34 (3.38) | 0.998 | 0.002 0.997 | 21.37 (7.11) | 101.06 | 66.87 (9.02) | 0.987 | 0.018 0.919 |
| (13): (h,t) | 0.704 (–0.21) | 52.95 | 36.78 (3.08) | 0.998 | 0.009 0.996 | –8.79 (6.91) | 140.03 | 96.92 (12.77) | 0.973 | 0.047 0.967 |
| Quadratic mean diameter | ||||||||||
| (4): (t) | −0.012 (–0.18) | 0.669 | 0.531 (3.75) | 0.987 | 0.652 0.985 | 1.021 (5.01) | 1.212 | 1.069 (5.22) | 0.984 | 0.779 0.423 |
| (10): (N,h,t) | –0.001 (0.27) | 0.340 | 0.266 (2.03) | 0.997 | 0.980 0.998 | 0.371 (1.66) | 0.598 | 0.494 (2.34) | 0.992 | 0.779 0.769 |
| (13): (N,t) | −0.002 (0.03) | 0.410 | 0.318 (1.99) | 0.995 | 0.906 0.997 | 0.598 (2.38) | 0.922 | 0.771 (3.59) | 0.981 | 0.619 0.636 |
| (13): (h,t) | −0.004 (0.39) | 0.387 | 0.309 (2.94) | 0.996 | 0.688 0.994 | 0.400 (2.54) | 0.758 | 0.571 (3.21) | 0.990 | 0.835 0.751 |
| Mean height | ||||||||||
| (4): (t) | −0.008 (–0.84) | 0.653 | 0.495 (3.36) | 0.991 | 0.059 0.992 | 1.045 (3.83) | 1.317 | 1.154 (4.80) | 0.985 | 0.440 0.525 |
| (10): (N,d,t) | −0.002 (–0.74) | 0.349 | 0.256 (2.37) | 0.997 | 0.133 0.998 | 0.399 (0.67) | 0.894 | 0.765 (3.61) | 0.985 | 0.440 0.807 |
| (13): (N,t) | −0.002 (–0.72) | 0.444 | 0.342 (2.74) | 0.996 | 0.435 0.998 | 0.746 (1.93) | 1.309 | 1.127 (5.17) | 0.974 | 0.036 0.649 |
| (13): (d,t) | –0.002 (−0.76) | 0.359 | 0.268 (2.42) | 0.997 | 0.349 0.998 | 0.377 (0.69) | 0.814 | 0.700 (3.26) | 0.988 | 0.198 0.817 |
| (Equation): (Predictors) | Estimation Dataset (Prediction) | Validation Dataset (Forecast) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| B (%B) | PR | AB (%AB) | R2 | SW p T p | B (%B) | PR | AB (%AB) | R2 | SW p T p | |
| Number of trees per hectare | ||||||||||
| (4): (t) | 21.52 (−15.22) | 465.27 | 327.35 (33.99) | 0.833 | 0.143 0.864 | 10.43 (−16.97) | 259.95 | 174.54 (32.12) | 0.907 | 0.117 0.960 |
| (10): (d,h,t) | 13.52 (−4.37) | 304.47 | 223.59 (23.27) | 0.929 | 0.296 0.915 | 121.51 (15.58) | 222.52 | 157.51 (27.24) | 0.952 | 0.117 0.565 |
| (13): (d,t) | 17.02 (−7.19) | 359.18 | 269.73 (28.24) | 0.901 | 0.586 0.893 | 111.22 (5.34) | 271.51 | 213.08 (36.72) | 0.916 | 0.496 0.598 |
| (13): (h,t) | 14.71 (−4.35) | 306.04 | 224.67 (23.32) | 0.932 | 0.223 0.907 | 124.60 (15.81) | 224.99 | 159.99 (27.63) | 0.952 | 0.101 0.556 |
| Quadratic mean diameter | ||||||||||
| (4): (t) | 0.066 (−2.32) | 3.171 | 2.697 (14.90) | 0.712 | 0.0004 0.919 | 1.342 (5.14) | 3.099 | 2.508 (10.68) | 0.701 | 0.582 0.295 |
| (10): (N,h,t) | 0.004 (0.13) | 1.069 | 0.877 (6.33) | 0.967 | 0.048 0.995 | 0.098 (0.34) | 1.501 | 1.096 (4.90) | 0.914 | 0.740 0.937 |
| (13): (N,t) | 0.009 (−0.43) | 2.432 | 2.014 (11.87) | 0.831 | 0.013 0.989 | 1.373 (5.97) | 2.850 | 2.223 (9.95) | 0.761 | 0.708 0.284 |
| (13): (h,t) | 0.008 (0.21) | 1.075 | 0.880 (6.25) | 0.967 | 0.024 0.990 | 0.104 (0.43) | 1.506 | 1.091 (4.84) | 0.913 | 0.719 0.934 |
| Mean height | ||||||||||
| (4): (t) | −0.087 (−3.46) | 3.479 | 2.872 (15.41) | 0.733 | 0.0004 0.906 | 1.515 (4.92) | 3.758 | 2.698 (10.32) | 0.730 | 0.147 0.359 |
| (10): (N,d,t) | 0.0004 (−0.80) | 0.941 | 0.805 (5.65) | 0.980 | 0.004 0.999 | 0.333 (0.90) | 1.617 | 1.315 (5.40) | 0.943 | 0.840 0.838 |
| (13): (N,t) | ‒0.0006 (−1.14) | 2.304 | 1.874 (11.29) | 0.883 | 3.9 × 10−5 0.999 | 1.545 (6.05) | 3.103 | 2.245 (9.19) | 0.835 | 0.106 0.350 |
| (13): (d,t) | −0.019 (−1.26) | 1.161 | 0.977 (6.58) | 0.970 | 0.064 0.976 | 0.196 (0.08) | 1.779 | 1.376 (5.49) | 0.929 | 0.976 0.904 |
| Scenario | Estimation Dataset (Prediction) | Validation Dataset (Forecast) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| B (%B) | PR | AB (%AB) | R2 | SW p T p | B (%B) | PR | AB (%AB) | R2 | SW p T p | |
| Mixed | −0.115 (−0.30) | 1.760 | 1.251 (6.23) | 0.968 | 0.097 0.907 | 0.993 (3.80) | 2.733 | 2.028 (7.38) | 0.988 | 0.580 0.678 |
| Fixed | −0.746 (−8.08) | 6.917 | 4.972 (20.70) | 0.510 | 0.098 0.452 | 4.352 (4.67) | 9.568 | 7.081 (27.70) | 0.867 | 0.104 0.082 |
| Scenario | Estimation Dataset (Prediction) | Validation Dataset (Forecast) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| B (%B) | PR | AB (%AB) | R2 | SW p T p | B (%B) | PR | AB (%AB) | R2 | SW p T p | |
| Mixed | −0.323 (−1.05) | 17.355 | 12.016 (5.33) | 0.966 | 0.008 0.973 | 19.281 (5.47) | 35.894 | 26.235 (7.86) | 0.980 | 0.028 0.381 |
| Fixed | −12.971 (−9.39) | 62.403 | 50.605 (20.87) | 0.583 | 0.360 0.176 | 57.935 (11.98) | 97.901 | 78.597 (24.49) | 0.862 | 0.119 0.015 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rupšys, P. Modeling Dynamics of Structural Components of Forest Stands Based on Trivariate Stochastic Differential Equation. Forests 2019, 10, 506. https://doi.org/10.3390/f10060506
Rupšys P. Modeling Dynamics of Structural Components of Forest Stands Based on Trivariate Stochastic Differential Equation. Forests. 2019; 10(6):506. https://doi.org/10.3390/f10060506
Chicago/Turabian StyleRupšys, Petras. 2019. "Modeling Dynamics of Structural Components of Forest Stands Based on Trivariate Stochastic Differential Equation" Forests 10, no. 6: 506. https://doi.org/10.3390/f10060506
APA StyleRupšys, P. (2019). Modeling Dynamics of Structural Components of Forest Stands Based on Trivariate Stochastic Differential Equation. Forests, 10(6), 506. https://doi.org/10.3390/f10060506





