Modeling Diameter Distribution of Black Alder (Alnus glutinosa (L.) Gaertn.) Stands in Poland

Abstract

We present diameter distribution models for black alder (Alnus glutinosa (L.) Gaertn.) derived from diameter measurements made at breast height in 844 circular sample plots set in 163 managed stands located in south-eastern Poland. A total of 22,530 trees were measured. Stand age ranged from six to 89 years. The model formulation was based on the two-parameter Weibull function and a non-parametric percentile-based method. Weibull function parameters were recovered from the first raw and second central moments estimated using the stand quadratic mean diameter. The same stand characteristic was used to predict values of 12 percentiles in the percentile-based method. The model performance was assessed using the k-fold cross-validation method. The goodness-of-fit statistics include the Kolmogorov–Smirnov statistic, mean error, root mean squared error, and two variants of the error index introduced by Reynolds. The percentile model developed, accurately predicted diameter distributions in 88.4% of black alder stands, as compared to 81.9% for the Weibull model (Kolmogorov–Smirnov test). Alternative statistical metrics assessing goodness-of-fit to empirical distributions suggested that the non-parametric percentile model was superior to the parametric Weibull model, especially in stands older than 20 years. In younger stands, the two models were accurate only in 57% of the cases, and did not differ significantly with respect to goodness-of-fit measures.

1. Introduction

The natural range of the black alder (Alnus glutinosa (L.) Gaertn.) extends through most of Europe, from central Scandinavia to the southern coast of the Mediterranean Sea [1,2]. In Poland, the black alder is widespread in the lowlands, especially in the northern and central parts of the country; in the south it is less common and generally does not occur above 500 m above sea level [3]. The black alder is an economically important species in Poland, covering 522,000 ha (5.7%) with a growing stock estimated at 137 million m³ (263 m³·ha⁻¹), which accounts for 5.3% of the country’s overall growing stock [4]. In wet soils with high groundwater levels, it mostly forms pure, even-aged, one-storey stands. On mesic sites, in mixed deciduous forests, the black alder may be used as a valuable admixture for improving timber production or for biocenotic considerations. Due to its robust root system and symbiosis with bacteria of genus Frankia, which produce nitrogen-fixing nodules on fine roots, it actively transforms its habitats [3]. In addition, as a result of open mineral metabolism, black alder leaf fall contributes 30–130 kg·ha⁻¹·year⁻¹ of nitrogen to the soil [1], and increases the availability of phosphorus, magnesium, manganese, and zinc [1]. These ecological properties of the black alder make it suitable for reclamation of post-industrial sites [5,6]. In addition to providing valuable timber, black alder stands for unique niches, offering habitats to riverine and riparian flora and fauna.

The implementation of economic and non-economic forest functions requires efficient forest management planning that provides reliable and detailed information about forest resources. The optimum level of detail required for economic decision-making includes data about the distribution of stand characteristics by tree-size classes [7]. Diameter distribution defined as the number of trees within a certain diameter range at breast height (DBH) [8,9], is crucial for the determination of stand volume and value [8], biodiversity [10], stability [11], development stage [12], and for predicting growth dynamics [13].

Accurate determination of diameter distribution entails substantial costs associated with measuring DBH for a large number of trees while conducting an inventory [14,15]. In practice, in order to reduce survey costs, only selected stand features are measured; these include quadratic mean diameter (QMD), mean tree height, basal area (BA), etc. Diameter distribution models can be used to estimate the number of trees falling into different DBH classes. The application of diameter distribution models in conjunction with stand characteristics generates results convergent with actual DBH measurements [16].

Diameter distribution modeling may also improve the utility of existing growth models. While complex individual tree-level models, which account for interactions between trees and their environment, accurately describe tree growth processes, they are impracticable due to the prohibitive costs of acquiring the necessary input data [17]. Diameter distribution models can be used with individual tree-level or taper models and can minimize the measurement work needed for their implementation [16,17,18]. The combination of diameter distribution models and individual tree-level or stand models gives rise to an integrated system that not only enhances the accuracy of stand characteristics assessment, but also ensures a convergence of estimates made at different levels of prediction [19].

Diameter distribution models are typically constructed using various theoretical distributions, including normal [20,21], log-normal [20,21], double normal [21,22], Weibull [8,23,24,25,26,27,28,29,30,31], Johnson S_B [32,33,34,35], and beta [16,18]. From among the above, the Weibull function is most often used for modeling unimodal diameter distributions, as it has a simple form of the cumulative function [7,8,36] and due to its flexibility in fitting distributions of various shapes and degrees of skewness and ease of parameter estimation. The parameters of the probability density function may be estimated using two methods—the parameter prediction method (PPM), in which they are predicted directly from stand characteristics, and the parameter recovery method (PRM), in which they are computed from the moments or percentiles of diameter distribution predicted from stand characteristics [37].

An alternative approach to the widely used parametric distributions is the percentile-based method, in which diameter distribution is defined by 12 percentiles estimated directly from stand characteristics [38]. The method has been applied in practice by Siipilehto [39], Kangas and Maltamo [40,41], Mehtätalo [14], Stankova and Diéguez-Aranda [42], and Stankova and Zlatanov [43], and has been deemed appropriate for describing multimodal distributions and those with irregular probability density functions [38,43].

The objective of the study was to develop a diameter distribution model for black alder stands using a two-parameter Weibull function and a non-parametric percentile-based approach. The predictive power of the resulting models was evaluated using a random sample of stands from the western part of the Sandomierz Basin in southeastern Poland.

2. Materials and Methods

2.1. Data Collection

The study material consisted of DBH measurements from 844 circular sample plots in 163 managed black alder stands, aged between 6 and 89 years, and located in southeastern Poland. Regularly spaced circular sample plots, numbering about 2 to 10, with area ranging from 100 to 1000 m² (depending on stand age) were established in each stand. In each plot, height (with an accuracy of 0.1 m) and DBH (twice, at right angles, with an accuracy of 0.1 cm, with the arithmetic mean of the two measurements adopted as the actual DBH) were measured for all living alders. A total of 22,530 trees were measured. An empirical diameter distribution for a given stand was obtained by combining the measurements from all sampled plots in that stand [21].

The collected data were used to calculate the basic stand variables widely used for the construction of diameter distribution models, that is, quadratic mean diameter (QMD; cm), stand density (SD; trees·ha⁻¹), Reineke stand density index (SDI; trees·ha⁻¹), Lorey’s mean height (HL; m), and basal area (BA; m²·ha⁻¹). Furthermore, site index (SI; m) was estimated by means of a formula developed for alder stands in Poland, assuming a base age of 100 years [44].

The parameters of diameter distribution models were developed for the entire set of 163 empirical diameter distributions. The predictive accuracy and precision of the models were evaluated by the k-fold cross-validation method [45,46,47]. To that end, the set of observations was divided at random into 10 parts; nine of them constituted a training dataset. The remaining one was a testing dataset. The procedure was repeated 10 times, so that each group of stands was used as a testing dataset once. The basic statistics for the studied stands and trees are given in

Table 1. Descriptive statistics for stand and tree variables.

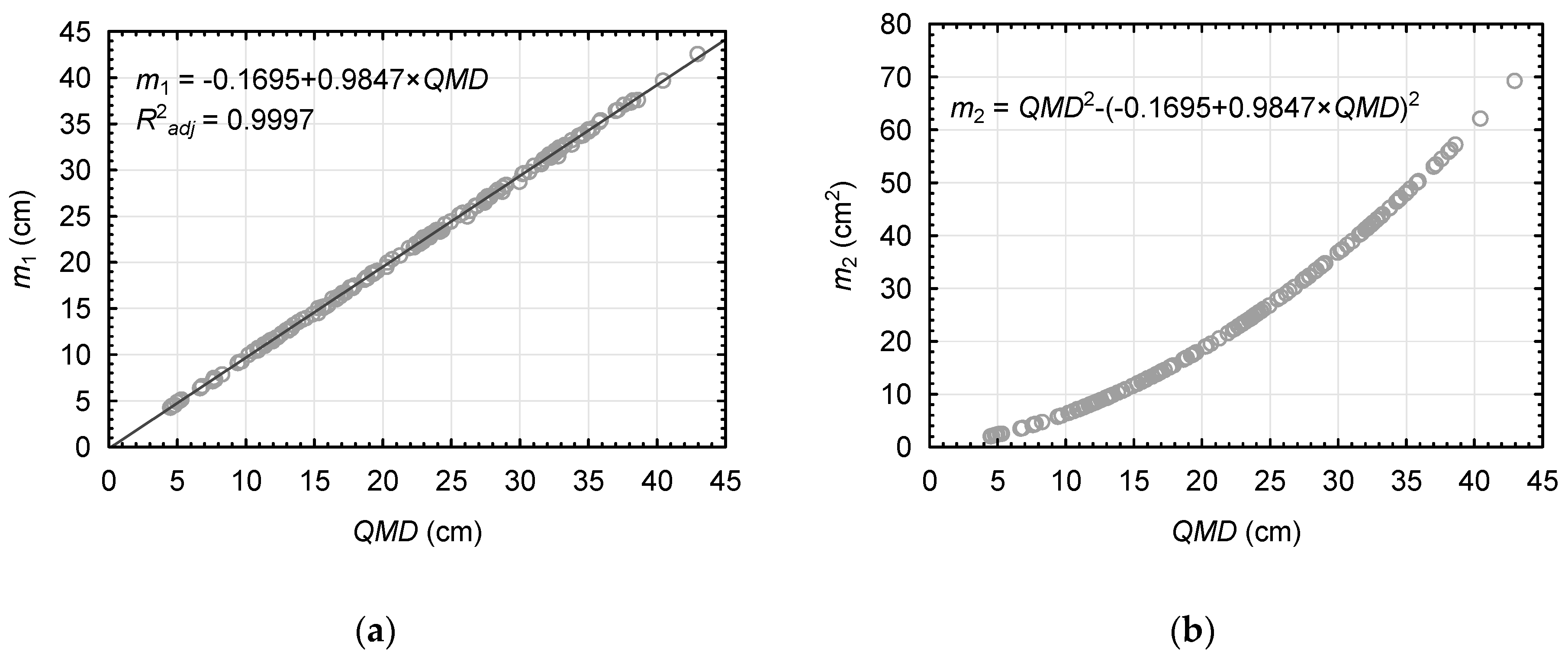
Statistics	Stand Variable							Tree Variable
	QMD	Age	SD	SDI	HL	SI	BA	DBH	TH	BA
Mean	21.99	44	1020	528	20.49	32.4	25.21	20.3	18.9	0.04120
StDev	9.44	23	885	129	6.37	2.4	9.11	10.6	6.8	0.03951
Min.	4.47	6	223	212	6.28	26.5	5.48	1.0	2.8	0.00008
Max.	42.95	89	4360	873	32.75	40.2	49.79	67.0	36.6	0.35257

QMD (cm), quadratic mean diameter; SD (stems·ha⁻¹), stand density; SDI (stems·ha⁻¹), Raineke stand density index; HL (m), Lorey’s mean height; SI (m), site index (base age 100 years), BA (m²·ha⁻¹), basal area; DBH (cm), diameter at breast height; TH (m), tree height; StDev, standard deviation.

.

2.2. Diameter Distribution Models

The diameter distribution of the studied black alder stands was described using a two-parameter Weibull distribution and a non-parametric percentile-based method.

The probability density function f(x) of a two-parameter Weibull distribution is given as [8]:

$$f\left(x\right)=\left(\frac{c}{b}\right){\left(\frac{x}{b}\right)}^{c-1}\exp \left\{-{\left(\frac{x}{b}\right)}^c\right\};x\ge 0;b,c>0,$$

(1)

with its cumulative distribution function F(x) being:

$$F\left(x\right)=1-\exp \{-{\left(\frac{x}{b}\right)}^c\};x\ge 0;b,c>0,$$

(2)

were x is DBH (cm) and b and c are the scale and shape parameters, respectively.

Among the many ways of estimating the parameters of a Weibull distribution, the moment method is deemed superior due to its simplicity and accuracy [48,49,50]. Moreover, if parameters are calculated based on the first raw moment (m₁) and the second central moment (m₂), the results are unbiased estimations of these moments from the sample which guarantees agreement of statistics between the empirical and fitted distributions. The parameters b and c of the Weibull distribution were estimated based on the first raw moment and the second central moment according to the formulas:

$$m_1=b\cdot \Gamma \left(1+\frac{1}{c}\right),$$

(3)

$$m_2=b^2\cdot \left(\Gamma \left(1+\frac{2}{c}\right)-{\Gamma }^2\left(1+\frac{1}{c}\right)\right),$$

(4)

where $\Gamma (\cdot )$ is the gamma function.

Transforming Equation (3) in terms of parameter b and substituting the result into Equation (4) gives:

$$b=\frac{m_1}{\Gamma \left(1+\frac{1}{c}\right)},$$

(5)

$$m_2=\frac{m_1^2}{{\Gamma }^2\left(1+\frac{1}{c}\right)}\cdot \left(\Gamma \left(1+\frac{2}{c}\right)-{\Gamma }^2\left(1+\frac{1}{c}\right)\right),$$

(6)

When the first raw moment and the second central moment are known, Equation (6) depends only on parameter c and may be solved iteratively after being transformed to:

$$\frac{m_1^2}{{\Gamma }^2\left(1+\frac{1}{c}\right)}\cdot \left(\Gamma \left(1+\frac{2}{c}\right)-{\Gamma }^2\left(1+\frac{1}{c}\right)\right)-m_2=0,$$

(7)

Parameter b may be then calculated directly from Equation (5).

In the PRM, moments, m₁ and m₂ are estimated from the stand characteristics recorded in the inventory. The first raw moment m₁, being the (arithmetic) mean diameter, may be expressed as a linear function of the QMD [42,43]:

$$m_1=a+b\cdot QMD,$$

(8)

where a and b are the equation coefficients.

The second central moment m₂, which is the variance of diameters, is calculated according to the formula [42,43]:

$$m_2=QM{D}^2-m_1^2,$$

(9)

The other approach to constructing a diameter distribution model is the percentile method proposed by Borders et al. [38], which defines the PDF by means of 12 percentiles, that is, 0th, 5th, 15th... 85th, 95th, and 100th. These percentiles are determined using empirical regression equations based on the actual stand characteristics. In the original version of the method, the percentile predicted with the greatest confidence, based on preliminary regression equations, is selected as a “driver percentile”. This work uses a version of the percentile method modified by Stankova and Zlatanov [43], without a driver percentile, in which the 12 percentiles are determined solely from stand characteristics. Preliminary analysis showed, that QMD was the best performing stand feature to predict values of the required percentiles. The parameters of the system of equations describing the empirical relationship between the 12 percentiles and the QMD of the stand were determined using seemingly unrelated regressions:

$$\{\begin{array}{l}{P}_0=a_0+b_{0}QMD\\ P_5=a_5+b_{5}QMD\\ P_{15}=a_{15}+b_{15}QMD\\ .\\ .\\ .\\ P_{100}=a_{100}+b_{100}QMD\end{array},$$

(10)

where P₀, P₅, P₁₅, ..., P₁₀₀ are percentiles of the empirical diameter distribution (cm), and a₀, a₅, a₁₅, ..., a₁₀₀ and b₀, b₅, b₁₅, ..., b₁₀₀ are equation coefficients.

2.3. Model Evaluation and Validation

At the stage of model parameterisation, goodness-of-fit to empirical data was evaluated using the adjusted coefficient of determination (R²_adj), the mean squared error (MSE), and the significance levels of regression models (F-test), and their coefficients (t-test).

The predictive performance of the models developed was estimated using the k-fold cross-validation method. The fit of the models to data from the actual stands (testing dataset) was evaluated by comparing empirical $F$ and predicted $\widehat{F}$ CDFs. The Kolmogorov–Smirnov statistic D_n was calculated to measure the maximum absolute distance between the observed and predicted CDFs [7,36,43]:

$$D_n=\underset{d}{\sup }\left|F\left(d_i\right)-\widehat{F}\left(d_i\right)\right|,$$

(11)

The average distances between the compared CDFs, expressed by means of the mean error (ME) and the root mean squared error (RMSE), were calculated for each stand from the following formulas:

$$ME=\frac{{\displaystyle \sum _{i=1}^n\left(\widehat{F}\left(d_i\right)-F\left(d_i\right)\right)}}{n},$$

(12)

$$RMSE=\sqrt{\frac{{\displaystyle \sum _{i=1}^n{\left(\widehat{F}\left(d_i\right)-F\left(d_i\right)\right)}^2}}{n}},$$

(13)

where d_i is the DBH of i-th tree in the stand and n is the number of trees.

In the case of diameter distribution modeling, it is important to not only determine differences between empirical and predicted CDFs, but also to find in which part of the distribution those differences occur. Practical implications of an error of one tree will substantially differ depending on whether that error arose in a small or large DBH class. A statistic which accounts for this additional criterion is the error index e, proposed by Reynolds et al. [36], which is the weighted sum of absolute differences between predicted and observed trees per hectare in all DBH classes [51]:

$$e=N{\displaystyle \sum _{k=1}^m\left|{\displaystyle \underset{{}_{L}d{}_k}{\overset{{}_{U}d{}_k}{\int }}w\left(d\right)d\widehat{F}\left(d\right)}-{\displaystyle \underset{{}_{L}d{}_k}{\overset{{}_{U}d{}_k}{\int }}w\left(d\right)dF\left(d\right)}\right|},$$

(14)

where N is the number of trees per unit of area (trees·ha⁻¹), w(d) is the weight assigned to a tree with a DBH of d, ${}_{L}d{}_k$ and ${}_{U}d{}_k$ are the lower and upper limits of k-th DBH class respectively, and m is the number of DBH classes. If the weight w(d) corresponds to tree volume, then the expression $N{\displaystyle {\int }_{{}_{L}d{}_k}^{{}_{U}d{}_k}w\left(d\right)d\widehat{F}\left(d\right)}$ is the predicted volume per hectare in the k-th DBH class, while $N{\displaystyle {\int }_{{}_{L}d{}_k}^{{}_{U}d{}_k}w\left(d\right)dF\left(d\right)}$ is the observed volume per hectare in that DBH class. If the effect of weights is eliminated, that is w(d) = 1, the above expressions correspond to the predicted and observed number of trees per hectare for the k-th DBH class [36]. This study used two variants of the error index, e_N and e_G, as calculated from the formulas below:

$$e_N={\displaystyle \sum _{k=1}^m\left|{\widehat{N}}_k-N_k\right|},$$

(15)

$$e_G={\displaystyle \sum _{k=1}^m\left|{\widehat{G}}_k-G_k\right|},$$

(16)

where ${\widehat{N}}_k$ and $N_k$ correspond to the predicted and observed number of trees per hectare for the k-th DBH class, ${\widehat{G}}_k$ and $G_k$ are the predicted and observed BAs (m²·ha⁻¹) for the k-th DBH class.

In the case of the Weibull distribution, the predicted number of trees in a given DBH class ${\widehat{N}}_k$ was calculated as the product of the overall number of trees per hectare (N) determined on the basis of field measurement and the probability p_k of the presence of trees in the k-th DBH class calculated from the difference in the CDF between the upper ${}_{U}d{}_k$ and lower ${}_{L}d{}_k$ DBH limits:

$${\widehat{N}}_k=N\cdot p_k,$$

(17)

$$p_k=\widehat{F}\left({}_{U}d{}_k\right)-\widehat{F}\left({}_{L}d{}_k\right),$$

(18)

In the case of the percentile method, the predicted number of trees in a given DBH class ${\widehat{N}}_k$ was determined from the following formula [38]:

$${\widehat{N}}_k=\left\{\frac{P_i-{}_{L}d{}_k}{P_i-P_{i-1}}\left(t_i-t_{i-1}\right)+\left(t_j-t_i\right)+\left(t_{j+1}-t_j\right)\frac{{}_{U}d{}_k-P_j}{P_{j+1}-P_j}\right\}\cdot N,$$

(19)

in which:

$$P_{i-1}\le {}_{L}d{}_k<P_i,$$

(20)

$$P_j<{}_{U}d{}_k\le P_{j+1},$$

(21)

where: P_i, P_j are values of the r-th percentile, t_i, t_j are the order of the r-th percentile expressed as (t_i = r/100), where {i – 1, i, j, j + 1} $\in$ r; r{0, 5, 15, 25, 35, 45, 55, 65, 75, 85, 95, 100}.

The predicted BA ${\widehat{G}}_k$ in the k-th DBH class was calculated from the formula:

$${\widehat{G}}_k={\widehat{N}}_k\cdot \frac{\pi \cdot {}_{M}d{}_k^2}{40000},$$

(22)

where ${}_{M}d{}_k$ is the middle DBH of the k-th DBH class.

Models were finally compared based on the differences revealed by the goodness-of-fit statistics for the 163 stands comprising the testing dataset in the cross-validation step. As the distributions of differences for all the analyzed statistics were not normal, they were compared using the Wilcoxon signed rank–test. At a significance level of α = 0.05, the null hypothesis (H₀: Median_{(differences)} = 0) was tested against the alternative hypothesis (H_A: Median_{(differences)} ≠ 0).

All calculations and analyses were performed in the R statistical software [52], using the following packages: base, caret [53], stats, and systemfit [54].

3. Results

3.1. Parametrization of the Diameter Distribution Models

The value of the first raw moment m₁, required to determine the scale parameter b and the shape parameter c of the two-parameter Weibull distribution (Equation (1)), was calculated from the empirical formula:

$$m_1=-0.1695+0.9847\cdot QMD,$$

(23)

The relationship between the first raw moment m₁ and the QMD was statistically significant (F_(1,161) = 554072.2; p < 0.0001), with the values of the constant term (t = −5.36; p < 0.0001) and slope (t = 744.36; p < 0.0001) being significantly different from 0 (Figure 1a). The adjusted determination coefficient was 0.9997. After substituting the above equation (Equation (23)) into the empirical formula (Equation (9)) for the second central moment m₂, the latter assumes the following form:

$$m_2=QM{D}^2-{\left(-0.1695+0.9847\cdot QMD\right)}^2,$$

(24)

with its graphical interpretation shown in Figure 1b.

Relationships between the 12 percentiles and the QMD in the stands studied are given in Figure 2. The fit of the developed system of seemingly unrelated equations assessed by McElroy’s R² is 0.9994, with R²_adj ranging from 0.850 to 0.998 for individual equations (

Table 2. Parameters and goodness-of-fit statistics for equations describing relationships between percentiles and the quadratic mean diameter (QMD) of black alder stands.

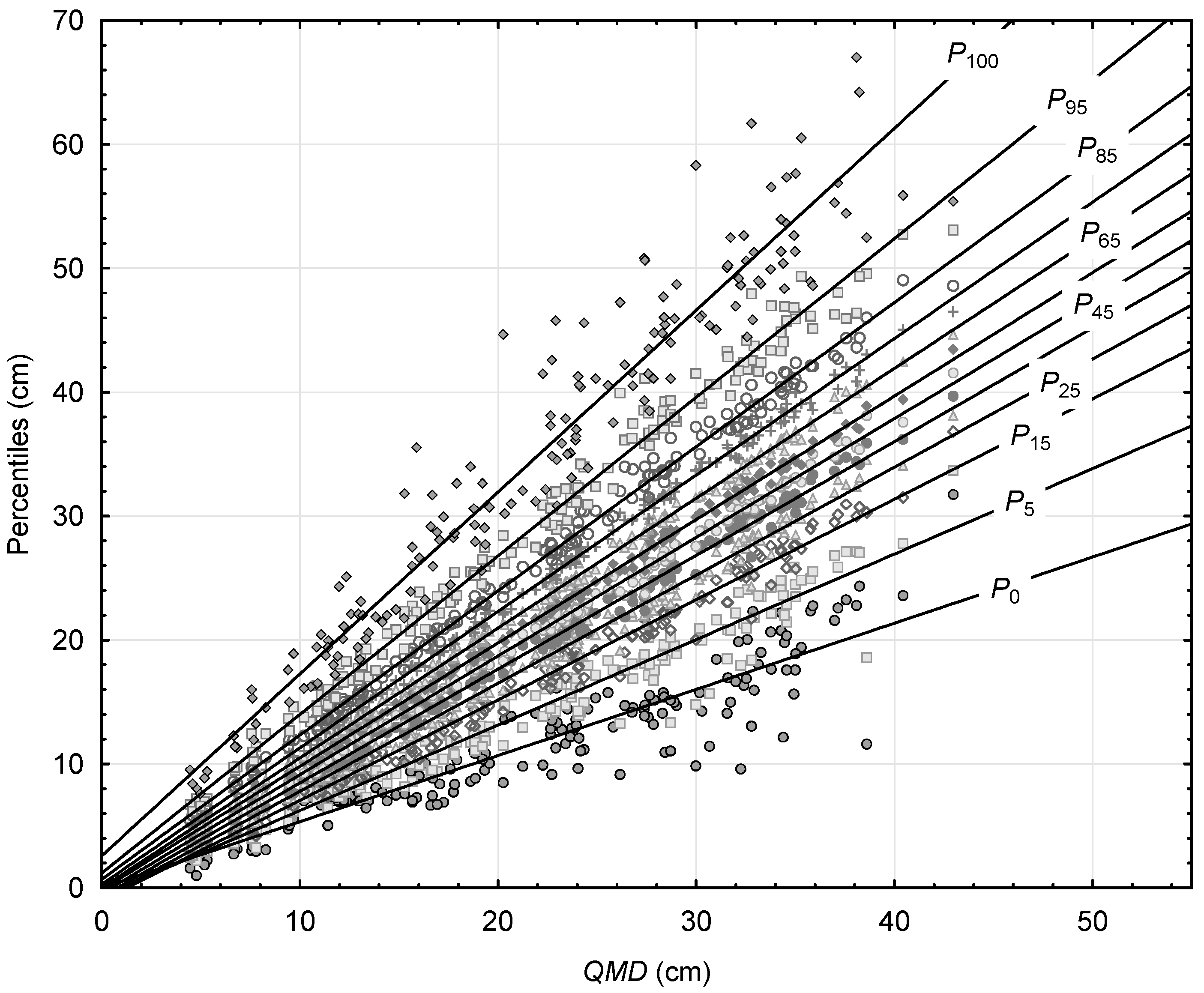
Percentiles	Parameters a0–100	Parameters b0–100	R2adj	MSE
P0 = a0 + b0 QMD	0.000	0.534 ***	0.850	4.70
P5 = a5 + b5 QMD	−0.663 ***	0.690 ***	0.949	2.34
P15 = a15 + b15 QMD	−1.039 ***	0.810 ***	0.985	0.89
P25 = a25 + b25 QMD	−0.929 ***	0.872 ***	0.992	0.56
P35 = a35 + b35 QMD	−0.714 ***	0.918 ***	0.996	0.32
P45 = a45 + b45 QMD	−0.451 ***	0.958 ***	0.997	0.21
P55 = a55 + b55 QMD	−0.155 *	0.996 ***	0.998	0.15
P65 = a65 + b65 QMD	0.000	1.048 ***	0.998	0.17
P75 = a75 + b75 QMD	0.284 ***	1.101 ***	0.998	0.23
P85 = a85 + b85 QMD	0.681 ***	1.164 ***	0.996	0.53
P95 = a95 + b95 QMD	1.186 ***	1.280 ***	0.988	1.76
P100 = a100 + b100 QMD	2.574 ***	1.468 ***	0.934	13.27

Significance levels: *** p < 0.001, * p < 0.05; R²_adj, adjusted coefficient of determination; MSE, mean squared error.

). The lowest goodness-of-fit, as expressed by the adjusted determination coefficient and mean squared error (MSE), was found for the extreme percentiles P₀ (R²_adj = 0.850; MSE = 4.70) and P₁₀₀ (R²_adj = 0.934; MSE = 13.27). Goodness-of-fit increased for percentiles closer to the center with the best fit obtained for P₅₅ (R²_adj = 0.998; MSE = 0.15).

3.2. Evaluation and Comparison of the Distribution Models

The Kolmogorov–Smirnov test used for comparing empirical and predicted distributions, revealed that the percentile and the Weibull models accurately reflected diameter distributions in 88.4% and 81.9% of black alder stands, respectively, at a significance level of α = 0.05. The share of cases in which the null hypothesis was not rejected depended on stand age, and in consecutive 20-year age classes amounted to 57.1%, 95.1%, 95.3%, and 90.2% for the percentile model and 57.1%, 77.1%, 90.2%, and 90.2% for the Weibull model. Both models poorly predicted diameter distributions for the youngest stands (1–20 years), with the proportion of poor fits significantly declining with stand age. In the second and third age classes, the percentile model was clearly superior to the Weibull model. Figure 3 shows the examples of best and worst fitted distributions in the various age classes.

The mean Kolmogorov–Smirnov statistic D_n was 0.0786 and 0.0919 for the overall set of studied stands, for the percentile and Weibull models, respectively (

Table 3. Goodness-of-fit statistics for Weibull and percentile diameter distribution models for different stand age classes.

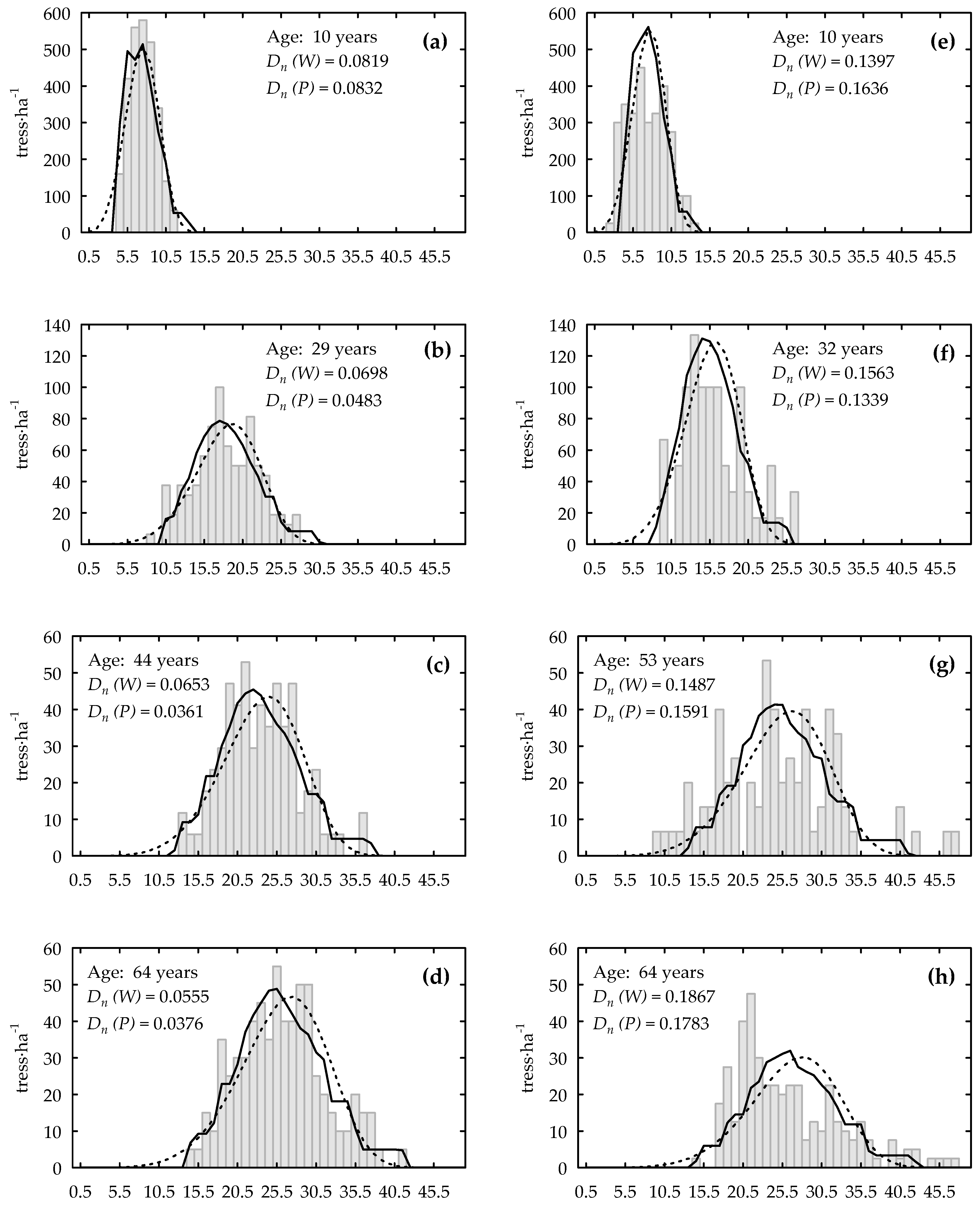
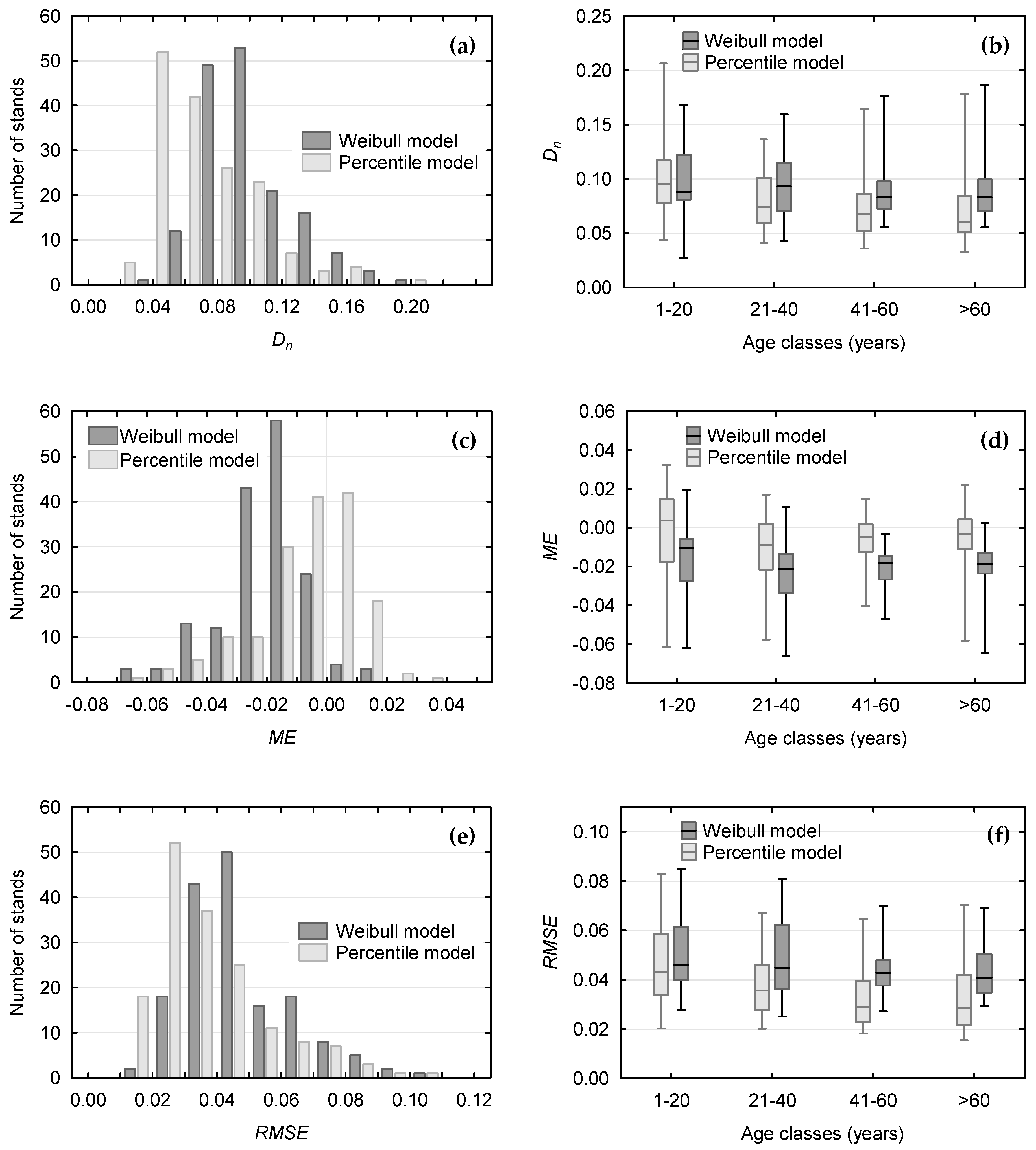
Distribution Models	Age Classes of Stands	Dn Statistic		ME		RMSE
		Mean	SD	Mean	SD	Mean	SD
Weibull	1–20 years	0.0977	0.0308	−0.0147	0.0175	0.0505	0.0180
	21–40 years	0.0937	0.0299	−0.0248	0.0162	0.0491	0.0181
	41–60 years	0.0881	0.0240	−0.0206	0.0099	0.0444	0.0133
	>60 years	0.0900	0.0277	−0.0209	0.0125	0.0456	0.0163
	All stands	0.0919	0.0279	−0.0207	0.0142	0.0471	0.0164
Percentile	1–20 years	0.0978	0.0368	−0.0018	0.0214	0.0473	0.0209
	21–40 years	0.0785	0.0259	−0.0122	0.0188	0.0384	0.0151
	41–60 years	0.0726	0.0282	−0.0063	0.0125	0.0331	0.0143
	>60 years	0.0717	0.0316	−0.0051	0.0155	0.0336	0.0177
	All stands	0.0786	0.0315	−0.0067	0.0171	0.0372	0.0175

ME, mean error; RMSE, root mean squared error; SD, standard deviation.

). The Wilcoxon signed-rank test revealed that the two models differed significantly in terms of that criterion (Z = 7.097; p < 0.05;

Table 4. Results of the Wilcoxon signed-rank test for comparison of goodness-of-fit statistics for the Weibull and percentile diameter distribution models.

Age Classes of Stands	Dn Statistic		ME		RMSE
	Z Statistic	p-Value	Z Statistic	p-Value	Z Statistic	p-Value
1–20 years	0.257	0.7971	4.741	0.0000	1.512	0.1310
21–40 years	4.130	0.0000	5.711	0.0000	5.204	0.0000
41–60 years	4.622	0.0000	5.841	0.0000	5.401	0.0000
>60 years	4.656	0.0000	5.841	0.0000	5.108	0.0000
All stands	7.097	0.0000	11.070	0.0000	8.936	0.0000

ME, mean error; RMSE, root mean squared error.

). In both models, the highest D_n statistic was found for stands in the first age class (Table 3), without significant differences between the models (Table 4). In subsequent age classes, the mean D_n statistic decreased, especially for the percentile model (Table 3, Figure 4), with the differences between the models being significant (Wilcoxon test, Table 4).

The mean difference (ME) between predicted and empirical CDFs was −0.0067 for the percentile model and −0.0207 for the Weibull model (Table 3). The observed absolute average differences were significantly smaller for the percentile models in all stand age classes (Table 3 and Table 4; Figure 4). RMSE differences between the predicted and empirical CDFs were 0.0372 and 0.0471 for the percentile and Weibull models, respectively (Table 3; Figure 4), and were statistically significant (Z = 8.936; p < 0.05; Table 4). For both models, RMSE was the highest in the first age class and generally decreased with stand age (Table 3; Figure 4). In the youngest stands (1–20 years), RMSE differences between the two models were not significant (Z = 1.512; p > 0.05; Table 4), in contrast to all other age classes, where statistical significance was obtained (Table 4).

The distribution of the error index e_N was similar for both diameter distribution models (Figure 5). The index ranged from 83.0 to 1677.4 trees·ha⁻¹ for the Weibull model and from 78.8 to 1997.3 trees·ha⁻¹ for the percentile model, with the mean values being 315.0 trees·ha⁻¹ and 314.0 trees·ha⁻¹, respectively (

Table 5. Error indexes e_N and e_G for the Weibull and percentile diameter distribution models for different stand age classes.

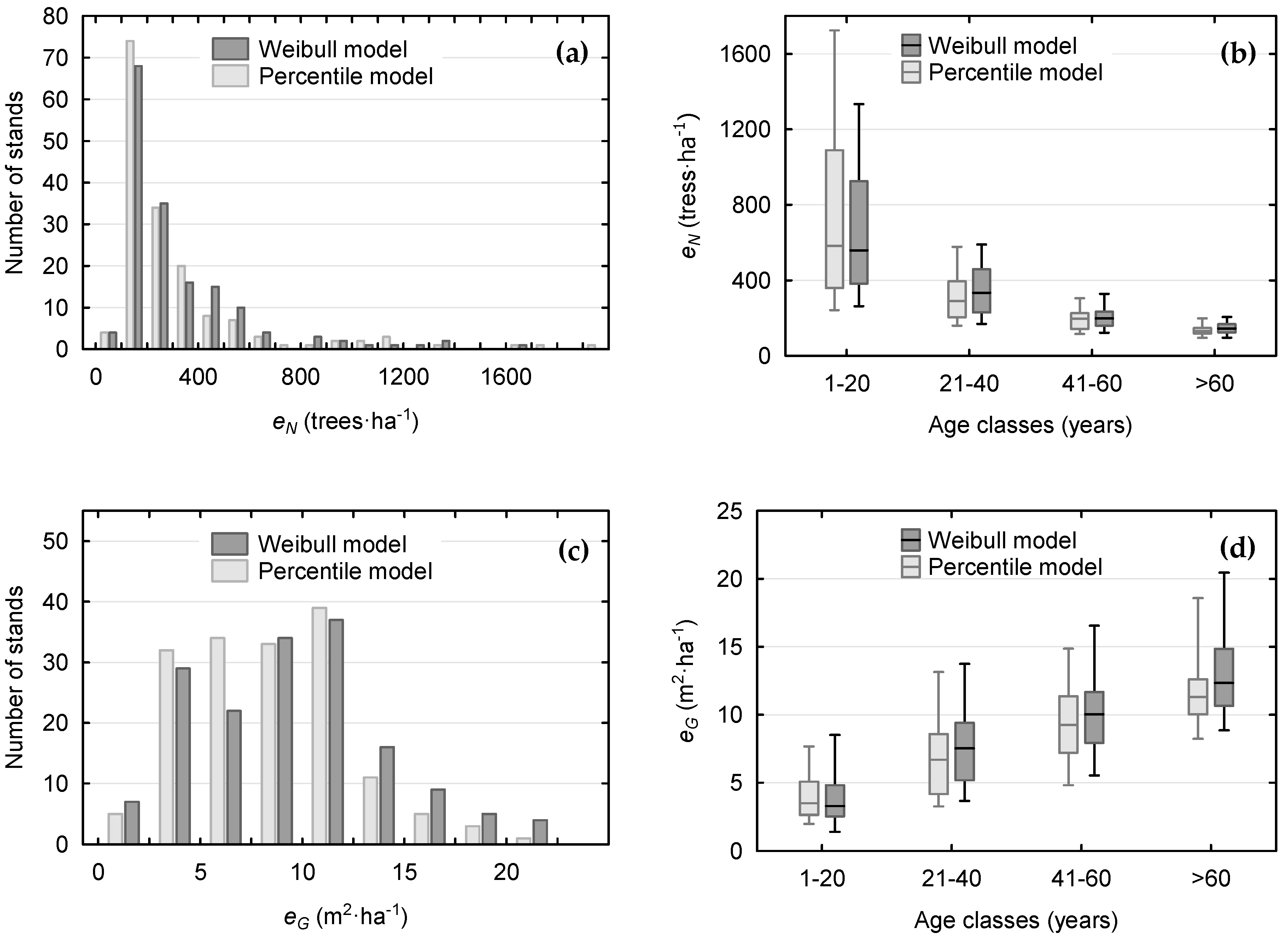
Distribution Models	Age Classes of Stands	eN		eG
		Mean	SD	Mean	SD
Weibull	1–20 years	675.7	378.6	4.10	2.17
	21–40 years	352.3	144.8	7.74	3.72
	41–60 years	207.4	70.3	10.24	3.67
	>60 years	146.5	34.6	13.04	3.42
	All stands	315.0	261.4	9.22	4.58
Percentile	1–20 years	749.1	483.7	3.92	1.59
	21–40 years	322.2	132.5	6.86	3.08
	41–60 years	194.3	66.0	9.50	3.55
	>60 years	136.0	29.6	11.74	2.91
	All stands	314.0	309.4	8.39	4.05

). Despite these similar results, the Wilcoxon signed-rank test for all stands revealed significant differences between the median values of e_N for the two models (Z = 4.499; p < 0.05;

Table 6. Results of the Wilcoxon signed-rank test for comparison of error indexes e_N and e_G for Weibull and percentile diameter distribution models.

Age Classes of Stands	eN		eG
	Z Statistic	p-Value	Z Statistic	p-Value
1–20 years	1.100	0.2712	0.566	0.5717
21–40 years	3.345	0.0008	4.371	0.0000
41–60 years	3.347	0.0008	3.979	0.0001
>60 years	4.306	0.0000	5.017	0.0000
All stands	4.499	0.0000	7.557	0.0000

). Significant differences between the Weibull and percentile models were found in stands older than 20 years, whereas in the youngest group of stands (1–20 years), the two models revealed similar e_N (Table 6; Figure 5). The same pattern was found for the error index e_G, which was calculated using the BAs of the various DBH classes as weights. Also in this case, the mean error index for the percentile model was lower than for the Weibull model, both, for all stands as a whole and for individual age classes (Table 5; Figure 5). Statistically significant differences were again found for stands older than 20 years, while in the youngest ones the null hypothesis could not be rejected (Wilcoxon signed-rank test; Table 6).

4. Discussion

The study led to the development of two diameter distribution models, which in conjunction with the previously proposed generalized height-diameter model for black alder [55] may serve as a useful tool supporting the management of alder stands. In the earlier models, the frequency of trees in the various DBH classes is predicted only from the QMD, which is a commonly used measure in forestry [56]. Borders and Patterson [26] emphasize that parsimony is a desirable feature of empirical models. A similar view is expressed by the authors, the more so as the constructed models of diameter distribution will be used mainly for practical applications rather than in scientific research. That is why, a simpler two-parameter form of the Weibull distribution was applied, especially, as it often gives better results as compared to the three-parameter form [18], and excludes the problem associated with the risk of obtaining a negative scale parameter as stated by Lei [57], and also by the present authors in a previous paper [21]. To prevent a negative value for this parameter, it is often arbitrarily fixed as half of the smallest DBH in a given stand [19,28,30,58,59]. On the other hand, the act of adopting an arbitrary value for a parameter describing the PDF remains controversial and theoretically unjustified.

The other approach to modeling diameter distributions was the non-parametric percentile-based method [38], in which it is not necessary to adopt a priori any theoretical function form, and so it can be used for modeling distributions of any shape. Maltamo et al. [18] pointed out, that there are no mathematical, and especially, no biological grounds for assuming any theoretical distribution for tree diameters. Furthermore, according to Zhang et al. [51] and Palahí et al. [16], the final evaluation of a given density function often depends on the applied method of estimation of its coefficient. In the case of the method proposed by Borders et al. [38], some objections may be raised as to the selection of a given number of percentiles and the assumption as to the existence of a relationship between percentile values and stand characteristic(s). Thus, for the sake of parsimony, the present study adopted 12 percentiles describing the distribution function, but without the application of a driver percentile, especially as Stankova and Zlatanov [43] reported that the simplified method was more accurate.

The main challenge in constructing diameter distribution models for a stand, group of stands, or another set of trees is to obtain the best possible approximation of their observed distributions using the basic stand characteristics available from inventory data. The developed percentile model accurately predicted diameter distributions in 88.4% of black alder stands as compared to 81.9% for the Weibull model (Kolmogorov–Smirnov test). Similar models developed for black pine plantations in Bulgaria led to 97% and 98% agreement for the percentile and Weibull models, respectively, but it should be noted that those results were obtained with the teaching dataset, for which the models were constructed [43]. A comparison of the proposed models using other statistics evaluating goodness-of-fit to empirical distributions indicated that the non-parametric percentile model was superior to the parametric Weibull model, especially in stands older than 20 years. In the youngest stands, the two models were accurate only in 57% of the cases and did not differ significantly with respect to goodness-of-fit. These findings differ from the models developed by Stankova and Zlatanov [43] for Austrian black pine plantations, where the two-parameter Weibull distribution was markedly better than the percentile model, especially in the youngest stands. The two-parameter Weibull distribution was similarly effective in characterizing DBH for young stands in a study by Bullock and Burkhart [60].

Both models were assessed by means of different statistics including ME, RMSE and error indexes e_N and e_G. While the first two rely only on differences in CDFs, the third requires information about the number of trees per hectare. In our analysis, we obtain this characteristics based on field measurements on sample plots of known area. There are also other ways like the application of existing whole stand models [34] or using airborne laser scanning data [15]. It seems that, regardless of the method used to determine the number of trees per hectare, the final conclusions regarding the comparison of our two models should not be affected. However, it should be expected that the range and variability of e_N and e_G will be larger compared to our results, especially when the stand density is predicted based on whole stand models.

According to Nord-Larsen and Cao [17], the use of the basic stand characteristics to estimate the frequency of trees in various DBH classes may be insufficient. This objection, in particular, pertains to the fact that stands treated according to different thinning regimes may reveal similar characteristics, while being completely different in terms of diameter distribution. Our study results, especially the values of goodness-of-fit statistics and their variation, confirm that while the distribution models generated accurate estimates for some stands, in other cases the predicted results were significantly different from the observed values (Figure 3). Such a situation may be caused not only by thinning, but also by natural factors affecting diameter distribution, such as heterogeneous site conditions and irregular tree density caused by wind or snow damages. Von Gadow et al. [61] noted that a given diameter distribution may correspond to many different spatial tree distributions, and so one should incorporate information about tree location in the process of diameter distribution modeling [62]. While a greater number of factors included in a model may certainly improve prediction quality, it may also decrease the application potential of the resulting solution, thus running contrary to the parsimony principle.

While some of the latest works devoted to diameter distributions of stands have applied remote sensing tools, such as airborne laser scanning [15], at the current stage of technological development, it is still necessary to estimate those distributions indirectly by means of prediction models [15]. It seems that the constructed models may provide valuable assistance to cutting-edge technologies in modeling diameter distributions for black alder stands. Nevertheless, the primary application of the developed models is the projection of future diameter distributions to optimize management processes in black alder stands [63]. This task may be facilitated by inclusion of predicted changes in QMD over time into elaborated distribution models.

5. Conclusions

Two diameter distribution models were developed for even-aged black alder stands in Poland to estimate the frequency of trees in the various DBH classes exclusively on the basis of the QMD. The percentile-based method was found to predict the diameter distribution very accurately and was superior to the Weibull model, but its application should be limited to stands older than 20 years. In younger stands, diameter distribution was not predicted well either by the percentile or Weibull models.