Beta-Diversity Modeling and Mapping with LiDAR and Multispectral Sensors in a Semi-Evergreen Tropical Forest
Abstract
1. Introduction
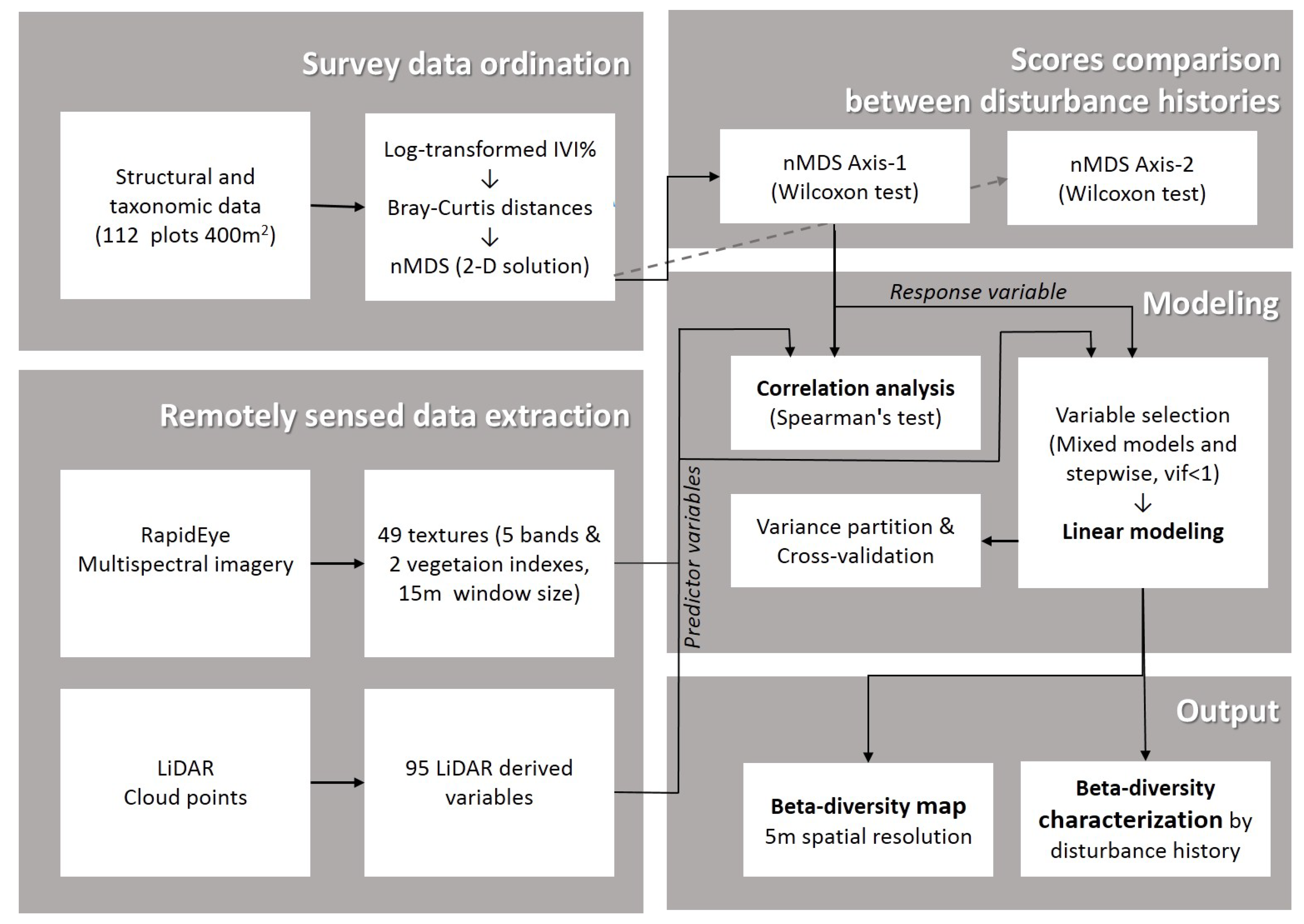
2. Materials and Methods
2.1. Study Site
2.2. Field Data Collection and Processing
2.3. Remotely Sensed Data
2.3.1. Multispectral Imagery
2.3.2. LiDAR
2.4. Correlation Test
2.5. Model Fitting
3. Results
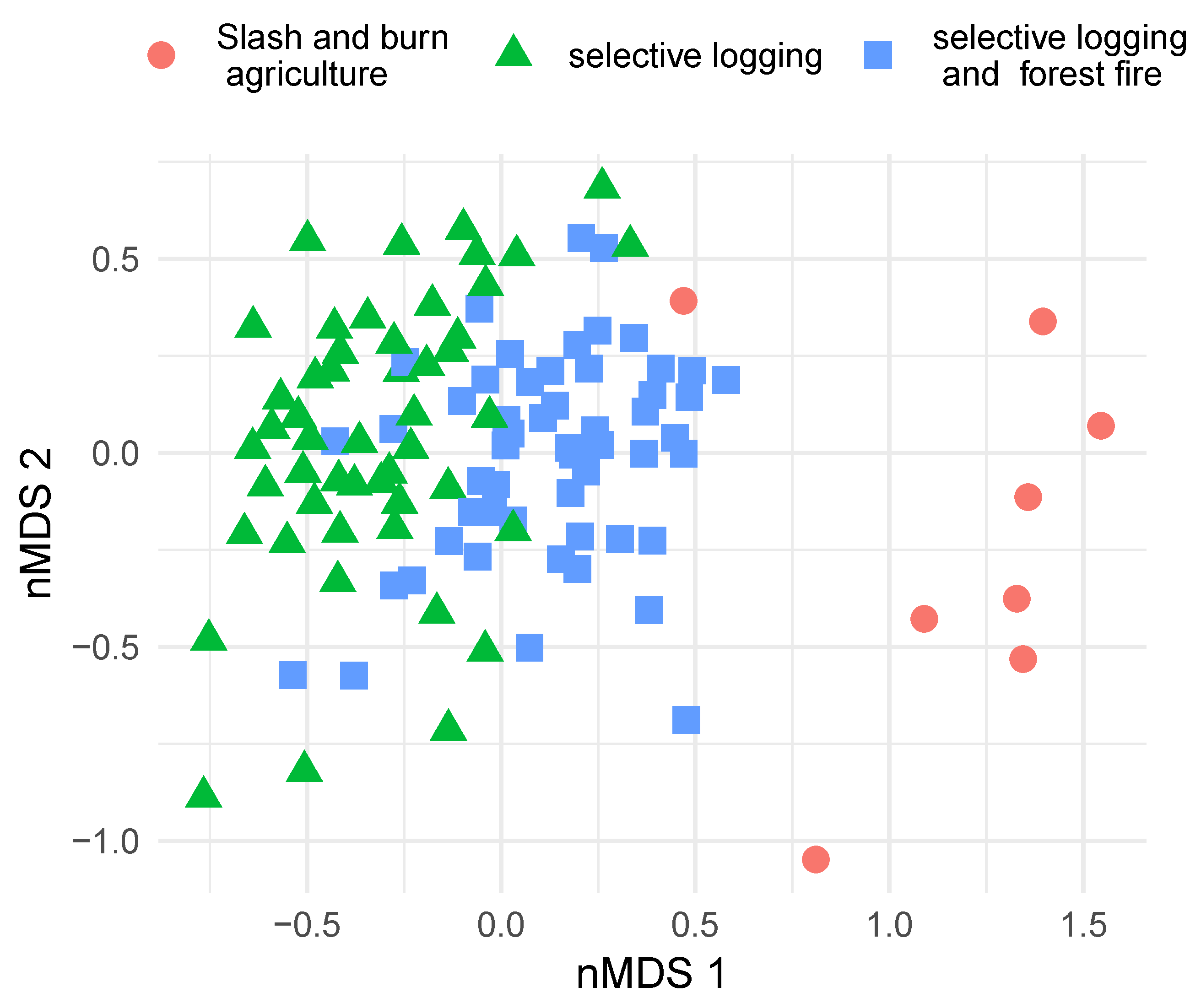
3.1. Species Compositional Ordination
3.2. Correlation Analysis
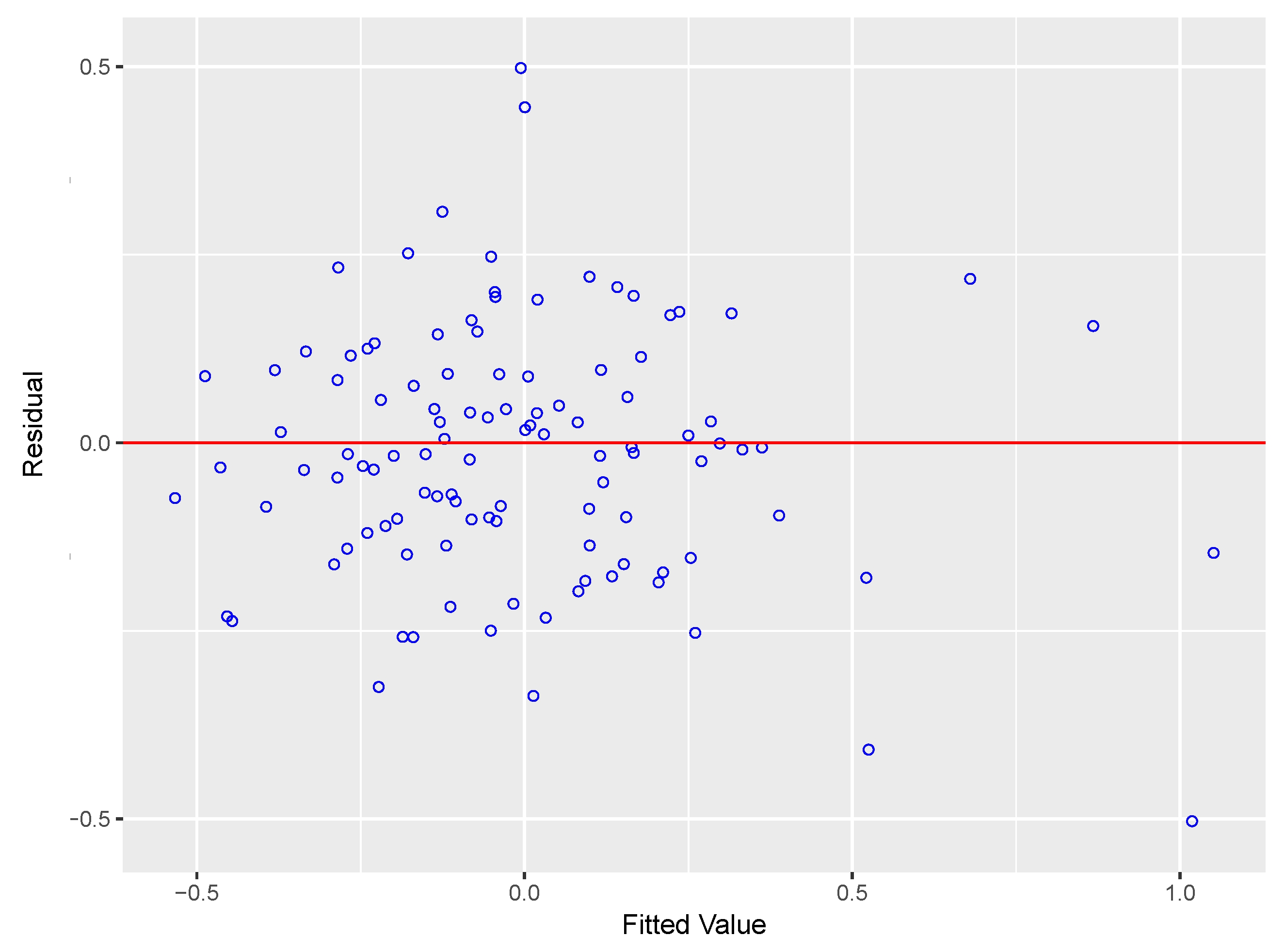
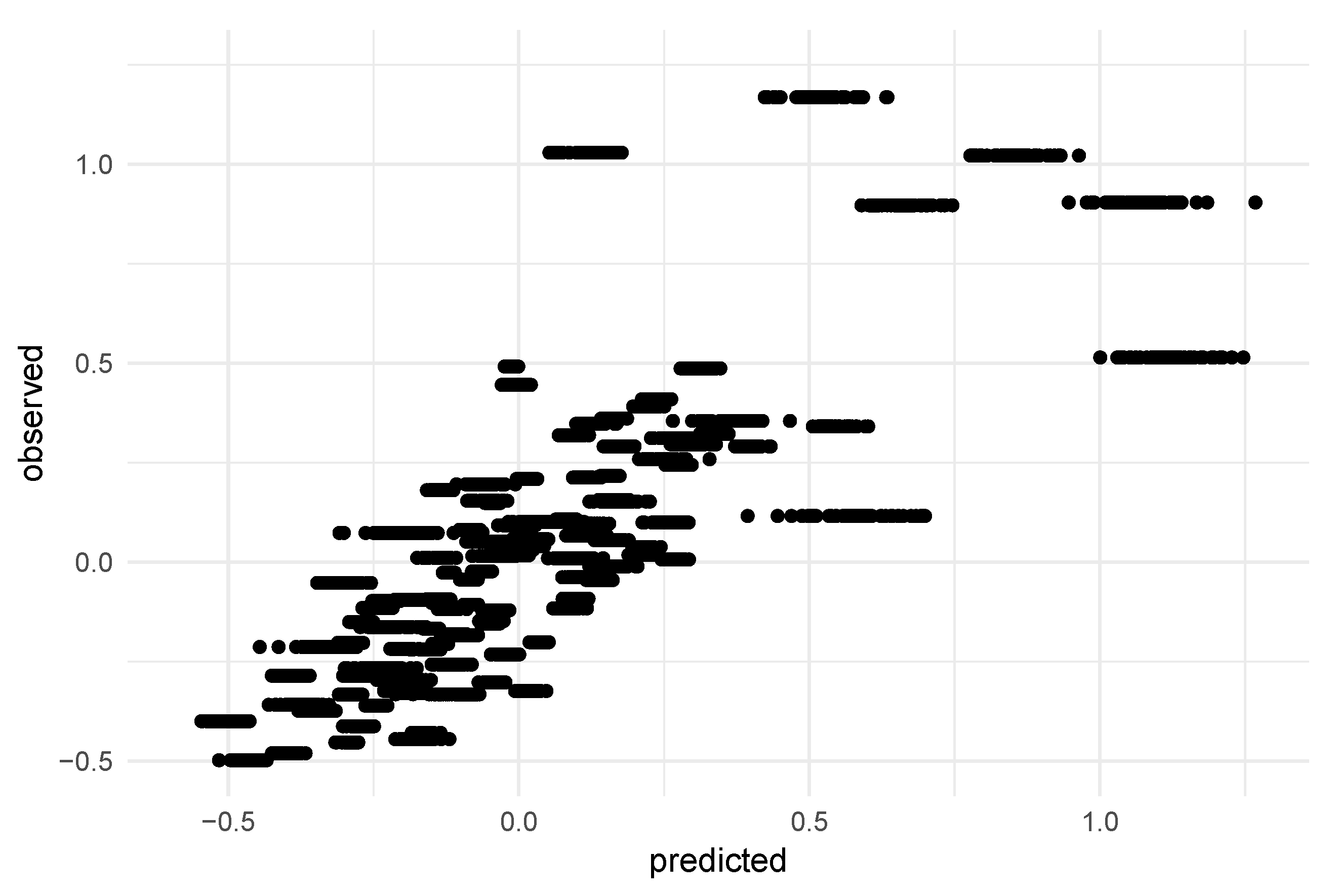
3.3. Predictive Model
3.4. Composition Mapping
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Frías, R. La selva tropical: Más que una numeralia fantástica. In Monitoreo de Biodiversidad y Recursos Naturales: ¿para qué? 3rd ed.; Chediack, S.E., Ed.; Comisión Nacional para el Conocimiento y Uso de la Biodiversidad: México DF, México, 2009; Chapter La selva t; pp. 39–43. [Google Scholar]
- Torres-Rojo, J.M.; Amador-Callejas, J. Características de los núcleos agrarios Forestales en México. In Desarrollo Forestal Comunitario, la Política pública; CIDE: México DF, México, 2015; Chapter Caracterís; pp. 15–37. [Google Scholar]
- Torres-Rojo, J.M.; Moreno-Sánchez, R.; Mendoza-Briseño, M.A. Sustainable Forest Management in Mexico. Curr. For. Rep. 2016, 2. [Google Scholar] [CrossRef]
- Trabanino, F.; Pulido-Salas, M.T. La Xiloteca en el Banco de Germoplasma-CICY: Referencia arqueobotánica para el área maya y para el uso sustentable de maderas de la península de Yucatán F. Desde Herb. CICY 2017, 9, 147–151. [Google Scholar]
- Rosell, J.; Wehenkel, C.; Pérez-Martínez, A.; Arreola, J.A.; García-Jácome, S.P.; Olguín, M.; Olgu, M. Updating bark proportions for the estimation of tropical timber volumes by indigenous community-nased forest enterprises in Quintana Roo. Forests 2017, 8, 338. [Google Scholar] [CrossRef]
- ENAIPROS: Estrategia Nacional de Manejo Forestal Sustentable para el Incremento de la Producción y Productividad. 2013–2018; Technical Report; Comisión Nacional Forestal: Zapopan, Jalisco, México, 2013.
- Jardel-Peláez, E.J. Guía para la Caracterización y Clasificación de Hábitats Forestales; Comisión Nacional Forestal: Zapopan, Jalisco, México, 2015; p. 118. [CrossRef]
- European Environment Agency. Terrestral Habitat Mapping in Europe: An Overview; Technical Report 1; European Environmental Agency: Copenhagen, Denmark, 2014. [Google Scholar] [CrossRef]
- Lindenmayer, D.; Franklin, J. Conserving Forest Biodiversity: A Comprehensive Multiscaled Approach; Island Press: Whashington, DC, USA, 2002; p. 352. [Google Scholar]
- Phua, M.H.; Ling, Z.Y.; Coomes, D.A.; Wong, W.; Korom, A.; Tsuyuki, S.; Ioki, K.; Hirata, Y.; Saito, H.; Takao, G. Seeing trees from space: Above-ground biomass estimates of intact and degraded montane rainforests from high-resolution optical imagery. iForest 2017, 10, 625–634. [Google Scholar] [CrossRef]
- Miyamoto, K.; Sato, T.; Olivos, E.A.A.; Orellana, G.C.; Stornaiuolo, C.M.R. Variation in tree community composition and carbon stock under natural and human disturbances in Andean forests, Peru. Forests 2018, 9, 390. [Google Scholar] [CrossRef]
- Finegan, B. Pattern and process in neotropical secondary rain forests: The first 100 years of succession. Trends Ecol. Evol. 1996, 11, 119–124. [Google Scholar] [CrossRef]
- Villa, P.M.; Martins, S.V.; de Oliveira Neto, S.N.; Rodrigues, A.C.; Safar, N.V.H.; Monsanto, L.D.; Cancio, N.M.; Ali, A. Woody species diversity as an indicator of the forest recovery after shifting cultivation disturbance in the northern Amazon. Ecol. Indic. 2018, 95, 687–694. [Google Scholar] [CrossRef]
- Van Ewijk, K.Y.; Randin, C.F.; Treitz, P.M.; Scott, N.A. Predicting fine-scale tree species abundance patterns using biotic variables derived from LiDAR and high spatial resolution imagery. Remote Sens. Environ. 2014, 150, 120–131. [Google Scholar] [CrossRef]
- Jamil, A.; Bayram, B. An object-based approach for tree species extraction from digital orthophoto maps. In Proceedings of the 2017 International Cartographic Conference, Washington, DC, USA, 2–7 July 2017; International Cartographic Association: Washington, DC, USA, 2018; Volume 1, pp. 1–7. [Google Scholar]
- Fang, F.; Mcneil, B.E.; Warner, T.A.; Maxwell, A.E.; Fang, F.; Mcneil, B.E.; Warner, T.A.; Maxwell, A.E. Combining high spatial resolution multi-temporal satellite data with leaf-on LiDAR to enhance tree species discrimination at the crown level. Int. J. Remote Sens. 2018, 39, 9054–9072. [Google Scholar] [CrossRef]
- Feilhauer, H.; Schmidtlein, S. Mapping continuous fields of forest alpha and beta diversity. Appl. Veg. Sci. 2009, 12, 429–439. [Google Scholar] [CrossRef]
- Rocchini, D.; Nagendra, H.; Ghate, R.; Cade, B.S. Spectral Distance Decay. Photogramm. Eng. Remote Sens. 2009, 75, 1225–1230. [Google Scholar] [CrossRef]
- Hernández-Stefanoni, J.L.; Gallardo-Cruz, J.A.; Meave, J.A.; Rocchini, D.; Bello-Pineda, J.; López-Martínez, J.O. Modeling α- and β-diversity in a tropical forest from remotely sensed and spatial data. Int. J. Appl. Earth Obs. Geoinf. 2012, 19, 359–368. [Google Scholar] [CrossRef]
- George-Chacón, S.P.; Dupuy, J.M.; Peduzzi, A.; Hernandez-Stefanoni, J.L. Combining high resolution satellite imagery and lidar data to model woody species diversity of tropical dry forests. Ecol. Indic. 2019, 101, 975–984. [Google Scholar] [CrossRef]
- Schmidtlein, S.; Sassin, J. Mapping of continuous floristic gradients in grasslands using hyperspectral imagery. Remote Sens. Environ. 2004, 92, 126–138. [Google Scholar] [CrossRef]
- Hakkenberg, C.R.; Peet, R.K.; Urban, D.L.; Song, C. Modeling plant composition as community continua in a forest landscape with LiDAR and hyperspectral remote sensing. Environ. Appl. 2018, 28, 177–190. [Google Scholar] [CrossRef]
- Ioki, K.; Tsuyuki, S.; Hirata, Y.; Phua, M.H.; Wong, W.V.C.; Ling, Z.Y.; Johari, S.A.; Korom, A.; James, D.; Saito, H.; et al. Evaluation of the similarity in tree community composition in a tropical rainforest using airborne LiDAR data. Remote Sens. Environ. 2016, 173, 304–313. [Google Scholar] [CrossRef]
- Adams, B.T.; Matthews, S.N.; Peters, M.P.; Prasad, A.; Iverson, L.R. Mapping floristic gradients of forest composition using an ordination-regression approach with landsat OLI and terrain data in the Central Hardwoods region. For. Ecol. Manag. 2019, 434, 87–98. [Google Scholar] [CrossRef]
- Fujiki, S.; Aoyagi, R.; Tanaka, A.; Imai, N.; Kusma, A.D.; Kurniawan, Y.; Lee, Y.F.; Sugau, J.B.; Pereira, J.T.; Samejima, H.; et al. Large-Scale mapping of tree-community composition as a surrogate of forest degradation in Bornean Tropical Rain Forest. Land 2016, 5, 45. [Google Scholar] [CrossRef]
- Gu, H.; Singh, A.; Townsend, P.A. Detection of gradients of forest composition in an urban area using imaging spectroscopy. Remote Sens. Environ. 2015, 167, 168–180. [Google Scholar] [CrossRef]
- Neumann, C.; Weiss, G.; Schmidtlein, S.; Itzerott, S.; Lausch, A.; Doktor, D.; Brell, M. Gradient-based assessment of habitat quality for spectral ecosystem monitoring. Remote Sens. 2015, 7, 2871–2898. [Google Scholar] [CrossRef]
- Magiera, A.; Feilhauer, H.; Waldhardt, R.; Wiesmair, M.; Otte, A.; Magiera, A.; Feilhauer, H.; Waldhardt, R.; Wiesmair, M.; Otte, A. Mapping Plant Functional Groups in Subalpine Grassland of the Greater Caucasus. Mt. Res. Dev. 2018, 38, 63–72. [Google Scholar] [CrossRef]
- Schmidtlein, S.; Zimmermann, P.; Scüpferling, R.; Weib, C. Mapping the floristic continuum: Ordination space position estimated from imaging spectroscopy. J. Veg. Sci. 2007, 18, 131–140. [Google Scholar] [CrossRef]
- Harris, A.; Charnock, R.; Lucas, R.M. Hyperspectral remote sensing of peatland floristic gradients. Remote Sens. Environ. 2015, 162, 99–111. [Google Scholar] [CrossRef]
- Borcard, D.; Gillet, G.F.; Legendre, P. Numerical Ecology with R; Springer: New York, NY, USA, 2011; p. 305. [Google Scholar]
- Hakkenberg, C.R.; Tarasi, D.D.; Peet, R.K. Community/Continuum in Biogeography. In International Encyclopedia of Geography: People, the Earth, Environment and Technology; Wiley Online Library: New York, NY, USA, 2017; pp. 2–6. [Google Scholar]
- Banda-R, K.; Delgado-Salinas, A.; Dexter, K.G.; Linares-Palomino, R.; Oliveira-Filho, A.; Prado, D.; Pullan, M.; Quintana, C.; Riina, R.; Rodríguez, G.M.; et al. Plant diversity patterns in neotropical dry forests and their conservation implications. Science 2016, 353, 1383–1387. [Google Scholar] [CrossRef]
- Chai, Z.; Wang, D. A comparison of species composition and community assemblage of secondary forests between the birch and pine-oak belts in the mid-altitude zone of the Qinling Mountains, China. PeerJ 2016, 4, e1900. [Google Scholar] [CrossRef] [PubMed]
- Mulatu, K.; Mora, B.; Kooistra, L.; Herold, M. Biodiversity Monitoring in Changing Tropical Forests: A Review of Approaches and New Opportunities. Remote Sens. 2017, 9, 1059. [Google Scholar] [CrossRef]
- Skidmore, A.; Pettorelli, N. Agree on biodiversity metrics to track from space. Nature 2015, 523, 5–7. [Google Scholar] [CrossRef] [PubMed]
- Schmeller, D.S.; Weatherdon, L.V.; Loyau, A.; Bondeau, A.; Brotons, L.; Brummitt, N.; Geijzendorffer, I.R.; Haase, P.; Kuemmerlen, M.; Martin, C.S.; et al. A suite of essential biodiversity variables for detecting critical biodiversity change. Biol. Rev. 2018, 93, 55–71. [Google Scholar] [CrossRef]
- GOFC-GOLD. A Sourcebook of Methods and Procedures for Monitoring Essential Biodiversity Variables in Tropical Forests with Remote Sensing; Technical Report; Land Cover Project Office, Wageningen University: Wageningen, The Netherlands, 2017. [Google Scholar]
- Gallardo-Cruz, J.A.; Hernández-Stefanoni, J.L.; Moser, D.; Martínez-Yrizar, A.; Llobet, S.; Meave, J. Relating species richness to the structure of continuous landscapes: Alternative methodological approaches. Ecosphere 2018, 9, e02189. [Google Scholar] [CrossRef]
- Palmer, M.W.; Earls, P.G.; Hoagland, B.W.; White, P.S.; Wohlgemuth, T. Quantitative tools for perfecting species lists. Environmetrics 2002, 13, 121–137. [Google Scholar] [CrossRef]
- Rocchini, D. Effects of spatial and spectral resolution in estimating ecosystem α-diversity by satellite imagery. Remote Sens. Environ. 2007, 111, 423–434. [Google Scholar] [CrossRef]
- Lausch, A.; Bannehr, L.; Beckmann, M.; Boehm, C.; Feilhauer, H.; Hacker, J.M.; Heurich, M.; Jung, A.; Klenke, R.; Neumann, C.; et al. Linking Earth Observation and taxonomic, structural and functional biodiversity: Local to ecosystem perspectives. Ecol. Indic. 2016, 70, 317–339. [Google Scholar] [CrossRef]
- Soriano-Luna, M.; Ángeles-Pérez, G.; Guevara, M.; Birdsey, R.; Pan, Y.; Vaquera-Huerta, H.; Valdez-Lazalde, J.R.; Johnson, K.; Vargas, R. Determinants of Above-Ground Biomass and Its Spatial Variability in a Temperate Forest Managed for Timber Production. Forests 2018, 9, 490. [Google Scholar] [CrossRef]
- Falkowski, M.J.; Evans, J.S.; Martinuzzi, S.; Gessler, P.E.; Hudak, A.T. Remote Sensing of Environment Characterizing forest succession with lidar data: An evaluation for the Inland. Remote Sens. Environ. 2009, 113, 946–956. [Google Scholar] [CrossRef]
- Hernández-Stefanoni, J.L.; Dupuy, J.M.; Johnson, K.D.; Birdsey, R.; Tun-Dzul, F.; Peduzzi, A.; Caamal-Sosa, J.P.; Sánchez-Santos, G.; López-Merlín, D. Improving species diversity and biomass estimates of Tropical Dry Forests using airborne LiDAR. Remote Sens. 2014, 6, 4741–4763. [Google Scholar] [CrossRef]
- Chazdon, R.L.; Letcher, S.G.; Breugel, M.V.; Bongers, F.; Finegan, B.; Martı, M.; Rica, C. Rates of change in tree communities of secondary Neotropical forests following major disturbances. Philos. Trans. R. Soc. 2007, 362, 273–289. [Google Scholar] [CrossRef]
- Dupuy, J.M.; Hernández-Stefanoni, J.L.; Hernández-Juárez, R.; Tetetla-Rangel, E.; López-Martínez, J.O.; Leyequién-Abarca, E.; Tun-Dzul, F.; May-Pat, F. Patterns and Correlates of Tropical Dry Forest Structure and Composition in a Highly Replicated Chronosequence in Yucatan, Mexico. Biotrópica 2012, 44, 151–162. [Google Scholar] [CrossRef]
- Asner, G.P. Biophysical and biochemical sources of variability in canopy reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Sánchez Santos, G.; Arreola Palacios, J.A.; López Merlín, D.; Maldonado Montero, V.; Olguín Álvarez, M.; Carrillo Negrete, O.; Puc Kauil, R. Sitio de Monitoreo Intensivo del Carbono en Quintana Roo; Technical Report; SEMARNAT, CONAFOR, REDD+, Norwegian Ministry of Foreign Affairs, PNUD, FAO: México DF, México, 2015.
- Bautista, F.; Palacio, G.; Ortiz-Pérez, M.; Batllori-Sampedro, E.; Castillo-González, M. El origen y el manejo maya de las geoformas, suelos y aguas en la Península de Yucatán. In Caracterización y Manejo de los Suelos de la Península de Yucatán: Implicaciones Agropecuarias, Forestales y Ambientales; Universidad Autónoma de Campeche, Universidad Autónoma de Yucatán, Instituto Nacional de Ecología: México DF, México, 2005; Chapter El Origen; pp. 21–32. [Google Scholar]
- García, E. Climas 1:40000. Atlas Nacional de México Vol. II; Instituto de Geografía, Universidad Nacional Autónoma de México: México DF, México, 1990. [Google Scholar]
- CONAFOR. Inventario Nacional Forestal y de Suelos México 2004–2009; Comisión Nacional Forestal: Zapopan, México, 2010.
- The Plant List. A Working List of All Known Plant Species. 2013. Available online: http://www.theplantlist.org/1/ (accessed on 26 April 2019).
- Mueller-Dombois, D.; Ellenberg, H. Aims and Methods of Vegetation Ecology; John Wiley and Sons: New York, NY, USA, 1974. [Google Scholar]
- Oksanen, J.; Blanchet, F.G.; Friendly, M.; Kindt, R.; Legendre, P.; Mcglinn, D.; Minchin, P.R.; Hara, R.B.O.; Simpson, G.L.; Solymos, P.; et al. Vegan: Community Ecology Package. 2018. Available online: https://cran.r-project.org/web/packages/vegan/index.html (accessed on 26 April 2019).
- R Core Team. R: A Language and Environment for Statistical Computing. 2018. Available online: https://www.R-project.org/ (accessed on 26 April 2019).
- Kruskal, J.B. Nonmetric multidimensional scaling. Psychometrika 1964, 29, 115–129. [Google Scholar] [CrossRef]
- Legendre, P.; Legendre, L. Numerical Ecology; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Imai, N.; Tanaka, A.; Samejima, H.; Baptist, J.; Pereira, J.T.; Titin, J.; Kurniawan, Y.; Kitayama, K. Tree community composition as an indicator in biodiversity monitoring of REDD +. For. Ecol. Manag. 2014, 313, 169–179. [Google Scholar] [CrossRef]
- Horler, D.N.H.; Dockray, M.; Barber, J. The red edge of leaf reflectance. Int. J. Remote Sens. 1983, 4, 273–288. [Google Scholar] [CrossRef]
- Schuster, C.; Förster, M.; Kleinschmit, B. Testing the red edge channel for improving land-use classifications based on high-resolution multi-spectral satellite data. Int. J. Remote Sens. 2012, 33, 5583–5599. [Google Scholar] [CrossRef]
- Planet. RAPIDEYETM IMAGERY PRODUCT SPECIFICATIONS Version 6.1. Technical Report January. 2016. Available online: https://www.planet.com/products/satellite-imagery/files/160625-RapidEyeImage-Product-Specifications.pdf (accessed on 26 April 2019).
- Chuvieco Salinero, E. Teledetección Ambiental, 3rd ed.; Ariel Ciencias: Barcelona, España, 2008; p. 613. [Google Scholar]
- Gao, X.; Huete, A.R.; Ni, W.; Miura, T. Optical-biophysical relationships of vegetation spectra without background contamination. Remote Sens. Environ. 2000, 74, 609–620. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Leeuwen, W.V.; Miura, T.; Glenn, E. MODIS vegetation indices. In Land Remote Sensing and Global Environmental Change; Springer: New York, NY, USA, 2011; Chapter 26; pp. 579–602. [Google Scholar] [CrossRef]
- Haralick, R. Statistical image texture analysis. In Handbook of Pattern Recognition and Image Processing; Academic Press: Cambridge, MA, USA, 1986; pp. 247–279. [Google Scholar]
- Kerr, J.T.; Packer, L. Habitat heterogeneity as a determinant of mammal species richness in high-energy regions. Nature 1997, 385, 252–254. [Google Scholar] [CrossRef]
- Wu, J.; Liang, S. Developing an Integrated Remote Sensing Based Biodiversity Index for Predicting Animal Species Richness. Remote Sens. 2018, 10, 739. [Google Scholar] [CrossRef]
- Hijmans, R.; van Etten, J.; Cheng, J.; Mattiuzzi, M.; Sumner, M.; Greenberg, J.A.; Bevan, A.; Shortridge, A. Raster: Geographic Data Analysis and Modeling. 2017. Available online: https://cran.r-project.org/web/packages/raster/index.html (accessed on 26 April 2019).
- Zvoleff, A. glcm: Calculate Textures from Grey-Level Co-Occurrence Matrices (GLCMs). 2016. Available online: https://cran.r-project.org/web/packages/glcm/index.html (accessed on 26 April 2019).
- McGaughey, R.J. FUSION / LDV: Software for LIDAR Data Analysis and Visualization; Portland, OR, USA, 2018. Available online: http://forsys.cfr.washington.edu/fusion/fusion_overview.html (accessed on 26 April 2019).
- Silva, C.A.; Crookston, N.L.; Hudak, A.T.; Vierling, L. LiDAR Data Processing and Visualization Version. 2017. Available online: http://cran.rproject.org/web/packages/rLiDAR/index.html (accessed on 26 April 2019).
- Rebekic, A.; Loncaric, Z.; Petrovic, S.; Maric, S. Pearson’s or Spearman’s correlation coefficient—Which one to use? Agricutlure 2015, 21, 47–54. [Google Scholar] [CrossRef]
- Zhou, X.; Stephens, M. Genome-wide efficient mixed-model analysis for association studies. Nat. Genet. 2012, 44, 821–824. [Google Scholar] [CrossRef]
- Pérez, P.; de los Campos, G. Genome-Wide Regression and Prediction with the BGLR Statistical Package. Genetics 2014, 198, 483–495. [Google Scholar] [CrossRef]
- Grömping, U. Relative Importance for Linear Regression in R: The Package relaimpo. J. Stat. Softw. 2006, 17, 139–147. [Google Scholar] [CrossRef]
- Hu, J.; Herbohn, J.; Chazdon, R.L.; Baynes, J.; Wills, J.; Meadows, J.; Sohel, M.S.I. Recovery of species composition over 46 years in a logged Australian tropical forest following different intensity silvicultural treatments. For. Ecol. Manag. 2018, 409, 660–666. [Google Scholar] [CrossRef]
- Solórzano, J.V.; Meave, J.A.; Gallardo-Cruz, J.A.; González, E.J.; Hernández-Stefanoni, J.L. Predicting old-growth tropical forest attributes from very high resolution (VHR)-derived surface metrics. Int. J. Remote Sens. 2017, 38, 492–513. [Google Scholar] [CrossRef]
- Knipling, E.B. Physical and physiological basis for the reflectance of visible and near-infrared radiation from vegetation. Remote Sens. Environ. 1970, 1, 155–159. [Google Scholar] [CrossRef]
- Pike, R.J.; Wilson, S.E. Elevation-relief ratio, hypsometric integral, and geomorphic area-altitude analysis. Bull. Geol. Soc. Am. 1971, 82, 1079–1084. [Google Scholar] [CrossRef]
- Chazdon, R.L.; Broadbent, E.N.; Rozendaal, D.M.A.; Bongers, F.; María, A.; Zambrano, A.; Aide, T.M.; Balvanera, P.; Becknell, J.M.; Boukili, V.; et al. Carbon sequestration potential of second-growth forest regeneration in the Latin American tropics. Sci. Adv. 2016, 2. [Google Scholar] [CrossRef]
- Gianola, D. Priors in Whole-Genome Regression: The Bayesian Alphabet Returns. Genom. Sel. 2013, 194, 573–596. [Google Scholar] [CrossRef]
- Crouzeilles, R.; Ferreira, M.S.; Chazdon, R.L.; Lindenmayer, D.B.; Sansevero, J.B.B.; Monteiro, L.; Iribarrem, A.; Latawiec, A.E.; Strassburg, B.B.N. Ecological restoration success is higher for natural regeneration than for active restoration in tropical forests. Sci. Adv. 2017, 3, e1701345. [Google Scholar] [CrossRef]
- Meli, P.; Holl, K.D.; María José, R.B.; Jones, H.; Jones, P.; Montoya, D.; Moreno Mateos, D. A global review of past land use, climate, and active vs. passive restoration effects on forest recovery. PLoS ONE 2017, 12, e0171368. [Google Scholar] [CrossRef]
- Guariguata, M.R.; Ostertag, R. Neotropical secondary forest succession: Changes in structural and functional characteristics. For. Ecol. Manag. 2001, 148, 185–206. [Google Scholar] [CrossRef]
- Chazdon, R.L. Tropical forest recovery: Legacies of human impact and natural disturbances. Perspect. Plant Ecol. Evol. Syst. 2003, 6, 51–71. [Google Scholar] [CrossRef]
- Curran, M.; Hellweg, S.; Jan, B. Is there any empirical support for biodiversity offset policy? Ecol. Appl. 2014, 24, 617–632. [Google Scholar] [CrossRef]
- Trujillo-Miranda, A.L.; Toledo-Aceves, T.; López-Barrera, F.; Gerez-Fernández, P. Active versus passive restoration: Recovery of cloud forest structure, diversity and soil condition in abandoned pastures. Ecol. Eng. 2018, 117, 50–61. [Google Scholar] [CrossRef]
- Whitworth, A.; Pillco-Huarcaya, R.; Downie, R.; Villacampa, J.; Braunholtz, L.D.; MacLeod, R. Long lasting impressions: After decades of regeneration rainforest biodiversity remains differentially affected following selective logging and clearance for agriculture. Glob. Ecol. Conserv. 2018, 13, e00375. [Google Scholar] [CrossRef]
- Lennox, G.; Gardner, T.; Thomson, J.; Ferreira, J.; Berenguer, E.; Lees, A.; Mac Nally, R.; Aragão, L.; Ferraz, S.; Louzada, J.; et al. Second rate or a second chance? Assessing biomass and biodiversity recovery in regenerating Amazonian forests. Glob. Chang. Biol. 2018, 9. [Google Scholar] [CrossRef]

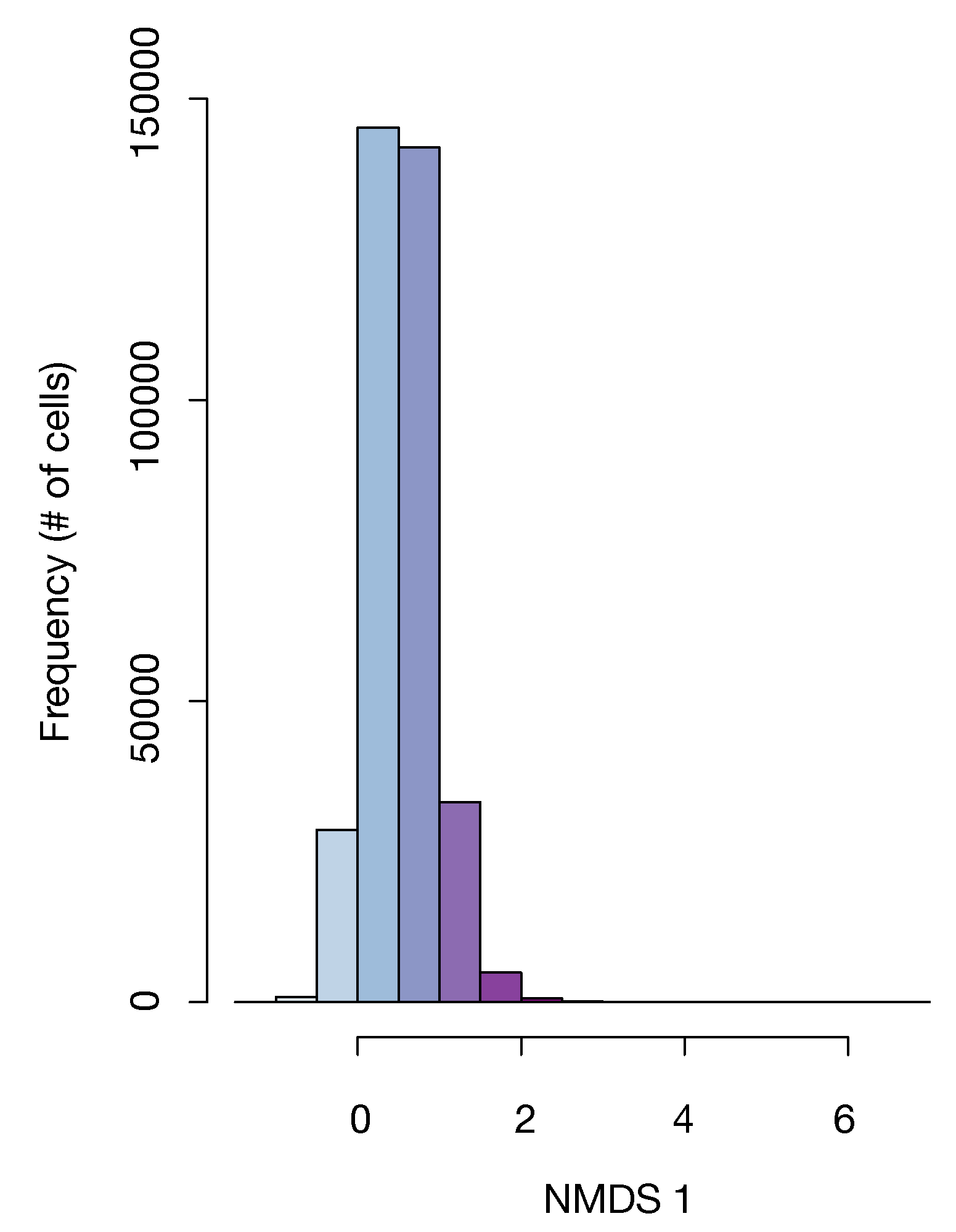
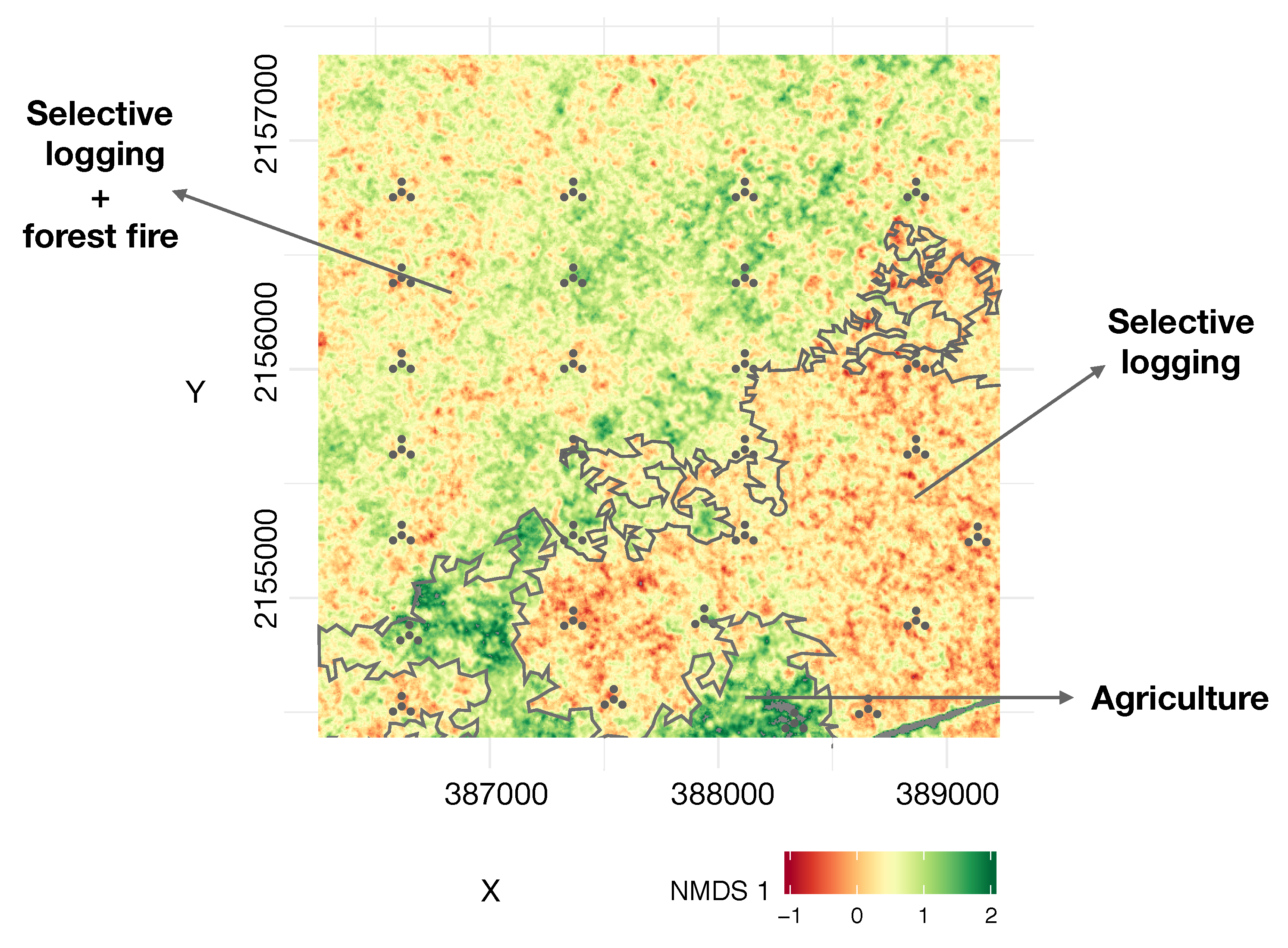
| Attribute | Agriculture | Selective Logging | S Logging + Fire |
|---|---|---|---|
| Tree density | stems/ha | stems/ha | stems/ha |
| Basal area | m/ha | m/ha | m/ha |
| 80p Biomass | kg/ind | kg/ind | kg/ind |
| Height | m | m | |
| Richness | species | species | species |
| Shannon index | |||
| IVI% dominant | Bursera simaruba | Gymnanthes lucida | Gymnanthes lucida |
| species | Psidia psipula | Manilkara zapota | Bursera simaruba |
| Textural Variable | LiDAR Variable | ||
|---|---|---|---|
| b3 variance | 0.780 | Canopy relief ratio | −0.616 |
| b3 mean | 0.767 | Height L3 moment | 0.547 |
| b2 variance | 0.747 | Height skewness | 0.537 |
| b2 mean | 0.738 | All above mean/first × 100 | 0.537 |
| reNDVI mean | −0.736 | Height L skewness | 0.535 |
| reNDVI variance | −0.735 | Canopy height model | −0.517 |
| b4 variance | 0.721 | Cover 7m threshold | −0.510 |
| b4 mean | 0.704 | All returns above mean | 0.461 |
| b5 variance | −0.440 | Height at 80th percentile | 0.437 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ochoa-Franco, A.d.P.; Valdez-Lazalde, J.R.; Ángeles-Pérez, G.; de los Santos-Posadas, H.M.; Hernández-Stefanoni, J.L.; Valdez-Hernández, J.I.; Pérez-Rodríguez, P. Beta-Diversity Modeling and Mapping with LiDAR and Multispectral Sensors in a Semi-Evergreen Tropical Forest. Forests 2019, 10, 419. https://doi.org/10.3390/f10050419
Ochoa-Franco AdP, Valdez-Lazalde JR, Ángeles-Pérez G, de los Santos-Posadas HM, Hernández-Stefanoni JL, Valdez-Hernández JI, Pérez-Rodríguez P. Beta-Diversity Modeling and Mapping with LiDAR and Multispectral Sensors in a Semi-Evergreen Tropical Forest. Forests. 2019; 10(5):419. https://doi.org/10.3390/f10050419
Chicago/Turabian StyleOchoa-Franco, Alejandra del Pilar, José René Valdez-Lazalde, Gregorio Ángeles-Pérez, Hector Manuel de los Santos-Posadas, José Luis Hernández-Stefanoni, Juan Ignacio Valdez-Hernández, and Paulino Pérez-Rodríguez. 2019. "Beta-Diversity Modeling and Mapping with LiDAR and Multispectral Sensors in a Semi-Evergreen Tropical Forest" Forests 10, no. 5: 419. https://doi.org/10.3390/f10050419
APA StyleOchoa-Franco, A. d. P., Valdez-Lazalde, J. R., Ángeles-Pérez, G., de los Santos-Posadas, H. M., Hernández-Stefanoni, J. L., Valdez-Hernández, J. I., & Pérez-Rodríguez, P. (2019). Beta-Diversity Modeling and Mapping with LiDAR and Multispectral Sensors in a Semi-Evergreen Tropical Forest. Forests, 10(5), 419. https://doi.org/10.3390/f10050419






