Intra-Ring Variations and Interrelationships for Selected Wood Anatomical and Physical Properties of Thuja Occidentalis L. †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Materials
2.2. Wood Ring Density and Width Measurement
2.3. Tracheid Length and Width Measurement
2.4. Microscopic Analysis of Tracheid Anatomical Properties
2.5. Statistical Analysis
3. Results and Discussion
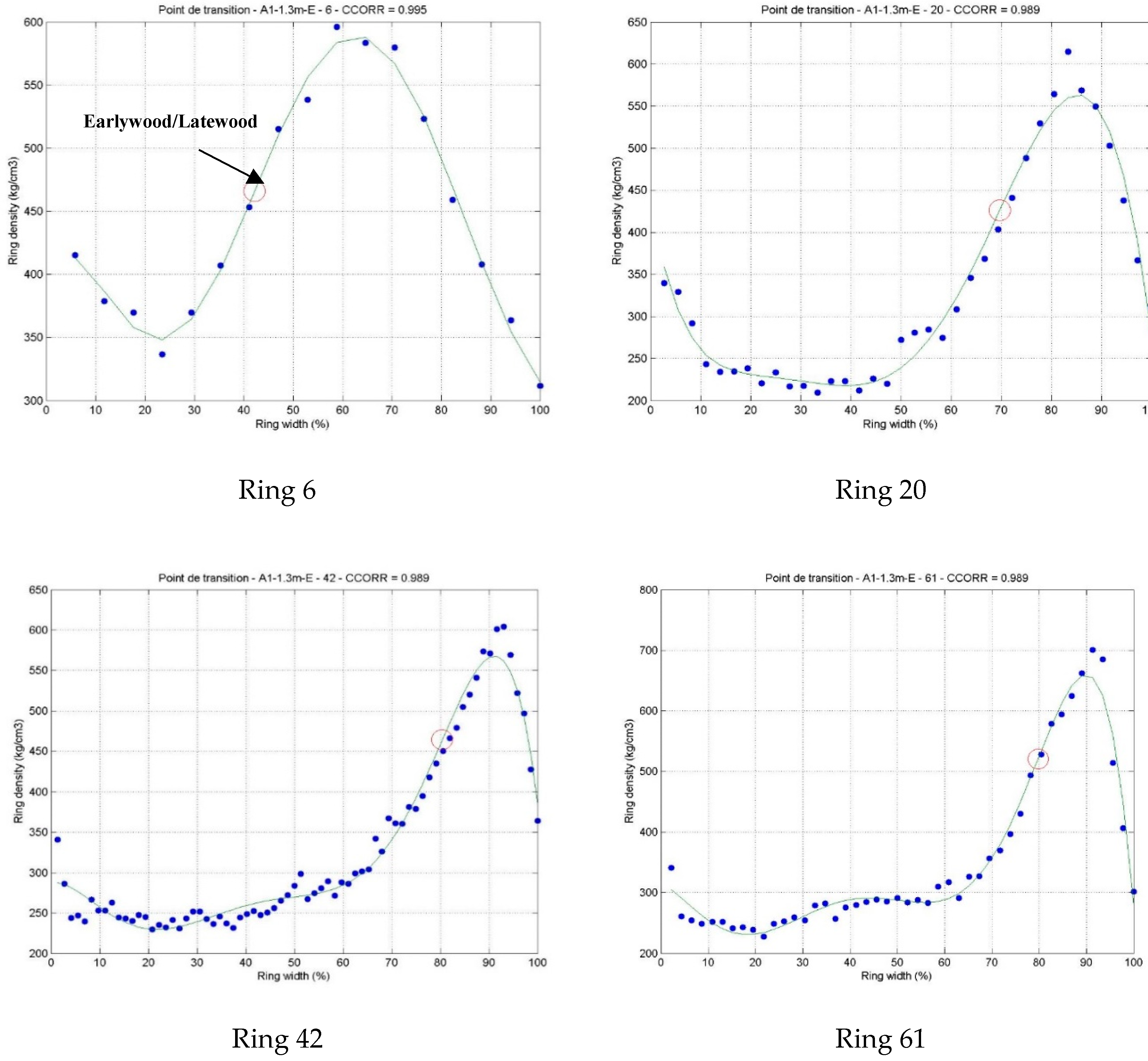
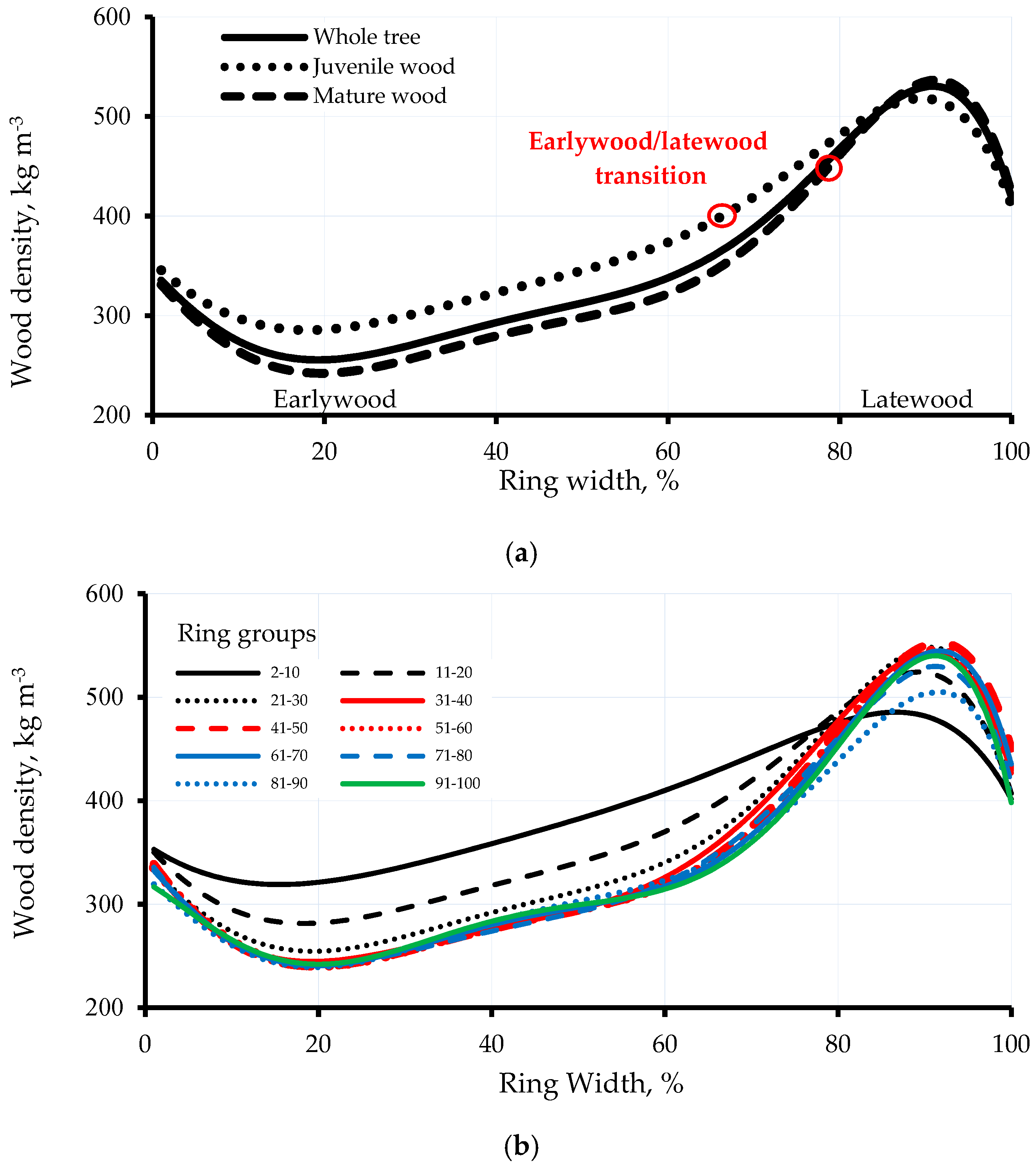
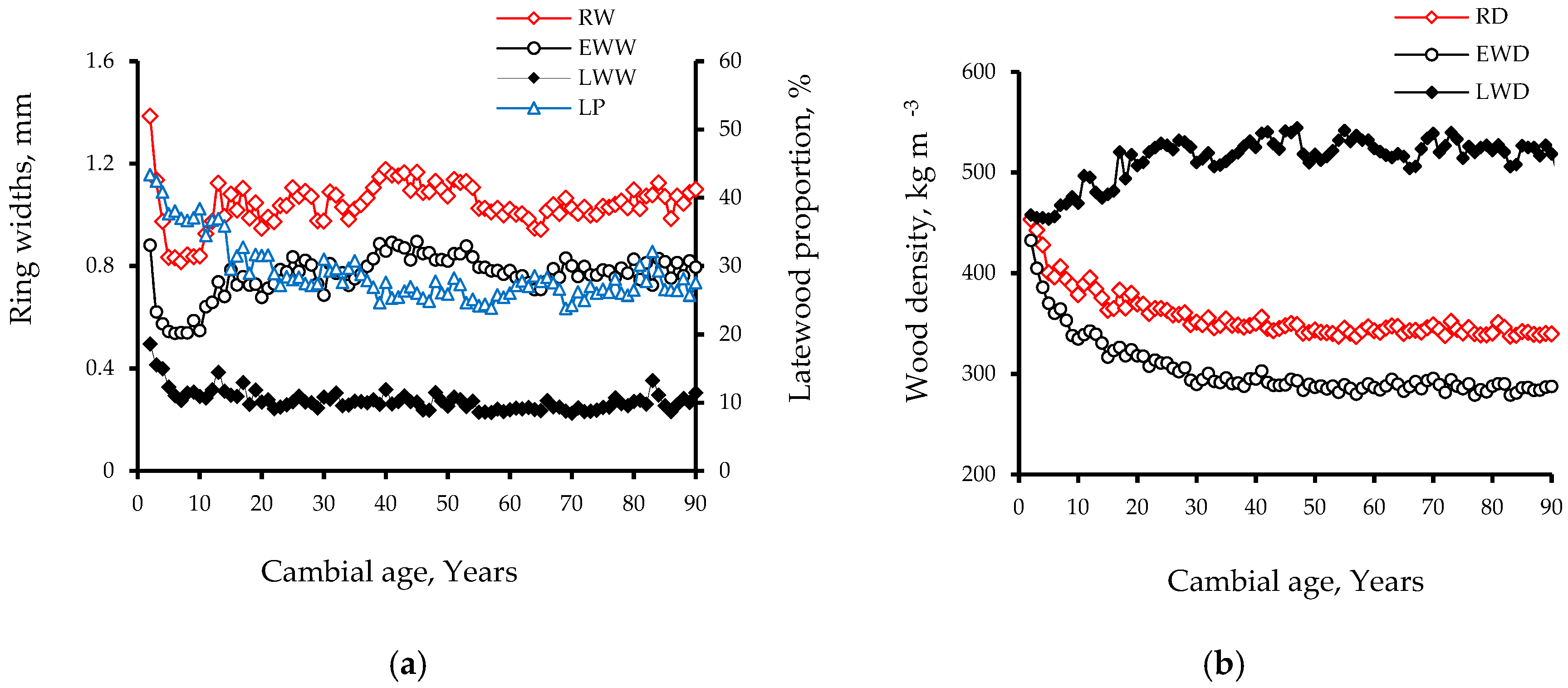
3.1. Intra-Ring Wood Density Variation and Anatomical Changes between Early-and Latewood
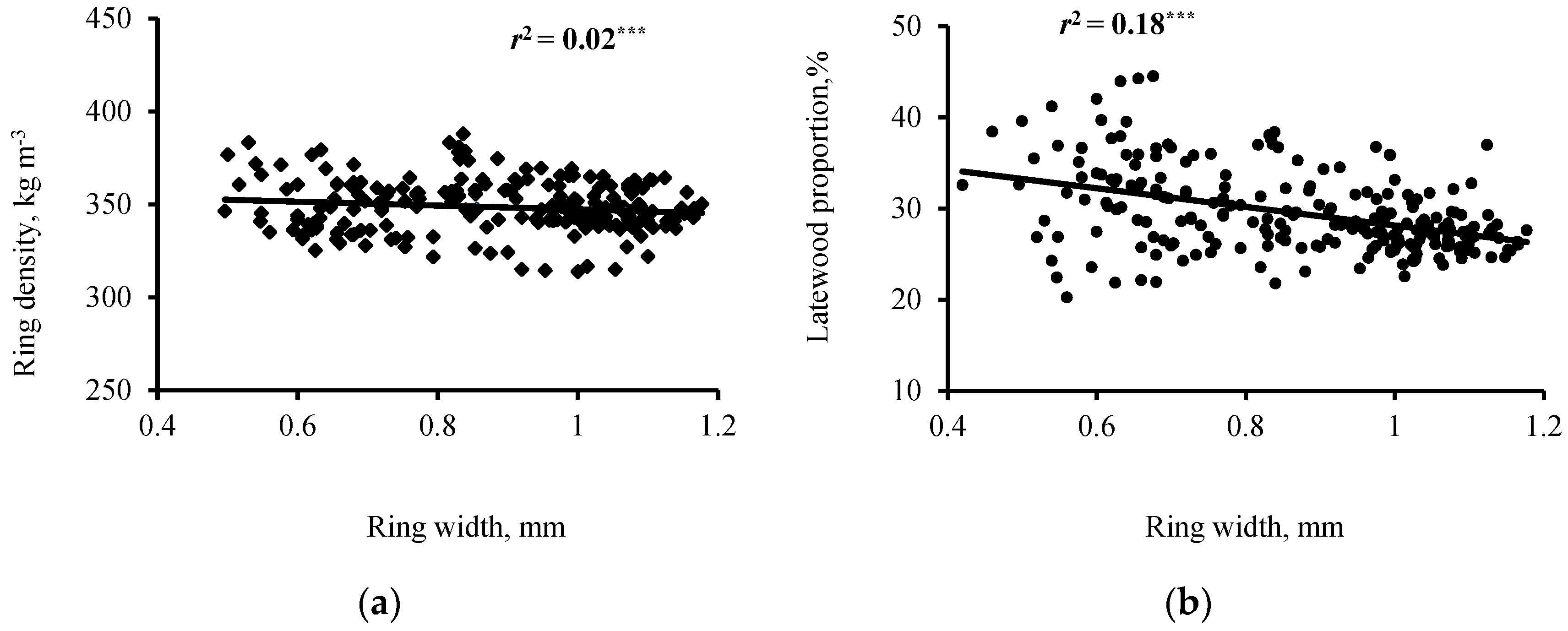
3.2. Interrelationships of Wood Ring Density and Width
3.3. Relationships between Ring Width and Tracheid Length and Width
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
References
- Fowells, H.A. Silvics of Forest Trees of the United States; U.S. Department of Agriculture Handbook; U.S. Department of Agriculture: Washington, DC, USA, 1965; p. 271.
- Taylor, A.M.; Gartner, B.L.; Morrell, J.J. Heartwood formation and natural durability—A review. Wood Fib. Sci. 2002, 34, 587–611. [Google Scholar]
- Koubaa, A.; Zhang, S.Y. (Eds.) White Cedar, Thuja occidentalis L. In Softwoods of Eastern Canada. Their Sylvics, Characteristics, Manufacturing and End-Uses; FPInnovations: Québec, QC, Canada, 2008; SP-526E, Chapter 11; p. 18. [Google Scholar]
- Haataja, B.A.; Laks, P.E. Properties of flakeboard made from northern white cedar. For. Prod. J. 1995, 45, 68–70. [Google Scholar]
- Johnston, W.F. Thuja occidentalis L. Northern white-cedar. In Silvics of North America. Volume 1: Conifers; Burns, R.M., Honkala, B.H., Eds.; U.S. Department of Agriculture: Washington, DC, USA, 1990; p. 654. [Google Scholar]
- Bouslimi, B.; Koubaa, A.; Bergeron, Y. Anatomical properties in Thuja occidentalis: Variation and relationship to biological processes. IAWA J. 2014, 35, 363–384. [Google Scholar] [CrossRef]
- Bouslimi, B.; Koubaa, A.; Bergeron, Y. Effects of biodegradation by brown-rot decay on selected wood properties in eastern white cedar (Thuja occidentalis L.). Int. Biodet. Biodeg. 2014, 87, 87–98. [Google Scholar] [CrossRef]
- Bouslimi, B. Variations Intra-Arbre, Intrasites et Intersites des Attributs de la Qualité du bois du Thuya Occidental (Thuja occidentalis L.). Ph.D. Thesis, Université du Québec en Abitibi-Témiscamingue (UQAT), Rouyn-Noranda, QC, Canada, 2014; p. 407. [Google Scholar]
- Zobel, B.J.; Van Buijtenen, J.P. Wood Variation: Its Causes and Control; Springer: Berlin, Germany, 1989; p. 363. [Google Scholar]
- Decoux, V.; Varcin, E.; Leban, J.M. Relationships between the intra-ring wood density assessed by X-ray densitometry and optical anatomical measurements in conifers. Consequences for the cell wall apparent density determination. Ann. For. Sci. 2004, 61, 251–262. [Google Scholar] [CrossRef] [Green Version]
- Koga, S.; Zhang, S.Y. Inter-tree and intra-tree variations in ring width and wood density components in balsam fir [Abies balsamea]. Wood Sci. Technol. 2004, 38, 149–162. [Google Scholar] [CrossRef]
- Abdul-Hamid, H.; Mencuccini, M. Age-and size-related changes in physiological characteristics and chemical composition of Acer pseudoplatanus and Fraxinus excelsior trees. Tree Physiol. 2009, 29, 27–38. [Google Scholar] [CrossRef]
- DeSoto, L.; De la Cruz, M.; Fonti, P. Intra-annual patterns of tracheid size in the Mediterranean tree Juniperus thurifera as an indicator of seasonal water stress. Can. J. For. Res. 2011, 41, 1280–1294. [Google Scholar] [CrossRef]
- Anfodillo, T.; Deslauriers, A.; Menardi, R.; Tedoldi, L.; Petit, G.; Ross, S. Widening of xylem conduits in a conifer tree depends on the longer time of cell expansion downwards along the stem. J. Exp. Bot. 2012, 63, 837–845. [Google Scholar] [CrossRef]
- Anfodillo, T.; Petit, G.; Crivellaro, A. Axial conduit widening in woody species: A still neglected anatomical pattern. IAWA J. 2013, 34, 352–364. [Google Scholar] [CrossRef]
- Bannan, M.W. Cambial behavior with reference to cell length and ring width in Thuja occidentalis L. Can. J. Bot. 1960, 38, 177–183. [Google Scholar] [CrossRef]
- Fromm, J. Xylem development in trees: From cambial divisions to mature wood cells. In Cellular Aspects of Wood Formation; Springer: Berlin, Germany, 2013; pp. 3–39. [Google Scholar]
- Rathgeber, C.B.; Decoux, V.; Leban, J.-M. Linking intra-tree-ring wood density variations and tracheid anatomical characteristics in Douglas fir (Pseudotsuga menziesii (Mirb.) Franco). Ann. For. Sci. 2006, 63, 699–706. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Nepveu, G.; Owoundi, R.E. Intratree and intertree variation in selected wood quality characteristics of European oak (Quercus petraea and Quercus robur). Can. J. For. Res. 1994, 24, 1818–1823. [Google Scholar] [CrossRef]
- Zhang, S. Effect of growth rate on wood specific gravity and selected mechanical properties in individual species from distinct wood categories. Wood Sci. Technol. 1995, 29, 451–465. [Google Scholar] [CrossRef]
- Koubaa, A.; Tony Zhang, S.Y.; Makni, S. Defining the transition from earlywood to latewood in black spruce based on intra-ring wood density profiles from X-ray densitometry. Ann. For. Sci. 2002, 59, 511–518. [Google Scholar] [CrossRef] [Green Version]
- Keunecke, D.; Evans, R.; Niemz, P. Microstructural properties of common yew and Norway spruce determined with SilviScan. IAWA J. 2009, 30, 165–178. [Google Scholar] [CrossRef]
- Alteyrac, J.; Cloutier, A.; Zhang, S.Y. Characterization of juvenile wood to mature wood transition age in black spruce (Picea mariana (Mill.) B.S.P.) at different stand densities and sampling heights. Wood Sci. Technol. 2006, 40, 124–138. [Google Scholar] [CrossRef]
- Koubaa, A.; Isabel, N.; Zhang, S.Y.; Beaulieu, J.; Bousquet, J. Transition from juvenile to mature wood in black spruce (Picea mariana (Mill.) B.S.P.). Wood Fib. Sci. 2005, 37, 445–455. [Google Scholar]
- Guller, B.; Isik, K.; Cetinay, S. Variations in the radial growth and wood density components in relation to cambial age in 30-year-old Pinus brutia Ten. at two test sites. Trees 2012, 26, 975–986. [Google Scholar] [CrossRef]
- Koga, S.; Zhang, S. Relationships between wood density and annual growth rate components in balsam fir (Abies balsamea). Wood Fib. Sci. 2002, 34, 146–157. [Google Scholar]
- Koubaa, A.; Zhangi, S.Y.; Isabel, N.; Beaulieu, J.; Bousquet, J. Phenotypic correlations between juvenile-mature wood density and growth in black spruce. Wood Fib. Sci. 2000, 32, 61–71. [Google Scholar]
- Bouslimi, B.; Koubaa, A.; Bergeron, Y. Variation of brown rot decay in eastern white cedar (Thuja occidentalis L.). BioResources 2013, 8, 4735–4755. [Google Scholar] [CrossRef]
- Grabner, M.; Wimmer, R.; Gierlinger, N.; Evans, R.; Downes, G. Heartwood extractives in larch and effects on X-ray densitometry. Can. J. For. Res. 2005, 35, 2781–2786. [Google Scholar] [CrossRef]
- Smith, D.-M. Maximum Moisture Content Method for Determining Specific Gravity of Small Wood Samples; Report No 2014; Forest Products Laboratory, Forest Service, U.S. Department of Agriculture: Madison, WI, USA, 1954; p. 9.
- Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree-Ring Bull. 1983, 43, 69–75. [Google Scholar]
- Franklin, C.L. Preparing thin sections of synthetic resin and wood 410 composites and a new maceration method for wood. Nature 1945, 155, 51–54. [Google Scholar] [CrossRef]
- Robertson, G.; Olson, J.; Allen, P.; Chan, B.; Seth, R. Measurement of fiber length, coarseness, and shape with the fiber quality analyzer. Tappi J. 1999, 82, 93–98. [Google Scholar]
- Seo, J.-W.; Eckstein, D.; Jalkanen, R. Screening various variables of cellular anatomy of Scots pines in subarctic Finland for climatic signals. IAWA J. 2012, 33, 417–429. [Google Scholar] [CrossRef]
- Denne, M.P. Definition of latewood according to Mork (1928). IAWA Bull. 1988, 10, 59–62. [Google Scholar] [CrossRef]
- Littell, R.C.; Milliken, G.A.; Stroup, W.W.; Wolfinger, R.D.; Schabenberber, O. SAS for Mixed Models, 2nd ed.; SAS Institute, Inc.: Cary, NC, USA, 2006; p. 814. [Google Scholar]
- SAS; SAS Institute, Inc.: Cary, NC, USA, 2008.
- De Kort, I.; Loeffen, V.; Baas, P. Ring width, density and wood anatomy of Douglas fir with different crown vitality. IAWA J. 1991, 12, 453–465. [Google Scholar] [CrossRef]
- Roque, R.M.; Tomazelo Filho, M. Relationships between anatomical features and intra-ring wood density profiles in Gmelina arborea applying X-ray densitometry. Cerne 2015, 13, 384–392. [Google Scholar]
- Nugroho, W.D.; Marsoem, S.N.; Yasue, K.; Fujiwara, T.; Nakajima, T.; Hayakawa, M.; Kubo, T. Radial variations in the anatomical characteristics and density of the wood of Acacia mangium of five different provenances in Indonesia. J. Wood Sci. 2012, 58, 185–194. [Google Scholar] [CrossRef]
- Hannrup, B.; Danell, Ö.; Ekberg, I.; Moëll, M. Relationships between wood density and tracheid dimensions in Pinus sylvestris L. Wood Fib. Sci. 2007, 33, 173–181. [Google Scholar]
- Wright, J.A.; Malan, F.S. Variation in Wood and Tracheid Properties of Pinus Maximinoi, P. Pseudostrobus and P. Patula. IAWA J. 1991, 12, 467–475. [Google Scholar] [CrossRef]
- Wang, L.; Payette, S.; Bégin, Y. Relationships between anatomical and densitometric characteristics of black spruce and summer temperature at tree line in northern Quebec. Can. J. For. Res. 2002, 32, 477–486. [Google Scholar] [CrossRef]
- Maeglin, R.R. Wisconsin Wood Density Survey; US Forest Products Laboratory Reseach Paper, Issue FPL 202; U.S. Forest Products Laboratory: Madison, WI, USA, 1973; p. 40. [Google Scholar]
- Koubaa, A.; Zhang, S.Y. Softwoods of Eastern Canada. Their Sylvics, Characteristics, Manufacturing and End-Use; Special Publication, SP-526F, Chapter 4, 8 and 10; FPInnovations: Québec, QC, Canada, 2008. [Google Scholar]
- Jozsa, L.A.; Middleton, G.R. A Discussion of Wood Quality Attributes and Their Practical Implications; Special Publication, SP-34; Forintek Canada Corp.: Sainte-Foy, QC, Canada, 1994; p. 42. [Google Scholar]
- Lachenbruch, B.; Moore, J.R.; Evans, R. Radial variation in wood structure and function in woody plants, and hypotheses for its occurrence. In Size-and Age-Related Changes in Tree Structure and Function; Springer: Berlin, Germany, 2011; pp. 121–164. [Google Scholar]
- Larson, P.R.; Kretschmann, D.E.; Clark, A., III; Isebrands, J.G. Formation and Properties of Juvenile Wood in Southern Pines: A Synopsis; USDA Forest Service, Forest Products Laborator: Washington, DC, USA, 2001; p. 42. [Google Scholar]
- Rathgeber, C.B.; Longuetaud, F.; Mothe, F.; Cuny, H.; Le Moguédec, G. Phenology of wood formation: Data processing, analysis and visualisation using R (package CAVIAR). Dendrochronologia 2011, 29, 139–149. [Google Scholar] [CrossRef]
- Deleuze, C.; Houllier, F. A Simple Process-based Xylem Growth Model for Describing Wood Microdensitometric Profiles. J. Theoret. Biol. 1998, 193, 99–113. [Google Scholar] [CrossRef]
- Wimmer, R. Intra-annual cellular characteristics and their implications for modeling softwood density. Wood Fib. Sci. 2007, 27, 413–420. [Google Scholar]
- Panshin, A.J.; De Zeeuw, C. Textbook of Wood Technology; McGraw-Hill Book Co.: New York, NY, USA, 1980; p. 772. [Google Scholar]
- Wheeler, E. Ultrastructural characteristics of red maple (Acer rubrum L.) wood. Wood Fib. Sci. 1982, 14, 43–53. [Google Scholar]
- Passialis, C.; Kiriazakos, A. Juvenile and mature wood properties of naturally-grown fir trees. Holz als Roh-und Werkstoff 2004, 62, 476–478. [Google Scholar] [CrossRef]
- Bannan, M. Sequential changes in rate of anticlinal division, cambial cell length, and ring width in the growth of coniferous trees. Can. J. Bot. 1967, 45, 1359–1369. [Google Scholar] [CrossRef]
- Zhang, S.Y. Effect of age on the variation, correlations and inheritance of selected wood characteristics in black spruce (Piceo mariana). Wood Sci. Technol. 1998, 32, 197–204. [Google Scholar]
- Abdel-Gadir, A.Y.; Krahmer, R.; McKimmy, M. Relationships between intra-ring variables in mature Douglas-fir trees from provenance plantations. Wood Fib. Sci. 2007, 25, 182–191. [Google Scholar]
- Zhang, S.Y.; Simpson, D.; Morgenstern, E.K. Variation in the relationship of wood density with growth in 40 black spruce (Picea mariana) families grown in New Brunswick. Wood Fib. Sci. 1996, 28, 91–99. [Google Scholar]
- Zhang, S.Y.; Morgenstern, E.K. Genetic variation and inheritance of wood density in black spruce (Picea mariana) and its relationship with growth: Implications for tree breeding. Wood Sci. Technol. 1996, 30, 63–75. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Jiang, Z.H. Variability of selected wood characteristics in 40 half-sib families of black spruce (Picea mariana). Wood Sci. Technol. 1998, 32, 71–82. [Google Scholar] [CrossRef]
- Bannan, M. Cambial behavior with reference to cell length and ring width in Picea. Can. J. Bot. 1963, 41, 811–822. [Google Scholar] [CrossRef]
- Chalk, L. Tracheid length, with special reference to sitka spruce (Picea sitchensis carr.). Forestry 1930, 4, 7–14. [Google Scholar] [CrossRef]
- Fujiwara, S.; Yang, K. The relationship between cell length and ring width and circumferential growth rate in five Canadian species. IAWA J. 2000, 21, 335–346. [Google Scholar] [CrossRef]
- Diaz-Váz, J.; Echols, R.; Knigge, W. Comparative investigation of the variation of tracheid dimensions and X-ray densitogrammes within the annual rings of two softwoods. Forstwissenschaftliches Cent. 1975, 94, 161–175. [Google Scholar] [CrossRef]
- Dutilleul, P.; Herman, M.; Avella-Shaw, T. Growth rate effects on correlations among ring width, wood density, and mean tracheid length in Norway spruce (Picea abies). Can. J. For. Res. 1998, 28, 56–68. [Google Scholar] [CrossRef]
- Adamopoulos, S.; Wimmer, R.; Milios, E. Tracheid length—Growth relationships of young Pinus brutia grown on reforestation sites. IAWA J. 2012, 33, 39–49. [Google Scholar] [CrossRef]

| Anatomical Properties | Earlywood (n = 392 cells) | Latewood (n = 366 cells) | ||||
|---|---|---|---|---|---|---|
| Means 1 | SD | CV | Means | SD | CV | |
| Cell radial diameter (µm) | 26.19 a | 4.63 | 17.69 | 23.58 b | 3.97 | 16.84 |
| Cell tangential diameter (µm) | 23.59 a | 4.13 | 17.54 | 25.42 b | 3.71 | 14.58 |
| Cell area (µm2) | 626.13 a | 180.70 | 28.86 | 608.75 b | 174.72 | 28.70 |
| Cell perimeter (µm) | 99.58 a | 14.80 | 14.87 | 97.99 b | 13.91 | 14.19 |
| Lumen radial diameter (µm) | 21.86 a | 4.49 | 20.53 | 12.97 b | 2.42 | 18.66 |
| Lumen tangential diameter (µm) | 19.25 a | 4.18 | 21.70 | 14.80 b | 2.70 | 18.25 |
| Lumen area (µm2) | 375.21 a | 120.04 | 31.99 | 165.81 b | 48.37 | 29.17 |
| Lumen perimeter (µm) | 82.21 a | 14.53 | 17.67 | 55.55 b | 7.91 | 14.25 |
| Cell wall thickness (µm) | 4.34 a | 1.81 | 41.76 | 10.61 b | 3.35 | 31.55 |
| Cell wall area (µm2) | 250.92 a | 99.67 | 39.72 | 442.94 b | 167.12 | 37.73 |
| Lumen (%) | 60.19 a | 11.61 | 17.88 | 28.53 b | 7.96 | 27.91 |
| Cell wall (%) | 39.78 a | 10.77 | 27.07 | 70.48 b | 7.96 | 11.13 |
| Lumen R/T 2 | 1.14 a | 0.34 | 28.50 | 0.90 b | 0.22 | 24.59 |
| Cell R/T 3 | 1.11 a | 0.45 | 30.13 | 0.93 b | 0.33 | 25.65 |
| Ring Groups 1 | Number | Means (kg m−3) | SD (kg m−3) | CV (%) | Max (kg m−3) | Min (kg m−3) |
|---|---|---|---|---|---|---|
| 2–10 | 4400 | 392.28 a | 105.65 | 26.93 | 762.07 | 171.13 |
| 11–20 | 4400 | 373.09 b | 102.35 | 27.43 | 766.59 | 194.57 |
| 21–30 | 4400 | 357.26 c | 110.02 | 30.80 | 733.92 | 191.91 |
| 31–40 | 4400 | 347.41 d | 108.89 | 31.34 | 732.23 | 195.72 |
| 41–50 | 4400 | 345.88 d | 113.43 | 32.79 | 854.73 | 200.02 |
| 51–60 | 4300 | 343.90 d | 110.03 | 32.00 | 687.39 | 194.20 |
| 61–70 | 4200 | 344.71 d | 107.35 | 31.14 | 669.32 | 191.98 |
| 71–80 | 3600 | 343.78 d | 110.91 | 32.26 | 715.60 | 194.75 |
| 81–90 | 2600 | 341.09 d | 110.09 | 32.28 | 676.99 | 185.76 |
| 91–100 | 1200 | 354.71 e | 118.45 | 33.39 | 704.61 | 198.02 |
| All data | 3,8500 | 354.41 | 109.72 | 31.04 | 854.74 | 171.13 |
| Fixed Effects | ||||
| Sources | Df 1 | F-Value | p-Value | VAR COMP (%) |
| Site | 2 | 1.48 | 0.24 | 0.11 |
| Ring groups | 10 | 331.33 | <0.0001 | 2.02 |
| Ring width | 99 | 943.24 | <0.0001 | 69.14 |
| Random Effects | ||||
| Sources | df | Z Value | p-Value | VAR COMP (%) |
| Tree | 14 | 4.38 | <0.0001 | 0.28 |
| Residual | 137 | 140.62 | <0.0001 | 28.44 |
| Juvenile Wood | ||||||||
|---|---|---|---|---|---|---|---|---|
| Wood Density Properties | RD | EWD | LWD | RW | EWW | LWW | LP | |
| Mature wood | RD | 1 | 0.92 *** | 0.53 *** | −0.1 ** | −0.15 ** | 0.05 ns | 0.23 *** |
| EWD | 0.89 *** | 1 | 0.31 *** | −0.1 ** | −0.11 ** | −0.02 ns | 0.15 ** | |
| LWD | 0.37 *** | 0.25 *** | 1 | 0.13 ** | 0.21 *** | −0.1 ** | −0.31 *** | |
| RW | −0.19 ** | −0.03 ns | 0.11 ** | 1 | 0.94 *** | 0.66 *** | −0.34 *** | |
| EWW | −0.23 *** | −0.02 ns | 0.26 *** | 0.96 *** | 1 | 0.36 *** | −0.58 *** | |
| LWW | −0.03 ns | −0.017 ns | −0.34 *** | 0.59 *** | 0.32 *** | 1 | 0.36 *** | |
| LP | 0.28 *** | 0.11 ** | −0.63 *** | −0.38 *** | −0.59 *** | 0.40 *** | 1 | |
| Ring Groups | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2–10 | 11–20 | 21–30 | 31–40 | 41–50 | 51–60 | 61–70 | 71–80 | 81–90 | |
| RD-EWD | 0.94 *** | 0.89 *** | 0.86 *** | 0.81 *** | 0.84 *** | 0.90 *** | 0.87 *** | 0.91 *** | 0.92 *** |
| RD-LWD | 0.81 *** | 0.57 *** | 0.21 *** | 0.43 *** | 0.36 *** | 0.25 *** | 0.27 *** | 0.33 *** | 0.14 * |
| EWD-LWD | 0.61 *** | 0.30 *** | 0.01 ns | 0.32 *** | 0.30 *** | 0.19 ** | 0.23 *** | 0.26 *** | 0.07 ns |
| RD-LP | 0.07 ns | 0.26 *** | 0.39 *** | 0.16 ** | 0.31 *** | 0.47 *** | 0.47 *** | 0.40 *** | 0.43 *** |
| LWD-LP | −0.05 ns | −0.22 *** | −0.57 *** | −0.63 *** | −0.61 *** | −0.55 *** | −0.53 *** | −0.57 *** | −0.68 *** |
| EWD-LP | −0.03 ns | 0.14 ** | 0.21 *** | −0.12 * | 0.02 ns | 0.27 *** | 0.2 *** | 0.24 *** | 0.32 *** |
| RD-RW | −0.13 * | −0.06 ns | −0.19 ** | −0.12 * | −0.12 * | −0.13 ** | −0.19 ** | −0.36 *** | −0.32 *** |
| EWD-RW | −0.10 ns | 0.07ns | −0.07 ns | 0.17 ** | 0.11 * | 0.10 * | −0.02 ns | −0.15 ** | −0.07 ns |
| LWD-RW | −0.06 ns | 0.15 ** | 0.13 * | 0.11 * | 0.25 *** | 0.11 * | 0.21 *** | −0.08 ns | −0.12 * |
| LP-RW | −0.29 *** | −0.28 *** | −0.42 *** | −0.39 *** | −0.52 *** | −0.39 *** | −0.46 *** | −0.36 *** | −0.29 *** |
| Characteristic | Tracheid Length | Tracheid Width | Ring Width | Tree Height | Tree Diameter |
|---|---|---|---|---|---|
| Tracheid length | 1 | ||||
| Tracheid width | 0.59 ** | 1 | |||
| Ring width | −0.12 ** | 0.11 ** | 1 | ||
| Tree height | 0.11 ** | 0.06 ns | −0.02 ns | 1 | |
| Tree diameter | 0.15 ** | 0.33 ** | 0.12 ** | 0.54 ** | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouslimi, B.; Koubaa, A.; Bergeron, Y. Intra-Ring Variations and Interrelationships for Selected Wood Anatomical and Physical Properties of Thuja Occidentalis L. Forests 2019, 10, 339. https://doi.org/10.3390/f10040339
Bouslimi B, Koubaa A, Bergeron Y. Intra-Ring Variations and Interrelationships for Selected Wood Anatomical and Physical Properties of Thuja Occidentalis L. Forests. 2019; 10(4):339. https://doi.org/10.3390/f10040339
Chicago/Turabian StyleBouslimi, Besma, Ahmed Koubaa, and Yves Bergeron. 2019. "Intra-Ring Variations and Interrelationships for Selected Wood Anatomical and Physical Properties of Thuja Occidentalis L." Forests 10, no. 4: 339. https://doi.org/10.3390/f10040339
APA StyleBouslimi, B., Koubaa, A., & Bergeron, Y. (2019). Intra-Ring Variations and Interrelationships for Selected Wood Anatomical and Physical Properties of Thuja Occidentalis L. Forests, 10(4), 339. https://doi.org/10.3390/f10040339






