Designing Operationally Relevant Daily Large Fire Containment Strategies Using Risk Assessment Results
Abstract
1. Introduction
2. Materials and Methods
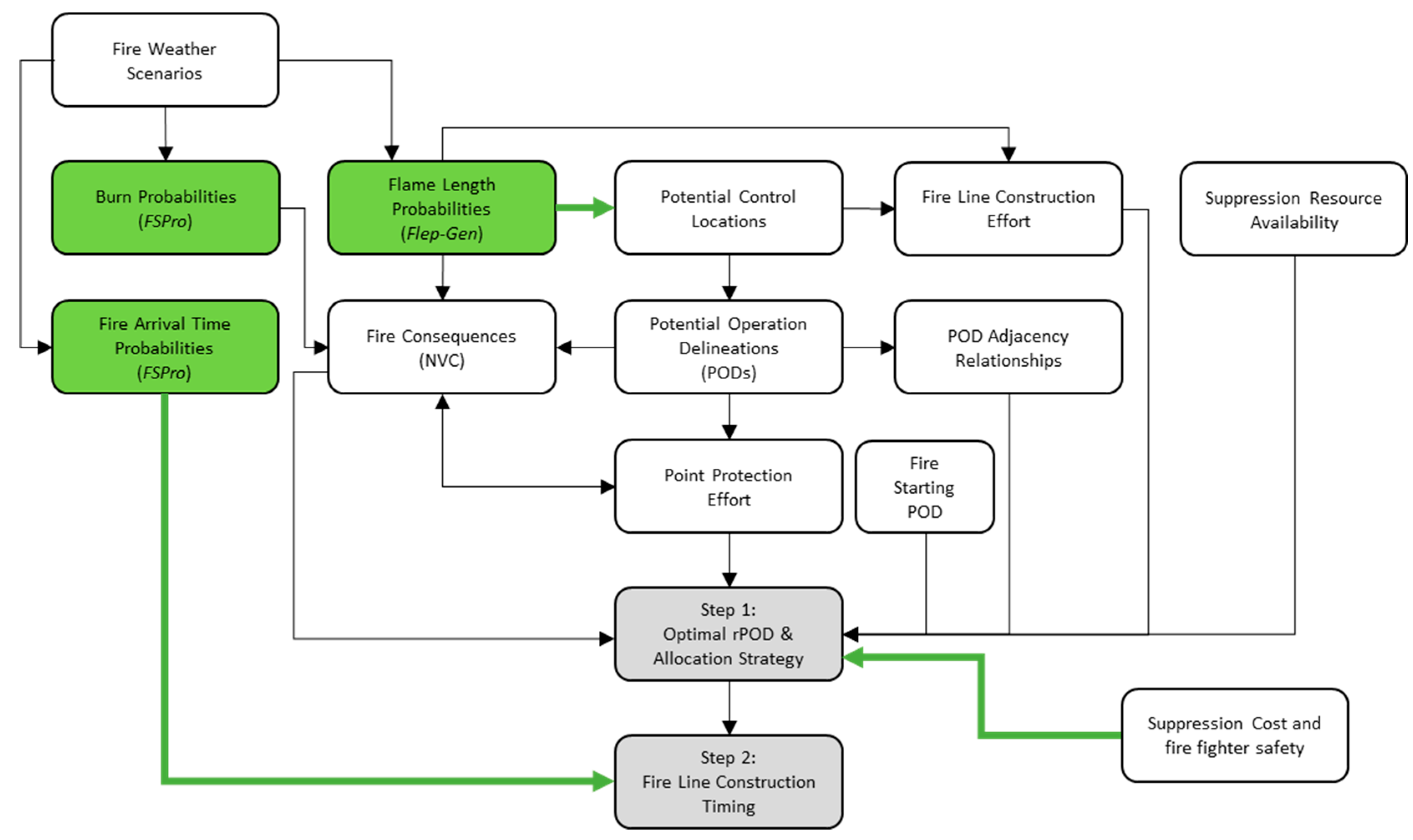
2.1. Modeling Overview
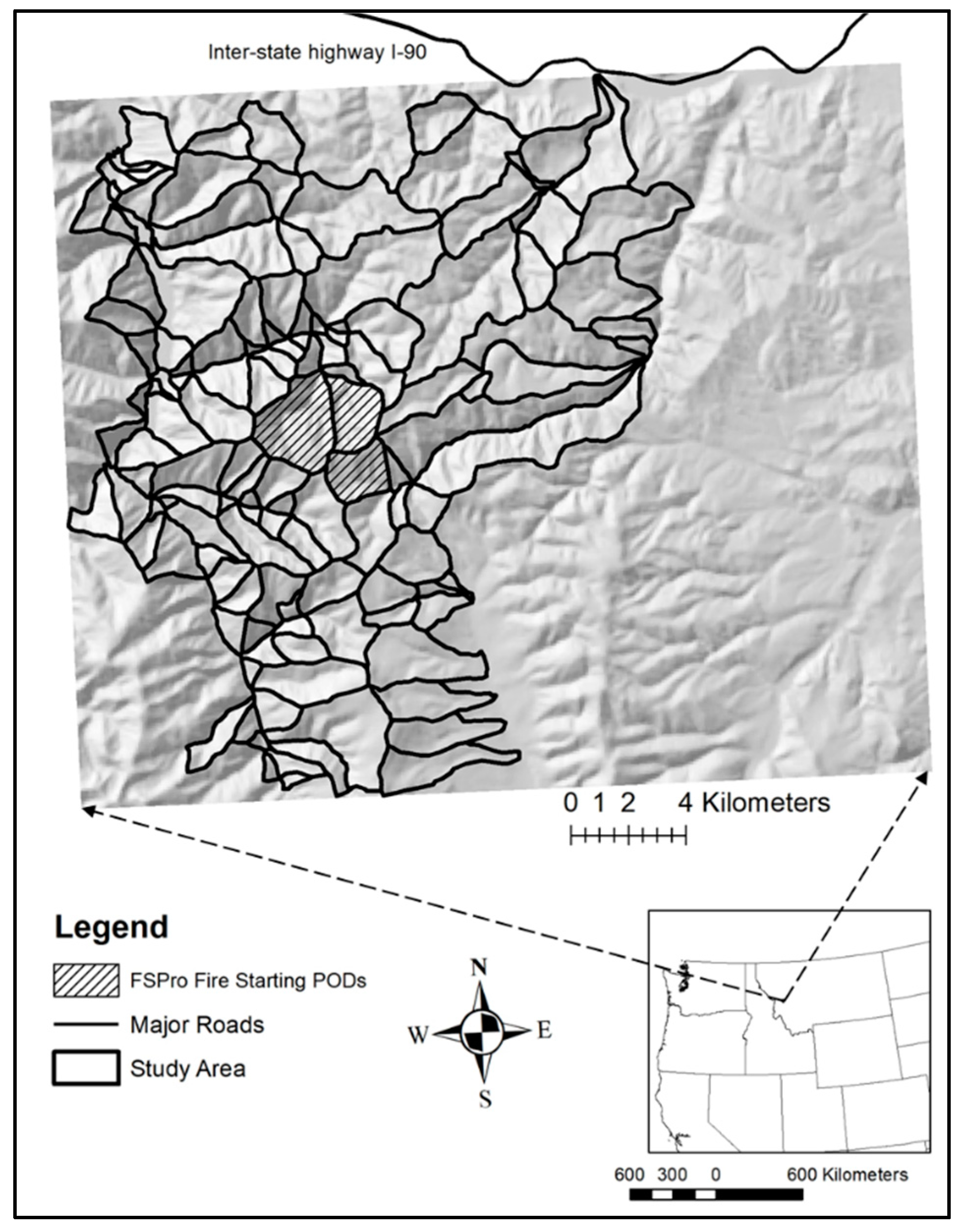
2.2. Case Study Location and Input Data Generation
2.3. Mathematical Formulation for rPOD Selection (the First Step Optimization)
2.4. Mathematical Formulation for Suppression Timing Adjustment (Second Step Optimization)
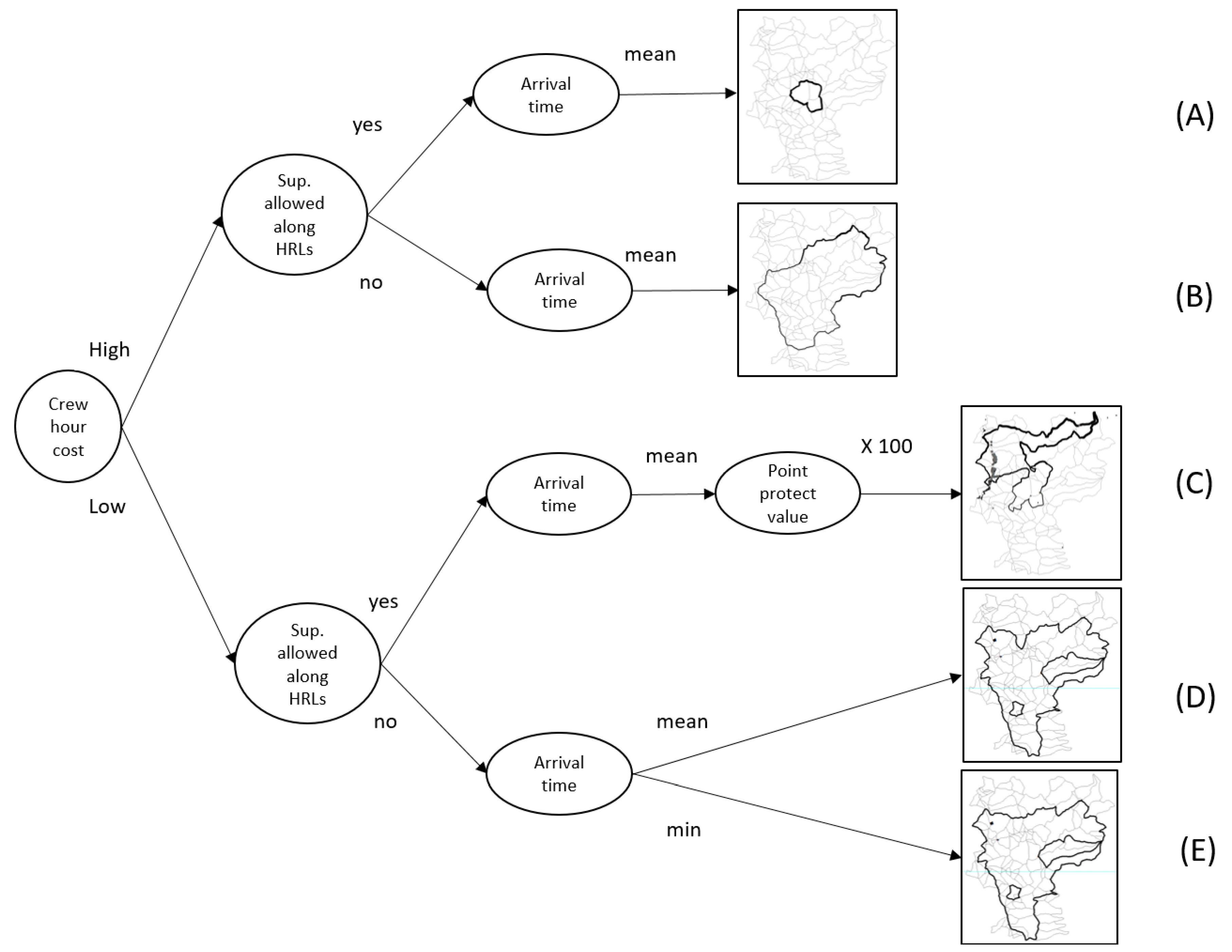
2.5. Scenarios Used for Model Assessment
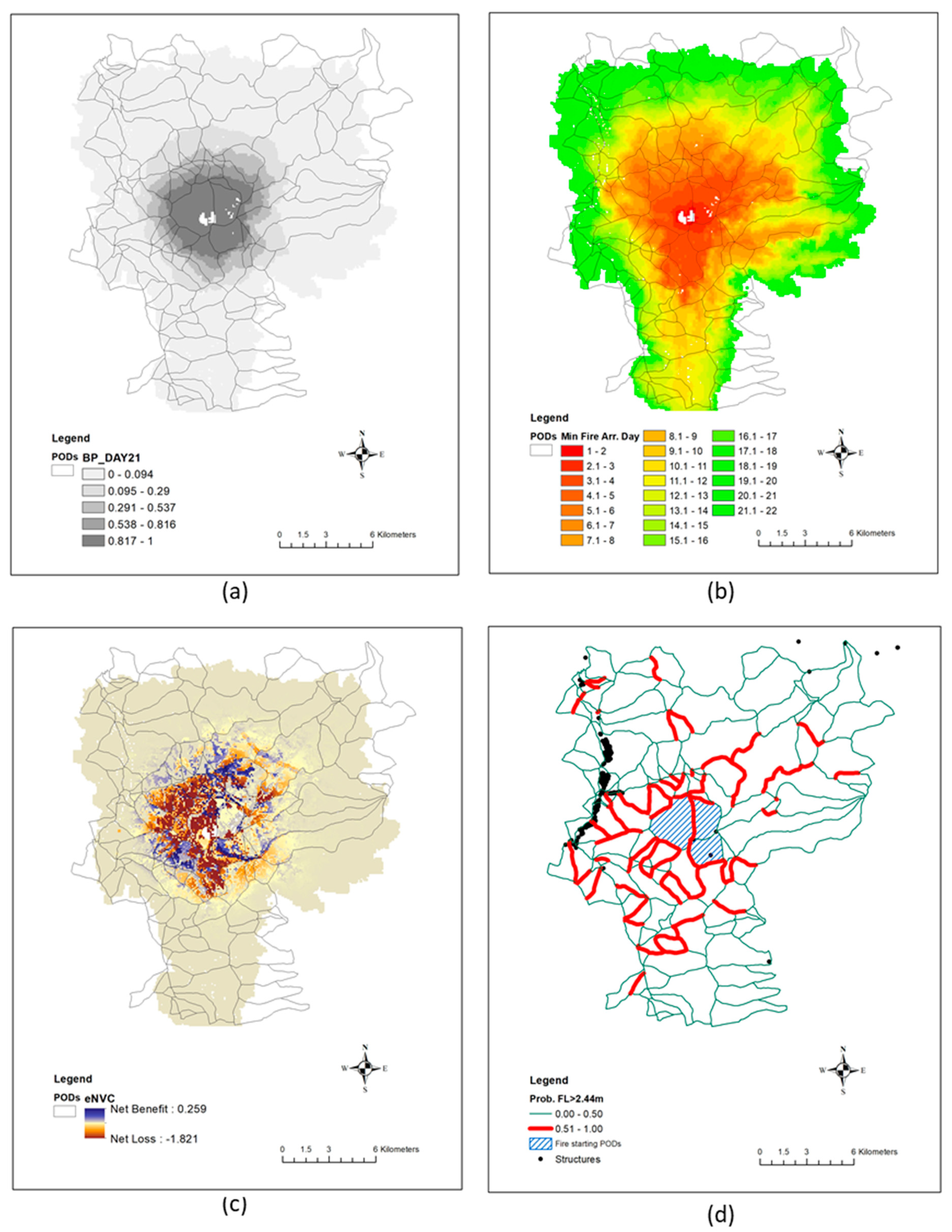
3. Results
3.1. Test Scenarios and Corresponding Containment Strategies
3.2. Development of Contingent rPOD Container
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Thompson, M.P. Modeling wildfire incident complexity dynamics. PLoS ONE 2013, 8, e63297. [Google Scholar] [CrossRef]
- McLennan, J.; Holgate, A.M.; Omodei, M.M.; Wearing, A.J. Decision making effectiveness in wildfire incident management teams. J. Conting. Crisis Manag. 2006, 14, 27–37. [Google Scholar] [CrossRef]
- Martell, D.L. A review of recent forest and wildland fire management decision support systems research. Curr. For. Rep. 2015, 1, 128–137. [Google Scholar] [CrossRef]
- Duff, T.J.; Tolhurst, K.G. Operational wildfire suppression modelling: A review evaluating development, state of the art and future directions. Int. J. Wildl. Fire 2015, 24, 735–748. [Google Scholar] [CrossRef]
- Petrovic, N.; Carlson, J.M. A decision-making framework for wildfire suppression. Int. J. Wildl. Fire 2012, 21, 927–937. [Google Scholar] [CrossRef]
- Dunn, C.J.; Calkin, D.E.; Thompson, M.P. Towards enhanced risk management planning, decision making and monitoring of US wildfire response. Int. J. Wildl. Fire 2017, 26, 551–556. [Google Scholar] [CrossRef]
- Pacheco, A.P.; Claro, J. Operational flexibility in forest fire prevention and suppression: A spatially explicit intra-annual optimization analysis, considering prevention, (pre) suppression, and escape costs. Eur. J. For. Res. 2018, 137, 895–916. [Google Scholar] [CrossRef]
- Minas, J.; Hearne, J.; Martell, D. An integrated optimization model for fuel management and fire suppression preparedness planning. Ann. Oper. Res. 2015, 232, 201–215. [Google Scholar] [CrossRef]
- Chow, J.Y.; Regan, A.C. Resource location and relocation models with rolling horizon forecasting for wildland fire planning. INFOR 2011, 49, 31–43. [Google Scholar] [CrossRef]
- Ntaimo, L.; Gallego-Arrubla, J.A.; Gan, J.; Stripling, C.; Young, J.; Spencer, T. A simulation and stochastic integer programming approach to wildfire initial attack planning. For. Sci. 2013, 59, 105–117. [Google Scholar] [CrossRef]
- Wei, Y.; Thompson, M.E.; Calkin, D.E.; Stonesifer, C.S. A simulation and optimisation procedure to model daily suppression resource transfers during a fire season in Colorado. Int. J. Wildl. Fire 2017, 26, 630–641. [Google Scholar] [CrossRef]
- Belval, E.J.; Calkin, D.E.; Wei, Y.; Stonesifer, C.S.; Thompson, M.P.; Masarie, A. Examining dispatching practices for Interagency Hotshot Crews to reduce seasonal travel distance and manage fatigue. Int. J. Wildl. Fire 2018, 27, 569–580. [Google Scholar] [CrossRef]
- Krasko, V.; Rebennack, S. Two-stage stochastic mixed-integer nonlinear programming model for post-wildfire debris flow hazard management: Mitigation and emergency evacuation. Eur. J. Oper. Res. 2017, 263, 265–282. [Google Scholar] [CrossRef]
- Wei, Y.; Rideout, D.B.; Hall, T.B. Toward efficient management of large fires: A mixed integer programming model and two iterative approaches. For. Sci. 2011, 57, 435–447. [Google Scholar]
- Belval, E.J.; Wei, Y.; Bevers, M. A mixed integer program to model spatial wildfire behavior and suppression placement decisions. Can. J. For. Res. 2015, 45, 384–393. [Google Scholar] [CrossRef]
- Belval, E.J.; Wei, Y.; Bevers, M. A stochastic mixed-integer program to model spatial wildfire behavior and suppression placement decisions with uncertain weather. Can. J. For. Res. 2016, 46, 234–248. [Google Scholar] [CrossRef]
- Van der Merwe, M.; Minas, J.P.; Ozlen, M.; Hearne, J.W. A mixed integer programming approach for asset protection during escaped wildfires. Can. J. For. Res. 2014, 45, 444–451. [Google Scholar] [CrossRef]
- Van der Merwe, M.; Ozlen, M.; Hearne, J.W.; Minas, J.P. Dynamic rerouting of vehicles during cooperative wildfire response operations. Ann. Oper. Res. 2017, 254, 467–480. [Google Scholar] [CrossRef]
- Roozbeh, I.; Ozlen, M.; Hearne, J.W. An Adaptive Large Neighbourhood Search for asset protection during escaped wildfires. Comp. Oper. Res. 2018, 97, 125–134. [Google Scholar] [CrossRef]
- Thompson, M.P.; MacGregor, D.G.; Calkin, D. Risk Management: Core Principles and Practices, and Their Relevance to Wildland Fire. General Technical Report RMRS-GTR-350; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2016; Volume 29, p. 350.
- Dunn, C.J.; Thompson, M.P.; Calkin, D.E. A framework for developing safe and effective large-fire response in a new fire management paradigm. For. Ecol. Manag. 2017, 404, 184–196. [Google Scholar] [CrossRef]
- Thompson, M.P.; MacGregor, D.G.; Dunn, C.J.; Calkin, D.E.; Phipps, J. Rethinking the Wildland Fire Management System. J. For. 2018, 116, 382–390. [Google Scholar] [CrossRef]
- Thompson, M.P.; Bowden, P.; Brough, A.; Scott, J.H.; Gilbertson-Day, J.; Taylor, A.; Anderson, J.; Haas, J.R. Application of wildfire risk assessment results to wildfire response planning in the southern Sierra Nevada, California, USA. Forests 2016, 7, 64. [Google Scholar] [CrossRef]
- O’Connor, C.D.; Thompson, M.P.; Rodríguez, Y.; Silva, F.R. Getting ahead of the wildfire problem: Quantifying and mapping management challenges and opportunities. Geosciences 2016, 6, 35. [Google Scholar] [CrossRef]
- O’Connor, C.D.; Calkin, D.E.; Thompson, M.P. An empirical machine learning method for predicting potential fire control locations for pre-fire planning and operational fire management. Int. J. Wildl. Fire 2017, 26, 587–597. [Google Scholar]
- Thompson, M.P.; Liu, Z.; Wei, Y.; Caggiano, M.D. Analyzing Wildfire Suppression Difficulty in Relation to Protection Demand. In Environmental Risks; IntechOpen: London, UK, 2018. [Google Scholar] [CrossRef]
- Thompson, M.P.; Riley, K.L.; Loeffler, D.; Haas, J.R. Modeling fuel treatment leverage: Encounter rates, risk reduction, and suppression cost impacts. Forests 2017, 8, 469. [Google Scholar] [CrossRef]
- Wei, Y.; Thompson, M.P.; Haas, J.R.; Dillon, G.K.; O’Connor, C.D. Spatial optimization of operationally relevant large fire confine and point protection strategies: Model development and test cases. Can. J. For. Res. 2018, 48, 480–493. [Google Scholar] [CrossRef]
- O’Connor, C.D.; Calkin, D.E. Engaging the fire before it starts: A case study from the 2017 Pinal Fire (Arizona). Wildfire 2019, 28, 14–18. [Google Scholar]
- Noonan-Wright, E.K.; Opperman, T.S.; Finney, M.A.; Zimmerman, G.T.; Seli, R.C.; Elenz, L.M.; Calkin, D.E.; Fiedler, J.R. Developing the US wildland fire decision support system. J. Combust. 2011. [Google Scholar] [CrossRef]
- Finney, M.A.; Grenfell, I.C.; McHugh, C.W.; Seli, R.C.; Trethewey, D.; Stratton, R.D.; Brittain, S. A method for ensemble wildland fire simulation. Environ. Model. Assess. 2011, 16, 153–167. [Google Scholar] [CrossRef]
- Calkin, D.E.; Thompson, M.P.; Finney, M.A.; Hyde, K.D. A real-time risk assessment tool supporting wildland fire decision making. J. For. 2011, 109, 274–280. [Google Scholar]
- Finney, M.A. The challenge of quantitative risk analysis for wildland fire. For. Ecol. Manag. 2005, 211, 97–108. [Google Scholar] [CrossRef]
- Scott, J.H.; Thompson, M.P.; Calkin, D.E. A wildfire risk assessment framework for land and resource management. In General Technical Report RMRS-GTR-315; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2013; 83p. [Google Scholar]
- Calkin, D.E.; Ager, A.; Thompson, M.P.; Finney, M.A.; Lee, D.C.; Quigley, T.M.; McHugh, C.W.; Riley, K.L.; Gilbertson-Day, J.M. A comparative risk assessment framework for wildland fire management: The 2010 cohesive strategy science report. In General Technical Report RMRS-GTR-262; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2011; 63p. [Google Scholar]
- Thompson, M.P.; Haas, J.R.; Gilbertson-Day, J.W.; Scott, J.H.; Langowski, P.; Bowne, E.; Calkin, D.E. Development and application of a geospatial wildfire exposure and risk calculation tool. Environ. Model. Softw. 2015, 63, 61–72. [Google Scholar] [CrossRef]
- Finney, M.A.; McHugh, C.W.; Grenfell, I.C.; Riley, K.L.; Short, K.C. A simulation of probabilistic wildfire risk components for the continental United States. Stoch. Environ. Res. Risk Assess. 2011, 25, 973–1000. [Google Scholar] [CrossRef]
- Scott, J.; Gilbertson-Day, J. Deterministic Generation of Flame-Length Probabilities for Use in Risk Assessments. Fire Continuum Conference. 21–24 May 2018. Missoula, MT. S11.2. Available online: http://firecontinuumconference.org/wp-content/uploads/2017/05/FINAL-Special-Session-Presentation-Abstracts-Fire-Continuum.pdf (accessed on 16 February 2019).
- Scott, J.H.; Burgan, R.E. Standard fire behavior fuel models: A comprehensive set for use with Rothermel’s surface fire spread model. In General Technical Report RMRS-GTR-153; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2005; 72p. [Google Scholar]
- Thompson, M.P.; Scott, J.; Helmbrecht, D.; Calkin, D.E. Integrated wildfire risk assessment: Framework development and application on the Lewis and Clark National Forest in Montana, USA. Integr. Environ. Assess. Manag. 2013, 9, 329–342. [Google Scholar] [CrossRef] [PubMed]
- Broyles, G. Fireline production rates. In Fire Management Report; USDA Forest Service, National Technology & Development Program: San Dimas, CA, USA, 2011; pp. 1151–1805. [Google Scholar]
- Andrews, P.L.; Heinsch, F.A.; Schelvan, L. How to generate and interpret fire characteristics charts for surface and crown fire behavior. In General Technical Report RMRS-GTR-253; USDA Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2011. [Google Scholar] [CrossRef]
- Mees, R.; Strauss, D.; Chase, R. Modeling wildland fire containment with uncertain flame length and fireline width. Int. J. Wildl. Fire 1993, 3, 179–185. [Google Scholar] [CrossRef]
- Canton-Thompson, J.; Gebert, K.M.; Thompson, B.; Jones, G.; Calkin, D.; Donovan, G. External Human Factors in Incident Management Team Decision making and Their Effect on Large Fire Suppression Expenditures. J. For. 2008, 106, 416–424. [Google Scholar] [CrossRef]
- Paveglio, T.B.; Moseley, C.; Carroll, M.S.; Williams, D.R.; Davis, E.J.; Paige, F.A. Categorizing the social context of the Wildland Urban Interface: Adaptive capacity for wildfire and community “archetypes”. For. Sci. 2015, 61, 298–310. [Google Scholar] [CrossRef]
- Evers, C.R.; Ager, A.A.; Nielsen-Pincus, M.; Palaiologou, P.; Bunzel, K. Archetypes of community wildfire exposure from national forests of the western US. Landsc. Urban Plan. 2019, 182, 55–66. [Google Scholar] [CrossRef]
- Wei, Y.; Thompson, M.P.; Scott, J.; O’connor, C. Test an Optimization Model to Support Multi-Day Large Fire Containment Decisions—A Case Study for the Ferguson Fire. In Proceedings of the 19th Symposium on Systems Analysis in Forest Resources, Puerto Varas, Chile, 3–7 March 2019; Available online: http://www.ssafr2019.cl/13/default/inicio (accessed on 3 April 2019).
- Haight, R.G.; Fried, J.S. Deploying Wildland Fire Suppression Resources with a Scenario-Based Standard Response Model. Informatioin 2007, 45, 31–39. [Google Scholar] [CrossRef]
- Ntaimo, L.; Arrubla, J.A.G.; Stripling, C.; Young, J.; Spencer, T. A stochastic programming standard response model for wildfire initial attack planning. Can. J. For. Res. 2012, 42, 987–1001. [Google Scholar] [CrossRef]
- Wei, Y.; Belval, E.; Bevers, M. Designing seasonal initial attack resource deployment and dispatch rules using a two-stage stochastic programming procedure. For. Sci. 2015, 61, 1021–1032. [Google Scholar]
- Wei, Y.; Bevers, M.; Belval, E.; Bird, B. A chance-constrained programming model to allocate wildfire initial attack resources for a fire season. For. Sci. 2015, 61, 278–288. [Google Scholar]
- Thompson, M.P.; Lauer, C.J.; Calkin, D.E.; Rieck, J.D.; Stonesifer, C.S.; Hand, M.S. Wildfire Response Performance Measurement: Current and Future Directions. Fire 2018, 1, 21. [Google Scholar] [CrossRef]
- Plucinski, M.P. Fighting Flames and Forging Firelines: Wildfire Suppression Effectiveness at the Fire Edge. Curr. For. Rep. 2019. [Google Scholar] [CrossRef]
- Smith, L.E. Sensitivity of fire size to fireline construction rates in a simulation model. Fire Technol. 1986, 22, 136–147. [Google Scholar] [CrossRef]
- Hirsch, K.G.; Martell, D.L. A review of initial attack fire crew productivity and effectiveness. Int. J. Wildl. Fire 1996, 6, 199–215. [Google Scholar] [CrossRef]
- Riley, K.; Thompson, M.; Scott, J.; Gilbertson, J. A Model-Based Framework to Evaluate Alternative Wildfire Suppression Strategies. Resources 2018, 7, 4. [Google Scholar] [CrossRef]



| Sets and Indices and Descriptions | |
| indices for PODs | |
| or | index of edges between each pair of adjacent PODs i and j with the first subscript smaller than the second subscript so that each edge is represented by only one pair of PODs. i = −1 represents areas out of the study area. |
| The set of boundaries (HRL) that fire line is not likely to hold due to predicted probability of flame length > 2.44 m. | |
| or | The set of boundaries with predicted fire arrival time at or after the tth planning period. We assumed resources available at period t can only be used to build fire lines along boundaries from this set. |
| Index of fire spread direction, from POD i to its adjacent POD j | |
| Index of suppression period (i.e., day) from one to tmax | |
| Index of each candidate point protection location, i.e., a structure | |
| Decision variables and descriptions | |
| 0/1 variable; 1 if POD i is selected as part of the rPOD | |
| 0/1 variable; 1 if fire line is constructed along edge (i,j) during suppression period t | |
| 0/1 variable tracking whether point protection would be applied at location a; 0 if not, 1 if applied | |
| 0/1 variable; 1 if fire spreads from POD i to j; 0 if not | |
| An auxiliary variable tracking the sequence each POD being included into the rPOD. Following the sequence, this model can form a contiguous rPOD starting from the fire starting PODs. | |
| Bookkeeping variable used to track the total resource time (i.e., crew hours) spent on containment and point protection during period t | |
| Parameters and descriptions | |
| The set of adjacent ignition PODs | |
| Expected total NVC in POD i; positive value represents fire benefits; negative value represents fire losses. | |
| Expected benefit (avoided loss), in terms of cNVC, from point protection at structure location a. | |
| The total number of point protection locations in POD i | |
| Resource time (i.e., number of crew hours) required for point protection at location a during period t | |
| A large positive constant (big M) that is larger than the number of PODs | |
| Expected resource time (i.e., crew hours) needed to build containment lines along edge calculated based on the predicted probabilities of multiple fire flame length levels. | |
| Resource time (i.e., crew hours) availability in each period t | |
| A point protection benefits multiplier. It can be set to a higher value to emphasis manager’s concern of losing structures. | |
| A selected weight in the objective function to penalize resource time (i.e., total crew hours) spent on large fire management | |
| The predicted fire arrival time (i.e., 2.3 days) to edge without suppression | |
| Additional sets and indices for the second step model | |
| The rPOD boundaries identified from the first step optimization | |
| The set of structures selected for point protection from the first step optimization | |
| Additional decision variables | |
| Variables used to track the time between fire line construction period (i.e., day) and fire arrival time along boundary | |
| The narrowest temporal gap between fire line construction period and fire arrival time for all rPOD boundaries | |
| Test Scenarios | Crew Hour Penalty in Equation (1)) | Suppression at HRL Is Allowed | Use (Mean or Min) Fire Arrival Time to Each Boundary | Weight in Equation (1)) |
|---|---|---|---|---|
| A | 1 | Yes | mean | 1 |
| high cost, high risk | ||||
| B | 1 | No | mean | 1 |
| high cost, low risk | ||||
| C | 0.0001 | Yes | mean | 100 |
| low cost, high risk structure protection | ||||
| D | 0.0001 | No | mean | 1 |
| low cost, low risk | ||||
| E | 0.0001 | No | min | 1 |
| low cost, low risk, earlier fire arrival |
| Test Scenario | rPOD Area (ha) | # of PODs | Line Length (m) | Crew Hour in Building Lines | Smallest Time Gap (day) | Total eNVC | # of Protected Structures | Mean Prob. of FL >8 ft |
|---|---|---|---|---|---|---|---|---|
| A | 1367 | 3 | 16,222 | 679 | 1.70 | −87.73 | 0 | 49.7% |
| B | 17,166 | 78 | 68,497 | 1835 | 12.54 | −284.87 | 0 | 14.0% |
| C | 9424 | 46 | 117,543 | 4116 | 2.70 | −81.02 | 123 | 32.9% |
| D | 17,298 | 81 | 118,557 | 3554 | 6.85 | −270.90 | 19 | 17.2% |
| E | 17,555 | 82 | 115,553 | 3487 | 6.85 | −271.09 | 19 | 17.7% |
| Crew Hour Penalty | rPOD Area (ha) | # of PODs | Line Length (m) | Crew Hour in Building Lines | Smallest Time Gap (Day) | Total eNVC | # of Structures Protected |
|---|---|---|---|---|---|---|---|
| Test scenario A with varying crew hour penalty ( in Equation (1)) | |||||||
| 1 | 1367 | 3 | 16,222 | 679 | 1.70 | −87.73 | 0 |
| 0.1 | 1367 | 3 | 16,222 | 679 | 1.70 | −87.73 | 0 |
| 0.01 | 1421 | 4 | 16,520 | 684 | 1.04 | −85.70 | 1 |
| 0.001 | 4683 | 23 | 50,636 | 1886 | 0.01 | −79.88 | 15 |
| 0.0001 | 7224 | 38 | 86,479 | 3133 | 2.70 | −80.30 | 74 |
| Test scenario B with varying crew hour penalty ( in Equation (1)) | |||||||
| 1 | 17,166 | 78 | 68,497 | 1835 | 12.54 | −284.87 | 0 |
| 0.1 | 17,166 | 78 | 68,497 | 1835 | 12.54 | −284.87 | 0 |
| 0.01 | 15,989 | 79 | 92,567 | 2706 | 8.39 | −271.86 | 1 |
| 0.001 | 16,620 | 81 | 99,493 | 2908 | 8.85 | −271.14 | 17 |
| 0.0001 | 19,090 | 87 | 130,983 | 3821 | 6.85 | −270.92 | 19 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Thompson, M.P.; Scott, J.H.; O’Connor, C.D.; Dunn, C.J. Designing Operationally Relevant Daily Large Fire Containment Strategies Using Risk Assessment Results. Forests 2019, 10, 311. https://doi.org/10.3390/f10040311
Wei Y, Thompson MP, Scott JH, O’Connor CD, Dunn CJ. Designing Operationally Relevant Daily Large Fire Containment Strategies Using Risk Assessment Results. Forests. 2019; 10(4):311. https://doi.org/10.3390/f10040311
Chicago/Turabian StyleWei, Yu, Matthew P. Thompson, Joe H. Scott, Christopher D. O’Connor, and Christopher J. Dunn. 2019. "Designing Operationally Relevant Daily Large Fire Containment Strategies Using Risk Assessment Results" Forests 10, no. 4: 311. https://doi.org/10.3390/f10040311
APA StyleWei, Y., Thompson, M. P., Scott, J. H., O’Connor, C. D., & Dunn, C. J. (2019). Designing Operationally Relevant Daily Large Fire Containment Strategies Using Risk Assessment Results. Forests, 10(4), 311. https://doi.org/10.3390/f10040311






