The Cumulative Effects of Forest Disturbance and Climate Variability on Streamflow in the Deadman River Watershed
Abstract
:1. Introduction
2. Materials and Methods
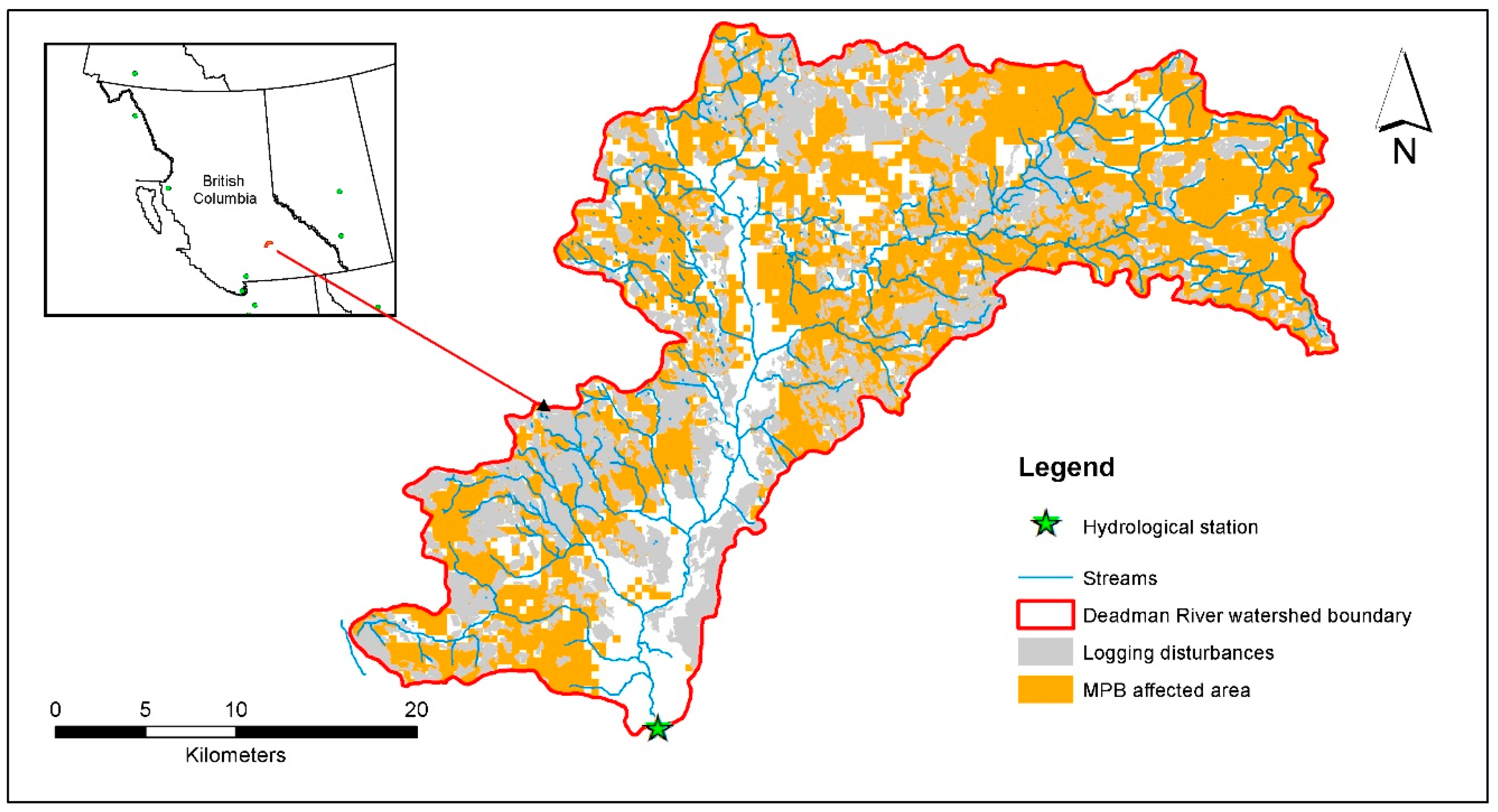
2.1. Watershed Description
2.2. Watershed Data
2.3. Cumulative Equivalent Clear-Cut Area
2.4. Cross-Correlation Analysis
2.5. Quantifying the Effects of Forest Disturbance and Climate Variability on Streamflow Components
2.5.1. Timeseries Trend Analysis
2.5.2. Modified Double Mass Curve
2.5.3. Sensitivity-Based Method
2.5.4. Paired-Year Approach
3. Results
3.1. Time-Trend Analysis of the Hydrometeorological Variables
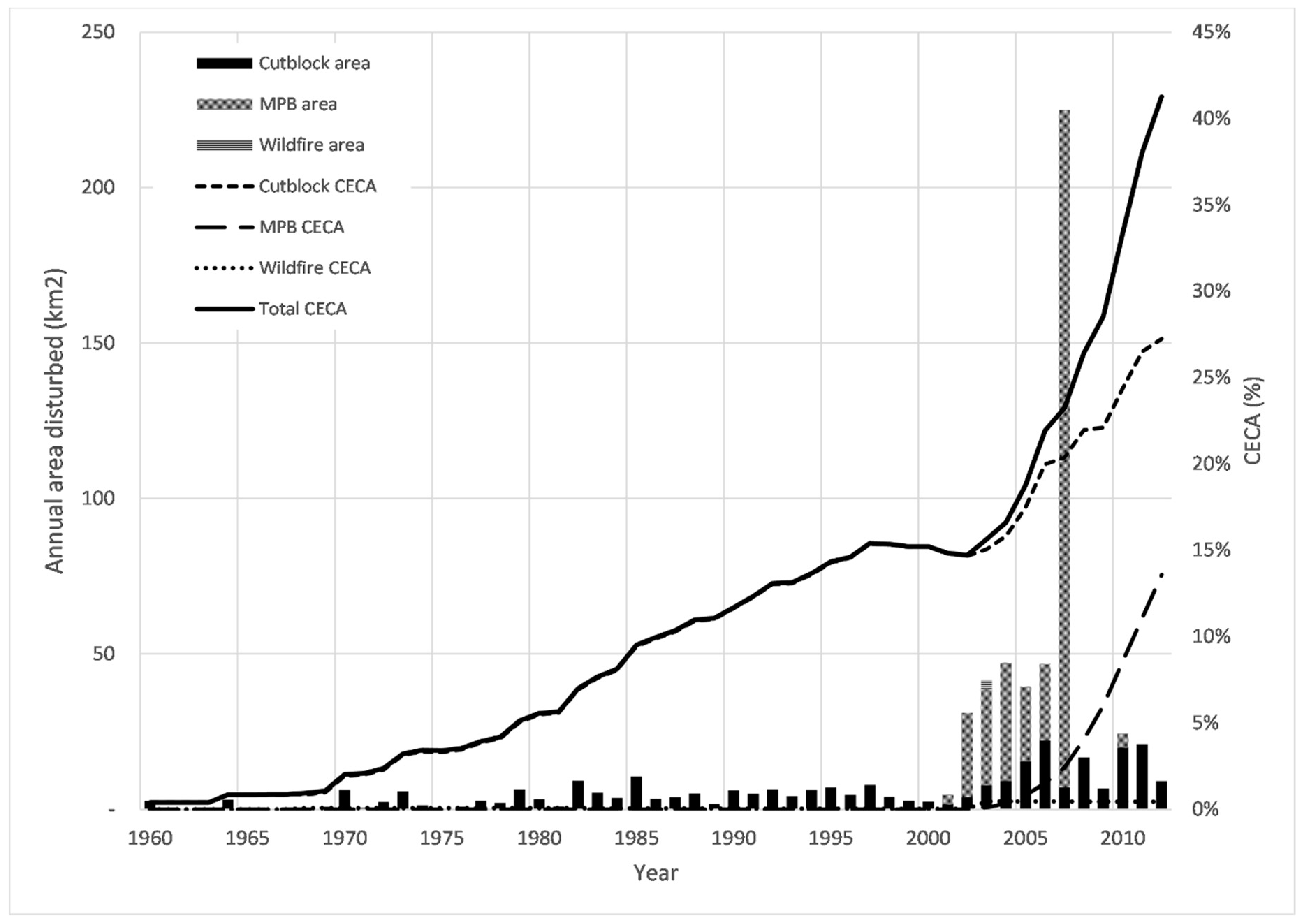
3.2. Cross-Correlation between Forest Disturbance and Streamflow Regime Components
3.3. Separation of the Effects Of Forest Disturbance and Climate Variability on Annual Mean Flow
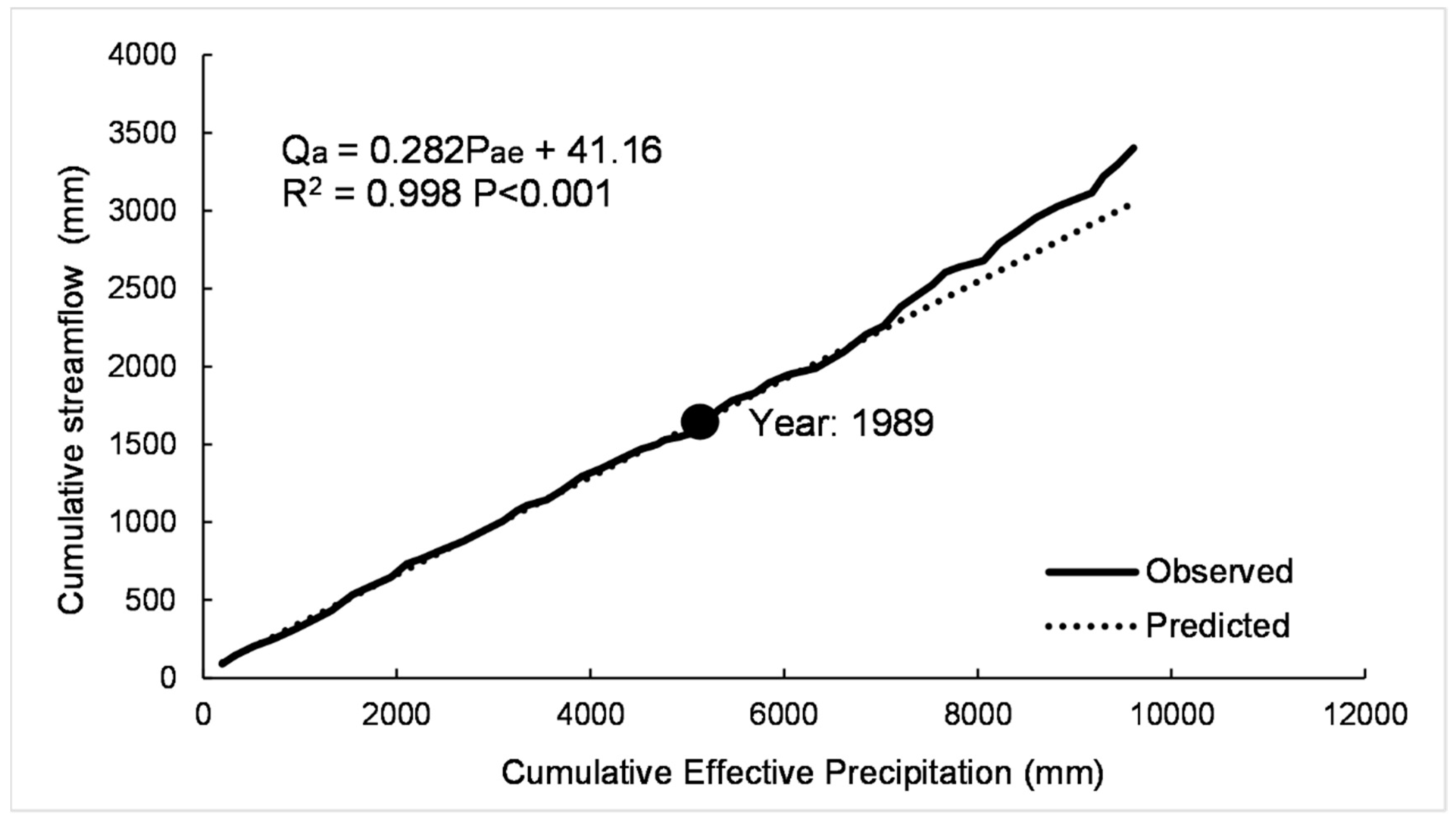
3.3.1. Modified Double Mass Curve
3.3.2. Sensitivity-Based Method
3.4. Separation of Effects Of Forest Disturbance and Climate Variability on High and Low Flows
4. Discussion
4.1. The Cumulative Effects of Forest Disturbance on Annual Mean Flow
4.2. Additive Effects of Cumulative Forest Disturbance and Climate Variability on Annual Mean Flow
4.3. The Cumulative Effects of Forest Disturbance on High and Low Flows
4.4. Management Implications
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Ellison, D.; Morris, C.E.; Locatelli, B.; Sheil, D.; Cohen, J.; Murdiyarso, D.; Gutierrez, V.; Noordwijk, M.V.; Creed, I.F.; Pokorny, J.; et al. Trees, forests and water: Cool insights for a hot world. Glob. Environ. Change 2017, 43, 51–61. [Google Scholar] [CrossRef] [Green Version]
- Wei, X.; Li, Q.; Zhang, M.; Giles-Hansen, K.; Liu, W.; Fan, H.; Wang, Y.; Zhou, G.; Piao, S.; Liu, S. Vegetation cover—Another dominant factor in determining global water resources in forested regions. Glob. Change Biol. 2018, 24, 786–795. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.; Liu, W.; Zhou, P. Quantifying the Relative Contributions of Forest Change and Climatic Variability to Hydrology in Large Watersheds: A Critical Review of Research Methods. Water 2013, 5, 728–746. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Liu, N.; Harper, R.; Li, Q.; Liu, K.; Wei, X.; Ning, D.; Hou, Y.; Liu, S. A global review on hydrological responses to forest change across multiple spatial scales: Importance of scale, climate, forest type and hydrological regime. J. Hydrol. 2017, 546, 44–59. [Google Scholar] [CrossRef]
- Zhang, L.; Hickel, K.; Shao, Q. Predicting afforestation impacts on monthly streamflow using the DWBM model. Ecohydrology 2016. [Google Scholar] [CrossRef]
- Ford, C.R.; Laseter, S.H.; Swank, W.T.; Vose, J.M. Can forest management be used to sustain water-based ecosystem services in the face of climate change? Ecol. Appl. 2011, 21, 2049–2067. [Google Scholar] [CrossRef] [PubMed]
- Kelly, C.N.; McGuire, K.J.; Miniat, C.F.; Vose, J.M. Streamflow response to increasing precipitation extremes altered by forest management. Geophys. Res. Lett. 2016, 43, 3727–3736. [Google Scholar] [CrossRef] [Green Version]
- Winkler, R.; Spittlehouse, D.; Boon, S. Streamflow Response to Clearcut Logging on British Columbia’s Okanagan Plateau. Ecohydrology 2017. [Google Scholar] [CrossRef]
- Li, Q.; Wei, X.; Zhang, M.; Liu, W.; Fan, H.; Zhou, G.; Giles-Hansen, K.; Liu, S.; Wang, Y. Forest cover change and water yield in large forested watersheds: A global synthetic assessment. Ecohydrology 2017, 10. [Google Scholar] [CrossRef]
- Bosch, J.M.; Hewlett, J.D. A review of catchment experiments to determine the effect of vegetation changes on water yield and evapotranspiration. J. Hydrol. 1982, 55, 3–23. [Google Scholar] [CrossRef]
- Brown, A.E.; Zhang, L.; McMahon, T.A.; Wes tern, A.W.; Vertessy, R.A. A review of paired catchment studies for determining changes in water yield resulting from alterations in vegetation. J. Hydrol. 2005, 310, 28–61. [Google Scholar] [CrossRef]
- Forest and Water on a Changing Planet:Vulnerability, Adaptation and Governance Opportunities. A Global Assessment Report. In Proceedings of the IUFRO World Series, Vienna, Austria, 10 July 2018; p. 192.
- Dey, P.; Mishra, A. Separating the impacts of climate change and human activities on streamflow: A review of methodologies and critical assumptions. J. Hydrol. 2017, 548, 278–290. [Google Scholar] [CrossRef]
- Liu, W.; Wei, X.; Li, Q.; Fan, H.; Duan, H.; Wu, J.; Giles-Hansen, K.; Zhang, H. Hydrological recovery in two large forested watersheds of southeastern China: The importance of watershed properties in determining hydrological responses to reforestation. Hydrol. Earth Syst. Sci. 2016, 20, 4747–4756. [Google Scholar] [CrossRef]
- Ruiz-Perez, G.; Koch, J.; Manfreda, S.; Caylor, K.; Frances, F. Calibration of a parsimonious distributed ecohydrological daily model in a data scarce basin using exclusively the spatio-temporal variation of NDVI. Hydrol. Earth System Sci. 2017, 21, 6235–6251. [Google Scholar] [CrossRef]
- Mikkelson, K.M.; Maxwell, R.M.; Ferguson, I.; Stednick, J.D.; McCray, J.E.; Sharp, J.O. Mountain pine beetle infestation impacts: modeling water and energy budgets at the hill-slope scale. Ecohydrology 2013, 6, 64–72. [Google Scholar] [CrossRef]
- Penn, C.A.; Bearup, L.A.; Maxwell, R.M.; Clow, D.W. Numerical experiments to explain multiscale hydrological responses to mountain pine beetle tree mortality in a headwater watershed. Water Resour. Res. 2016, 52, 3143–3161. [Google Scholar] [CrossRef] [Green Version]
- Schnorbus, M.; Bennett, K.; Werner, A. Quantifying the water resource impacts of mountain pine beetle and associated salvage harvest operations across a range of watershed scales: Hydrologic modelling of the Fraser River Basin. In Information Report BC-X-423; Natural Resources Canada, Canadian Forest Service, Pacific Forestry Centre: Victoria, BC, Canada, 2010. [Google Scholar]
- White, J.C.; Wulder, M.A.; Hermosilla, T.; Coops, N.C.; Hobart, G.W. A nationwide annual characterization of 25years of forest disturbance and recovery for Canada using Landsat time series. Remote Sens. Environ. 2017, 194, 303–321. [Google Scholar] [CrossRef]
- Reid, L.M. Cumulative watershed effects and watershed analysis. In River Ecology and Management: Lessons from the Pacific Coastal Ecoregion; Naiman, R.J., Bilby, R.E., Eds.; Springer: New York, NY, USA, 1998; pp. 476–501. [Google Scholar]
- Schindler, D.W.; Donahue, W.F. An impending water crisis in Canada’s western prairie provinces. Proc. Natl. Acad. Sci. USA 2006, 103, 7210. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.; Zhang, M. Quantifying streamflow change caused by forest disturbance at a large spatial scale: A single watershed study. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Wei, X. Contrasted hydrological responses to forest harvesting in two large neighbouring watersheds in snow hydrology dominant environment: implications for forest management and future forest hydrology studies. Hydrol. Process. 2014, 28, 6183–6195. [Google Scholar] [CrossRef]
- Winkler, R.; Boon, S. Revised Snow Recovery Estimates for Pine-dominated Forests in Interior British Columbia; Extension note 116; Ministry of Forests, Lands and Natural Resource Operations: Kamloops, BC, Canada, 2015.
- Winkler, R.D.; Moore, R.D.; Redding, T.E.; Spittlehouse, D.L.; Smerdon, B.D.; Carlyle-Moses, D.E. The Effects of Forest Disturbance on Hydrologic Processes and Watershed Response (Chapter 7). In Compendium of Forest Hydrology and Geomorphology in British Columbia; British Columbia: Victoria, BC, Canada, 2010. [Google Scholar]
- Moore, D.R.; Wondzell, S.M. Physical Hydrology and the Effects of Forest Harvesting in the Pacific Northwest: A Review. JAWRA 2005, 41, 763–784. [Google Scholar] [CrossRef]
- British Columbia Ministry of Forests. Forest Practices Code of British Columbia. In Coastal Watershed Assessment Procedure Guidebook (CWAP) and Interior Watershed Assessment Procedure Guidebook (IWAP); British Columbia Ministry of Forests: Victoria, BC, Canada, 1999. [Google Scholar]
- Jones, J.A.; Perkins, R.M. Extreme flood sensitivity to snow and forest harvest, western Cascades, Oregon, United States. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Wei, X. Alteration of flow regimes caused by large-scale forest disturbance: a case study from a large watershed in the interior of British Columbia, Canada. Ecohydrology 2014, 7, 544–556. [Google Scholar] [CrossRef]
- Liu, W.; Wei, X.; Liu, S.; Liu, Y.; Fan, H.; Zhang, M.; Yin, J.; Zhan, M. How do climate and forest changes affect long-term streamflow dynamics? A case study in the upper reach of Poyang River basin. Ecohydrology 2015, 8, 46–57. [Google Scholar] [CrossRef]
- Bruijnzeel, L.A. Hydrological functions of tropical forests: not seeing the soil for the trees? Agric. Ecosyst. Environ. 2004, 104, 185–228. [Google Scholar] [CrossRef]
- Ecoscape Environmental Consultants Ltd. Deadman River Sensitive Habitat Inventory and Mapping (SHIM)-2009–2011; Inventory Summary Report; Skeetchestn Indian Band: Kelowna, BC, Canada, 2012; p. 28. [Google Scholar]
- Walton, A. Provincial-Level Projection of the Current Mountain Pine Beetle Outbreak: Update of the Infestation Projection Based on the Provincial Aerial Overview Surveys of Forest Health Conducted from 1999 through 2012 and the BCMPB Model (Year 10). BC Forest Service, 2013. Available online: https://www.google.com.sg/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=2ahUKEwjPw-Tvn8zgAhWDLqYKHdg5AnIQFjAAegQIARAC&url=https%3A%2F%2Fwww.for.gov.bc.ca%2Fftp%2Fhre%2Fexternal%2F!publish%2Fweb%2Fbcmpb%2Fyear10%2FBCMPB.v10.BeetleProjection.Update.pdf&usg=AOvVaw1l11YYPl_TOX7qhgj15tq1 (accessed on 11 January 2019).
- Wang, T.; Hamann, A.; Spittlehouse, D.; Carroll, C. Locally Downscaled and Spatially Customizable Climate Data for Historical and Future Periods for North America. PLoS ONE 2016, 11, e0156720. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Wei, X.; Li, Q. A quantitative assessment on the response of flow regimes to cumulative forest disturbances in large snow-dominated watersheds in the interior of British Columbia, Canada. Ecohydrology 2016, 9, 843–859. [Google Scholar] [CrossRef]
- Li, Q.; Wei, X.; Zhang, M.; Liu, W.; Giles-Hansen, K.; Wang, Y. The cumulative effects of forest disturbance and climate variability on streamflow components in a large forest-dominated watershed. J. Hydrol. 2018, 557, 448–459. [Google Scholar] [CrossRef]
- Lewis, D.; Huggard, D. A Model to Quantify Effects of Mountain Pine Beetle on Equivalent Clearcut Area. Streamline Watershed Manag. Bull. 2010, 13, 42–51. [Google Scholar]
- Axelson, J.N.; Alfaro, R.I.; Hawkes, B.C. Influence of fire and mountain pine beetle on the dynamics of lodgepole pine stands in British Columbia, Canada. For. Ecol. Manage. 2009, 257, 1874–1882. [Google Scholar] [CrossRef]
- Baker, E.H.; Painter, T.H.; Schneider, D.; Meddens, A.J.H.; Hicke, J.A.; Molotch, N.P. Quantifying insect-related forest mortality with the remote sensing of snow. Remote Sens. Environ. 2017, 188, 26–36. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Hyndman, R.J.; Khandakar, Y. Automatic time series forecasting: the forecast package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef]
- Liu, W.; Wei, X.; Fan, H.; Guo, X.; Liu, Y.; Zhang, M.; Li, Q. Response of flow regimes to deforestation and reforestation in a rain-dominated large watershed of subtropical China. Hydrol. Process. 2015, 29, 5003–5015. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Oxford University Press: New York, NY, USA, 1975; p. 202. [Google Scholar]
- Déry, S.J.; Wood, E.F. Decreasing river discharge in northern Canada. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Razavi, S.; Vogel, R. Prewhitening of hydroclimatic time series? Implications for inferred change and variability across time scales. J. Hydrol. 2018, 557, 109–115. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–82. [Google Scholar] [CrossRef]
- Hamon, W.R. Computation of Direct Runoff Amounts From Storm Rainfall. IAHS 1963, 63, 52–62. [Google Scholar]
- Lu, J.; Sun, G.; McNulty, S.G.; Amatya, D. A comparison of six potential evapotranspiration methods for regional use in the Southeastern United States. JAWRA 2005, 41, 621–633. [Google Scholar] [CrossRef]
- McMahon, T.A.; Peel, M.C.; Lowe, L.; Srikanthan, R.; McVicar, T.R. Estimating actual, potential, reference crop and pan evaporation using standard meteorological data: a pragmatic synthesis. Hydrol. Earth Syst. Sci. 2013, 17, 1331–1363. [Google Scholar] [CrossRef]
- Budyko, M.I. Climate and Life; Academic Press: London, UK, 1974; Volume 18. [Google Scholar]
- Zhang, L.; Hickel, K.; Dawes, W.R.; Chiew, F.H.S.; Western, A.W.; Briggs, P.R. A rational function approach for estimating mean annual evapotranspiration. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Cai, T.; Wei, X.; Zhang, M.; Ju, C. Effect of forest recovery on summer streamflow in small forested watersheds, Northeastern China. Hydrol. Process. 2012, 26, 1208–1214. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Li, Y.; Piao, S.; Li, L.Z.X.; Chen, A.; Wang, X.; Ciais, P.; Huang, L.; Lian, X.; Peng, S.; Zeng, Z.; et al. Divergent hydrological response to large-scale afforestation and vegetation greening in China. Sci. Adv. 2018, 4. [Google Scholar] [CrossRef] [PubMed]
- Koster, R.D.; Suarez, M.J. A Simple Framework for Examining the Interannual Variability of Land Surface Moisture Fluxes. J. Climate 1999, 12, 1911–1917. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Dunne, K.A. Macroscale water fluxes 1. Quantifying errors in the estimation of basin mean precipitation. Water Resour. Res. 2002, 38, 1–14. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G.; Lombardo, F. Untenable nonstationarity: An assessment of the fitness for purpose of trend tests in hydrology. Adv. Water Resour. 2018, 111, 132–155. [Google Scholar] [CrossRef]
- Mikkelson, K.M.; Bearup, L.A.; Maxwell, R.M.; Stednick, J.D.; McCray, J.E.; Sharp, J.O. Bark beetle infestation impacts on nutrient cycling, water quality and interdependent hydrological effects. Biogeochemistry 2013, 115, 1–21. [Google Scholar] [CrossRef]
- Zhang, M.; Wei, X.; Li, Q. Do the hydrological responses to forest disturbances in large watersheds vary along climatic gradients in the interior of British Columbia, Canada? Ecohydrology 2017, 10, e1840. [Google Scholar] [CrossRef]
- Berghuijs Wouter, R.; Larsen Joshua, R.; van Emmerik Tim, H.M.; Woods Ross, A. A Global Assessment of Runoff Sensitivity to Changes in Precipitation, Potential Evaporation, and Other Factors. Water Resour. Res. 2017, 53, 8475–8486. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M. The effects of cumulative forest disturbances on hydrology in the interior of British Columbia, Canada. Ph.D. Thesis, The University of British Columbia (Okanagan), Kelowna, BC, Canada, June 2013. [Google Scholar]
- Zhang, M.; Wei, X.; Sun, P.; Liu, S. The effect of forest harvesting and climatic variability on runoff in a large watershed: The case study in the Upper Minjiang River of Yangtze River basin. J. Hydrol. 2012, 464–465, 1–11. [Google Scholar] [CrossRef]
- Zhang, M.; Wei, X. The effects of cumulative forest disturbance on streamflow in a large watershed in the central interior of British Columbia, Canada. HESS 2012, 16, 2021–2034. [Google Scholar] [CrossRef] [Green Version]
- Roa-García, M.C.; Brown, S.; Schreier, H.; Lavkulich, L.M. The role of land use and soils in regulating water flow in small headwater catchments of the Andes. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Clark, K.L.; Skowronski, N.; Gallagher, M.; Renninger, H.; Schäfer, K. Effects of invasive insects and fire on forest energy exchange and evapotranspiration in the New Jersey pinelands. Agric. For. Meteorol. 2012, 166–167, 50–61. [Google Scholar] [CrossRef]
- Du, E.; Link, T.E.; Wei, L.; Marshall, J.D. Evaluating hydrologic effects of spatial and temporal patterns of forest canopy change using numerical modelling. Hydrol. Process. 2016, 30, 217–231. [Google Scholar] [CrossRef]
- Buttle, J.M.; Metcalfe, R.A. Boreal forest disturbance and streamflow response, northeastern Ontario. Can. J. Fish. Aquat. Sci. 2000, 57, 5–18. [Google Scholar] [CrossRef] [Green Version]
- Wilk, J.; Andersson, L.; Plermkamon, V. Hydrological impacts of forest conversion to agriculture in a large river basin in northeast Thailand. Hydrol. Process. 2001, 15, 2729–2748. [Google Scholar] [CrossRef]
- Chen, W.; Wei, X. Assessing the relations between aquatic habitat indicators and forest harvesting at watershed scale in the interior of British Columbia. For. Ecol. Manage. 2008, 256, 152–160. [Google Scholar] [CrossRef]
- Stednick, J.D. Monitoring the effects of timber harvest on annual water yield. J. Hydrol. 1996, 176, 79–95. [Google Scholar] [CrossRef]
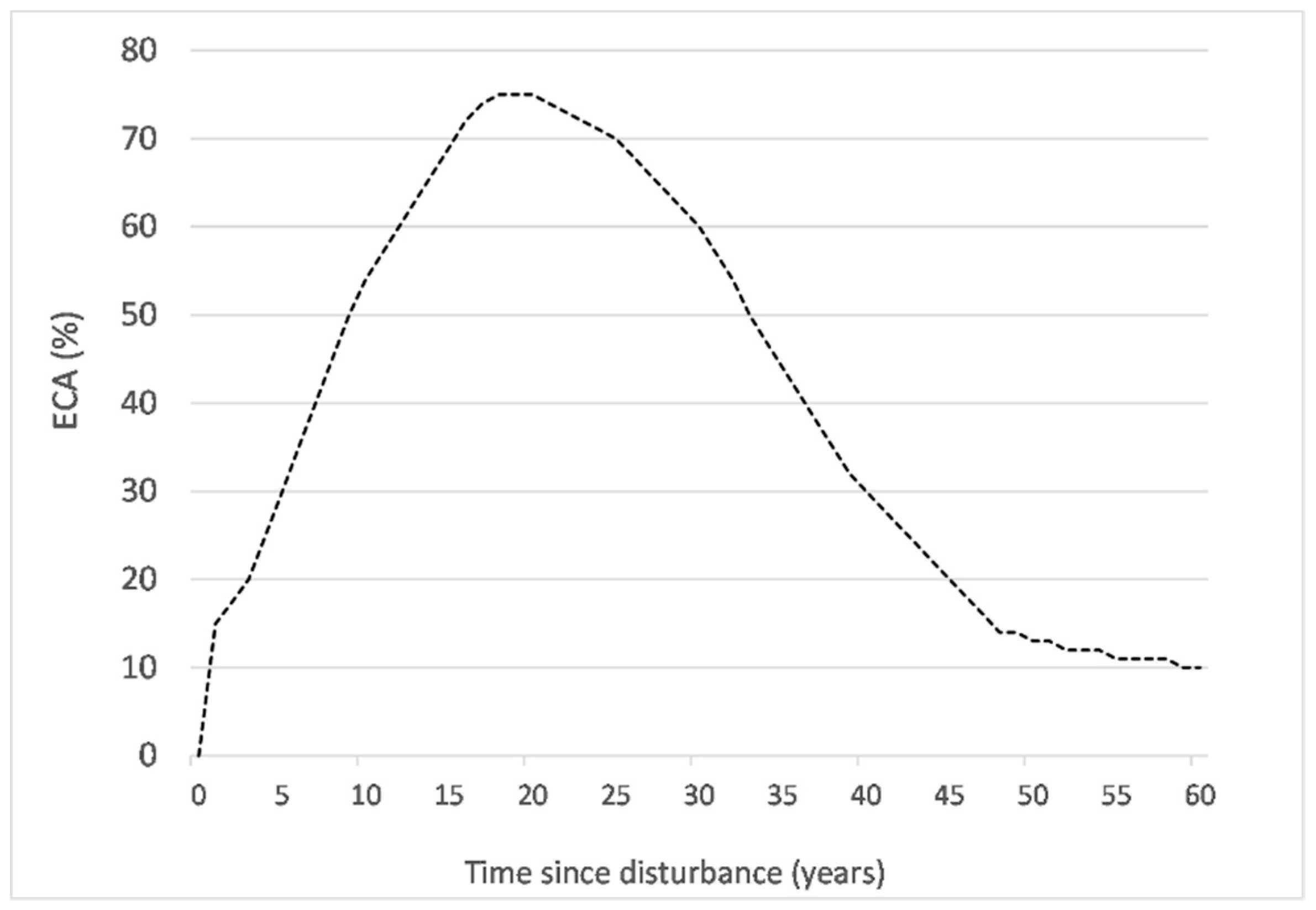
| Height (m) | Hydrologic Recovery (%) | ECA (%) |
|---|---|---|
| 0 ≤ 3 | 0 | 100 |
| 3 ≤ 5 | 25 | 75 |
| 5 ≤ 7 | 50 | 50 |
| 7 ≤ 9 | 75 | 25 |
| >9 | 90 | 10 |
| Season | Tmax | Tmin | Tmean | P | PET | AET | Q5% | Q95% | Qmean | |
|---|---|---|---|---|---|---|---|---|---|---|
| Annual | tau | 0.19 | 0.25 | 0.23 | −0.02 | 0.25 | 0.06 | –0.04 | 0.24 | 0.01 |
| p-value | 0.05 | 0.01 | 0.01 | 0.87 | 0.01 | 0.55 | 0.73 | 0.02 | 0.95 | |
| Spring | tau | 0.08 | 0.18 | 0.15 | 0.21 | 0.17 | 0.25 | –0.01 | 0.05 | –0.06 |
| p-value | 0.41 | 0.05 | 0.11 | 0.02 | 0.08 | 0.01 | 0.91 | 0.59 | 0.55 | |
| Summer | tau | 0.09 | 0.25 | 0.13 | 0.04 | 0.16 | 0.08 | –0.08 | 0.11 | –0.01 |
| p-value | 0.35 | 0.01 | 0.17 | 0.68 | 0.09 | 0.42 | 0.45 | 0.29 | 0.96 | |
| Autumn | tau | 0.16 | 0.04 | 0.06 | 0.05 | 0.10 | 0.05 | 0.06 | 0.26 | 0.23 |
| p-value | 0.08 | 0.71 | 0.50 | 0.60 | 0.27 | 0.57 | 0.54 | 0.01 | 0.02 | |
| Winter | tau | 0.13 | 0.15 | 0.12 | –0.07 | 0.11 | 0.10 | 0.13 | 0.21 | 0.14 |
| p-value | 0.15 | 0.10 | 0.20 | 0.47 | 0.24 | 0.27 | 0.20 | 0.04 | 0.15 |
| Hydrological Variables | Cross-Correlation with CECA (Pre-Whitened Using ARIMA (2, 2, 1)) | ||
|---|---|---|---|
| ARIMA Model Used to Pre-Whiten | Coefficients | Lag | |
| Annual mean flow (Q) | (1, 3, 0) | 0.32 | 8 |
| High flow (Q5%) | (0, 1, 1) | 0.33 | 8 |
| Low flow (Q95%) | (0, 1, 2) | 0.32 | 4 |
| Method | Selected Periods | ∆Q (mm) | ∆Qf (mm) | ∆Qc (mm) | Rf (%) | Rc (%) | CECA (%) |
|---|---|---|---|---|---|---|---|
| MDMC | 1990–1994 | 17.53 | 13.71 | 3.82 | 78.23 | 21.77 | 14.56 |
| 1995–1999 | 30.53 | 14.23 | 16.30 | 46.62 | 53.38 | 17.32 | |
| 2000–2004 | 3.02 | 4.63 | −1.61 | 74.18 | 25.82 | 18.21 | |
| 2005–2009 | 21.57 | 19.71 | 1.85 | 91.40 | 8.60 | 32.43 | |
| 2010–2012 | 27.12 | 34.20 | −7.08 | 82.85 | 17.15 | 51.67 | |
| 1990–2012 | 19.95 | 16.59 | 2.66 | 86.20 | 13.80 | 24.68 | |
| Sensitivity-based method | 1990–2012 | 19.65 | 10.75 | 8.90 | 54.70 | 45.30 | 24.68 |
| Flow (m3s−1) | Q5% | Q95% |
|---|---|---|
| Reference | 8.07 | 0.26 |
| Disturbance | 12.74 | 0.31 |
| Change (m3s−1) | 4.67 | 0.05 |
| Change (%) | 58% | 19% |
| p-value | <0.001 | <0.001 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giles-Hansen, K.; Li, Q.; Wei, X. The Cumulative Effects of Forest Disturbance and Climate Variability on Streamflow in the Deadman River Watershed. Forests 2019, 10, 196. https://doi.org/10.3390/f10020196
Giles-Hansen K, Li Q, Wei X. The Cumulative Effects of Forest Disturbance and Climate Variability on Streamflow in the Deadman River Watershed. Forests. 2019; 10(2):196. https://doi.org/10.3390/f10020196
Chicago/Turabian StyleGiles-Hansen, Krysta, Qiang Li, and Xiaohua Wei. 2019. "The Cumulative Effects of Forest Disturbance and Climate Variability on Streamflow in the Deadman River Watershed" Forests 10, no. 2: 196. https://doi.org/10.3390/f10020196
APA StyleGiles-Hansen, K., Li, Q., & Wei, X. (2019). The Cumulative Effects of Forest Disturbance and Climate Variability on Streamflow in the Deadman River Watershed. Forests, 10(2), 196. https://doi.org/10.3390/f10020196





