Response of Four Tree Species to Changing Climate in a Moisture-Limited Area of South Siberia
Abstract
1. Introduction
2. Materials and Methods
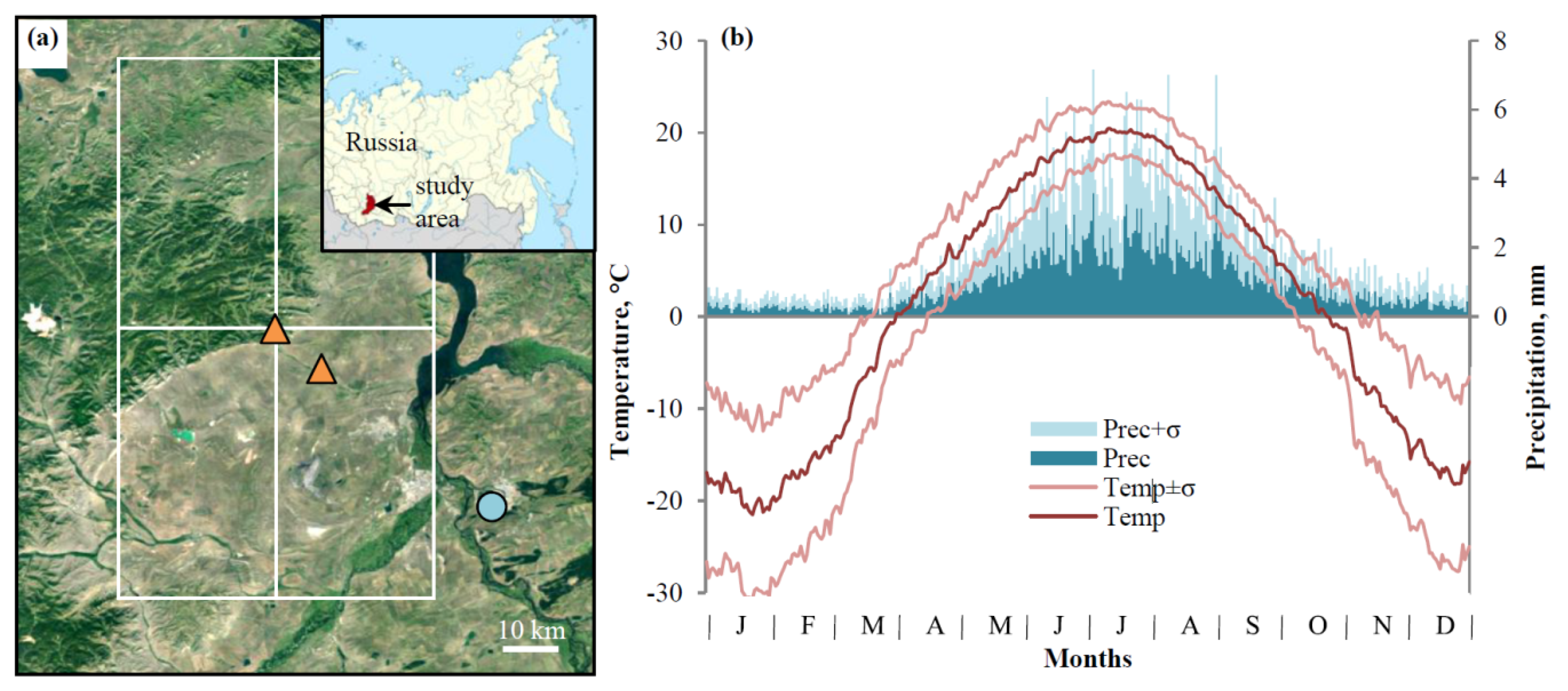
2.1. Study Area and Sampling Sites
2.2. Climatic Data
2.3. Dendrochronological Data
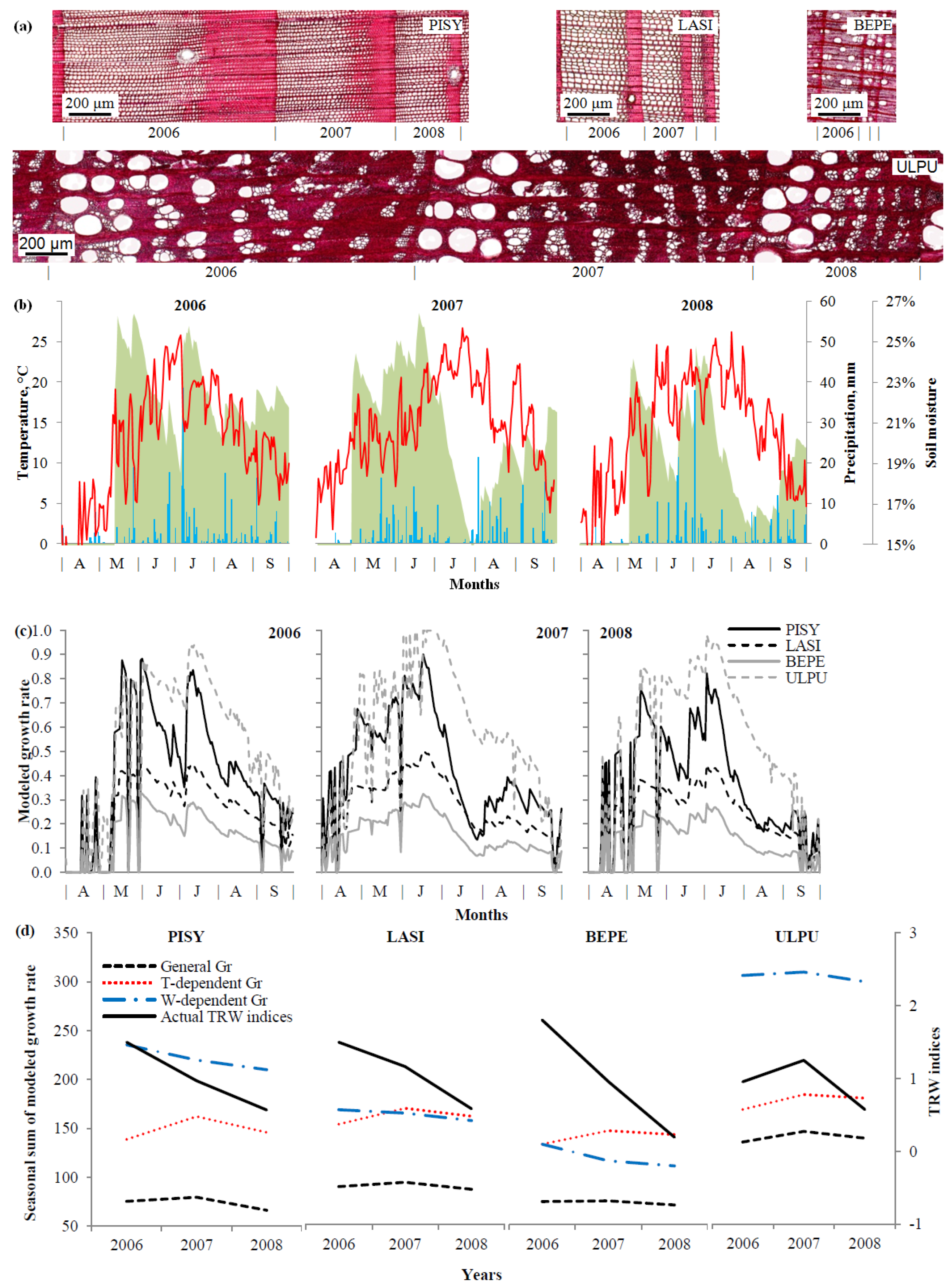
2.4. Tree-Ring Formation Modeling
3. Results
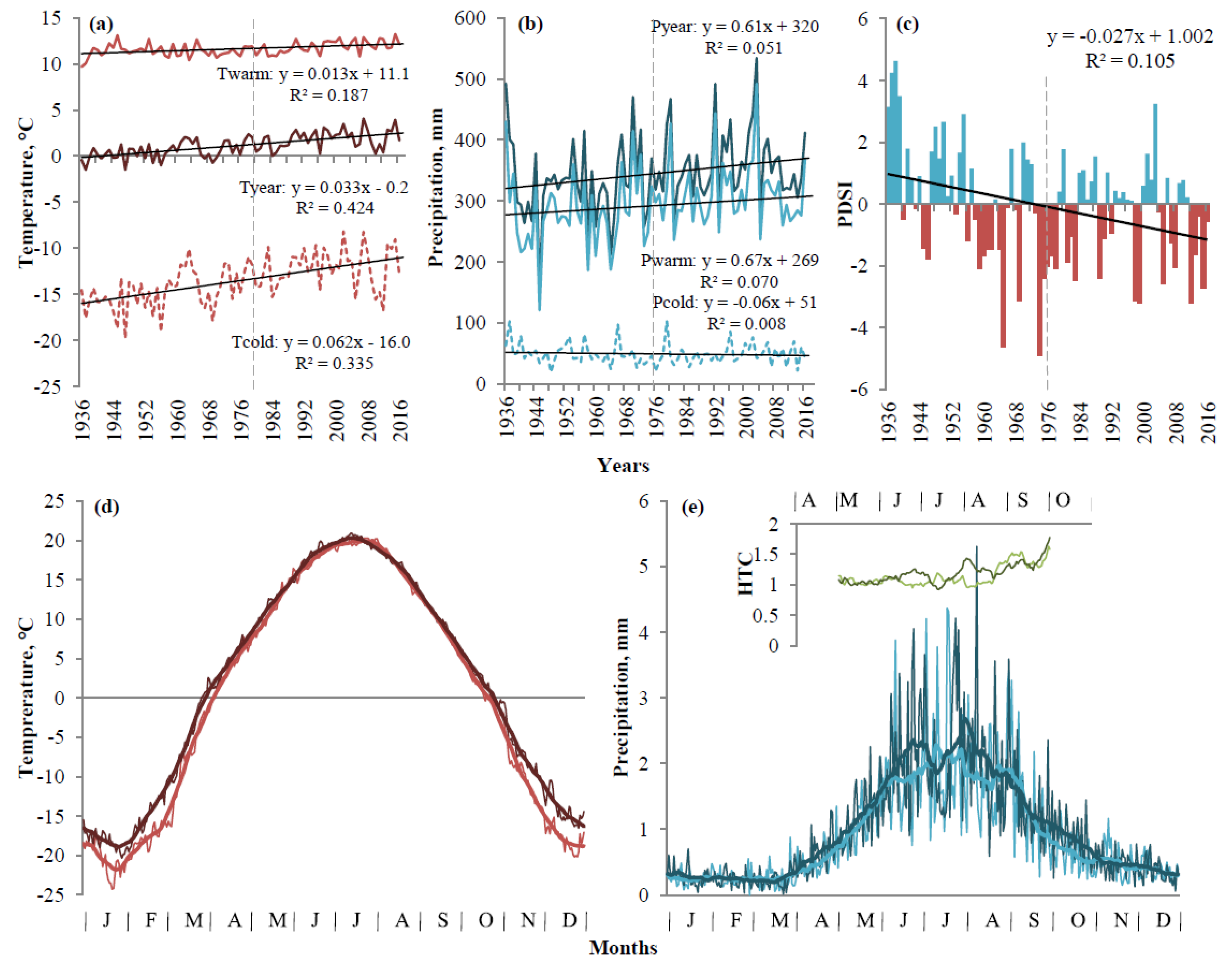
3.1. Regional Climate Change
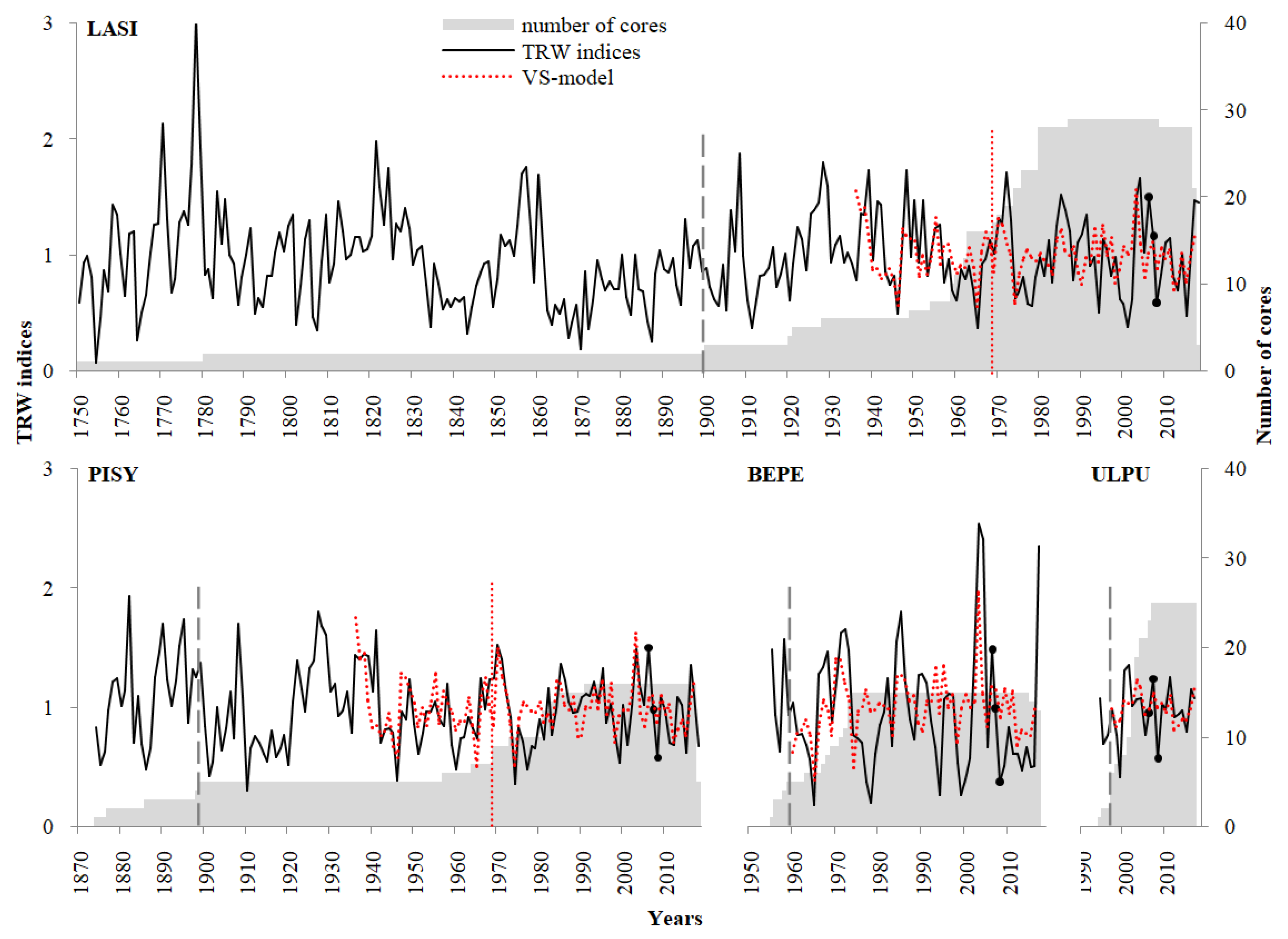
3.2. Tree-Ring Width Chronologies
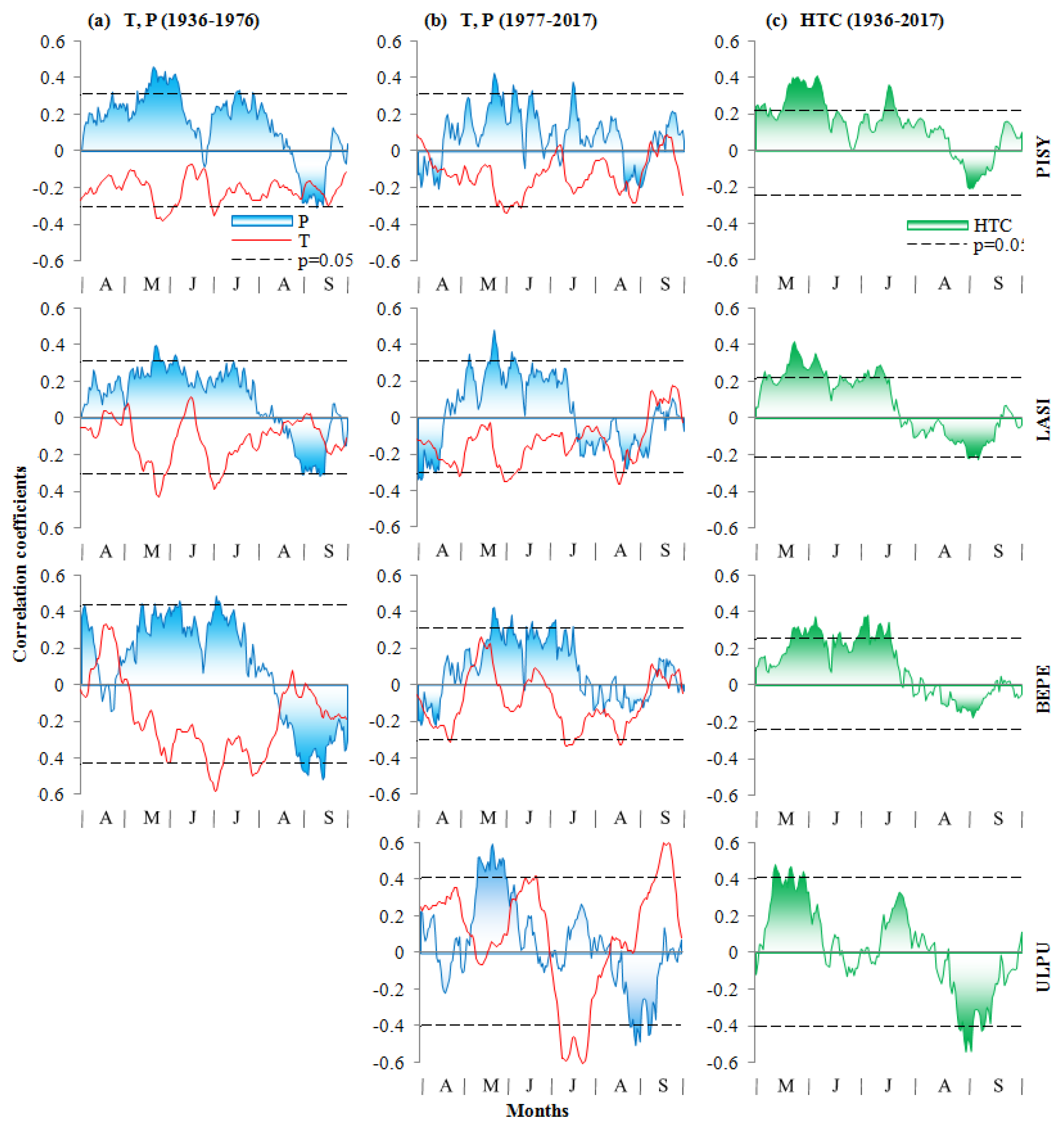
3.3. Climate–Growth Relationships
3.4. Growth Modeling
4. Discussion
4.1. Growth Patterns of Considered Species
4.2. Climatic Response and Growth Modeling of Trees
4.3. Prospects of Tree Stands Dynamics Under Climate Change
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dai, A.; Trenberth, K.E.; Karl, T.R. Global variations in droughts and wet spells: 1900–1995. Geophys. Res. Lett. 1998, 25, 3367–3370. [Google Scholar] [CrossRef]
- Dulamsuren, C.; Khishigjargal, M.; Leuschner, C.; Hauck, M. Response of tree-ring width to climate warming and selective logging in larch forests of the Mongolian Altai. J. Plant Ecol. 2014, 7, 24–38. [Google Scholar] [CrossRef]
- Flanagan, P.X.; Basara, J.B.; Xiao, X. Long-term analysis of the asynchronicity between temperature and precipitation maxima in the United States Great Plains. Int. J. Climatol. 2017, 37, 3919–3933. [Google Scholar] [CrossRef]
- Rogers, J.C.; Mosely-Thompson, E. Atlantic Arctic cyclones and mild Siberian winters of the 1980s. Geophys. Res. Lett. 1995, 22, 799–802. [Google Scholar] [CrossRef]
- Savelieva, N.I.; Semiletov, I.P.; Vasilevskaya, L.N.; Pugach, S.P. A climate shift in seasonal values of meteorological and hydrological parameters for Northeastern Asia. Prog. Oceanogr. 2000, 47, 279–297. [Google Scholar] [CrossRef]
- Davi, N.K.; Jacoby, G.C.; Curtis, A.E.; Baatarbileg, N. Extension of drought records for central Asia using tree rings: West-central Mongolia. J. Clim. 2006, 19, 288–299. [Google Scholar] [CrossRef]
- IPCC Climate Change. The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK, 2013; p. 1535. [Google Scholar]
- Kattsov, V.M.; Semenov, S.M. (Eds.) Second Roshydromet Assessment Report on Climate Change and Its Consequences in Russian Federation; Roshydromet: Moscow, Russia, 2014; p. 54. [Google Scholar]
- Liu, X.; Pan, Y.; Zhu, X.; Yang, T.; Bai, J.; Sun, Z. Drought evolution and its impact on the crop yield in the North China Plain. J. Hydrol. 2018, 564, 984–996. [Google Scholar] [CrossRef]
- Liu, H.; Park Williams, A.; Allen, C.D.; Guo, D.; Wu, X.; Anenkhonov, O.A.; Liang, E.; Sandanov, D.V.; Yin, Y.; Qi, Z.; et al. Rapid warming accelerates tree growth decline in semi-arid forests of Inner Asia. Glob. Chang. Biol. 2013, 19, 2500–2510. [Google Scholar] [CrossRef]
- McDowell, N.; Pockman, W.T.; Allen, C.D.; Breshears, D.D.; Cobb, N.; Kolb, T.; Plaut, J.; Sperry, J.; West, A.; Williams, D.G.; et al. Mechanisms of plant survival and mortality during drought: Why do some plants survive while others succumb to drought? N. Phytol. 2008, 178, 719–739. [Google Scholar] [CrossRef]
- Carnicer, J.; Barbeta, A.; Sperlich, D.; Coll, M.; Peñuelas, J. Contrasting trait syndromes in angiosperms and conifers are associated with different responses of tree growth to temperature on a large scale. Front. Plant Sci. 2013, 4, 409. [Google Scholar] [CrossRef]
- Matheny, A.M.; Bohrer, G.; Garrity, S.R.; Morin, T.H.; Howard, C.J.; Vogel, C.S. Observations of stem water storage in trees of opposing hydraulic strategies. Ecosph. 2015, 6, 1–13. [Google Scholar] [CrossRef]
- Hu, G.; Liu, H.; Shangguan, H.; Wu, X.; Xu, X.; Williams, M. The role of heartwood water storage for semi-arid trees under drought. Agric. For. Meteorol. 2018, 256–257, 534–541. [Google Scholar] [CrossRef]
- Piper, F.I.; Fajardo, A. Foliar habit, tolerance to defoliation and their link to carbon and nitrogen storage. J. Ecol. 2014, 102, 1101–1111. [Google Scholar] [CrossRef]
- Nazimova, D.I.; Polikarpov, N.P. Forest zones of Siberia as determined by climatic zones and their possible transformation trends under global change. Silva Fenn. 1996, 30, 201–208. [Google Scholar] [CrossRef][Green Version]
- Babushkina, E.A.; Belokopytova, L.V.; Zhirnova, D.F.; Shah, S.K.; Kostyakova, T.V. Climatically driven yield variability of major crops in Khakassia (South Siberia). Int. J. Biometeorol. 2018, 62, 939–948. [Google Scholar] [CrossRef]
- Wang, C.W. The Forests of China, with a Survey of Grassland and Desert Vegetation; Harvard University: Cambridge, UK, 1961. [Google Scholar]
- Wesche, K.; Walther, D.; VonWehrden, H.; Hensen, I. Trees in the desert: Reproduction and genetic structure of fragmented Ulmus pumila forests in Mongolian drylands. Flora Morphol. Distrib. Funct. Ecol. Plants 2011, 206, 91–99. [Google Scholar] [CrossRef]
- Mamyshev, K.V. Biology and morphological characteristics of Ulmus pumila L. in the system of belts Uybat steppe. Theor. Appl. Sci. 2014, 3, 76–80. [Google Scholar] [CrossRef]
- Fritts, H.C. Tree Rings and Climate; Academic Press: London, UK, 1976. [Google Scholar]
- Vaganov, E.A.; Hughes, M.K.; Shashkin, A.V. Growth Dynamics of Conifer Tree Rings: Images of Past and Future; Springer: Berlin, Germany, 2006. [Google Scholar]
- Cook, E.R.; Kairiukstis, L.A. Methods of Dendrochronology: Applications in the Environmental Sciences; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1990. [Google Scholar] [CrossRef]
- Hughes, M.K.; Swetnam, T.W.; Diaz, H.F. (Eds.) Dendroclimatology: Progress and Prospects; Springer: New York, NY, USA, 2010. [Google Scholar]
- Misson, L. MAIDEN: A model for analyzing ecosystem processes in dendroecology. Can. J. For. Res. 2004, 34, 874–887. [Google Scholar] [CrossRef][Green Version]
- Dufrene, E.; Davi, H.; Francois, C.; le Maire, G.; Le Dantec, V.; Granier, A. Modelling carbon and water cycles in a beech forest. Part I: Model description and uncertainty analysis on modelled NEE. Ecol. Modell. 2005, 185, 407–436. [Google Scholar] [CrossRef]
- Buckley, L.B.; Urban, M.C.; Angilletta, M.J.; Crozier, L.G.; Rissler, L.J.; Sears, M.W. Can mechanism inform species’ distribution models? Ecol. Lett. 2010, 13, 1041–1054. [Google Scholar] [CrossRef]
- Drew, D.M.; Downes, G.M.; Battaglia, M. CAMBIUM, a process-based model of daily xylem development in Eucalyptus. J. Theor. Biol. 2010, 264, 395–406. [Google Scholar] [CrossRef] [PubMed]
- Shishov, V.V.; Tychkov, I.I.; Popkova, M.I.; Ilyin, V.A.; Bryukhanova, M.V.; Kirdyanov, A.V. VS-oscilloscope: A new tool to parameterize tree radial growth based on climate conditions. Dendrochronologia 2016, 39, 42–50. [Google Scholar] [CrossRef]
- Tychkov, I.I.; Sviderskaya, I.V.; Babushkina, E.A.; Popkova, M.I.; Vaganov, E.A.; Shishov, V.V. How can the parameterization of a process-based model help us understand real tree-ring growth? Trees 2019, 33, 345–357. [Google Scholar] [CrossRef]
- Liang, W.; Heinrich, I.; Simard, S.; Helle, G.; Dorado Linan, I.; Heinken, T. Climate signals derived from cell anatomy of Scots pine in NE Germany. Tree Physiol. 2013, 33, 833–844. [Google Scholar] [CrossRef] [PubMed]
- Carrer, M.; Castagneri, D.; Prendin, A.L.; Petit, G.; von Arx, G. Retrospective analysis of wood anatomical traits reveals a recent extension in tree cambial activity in two high-elevation conifers. Front. Plant Sci. 2017, 8, 737. [Google Scholar] [CrossRef] [PubMed]
- Lobanov, A.I.; Varaksin, G.S. Effect of seeding method and microtopography on vegetation and condition of Siberian elm stands in shelter forest belts of arid steppe zone of Khakassia. For. J. 2012, 2, 28–34. [Google Scholar]
- Shiyatov, S.G. Dendrochronology of the Higher Timberline on the Urals; Nauka: Moscow, Russia, 1986. [Google Scholar]
- Wigley, T.M.L.; Briffa, K.R.; Jones, P.D. On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. J. Appl. Meteorol. Climatol. 1984, 23, 201–213. [Google Scholar] [CrossRef]
- Alisov, B.P. Climate of the USSR; Moscow State University: Moscow, Russia, 1956. [Google Scholar]
- Bazhenova, O.I.; Tyumentseva, E.M. The structure of contemporary denudation in the steppes of the Minusinskaya depression. Geogr. Nat. Resour. 2010, 31, 362–369. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Babushkina, E.; Belokopytova, L.; Zhirnova, D.; Barabantsova, A.; Vaganov, E. Divergent growth trends and climatic response of Picea obovata along elevational gradient in Western Sayan Mountains, Siberia. J. Mt. Sci. 2018, 15, 2378–2397. [Google Scholar] [CrossRef]
- Selyaniniov, G.T. Principles of agroclimatic regional planning in USSR. In Questions of Agroclimatic Zoning of the USSR; Davitaya, F.F., Shulgina, A.I., Eds.; Ministry of Agriculture of the USSR: Moscow, Russia, 1958; pp. 18–26. [Google Scholar]
- Van der Schrier, G.; Barichivich, J.; Briffa, K.R.; Jones, P.D. A scPDSI-based global data set of dry and wet spells for 1901–2009. J. Geophys. Res. Atmos. 2013, 118, 4025–4048. [Google Scholar] [CrossRef]
- Cherenkova, E.A.; Zolotokrylin, A.N. On the comparability of some quantitative drought indices. Fundam. Appl. Climatol. 2016, 2, 79–94. [Google Scholar] [CrossRef]
- Rice, J.A. Mathematical Statistics and Data Analysis, 3rd ed.; Thomson/Brooks/Cole: Belmont, CA, USA, 2007. [Google Scholar]
- Rinn, F. TSAP-Win: Time Series Analysis and Presentation for Dendrochronology and Related Applications: User Reference; RINNTECH: Heidelberg, Germany, 2003. [Google Scholar]
- Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree Ring Bull. 1983, 43, 68–78. [Google Scholar]
- Cook, E.R.; Krusic, P.J. Program ARSTAN: A Tree-Ring Standardization Program Based on Detrending and Autoregressive Time Series Modeling, with Interactive Graphics; Lamont-Doherty Earth Observatory, Columbia University: New York, NY, USA, 2005. [Google Scholar]
- Vaganov, E.A.; Anchukaitis, K.J.; Evans, M.N. How well understood are the processes that create dendroclimatic records? A mechanistic model of the climatic control on conifer tree-ring growth dynamics. In Dendroclimatology: Progress and Prospects; Hughes, M.K., Swetnam, T.W., Diaz, H.F., Eds.; Springer: New York, USA, 2011; pp. 37–75. [Google Scholar]
- Chetin, Y.I. Features of growth and drought tolerance of larch, pine, spruce and birch in cultures of the agroforestmeliorative zone of Western Siberia. In Works on Forestry of Siberia, Proceedings of the Conference on Rationalization of Siberian Forestry, Novosibirsk, Russia, 12–15 September 1957; AS USSR: Novosibirsk, Russia, 1958; Volume 4, pp. 328–338. [Google Scholar]
- Niinemets, Ü.; Valladares, F. Tolerance to shade, drought, and waterlogging of temperate Northern Hemisphere trees and shrubs. Ecol. Monogr. 2006, 76, 521–547. [Google Scholar] [CrossRef]
- Carrer, M.; Urbinati, C. Age-dependent tree-ring growth responses to climate in Larix decidua and Pinus cembra. Ecol. 2004, 85, 730–740. [Google Scholar] [CrossRef]
- Esper, J.; Niederer, R.; Bebi, P.; Frank, D. Climate signal age effects—Evidence from young and old trees in the Swiss Engadin. For. Ecol. Manag. 2008, 255, 3783–3789. [Google Scholar] [CrossRef]
- Dorado Linan, I.; Gutiérrez, E.; Heinrich, I.; Andreu-Hayles, L.; Muntán, E.; Campelo, F.; Helle, G. Age effects and climate response in trees: A multi-proxy tree-ring test in old-growth life stages. Eur. J. For. Res. 2012, 131, 933–944. [Google Scholar] [CrossRef]
- Kraus, C.; Zang, C.; Menzel, A. Elevational response in leaf and xylem phenology reveals different prolongation of growing period of common beech and Norway spruce under warming conditions in the Bavarian Alps. Eur. J. For. Res. 2016, 135, 1011–1023. [Google Scholar] [CrossRef]
- Babushkina, E.A.; Vaganov, E.A.; Belokopytova, L.V.; Shishov, V.V.; Grachev, A.M. Competitive strength effect in the climate response of Scots pine radial growth in south-central Siberia forest-steppe. Tree Ring Res. 2015, 71, 106–117. [Google Scholar] [CrossRef]
- Babushkina, E.A.; Belokopytova, L.V.; Shah, S.K.; Zhirnova, D.F. Past crops yield dynamics reconstruction from tree-ring chronologies in the forest-steppe zone based on low- and high-frequency components. Int. J. Biometeorol. 2018, 62, 861–871. [Google Scholar] [CrossRef]
- Ghelardini, L. Bud Burst Phenology, Dormancy Release and Susceptibility to Dutch Elm Disease in Elms (Ulmus spp.). Ph.D. Thesis, Swedish University of Agricultural Sciences, Uppsala, Sweden, 2007. [Google Scholar]
- Park, G.E.; Lee, D.K.; Kim, K.W.; Batkhuu, N.O.; Tsogtbaatar, J.; Zhu, J.J.; Jin, Y.; Park, P.S.; Hyun, J.O.; Kim, H.S. Morphological characteristics and water-use efficiency of Siberian elm trees (Ulmus pumila L.) within arid regions of northeast Asia. Forests 2016, 7, 280. [Google Scholar] [CrossRef]
- Tyree, M.T.; Zimmermann, M.H. Xylem Structure and the Ascent of Sap; Springer: Berlin, Germany, 2002. [Google Scholar]
- Solla, A.; Martín, J.A.; Corral, P.; Gil, L. Seasonal changes in wood formation of Ulmus pumila and U. minor and its relation with Dutch elm disease. N. Phytol. 2005, 166, 1025–1034. [Google Scholar] [CrossRef] [PubMed]
- Cochard, H.; Tyree, M.T. Xylem dysfunction in Quercus: Vessel sizes, tyloses, cavitation and seasonal changes in embolism. Tree Physiol. 1990, 6, 393–407. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, C.; Zhang, Q.; Quan, X. Heartwood and sapwood allometry of seven Chinese temperate tree species. Ann. For. Sci. 2010, 67, 410. [Google Scholar] [CrossRef]
- Millers, M. The proportion of heartwood in conifer (Pinus sylvestris L., Picea abies [L.] H. Karst.) trunks and its influence on trunk wood moisture. J. For. Sci. 2013, 59, 295–300. [Google Scholar] [CrossRef]
- Urli, M.; Porté, A.J.; Cochard, H.; Guengant, Y.; Burlett, R.; Delzon, S. Xylem embolism threshold for catastrophic hydraulic failure in angiosperm trees. Tree Physiol. 2013, 33, 672–683. [Google Scholar] [CrossRef]
- Ren, P.; Rossi, S.; Camarero, J.J.; Ellison, A.M.; Liang, E.; Peñuelas, J. Critical temperature and precipitation thresholds for the onset of xylogenesis of Juniperus przewalskii in a semi-arid area of the north-eastern Tibetan Plateau. Ann. Bot. 2017, 121, 617–624. [Google Scholar] [CrossRef]
- Swidrak, I.; Gruber, A.; Oberhuber, W. Xylem and phloem phenology in co-occurring conifers exposed to drought. Trees 2014, 28, 1161–1171. [Google Scholar] [CrossRef]

| Species | Coordinates | Sample | Chronology | Period of EPS > 0.85 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Latitude (N) | Longitude (E) | Altitude, m a.s.l. | Time Span, year | Length, year | Number of Trees/Cores | stdev | sens | r-bar | Time Span, year | Min Number of Trees | |
| Pinus sylvestris | 54°00′ | 90°59′ | 600–640 | 1874–2018 | 145 | 13/16 | 0.330 | 0.299 | 0.583 | 1899–2018 | 5 |
| Larix sibirica | 54°00′ | 90°59′ | 600–640 | 1750–2018 | 269 | 22/29 | 0.385 | 0.338 | 0.524 | 1900–2018 | 3 |
| Betula pendula | 54°00′ | 90°59′ | 600–640 | 1955–2017 | 63 | 15/15 | 0.518 | 0.432 | 0.532 | 1956–2017 | 3 |
| Ulmus pumila | 53°54′ | 91°11′ | ~310 | 1994–2017 | 24 | 18/30 | 0.229 | 0.294 | 0.563 | 1997–2017 | 6 |
| Species | Larix sibirica | Pinus sylvestris | Betula pendula |
|---|---|---|---|
| 1955–2017 (n = 63 years) | |||
| Pinus sylvestris | 0.677 * | ||
| Betula pendula | 0.781 * | 0.575 * | |
| 1994–2017 (n = 24 years) | |||
| Pinus sylvestris | 0.626 * | ||
| Betula pendula | 0.775 * | 0.563 * | |
| Ulmus pumila | 0.116 | 0.288 | 0.184 |
| Parameter | Description | Pinus sylvestris | Larix sibirica | Betula pendula | Ulmus pumila |
|---|---|---|---|---|---|
| Tmin | Minimum daily temperature (low threshold) for tree growth (°C) | 5 | 5 | 6 | 1 |
| Topt1 | Lower end of range of optimal daily temperatures for tree growth (°C) | 11 | 15 | 19 | 15 |
| Topt2 | Upper end of range of optimal daily temperatures for tree growth (°C) | 26 | 24 | 24 | 25 |
| Tmax | Maximum daily temperature (upper threshold) for tree growth, °C | 32 | 30 | 31 | 30 |
| Wmin | Minimum soil moisture (low threshold) for tree growth, calculated as a ratio of water volume to soil volume | 0.048 | 0.028 | 0.055 | 0.003 |
| Wopt1 | Lower end of range of the optimal soil moistures for tree growth (ratio) | 0.15 | 0.275 | 0.35 | 0.175 |
| Wopt2 | Upper end of range of the optimal soil moistures for tree growth (ratio) | 0.325 | 0.4 | 0.4 | 0.425 |
| Wmax | Maximum soil moisture (upper threshold) for tree growth (ratio) | 0.675 | 0.65 | 0.525 | 0.55 |
| Tbeg | Temperature sum for initiation of growth (°C) | 100 | 90 | 115 | 105 |
| tbeg | Time period for calculation of temperature sum (days) | 10 | 10 | 10 | 10 |
| lr | Depth of root system (mm) | 600 | 700 | 650 | 500 |
| Pmax | Maximum daily precipitation for saturated soil (mm/day) | 40 | 50 | 45 | 35 |
| C1 | Fraction of precipitation penetrating soil (not caught by crown; relative unit) | 0.5 | 0.5 | 0.44 | 0.4 |
| C2 | First coefficient for calculation of transpiration * (mm/day) | 0.25 | 0.21 | 0.16 | 0.12 |
| C3 | Second coefficient for calculation of transpiration (relative unit per °C) | 0.110 | 0.135 | 0.165 | 0.105 |
| Calibration period | 1970–2017 | 1970–2017 | 1960–2016 | 1997–2017 | |
| R | Correlation between model and actual series | 0.627 | 0.594 | 0.619 | 0.546 |
| R2 | Coefficient of determination | 0.394 | 0.352 | 0.383 | 0.298 |
| Synch | Synchronicity between model and actual series (%) | 72.9 | 72.3 | 64.9 | 76.2 |
| Verification period | 1936–1969 | 1936–1969 | |||
| R | Correlation between model and actual series | 0.584 | 0.458 | ||
| R2 | Coefficient of determination | 0.342 | 0.210 | ||
| Synch | Synchronicity between model and actual series (%) | 73.5 | 67.6 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Babushkina, E.A.; Zhirnova, D.F.; Belokopytova, L.V.; Tychkov, I.I.; Vaganov, E.A.; Krutovsky, K.V. Response of Four Tree Species to Changing Climate in a Moisture-Limited Area of South Siberia. Forests 2019, 10, 999. https://doi.org/10.3390/f10110999
Babushkina EA, Zhirnova DF, Belokopytova LV, Tychkov II, Vaganov EA, Krutovsky KV. Response of Four Tree Species to Changing Climate in a Moisture-Limited Area of South Siberia. Forests. 2019; 10(11):999. https://doi.org/10.3390/f10110999
Chicago/Turabian StyleBabushkina, Elena A., Dina F. Zhirnova, Liliana V. Belokopytova, Ivan I. Tychkov, Eugene A. Vaganov, and Konstantin V. Krutovsky. 2019. "Response of Four Tree Species to Changing Climate in a Moisture-Limited Area of South Siberia" Forests 10, no. 11: 999. https://doi.org/10.3390/f10110999
APA StyleBabushkina, E. A., Zhirnova, D. F., Belokopytova, L. V., Tychkov, I. I., Vaganov, E. A., & Krutovsky, K. V. (2019). Response of Four Tree Species to Changing Climate in a Moisture-Limited Area of South Siberia. Forests, 10(11), 999. https://doi.org/10.3390/f10110999







