Predicting Growing Stock Volume of Eucalyptus Plantations Using 3-D Point Clouds Derived from UAV Imagery and ALS Data
Abstract
:1. Introduction
2. Materials and Methods
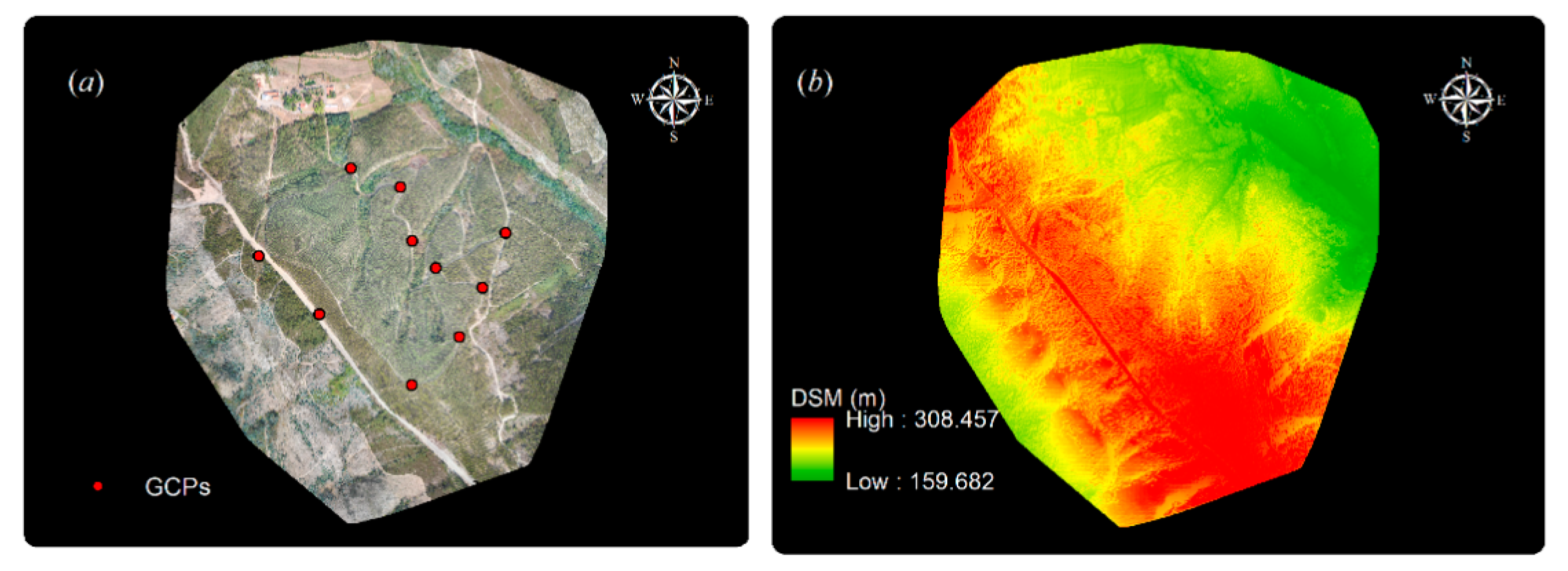
2.1. Study Area
2.2. Field Measurements and Field Volume Estimation
2.3. ALS Acquisition
2.4. UAV Data Acquisition and Use
2.5. 3D Model Generation and Preprocessing Point Clouds
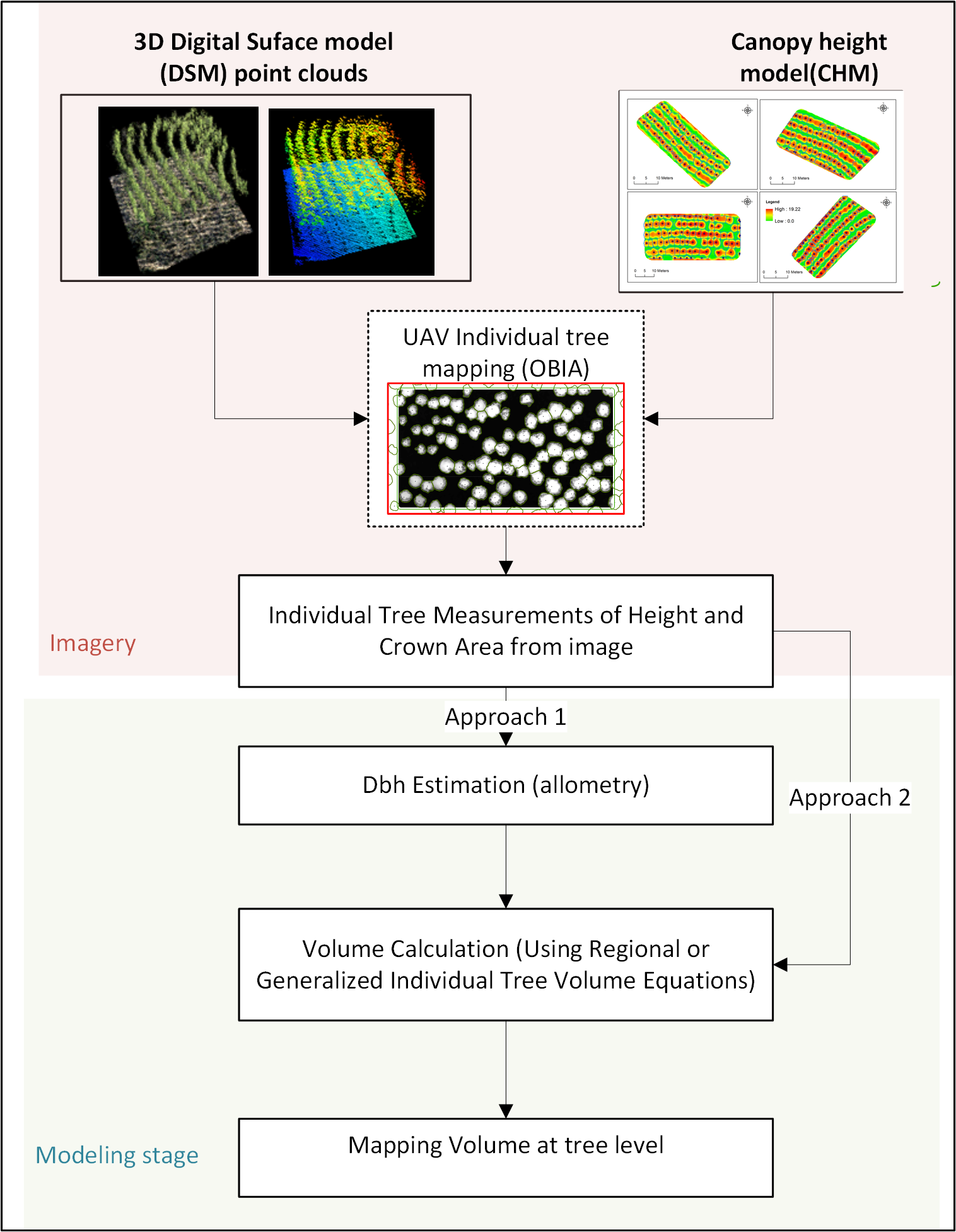
2.6. ITC Process to Derive ALS- and SfM-Variables
2.7. Individual Tree Volume Estimation
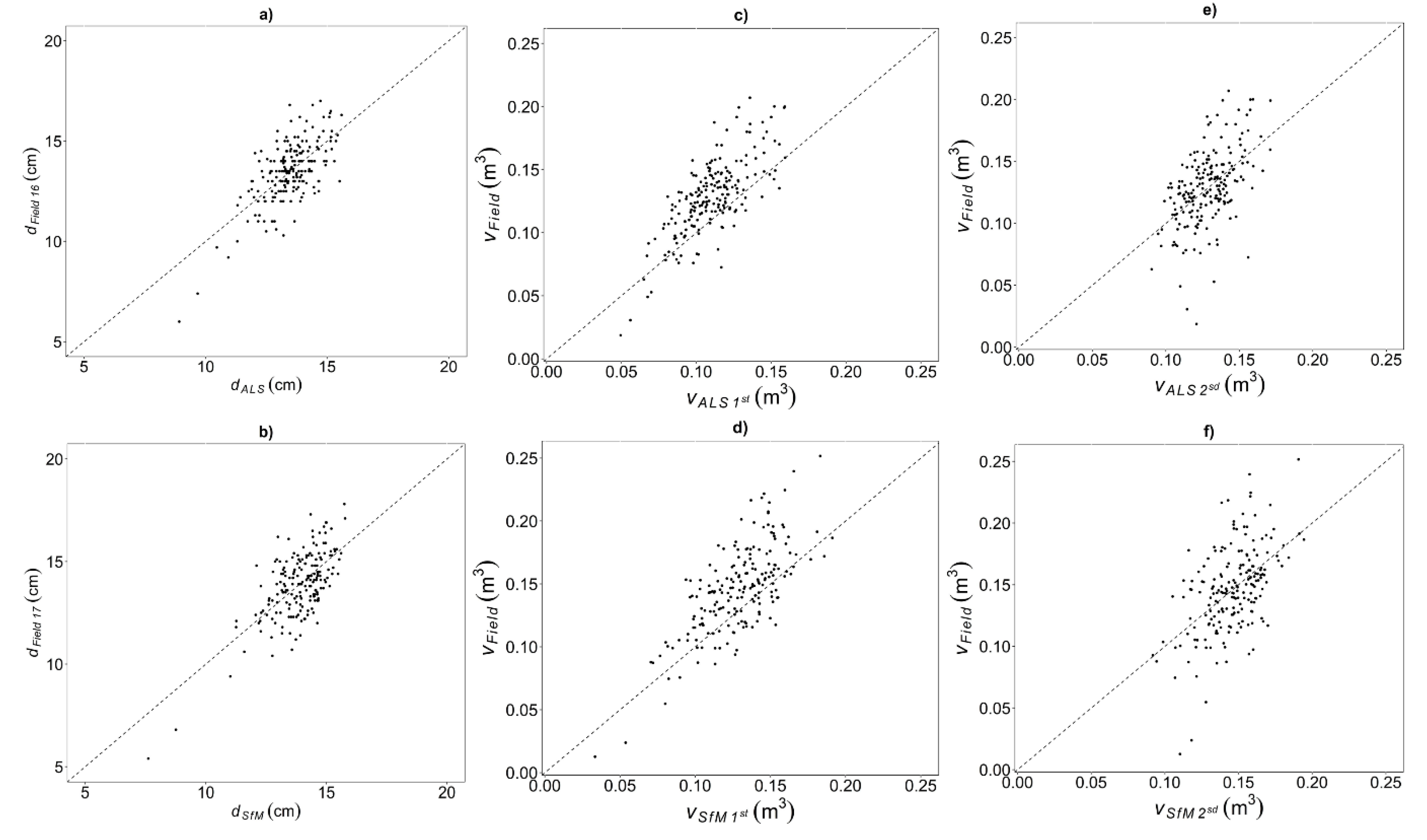
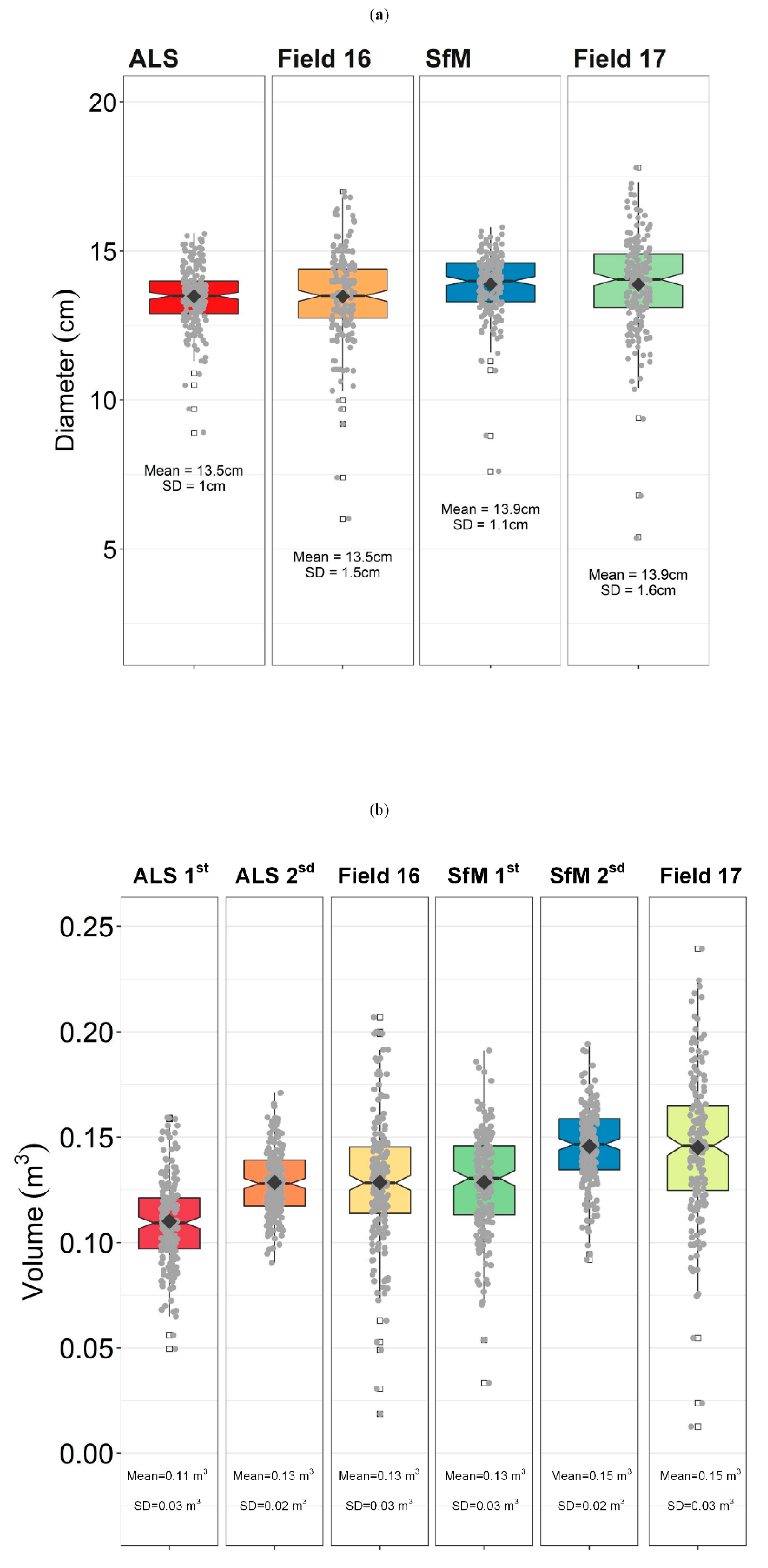
3. Results
Field, ALS and SfM Volume Estimation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Burkhart, H.E.; Tomé, M. Modeling Forest Trees and Stands; Springer Science & Business Media: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest Inventory with Terrestrial LiDAR: A Comparison of Static and Hand-Held Mobile Laser Scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef]
- Williams, M.S.; Bechtold, W.A.; LaBau, V.J. Five Instruments for Measuring Tree Height: An Evaluation. South. J. Appl. For. 1994, 18, 76–82. [Google Scholar] [CrossRef] [Green Version]
- Thenkabail, P.S.; Durrieu, S.; Véga, C.; Bouvier, M.; Gosselin, F.; Renaud, J.-P.; Saint-André, L. Optical Remote Sensing of Tree and Stand Heights. In Land Resources Monitoring, Modeling, and Mapping with Remote Sensing; CRC Press: Boca Raton, FL, USA, 2015; pp. 449–485. [Google Scholar]
- Díaz-Varela, R.A.; de la Rosa, R.; León, L.; Zarco-Tejada, P.J. High-Resolution Airborne UAV Imagery to Assess Olive Tree Crown Parameters Using 3D Photo Reconstruction: Application in Breeding Trials. Remote Sens. 2015, 7, 4213–4232. [Google Scholar] [CrossRef] [Green Version]
- Panagiotidis, D.; Abdollahnejad, A.; Surový, P.; Chiteculo, V. Determining Tree Height and Crown Diameter from High-Resolution UAV Imagery. Int. J. Remote Sens. 2016, 1–19. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote Sensing Technologies for Enhancing Forest Inventories: A Review. Can. J. Remote Sens. 2016, 1–23. [Google Scholar] [CrossRef]
- Giannetti, F.; Puletti, N.; Quatrini, V.; Travaglini, D.; Bottalico, F.; Corona, P.; Chirici, G. Integrating Terrestrial and Airborne Laser Scanning for the Assessment of Single-Tree Attributes in Mediterranean Forest Stands. Eur. J. Remote Sens. 2018, 51, 795–807. [Google Scholar] [CrossRef]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F. Terrestrial Laser Scanning in Forest Inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Abegg, M.; Kükenbrink, D.; Zell, J.; Schaepman, M.E.; Morsdorf, F. Terrestrial Laser Scanning for Forest Inventories—Tree Diameter Distribution and Scanner Location Impact on Occlusion. Forests 2017, 8, 184. [Google Scholar] [CrossRef]
- Liu, G.; Wang, J.; Dong, P.; Chen, Y.; Liu, Z. Estimating Individual Tree Height and Diameter at Breast Height (DBH) from Terrestrial Laser Scanning (TLS) Data at Plot Level. Forests 2018, 9, 398. [Google Scholar] [CrossRef]
- Baltsavias, E.P. A Comparison between Photogrammetry and Laser Scanning. ISPRS J. Photogramm. Remote Sens. 1999, 54, 83–94. [Google Scholar] [CrossRef]
- Næsset, E. Determination of Mean Tree Height of Forest Stands by Digital Photogrammetry. Scand. J. For. Res. 2002, 17, 446–459. [Google Scholar] [CrossRef]
- Næsset, E. Predicting Forest Stand Characteristics with Airborne Scanning Laser Using a Practical Two-Stage Procedure and Field Data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- White, J.; Wulder, M.; Vastaranta, M.; Coops, N.; Pitt, D.; Woods, M. The Utility of Image-Based Point Clouds for Forest Inventory: A Comparison with Airborne Laser Scanning. Forests 2013, 4, 518–536. [Google Scholar] [CrossRef] [Green Version]
- Fritz, A.; Kattenborn, T.; Koch, B. UAV-Based Photogrammetric Point Clouds—Tree Stem Mapping in Open Stands in Comparison to Terrestrial Laser Scanner Point Clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 40, 141–146. [Google Scholar] [CrossRef]
- Gobakken, T.; Bollandsås, O.M.; Næsset, E. Comparing Biophysical Forest Characteristics Estimated from Photogrammetric Matching of Aerial Images and Airborne Laser Scanning Data. Scand. J. For. Res. 2015, 30, 73–86. [Google Scholar] [CrossRef]
- Maltamo, M.; Næsset, E.; Vauhkonen, J. Forestry Applications of Airborne Laser Scanning. Concepts Case Stud. Manag. Ecosys 2014, 27, 2014. [Google Scholar]
- Naesset, E. Estimating Timber Volume of Forest Stands Using Airborne Laser Scanner Data. Remote Sens. Environ. 1997, 61, 246–253. [Google Scholar] [CrossRef]
- Hyyppä, J.; Hyyppä, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of Methods of Small-Footprint Airborne Laser Scanning for Extracting Forest Inventory Data in Boreal Forests. Int. J. Remote Sens. 2008, 29, 1339–1366. [Google Scholar] [CrossRef]
- Van Leeuwen, M.; Nieuwenhuis, M. Retrieval of Forest Structural Parameters Using LiDAR Remote Sensing. Eur. J. For. Res. 2010, 129, 749–770. [Google Scholar] [CrossRef]
- Puliti, S.; Gobakken, T.; Ørka, H.O.; Næsset, E. Assessing 3D Point Clouds from Aerial Photographs for Species-Specific Forest Inventories. Scand. J. For. Res. 2017, 32, 68–79. [Google Scholar] [CrossRef]
- Tuominen, S.; Balazs, A.; Saari, H.; Pölönen, I.; Sarkeala, J.; Viitala, R. Unmanned Aerial System Imagery and Photogrammetric Canopy Height Data in Area-Based Estimation of Forest Variables. Silva Fenn. 2015, 49. [Google Scholar] [CrossRef]
- Bohlin, J.; Wallerman, J.; Fransson, J.E. Forest Variable Estimation Using Photogrammetric Matching of Digital Aerial Images in Combination with a High-Resolution DEM. Scand. J. For. Res. 2012, 27, 692–699. [Google Scholar] [CrossRef]
- Nurminen, K.; Karjalainen, M.; Yu, X.; Hyyppä, J.; Honkavaara, E. Performance of Dense Digital Surface Models Based on Image Matching in the Estimation of Plot-Level Forest Variables. ISPRS J. Photogramm. Remote Sens. 2013, 83, 104–115. [Google Scholar] [CrossRef]
- St-Onge, B.; Vega, C.; Fournier, R.A.; Hu, Y. Mapping Canopy Height Using a Combination of Digital Stereo-photogrammetry and Lidar. Int. J. Remote Sens. 2008, 29, 3343–3364. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Diaz-Varela, R.; Angileri, V.; Loudjani, P. Tree Height Quantification Using Very High Resolution Imagery Acquired from an Unmanned Aerial Vehicle (UAV) and Automatic 3D Photo-Reconstruction Methods. Eur. J. Agron. 2014, 55, 89–99. [Google Scholar] [CrossRef]
- Goodbody, T.R.; Coops, N.C.; White, J.C. Digital Aerial Photogrammetry for Updating Area-Based Forest Inventories: A Review of Opportunities, Challenges, and Future Directions. Curr. For. Rep. 2019, 5, 55–75. [Google Scholar] [CrossRef] [Green Version]
- Iglhaut, J.; Cabo, C.; Puliti, S.; Piermattei, L.; O’Connor, J.; Rosette, J. Structure from Motion Photogrammetry in Forestry: A Review. Curr. For. Rep. 2019, 1–14. [Google Scholar] [CrossRef]
- White, J.C.; Stepper, C.; Tompalski, P.; Coops, N.C.; Wulder, M.A. Comparing ALS and Image-Based Point Cloud Metrics and Modelled Forest Inventory Attributes in a Complex Coastal Forest Environment. Forests 2015, 6, 3704–3732. [Google Scholar] [CrossRef]
- Baltsavias, E.; Gruen, A.; Eisenbeiss, H.; Zhang, L.; Waser, L.T. High-quality Image Matching and Automated Generation of 3D Tree Models. Int. J. Remote Sens. 2008, 29, 1243–1259. [Google Scholar] [CrossRef]
- Véga, C.; St-Onge, B. Height Growth Reconstruction of a Boreal Forest Canopy over a Period of 58 Years Using a Combination of Photogrammetric and Lidar Models. Remote Sens. Environ. 2008, 112, 1784–1794. [Google Scholar] [CrossRef]
- Waser, L.T.; Baltsavias, E.; Ecker, K.; Eisenbeiss, H.; Feldmeyer-Christe, E.; Ginzler, C.; Küchler, M.; Zhang, L. Assessing Changes of Forest Area and Shrub Encroachment in a Mire Ecosystem Using Digital Surface Models and CIR Aerial Images. Remote Sens. Environ. 2008, 112, 1956–1968. [Google Scholar] [CrossRef]
- Vastaranta, M.; Wulder, M.A.; White, J.C.; Pekkarinen, A.; Tuominen, S.; Ginzler, C.; Kankare, V.; Holopainen, M.; Hyyppä, J.; Hyyppä, H. Airborne Laser Scanning and Digital Stereo Imagery Measures of Forest Structure: Comparative Results and Implications to Forest Mapping and Inventory Update. Can. J. Remote Sens. 2013, 39, 382–395. [Google Scholar] [CrossRef]
- Pitt, D.G.; Woods, M.; Penner, M. A Comparison of Point Clouds Derived from Stereo Imagery and Airborne Laser Scanning for the Area-Based Estimation of Forest Inventory Attributes in Boreal Ontario. Can. J. Remote Sens. 2014, 40, 214–232. [Google Scholar] [CrossRef]
- Rahlf, J.; Breidenbach, J.; Solberg, S.; Næsset, E.; Astrup, R. Comparison of Four Types of 3D Data for Timber Volume Estimation. Remote Sens. Environ. 2014, 155, 325–333. [Google Scholar] [CrossRef]
- Ota, T.; Ogawa, M.; Shimizu, K.; Kajisa, T.; Mizoue, N.; Yoshida, S.; Takao, G.; Hirata, Y.; Furuya, N.; Sano, T. Aboveground Biomass Estimation Using Structure from Motion Approach with Aerial Photographs in a Seasonal Tropical Forest. Forests 2015, 6, 3882–3898. [Google Scholar] [CrossRef] [Green Version]
- Holopainen, M.; Vastaranta, M.; Karjalainen, M.; Karila, K.; Kaasalainen, S.; Honkavaara, E.; Hyyppä, J. Forest Inventory Attribute Estimation Using Airborne Laser Scanning, Aerial Stereo Imagery, Radargrammetry and Interferometry-Finnish Experiences of the 3D Techniques. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 2, 63. [Google Scholar] [CrossRef]
- Tanhuanpää, T.; Saarinen, N.; Kankare, V.; Nurminen, K.; Vastaranta, M.; Honkavaara, E.; Karjalainen, M.; Yu, X.; Holopainen, M.; Hyyppä, J. Evaluating the Performance of High-Altitude Aerial Image-Based Digital Surface Models in Detecting Individual Tree Crowns in Mature Boreal Forests. Forests 2016, 7, 143. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.; Turner, C. Assessing the Feasibility of UAV-Based LiDAR for High Resolution Forest Change Detection. Proc. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, B7. [Google Scholar] [CrossRef]
- Lisein, J.; Pierrot-Deseilligny, M.; Bonnet, S.; Lejeune, P. A Photogrammetric Workflow for the Creation of a Forest Canopy Height Model from Small Unmanned Aerial System Imagery. Forests 2013, 4, 922–944. [Google Scholar] [CrossRef] [Green Version]
- Wallace, L.; Lucieer, A.; Malenovský, Z.; Turner, D.; Vopěnka, P. Assessment of Forest Structure Using Two UAV Techniques: A Comparison of Airborne Laser Scanning and Structure from Motion (SfM) Point Clouds. Forests 2016, 7, 62. [Google Scholar] [CrossRef]
- Jaakkola, A.; Hyyppä, J.; Yu, X.; Kukko, A.; Kaartinen, H.; Liang, X.; Hyyppä, H.; Wang, Y. Autonomous Collection of Forest Field Reference—The Outlook and a First Step with UAV Laser Scanning. Remote Sens. 2017, 9, 785. [Google Scholar] [CrossRef]
- Dandois, J.P.; Ellis, E.C. Remote Sensing of Vegetation Structure Using Computer Vision. Remote Sens. 2010, 2, 1157–1176. [Google Scholar] [CrossRef] [Green Version]
- Dandois, J.P.; Olano, M.; Ellis, E.C. Optimal Altitude, Overlap, and Weather Conditions for Computer Vision UAV Estimates of Forest Structure. Remote Sens. 2015, 7, 13895–13920. [Google Scholar] [CrossRef] [Green Version]
- Dandois, J.P.; Ellis, E.C. High Spatial Resolution Three-Dimensional Mapping of Vegetation Spectral Dynamics Using Computer Vision. Remote Sens. Environ. 2013, 136, 259–276. [Google Scholar] [CrossRef]
- Zahawi, R.A.; Dandois, J.P.; Holl, K.D.; Nadwodny, D.; Reid, J.L.; Ellis, E.C. Using Lightweight Unmanned Aerial Vehicles to Monitor Tropical Forest Recovery. Biol. Conserv. 2015, 186, 287–295. [Google Scholar] [CrossRef]
- Guerra-Hérnandez, J.; González-Ferreiro, E.; Sarmento, A.; Silva, J.; Nunes, A.; Correia, A.C.; Fontes, L.; Tomé, M.; Díaz-Varela, R. Short Communication. Using High Resolution UAV Imagery to Estimate Tree Variables in Pinus Pinea Plantation in Portugal. For. Syst. 2016, 25, 9. [Google Scholar] [CrossRef]
- Mohan, M.; Silva, C.A.; Klauberg, C.; Jat, P.; Catts, G.; Cardil, A.; Hudak, A.T.; Dia, M. Individual Tree Detection from Unmanned Aerial Vehicle (UAV) Derived Canopy Height Model in an Open Canopy Mixed Conifer Forest. Forests 2017, 8, 340. [Google Scholar] [CrossRef]
- Thiel, C.; Schmullius, C. Comparison of UAV Photograph-Based and Airborne Lidar-Based Point Clouds over Forest from a Forestry Application Perspective. Int. J. Remote Sens. 2017, 38, 2411–2426. [Google Scholar] [CrossRef]
- Cardil, A.; Vepakomma, U.; Brotons, L. Assessing Pine Processionary Moth Defoliation Using Unmanned Aerial Systems. Forests 2017, 8, 402. [Google Scholar] [CrossRef]
- Navarro, J.; Algeet, N.; Fernández-Landa, A.; Esteban, J.; Rodríguez-Noriega, P.; Guillén-Climent, M. Integration of UAV, Sentinel-1, and Sentinel-2 Data for Mangrove Plantation Aboveground Biomass Monitoring in Senegal. Remote Sens. 2019, 11, 77. [Google Scholar] [CrossRef]
- Puliti, S.; Ørka, H.O.; Gobakken, T.; Næsset, E. Inventory of Small Forest Areas Using an Unmanned Aerial System. Remote Sens. 2015, 7, 9632–9654. [Google Scholar] [CrossRef] [Green Version]
- Torresan, C.; Berton, A.; Carotenuto, F.; Di Gennaro, S.F.; Gioli, B.; Matese, A.; Miglietta, F.; Vagnoli, C.; Zaldei, A.; Wallace, L. Forestry Applications of UAVs in Europe: A Review. Int. J. Remote Sens. 2017, 38, 2427–2447. [Google Scholar] [CrossRef]
- Whitehead, K.; Hugenholtz, C.H. Remote Sensing of the Environment with Small Unmanned Aircraft Systems (UASs), Part 1: A Review of Progress and Challenges 1. J. Unmanned Veh. Syst. 2014, 2, 69–85. [Google Scholar] [CrossRef]
- Tang, L.; Shao, G. Drone Remote Sensing for Forestry Research and Practices. J. For. Res. 2015, 1–7. [Google Scholar] [CrossRef]
- Guerra-Hernández, J.; González-Ferreiro, E.; Monleón, V.; Faias, S.; Tomé, M.; Díaz-Varela, R. Use of Multi-Temporal UAV-Derived Imagery for Estimating Individual Tree Growth in Pinus Pinea Stands. Forests 2017, 8, 300. [Google Scholar] [CrossRef]
- Pádua, L.; Hruška, J.; Bessa, J.; Adão, T.; Martins, L.M.; Gonçalves, J.A.; Peres, E.; Sousa, A.M.; Castro, J.P.; Sousa, J.J. Multi-Temporal Analysis of Forestry and Coastal Environments Using UASs. Remote Sens. 2017, 10, 24. [Google Scholar] [CrossRef]
- Hall, S.A.; Burke, I.C.; Box, D.O.; Kaufmann, M.R.; Stoker, J.M. Estimating Stand Structure Using Discrete-Return Lidar: An Example from Low Density, Fire Prone Ponderosa Pine Forests. For. Ecol. Manag. 2005, 208, 189–209. [Google Scholar] [CrossRef]
- Järnstedt, J.; Pekkarinen, A.; Tuominen, S.; Ginzler, C.; Holopainen, M.; Viitala, R. Forest Variable Estimation Using a High-Resolution Digital Surface Model. ISPRS J. Photogramm. Remote Sens. 2012, 74, 78–84. [Google Scholar] [CrossRef]
- González-Ferreiro, E.; Diéguez-Aranda, U.; Miranda, D. Estimation of Stand Variables in Pinus Radiata D. Don Plantations Using Different LiDAR Pulse Densities. Forestry 2012, 85, 281–292. [Google Scholar] [CrossRef]
- González-Ferreiro, E.; Diéguez-Aranda, U.; Crecente-Campo, F.; Barreiro-Fernández, L.; Miranda, D.; Castedo-Dorado, F. Modelling Canopy Fuel Variables for Pinus Radiata D. Don in NW Spain with Low-Density LiDAR Data. Int. J. Wildland Fire 2014, 23, 350–362. [Google Scholar] [CrossRef]
- Montaghi, A.; Corona, P.; Dalponte, M.; Gianelle, D.; Chirici, G.; Olsson, H. Airborne Laser Scanning of Forest Resources: An Overview of Research in Italy as a Commentary Case Study. Int. J. Appl. Earth Obs. Geoinformation 2013, 23, 288–300. [Google Scholar] [CrossRef]
- Corona, P.; Cartisano, R.; Salvati, R.; Chirici, G.; Floris, A.; Di Martino, P.; Marchetti, M.; Scrinzi, G.; Clementel, F.; Torresan, C. Airborne Laser Scanning to Support Forest Resource Management under Alpine, Temperate and Mediterranean Environments in Italy. Eur. J. Remote Sens. 2012, 45, 27–37. [Google Scholar]
- González-Olabarria, J.-R.; Rodríguez, F.; Fernández-Landa, A.; Mola-Yudego, B. Mapping Fire Risk in the Model Forest of Urbión (Spain) Based on Airborne LiDAR Measurements. For. Ecol. Manag. 2012, 282, 149–156. [Google Scholar] [CrossRef]
- Guerra-Hernández, J.; Görgens, E.B.; García-Gutiérrez, J.; Rodriguez, L.C.E.; Tomé, M.; González-Ferreiro, E. Comparison of ALS Based Models for Estimating Aboveground Biomass in Three Types of Mediterranean Forest. Eur. J. Remote Sens. 2016, 49, 185–204. [Google Scholar] [CrossRef]
- Montealegre, A.L.; Lamelas, M.T.; Tanase, M.A.; de la Riva, J. Estimación de La Severidad En Incendios Forestales a Partir de Datos LiDAR-PNOA y Valores de Composite Burn Index. Rev. Teledetec. 2017, 49, 1–16. [Google Scholar] [CrossRef]
- Montealegre, A.L.; Lamelas, M.T.; de la Riva, J.; García-Martín, A.; Escribano, F. Use of Low Point Density ALS Data to Estimate Stand-Level Structural Variables in Mediterranean Aleppo Pine Forest. For. Int. J. For. Res. 2016, 89, 373–382. [Google Scholar] [CrossRef]
- Domingo, D.; Alonso, R.; Lamelas, M.T.; Montealegre, A.L.; Rodríguez, F.; de la Riva, J. Temporal Transferability of Pine Forest Attributes Modeling Using Low-Density Airborne Laser Scanning Data. Remote Sens. 2019, 11, 261. [Google Scholar] [CrossRef]
- Silva, C.A.; Klauberg, C.; Hudak, A.T.; Vierling, L.A.; Liesenberg, V.; Carvalho, S.P.E.; Rodriguez, L.C. A Principal Component Approach for Predicting the Stem Volume in Eucalyptus Plantations in Brazil Using Airborne LiDAR Data. For. Int. J. For. Res. 2016, 89, 422–433. [Google Scholar] [CrossRef]
- Kachamba, D.J.; Ørka, H.O.; Gobakken, T.; Eid, T.; Mwase, W. Biomass Estimation Using 3D Data from Unmanned Aerial Vehicle Imagery in a Tropical Woodland. Remote Sens. 2016, 8, 968. [Google Scholar] [CrossRef]
- St-Onge, B.; Audet, F.-A.; Bégin, J. Characterizing the Height Structure and Composition of a Boreal Forest Using an Individual Tree Crown Approach Applied to Photogrammetric Point Clouds. Forests 2015, 6, 3899–3922. [Google Scholar] [CrossRef]
- Mielcarek, M.; Stereńczak, K.; Khosravipour, A. Testing and Evaluating Different LiDAR-Derived Canopy Height Model Generation Methods for Tree Height Estimation. Int. J. Appl. Earth Obs. Geoinformation 2018, 71, 132–143. [Google Scholar] [CrossRef]
- Guerra-Hernández, J.; Cosenza, D.N.; Rodriguez, L.C.E.; Silva, M.; Tomé, M.; Díaz-Varela, R.A.; González-Ferreiro, E. Comparison of ALS-and UAV (SfM)-Derived High-Density Point Clouds for Individual Tree Detection in Eucalyptus Plantations. Int. J. Remote Sens. 2018, 39, 5211–5235. [Google Scholar]
- Maltamo, M.; Eerikäinen, K.; Packalén, P.; Hyyppä, J. Estimation of Stem Volume Using Laser Scanning-Based Canopy Height Metrics. Forestry 2006, 79, 217–229. [Google Scholar] [CrossRef]
- Hentz, Â.M.; Silva, C.A.; Dalla Corte, A.P.; Netto, S.P.; Strager, M.P.; Klauberg, C. Estimating Forest Uniformity in Eucalyptus Spp. and Pinus Taeda L. Stands Using Field Measurements and Structure from Motion Point Clouds Generated from Unmanned Aerial Vehicle (UAV) Data Collection. For. Syst. 2018, 27, 5. [Google Scholar] [CrossRef]
- Roussel, J.-R.; Caspersen, J.; Béland, M.; Thomas, S.; Achim, A. Removing Bias from LiDAR-Based Estimates of Canopy Height: Accounting for the Effects of Pulse Density and Footprint Size. Remote Sens. Environ. 2017, 198, 1–16. [Google Scholar] [CrossRef]
- Tomé, M.; Tomé, J.; Ribeiro, F.; Faias, S. Equações de Volume Total, Volume Percentual e de Perfil Do Tronco Para Eucalyptus Globulus Labill. Em Portugal. Silva Lusit. 2007, 15, 25–39. [Google Scholar]
- McGaughey, R.J. FUSION/LDV: Software for LIDAR Data Analysis and Visualization; Version 3.60+; Pacific Northwest Research Station, United States Department of Agriculture Forest Service: Seattle, WA, USA, 2017.
- Isenburg, M. LAStools—Efficient Tools for LiDAR Processing; Version 160921; Academic: Cambridge, MA, USA, 2016. [Google Scholar]
- González-Ferreiro, E.; Diéguez-Aranda, U.; Barreiro-Fernández, L.; Buján, S.; Barbosa, M.; Suárez, J.C.; Bye, I.J.; Miranda, D. A Mixed Pixel-and Region-Based Approach for Using Airborne Laser Scanning Data for Individual Tree Crown Delineation in Pinus Radiata D. Don Plantations. Int. J. Remote Sens. 2013, 34, 7671–7690. [Google Scholar] [CrossRef]
- Vanclay, J.K.; Skovsgaard, J.P. Evaluating Forest Growth Models. Ecol. Model. 1997, 98, 1–12. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B.; Chen, H.J. A Comparative Study of Various Tests for Normality. J. Am. Stat. Assoc. 1968, 63, 1343–1372. [Google Scholar] [CrossRef]
- Iizuka, K.; Yonehara, T.; Itoh, M.; Kosugi, Y. Estimating Tree Height and Diameter at Breast Height (DBH) from Digital Surface Models and Orthophotos Obtained with an Unmanned Aerial System for a Japanese Cypress (Chamaecyparis Obtusa) Forest. Remote Sens. 2017, 10, 13. [Google Scholar] [CrossRef]
- Chisholm, R.A.; Cui, J.; Lum, S.K.; Chen, B.M. UAV LiDAR for Below-Canopy Forest Surveys. J. Unmanned Veh. Syst. 2013, 1, 61–68. [Google Scholar] [CrossRef]
- Cosenza, D.N.; Soares, V.P.; Leite, H.G.; Gleriani, J.M.; do Amaral, C.H.; Gripp Júnior, J.; da Silva, A.A.L.; Soares, P.; Tomé, M. Airborne Laser Scanning Applied to Eucalyptus Stand Inventory at Individual Tree Level. Pesqui. Agropecuária Bras. 2018, 53, 1373–1382. [Google Scholar] [CrossRef]
- Persson, A.; Holmgren, J.; Söderman, U. Detecting and Measuring Individual Trees Using an Airborne Laser Scanner. Photogramm. Eng. Remote Sens. 2002, 68, 925–932. [Google Scholar]
- Popescu, S.C. Estimating Biomass of Individual Pine Trees Using Airborne Lidar. Biomass Bioenergy 2007, 31, 646–655. [Google Scholar] [CrossRef]
- Zhao, K.; Popescu, S.; Nelson, R. Lidar Remote Sensing of Forest Biomass: A Scale-Invariant Estimation Approach Using Airborne Lasers. Remote Sens. Environ. 2009, 113, 182–196. [Google Scholar] [CrossRef]
- Korpela, I. Individual Tree Measurements by Means of Digital Aerial Photogrammetry; Finnish Society of Forest Science: Helsinki, Finland, 2004; Volume 3. [Google Scholar]
- St-Onge, B.; Jumelet, J.; Cobello, M.; Véga, C. Measuring Individual Tree Height Using a Combination of Stereophotogrammetry and Lidar. Can. J. For. Res. 2004, 34, 2122–2130. [Google Scholar] [CrossRef]
- Jensen, J.L.; Mathews, A.J. Assessment of Image-Based Point Cloud Products to Generate a Bare Earth Surface and Estimate Canopy Heights in a Woodland Ecosystem. Remote Sens. 2016, 8, 50. [Google Scholar] [CrossRef]
- Hopkinson, C.; Chasmer, L.; Hall, R.J. The Uncertainty in Conifer Plantation Growth Prediction from Multi-Temporal Lidar Datasets. Remote Sens. Environ. 2008, 112, 1168–1180. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Kukko, A.; Maltamo, M.; Kaartinen, H. Change Detection Techniques for Canopy Height Growth Measurements Using Airborne Laser Scanner Data. Photogramm. Eng. Remote Sens. 2006, 72, 1339–1348. [Google Scholar] [CrossRef]
- Gatziolis, D.; Fried, J.S.; Monleon, V.S. Challenges to Estimating Tree Height via LiDAR in Closed-Canopy Forests: A Parable from Western Oregon. For. Sci. 2010, 56, 139–155. [Google Scholar]
- Milas, A.S.; Arend, K.; Mayer, C.; Simonson, M.A.; Mackey, S. Different Colours of Shadows: Classification of UAV Images. Int. J. Remote Sens. 2017, 38, 3084–3100. [Google Scholar] [CrossRef]
- Laliberte, A.S.; Herrick, J.E.; Rango, A.; Winters, C. Acquisition, Orthorectification, and Object-Based Classification of Unmanned Aerial Vehicle (UAV) Imagery for Rangeland Monitoring. Photogramm. Eng. Remote Sens. 2010, 76, 661–672. [Google Scholar] [CrossRef]
- Ke, Y.; Quackenbush, L.J. A Review of Methods for Automatic Individual Tree-Crown Detection and Delineation from Passive Remote Sensing. Int. J. Remote Sens. 2011, 32, 4725–4747. [Google Scholar] [CrossRef]
- Nuijten, R.J.; Coops, N.C.; Goodbody, T.R.; Pelletier, G. Examining the Multi-Seasonal Consistency of Individual Tree Segmentation on Deciduous Stands Using Digital Aerial Photogrammetry (DAP) and Unmanned Aerial Systems (UAS). Remote Sens. 2019, 11, 739. [Google Scholar] [CrossRef]
- Frey, J.; Kovach, K.; Stemmler, S.; Koch, B. UAV Photogrammetry of Forests as a Vulnerable Process. A Sensitivity Analysis for a Structure from Motion RGB-Image Pipeline. Remote Sens. 2018, 10, 912. [Google Scholar] [CrossRef]
- Fraser, B.; Congalton, R. Issues in Unmanned Aerial Systems (UAS) Data Collection of Complex Forest Environments. Remote Sens. 2018, 10, 908. [Google Scholar] [CrossRef]
- Ni, W.; Sun, G.; Pang, Y.; Zhang, Z.; Liu, J.; Yang, A.; Wang, Y.; Zhang, D. Mapping Three-Dimensional Structures of Forest Canopy Using UAV Stereo Imagery: Evaluating Impacts of Forward Overlaps and Image Resolutions With LiDAR Data as Reference. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3578–3589. [Google Scholar] [CrossRef]


| Plot | d | h | ||||
|---|---|---|---|---|---|---|
| Mean | Mean | Mean | ||||
| Dec 2016 | Sep 2017 | Dec 2016 | Sep 2017 | Dec 2016 | Sep 2017 | |
| P1 | 13.2 | 13.4 | 19.4 | 20.9 | 0.13 | 0.14 |
| P2 | 12.9 | 13.3 | 18.8 | 19.9 | 0.12 | 0.15 |
| P3 | 13.4 | 13.8 | 18.6 | 20.0 | 0.13 | 0.15 |
| P4 | 13.8 | 14.1 | 18.8 | 19.8 | 0.13 | 0.15 |
| P5 | 13.7 | 14.0 | 18.3 | 19.7 | 0.13 | 0.15 |
| P6 | 13.8 | 14.2 | 17.6 | 19.1 | 0.13 | 0.14 |
| Min. | 5.3 | 5.4 | 9.9 | 10.3 | 0.01 | 0.01 |
| Mean | 13.5 | 13.8 | 18.6 | 19.9 | 0.13 | 0.14 |
| Max. | 17.3 | 17.8 | 22.8 | 23.5 | 0.24 | 0.26 |
| SD | 1.7 | 1.7 | 1.5 | 1.6 | 0.03 | 0.04 |
| Approach | Dependent variable | Predictors | Parameter estimate | Standard error | p-value | Mef | RMSE (cm) | rRMSE (%) | bias (cm) |
| 1st | dSfM | Constant | 0.863 | 1.170 | < 0.001 | 0.45 | 1.17 | 8.49 | 0.38 |
| hSfM | 0.907 | 0.108 | < 0.001 | ||||||
| caSfM | 0.037 | 0.037 | 0.013 | ||||||
| dALS | Constant | 0.564 | 0.151 | < 0.001 | 0.47 | 1.12 | 8.31 | 0.35 | |
| hALS | 1.042 | 0.090 | < 0.001 | ||||||
| caALS | 0.062 | 0.015 | < 0.001 | ||||||
| Approach | Dependent variable | Predictors | Parameter estimate | Standard error | p-value | Mef | RMSE (m3) | rRMSE (%) | bias (m3) |
| 2nd | vSfM | Constant | 0.004 | 0.002 | 0.082 | 0.43 | 0.030 | 20.31 | 0.0016 |
| hSfM | 1.192 | 0.201 | < 0.001 | ||||||
| caSfM | 0.151 | 0.035 | < 0.001 | ||||||
| vALS | Constant | 0.001 | 0.000 | 0.106 | 0.46 | 0.026 | 19.97 | 0.0004 | |
| hALS | 1.828 | 0.224 | < 0.001 | ||||||
| caALS | 0.024 | 0.037 | < 0.001 |
| Plot | dALS (cm) | dSfM (cm) | vALS (m3) | vSfM (m3) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ALS | Field 16 | SfM | Field 17 | ALS 1st | ALS 2sd | Field 16 | SfM 1st | SfM 2sd | Field 17 | |
| P1 | 14.1 | 13.3 | 14.3 | 13.4 | 0.13 | 0.15 | 0.13 | 0.15 | 0.15 | 0.14 |
| P2 | 13.4 | 12.5 | 14.0 | 13.4 | 0.11 | 0.14 | 0.11 | 0.13 | 0.15 | 0.14 |
| P3 | 13.1 | 13.3 | 13.9 | 14.0 | 0.10 | 0.13 | 0.12 | 0.12 | 0.14 | 0.15 |
| P4 | 13.4 | 13.8 | 13.8 | 14.3 | 0.11 | 0.14 | 0.13 | 0.12 | 0.14 | 0.15 |
| P5 | 13.5 | 13.8 | 14.0 | 14.2 | 0.11 | 0.14 | 0.13 | 0.13 | 0.15 | 0.15 |
| P6 | 13.2 | 14.2 | 13.1 | 14.0 | 0.11 | 0.16 | 0.14 | 0.12 | 0.14 | 0.14 |
| Min. | 8.9 | 6.0 | 7.6 | 5.4 | 0.05 | 0.05 | 0.02 | 0.03 | 0.09 | 0.01 |
| Mean | 13.5 | 13.5 | 13.9 | 13.9 | 0.11 | 0.15 | 0.13 | 0.13 | 0.15 | 0.15 |
| Max. | 15.6 | 17.0 | 15.8 | 17.8 | 0.16 | 0.20 | 0.21 | 0.19 | 0.19 | 0.25 |
| SD | 1.0 | 1.5 | 1.1 | 1.6 | 0.02 | 0.02 | 0.03 | 0.02 | 0.02 | 0.03 |
| t-test p-value | 0.98 | 0.98 | <0.001 | 0.99 | <0.001 | 0.98 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerra-Hernández, J.; Cosenza, D.N.; Cardil, A.; Silva, C.A.; Botequim, B.; Soares, P.; Silva, M.; González-Ferreiro, E.; Díaz-Varela, R.A. Predicting Growing Stock Volume of Eucalyptus Plantations Using 3-D Point Clouds Derived from UAV Imagery and ALS Data. Forests 2019, 10, 905. https://doi.org/10.3390/f10100905
Guerra-Hernández J, Cosenza DN, Cardil A, Silva CA, Botequim B, Soares P, Silva M, González-Ferreiro E, Díaz-Varela RA. Predicting Growing Stock Volume of Eucalyptus Plantations Using 3-D Point Clouds Derived from UAV Imagery and ALS Data. Forests. 2019; 10(10):905. https://doi.org/10.3390/f10100905
Chicago/Turabian StyleGuerra-Hernández, Juan, Diogo N. Cosenza, Adrian Cardil, Carlos Alberto Silva, Brigite Botequim, Paula Soares, Margarida Silva, Eduardo González-Ferreiro, and Ramón A. Díaz-Varela. 2019. "Predicting Growing Stock Volume of Eucalyptus Plantations Using 3-D Point Clouds Derived from UAV Imagery and ALS Data" Forests 10, no. 10: 905. https://doi.org/10.3390/f10100905
APA StyleGuerra-Hernández, J., Cosenza, D. N., Cardil, A., Silva, C. A., Botequim, B., Soares, P., Silva, M., González-Ferreiro, E., & Díaz-Varela, R. A. (2019). Predicting Growing Stock Volume of Eucalyptus Plantations Using 3-D Point Clouds Derived from UAV Imagery and ALS Data. Forests, 10(10), 905. https://doi.org/10.3390/f10100905











