Finer Resolution Estimation and Mapping of Mangrove Biomass Using UAV LiDAR and WorldView-2 Data
Abstract
1. Introduction
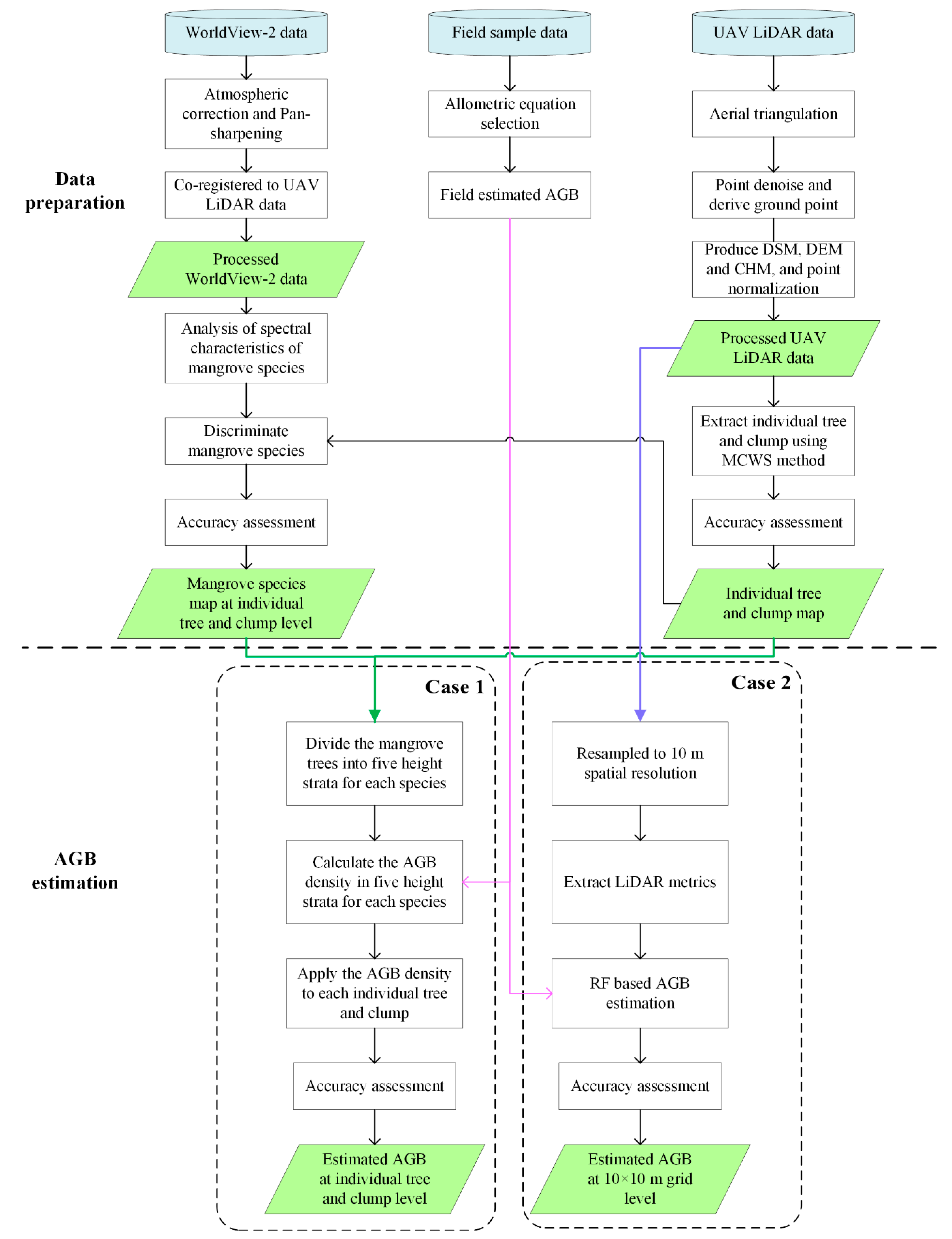
2. Materials and Methods
2.1. Study Site
2.2. Field Data Collection
2.3. Remote Sensing Data and Processing
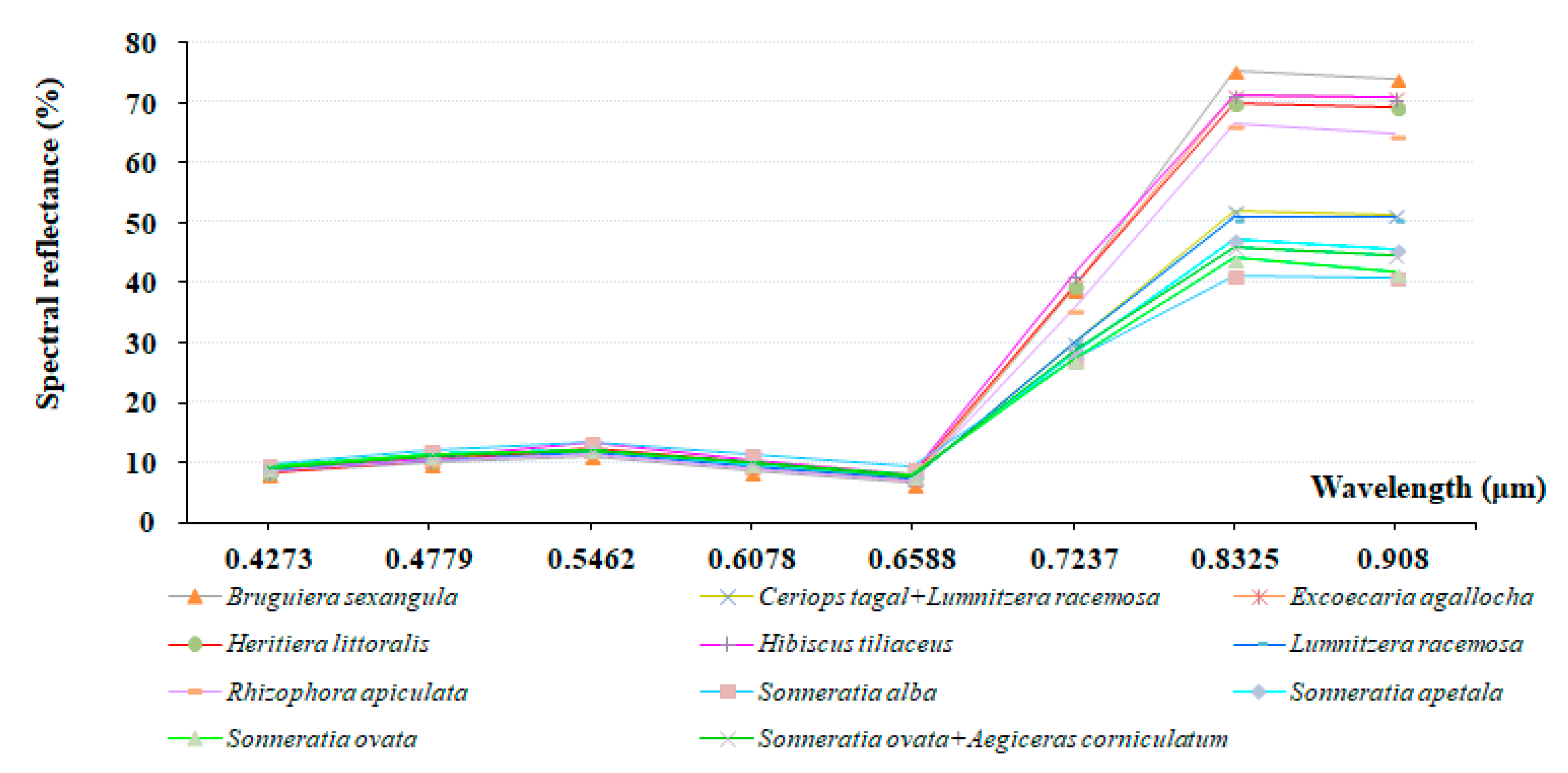
2.3.1. WorldView-2 Imagery
2.3.2. UAV LiDAR Data and Mangrove Canopy Height Model Production
2.4. Mangrove Species Classification and Individual Tree Detection
2.5. AGB Estimation
2.6. Accuracy Assessment
2.6.1. Validation Mangrove Classification
2.6.2. Validation Biomass Result
2.6.3. Individual Tree Detection
3. Results
3.1. Individual Mangrove Tree Extraction
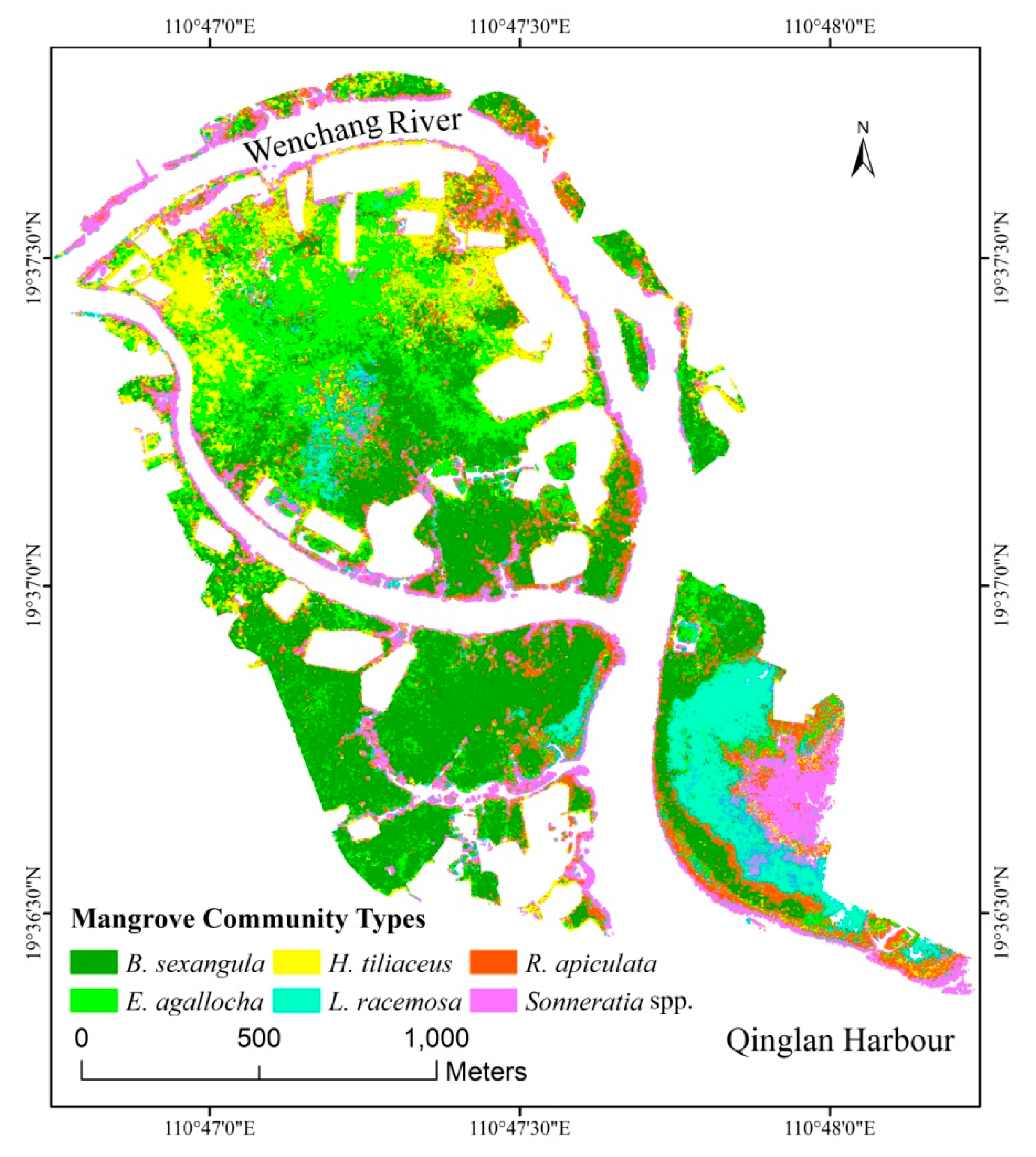
3.2. Finer Resolution Mangrove Classification
3.3. AGB Estimates and Prediction
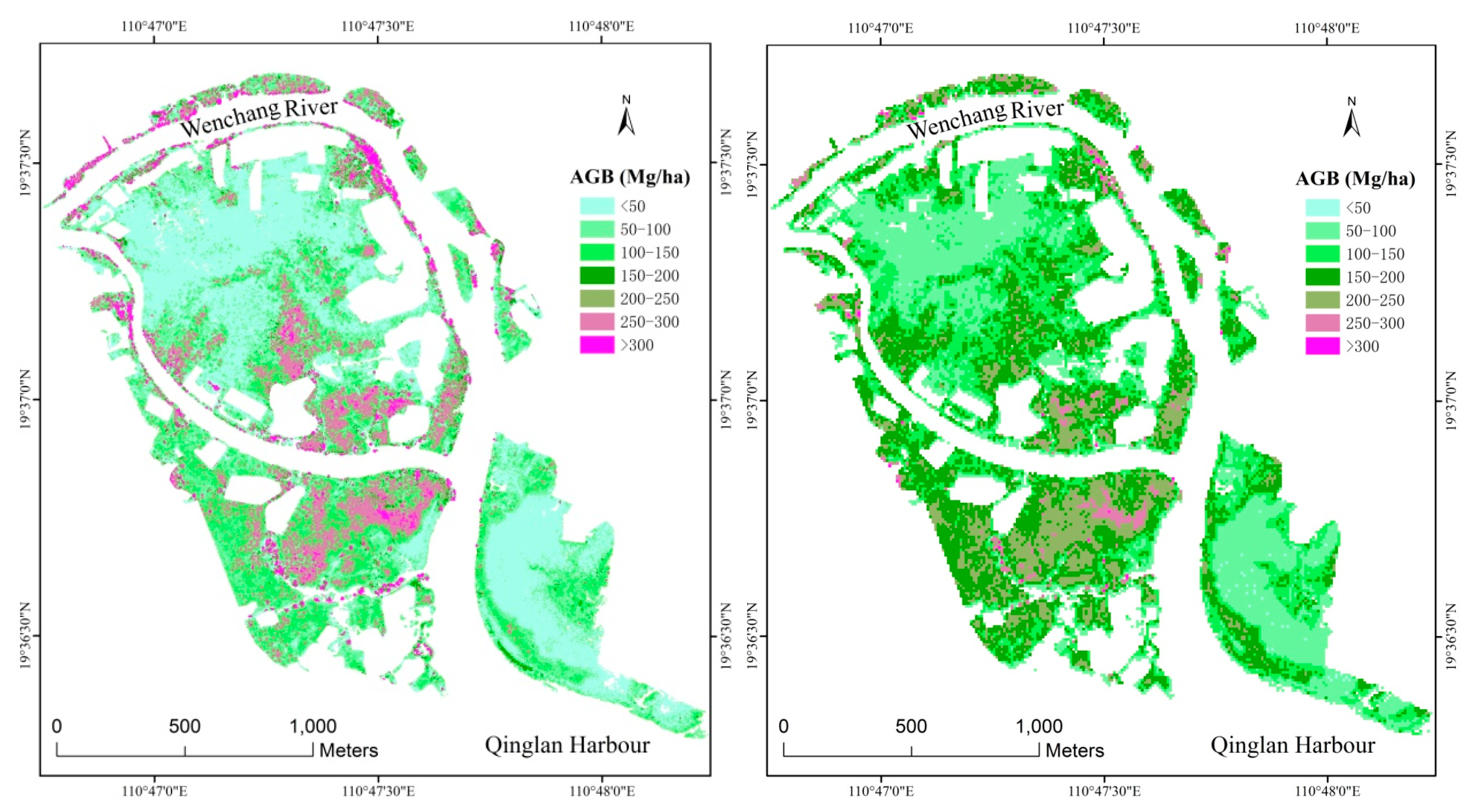
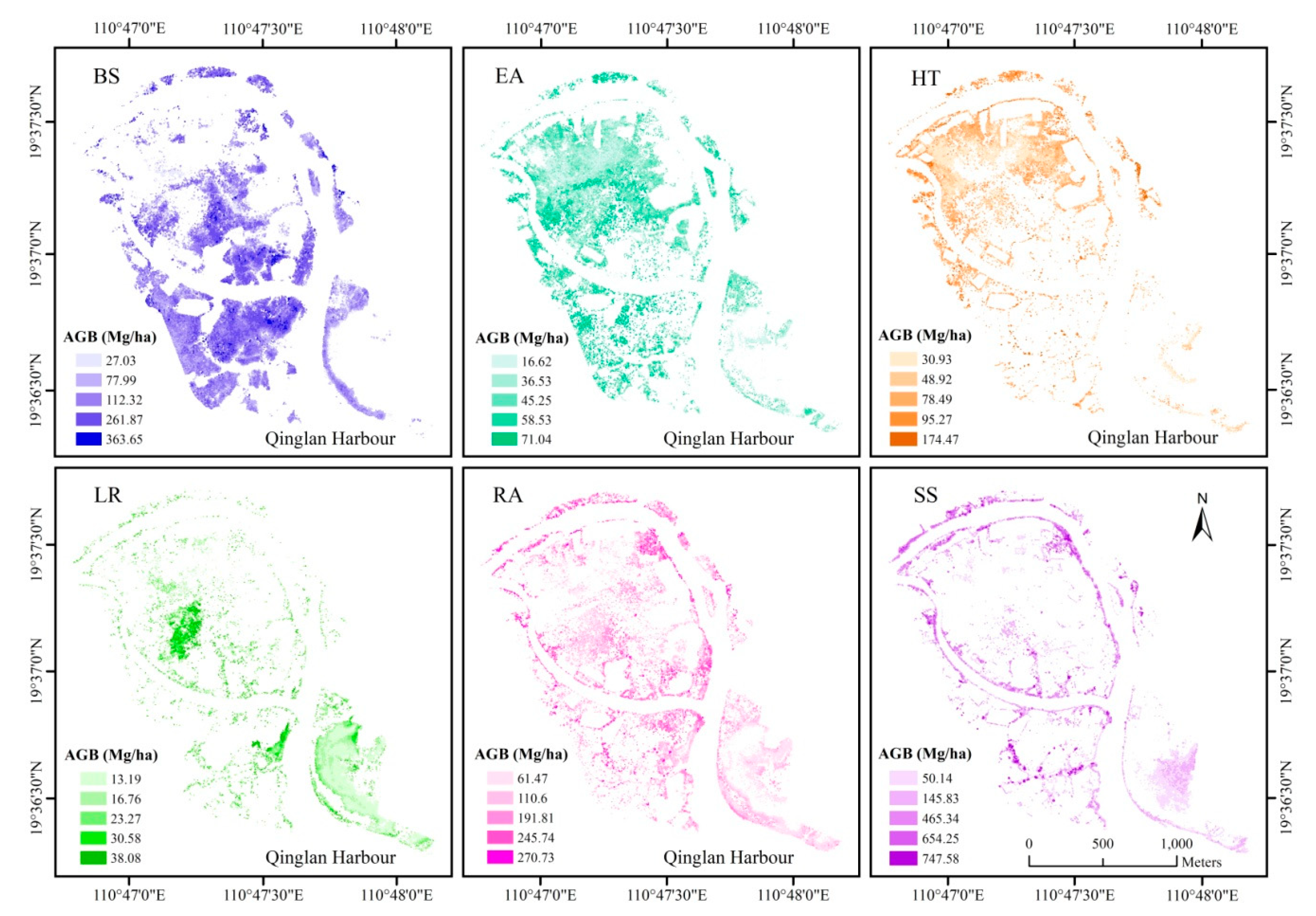
3.4. Spatial Distribution of Mangrove AGB
4. Discussion
4.1. Effect of Mangrove DBH on Individual Tree Segmentation
4.2. Comparison of the Individual Tree-Based Inference Method and the Grid-Based RF Model Method
4.3. AGB Comparison with Mangroves in Other Areas
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| DBH1 | DBH2 | DBH3 | DBH4 | DBH5 | DBH6 | DBH7 | DBH8 | DBH9 | DBH10 | DBH11 | DBH12 | DBH13 | DBH14 | DBH15 | DBH16 | DBH17 | DBH18 | DBH19 | DBH20 | DBH21 | Max. | Min. | Mean | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DBH1 | 1 | |||||||||||||||||||||||
| DBH2 | 0.094 | 1 | ||||||||||||||||||||||
| DBH3 | 0.078 | 0.173 | 1 | |||||||||||||||||||||
| DBH4 | 0.157 | −0.244 | 0.258 | 1 | ||||||||||||||||||||
| DBH5 | −0.002 | −.202 | 0.258 | 0.834 ** | 1 | |||||||||||||||||||
| DBH6 | 0.243 | −0.213 | 0.146 | 0.804 ** | 0.814 ** | 1 | ||||||||||||||||||
| DBH7 | 0.292 | −0.374 * | −0.154 | 0.611 ** | 0.541 ** | 0.676 ** | 1 | |||||||||||||||||
| DBH8 | 0.084 | −0.276 | −0.275 | 0.262 | 0.226 | 0.469 ** | 0.604 ** | 1 | ||||||||||||||||
| DBH9 | 0.086 | −0.248 | −0.208 | 0.323 * | 0.304 * | 0.523 ** | 0.576 ** | 0.535 ** | 1 | |||||||||||||||
| DBH10 | −0.044 | −0.064 | −0.306 * | −0.045 | 0.072 | 0.152 | 0.338 * | 0.568 ** | 0.489 ** | 1 | ||||||||||||||
| DBH11 | −0.034 | −0.097 | −0.124 | 0.197 | 0.289 | 0.400 ** | 0.475 ** | 0.315 * | 0.608 ** | 0.347 * | 1 | |||||||||||||
| DBH12 | −0.056 | 0.084 | −0.284 | −0.145 | −0.085 | 0.074 | 0.124 | 0.241 | 0.509 ** | 0.508 ** | 0.617 ** | 1 | ||||||||||||
| DBH13 | −0.074 | −0.164 | −0.268 | −0.266 | −0.131 | −0.158 | 0.003 | 0.117 | 0.184 | 0.147 | 0.295 * | 0.141 | 1 | |||||||||||
| DBH14 | 0.087 | −0.016 | −0.249 | −0.265 | −0.154 | −0.083 | −0.052 | 0.328 * | 0.381 ** | 0.442 ** | 0.275 | 0.390 ** | 0.624 ** | 1 | ||||||||||
| DBH15 | −0.094 | 0.075 | −0.211 | −0.085 | −0.049 | −0.023 | 0.008 | −0.037 | 0.217 | 0.088 | 0.485 ** | 0.531 ** | 0.609 ** | 0.345 * | 1 | |||||||||
| DBH16 | −0.081 | −0.147 | −0.197 | −0.229 | −0.115 | −0.149 | −0.020 | −0.026 | 0.019 | −0.043 | 0.286 | 0.146 | 0.835 ** | 0.393 ** | 0.659 ** | 1 | ||||||||
| DBH17 | 0.087 | −0.045 | −0.053 | −0.142 | −0.028 | 0.018 | −0.004 | −0.036 | 0.036 | −0.040 | 0.334 * | 0.106 | 0.823 ** | 0.347 * | 0.623 ** | 0.831 ** | 1 | |||||||
| DBH18 | 0.008 | −0.098 | −0.188 | −0.147 | −0.060 | 0.026 | 0.039 | 0.181 | 0.551 ** | 0.234 | 0.405 ** | 0.357 * | 0.687 ** | 0.791 ** | 0.402 ** | 0.376 * | 0.464 ** | 1 | ||||||
| DBH19 | −0.056 | −0.105 | −0.119 | −0.081 | −0.040 | −0.008 | 0.056 | 0.221 | 0.294 * | 0.109 | 0.200 | 0.145 | 0.499 ** | 0.543 ** | 0.096 | 0.139 | 0.218 | 0.764 ** | 1 | |||||
| DBH20 | −0.066 | −0.103 | −0.058 | −0.058 | 0.042 | 0.062 | 0.059 | 0.102 | −0.031 | 0.079 | 0.298 * | −0.016 | 0.170 | 0.117 | 0.056 | 0.408 ** | 0.159 | −0.058 | −0.044 | 1 | ||||
| DBH21 | −0.039 | −0.079 | −0.097 | −0.134 | −0.066 | −0.031 | −0.017 | 0.102 | 0.383 ** | 0.132 | 0.269 | 0.201 | 0.522 ** | 0.628 ** | 0.133 | 0.176 | 0.262 | 0.866 ** | 0.892 ** | −0.033 | 1 | |||
| Max. | 0.126 | −0.294 | −0.320 * | 0.130 | 0.207 | 0.393 ** | 0.465 ** | 0.574 ** | 0.528 ** | 0.462 ** | 0.622 ** | 0.519 ** | 0.518 ** | 0.532 ** | 0.469 ** | 0.463 ** | 0.422 ** | 0.467 ** | 0.382 ** | 0.379 * | 0.307 * | 1 | ||
| Min. | −0.306 * | −0.120 | −0.162 | 0.031 | −0.001 | −0.090 | 0.140 | −0.012 | −0.155 | −0.076 | 0.006 | −0.110 | 0.001 | −0.241 | 0.156 | 0.092 | −0.031 | −0.251 | −0.215 | 0.038 | −0.265 | −0.159 | 1 | |
| Mean | −0.005 | −0.250 | −0.518 ** | −0.151 | −0.037 | 0.040 | 0.260 | 0.372 * | 0.412 ** | 0.488 ** | 0.487 ** | 0.565 ** | 0.692 ** | 0.628 ** | 0.660 ** | 0.634 ** | 0.483 ** | 0.493 ** | 0.296 * | 0.306 * | 0.309 * | 0.791 ** | 0.142 | 1 |
| DA | −0.211 | −0.356 * | −0.388 ** | −0.116 | −0.024 | −0.002 | 0.302 * | 0.309 * | 0.371 * | 0.289 | 0.360 * | 0.226 | 0.799 ** | 0.394 ** | 0.569 ** | 0.637 ** | 0.603 ** | 0.522 ** | 0.395 ** | 0.054 | 0.391 ** | 0.556 ** | 0.086 | 0.695 ** |
References
- Saenger, P. Mangrove Ecology, Silviculture and Conservation; Kluwer Academic: Dordrecht, The Nederlands, 2003. [Google Scholar]
- Constanza, R.; d’Arge, R.; de Groot, R.; Farber, S.; Grasso, M.; Hannon, B.; Limberg, K.; Naeem, S.; O’Neill, R.V.; Paruelo, J.; et al. The value of the world’s ecosystem service and natural capital. Ecol. Econ. 1997, 25, 3–15. [Google Scholar] [CrossRef]
- Donato, D.C.; Kauffman, J.B.; Murdiyarso, D.; Kurnianto, S.; Stidham, M.; Kanninen, M. Mangroves among the most carbon–rich forests in the tropics. Nat. Geosci. 2011, 4, 293–297. [Google Scholar] [CrossRef]
- Barbier, E.B.; Hacker, S.D.; Kennedy, C.; Koch, E.W.; Stier, A.C.; Silliman, B.R. The value of estuarine and coastal ecosystem services. Ecol. Monogr. 2011, 81, 169–193. [Google Scholar] [CrossRef]
- Hickey, S.M.; Callow, N.J.; Phinn, S.; Lovelock, C.E.; Duarte, C.M. Spatial complexities in aboveground carbon stocks of a semi–arid mangrove community: A remote sensing height–biomass–carbon approach. Estuar. Coast. Shelf Sci. 2018, 200, 194–201. [Google Scholar] [CrossRef]
- Giri, C.; Ochieng, E.; Tieszen, L.L.; Zhu, Z.; Singh, A.; Loveland, T.; Masek, J.; Duke, N. Status and distribution of mangrove forests of the world using earth observation satellite data. Glob. Ecol. Biogeogr. 2011, 20, 154–159. [Google Scholar] [CrossRef]
- Hamilton, S.E.; Friess, D.A. Global carbon stocks and potential emissions due to mangrove deforestation from 2000 to 2012. Nat. Clim. Chang. 2018, 8, 240–244. [Google Scholar] [CrossRef]
- Fehrmann, L.; Kleinn, C. General considerations about the use of allometric equations for biomass estimation on the example of Norway spruce in central Europe. Ecol. Manag. 2006, 236, 412–421. [Google Scholar] [CrossRef]
- Komiyama, A.; Ong, J.E.; Poungparn, S. Allometry, biomass, and productivity of mangrove forests: A review. Aquat. Bot. 2008, 8, 128–137. [Google Scholar] [CrossRef]
- Ketterings, Q.M.; Coe, R.; van Noordwijk, M.; Ambagu, Y.; Palm, C.A. Reducing uncertainty in use of allometric biomass equations for predicting above–ground tree biomass in mixed secondary forests. Ecol. Manag. 2001, 146, 199–202. [Google Scholar] [CrossRef]
- Overman, J.P.M.; Witte, H.J.L.; Saldarriaga, J.G. Evaluation of regression models for above–ground biomass determination in Amazon rainforest. J. Trop. Ecol. 1994, 10, 207–218. [Google Scholar] [CrossRef]
- Proisy, C.; Couteron, P.; Fromard, F. Predicting and mapping mangrove biomass from canopy grain analysis using Fourier–based textural ordination of IKONOS images. Remote Sens. Environ. 2007, 109, 379–392. [Google Scholar] [CrossRef]
- Jachowski, N.R.A.; Quak, M.S.Y.; Friess, D.A.; Duangnamon, D.; Webb, E.; Ziegler, A.D. Mangrove biomass estimation in Southwest Thailand using machine learning. Appl. Geogr. 2013, 45, 311–321. [Google Scholar] [CrossRef]
- Hamdan, O.; Aziz, H.K.; Hasmadi, I.M. L–band ALOS PALSAR for biomass estimation of Matang Mangroves, Malaysia. Remote Sens. Environ. 2014, 155, 69–78. [Google Scholar] [CrossRef]
- Hartoko, A.; Chayaningrum, S.; Febrianti, D.A.; Ariyanto, D. Carbon biomass algorithms development for mangrove vegetation in Kemujan, Parang Island Karimunjawa National Park and Demak Coastal Area—Indonesia. Procedia Environ. Sci. 2015, 23, 39–47. [Google Scholar] [CrossRef]
- Aslan, A.; Rahman, A.F.; Warren, M.W.; Robeson, S.M. Mapping spatial distribution and biomass of coastal wetland vegetation in Indonesian Papua by combining active and passive remotely sensed data. Remote Sens. Environ. 2016, 183, 65–81. [Google Scholar] [CrossRef]
- Castillo, J.A.A.; Apan, A.A.; Maraseni, T.N.; Salmo, S.G., III. Estimation and mapping of above–ground biomass of mangrove forests and their replacement land uses in the Philippines using Sentinel imagery. ISPRS J. Photogramm. Remote Sens. 2017, 134, 70–85. [Google Scholar] [CrossRef]
- Pham, L.T.H.; Brabyn, L. Monitoring mangrove biomass change in Vietnam using SPOT images and an object–based approach combined with machine learning algorithms. ISPRS J. Photogramm. Remote Sens. 2017, 128, 86–97. [Google Scholar] [CrossRef]
- Dalponte, M.; Frizzera, L.; Ørka, H.O.; Gobakken, T.; Næsset, E.; Gianelle, D. Predicting stem diameters and aboveground biomass of individual trees using remote sensing data. Ecol. Indic. 2018, 85, 367–376. [Google Scholar] [CrossRef]
- Owers, C.J.; Rogers, K.; Woodroffe, C.D. Terrestrial laser scanning to quantify above–ground biomass of structurally complex coastal wetland vegetation. Estuar. Coast. Shelf Sci. 2018, 204, 164–176. [Google Scholar] [CrossRef]
- Demir, N. Using UAVs for detection of trees from digital surface models. J. For. Res. 2018, 29, 813–821. [Google Scholar] [CrossRef]
- Kestur, R.; Angural, A.; Bashir, B.; Omkar, S.N.; Anand, G.; Meenavathi, M.B. Tree Crown Detection, Delineation and Counting in UAV Remote Sensed Images: A Neural Network Based Spectral–Spatial Method. J. Indian Soc. Remote Sens. 2018, 46, 991–1004. [Google Scholar] [CrossRef]
- Disney, M.; Burt, A.; Calders, K.; Schaaf, C.; Stovall, A. Innovations in ground and airborne technologies as reference and for training and validation: Terrestrial laser scanning (TLS). Surv. Geophys. 2019. [Google Scholar] [CrossRef]
- Kędra, K.; Barbeito, I.; Dassot, M.; Vallet, P.; Gazda, A. Single–image photogrammetry for deriving tree architectural traits in mature forest stands: A comparison with terrestrial laser scanning. Ann. For. Sci. 2019, 76, 5. [Google Scholar] [CrossRef]
- Carrijo, J.V.N.; de Freitas Ferreira, A.B.; Ferreira, M.C.; de Aguiar, M.C.; Miguel, E.P.; Matricardi, E.A.T.; Rezende, A.V. The growth and production modeling of individual trees of Eucalyptus urophylla plantations. J. For. Res. 2019. [Google Scholar] [CrossRef]
- Yin, D.; Wang, L. Individual mangrove tree measurement using UAV–based LiDAR data: Possibilities and challenges. Remote Sens. Environ. 2019, 223, 34–49. [Google Scholar] [CrossRef]
- Shao, Z.F.; Zhang, L.J.; Wang, L. Stacked sparse autoencoder modeling using the synergy of airborne LiDAR and satellite optical and SAR data to map forest above-ground biomass. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5569–5582. [Google Scholar] [CrossRef]
- Baral, S. Mapping Carbon Stock Using High Resolution Satellite Images in Sub–Tropical Forest of Nepal; University of Twente University of Faculty of Geo-Information and Earth Observation (ITC): Enschede, The Netherlands, 2011. [Google Scholar]
- Maharjan, S. Estimation and Mapping above Ground Woody Carbon Stocks Using LiDAR Data and Digital Camera Imagery in the Hilly Forests of Gorkha, Nepal; University of Twente University of Faculty of Geo-Information and Earth Observation (ITC): Enschede, The Netherlands, 2012. [Google Scholar]
- Karna, Y.K.; Hussin, Y.A.; Gilani, H.; Bronsveld, M.C.; Murthy, M.S.R.; Qamer, F.M.; Karky, B.S.; Bhattarai, T.; Aigong, X.; Baniya, C.B. Integration of WorldView–2 and airborne LiDAR data for tree species level carbon stock mapping in Kayar Khola watershed, Nepal. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 280–291. [Google Scholar] [CrossRef]
- Zhang, L.; Shao, Z.; Liu, J.; Cheng, Q. Deep learning based retrieval of forest aboveground biomass from combined lidar and landsat 8 data. Remote Sens. 2019, 11, 1459. [Google Scholar] [CrossRef]
- Nandy, S.; Ghosh, S.; Kushwaha, S.P.S.; Kumar, A.S. Remote sensing–based forest biomass assessment in northwest Himalayan landscape. In Remote Sensing of Northwest Himalayan Ecosystems; Navalgund, R.R., Kumar, A.S., Nandy, S., Eds.; Springer: Singapore, 2019. [Google Scholar]
- Meyer, V.; Saatchi, S.; Ferraz, A.; Xu, L.; Duque, A.; García, M.; Chave, J. Forest degradation and biomass loss along the Chocó region of Colombia. Carbon Balance Manag. 2019, 14, 2. [Google Scholar] [CrossRef]
- Kellner, J.R.; Armston, J.; Birrer, M.; Cushman, K.C.; Duncanson, L.; Eck, C.; Falleger, C.; Imbach, B.; Král, K.; Krůček, M.; et al. New Opportunities for Forest Remote Sensing Through Ultra High Density Drone LiDAR. Surv. Geophys. 2019. [Google Scholar] [CrossRef]
- Hamilton, S.E.; Castellanos–Galindo, G.A.; Millones–Mayer, M.; Chen, M. Remote sensing of mangrove forests: Current techniques and existing databases. In Threats to Mangrove Forests; Makowski, C., Finkl, C.W., Eds.; Coastal Research Library: Boca Raton, FL, USA, 2018; Volume 25, pp. 497–520. [Google Scholar]
- Fragoso–Campón, L.; Quirós, E.; Mora, J.; Gallego, J.A.G.; Durán–Barroso, P. Overstory–understory land cover mapping at the watershed scale: Accuracy enhancement by multitemporal remote sensing analysis and LiDAR. Environ. Sci. Pollut. Res. 2019. [Google Scholar] [CrossRef] [PubMed]
- Cintron, G.; Schaeffer–Novelli, S.Y. Methods for studying Mangrove structure. In The Mangrove Ecosystems: Research Methods; Snedaker, S.C., Snedaker, J., Eds.; UNESCO: Paris, France, 1984; pp. 91–113. [Google Scholar]
- Clough, B.F.; Scott, K. Allometric relationships for estimating above–ground biomass in six mangrove species. For. Ecol. Manag. 1989, 27, 117–127. [Google Scholar] [CrossRef]
- Hossain, M.; Siddique, M.R.H.; Saha, S.; Abdullah, S.M.R. Allometric models for biomass, nutrients and carbon stock in Excoecaria agallocha of the Sundarbans, Bangladesh. Wetl. Ecol. Manag. 2015, 23, 765–774. [Google Scholar] [CrossRef]
- Ong, J.E.; Gong, W.K.; Wong, C.H. Allometry and partitioning of the mangrove, Rhizophora apiculata. For. Ecol. Manag. 2004, 188, 395–408. [Google Scholar] [CrossRef]
- Fromard, F.; Puig, H.; Mougin, E.; Marty, G.; Betoulle, J.L.; Cadamuro, L. Structure of above–ground biomass and dynamics of mangrove ecosystems: New data from French Guiana. Oecologia 1998, 115, 39–53. [Google Scholar] [CrossRef]
- Tam, N.F.Y.; Wong, Y.S.; Lan, C.Y.; Chen, G.Z. Community structure and standing crop biomass of a mangrove forest in Futian Nature Reserve, Shenzhen, China. Hydrobiologia 1995, 295, 193–201. [Google Scholar] [CrossRef]
- Kusmana, C.; Hidayat, T.; Tiryana, T.; Rusdiana, O. Allometric models for above-and below–ground biomass of Sonneratia spp. Glob. Ecol. Conserv. 2018, 15, e00417. [Google Scholar] [CrossRef]
- Komiyama, A.; Poungparn, S.; Kato, S. Common allometric equations for estimating the tree weight of mangroves. J. Trop. Ecol. 2005, 21, 471–477. [Google Scholar] [CrossRef]
- Wang, D.; Wan, B.; Qiu, P.; Su, Y.; Guo, Q.; Wang, R.; Sun, F.; Wu, X. Evaluating the Performance of Sentinel-2, Landsat 8 and Pléiades-1 in Mapping Mangrove Extent and Species. Remote Sens. 2018, 10, 1468. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Leboeuf, A.; Beaudoin, A.; Fournier, R.A.; Guindon, L.; Luther, J.E.; Lambert, M.-C. A shadow fraction method for mapping biomass of northern boreal black spruce forests using QuickBird imagery. Remote Sens. Environ. 2007, 110, 488–500. [Google Scholar] [CrossRef]
- Holmgren, J.; Persson, A.; Söderman, U. Species identification of individual trees by combining high resolution LiDAR data with multi–spectral images. Int. J. Remote Sens. 2008, 29, 1537–1552. [Google Scholar] [CrossRef]
- Othmani, A.; Piboule, A.; Krebs, M.; Stolz, C.; Voon, L.L.Y. Towards automated and operational forest inventories with T–LiDAR. In Proceedings of the 11th International Conference on LiDAR Applications for Assessing Forest Ecosystems (SilviLaser 2011), Hobart, Australia, 16–20 October 2011. [Google Scholar]
- Sousa, A.M.O.; Gonçalves, A.C.; Mesquita, P.; da Silva, J.R.M. Biomass estimation with high resolution satellite images: A case study of Quercus rotundifolia. ISPRS J. Photogramm. Remote Sens. 2015, 101, 69–79. [Google Scholar] [CrossRef]
- Aihua Li Glenn, N.F.; Olsoy, P.J.; Mitchell, J.J.; Shrestha, R. Aboveground biomass estimates of sagebrush using terrestrial and airborne LiDAR data in a dryland ecosystem. Agric. For. Meteorol. 2015, 213, 138–147. [Google Scholar]
- Dalponte, M.; Coomes, D.A. Tree–centric mapping of forest carbon density from airborne laser scanning and hyperspectral data. Methods Ecol. Evol. 2016, 7, 1236–1245. [Google Scholar] [CrossRef]
- Stovall, A.E.L.; Anderson–Teixeira, K.J.; Shugart, H.H. Assessing terrestrial laser scanning for developing non–destructive biomass allometry. For. Ecol. Manag. 2018, 427, 217–229. [Google Scholar] [CrossRef]
- Bazezew, M.N.; Hussin, Y.A.; Kloosterman, E.H. Integrating airborne LiDAR and terrestrial laser scanner forest parameters for accurate above–ground biomass/carbon estimation in Ayer Hitam tropical forest, Malaysia. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 638–652. [Google Scholar] [CrossRef]
- Wang, L.; Gong, P.; Biging, G.S. Individual tree–crown delineation and treetop detection in high–spatial–resolution aerial imagery. Photogramm. Eng. Remote Sens. 2004, 70, 351–357. [Google Scholar] [CrossRef]
- Duro, D.C.; Franklin, S.E.; Dubé, M.G. A comparison of pixel-based and object-based image analysis with selected machine learning algorithms for the classification of agricultural landscapes using SPOT-5 HRG imagery. Remote Sens. Environ. 2012, 118, 259–272. [Google Scholar] [CrossRef]
- Yin, D.; Wang, L. How to assess the accuracy of the individual tree-based forest inventory derived from remotely sensed data: A review. Int. J. Remote Sens. 2016, 37, 4521–4553. [Google Scholar] [CrossRef]
- Strîmbu, V.F.; Strîmbu, B.M. A graph-based segmentation algorithm for tree crown extraction using airborne LiDAR data. ISPRS J. Photogramm. Remote Sens. 2015, 104, 30–43. [Google Scholar] [CrossRef]
- Zhou, T.; Popescu, S.; Lawing, A.; Eriksson, M.; Strimbu, B.; Bürkner, P. Bayesian and classical machine learning methods: A comparison for tree species classification with LiDAR waveform signatures. Remote Sens. 2018, 10, 39. [Google Scholar] [CrossRef]
- Pouliot, D.A.; King, D.J.; Bell, F.W.; Pitt, D.G. Automated tree crown detection and delineation in high-resolution digital camera imagery of coniferous forest regeneration. Remote Sens. Environ. 2002, 82, 322–334. [Google Scholar] [CrossRef]
- Kusmana, C.; Sabiham, S.; Abe, K.; Watanabe, H. An estimation of above ground tree biomass of a mangrove forest in East Sumatra, Indonesia. Tropics. 1992, 1, 243–257. [Google Scholar] [CrossRef]
- Mitra, A.; Zaman, S. Abiotic Variables of the Marine and Estuarine Ecosystems. In Basics of Marine and Estuarine Ecology; Mitra, A., Zaman, S., Eds.; Springer: New Delhi, India, 2016; pp. 182–184. [Google Scholar]
- Zan, Q.J.; Wang, Y.J.; Liao, B.W.; Zheng, D.Z. Biomass and net productivity of Sonneratia apetala, S. caseolaris mangrove man-made forest. J. Wuhan Bot. Res. 2001, 19, 391–396. [Google Scholar]
- Han, W.D.; Gao, X.M.; Teunissen, E. Study on Sonneratia apetala productivity in restored forests in Leizhou Peninsula, China. J. For. Res. 2001, 12, 229–234. [Google Scholar]
- Komiyama, A.; Ogino, K.; Aksomkoae, S.; Sabhasri, S. Root biomass of a mangrove forest in southern Thailand 1: Estimation by the trench method and the zonal structure of root biomass. J. Trop. Ecol. 1987, 3, 97–108. [Google Scholar] [CrossRef]
- Mall, L.P.; Singh, V.P.; Garge, A. Study of biomass, litter fall, litter decomposition and soil respiration in monogeneric mangrove and mixed mangrove forests of Andaman Islands. Trop. Ecol. 1991, 32, 144–152. [Google Scholar]
- Alongi, D.M.; Dixon, P. Mangrove primary production and above and below–Ground biomass in Sawi Bay, southern Thailand. Phuket Mar. Biol. Cent. Spec. Publ. 2000, 22, 31–38. [Google Scholar]
- Phan, S.M.; Nguyen, H.T.T.; Nguyen, T.K.; Lovelock, C. Modelling above ground biomass accumulation of mangrove plantations in Vietnam. For. Ecol. Manag. 2019, 432, 376–386. [Google Scholar] [CrossRef]
- Putz, F.; Chan, H.T. Tree growth, dynamics, and productivity in a mature mangrove forest in Malaysia. For. Ecol. Manag. 1986, 17, 211–230. [Google Scholar] [CrossRef]
- Komiyama, A.; Moriya, H.; Prawiroatmodjo, S.; Toma, T.; Ogino, K. Forest primary productivity. In Biological System of Mangrove; Ogino, K., Chihara, M., Eds.; Ehime University: Matsuyama, Japan, 1988; pp. 97–117. [Google Scholar]


| Species | Count | Density (Individuals·100 m−2) | RD (%) | F (%) | ReF (%) | BA (m2) | Dominance (m2 ha−1) | RDo (%) | IVI |
|---|---|---|---|---|---|---|---|---|---|
| B. sexangula | 1063 | 8.93 | 27.74 | 67.31 | 20.02 | 16.514 | 13.877 | 46.75 | 31.50 |
| E. agallocha | 694 | 5.83 | 18.11 | 71.11 | 21.15 | 4.462 | 3.750 | 12.63 | 17.30 |
| H. tiliaceus | 250 | 2.10 | 6.53 | 35.56 | 10.58 | 1.371 | 1.152 | 3.88 | 7.00 |
| H. littoralis | 18 | 0.15 | 0.47 | 4.44 | 1.32 | 1.187 | 0.997 | 3.36 | 1.72 |
| X. granatum | 98 | 0.82 | 2.56 | 31.11 | 9.25 | 0.887 | 0.745 | 2.51 | 4.77 |
| R. apiculata | 402 | 3.38 | 10.49 | 35.56 | 10.58 | 3.938 | 3.309 | 11.15 | 10.74 |
| A. corniculatum | 469 | 3.94 | 12.24 | 8.89 | 2.64 | 0.655 | 0.550 | 1.85 | 5.58 |
| K. candel | 4 | 0.03 | 0.10 | 6.67 | 1.98 | 0.009 | 0.007 | 0.03 | 0.70 |
| L. racemosa | 543 | 4.56 | 14.17 | 28.89 | 8.59 | 1.516 | 1.274 | 4.29 | 9.02 |
| C. tagal | 112 | 0.94 | 2.92 | 2.22 | 0.66 | 0.213 | 0.179 | 0.60 | 1.39 |
| S. ovata | 50 | 0.42 | 1.31 | 13.33 | 3.97 | 1.453 | 1.221 | 4.12 | 3.13 |
| S. apetala | 48 | 0.40 | 1.25 | 13.33 | 3.97 | 1.859 | 1.562 | 5.26 | 3.49 |
| S. alba | 81 | 0.68 | 2.11 | 17.78 | 5.29 | 1.259 | 1.058 | 3.57 | 3.66 |
| Total | 3832 | 32.20 | 100.00 | 336.20 | 100.00 | 35.322 | 29.682 | 100.00 | 100.00 |
| No. | Species | Allometric Equations | References |
|---|---|---|---|
| 1 | B. sexangula | AGB = 0.168 × DBH2.42 | [38] |
| 2 | E. agallocha | LogAGB = 1.0996 × logDBH2 − 0.8572 | [39] |
| 3 | R. apiculata | AGB = 0.235 × DBH2.420 | [40] |
| 4 | C. tagal | AGB = 0.1885 × DBH2.3379 | [38] |
| 5 | L. racemosa | AGB = 0.1023 × DBH2.50 | [41] |
| 6 | A. corniculatum | LogAGB = 1.496 + 0.465 × log (DBH2 × H) | [42] |
| 7 | X. granatum | AGB = 0.0823 × DBH2.5883 | [38] |
| 8 | K. candel | LogAGB = 2.814 + 1.053 × log (DBH2 × H) | [42] |
| 9 | Sonneratia spp. (S. ovata, S. apetala, and S. alba) | AGB = 0.258 × DBH2.287 | [43] |
| 10 | Others (H. littoralis, H. tiliaceus) | AGB = 0.251 × ρ × DBH2.46 | [44] |
| LiDAR Metrics | Explanation |
|---|---|
| CC1.3 | Canopy cover above 1.3 m. |
| HSD | Standard deviation of heights. |
| D01 | The number of canopy return points in the 1th slice relative to the total points. There are 12 density metrics in this study from 0 to 24 m with an interval of 2 m |
| HVAR | Variance of heights. |
| HIQ | Interquartile distance of percentile height. |
| H05 | The 5th percentile of height. |
| H10 | The 10th percentile of height. |
| H80 | The 80th percentile of height. |
| H90 | The 90th percentile of height. |
| H95 | The 95th percentile of height. |
| CTHK | Canopy thickness. |
| Number of Mismatches | Number of Segmentations | TA | |||
|---|---|---|---|---|---|
| Type | Commission | Omission | Sum | ||
| Number | 221 | 47 | 268 | 2132 | 87.43% |
| Ratio (%) | 10.37 | 2.2 | 12.57 | ||
| Scenario | Item | |Di| ≤ 0.1 | 0.1 < |Di| ≤ 0.2 | 0.2 < |Di| ≤ 0.3 | 0.3 < |Di| ≤ 0.4 | |Di| > 0.4 | Total | DA |
|---|---|---|---|---|---|---|---|---|
| All species except A. corniculatum | No. plots | 5 | 7 | 5 | 9 | 19 | 45 | |
| Percentage (%) | 11.11 | 15.56 | 11.11 | 20.00 | 42.22 | 100.00 | 57.78 | |
| No. OS plots | 1 | 1 | 0 | 0 | 4 | 6 | ||
| No. US plots | 4 | 6 | 5 | 9 | 15 | 39 | ||
| All species | No. plots | 4 | 7 | 4 | 8 | 22 | 45 | |
| Percentage (%) | 8.89 | 15.56 | 8.89 | 17.78 | 48.89 | 100.00 | 51.11 | |
| No. OS plots | 1 | 1 | 0 | 0 | 3 | 5 | ||
| No. US plots | 3 | 6 | 4 | 8 | 19 | 40 |
| Predicted | Producer Accuracy (%) | User Accuracy (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BS | EA | HT | LR | RA | SS | Sum | ||||
| Observed | BS | 470 | 14 | 1 | 3 | 18 | 4 | 510 | 92.16 | 82.89 |
| EA | 37 | 158 | 15 | 3 | 13 | 0 | 226 | 69.91 | 74.53 | |
| HT | 6 | 26 | 219 | 2 | 4 | 5 | 262 | 83.59 | 90.12 | |
| LR | 3 | 7 | 1 | 321 | 11 | 11 | 354 | 90.68 | 93.31 | |
| RA | 51 | 7 | 6 | 10 | 165 | 10 | 249 | 66.27 | 74.66 | |
| SS | 0 | 0 | 1 | 5 | 10 | 423 | 439 | 96.36 | 93.38 | |
| Sum | 567 | 212 | 243 | 344 | 221 | 453 | 2040 | Overall accuracy = 86.08% | ||
| Species | Mean Tree Height (m) | Patch Number | Mean Area of Patches (m2) | Total Area (ha) | Percentage of Total Area (%) |
|---|---|---|---|---|---|
| BS | 8.00 | 117,413 | 6.26 | 73.53 | 35.01 |
| EA | 5.03 | 76,348 | 5.21 | 39.81 | 18.96 |
| SS | 7.84 | 42,738 | 6.03 | 25.78 | 12.28 |
| RA | 6.90 | 41,450 | 6.24 | 25.88 | 12.32 |
| HT | 5.85 | 40,334 | 6.19 | 24.95 | 11.88 |
| LR | 3.78 | 50,467 | 3.97 | 20.05 | 9.55 |
| Sum | 6.43 | 368,750 | 5.69 | 209.99 | 100.00 |
| Level 1 | Level 2 | Level 3 | Level 4 | Level 5 | ||
|---|---|---|---|---|---|---|
| BS | Height | <5.54 | 5.54–7.48 | 7.48–8.91 | 8.91–10.94 | 10.94–19.21 |
| AGB | 27.03 | 77.99 | 112.32 | 261.87 | 363.65 | |
| EA | Height | <3.61 | 3.61–4.77 | 4.77–5.89 | 5.89–7.51 | 7.51–15.77 |
| AGB | 16.62 | 36.53 | 45.25 | 58.53 | 71.04 | |
| HT | Height | <4.77 | 4.77–6.34 | 6.34–8.17 | 8.17–10.82 | 10.82–19.53 |
| AGB | 30.93 | 48.92 | 78.49 | 95.27 | 174.47 | |
| LR | Height | <3.25 | 3.25–4.33 | 4.33–5.25 | 5.25–6.07 | 6.07–8.81 |
| AGB | 13.19 | 16.76 | 23.27 | 30.58 | 38.08 | |
| RA | Height | <5.64 | 5.64–7.46 | 7.44–9.46 | 9.46–12.15 | 12.15–20.20 |
| AGB | 61.47 | 110.60 | 191.81 | 245.74 | 270.73 | |
| SS | Height | <5.92 | 5.92–8.85 | 8.85–11.33 | 11.33–14.20 | 14.20–21.85 |
| AGB | 50.14 | 145.83 | 465.34 | 654.25 | 747.58 | |
| Individual Tree-Based Inference Method | Grid-Based RF Model Method | |
|---|---|---|
| Merits | (1) The AGB is extrapolated on the basis of species, height stratification. The precise tree height can be obtained from LiDAR point cloud data. (2) Finer estimation and mapping of biomass can be conducted on the tree scale, which is more conducive to accurate and differentiated management. (3) Producing large amount of data and detail expression, so it is suitable for application in management or management decision-making in small or specific areas. | (1) Using the RF selection of LiDAR indexes, the relationship of AGB = f (LiDAR indexes) is constructed, and the equal area extrapolation of sample-plot AGB is conducted. (2) The method is relatively mature, and it is the popular method for AGB estimation and mapping at present. (3) The amount of data produced is moderate, the operation speed is fast, and it is suitable for application in government decision-making at the regional level. |
| Demerits | (1) The extrapolation of AGB lacks a strictly mathematical model. And using tree height stratification to extrapolate AGB, it implies a premise that there is an internal relationship between tree height and AGB, but how this relationship is still not clear. (2) Owing to the survival competition of cluster mangroves, the individuals may tend to have taller tree height, but not necessarily have larger DBH. The AGB estimated by species-specific allometric models based on DBH is also not necessarily suitable for the AGB estimation based on height stratification. (3) Because the individual tree segmentation is mainly based on the CHM layer, the AGB of the lower wood layer under the CHM layer may be ignored. | (1) The AGB extrapolation method is affected by the distribution details of gaps or non-trees in sample plots. (2) AGB estimation based on LiDAR indices focus on the external structural characteristics of plants, such as tree height, and crown width, while neglecting the inherent characteristics of plants, such as wood density, which affects the accuracy of AGB estimation. (3) This extrapolation is not conducive to the fine expression of AGB at the mangrove plant type and individual tree level. |
| Commonground | The initial AGB values for extrapolation depend on the estimation of species-specific allometric models in the field survey. | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, P.; Wang, D.; Zou, X.; Yang, X.; Xie, G.; Xu, S.; Zhong, Z. Finer Resolution Estimation and Mapping of Mangrove Biomass Using UAV LiDAR and WorldView-2 Data. Forests 2019, 10, 871. https://doi.org/10.3390/f10100871
Qiu P, Wang D, Zou X, Yang X, Xie G, Xu S, Zhong Z. Finer Resolution Estimation and Mapping of Mangrove Biomass Using UAV LiDAR and WorldView-2 Data. Forests. 2019; 10(10):871. https://doi.org/10.3390/f10100871
Chicago/Turabian StyleQiu, Penghua, Dezhi Wang, Xinqing Zou, Xing Yang, Genzong Xie, Songjun Xu, and Zunqian Zhong. 2019. "Finer Resolution Estimation and Mapping of Mangrove Biomass Using UAV LiDAR and WorldView-2 Data" Forests 10, no. 10: 871. https://doi.org/10.3390/f10100871
APA StyleQiu, P., Wang, D., Zou, X., Yang, X., Xie, G., Xu, S., & Zhong, Z. (2019). Finer Resolution Estimation and Mapping of Mangrove Biomass Using UAV LiDAR and WorldView-2 Data. Forests, 10(10), 871. https://doi.org/10.3390/f10100871






