Uncertainty in Forest Net Present Value Estimations
Abstract
:1. Introduction
2. Objective
3. Material and Methods
3.1. Data
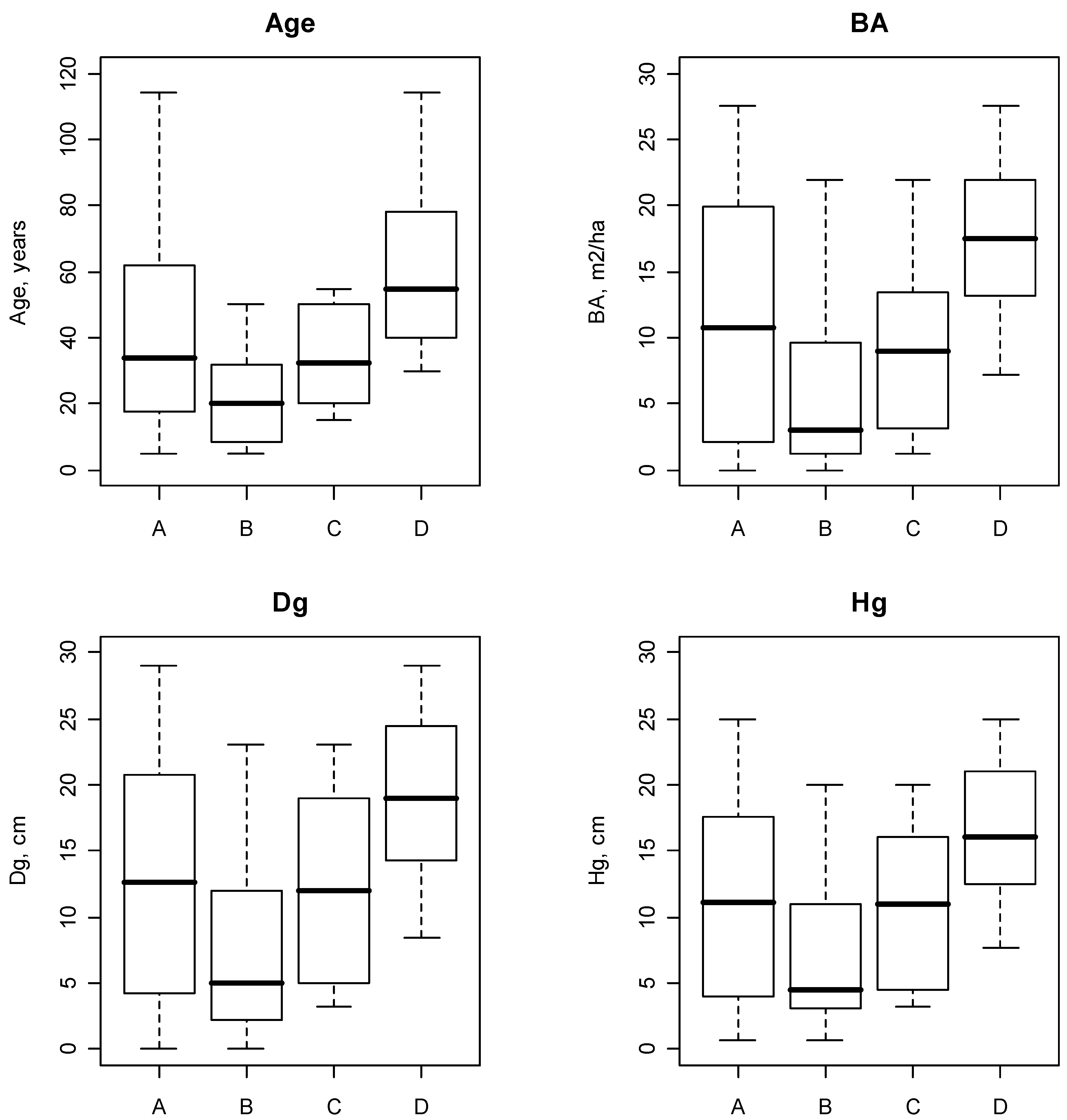
3.2. Simulation of the Sources of Uncertainty
3.3. Analysis of the Uncertainty
4. Results
| 3 % | 4 % | 5 % | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Forest property | Uinventory | Ugrowth | Uprice | meanNPV | BIAS%NPV | SD%NPV | meanNPV | BIAS%NPV | SD%NPV | meanNPV | BIAS%NPV | SD%NPV |
| A | • | 142,140.9 | 12.2 | 5.1 | 123,038.6 | 14.4 | 6.5 | 112,439.9 | 18.1 | 7.6 | ||
| A | • | 128,507.9 | 1.4 | 1.7 | 109,728.8 | 2.1 | 1.3 | 97,236.1 | 2.1 | 1.4 | ||
| A | • | 124,846.2 | −1.5 | 3.4 | 106,930.3 | −0.5 | 2.4 | 95,661.8 | 0.5 | 2.0 | ||
| A | • | • | • | 143,469.5 | 13.2 | 6.5 | 125,119.5 | 16.4 | 6.4 | 115,839.1 | 21.7 | 6.8 |
| B | • | 87,042.1 | 8.9 | 7.4 | 63,659.0 | 16.5 | 9.9 | 49,849.9 | 24.3 | 11.1 | ||
| B | • | 79,864.9 | −0.1 | 4.1 | 55,853.2 | 2.2 | 3.6 | 41,231.2 | 2.8 | 4.4 | ||
| B | • | 76,160.0 | −4.7 | 5.8 | 52,502.4 | −3.9 | 4.7 | 39,230.1 | −2.1 | 4.8 | ||
| B | • | • | • | 84,661.3 | 5.9 | 9.3 | 62,515.1 | 14.4 | 9.8 | 49,896.3 | 24.5 | 12.6 |
| C | • | 120,940.7 | 13.5 | 7.5 | 95,619.7 | 19.7 | 9.4 | 80,878.8 | 29.6 | 12.0 | ||
| C | • | 107,330.0 | 0.7 | 3.2 | 81,492.2 | 2.0 | 3.1 | 64,357.0 | 3.2 | 3.3 | ||
| C | • | 103,493.5 | −2.9 | 6.4 | 78,387.9 | −1.9 | 4.9 | 62,126.2 | −0.4 | 4.6 | ||
| C | • | • | • | 118,141.0 | 10.9 | 9.4 | 95,007.3 | 19.0 | 9.7 | 80,928.5 | 29.7 | 10.9 |
| D | • | 204,107.4 | 14.1 | 5.8 | 186,286.6 | 15.4 | 7.2 | 177,365.5 | 18.6 | 8.1 | ||
| D | • | 183,501.9 | 2.6 | 1.5 | 165,762.0 | 2.7 | 1.3 | 153,543.8 | 2.7 | 1.3 | ||
| D | • | 179,539.0 | 0.4 | 3.6 | 162,407.2 | 0.6 | 2.3 | 151,240.5 | 1.2 | 1.9 | ||
| D | • | • | • | 209,108.8 | 16.9 | 7.3 | 191,775.9 | 18.8 | 7.4 | 184,321.2 | 23.3 | 7.3 |
| 3 % | 4 % | 5 % | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Forest property | Uinventory | Ugrowth | Uprice | meanNPV | BIAS%NPV | SD%NPV | meanNPV | BIAS%NPV | SD%NPV | meanNPV | BIAS%NPV | SD%NPV |
| A | • | 5,685.6 | 12.2 | 25.9 | 4,921.5 | 14.4 | 30.4 | 4497.6 | 18.1 | 33.6 | ||
| A | • | 5,140.3 | 1.4 | 15.3 | 4,389.2 | 2.1 | 15.5 | 3889.4 | 2.1 | 18.8 | ||
| A | • | 4,993.8 | −1.5 | 9.9 | 4,277.2 | −0.5 | 9.1 | 3826.5 | 0.5 | 8.7 | ||
| A | • | • | • | 5,738.8 | 13.2 | 32.8 | 5,004.8 | 16.4 | 35.3 | 4633.6 | 21.7 | 39.3 |
| B | • | 3,481.7 | 8.9 | 22.9 | 2,546.4 | 16.5 | 27.7 | 1994.0 | 24.3 | 29.6 | ||
| B | • | 3,194.6 | −0.1 | 20.6 | 2,234.1 | 2.2 | 20.5 | 1649.2 | 2.8 | 24.6 | ||
| B | • | 3,046.4 | −4.7 | 12.6 | 2,100.1 | −3.9 | 11.6 | 1569.2 | −2.1 | 11.6 | ||
| B | • | • | • | 3,386.5 | 5.9 | 34.8 | 2,500.6 | 14.4 | 38.1 | 1995.9 | 24.5 | 41.8 |
| C | • | 4,837.6 | 13.5 | 29.7 | 3,824.8 | 19.7 | 35.0 | 3235.2 | 29.6 | 40.8 | ||
| C | • | 4,293.2 | 0.7 | 17.7 | 3,259.7 | 2.0 | 16.9 | 2574.3 | 3.2 | 20.2 | ||
| C | • | 4,139.7 | −2.9 | 11.2 | 3,135.5 | −1.9 | 9.8 | 2485.0 | −0.4 | 9.3 | ||
| C | • | • | • | 4,725.6 | 10.9 | 37.1 | 3,800.3 | 19.0 | 41.1 | 3237.1 | 29.7 | 46.4 |
| D | • | 8,164.3 | 14.1 | 30.4 | 7,451.5 | 15.4 | 35.4 | 7094.6 | 18.6 | 40.9 | ||
| D | • | 7,340.1 | 2.6 | 8.6 | 6,630.5 | 2.7 | 9.2 | 6141.8 | 2.7 | 11.1 | ||
| D | • | 7,181.6 | 0.4 | 7.9 | 6,496.3 | 0.6 | 6.6 | 6049.6 | 1.2 | 6.0 | ||
| D | • | • | • | 8,364.4 | 16.9 | 31.2 | 7,671.0 | 18.8 | 33.7 | 7372.8 | 23.3 | 39.1 |
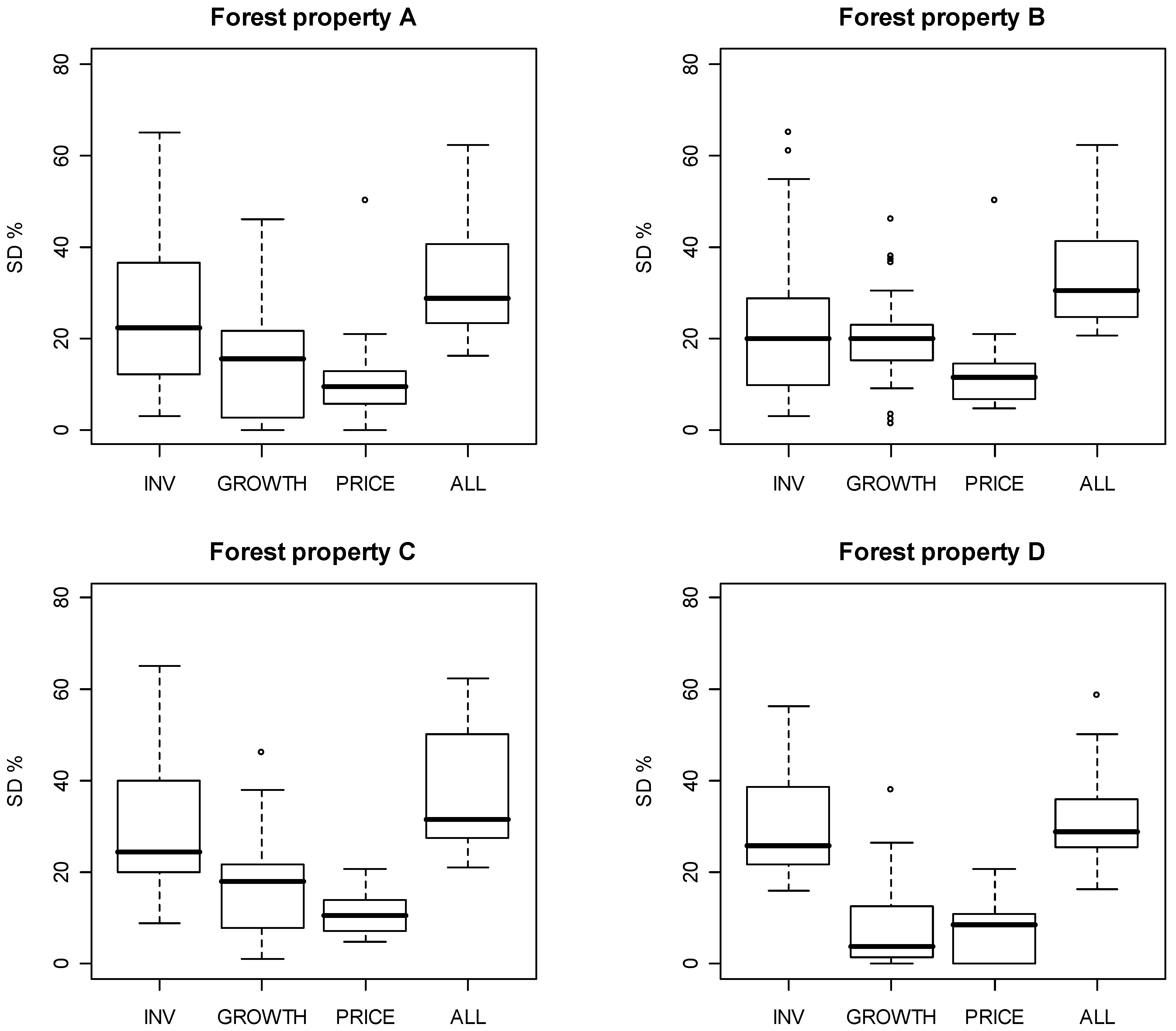
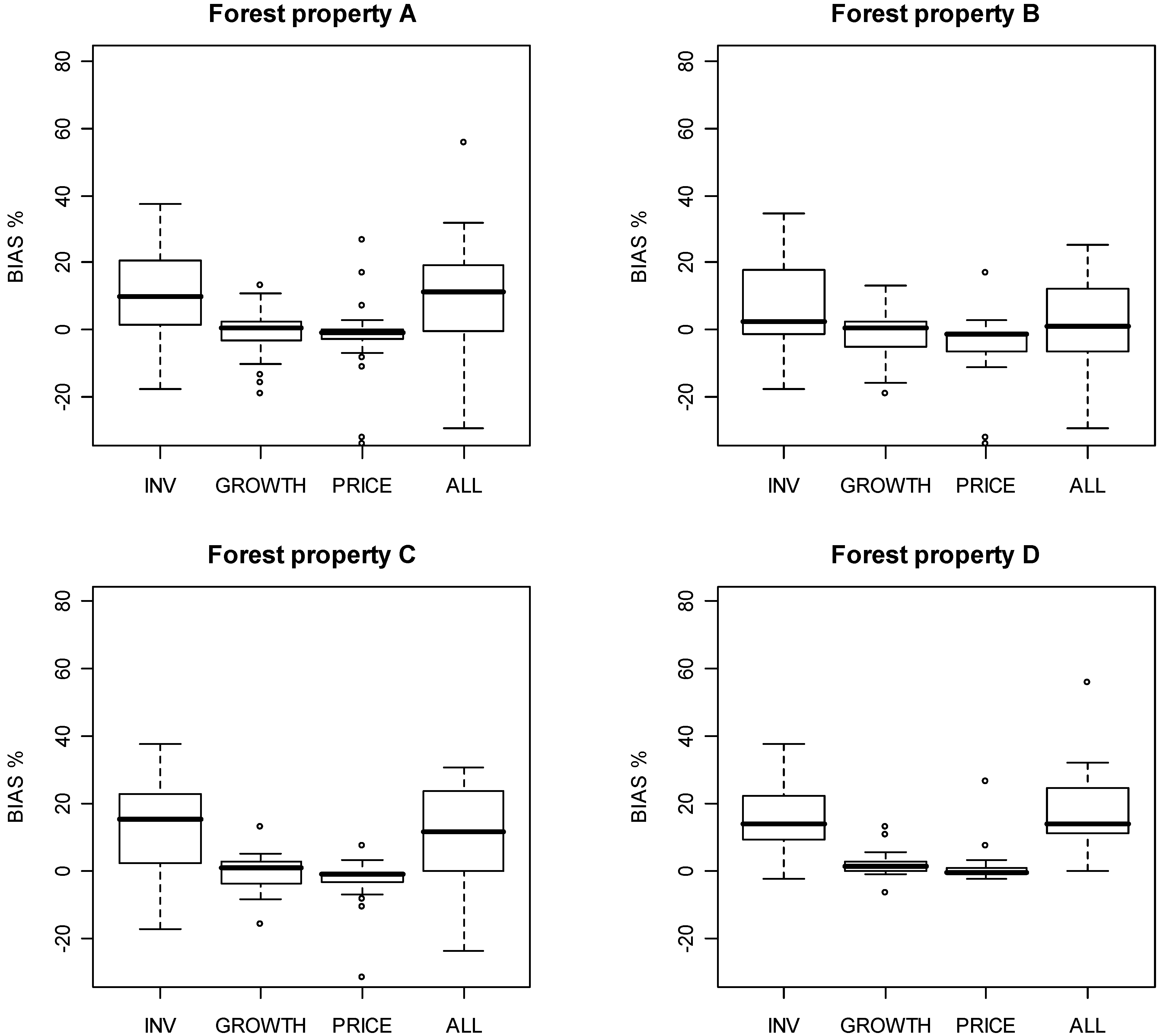
5. Discussion
6. Conclusions
Acknowledgments
References
- Holopainen, M.; Viitanen, K. Käsitteistä ja epävarmuudesta metsäkiinteistöjen taloudellisen arvon määrittämisessä. Metsätieteen aikakauskirja 2009, 2, 135–140. [Google Scholar]
- Duerr, W.A. Fundamentals of Forestry Economics; McGraw-Hill Book Company: New York, NY, USA, 1960. [Google Scholar]
- Packalén, P. Using Airborne Laser Scanning Data And Digital Aerial Photographs To Estimate Growing Stock By Tree Species. PhD thesis, Faculty of Forest Sciences, University of Joensuu, Joensuu, Sweden, 2009. [Google Scholar]
- Næsset, E. Estimating timber volume of forest stands using airborne laser scanner data. Remote Sens. Environ. 1997, 61, 246–253. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Næsset, E. Accuracy of forest inventory using airborne laser-scanning: Evaluating the first Nordic full-scale operational project. Scand. J. For. Res. 2004, 19, 554–557. [Google Scholar] [CrossRef]
- Holmgren, J. Estimation of Forest Variables Using Airborne Laser Scanning. PhD Thesis, Swedish University of Agricultural Sciences, Umeå, Sweden, 2003. [Google Scholar]
- Packalén, P.; Maltamo, M. Predicting the plot volume by tree species using airborne laser scanning and aerial photographs. Forest Sci. 2006, 56, 611–622. [Google Scholar]
- Packalén, P.; Maltamo, M. Estimation of species-specific diameter distributions using airborne laser scanning and aerial photographs. Can. J. For. Res. 2008, 38, 1750–1760. [Google Scholar] [CrossRef]
- Peuhkurinen, J.; Maltamo, M.; Malinen, J. Estimating species-specific diameter, distributions and saw log recoveries of boreal forests from airborne laser scanning data and aerial photographs: a distribution-based approach. Silva Fenn. 2008, 42, 625–641. [Google Scholar] [CrossRef]
- Holopainen, M.; Vastaranta, M.; Rasinmäki, J.; Kalliovirta, J.; Mäkinen, A.; Haapanen, R.; Melkas, T.; Yu, X.; Hyyppä, J. Uncertainty in timber assortment estimates predicted from forest inventory data. Eur. J. For. Res. 2010. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T.; Holmgren, J.; Hyyppä, H.; Hyyppä, J.; Maltamo, M.; Nilsson, M.; Olsson, H.; Persson, Å.; Söderman, U. Laser scanning of forest resources: the Nordic experience. Scand. J. For. Res. 2004, 19, 482–499. [Google Scholar] [CrossRef]
- Hyyppä, J.; Hyyppä, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of methods of small-footprint airborne laser scanning for extracting forest inventory data in boreal forests. Int. J. Remote Sens. 2008, 29, 1339–1366. [Google Scholar] [CrossRef]
- Hyyppä, J.; Hyyppä, H.; Yu, X.; Kaartinen, H.; Kukko, H.; Holopainen, M. Forest inventory using small-footprint airborne lidar. In Topographic Laser Ranging and Scanning: Principles and Processing; Shan, J., Toth, C., Eds.; CRC/ Taylor &Francis, Book News, Inc.: Portland, OR, USA, 2009; pp. 335–370. [Google Scholar]
- Koch, B.; Straub, C.; Dees, M.; Wang, Y.; Weinacker, H. Airborne laser data for stand delineation and information extraction. Int. J. Remote Sens. 2009, 30, 935–963. [Google Scholar] [CrossRef]
- Burkhart, H.E; Stuck, R.D.; Leuschner, W.A.; Reynolds, M.A. Allocating inventory resources for multiple-use planning. Can. J. For. Res. 1978, 8, 100–110. [Google Scholar] [CrossRef]
- Hamilton, D.A. Specifying precision in natural resource inventories. In Integrated Inventories of Renewable Resources: Proceedings of the Workshop; General technical report RM 55; USDA Forest Service: Tucson, AZ, USA, 1978; pp. 276–281. [Google Scholar]
- Ståhl, G. Optimizing the Utility of Forest Inventory Activities. PhD thesis, Swedish University of Agricultural Sciences, Department of Biometry and Forest Management, Umeå, Sweden, 1994. [Google Scholar]
- Eid, T. Use of uncertain inventory data in forestry scenario models and consequential incorrect harvest decisions. Silva Fenn. 2000, 34, 89–100. [Google Scholar] [CrossRef]
- Holmström, H.; Kallur, H.; Ståhl, G. Cost-plus-loss analyses of forest inventory strategies based on kNN-assigned reference sample plot data. Silva Fenn. 2003, 37, 381–398. [Google Scholar] [CrossRef]
- Eid, T.; Gobakken, T.; Næsset, E. Comparing stand inventories for large areas based on photo-interpretation and laser scanning by means of cost-plus-loss analyses. Scand. J. For. Res. 2004, 19, 512–523. [Google Scholar] [CrossRef]
- Duvemo, K.; Lämås, T. The influence of forest data quality on planning processes in forestry. Scand. J. For. Res. 2006, 21, 327–339. [Google Scholar] [CrossRef]
- Holopainen, M.; Talvitie, T. Effects of data acquisition accuracy on timing of stand harvests and expected net present value. Silva Fenn. 2006, 40, 531–543. [Google Scholar] [CrossRef]
- Barth, A. Spatially Comprehensive Data for Sorestry Scenario Analysis—Consequences of Errors and MEthods to Enhace Usability. PhD thesis, Swedish University of Agriculture Sciences, Faculty of Forest sciences, Umeå, Sweden, 2007. [Google Scholar]
- Mäkinen, A.; Holopainen, M.; Rasinmäki, J.; Kangas, A. Propagating the errors of initial forest variables through stand- and tree-level growth simulators. Eur. J. For. Res. 2009. [Google Scholar] [CrossRef]
- Kangas, A. Methods for assessing uncertainty of growth and yield predictions. Can. J. For. Res. 1999, 29, 1357–1364. [Google Scholar] [CrossRef]
- Gertner, G.; Dzialowy, P.J. Effects of measurement errors on an individual tree-based growth projection system. Can. J. For. Res. 1984, 14, 311–316. [Google Scholar] [CrossRef]
- Mowrer, H.T. Estimating components of propagated variance in growth simulation model projections. Can. J. For. Res. 1991, 21, 379–386. [Google Scholar] [CrossRef]
- Kangas, A. On the prediction bias and variance in long-term growth Projections. Forest Ecol. manag. 1997, 96, 207–216. [Google Scholar] [CrossRef]
- Mäkinen, A. Uncertainty in Forest Simulators and Forest Planning Systems. PhD thesis, University of Helsinki, Faculty of Agriculture and Forestry, Department of Forest Sciences, Helsinki, Finland, 2010. [Google Scholar]
- Airaksinen, M. Summa-arvomenetelmä metsän markkina-arvon määrittämisessä (The Summation Approach for Determining the Market Value of Forest Properties). PhD thesis, Helsinki University of Technology, Espoo, Finland, 2008. [Google Scholar]
- Insley, M. A real option approach to the valuation of a forestry investment. J. Environ. Econ. Manag. 2002, 44, 471–492. [Google Scholar] [CrossRef]
- Insley, M.; Rollins, K. On solving the multirotational timber harvesting with stochastic prices: a linear complementarity formulation, AM. J. Agric. Econ. 2005, 87, 735–755. [Google Scholar] [CrossRef]
- Yoshimoto, A. Threshold price as economic indicator for sustainable forest management under stochastic log price. J. Forest. Res. 2009, 14, 193–202. [Google Scholar] [CrossRef]
- Clarke, H.R.; Reed, W.J. The tree-cutting problem in a stochastic environment. J. Econ. Syn. Control 1989, 13, 569–595. [Google Scholar] [CrossRef]
- Thomson, T.A. Optimal forest rotation when stumpage prices follow a diffusion process. Land Econ. 1992, 68, 329–342. [Google Scholar] [CrossRef]
- Yoshimoto, A.; Shoji, I. Searching for an optimal rotation age for forest stand management under stochastic log price. Eur. J. Operat. Res. 1998, 105, 100–112. [Google Scholar] [CrossRef]
- Holopainen, M.; Mäkinen, A.; Rasinmäki, J.; Hyytiäinen, K.; Bayazidi, S.; Pietilä, I. Comparison of various sources of uncertainty in stand-level net present value estimates. Forest Policy Econ. 2010, 12, 77–386. [Google Scholar] [CrossRef]
- Mäkelä, A. Performance analyses of a process based stand growth model using Monte-Carlo techniques. Scand. J. For. Res. 1988, 3, 315–331. [Google Scholar] [CrossRef]
- Tokola, T.; Kangas, A.; Kalliovirta, J.; Mäkinen, A.; Rasinmäki, J. SIMO—SIMulointi ja Optimointi uuteen metsäsuunnitteluun. Metsätieteen aikakauskirja 2006, 1, 60–65. [Google Scholar]
- Rasinmäki, J.; Kalliovirta, J.; Mäkinen, A. An adaptable simulation framework for multiscale forest resource data. Comput. Electron. Agric. 2009, 66, 76–84. [Google Scholar] [CrossRef]
- Packalén, P.; Maltamo, M. The k-MSN method in the prediction of species specific stand attributes using airborne laser scanning and aerial photographs. Remote Sens. Environ. 2007, 109, 328–341. [Google Scholar] [CrossRef]
- Mäkinen, A.; Kangas, A.; Mehtätalo, L. Correlations, distributions, and trends in forest inventory errors and their effects on forest planning. Can. J. For. Res. 2010, 40, 1386–1396. [Google Scholar] [CrossRef]
- Hyvän metsänhoidon suositukset; Metsätalouden kehittämiskeskus Tapio: Helsinki, Finland, 2010.
- Kilkki, P. Use of the Weibull function in estimating the basal area dbh-distribution. Silva Fenn. 1989, 23, 311–318. [Google Scholar] [CrossRef]
- Siipilehto, J. Improving the accuracy of predicted basal-area diameter distribution in advanced stands by determining stem number. Silva Fenn. 1999, 33, 281–301. [Google Scholar] [CrossRef]
- Maltamo, M.; Kangas, A. Percentile based basal area diameter distribution models for scots pine, norway spruce and birch species. Silva Fenn. 2000, 34, 371–380. [Google Scholar]
- Laasasenaho, J. Taper curve and volume functions for pine, spruce and birch. Commun. Inst. For. Fenn. 1982, 108, 1–74. [Google Scholar]
- Näsberg, M. Mathematical Programming Models for Optimal Log Bucking; Linköping Studies in Science and Technology; Dissertation No. 132; Department Mathematics, Linköping University: Linköping, Sweden, 1985. [Google Scholar]
- Hyyppä, J.; Hyyppä, H.; Inkinen, M.; Engdahl, M.; Linko, S.; Zhu, Y-H. Accuracy comparison of various remote sensing data sources in the retrieval of forest stand attributes. Forest Ecol. Manag. 2000, 128, 109–120. [Google Scholar]
- Holopainen, M.; Haapanen, R.; Tuominen, S.; Viitala, R. Performance of airborne laser scanning- and aerial photograph-based statistical and textural features in forest variable estimation. In Proceedings of the Silvilaser 2008: 8th International Conference on LiDAR Applications in Forest Assessment and Inventory, Edinburgh, UK, September 2008; Hill, R., Rossette, J., Suárez, J., Eds.; Bournemouth University: Edinburgh, UK, 2008; pp. 105–112. [Google Scholar]
- Lim, K.; Treitz, P.; Wulder, M.; St.Onge, B.; Flood, M. LIDAR remote sensing of forest structure. Prog. Phys. Geog. 2008, 27, 88–106. [Google Scholar] [CrossRef]
- Attfield, C.L.F.; Demery, D.; Duck, N.W. Rational Expectations in Macro-Economics. An Introduction to Theory and Evidence, 2nd ed.; Basil Blackwell: Oxford, UK, 1991. [Google Scholar]
- Haight, R.G.; Holmes, T.P. Stochastic price models and optimal tree cutting: results for loblolly pine. Nat. Resour. Mod. 1991, 5, 423–443. [Google Scholar]
- Plantinga, A.J. The optimal timber rotation: an option value approach. Forest Sci. 1998, 44, 192–202. [Google Scholar]
- Brazee, R.J.; Bulte, E. Optimal harvesting and thinning with stochastic prices. Forest Sci. 2000, 46, 23–31. [Google Scholar]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Holopainen, M.; Mäkinen, A.; Rasinmäki, J.; Hyytiäinen, K.; Bayazidi, S.; Vastaranta, M.; Pietilä, I. Uncertainty in Forest Net Present Value Estimations. Forests 2010, 1, 177-193. https://doi.org/10.3390/f1030177
Holopainen M, Mäkinen A, Rasinmäki J, Hyytiäinen K, Bayazidi S, Vastaranta M, Pietilä I. Uncertainty in Forest Net Present Value Estimations. Forests. 2010; 1(3):177-193. https://doi.org/10.3390/f1030177
Chicago/Turabian StyleHolopainen, Markus, Antti Mäkinen, Jussi Rasinmäki, Kari Hyytiäinen, Saeed Bayazidi, Mikko Vastaranta, and Ilona Pietilä. 2010. "Uncertainty in Forest Net Present Value Estimations" Forests 1, no. 3: 177-193. https://doi.org/10.3390/f1030177
APA StyleHolopainen, M., Mäkinen, A., Rasinmäki, J., Hyytiäinen, K., Bayazidi, S., Vastaranta, M., & Pietilä, I. (2010). Uncertainty in Forest Net Present Value Estimations. Forests, 1(3), 177-193. https://doi.org/10.3390/f1030177






