Moving Mesh Strategies of Adaptive Methods for Solving Nonlinear Partial Differential Equations
Abstract
:1. Introduction
2. The Improved Moving Mesh PDEs
2.1. Analysis of Huang’s MMPDEs
2.2. The Moving Mesh Equation Based on the Characteristic Line
2.3. The Proposed Moving Mesh Equations
3. The Numerical Algorithms
4. Experiments
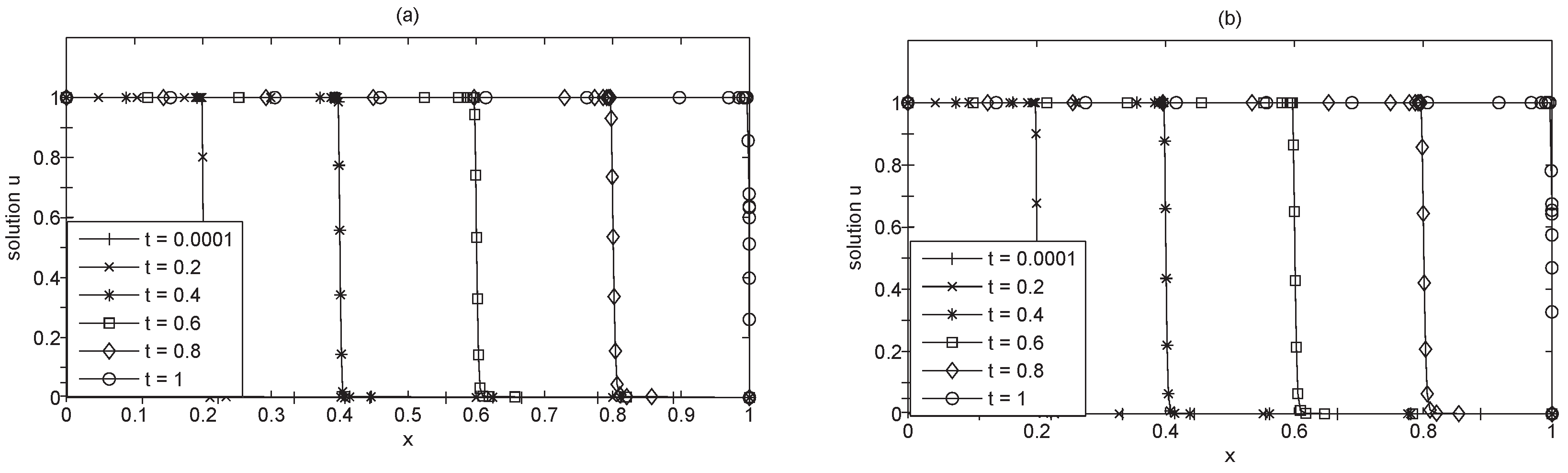
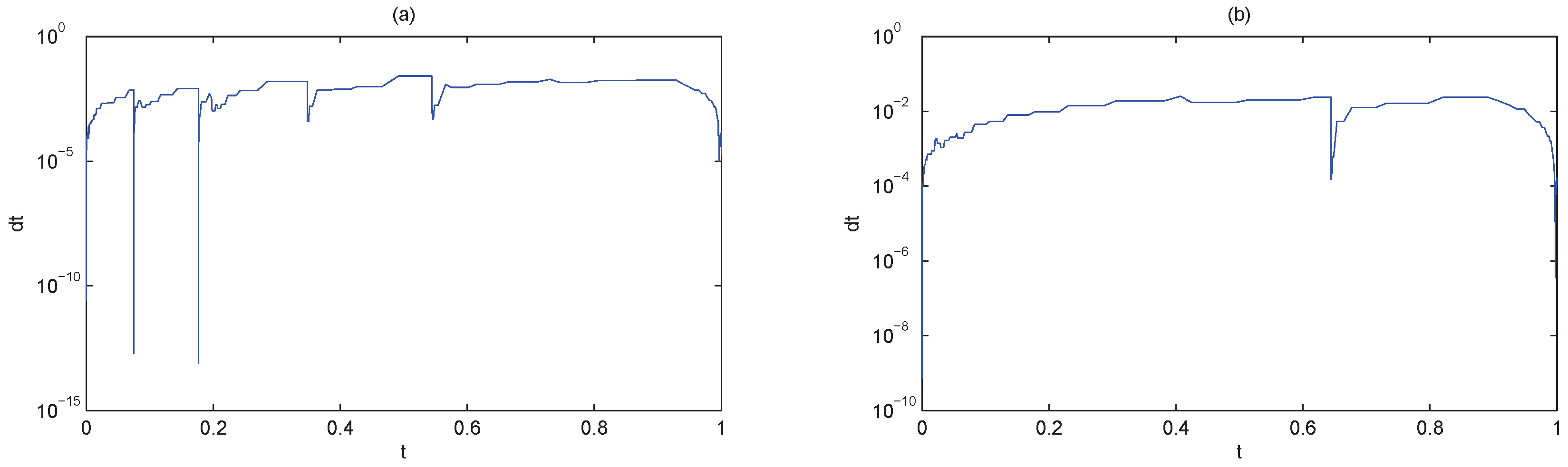
4.1. Advection-Diffusion Equation
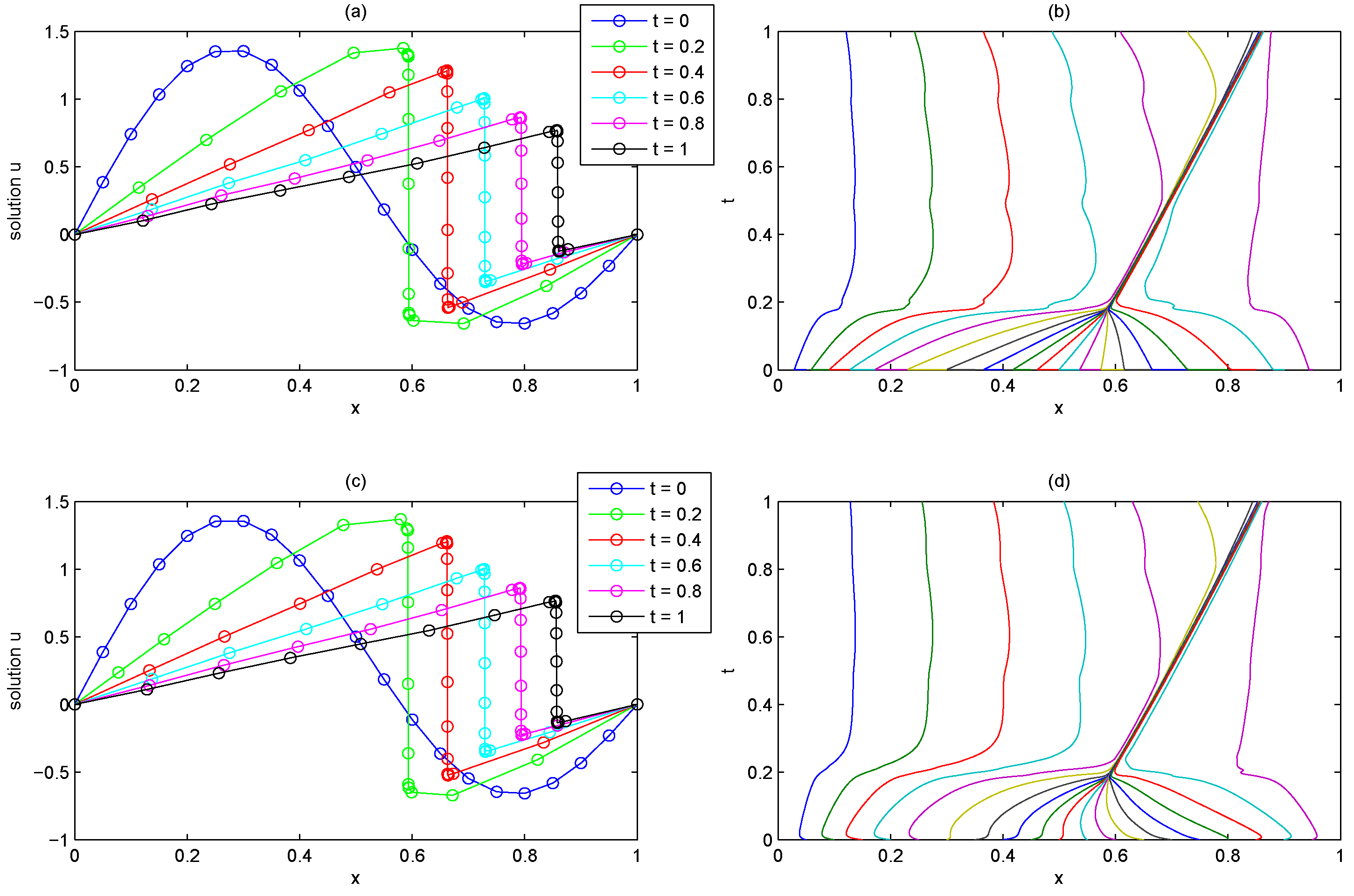
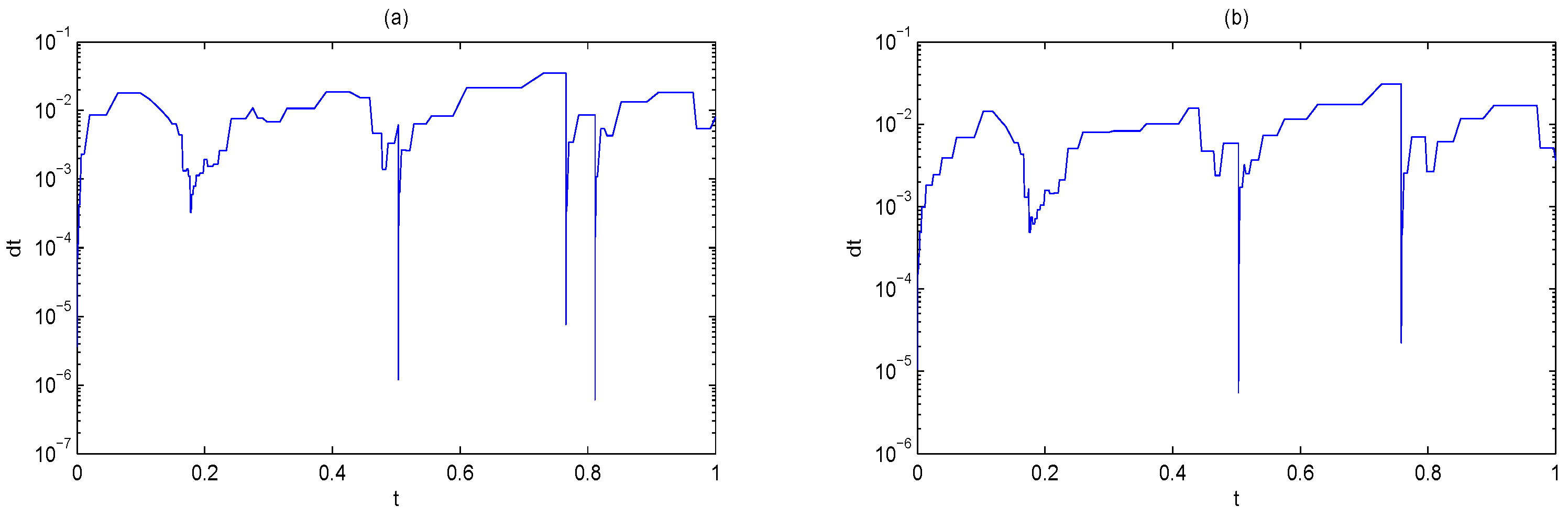
4.2. Burgers Equation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Meis, T.; Marcowitz, U. Numerical Solution of Partial Differential Equations; Springer: New York, NY, USA, 2012. [Google Scholar]
- Gutierrez, J.M. Numerical Properties of Different Root-Finding Algorithms Obtained for Approximating Continuous Newton’s Method. Algorithms 2015, 8, 1210–1218. [Google Scholar] [CrossRef]
- Ullah, M.Z.; Ahmad, F.; Serra-Capizzano, S. Constructing Frozen Jacobian Iterative Methods for Solving Systems of Nonlinear Equations, Associated with ODEs and PDEs Using the Homotopy Method. Algorithms 2016, 9, 18. [Google Scholar]
- Gao, Q.J.; Wu, Z.M.; Zhang, S.G. Applying multiquadric quasi-interpolation for boundary detection. Comput. Math. Appl. 2011, 62, 4356–4361. [Google Scholar] [CrossRef]
- Liseikin, V.D. Grid Generation Methods; Springer: New York, NY, USA, 2009. [Google Scholar]
- Huang, W.; Russell, R.D. Adaptive Moving Mesh Methods; Springer: New York, NY, USA, 2011. [Google Scholar]
- Miller, K.; Miller, R.N. Moving finite elements. I. SIAM J. Numer. Anal. 1981, 18, 1019–1032. [Google Scholar] [CrossRef]
- Dorfi, E.A.; Drury, L.O.C. Simple adaptive grids for 1-D initial value problems. J. Comput. Phys. 1987, 69, 175–195. [Google Scholar] [CrossRef]
- Huang, W.Z.; Ren, Y.; Russell, R.D. Moving mesh partial differential equations (MMPDEs) based on the equidistribution principle. SIAM J. Sci. Comput. 1994, 31, 709–730. [Google Scholar] [CrossRef]
- Budd, C.J.; Huang, W.; Russell, R.D. Moving mesh methods for problems with blow-up. SIAM J. Sci. Comput. 1996, 17, 305–327. [Google Scholar] [CrossRef]
- Huang, W.Z.; Russell, R.D. Analysis of moving mesh partial differential equations with spatial smoothing. SIAM J. Numer. Anal. 1997, 34, 1106–1126. [Google Scholar] [CrossRef]
- Huang, W. Practical aspects of formulation and solution of moving mesh partial differential equations. J. Comput. Phys. 2001, 171, 753–775. [Google Scholar] [CrossRef]
- Li, R.; Tang, T.; Zhang, P. Moving mesh methods in multiple dimensions based on harmonic maps. J. Comput. Phys. 2001, 170, 562–588. [Google Scholar] [CrossRef]
- Li, R.; Tang, T.; Zhang, P. A moving mesh finite element algorithm for singular problems in two and three space dimensions. J. Comput. Phys. 2002, 177, 365–393. [Google Scholar] [CrossRef]
- Tan, Z.; Zhang, Z.; Huang, Y.; Tang, T. Moving mesh methods with locally varying time steps. J. Comput. Phys. 2004, 200, 347–367. [Google Scholar] [CrossRef]
- Tang, T. Moving mesh methods for computational fluid dynamics. Contemp. Math. 2005, 383, 141–174. [Google Scholar]
- Tang, H.Z. A moving mesh method for the Euler flow calculations using a directional monitor function. Commun. Comput. Phys. 2006, 1, 656–676. [Google Scholar]
- Yao, J.; Liu, G.R.; Qian, D.; Chen, C.-L.; Xu, G.X. A moving-mesh gradient smoothing method for compressible CFD problems. Math. Mod. Meth. Appl. Sci. 2013, 23, 273–305. [Google Scholar] [CrossRef]
- Browne, P.A.; Budd, C.J.; Piccolo, C.; Cullen, M. Fast three dimensional r-adaptive mesh redistribution. J. Comput. Phys. 2014, 275, 174–196. [Google Scholar] [CrossRef]
- Lee, T.E.; Baines, M.J.; Langdon, S. A finite difference moving mesh method based on conservation for moving boundary problems. J. Comput. Appl. Math. 2015, 288, 1–17. [Google Scholar] [CrossRef]
- Lu, C.; Huang, W.; Qiu, J. An Adaptive Moving Mesh Finite Element Solution of the Regularized Long Wave Equation. 2016; arXiv:1606.06541. [Google Scholar]
- De Boor, C. Good Approximation by Splines with Variable Knots, II. In Conference on the Numerical Solution of Differential Equations; Springer: Heidelberg/Berlin, Germany, 1974. [Google Scholar]
- Budd, C.J.; Huang, W.; Russell, R.D. Adaptivity with moving grids. Acta Numer. 2009, 18, 111–241. [Google Scholar] [CrossRef]
- Huang, W.; Russell, R.D. Moving mesh strategy based on a gradient flow equation for two-dimensional problems. SIAM J. Sci. Comput. 1998, 20, 998–1015. [Google Scholar] [CrossRef]
- Huang, W.; Kamenski, L. A geometric discretization and a simple implementation for variational mesh generation and adaptation. J. Comput. Phys. 2015, 301, 322–337. [Google Scholar] [CrossRef]
- Luo, D.; Huang, W.; Qiu, J. A hybrid LDG-HWENO scheme for KdV-type equations. J. Comput. Phys. 2016, 313, 754–774. [Google Scholar] [CrossRef]
- Ngo, C.; Huang, W. A Study on Moving Mesh Finite Element Solution of the Porous Medium Equation. 2016; arXiv:1605.03570. [Google Scholar]
- Ong, B.; Russell, R.; Ruuth, S. An hr Moving Mesh Method for One-Dimensional Time-Dependent PDEs. In Proceedings of the 21st International Meshing Roundtable; Springer: Berlin/Heidelberg, Germany, 2013; pp. 39–54. [Google Scholar]
- Uzunca, M.; Karasozen, B.; Kucukseyhan, T. Moving Mesh Discontinuous Galerkin Methods for PDEs with Traveling Waves. Appl. Math. Comput. 2017, 292, 9–18. [Google Scholar] [CrossRef]
- Wu, Z.M. Dynamical knot and shape parameter setting for simulating shock wave by using multi-quadric quasi-interpolation. Eng. Anal. Bound. Elem. 2005, 29, 354–358. [Google Scholar] [CrossRef]
- Zhu, C.G.; Wang, R.H. Numerical solution of Burgers’ equation by cubic B-spline quasi-interpolation. Appl. Math. Comput. 2009, 208, 260–272. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations. II; Springer: New York, NY, USA, 1991. [Google Scholar]
- Soheili, A.R.; Kerayechian, A.; Davoodi, N. Adaptive numerical method for Burgers-type nonlinear equations. Appl. Math. Comput. 2012, 219, 3486–3495. [Google Scholar] [CrossRef]
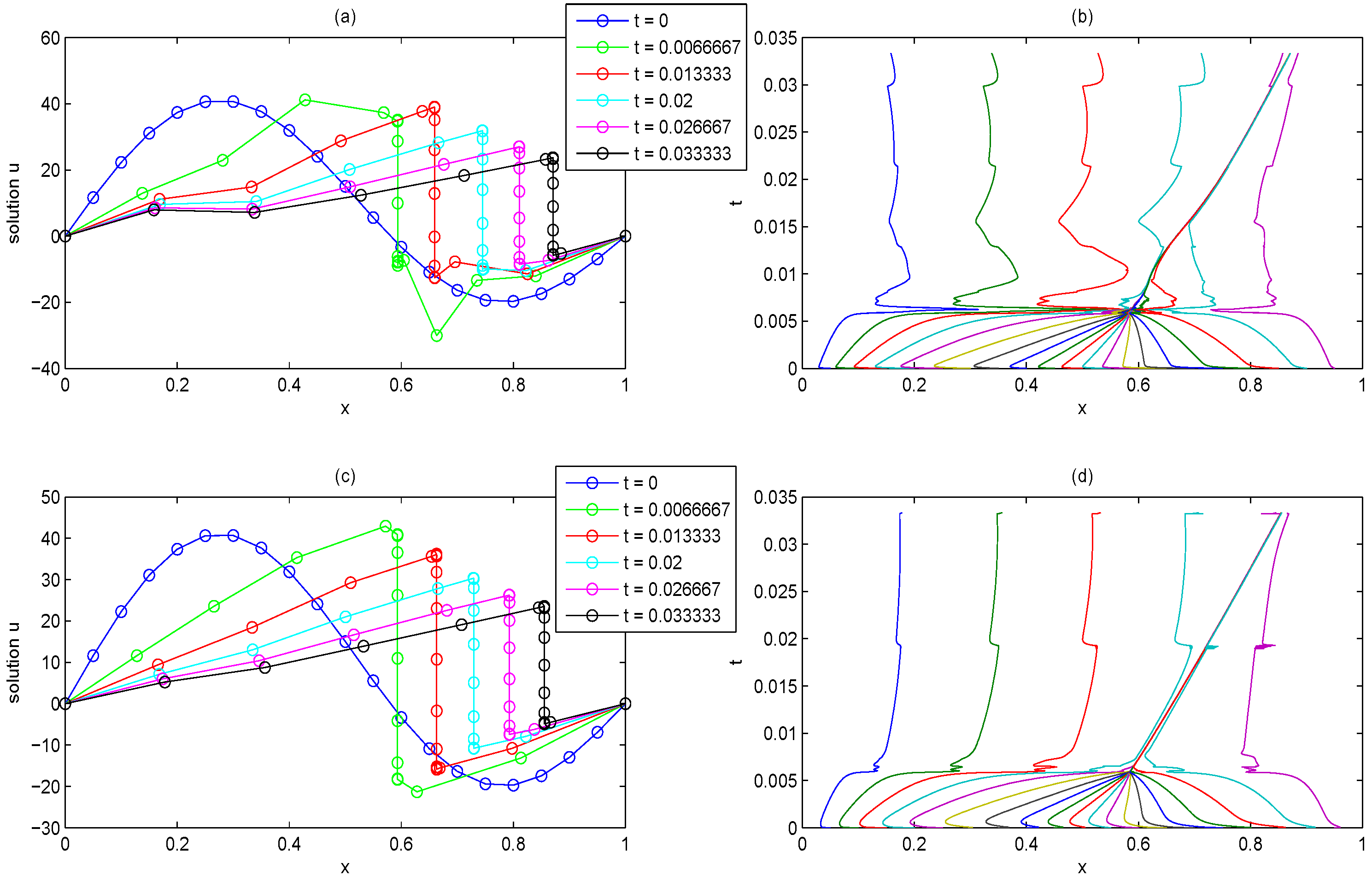
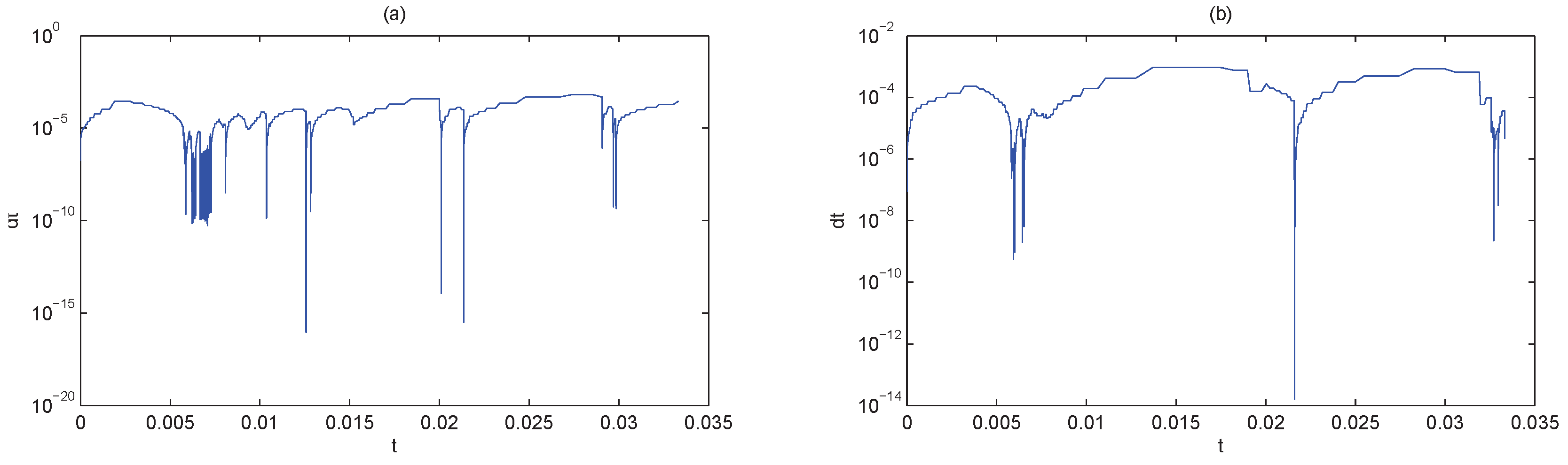
| Huang’s method | The Proposed Method | |||
|---|---|---|---|---|
| Computational Time (s) | Iterations | Computational Time (s) | Iterations | |
| Advection-diffusion equation | 2.47354 | 664 | 1.86607 | 279 |
| Burgers equation with | 1.11280 | 258 | 0.89543 | 254 |
| Burgers equation with | 4.6116 | 1236 | 2.43196 | 1154 |
| Burgers equation with | 4.85784 | 2205 | 4.14323 | 2008 |
| Burgers equation with | 8.48143 | 23,014 | 8.05290 | 8837 |
| Burgers equation with | 70.785286 | 30,167 | 15.54634 | 13,053 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Q.; Zhang, S. Moving Mesh Strategies of Adaptive Methods for Solving Nonlinear Partial Differential Equations. Algorithms 2016, 9, 86. https://doi.org/10.3390/a9040086
Gao Q, Zhang S. Moving Mesh Strategies of Adaptive Methods for Solving Nonlinear Partial Differential Equations. Algorithms. 2016; 9(4):86. https://doi.org/10.3390/a9040086
Chicago/Turabian StyleGao, Qinjiao, and Shenggang Zhang. 2016. "Moving Mesh Strategies of Adaptive Methods for Solving Nonlinear Partial Differential Equations" Algorithms 9, no. 4: 86. https://doi.org/10.3390/a9040086
APA StyleGao, Q., & Zhang, S. (2016). Moving Mesh Strategies of Adaptive Methods for Solving Nonlinear Partial Differential Equations. Algorithms, 9(4), 86. https://doi.org/10.3390/a9040086





