A Differentiated Anonymity Algorithm for Social Network Privacy Preservation

Abstract

Devising methods to publish social network data in a form that affords utility without compromising privacy remains a longstanding challenge, while many existing methods based on k-anonymity algorithms on social networks may result in nontrivial utility loss without analyzing the social network topological structure and without considering the attributes of sparse distribution. Toward this objective, we explore the impact of the attributes of sparse distribution on data utility. Firstly, we propose a new utility metric that emphasizes network structure distortion and attribute value loss. Furthermore, we design and implement a differentiated k-anonymity l-diversity social network anonymity algorithm, which seeks to protect users’ privacy in social networks and increase the usability of the published anonymized data. Its key idea is that it divides a node into two child nodes and only anonymizes sensitive values to satisfy anonymity requirements. The evaluation results show that our method can effectively improve the data utility as compared to generalized anonymizing algorithms.

1. Introduction

Nowadays, partly driven by many Web 2.0 applications, more and more social network data are publicly available and analyzed in one way or another, as the social network data has significant application value for commercial and research purposes [1]. However, the social network data often have privacy information of individuals. It has become a major concern to prevent individual privacy disclosure when publishing the social network data. Additionally, the k-anonymity l-diversity models aim to sanitize the published graph, eventually leading to data usability reduction for published social network data. Therefore, the tradeoff between the individual’s privacy security and data utility while publishing the social network data has become a major concern [2,3,4].

Generally, the social networks are modelled as graphs in which nodes and edges correspond to social entities and social links between them, respectively, while users’ attributes and graph structures are composed of the corresponding social network data [5].

Although researchers have proposed various anonymous models based on k-anonymity [6] to achieve privacy protection in existing research [7,8,9], the balance between privacy safety and data utility is still new in the field of social network publishing [4]. The existing approaches may prevent leakage of some privacy information when publishing social network data, but may result in nontrivial utility loss without exploring the attribute of sparse distribution and without recognizing the fact that different nodes have different impacts on the network structure. Statistics from security research institutions show that many existing methods have the problem of excessive anonymity for preserving sensitive attributes [10]. According to a report from Google data, nearly 30% of the users marked attributes, and the users with >4 attributes do not exceed 5%. This may hedge that user attribute distribution is relatively sparse in social networks. Additionally, in realistic social networks, almost every attribute has a rich diversity of values, only some of which are sensitive. It is claimed that existing privacy-preserving algorithms do not distinguish between the sensitivity of privacy attribute values, therefore, non-sensitive information is altered and this leads to a lower usability of the published data [6,11]. 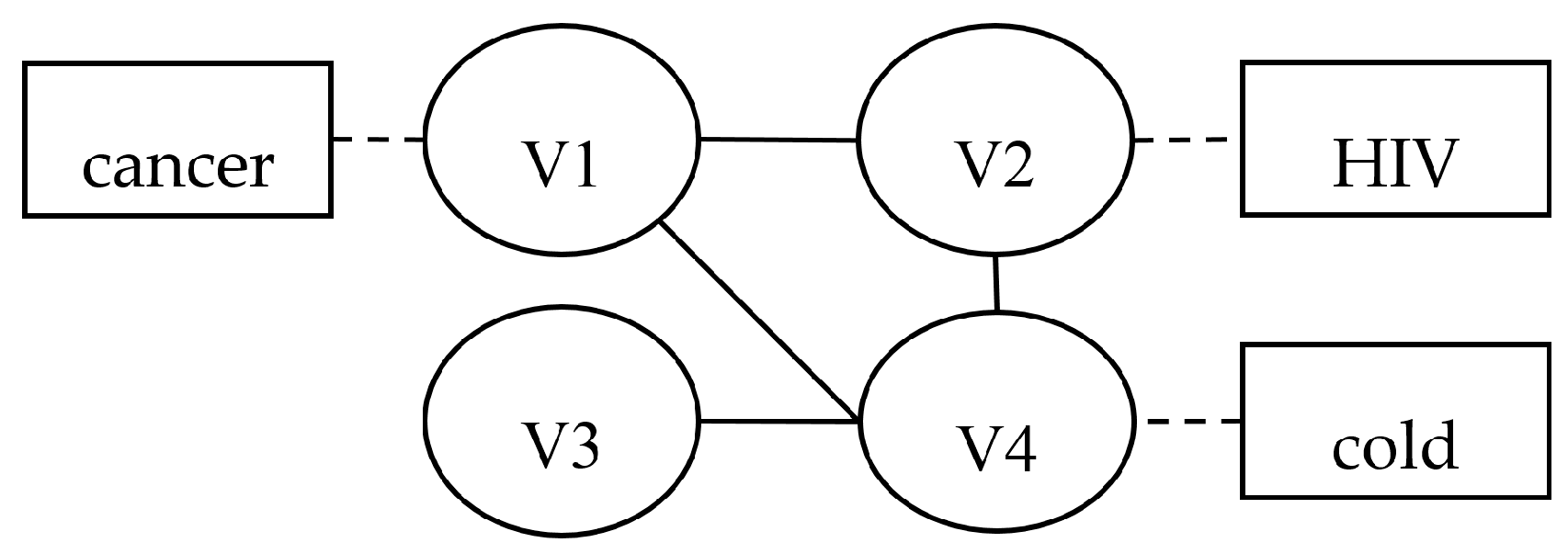For example, as depicted in Figure 1, the human disease network has various values. Most people generally consider the disease HIV as private, while considering the disease cold as non-sensitive information. Meanwhile, node V3 does not mark health status. Thus, the human disease network in Figure 1 is sparse and the existing methods may lead to excessive data utility loss for published data. To tackle this issue, we explored the attributes’ sparse distribution and studied differentiated sensitivity of varied attribute values, proposing a finer granular anonymization algorithm that shifts anonymous objects from the attribute to some sensitive attribute values.

In addition, most previous works take the total number of modified edges or modified nodes as the only metric to measure the social network utility loss without considering the graph structure interference. The lack of exploring utility is partially responsible for the high rate of structure interference in publishing data and contributes to the decrease of data availability. To approach this dearth of research on anonymized data utility for anonymity algorithms, we have undertaken to develop a proper utility function targeted at measuring both information loss and network structure interference that have been shown to be essential for data integrity and authenticity.

To date, many researchers have put forward a variety of personalized privacy protection models and algorithms to improve the published data utility. These personalized anonymous models almost insist that individuals in social networks have different privacy protection requirements and put users who have different privacy protection needs into different anonymous equivalence group. For example, Jiao et al. [12] divided user privacy protection needs into S (ultra), H (high), M (middle), and L (low) levels, then put forward a personalized k-degree-l-diversity anonymity model. Wang [13] proposed a personal privacy protection scheme based on a social network subset. The scheme divided social networks into three levels according to the attacker’s background knowledge: levels a, b, and c. For level a, the scheme removes all node labels; for level b, it releases the sub-structure of the social network graph that could satisfy the requirement of k-anonymity; and, for level c, it releases the sub-structure that could satisfy the requirement of l-diversity anonymity. However, when the social network scale is very large, setting different privacy requirements for each user will significantly increase the time complexity of the algorithm. More importantly, these personalized privacy protection strategies ignore the fact that the influence of each individual is different in a social network.

Above all, in this paper, we treat node attributes as sensitive information (such as salary) that has to be protected and the node degree as background knowledge. Then we propose a differentiated graph anonymity algorithm based on the k-degree-l-diversity model targeted at reducing the utility loss for anonymity. The key idea of our model is that we consider the differences of node importance and attribute value sensitivity. The major contributions of this paper are as follows:

First, a novel utility metric for measuring the published utility loss, named UL(G,G’), is proposed based on the attribute distribution and network structure. Our metric focuses on the different influences of node (edge) modification to both the network data information and the network structure instead of purely the number of node (edge) modifications. We believe that our metric is a better measurement of the utility loss when compared with other existing utility metrics. As this metric assumes each node modification has an equal impact on the original social network properties, the existing k-anonymization algorithms based on this metric has natural flaws in providing high-utility anonymized social network data. Therefore, we designed an algorithm that caters to our metric to improve published anonymized data utility. Although our metric has slightly higher computing complexity, the measurement is more comprehensive and conducive to selecting anonymity operations that can result in less utility loss.

Second, a heuristic anonymizing algorithm, called DKDLD-UL, namely due to the differentiated k-degree-l-diversity anonymity based on data utility, is designed to modify a given social network G to G’ aiming at preserving attribute privacy with relatively low utility loss. On one hand, we make differential protection for diverse sensitive attribute values by the fuzzy function and establish a sensitivity matrix according all possible attribute values for each sensitive attribute having different sensitivity. On the other hand, we implement differential anonymizing operations for different important nodes based on the key node analysis in social network analysis. Above all, we propose the differentiated protection algorithm to prevent privacy information leakage while reducing data utility loss as much as possible.

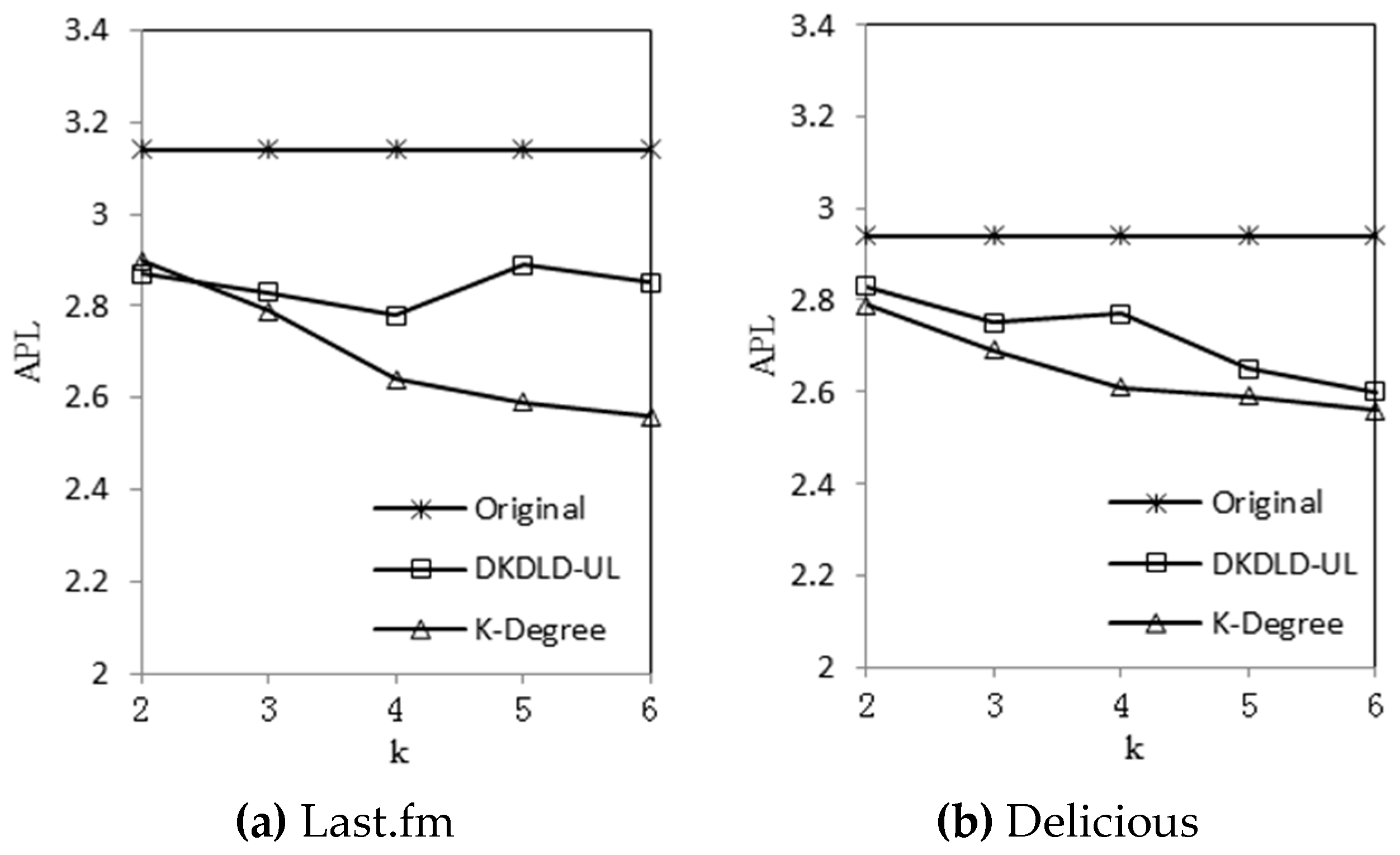
The rest of the paper is organized as follows. Section 2 briefly provides some background knowledge and reviews related works about social network data anonymity. Section 3 details the novel utility measure model based on the structure of topological similarity of the social network, then presents the differentiated protection algorithm based on the proposed utility metric. Section 4 reports the experimental results. Finally, Section 5 concludes the paper.

2. Problem Description

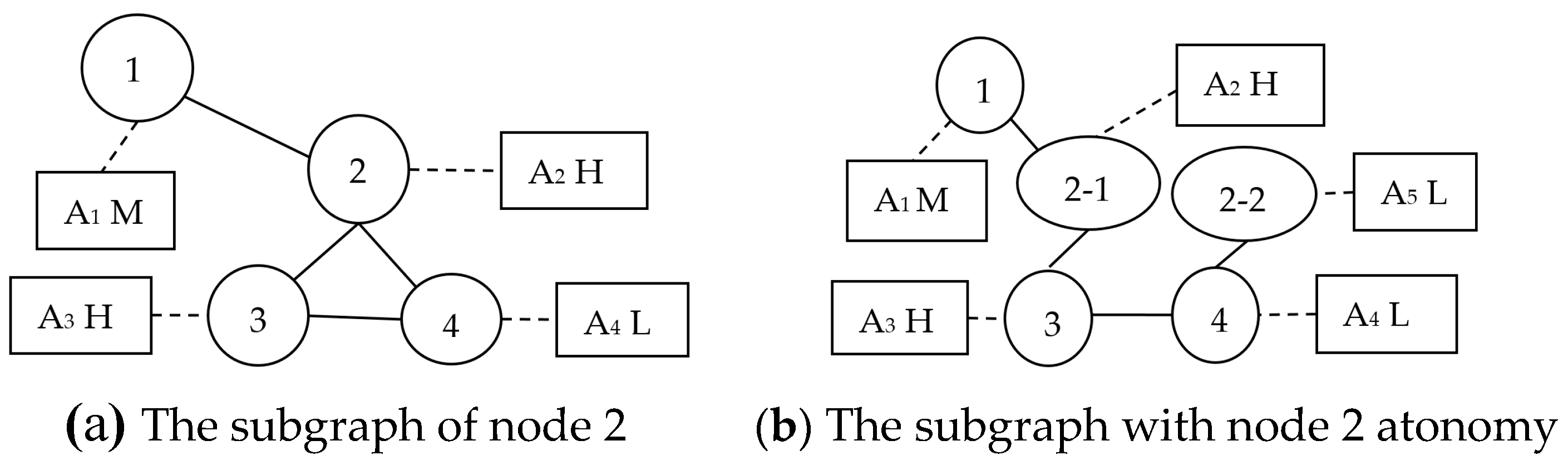
We first present the terminology that will be used in this paper. We focus on the attribute privacy-preserving problem for an un-weighted, undirected, simple graph with a privacy attribute. Figure 2 shows an example of such a graph. A social network graph is defined as follows:

Definition 1.

Social Network Graph [14]. The social network data is modeled by a graph with a four tuple G = (V, E, A, S). V is a set of nodes representing users; E ⊆ V × V is a set of edges representing social relations between users; A= {A₁, A₂,…, A_n} is a set of attribute nodes representing all users’ possible values of the privacy attribute, and A_i corresponds to any privacy attribute values in a social network. For example, for the attribute called health-state, pneumonia and influenza, as two different property values form two different attribute nodes showed by A₁ = pneumonia, A₂ = influenza. S = {H, M, L}, is the set of the sensitivity of privacy attribute values; S(A_i) represents the sensitivity of attribute value Ai, and Si is the short name of S(Ai), as shown in Figure 2.

Definition 2.

Structural Re-identification Attack (SRA) [15]. Given a social network G(V, E), its published graph G’(V’, E’), a target entity t∈V, and the attacker background knowledge F(t), the attacker performs the structural re-identification attack by searching for all of the vertices in G’ that could be mapped to t, i.e., VF (t) = {v∈V’|F(v) = F(t)}. If |VF (t)| << |V’|, then t has a high probability to be re-identified.

Definition 3.

K-degree Anonymity [15]. Given a graph G = (V, E) with V = {v₁, v₂, …,v_n} and d(v_i) =|{u∈V : (u, v_i)∈E}|, and the type of attacker’s background knowledge F, the degree sequence of G is defined to be the sequence P = (d(v₁), d(v₂), …, d(v_n)). P can be divided into a group of subsequences [[d(1), …, d(i₁)], [d(i₁ + 1), …, d(i₂)], …, [d(i_m + 1), …, P(j)]] such that G satisfies k-degree anonymity if, for every vertex v_i∈V, there exist at least k–1 other vertices in G with the same degree as v_i. In other words, for any subsequences P_y = [d(i_y + 1), …, d(i_y+1)], P_y satisfies two constraints: (1) All of the elements in P_y share the same degree (d(i_y + 1) = d(i_y + 2) = … = d(i_y+1)); and (2) P_y has size of at least k, namely (|i_y+1 − i_y| ≥ k).

Definition 4.

L-diversity Anonymity [16]. Given an anonymized graph G’ = (V’, E’, A’, S), G’ satisfies l-diversity anonymity if, for any privacy attribute values A_i’, there exists at least l–1 different attribute values in an equivalence group.

Definition 5.

Attribute Value Sensitivity Function. The sensitivity of privacy attribute values are usually established by a membership function. We use a trapezoidal distribution membership function sensitivity(x) which ranges from [0, 1] to determine the attribute value sensitivity S as shown in Equation (1). The independent variable x is any privacy attribute value from the set A, the sensitivity of x is written S(x), and we classify the privacy sensitivity into three categories which are denoted by H (high), M (middle), and L (low). The following three parts show the details of three categories.

$$\begin{array}{l}sensitivity(x)=\{\begin{array}{l}0,x\le a\\ \frac{x-a}{b-a},a<x\le b\\ 1,x>b\end{array}\\ s.t.\{\begin{array}{l}x\le a:S=L\\ a<x\le b:S=M\\ x>b:S=H\end{array}\end{array}$$

(1)

(1) When x ≤ a, S(x) = L, L is the shorthand of low. We think the attribute value x may have little chance to be privacy information, so it can be published without anonymity, such as the attribute value “cold”, as almost no person will think of “cold” as private information. Many existing privacy-preserving algorithms do not distinguish between the sensitivity of attribute values, so that even non-sensitive information is anonymized, which leads to a lower usability of the published data.

(2) When a < x ≤ b, S(x) = M, M is middle, which means attribute value x has the potential to be private information. Thus, we take one time division for nodes whose attribute value sensitivity is M before publishing data.

(3) When x > b, S(x) = H, attribute value x is usually considered as private information, so we take two, or more, time node divisions.

Above all, when S(Ai) = M or S(Ai) = H, we consider the attribute value Ai as private, and add user node Vi to the sensitive vertex set SV. The critical points a, b are two threshold values, for the convenience of the experiment, we set the threshold based on experience: a = 0.6, b = 0.8. However, for the practical application, it should be established by statistics and analysis.

3. The Differentiated Attribute-Preserving Model

In this section, we detail the sensitive label-preserving model based data utility: the DKDLD-UL anonymity model. In our work, we aim at improving the utility of the graph G’ anonymized from the original graph G while achieving high privacy protection to resist the re-identification attack, which is one of the most serious privacy problems in social network data publishing, upon the user nodes’ degree as background knowledge. Our model is divided into two modules:

3.1. Graph Utility Measurement

As pointed out in previous sections, the number of edge or node additions (deletions) is the most common utility loss measurement, though this metric is not effective as it neglects the different impacts of various graph operations on the social network structure. To settle this problem, in this paper, we try design a proper utility loss metric function named UL(G,G’) shown in Equation (2). This metric measures both the structure interference and information loss of different anonymizing operations. Then we may optimize the 3 anonymizing operations according to the metric. Thus, the anonymity algorithm proposed in Section 3.2 may result in higher data utility based on the data utility metric UL.

$$\begin{array}{l}\mathrm{UL}(\mathrm{G},{\mathrm{G}}^{\prime })=a\cdot \left(TC\right)+b\cdot \left(IL\right)\\ s.t.\{\begin{array}{c}TC=\alpha \cdot \frac{AP{L}^{\prime }-APL}{APL}+\beta \cdot \frac{C{C}^{\prime }-CC}{CC}\\ IL=\frac{\left|SV\cap KV\right|}{\left|V\right|}\\ a+b=1\\ \alpha +\beta =1\end{array}\end{array}$$

(2)

where G is the original social network graph and G’ is the published anonymous graph. The formula TC captures the variable quantity of the social network structure and the formula IL measures the attributes’ information loss. The constants a, b are used to trade off the information loss and structure interference, and the social network publisher may modulate a, b based on the purpose of publishing the data. For example, if the published data is targeted at analyzing characteristics of the network structure, then the publisher may make a larger than b.

The APL and CC represent, respectively, the average path length and clustering coefficient of graph G that have been shown to be essential for evaluating the structure of the social network graph [3,6,11], while APL’ and CC’ are two parameters measuring the topology features of G’; The constant α, β may be different values, respectively, according to different social networks.

The set SV is the set of sensitive vertices whose S is H or M, and we must protect these nodes’ information before publishing social network data; the set KV is the set of key nodes in the social network which are important for the social network graph structure.

3.2. The Differentiated Attribute-Preserving Algorithm

The optimal k-anonymization problem (i.e., k-anonymization with minimum utility loss) on social networks is NP-hard [17]. To simplify the problem, after introducing the UL(G,G’) model-based utility measurement, we are ready to present the DKDLD-UL anonymity algorithm that tries to anonymize a given social network by user node segmentation with utility loss as small as possible (to be near the optimal function Min UL(G,G’)). In the following, we first present the basic idea of the DKDLD-UL algorithm and then detail the algorithm steps in Algorithm 1.

3.2.1. Basic Idea

Given a graph G(V,E,A,S), the attacker’s background knowledge F, which is the degree of the target node and the privacy requirement k, l, we perform node(Vi∈V) segmentation operations one at a time on G to achieve k-d-l-d anonymity. To achieve the differentiated anonymity of targeting for decreasing utility loss, our DKDLD-UL algorithm will run the following two main steps:

Firstly, we define the sensitivity for privacy attribute values with Equation (1), only considering attribute values with S equal to H or M as the privacy, and then put nodes which have privacy attribute values into the privacy-preserving requirements list SV = {Vi}.

Secondly, for targeting node differentiation, we classify the user node set SV into two categories by the key node analysis in social network analysis according to the “80/20 Rule” for the convenience in evaluating the experimental algorithm. The details are as follows:

We choose 20% of the nodes from the set V as key nodes on the basis of the research on four indicators which are commonly used in undirected network node importance analysis and then put them into the set KV = {Vt}, simultaneously considering other nodes as general nodes GV. The four indicators mentioned above are as follows:

Degree Centrality

$${\mathrm{DC}}_{\mathrm{i}}=\frac{{\mathrm{K}}_{\mathrm{i}}}{\mathrm{N}-1}$$

(3)

where Ki is the degree or node Vi and N is number of nodes in set V. However, it has its limits by only considering that the greater the degree of a node, the more important the node.

Betweeness Centrality (BC)

$${\mathrm{BC}}_{\mathrm{i}}={\displaystyle \sum _{\mathrm{s}\ne \mathrm{i}\ne \mathrm{t}}\frac{{\mathrm{n}}_{\mathrm{st}}^{\mathrm{i}}}{{\mathrm{g}}_{\mathrm{st}}}}$$

(4)

where g_st is the number of the shortest path length between node s and node t and ${\mathrm{n}}_{\mathrm{st}}^{\mathrm{i}}$ is the number though node i. The index BC depicts the influence of nodes on the network information flow.

Closeness Centrality

$${\mathrm{CC}}_{\mathrm{i}}=\frac{1}{{\mathrm{d}}_{\mathrm{i}}}=\frac{\mathrm{N}}{{\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{N}}{\mathrm{d}}_{\mathrm{ij}}}}$$

(5)

where d_ij is the distance between node V_i and node V_j. In experiments, the parameter shows an effective description of a node’s topological importance.

Eigenvector Centrality

$${\mathrm{x}}_{\mathrm{i}}=\mathrm{c}{\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{N}}{\mathrm{a}}_{\mathrm{ij}}{\mathrm{x}}_{\mathrm{j}}}$$

(6)

where c is a constant and A = (a_ij) is the adjacency matrix. This shows not only a high number of neighbor nodes but is also an effective description of a node’s topological importance.

Above all, in the simulation experiments, we use the last three indicators to mine the central nodes and we may change the measure index of different social networks.

Thirdly, for the two sets of nodes in the network, we use different anonymizing operations separately from node division operations for key nodes in set KV, and with privacy attribute value generalization operations for other nodes in set GV.

3.2.2. Algorithm Framework

Algorithm 1 shows the pseudocode of the DKDLD-UL algorithm.

Algorithm 1. The DKDLD-UL Algorithm

Input: Graph G(V, E, VA, S), k, l, F, and KV

Output: DKDLD-UL anonymity graph G*.

1. for(i = 1;i< = |V|;i++)

2. {  S.Vi = sensitivity(Vi);                 // Generate node attribute sensitivity

3.    if (S.Vi = M or H) then

4.      SV←Vi;         // put Vi into privacy-preserving requirement vertices set SV

5.    end if }

6. while (node Vt in SV) and (Vt is key node) do

7.    KV←Vt;           // Generated attribute generalization node sequence set KV

8.    Vt.VA = [min, max]  //min(max) is the minimal(maximum) attribute value in sequence Vt

9. else if

10.   GV←Vt;                 // Generate node segmentation sequence set GV

11.   Vt-1, Vt-2←new node(Vt)         // divide the current node into two new nodes

12.     For each social edge Ei of Vt

13.   Distribute by k-degree(Ei, Vt-1, Vt-2);       // assign Ei to meet k-degree anonymity

14.    For each attribute VAi of Vt

15.   Distribute by l-diversity(VAi, Vt-1, Vt-2)          // assign VAi to meet l-diversity

16. end while;

17. Return G*;

The progress of generating the DKDLD-UL anonymity graph G’ needs only to scan the sensitivity S of all nodes in the original graph G and scan the sensitivity node set SV for implementing node division or node attribute generation once, respectively; therefore, the time complexity of the DKDLD-UL algorithm is O(n²).

As we defined G = (V, E, A, S), we should make the graph as a set of (nodes, edges, attribute values, attribute values sensitivity). However, for facilitating writing, we use the node’s degree to replace the edge set of the node. Thus, we describe a social network graph by a tuple set (node, number of neighbor, attribute values, sensitivity). For example, if using Algorithm 1 to protect graph G = [(2,3,A₂,H), (3,2,A₃,H), (4,2,A₄,L), (1,1,A₁,M)] shown in Figure 3a, we get the DKDLD-UL anonymity graph G’ = [(2-1,2,A2,H), (3,2,A3,H), (4,2,A4,L), (1,1,A1,M), (2-2,1,A5,L)] shown in Figure 3b.

Firstly, as S(A₂) = H, S(A₃) = H, S(A₁) = M,S(A₄) = L, we obtain the privacy-preserving requirement node set SV = {V₂,V₃,V₁}.

Secondly, in Figure 3a, the differences between all nodes in set SV is small, so all nodes are general nodes, namely GV = {V₂, V₃, V₁}.

Thirdly, as node V₂ in set GV = {V₂, V₃, V₁}, the algorithm divides V₂ into child nodes V_2-1, V_2-2. For attribute values, it sets sensitivity attribute value for V_2-1 and sets non-sensitivity attribute value for node V_2-2. For social edges, it divides the edges of node V₂ according to attribute similarity and remains the edge of other nodes, such as S(A₁) = M, S(A₃) = H, so edges (V₁,V₂), (V₂,V₃) are inherited by node V_2-1, S(A₄) = L, and edge (V₂,V₄) is inherited by node V_2-2. Therefore, we obtain edges = {(V₁, V_2-1), (V_2-1, V₃), (V_2-2, V₄), (V₃, V₄)} in Figure 3b.

Above all, Figure 3b is an anonymous security graph that satisfies differentiated 2-degree-2-diversity anonymity.

4. Experiments

In this section, we report the empirical results that we collected to evaluate the performance of our proposed DKDLD-UL model. All of the experiments have been implemented using MATLAB2010a provided by Mathworks in America and Gephi software [18]. The experiments were conducted on a PC having a 2.13 GHz Intel Duo processor with 2 GB of RAM under the Windows 7 operating system.

4.1. Datasets

Two real datasets are used in our tests: Last.fm dataset and Delicious dataset.

The Last.fm Dataset contains social networking, tagging, and music artist listening information from the Last.fm online music website [19] with 1892 users and 12,717 edges.

The Delicious dataset contains social networking, bookmarking, and tagging information from the Delicious social bookmarking system [20]. It consists of 1867 nodes and 15,328 edges.

4.2. Results and Analysis

This section compares our algorithm DKDLD-UL with the personalized k-degree anonymizing algorithm [12]. The compared algorithm in [12], based on k-degree-l-diversity anonymity model, is called k-degree and is intended to improve the utility of anonymous data. Additionally, this algorithm caters to the individuals’ personalized privacy requirements while ignoring the fact that the influence of each individual is different in a social network. However, our algorithm chooses a new research perspective and explores the differentiated influence. Therefore, the DKDLD-UL algorithm is very similar to the k-degree algorithm and we believe that our algorithm may work better than the compared algorithm. Importantly, we compare the effectiveness of the above two algorithms by examining three dimensions through experimentation: running time, anonymity cost, and utility loss.

4.2.1. Experiment 1: Running Time

We present the running time of our DKDLD-UL algorithm and compared it with the K-Degree algorithm as k increases in two datasets, respectively (Figure 4). From the figures, we can observe that both our algorithm and the compared algorithm are very efficient; the largest running time is less than 30 s. However, the compared algorithm works much better since, when we generate the KV and GV set, it takes time to compute the nodes’ importance index mentioned in Equations (4)–(6) and choose the optimized node segmentation operations by function UL(G,G’). This aims at decreasing the utility loss as much as possible, however, this process does not exist in the compared algorithm.

4.2.2. Experiment 2: Anonymity Cost

In this part of the experiment, we calculate the anonymous cost that represents the number of anonymity operations, defined as follows:

$$\mathrm{A}.\mathrm{Cos}\mathrm{t}(\mathrm{G},{\mathrm{G}}^{\prime })=\left|\mathrm{KV}\right|+\left|\mathrm{GV}\right|$$

(7)

where G’ = (V’, E’) is the anonymity graph, |KV| and |GV| indicate the number of attribute generation and node segmentation operations, respectively.

Since the DKDLD-UL algorithm shifts the objects of protection from the sensitive attribute to the privacy attribute values, accurately targeting differentiated protection, while the K-degree anonymous algorithm considers all values of the sensitive attribute as privacy attributes and then performs general anonymizing operations. The DKDLD-UL algorithm can both satisfy the requirement of privacy protection and reduce the loss of information. Therefore, our DKDLD-UL algorithm works better than the k-degree model on anonymity cost, as shown in Figure 5.

4.2.3. Experiment 3: Utility Loss

In the third set of experiments, we examine how well the published graph represents the original graph with two topological structure indicators, APL [6,13] and CC [6,11,13], which are essential for the graph structure.

Figure 6 and Figure 7 show the APL and CC results with respect to different k values on two datasets. Generally, the DKDLD-UL method works better in terms of preserving graph properties than the compared k-degree algorithm. Taking the APL value as an example; as depicted in Figure 6a,b, the straight line indicates the APL of the original graph. Although the utility loss rises with the increase of the variant k by both methods, the APL deviates less from its original values by using our DKDLD-UL algorithm, compared with k-degree algorithm. Meanwhile, our algorithm considers the sensitivity of the individual’s attributes and key graph structures, and provides differentiated preservation for the individuals.

5. Future Work and Limitations

Our algorithm is far superior to the usual k-anonymity used for privacy. Although it focuses on the attribute privacy-preserving problem for an unweighted undirected graph, it has good scalability with reasonable hardware costs. However, different sizes of networks may yield different results, and we will discuss this problem in future work.

6. Conclusions

In this paper, we proposed a proper utility model UL(G,G’), and designed a graph anonymity algorithm DKDLD-UL aimed at providing differentiated privacy preservation from a structure attack. By dividing attribute values with different sensitivity, we reduce the loss of data authenticity and integrity. Meanwhile we choose different kinds of anonymity operations, targeting key nodes and general nodes according to the scenario that key nodes have vital influence to the overall structure of the graph. Above all, the advantages of our method is that it shifts anonymous objects from the privacy attributes to some sensitive attribute values and optimizes anonymous operations according to a proper utility evaluation model targeting less information loss and structure distortion. Experimental evaluation on a real dataset shows our approach outperforms the existing approaches in terms of improving the utility of anonymized data with the same degree of privacy preservation.