Evaluation of Cloud Services: A Fuzzy Multi-Criteria Group Decision Making Method ^†

Abstract

This paper presents a fuzzy multi-criteria group decision making method for evaluating the performance of Cloud services in an uncertain environment. Intuitionistic fuzzy numbers are used to better model the subjectivity and imprecision in the performance evaluation process. An effective algorithm is developed based on the technique for order preference by similarity to the ideal solution and the Choquet integral operator for adequately solving the performance evaluation problem. An example is presented for demonstrating the applicability of the proposed method for solving the multi-criteria group decision making problem in real situations.

1. Introduction

With the rapid development of information and communication technologies and increasing globalization, Cloud computing is becoming popular in which computing infrastructure and solutions are delivered as a service [1]. Clouds are next-generation data-storage and computing systems with virtualization as the core, enabling available technologies to interconnect and manage distributed computers where resources are dynamically provisioned on demand [2]. The use of Clouds greatly helps organizations create and maintain their competitive advantages and improve their overall performance in the marketplace. It often provides organizations with numerous benefits including (a) the reduction of costs in managing and maintaining organizational information systems; (b) increased productivity; (c) improved collaboration; and (d) the flexibility that individual employees seek [3].

The popularity of cloud services results in their proliferation in the marketplace. As a result, adequately evaluating and selecting the most appropriate Cloud service in a specific situation with respect to specific user requirements has become a significant challenge for decision makers in various organizations [1,3]. Often, there are various trade-offs between different user requirements that can be accommodated by various Cloud services. This makes it difficult to evaluate the overall appropriateness of available Cloud services for implementation in a given situation.

Evaluating the performance of Cloud services for implementation in an organization is complex and challenging. This is due to (a) the involvement of multiple decision makers in evaluating the appropriateness of available Cloud services with respect to multiple, often conflicting criteria; (b) the presence of subjectivity and imprecision inherent in the evaluation process [2]; and (c) the need to adequately consider the interest of multiple decision makers in a comprehensive manner.

Much research has been done on the development of numerous methods for dealing with the Cloud service performance evaluation and selection problem [3,4,5,6]. Garg et al. [3], for example, use analytic hierarchy process to evaluate the performance of Cloud services in an organization. This process consists of three steps including (a) problem decomposition; (b) priority judgment; and (c) priority aggregation. In problem decomposition, a hierarchy structure of problem evaluation is developed for describing the relationship between the goal of the Cloud service selection, the evaluation criteria, and the available Cloud services. In the priority judgment, pairwise comparisons are conducted to determine the relative importance of the criteria and the performance of the Cloud service. In the priority aggregation, the overall rankings of these Cloud services across all the evaluation criteria are determined based on the aggregation of the priority judgments in the second phase along the utility theory in a specific situation.

Saripalli and Pingali [5] apply the simple additive weighting (SAW) method for dealing with the Cloud service performance evaluation and selection problem. A Delphi method is used to assess the relative importance of each criterion through an expert interview. The SAW method is then employed to determine the overall performance of each alternative across all the criteria on which the ranking of the Cloud service is determined.

Menzel et al. [6] present an integrated method using the analytic network process (ANP) and zero-one goal programming for evaluating the performance of Cloud services. ANP is used to calculate the weightings for the evaluation and selection criteria. The information obtained from the ANP is then used in the zero-one goal programming for determining the overall ranking of the available Cloud services.

The methods discussed above have shown their applicability in solving various Cloud services’ evaluation and selection problems from different perspectives under various circumstances. There are, however, some specific issues and concerns that stop them from their effective use in solving this kind of problem, including (a) the failure to adequately handle the various requirements of the decision makers; (b) tedious and complex mathematical computation required; and (c) high cognitive demand on the decision makers [7,8,9].

To overcome the shortcomings of these methods above, this paper formulates the process of evaluating the performance of Cloud services as a multi-criteria group decision making problem, and presents a fuzzy multi-criteria group decision making method for evaluating the performance of Cloud services. Intuitionistic fuzzy numbers [10] are used to better model the inherent subjectivity and imprecision of the evaluation process. An effective algorithm is developed based on the technique for order preference by similarity to ideal solution (TOPSIS) and the Choquet integral operator for adequately dealing with the performance evaluation problem. An example is presented to demonstrate the applicability of the proposed fuzzy multi-criteria group decision making method for solving the multi-criteria group decision making problem in real situations.

2. The Cloud Service Performance Evaluation and Selection Problem

Cloud computing is widely used to enable individual organizations to access specific information technologies at a much lower cost. It allows these organizations to rapidly expand their operations by giving them the ability to quickly and cost-effectively roll-out new products and services, and at the same time, serve their customers better across the world [11]. Furthermore, the adoption of Cloud computing can lead to (a) the reduction in initial capital expenditure [12]; (b) minimal management [1]; (c) optimized resources utilization [13,14]; and (d) improved energy efficiency [15], increased scalability, increased agility, reduction of information technology infrastructure complexity, and improved alignment between businesses and information technology services [16].

There is an upward trend in the adoption of Cloud computing [17,18]. A KPMG survey [19] reveals that 81% of organizations are either planning their initial forays, are in the early stage of implementation, or have a full implementation of Cloud computing. Many organizations have started building applications on the Cloud infrastructure and making their businesses agile by using flexible and elastic Cloud services [4]. Moving applications and data into the Cloud, however, is not a straightforward process. This is because numerous challenges exist to leverage the full potential that Cloud computing can offer.

With the growth of public Cloud service offerings, it has become increasingly difficult for Cloud service customers to decide which provider(s) can fulfill their requirements for quality Cloud services [1]. For example, each Cloud service might offer similar services at different prices and performance levels with different sets of features. While one provider might be cheaper for storage services, they may be more expensive for computation. Given the diversity of Cloud service offerings, it is an important challenge for organizations to discover the suitable Cloud providers who can satisfy their requirements. There may be trade-offs between different user requirements fulfilled by different Cloud service providers. As a result, it is not sufficient to just discover multiple Cloud services. It is important to determine the most suitable Cloud service through a comprehensive performance evaluation in a specific situation [3].

The performance evaluation of available Cloud services with respect to a set of specific criteria is complex [20]. This is due to the presence of the multi-dimensional nature of the evaluation process and the presence of vagueness of the decision making process [21]. To effectively deal with this problem, an overall evaluation of individual Cloud services is desirable. In order to adequately measure the performance of the available Cloud services, it is important to first define the suitable criteria for ensuring that the evaluation and selection process produces an accurate and effective outcome for specific organizations.

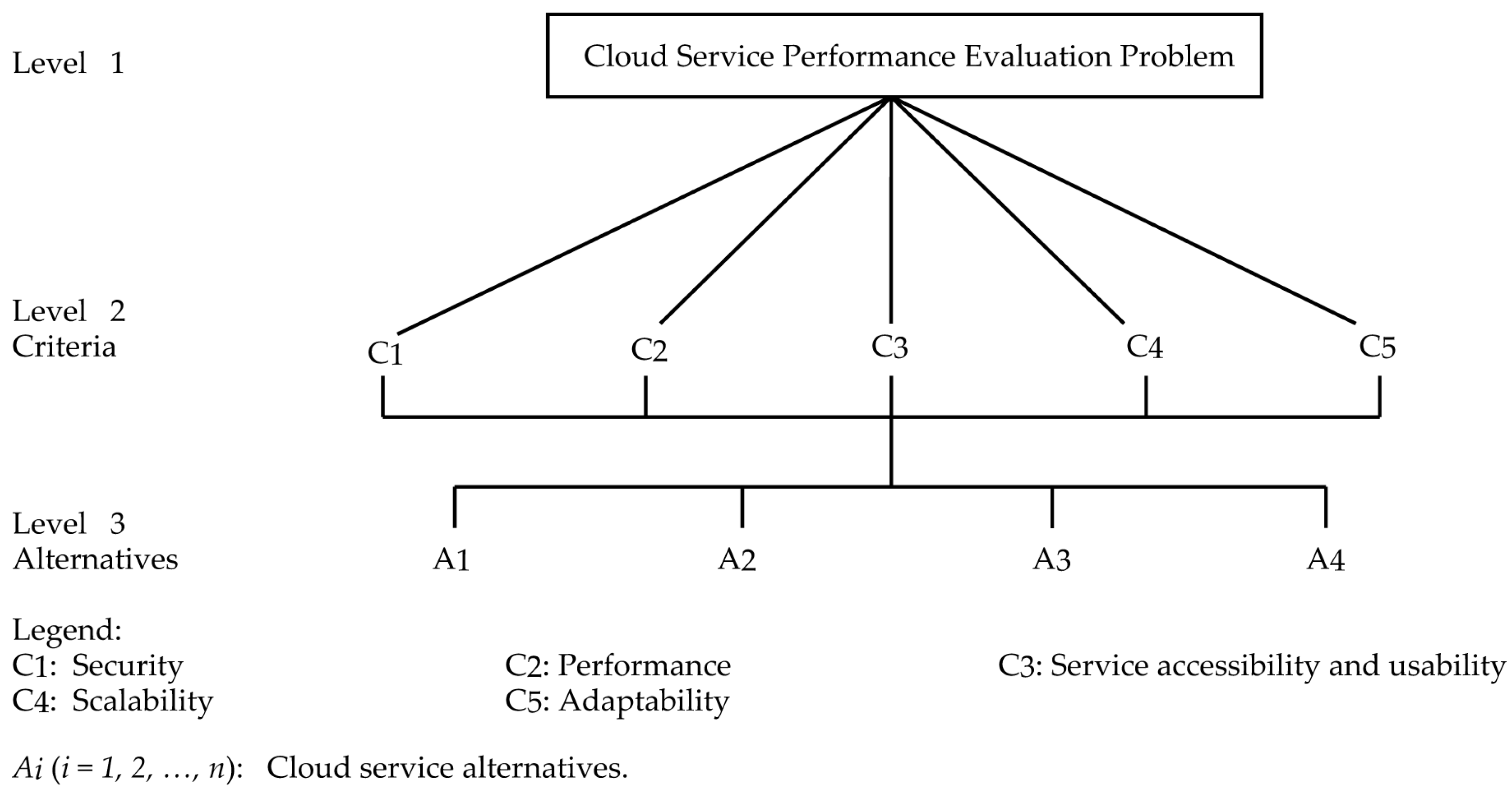
Much research has been done on identifying the relevant criteria for evaluating the performance of Cloud services [1,3,5,6,8,12,13,14,15,16,17,18,19,20,21,22]. A review of the related literature leads to the classification of the evaluation criteria into (a) security, (b) performance, (c) accessibility, (d) usability, (e) scalability, and (f) adaptability. Figure 1 shows the hierarchical structure of the Cloud service performance evaluation problem.

Security (C₁) refers to the ability of a Cloud service to protect the organizational data in terms of their confidentiality and privacy. It is one of the major concerns for organizations when they consider moving their businesses to a Cloud environment. There is a great deal of uncertainty and risks related to the use of networks, hosts, applications, and data in the adoption of Cloud services.

Hosting data under another organization’s control is always a critical issue which requires stringent security policies employed by the Cloud service provider. Avram et al. [22] and Hung et al [23] believe that the support and maintenance provided by the Cloud services provider and the security of the system are the main factors to be used for the selection of the most suitable Cloud service. Godse and Mulik [8] state that a positive user perception of the level of security and privacy of a specific Cloud service positively influences the actual selection of such a service in the real world. Garg et al. [3] point out that there is a significant relationship between the level of the security and privacy concerns and a willingness to provide personal and sensitive information. Julisch and Hall [24] state that, due to the concept of resource pooling with other Clouds, the clients’ data is available both to the third-party Cloud and the Cloud in use. Park and Kim [25] state that an acceptance of the Cloud services is largely affected by the security, perceived mobility, quality of the service, connectedness, and satisfaction of individual users in the evaluation and selection process. This shows that security is a critical criterion for evaluating the appropriateness of Cloud service for implementation.

Performance (C₂) is used to measure the quality of the service that a Cloud service provides. There are many different solutions that a Cloud service can provide for addressing the needs of different organizations. It is therefore important for individual organizations to understand how their applications perform on the different Clouds and whether these application deployments meet their expectations [3,5,26]. Martens and Teuteberg [27] show that organizations need to understand how their applications perform on different Clouds and whether these applications meet their expectations and requirements for achieving the competitive position in the market place. Zeng et al. [28] claim that the performance of the Cloud service is important for improving the operational effectiveness of an organization.

Service accessibility and usability (C₃) refers to the simplicity of the use of a Cloud service for supporting the business operations. The easier it is to use a Cloud service, the faster an organization can switch to it [5,21]. Limam and Boutaba [29] state that a Cloud service needs to enhance the accessibility to many information resources which are locked either in proprietary or inaccessible desktop applications. Quinton et al. [30] believe that the usability of a Cloud service should include multiple factors such as accessibility, learnability, and operability of a Cloud service.

Scalability (C₄) refers to the ability of a Cloud service to fit a problem as the scope of that problem increases. It depends on the automatic resizing and reconfiguration of Cloud resources [6]. The focus here is on how the Cloud service has the ability to make good use of available resources at different workload levels to avoid an excessive delay and unproductive consumption of organizational resources. Garg et al. [3] state that the scalability of a Cloud service is an important quality measure for an organization who wants to move to the Cloud. This is because the costs of using a Cloud service increase, particularly at peak times if the Cloud does not allow an application to scale well vertically. Saripalli and Pingali [5] believe that a Cloud service should have the ability to be scaled up to easily meet the demand through replication and distribution of the requests across a pool or farm of available servers in a specific situation.

Adaptability (C₅) reflects on the ability of the Cloud service to adjust the services based on customers’ requests [1,5,21,31,32]. Menzel et al. [6] and Karim et al. [33] state that Cloud services should be able to create a pool of resources that are flexible enough to handle many different sorts of applications. Such resources can be brought online or torn down to meet the demand of the organization in a given situation.

Given the evaluation criteria identified as above, the available Cloud services have to be evaluated by multiple decision makers to determine the most suitable Cloud service for implementation. With the multi-dimensional nature of such an evaluation problem, the use of a multi-criteria group decision making methodology is appropriate and necessary.

3. A Fuzzy Multi-Criteria Group Decision Making Method

Evaluating the performance of the available Cloud services with respect to multiple, usually conflicting criteria in a specific situation is always challenging due to (a) the availability of multiple Cloud services; (b) the multi-dimensional nature of the decision making problem; (c) the involvement of multiple decision makers; and (d) the presence of subjectivity and imprecision involved in the decision making process [34]. To overcome these concerns, this paper presents a fuzzy multi-criteria decision making method based on the fusion of several concepts including (a) the TOPSIS method; (b) the Choquet integral operator; and (c) intuitionistic fuzzy numbers.

Modelled as a multi-criteria group decision making problem, the performance evaluation of available Cloud services involves (a) discovering all the alternatives; (b) identifying the evaluation criteria; (c) assessing the alternatives’ performance ratings and the criteria weightings by individual decision makers; (d) aggregating the alternative ratings and criteria weightings for producing an overall performance value for each alternative across all the criteria; and (e) selecting the best alternative in the given situation [35,36].

To better model the subjectivity and imprecision of the human decision making process, interval-valued intuitionistic fuzzy numbers are used by the decision maker for assigning the weightings of the evaluation criteria. Interval-valued intuitionistic fuzzy numbers [10] are the generalization of the intuitionistic fuzzy numbers. The values of the membership function and non-membership function of interval-valued intuitionistic fuzzy numbers are represented as intervals rather than exact numbers. In many real situations, it is often difficult to define the membership grade of an element because decision makers often do not agree on the same membership grade for an element. To effectively deal with this situation, a hesitant fuzzy set is introduced [37] as a generalization of fuzzy sets.

For the multi-criteria group decision making problem, let A = {A₁, A₂, ..., A_n} be the set of n alternatives, C = {C₁, C₂, ..., C_m} be the set of m criteria and D = {D₁, D₂, ..., D_s} be the set of decision makers. The performance of the alternatives A_i (i = 1, 2, …, n) with respect to criteria C_j (j = 1, 2, …, m) which is assessed by individual decision makers D_k (k = 1, 2, …, s) is measured by an interval-valued intuitionistic hesitant fuzzy element [37].

In this paper, an interval-valued intuitionistic hesitant fuzzy Choquet integral operator [38] is introduced for dealing with the hesitant fuzzy multi-criteria decision making problem in an efficient and effective manner. The procedure for the adoption of the interval-valued intuitionistic hesitant fuzzy Choquet integral operator in the fuzzy multi-criteria group decision making process includes the following steps:

Step 1. Construct an interval-valued intuitionistic hesitant fuzzy decision matrix [39] $Z={(h_{ij})}_{n\times m}$ where $h_{ij}=\left\{{\alpha }_{ij}|{\alpha }_{ij}\in h_{ij}\right\}=\left\{\left(\left[{\mu }_{{\alpha }_{ij}}^{-},{\mu }_{{\alpha }_{ij}}^{+}\right],\left[{\nu }_{{\alpha }_{ij}}^{-},{\nu }_{{\alpha }_{ij}}^{+}\right]\right)|{\alpha }_{ij}\in h_{ij}\right\}$ denotes an interval-valued intuitionistic hesitant fuzzy element, and alternative A_i is evaluated by each decision maker D_k with respect to criteria C_j. The hesitant fuzzy decision making matrix for each decision maker Z_k can be represented as in (1).

$$Z^k=\left[\begin{array}{cccc}{h}_{11}^k& h_{12}^k& \mathrm{...}& h_{1m}^k\\ h_{21}^k& h_{22}^k& \mathrm{...}& h_{2m}^k\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ h_{n1}^k& h_{n2}^k& \mathrm{...}& h_{nm}^k\end{array}\right]$$

(1)

Step 2. Obtain the overall interval-valued intuitionistic hesitant fuzzy decision matrix by averaging the fuzzy assessments made by individual decision makers as given in (1).

$$Z=\left[\begin{array}{cccc}{h}_{11}& h_{12}& \mathrm{...}& h_{1m}\\ h_{21}& h_{22}& \mathrm{...}& h_{2m}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ h_{n1}& h_{n2}& \mathrm{...}& h_{nm}\end{array}\right]$$

(2)

Step 3. Determine the fuzzy measures of the criteria set given as in (2) as follows:

$$\lambda +1={\displaystyle \prod _{i=1}^m(1+\lambda \mu (x_i)}$$

(3)

Step 4. Calculate the preference of one permutation to others based on the score function S(h) by using (4).

$$S(h)={\displaystyle {\sum }_{\alpha \in h}S(\alpha )/\#h}$$

(4)

where #h is the number of the elements in h.

Step 5: Aggregate all interval-valued intuitionistic hesitant fuzzy elements ${[h_{ij}]}_{n\times m}$ into h_i (i = 1, 2, …, n) of the alternatives A_i using the interval-valued intuitionistic hesitant fuzzy Choquet integral operator [39] as in (5).

$$IVIHFCI(h_1,h_2,\mathrm{...},h_m)=\left\{\left(\begin{array}{l}\left[{\displaystyle \prod _{i=1}^m{({\mu }_{{\alpha }_{\sigma (i)}}^{-})}^{\mu (A_{\sigma (i)})-\mu (A_{\sigma (i-1)})},{\displaystyle \prod _{i=1}^m{({\mu }_{{\alpha }_{\sigma (i)}}^{+})}^{\mu (A_{\sigma (i)})-\mu (A_{\sigma (i-1)})}}}\right],\\ \left[1-{\displaystyle \prod _{i=1}^m{(1-{\nu }_{{\alpha }_{\sigma (i)}}^{-})}^{\mu (A_{\sigma (i)})-\mu (A_{\sigma (i-1)})},1-{\displaystyle \prod _{i=1}^m{(1-{\nu }_{{\alpha }_{\sigma (i)}}^{+})}^{\mu (A_{\sigma (i)})-\mu (A_{\sigma (i-1)})}}}\right]\times |{\alpha }_{\sigma (1)}\in h_{\sigma (1)},\mathrm{...}{\alpha }_{\sigma (m)}\in h_{\sigma (m)}\end{array}\right)\right\}$$

(5)

where (σ(1), σ(2), …, σ(m)) is a permutation of (1, 2, …, m), such that $h_{\sigma (1)}\ge h_{\sigma (2)}\ge \mathrm{....}{h}_{\sigma (m)}.$

Steps 6–9 are derived based on the procedure developed by Xu and Yager [40].

Step 6. The interval-valued intuitionistic hesitant fuzzy positive-ideal solution (h⁺) and interval-valued intuitionistic hesitant fuzzy negative-ideal solution (h⁻) are given as in (6) and (7). Here B and C indicate the benefit and the cost criteria, respectively.

$$h^{+}=\left\{\begin{array}{l}\left(\left[\max {\mu }_{{\alpha }_{ij}}^{-},\max {\mu }_{{\alpha }_{ij}}^{+}\right],\left[\min {\nu }_{{\alpha }_{ij}}^{-},\min {\nu }_{{\alpha }_{ij}}^{+}\right]\right)|{\alpha }_{ij}\in B),\\ \left(\left[\min {\mu }_{{\alpha }_{ij}}^{-},\min {\mu }_{{\alpha }_{ij}}^{+}\right],\left[\max {\nu }_{{\alpha }_{ij}}^{-},\max {\nu }_{{\alpha }_{ij}}^{+}\right]\right)|{\alpha }_{ij}\in C)\end{array}\right\}$$

(6)

$$h^{-}=\left\{\begin{array}{l}\left(\left[\min {\mu }_{{\alpha }_{ij}}^{-},\min {\mu }_{{\alpha }_{ij}}^{+}\right],\left[\max {\nu }_{{\alpha }_{ij}}^{-},\max {\nu }_{{\alpha }_{ij}}^{+}\right]\right)|{\alpha }_{ij}\in B),\\ \left(\left[\max {\mu }_{{\alpha }_{ij}}^{-},\max {\mu }_{{\alpha }_{ij}}^{+}\right],\left[\min {\nu }_{{\alpha }_{ij}}^{-},\min {\nu }_{{\alpha }_{ij}}^{+}\right]\right)|{\alpha }_{ij}\in C)\end{array}\right\}$$

(7)

${\alpha }^{+}$ and ${\alpha }^{-}$ represent the largest and the smallest interval-valued intuitionistic fuzzy values respectively and are denoted as follows:

$${\alpha }^{+}=\left(\left[\max {\mu }_{{\alpha }_{ij}}^{-},\max {\mu }_{{\alpha }_{ij}}^{+}\right],\left[\min {\nu }_{{\alpha }_{ij}}^{-},\min {\nu }_{{\alpha }_{ij}}^{+}\right]\right)$$

$${\alpha }^{-}=\left(\left[\min {\mu }_{{\alpha }_{ij}}^{-},\min {\mu }_{{\alpha }_{ij}}^{+}\right],\left[\max {\nu }_{{\alpha }_{ij}}^{-},\max {\nu }_{{\alpha }_{ij}}^{+}\right]\right)$$

where ${\alpha }^{+}=([1,1],[0,0]$ and ${\alpha }^{-}=([0,0],[1,1]).$

Step 7. Calculate the distances $d(A_i,{\alpha }^{+})$ and $d(A_i,{\alpha }^{-})$ between the alternative A_i and the interval-valued intuitionistic hesitant fuzzy positive-ideal solution (h⁺) and the interval-valued intuitionistic hesitant fuzzy negative-ideal solution (h⁻) respectively by using the interval-valued hesitant fuzzy Euclidean distance [38] by using (8) and (9), respectively.

$$d(A_i,{\alpha }^{+})=\sqrt{\frac{1}{2m}{\displaystyle \sum _{j=1}^m\left({\left|{\mu }_{{\alpha }_{ij}}^{+}-{\mu }_{{\alpha }_j}^{+}\right|}^2+{\left|{\nu }_{{\alpha }_{ij}}^{+}-{\nu }_{{\alpha }_j}^{+}\right|}^2\right)}}$$

(8)

$$d(A_i,{\alpha }^{-})=\sqrt{\frac{1}{2m}{\displaystyle \sum _{j=1}^m\left({\left|{\mu }_{{\alpha }_{ij}}^{-}-{\mu }_{{\alpha }_j}^{-}\right|}^2+{\left|{\nu }_{{\alpha }_{ij}}^{-}-{\nu }_{{\alpha }_j}^{-}\right|}^2\right)}}$$

(9)

Step 8. Compute the closeness coefficient value for each alternative across all the evaluation criteria by using (10) as follows

$$C{C}_i=\frac{d(A_i,{\alpha }^{-})}{d(A_i,{\alpha }^{+})+d(A_i,{\alpha }^{-})}$$

(10)

where i = 1, 2, …, n.

Step 9. Rank all the alternatives A_i (i = 1, 2, …, n) based on the descending order of the closeness of coefficient values. The larger the closeness coefficient value is, the more preferred the alternative A_i.

4. An Example

Company A is an e-learning services provider with more than 50 employees located in Taiwan. The company’s main activities include e-learning content development and delivery business through direct marketing. As the e-learning content is the most precious corporate asset, content security and piracy are the company’s top concerns. Company A is particularly worried about its e-learning content being pirated on the Internet as it could cause a devastating business loss to the company. Up till now, Company A still has not found a suitable Digital Rights Management solution to resolve the data security and piracy issue on the Internet. As a result, Company A is seeking a suitable Cloud service that is capable of customizing a private e-learning platform to suit the company’s specific purposes.

To start with the Cloud service performance evaluation process, the team has identified several Cloud service alternatives and the evaluation criteria through a comprehensive investigation. Four potential Cloud service alternatives and five criteria are determined for evaluating the performance of the most suitable Cloud service alternative. The four potential Cloud service alternatives are identified which include (a) iCloud, (b) hiCloud, (c) Cloud drive, and (d) SmartCLOUD. The five most important criteria that are relevant for the performance evaluation of Cloud service alternatives are used including security (C₁), performance (C₂), service accessibility and usability (C₃), scalability (C₄), and adaptability (C₅). The proposed fuzzy multicriteria decision making method presented in Section 3 is used for evaluating the performance of Cloud service alternatives. The steps followed are illustrated in the following:

Step 1. Constr0uct an interval-valued intuitionistic hesitant fuzzy decision matrix by each decision maker. In the evaluation process, it is necessary for the decision makers to provide their own evaluation in relation to all the available alternatives.

Table 1. The interval-valued intuitionistic hesitant fuzzy decision matrix for decision maker 1.

Alternatives	C1	C2	C3	C4	C5
A1	{([0.4,0.5],[0.6,0.9]) ([0.1,0.3],[0.2,0.6])}	{([0.4,0.6],[0.3,0.7]) ([0.2,0.3],[0.5,0.8])}	{([0.3,0.6],[0.3,0.6]) ([0.4,0.7],[0.5,0.8])}	{([0.4,0.6],[0.7,0.8]) ([0.1,0.4],[0.2,0.6])}	{([0.3,0.6],[0.5,0.8]) ([0.5,0.8],[0.6,0.7])}
A2	{([0.2,0.3],[0.5,0.6]) ([0.4,0.7],[0.3,0.4])}	{([0.3,0.5],[0.4,0.7]) ([0.2,0.6],[0.5,0.9])}	{([0.6,0.7],[0.4,0.8]) ([0.1,0.5],[0.3,0.6])}	{([0.4,0.9],[0.3,0.7]) ([0.5,0.7],[0.2,0.4])}	{([0.2,0.6],[0.5,0.6]) ([0.4,0.7],[0.5,0.7])}
A3	{([0.5,0.9],[0.2,0.7]) ([0.3,0.7],[0.4,0.9])}	{([0.1,0.4],[0.5,0.8]) ([0.1,0.3],[0.3,0.7])}	{([0.5,0.9],[0.3,0.7]) ([0.3,0.7],[0.1,0.2])}	{([0.3,0.8],[0.2,0.7]) ([0.4,0.7],[0.6,0.9])}	{([0.5,0.9],[0.2,0.7]) ([0.3,0.6],[0.4,0.5])}
A4	{([0.3,0.4],[0.5,0.8]) ([0.1,0.5],[0.6,0.8])}	{([0.2,0.5],[0.4,0.7]) ([0.1,0.6],[0.6,0.8])}	{([0.5,0.8],[0.1,0.4]) ([0.3,0.4],[0.5,0.7])}	{([0.2,0.4],[0.6,0.9]) ([0.3,0.7],[0.4,0.8])}	{([0.2,0.5],[0.6,0.8]) ([0.1,0.4],[0.5,0.9])}

,

Table 2. The interval-valued intuitionistic hesitant fuzzy decision matrix for decision maker 2.

Alternatives	C1	C2	C3	C4	C5
A1	{([0.1,0.4],[0.5,0.8]) ([0.1,0.3],[0.3,0.7])}	{([0.5,0.9],[0.2,0.7]) ([0.3,0.6],[0.4,0.5])}	{([0.4,0.9],[0.3,0.7]) ([0.5,0.7],[0.2,0.4])}	{([0.5,0.9],[0.2,0.7]) ([0.3,0.7],[0.4,0.9])}	{([0.2,0.3],[0.5,0.6]) ([0.4,0.7],[0.3,0.4])}
A2	{([0.4,0.6],[0.7,0.8]) ([0.1,0.4],[0.2,0.6])}	{([0.2,0.5],[0.6,0.8]) ([0.1,0.4],[0.5,0.9])}	{([0.1,0.4],[0.5,0.8]) ([0.1,0.3],[0.3,0.7])}	{([0.1,0.4],[0.5,0.8]) ([0.1,0.3],[0.3,0.7])}	{([0.2,0.5],[0.6,0.8]) ([0.1,0.4],[0.5,0.9])}
A3	{([0.4,0.9],[0.3,0.7]) ([0.5,0.7],[0.2,0.4])}	{([0.2,0.3],[0.5,0.6]) ([0.4,0.7],[0.3,0.4])}	{([0.5,0.9],[0.2,0.7]) ([0.3,0.6],[0.4,0.5])}	{([0.6,0.7],[0.4,0.8]) ([0.1,0.5],[0.3,0.6])}	{([0.4,0.6],[0.7,0.8]) ([0.1,0.4],[0.2,0.6])}
A4	{([0.5,0.9],[0.2,0.7]) ([0.3,0.6],[0.4,0.5])}	{([0.6,0.7],[0.4,0.8]) ([0.1,0.5],[0.3,0.6])}	{([0.5,0.9],[0.2,0.7]) ([0.3,0.7],[0.4,0.9])}	{([0.4,0.9],[0.3,0.7]) ([0.5,0.7],[0.2,0.4])}	{([0.4,0.9],[0.3,0.7]) ([0.5,0.7],[0.2,0.4])}

and

Table 3. The interval-valued intuitionistic hesitant fuzzy decision matrix for decision maker 3.

Alternatives	C1	C2	C3	C4	C5
A1	{([0.1,0.4],[0.5,0.8]) ([0.1,0.3],[0.3,0.7])}	{([0.4,0.6],[0.7,0.8]) ([0.1,0.4],[0.2,0.6])}	{([0.5,0.9],[0.2,0.7]) ([0.3,0.6],[0.4,0.5])}	{([0.5,0.9],[0.2,0.7]) ([0.3,0.6],[0.4,0.5])}	{([0.5,0.9],[0.2,0.7]) ([0.3,0.6],[0.4,0.5])}
A2	{([0.3,0.5],[0.4,0.7]) ([0.2,0.6],[0.5,0.9])}	{([0.3,0.6],[0.3,0.6]) ([0.4,0.7],[0.5,0.8])}	{([0.5,0.9],[0.2,0.7]) ([0.3,0.6],[0.4,0.5])}	{([0.4,0.6],[0.3,0.7]) ([0.2,0.3],[0.5,0.8])}	{([0.2,0.5],[0.6,0.8]) ([0.1,0.4],[0.5,0.9])}
A3	{([0.4,0.9],[0.3,0.7]) ([0.5,0.7],[0.2,0.4])}	{([0.1,0.4],[0.5,0.8]) ([0.1,0.3],[0.3,0.7])}	{([0.1,0.4],[0.5,0.8]) ([0.1,0.3],[0.3,0.7])}	{([0.3,0.5],[0.4,0.7]) ([0.2,0.6],[0.5,0.9])}	{([0.4,0.9],[0.2,0.7]) ([0.2,0.6],[0.4,0.5])}
A4	{([0.4,0.6],[0.7,0.8]) ([0.1,0.4],[0.2,0.6])}	{([0.4,0.6],[0.3,0.7]) ([0.2,0.3],[0.5,0.8])}	{([0.4,0.9],[0.3,0.7]) ([0.5,0.7],[0.2,0.4])}	{([0.3,0.6],[0.3,0.6]) ([0.4,0.7],[0.5,0.8])}	{([0.2,0.3],[0.5,0.6]) ([0.4,0.7],[0.3,0.4])}

show the evaluation of each decision maker D_k for all the alternatives A_i (i = 1, 2, …, n) with respect to the criteria C_j (j = 1, 2, …, m).

Step 2. The overall interval-valued intuitionistic hesitant fuzzy decision matrix is obtained by averaging the fuzzy assessments made by individual decision makers as in (1).

Step 3. The fuzzy measures of criteria C are determined as shown below by using λ = 0.5.

$$\mu (C_1)=0.6,\mu (C_2)=0.5,\mu (C_3)=0.3,\mu (C_4)=0.2,\mu (C_5)=0.2$$

Step 4. The preference of one permutation over others is obtained below by using the score function derived in (4).

S(h₁₁) = 0.638, S(h₁₂) = 0.532, S(h₁₃) = 0.581, S(h₁₄) = 0.359, S(h₁₅) = 0.214.

Step 5: Aggregate all interval-valued intuitionistic hesitant fuzzy elements ${[h_{ij}]}_{n\times m}$ into h_i (i = 1, 2, …, n) of the alternatives A_i by using (5). The results are calculated as:

h₁ = {([0.62,0.77],[0.12,0.15])([0.41,0.52][0.38,0.48])([0.43,0.55],[0.27,0.42])([0.32,0.39],[0.58,0.65])([0.37,0.26],[0.48,0.52])}

h₂ = {([0.48,0.56],[0.24,0.31])([0.46,0.49][0.27,0.48])([0.11,0.17],[0.63.0.82])([0.13,0.25],[0.56,0.72])([0.28,0.39],[0.37,0.64])}

h₃ = {([0.27,0.36],[0.52,0.61])([0.32,0.43][0.39,0.48])([0.32,0.41],[0.45.0.64])([0.38,0.49],[0.34,0.52]) ([0.36,0.54],[0.49,0.55])}

h₄ = {([0.14,0.24],[0.53,0.74])([0.22,0.38][0.48,0.63])([0.21,0.28],[0.46,0.73])([0.17,0.26],[0.48,0.68]) ([0.29,0.36],[0.43,0.48])}

Step 6. The interval-valued intuitionistic hesitant fuzzy positive-ideal solution (h⁺) and interval-valued intuitionistic hesitant fuzzy negative-ideal solution (h⁻) are given as:

h⁺ = {([1,1],[0,0])([1,1],[0,0])([1,1][0,0])([1,1][0,0])([1,1][0,0])}

h⁻ = {([0,0],[1,1])([0,0],[1,1])([0,0][1,1])([0,0][1,1])([0,0][1,1])}

Step 7. The distance between the alternative A_i from the interval-valued intuitionistic hesitant fuzzy positive-ideal solution (h⁺) and the interval-valued intuitionistic hesitant fuzzy negative-ideal solution (h⁻) are calculated by using (8) and (9).

$$\begin{array}{l}d(A_1,h^{+})=0.571,d(A_1,h^{-})=0.439\\ d(A_2,h^{+})=0.526,d(A_2,h^{-})=0.435\\ d(A_3,h^{+})=0.492,d(A_3,h^{-})=0.479\\ d(A_4,h^{+})=0.548,d(A_4,h^{-})=0.371\end{array}$$

Step 8. By using (10), the closeness coefficient value of each alternative can be calculated as shown in

Table 4. The closeness coefficient of the Cloud service alternatives and their rankings.

Alternatives	Value	Ranking
A1	0.714	2
A2	0.653	3
A3	0.628	4
A4	0.739	1

.

Step 9. The ranking of each alternative can be determined based on the closeness coefficient obtained in Table 4. Table 4 also shows that alternative A₄ is the best performing Cloud service alternative, as compared to the other alternatives as it has the highest closeness coefficient value of 0.739.

The result shows that SmartCLOUD Cloud service alternative is the ideal solution for Company A as it is capable of meeting the company’s specific purposes for improving its business operation.

The developed fuzzy multicriteria group decision making method is an extension of the work of Joshi and Kumar [36]. The extension mainly focuses on (a) the use of an overall interval-valued intuitionistic hesitant fuzzy decision matrix that is obtained by averaging the fuzzy assessments made by all the decision makers shown as in Step 2; and (b) the adoption of the interval-valued hesitant fuzzy Euclidean distance for calculating the positive and negative ideal solutions in this paper. Such an extension simplifies the extensive computation process usually required in existing fuzzy multicriteria group decision making methods including that of Joshi and Kumar [36].

To demonstrate the effectiveness of the proposed fuzzy multicriteria group decision making model presented in Section 3, a comparative study on the relative performance of the proposed model with comparable multicriteria group decision making methods is conducted.

Five other methods [40,41,42,43,44] are used in the comparative study here as examples to show the performance of the fuzzy multicriteria group decision making model developed. The result shows that the proposed fuzzy multicriteria group decision making model produces consistent ordering results as compared to most of the multicriteria group decision making methods. The advantage of the proposed fuzzy multicriteria group decision making model over the other multicriteria group decision making methods is due to its simplicity in concept and its efficiency in computation.

Table 5. Results of the comparative study

Methods	Ordering
Xu and Yager [40]	A4 > A1 > A2 > A3
Chen and Tsao [41]	A4 > A2 > A1 > A3
Ye [42]	A1 > A4 > A2 > A3
Intepe et al. [43]	A4 > A1 > A3 > A2
Chen [44]	A4 > A1 > A2 > A3
The proposed algorithm	A4 > A1 > A2 > A3

shows the results of the comparative study.

The discussion above demonstrates that the proposed fuzzy multi-criteria group decision making model is useful for solving real multi-criteria group decision making problems. Furthermore, the underlying principle of the proposed model which is based on the TOPSIS method and the Choquet integral operator is logical and comprehensible, and the computation involved is simple and straightforward, in particular when interval-valued intuitionistic fuzzy numbers are present as in the comparative studies shown above.

5. Conclusion

This paper has presented a fuzzy multi-criteria group decision making method for evaluating the performance of Cloud services. The inherent subjectivity and imprecision of the evaluation process is modeled by using interval-valued intuitionistic fuzzy numbers. An effective algorithm is developed based on the TOPSIS method and the Choquet integral operator for adequately dealing with the Cloud service performance evaluation problem. With the use of an example of a company in Taiwan, the proposed fuzzy multi-criteria group decision making method has demonstrated a number of advantages for adequately dealing with the problem of evaluating the performance of alternative Cloud services, including the capability to adequately handle the group decision making process, and the ability to deal with the subjectivity and imprecision inherent in the Cloud service performance evaluation problem. The method is found to be effective and efficient, due to the comprehensibility of its underlying concepts and the straightforward computation process.