1. Introduction
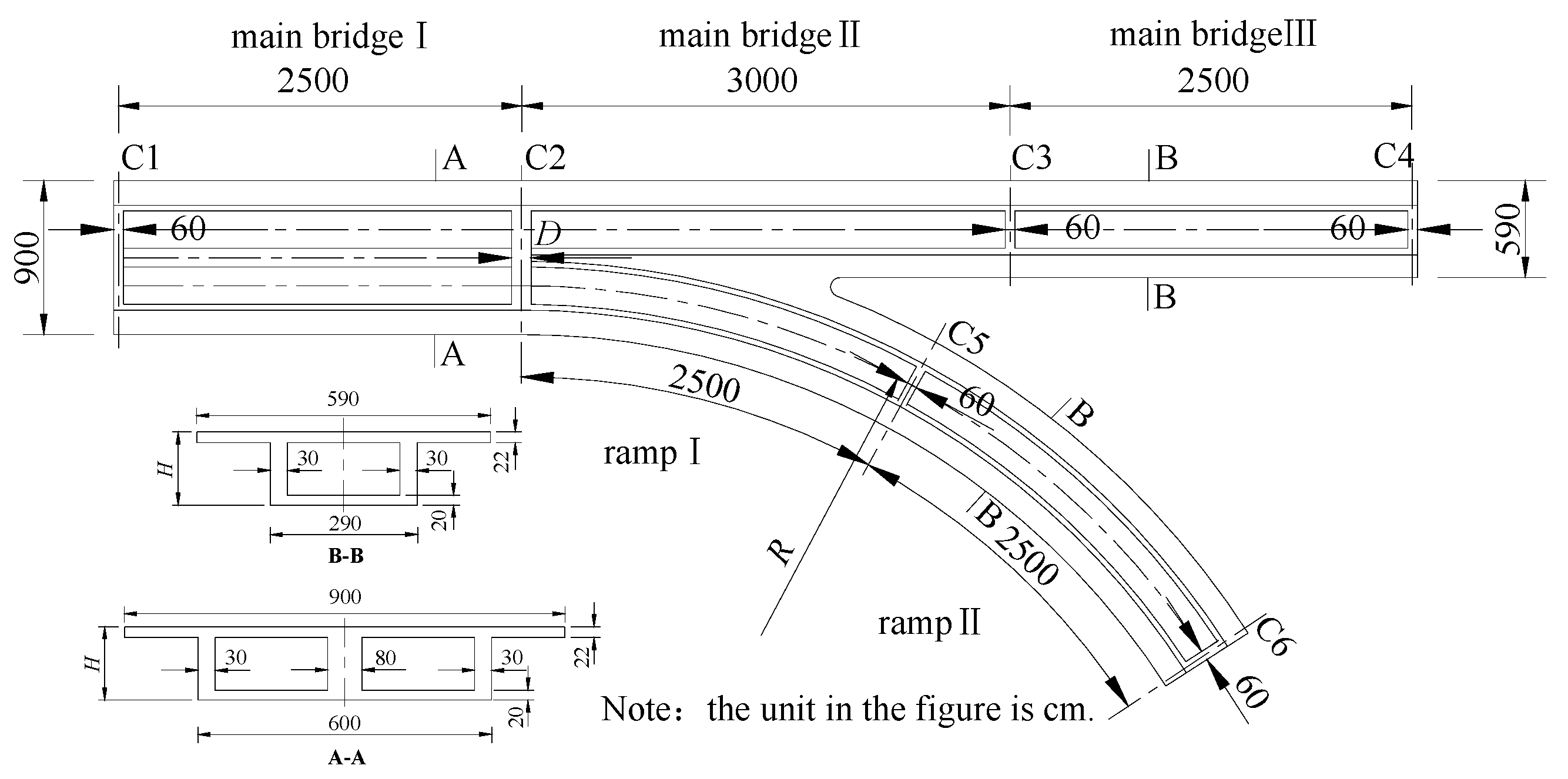
With continuous economic development, urban traffic congestion is increasingly becoming a serious problem. Overpasses play an important role in solving the urban traffic problem. As the connecting structure of the main bridge and ramps in urban overpasses, an irregularly-shaped bridge, as shown in
Figure 1a, can solve the conflict of bridge and ground transportation effectively to improve the driving efficiency and keep it in harmony with the environment [
1]. However, an irregularly-shaped bridge usually adopts the thin-walled box girder, which suffers salient restrained torsion and shear lag effects [
2]. The main bridge and ramp are contacted and restricted with each other at the crotch of the irregularly-shaped bridge, which results in a complicated strained condition and varying degrees of damage. In recent years, the collapse of irregular-shaped bridges have happened several times in China, as illustrated in
Figure 1b [
3]. The optimal design of such structures can be extremely useful to improve this situation. Foti et al. [
4,
5] had studied the dynamic behaviors of a pedestrian bridge before retrofitting, and after, using experimental and numerical methods. The dynamic interaction between pedestrians and the bridge and the damping factor were investigated. Due to the change of mass and stiffness of the footbridge caused by retrofitting using glass fiber-reinforced polymers (GFRPs), the dynamic behavior was indeed modified. Dynamic interaction still existed, and the modal damping factors for the main modes of bending vibration almost doubled after retrofitting. Therefore, the dynamic interaction problem highlights the need to perform specific dynamic analysis during the design phase of light and slender bridges to avoid resonance. For the design of irregularly-shaped bridges, many parameters affect its mechanical properties. One of the key aspects of an optimization study is the sensitivity analysis of influence parameters. How to determine the major influence parameters of the design indices and find the optimal parameter levels for an irregularly-shaped bridge are becoming the focus of attention and demand for engineers.
The thin-walled box girder adopted in irregularly-shaped bridges usually suffers from the influence of torsion, distortion, warping, and shear lag, which causes a severely uneven stress distribution [
6,
7]. Many researchers have studied the calculation principles and analysis methods for the thin-walled box girder [
8,
9,
10,
11,
12]. However, the mechanical property of an irregularly-shaped bridge is different from the conventional straight and curved thin-walled box girder bridge. The traditional analytical method is unsuitable to solve this problem. Finite element analysis (FEA) is a widely used numerical calculation method, which provides an effective way to analyze the static and dynamic properties of structures [
13,
14,
15,
16,
17]. Through numerical simulation, the influence of design parameters on mechanical properties of irregularly-shaped bridges and curved bridges have been studied and demonstrated [
1,
18]. However, the investigation on multi-indices optimization for the mechanical properties of irregularly-shaped bridges is relatively scarce [
19,
20]. Due to numerous parameters affecting the strained condition of irregularly-shaped bridges, the influence of a single parameter is not able to reflect the effect of parameters in combination. Moreover, the comprehensive combination tests of influence parameters need repeated and complicated numerical modeling and analysis, which is difficult to be achieved due to the large degree of testing and calculation. The classical optimization procedures, such as back propagation neural networks (BPNN), support vector machines (SVM), and genetic algorithms (GA), need significant amounts of numerical simulation with different parameter combinations, which also makes the optimization design more complex. Even for a simple problem, the objective functions are calculated based on a large number of training samples. By utilizing the orthogonal test method to optimize the design process, the representative parameter combinations are selected to be analyzed, which reduces the complexity of tests to a large extent.
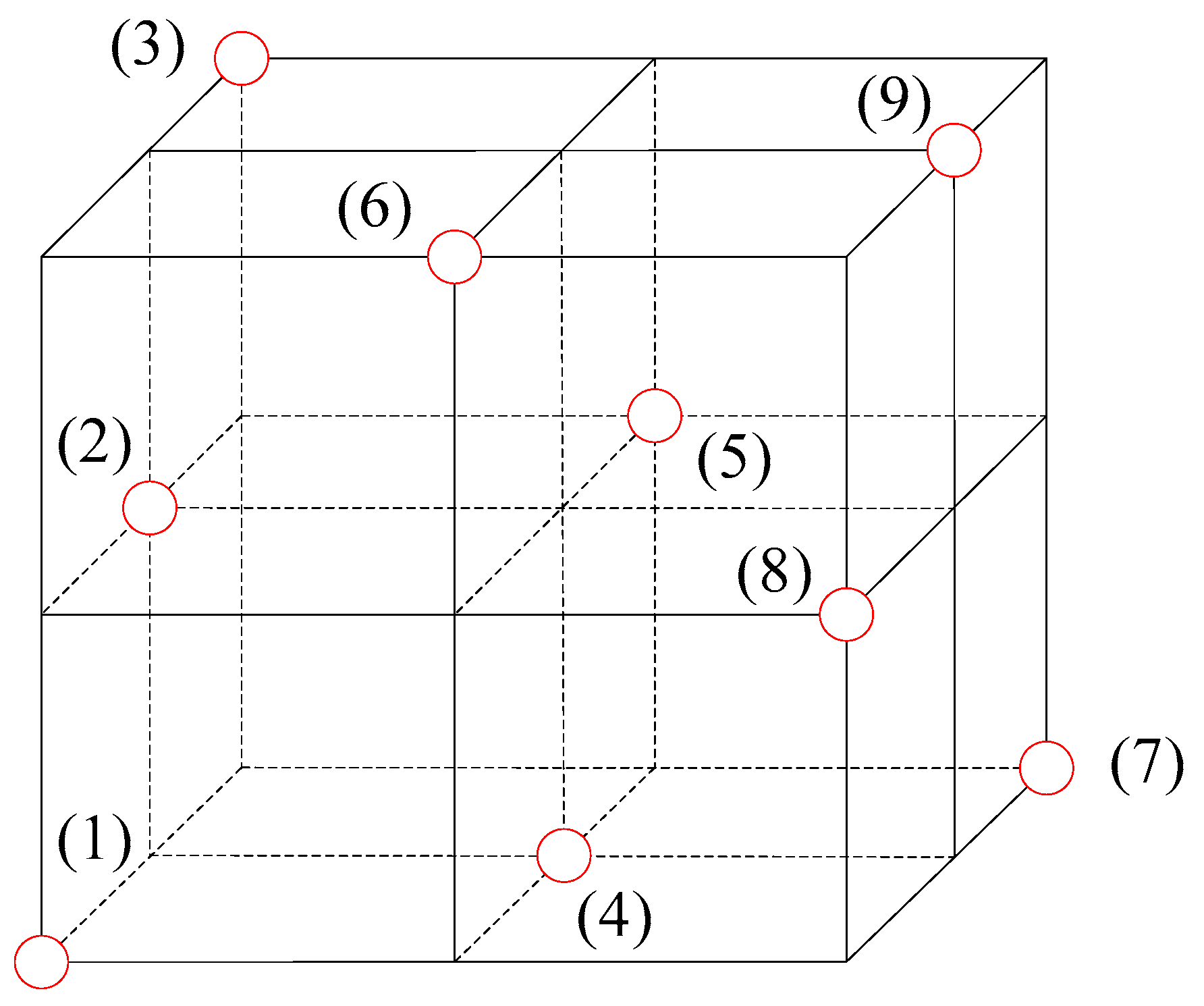
The orthogonal test method provides a scientific and efficient way to arrange and analyze the multi-factors test. It can infer the comprehensive test results based on a limited number of tests, and has been widely used for test design and parameter optimization [
21,
22,
23,
24,
25,
26]. Taking the test with three factors and three levels, for example, the number of comprehensive tests is 3
3 = 27, while only nine orthogonal tests can analyze the sensitivity of factors and determine the preferred levels. As shown in
Figure 2, nine test points regularly distributed throughout the comprehensive test points, which shows a strong representation and is able to better reflect the basic information in the optimal selection space. The optimum condition determined by part tests has the same trends as that obtained by comprehensive tests.
The orthogonal test method can effectively reduce the complexity of testing analysis. However, there is still a large calculated amount, unreasonable weight, and human factor influence in the analysis process of the multi-indices orthogonal test [
27]. In this paper, the index system for the mechanical properties of an irregularly-shaped bridge is established based on the AHP and orthogonal test methods. Maximum stress, the stress variation coefficient, and torsion vibration fundamental frequency are selected as test indices. The influence of the ramp radius, bifurcation diaphragm stiffness, box girder height, and supporting condition on each test index is analyzed by the orthogonal test method. On this basis, weights of factors and levels in the test indices for mechanical properties of an irregularly-shaped bridge are calculated by the proposed comprehensive weight analysis approach. Based on the weight value, the influence order and optimal values of parameters are determined. Experimental results indicate that the proposed comprehensive weight analysis method used for the analysis of the multi-indices orthogonal test can decrease the calculation amount, reasonably determine the weight, and reflect parameter influences objectively, which provides an effective way for parameter sensitivity analysis and design optimization. Additionally, a limitation of the method employed is that correlations and coupling effects between the variables are not considered and analyzed. The fundamental purpose is to investigate the effect of every variable on the overall mechanical properties and determine their weights. In the future, the correlation and coupling effects between variables will be paid more attention and intensively studied.
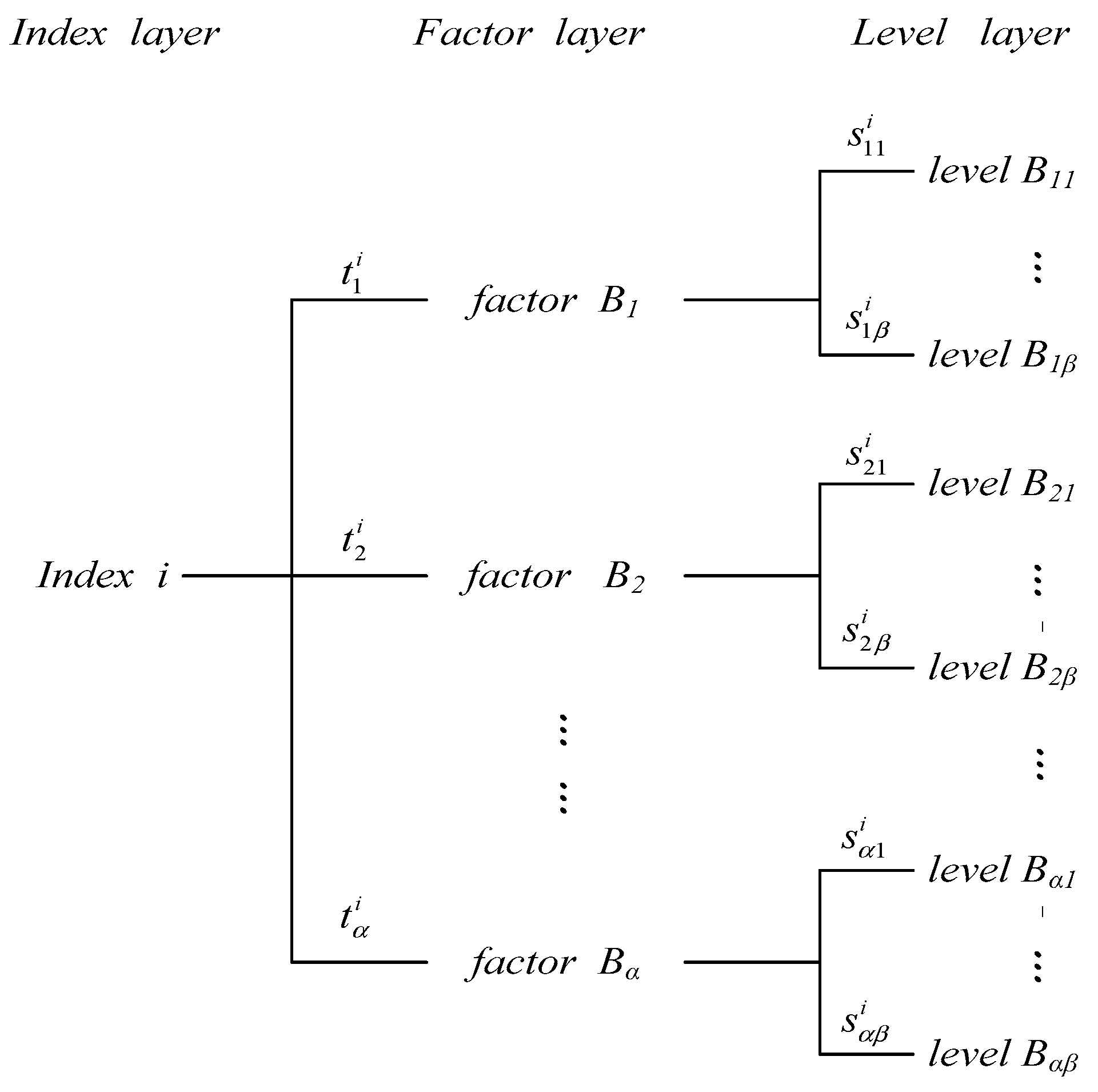
4. Construction of the Index System and the Determination of Factors and Levels
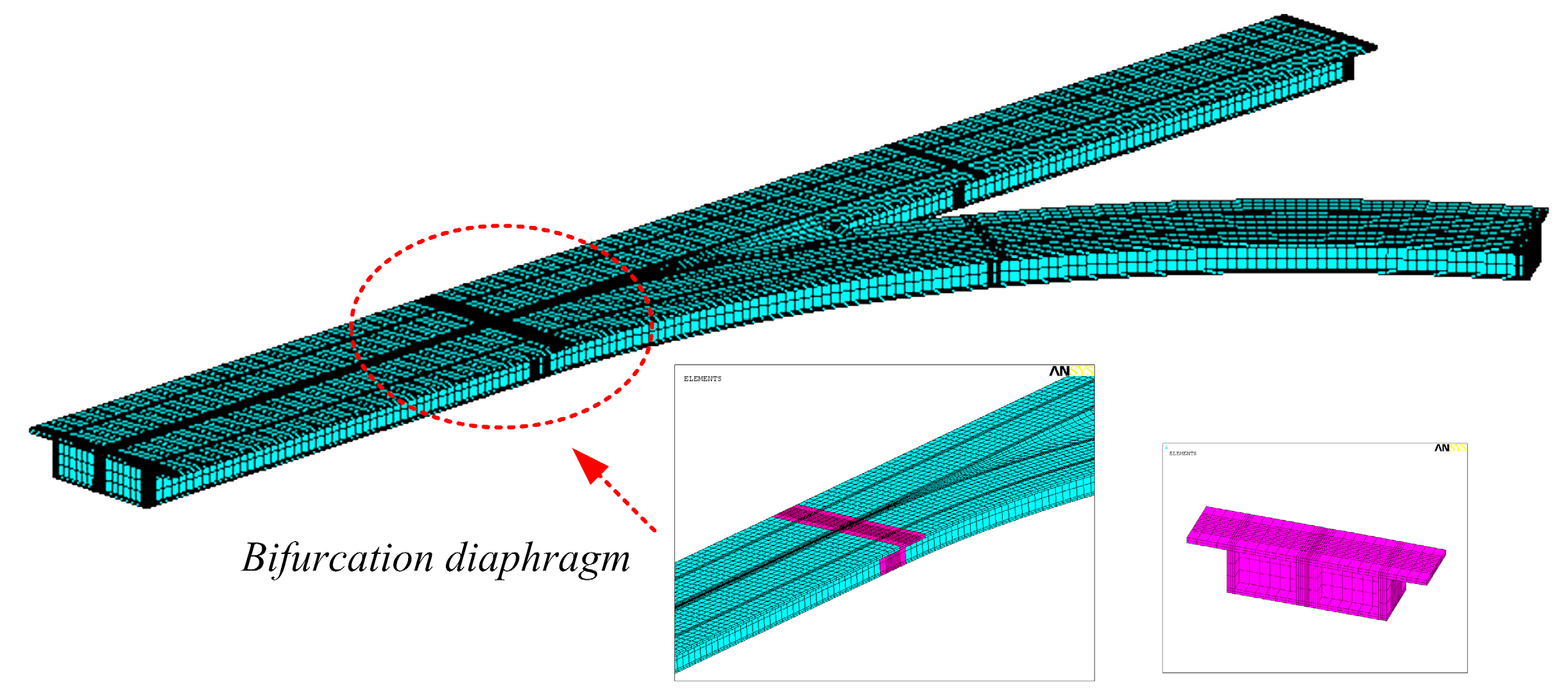
The irregularly-shaped bridge is a continuous structure with three spans. The top plate of the bifurcation diaphragm is under the effect of the hogging moment and tensile stress, which can easily result in cracking and breaking of the concrete in the top plate. Moreover, the bifurcation diaphragm is located at the crotch of main bridge and ramp. It is affected by the coupling effect of constraints, torsion, and shear lag, which makes the distribution of tensile stress seriously uneven. Research on the maximum stress and uneven stress distribution in the top plate of the bifurcation diaphragm is essential to improve the design security of irregularly-shaped bridges. Meanwhile, the torsion vibration fundamental frequency of the irregularly-shaped bridge should be greater than the external excitation frequency to avoid torsional resonance and improve its dynamic characteristics [
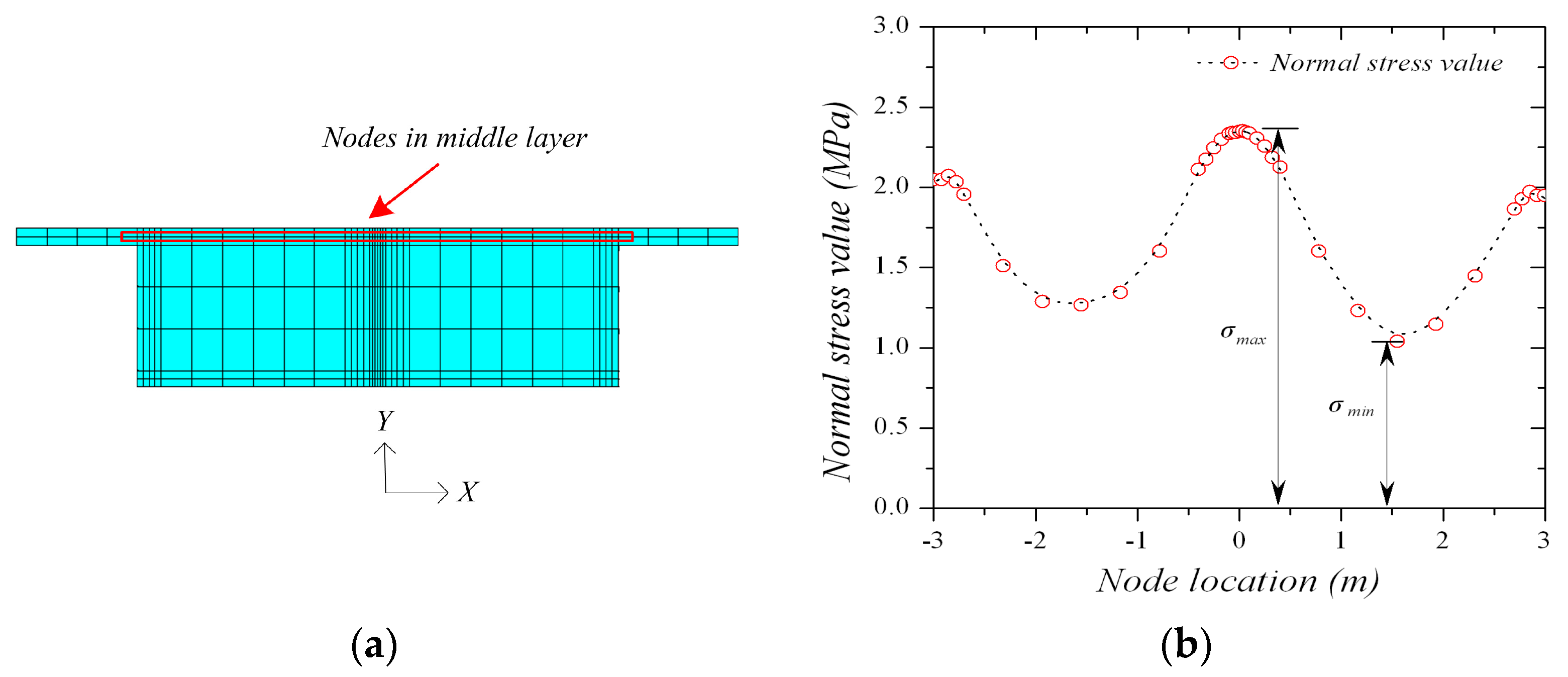
5]. The middle section of the bifurcation diaphragm is selected and the nodes in the middle layer of the top plate are adopted as study objects, which are shown in
Figure 6a. Taking into account the static and dynamic characteristics, the maximum stress (
), the stress variation coefficient (
) of selected nodes under a dead load condition, and the torsion vibration fundamental frequency (
) of the bridge are regarded as the indices to reflect the parameter influences on the mechanical properties. Hierarchical structure and index weights are listed in
Table 4. The stress variation coefficient (
) is the ratio of the maximum normal stress (
) to the minimum normal stress (
), which can be calculated by Equation (12). The calculation results are shown in
Figure 6b.
Based on the relative importance of maximum stress, the stress variation coefficient, and the torsion vibration fundamental frequency to the mechanical properties of the irregularly-shaped bridge, the comparative judgment matrix is established as follows:
The eigenvector for matrix
A can be calculated according to Equation (1), and is shown as follows:
The consistency ratio CR is calculated by Equation (4). If , then the extent of inconsistency for comparison judgment matrix is permitted.
The orthogonal test is carried out for every index to investigate the influence of parameters. In practice, the span is an important factor affecting the strained condition of the bridge structure. However, it is restricted by topographical conditions. Therefore, the influence of other parameters on mechanical properties is demonstrated for the irregularly-shaped bridge with a certain span. In this paper, ramp radius, bifurcation diaphragm stiffness, box girder height, and supporting condition, which can strongly affect the mechanical properties of an irregularly-shaped bridge, are selected as the influence factors for mechanical properties in the irregularly-shaped bridge design [
3]. The change of the bifurcation diaphragm stiffness is simulated by thickness variation.
The ramp is a curved beam with a small radius in numerical simulation of the irregularly-shaped bridge. Based on the standard requirements of urban overpass design and the rationality for irregularly-shaped bridge design [
29], the variation ranges for design parameters are determined as ramp radius: 30–50 m, box girder height: 1.6–2.0 m, bifurcation diaphragm thickness: 1.2–2.0 m, and supporting conditions are listed in
Table 5. The selected ranges of values are determined by the statistics for the design parameters of the irregularly-shaped bridge in practical engineering and are consistent with the standard requirements. Therefore, they are representative and reasonable for the optimization design of an irregularly-shaped bridge. The parameters are taken as the factors of the orthogonal test and every parameter is divided into three levels. The factors and levels are listed in
Table 6.
5. Sensitivity Analysis and Design Optimization of Parameters
Based on the factors and levels in
Table 6, an orthogonal test is adopted to arrange numerical simulation tests for analyzing the influence of parameters on test indices, including maximum stress, the stress variation coefficient, and the torsion vibration fundamental frequency. The orthogonal test is carried out utilizing an orthogonal array,
, and test results are listed in
Table 7.
In order to determine the influence order of factors and optimal levels, orthogonal analysis is conducted for the test indices. The analysis results are listed in
Table 8.
ki (
i = 1, 2, 3) represents the corresponding index value at each parameter level and
R denotes the difference between the largest and the smallest values of
ki. It is apparent that the parameter with the largest
R value has the most significant influence on the test index.
5.1. Result Analysis for a Single Index
5.1.1. Influence of Parameters on Maximum Stress
The influence of changing parameters on maximum stress is illustrated in
Figure 7. As can be seen from
Figure 7, the maximum stresses decrease with the increase of box girder height and bifurcation diaphragm thickness, while the influences of the ramp radius and supporting condition are negligible. The growth of the box girder height increases the flexural rigidity to make the vertical bending stress smaller. Vertical bending stress plays the most important role in the normal stress of the top plate, which results in the decrease of the maximum stress. With the bifurcation diaphragm thickness increasing, the torsional stiffness of the bridge increases to resist the torsion and distortion, which decreases the maximum stress. According to range
R, it can be found that the influence degree of factors on the maximum stress is: box girder height > bifurcation diaphragm stiffness > ramp radius > supporting condition. The box girder height and bifurcation diaphragm stiffness are the major influencing factors for maximum stress. In the design of an irregularly-shaped bridge, the smaller maximum stress is conducive to bridge security. As can been seen from
Table 7, the minimum value of the maximum stress index can be obtained when the box girder height is 2 m and the bifurcation diaphragm thickness is 2 m. For the maximum stress index, the ramp radius and the supporting condition can adopt reasonable values due to their negligible influence.
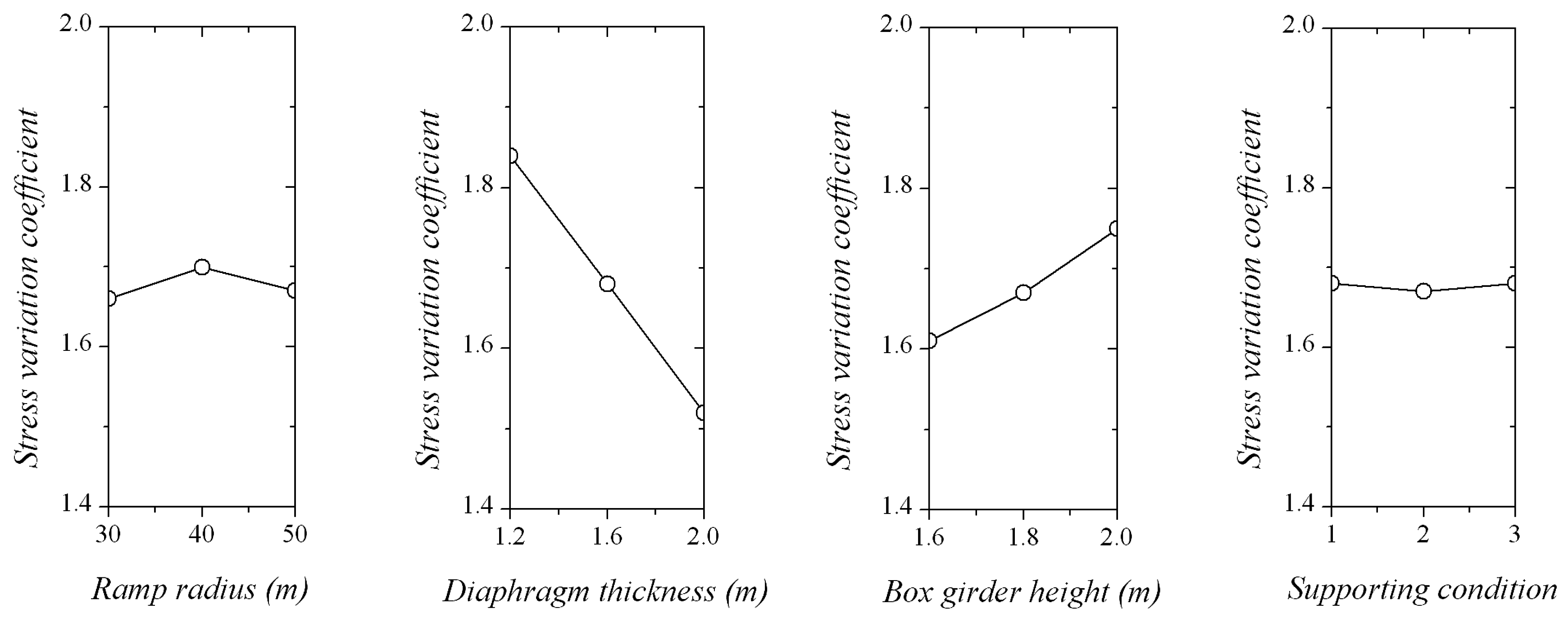
5.1.2. Influence of Parameters on the Stress Variation Coefficient
The influence of parameters on the stress variation coefficient is shown in
Figure 8. From
Figure 8, it can be obtained that the stress variation coefficient decreases with the increase of the bifurcation diaphragm thickness and increases with the growth of the box girder height. The influence of the ramp radius and supporting condition are relatively insignificant. The increase of the bifurcation diaphragm thickness enhances the torsional stiffness, which improves the ability to resist torsion and distortion and reduces the uneven stress distribution. Increasing the box girder height increases the flexural rigidity and torsional stiffness of the bridge, simultaneously. The vertical bending stress in the total vertical stress quickly decreases, while distortion and warping stress reduce insignificantly [
18]. This makes the impact of distortion and warping more significant. Therefore, the stress distribution is seriously uneven and the stress variation coefficient becomes larger. Based on the range of
R values, it can be found that the influence of factors on the stress variation coefficient is: bifurcation diaphragm stiffness > box girder height > ramp radius > supporting condition. Bifurcation diaphragm stiffness and box girder height are the first two factors affecting the uneven stress distribution. The smaller the stress variation coefficient is, the more uniform the stress distribution. The optimal parameter combination for the stress distribution index is: a bifurcation diaphragm thickness of 2 m and box girder height of 1.6 m, while the ramp radius and supporting condition can adopt reasonable values due to their negligible influence.
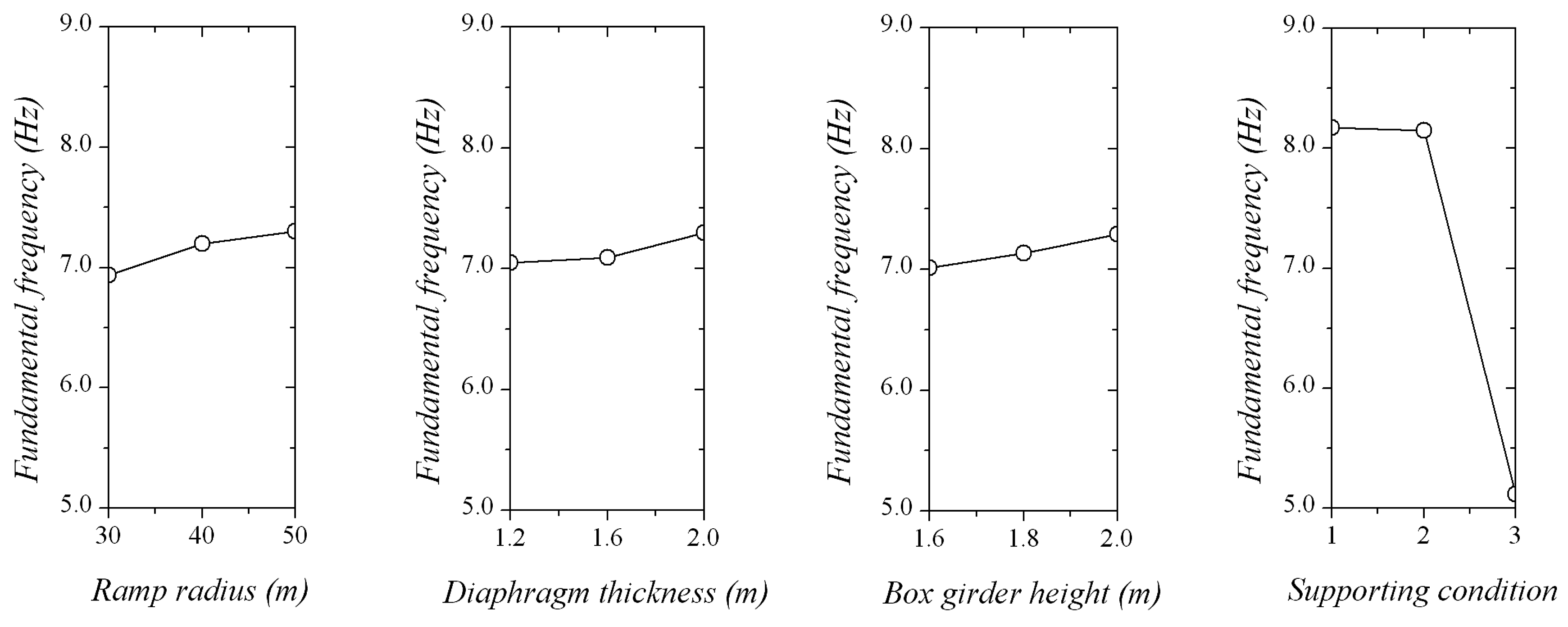
5.1.3. Influence of Parameters on the Torsion Vibration Fundamental Frequency
The influence of parameters on the torsion vibration fundamental frequency is illustrated in
Figure 9. The supporting condition plays the most significant role in the influence of parameters on the torsion vibration fundamental frequency. Supporting condition ③ can reduce the torsion vibration fundamental frequency by a great degree by comparing with others factors. Vertical single supports are set at the end of irregularly-shaped bridge in supporting condition ③. The torsional stiffness decreases and the ability to resist torsional vibration weakens, which leads to the serious decline of the torsion vibration fundamental frequency. According to the range of
R values, the influences of factors on the torsion vibration fundamental frequency is in the following order: supporting condition > ramp radius > box girder height > bifurcation diaphragm stiffness. The supporting condition becomes the first factor to affect the torsional vibration of the irregularly-shaped bridge. The larger torsion vibration fundamental frequency is conducive to avoiding torsional vibration stimulated by the external environment. For driving safety, the parameter combination leading to the maximum torsion vibration fundamental frequency is: supporting condition ① or ②, a ramp radius of 50 m, a bifurcation diaphragm thickness of 2.0 m, and a box girder height 2.0 m.
5.2. Result Analysis for the Mechanical Properties of an Irregularly-Shaped Bridge
5.2.1. Parameter Optimization Based on the Overall Balance Method
According to the orthogonal analysis results for indices, the overall balance method comprehensively considers the influence order of factors and the advantages of levels to determine the final optimal parameter combination. Ramp radius mainly affects the torsion vibration fundamental frequency, and the influence on maximum stress and the stress variation coefficient are negligible. Therefore, optimal ramp radius is selected based on the torsion vibration fundamental frequency. With increasing ramp radius, the torsion vibration fundamental frequency continues to increase. A ramp radius of 50 m is selected as the optimal level. Bifurcation diaphragm stiffness is the first influencing factor for the stress variation coefficient and the second influencing factor for maximum stress. The stress variation coefficient and maximum stress are all decreasing with an increase of the bifurcation diaphragm thickness. The optimal value of the bifurcation diaphragm thickness is 2.0 m. Box girder height affects maximum stress and the stress variation coefficient significantly. With the box girder height increasing, the maximum stress reduces and the stress variation coefficient becomes larger. Taking into account of optimization principles for both factors, the optimal box girder height is determined to be 1.8 m. Supporting condition mainly affects the torsion vibration fundamental frequency. In order to obtain the maximum torsion vibration fundamental frequency, ① is the optimal supporting condition selected. Comprehensively considering all of the above influences for indices, the optimal parameter combination for the mechanical properties of an irregularly-shaped bridge is: ramp radius R = 50 m, bifurcation diaphragm thickness D = 2.0 m, box girder height H = 1.8 m, and supporting condition ①.
5.2.2. Parameter Optimization Based on the Comprehensive Weight Analysis Method
Optimization conditions for a single index are inconsistent with each other. Overall balance methods determine the optimal parameter combination based on the influence of factors on multiple indices. However, it is seriously affected by subjective factors and is difficult to be selected as the actual optimal parameters. Therefore, it is a more favorable method of quantitative analysis to determine the factor influence order and the accurate optimal parameters for calculating the influence weights of factors and levels to the mechanical properties of the irregularly-shaped bridge based on the test index values.
Based on the influence weight matrixes (
,
,
) of factors to indices, the influence weight matrix
of factors to mechanical properties of the irregularly-shaped bridge is shown in
Table 9.
According to the influence weight matrixes (
,
,
) of levels to indices, the influence weight matrix
of levels to mechanical properties of the irregularly-shaped bridge is shown in
Table 10.
As can be seen from weight matrix
in
Table 9, the influence rank of factors is: supporting condition > bifurcation diaphragm stiffness > box girder height > ramp radius. Comparing the weights of levels in the same factor in matrix
listed in
Table 10, the optimal mechanical properties of the irregularly-shaped bridge are obtained when ramp radius, bifurcation diaphragm thickness, box girder height, and supporting condition are
R = 50 m,
D = 2.0 m,
H = 2.0 m, and supporting condition ①, respectively.
In order to compare the optimal parameter combinations for multiple indices obtained from the overall balance method and comprehensive weight analysis, mechanical properties of the irregularly-shaped bridge under two conditions are illustrated in
Table 11.
As can be seen from
Table 11, the comprehensive weight analysis method is superior to the overall balance method. For the comprehensive weight analysis method, maximum stress decreases by 13.4% compared with the overall balance method. There are also significant improvements for the torsion vibration fundamental frequency and the stress variation coefficient. The results indicate that the comprehensive weight analysis method is able to accurately determine the influence order and optimal values of parameters for mechanical properties of the irregularly-shaped bridge.