A Modified Iterative Algorithm for Split Feasibility Problems of Right Bregman Strongly Quasi-Nonexpansive Mappings in Banach Spaces with Applications

Abstract

In this paper, we present a new iterative scheme for finding a common element of the solution set $\mathcal{F}$ of the split feasibility problem and the fixed point set $F(T)$ of a right Bregman strongly quasi-nonexpansive mapping T in p-uniformly convex Banach spaces which are also uniformly smooth. We prove strong convergence theorem of the sequences generated by our scheme under some appropriate conditions in real p-uniformly convex and uniformly smooth Banach spaces. Furthermore, we give some examples and applications to illustrate our main results in this paper. Our results extend and improve the recent ones of some others in the literature.

1. Introduction

Let $E_1$, $E_2$ be Banach spaces and C, Q be nonempty closed convex subsets of $E_1$ and $E_2$, respectively. Let A$:E_1\to E_2$ be a bounded linear operator. The split feasibility problem (shortly, (SFP)) is as follows:

$$\text{Find}x\in C\text{such}\text{that}Ax\in Q.$$

(1)

We denote the solution set of the problem (SFP) by $\mathcal{F}:=\{x\in C:Ax\in Q\}=C\cap A^{-1}(Q).$ It is worth mentioning that (SFP) in finite-dimensional spaces was first introduced by Censor and Elfving [1] for modelling inverse problems which arise from phase retrievals and medical image reconstruction.

Note that, in finite dimensional Hilbert spaces, the strong convergence of a sequence is equivalent to the weak convergence and the boundedness of a sequence implies that there exists a strongly convergent subsequence. However, in infinite dimensional Hilbert spaces, the strong convergence of a sequence is not equivalent to the weak convergence and the boundedness of a sequence implies that there exists a weakly convergent subsequence. So, for some algorithms, we can prove only strong convergence theorems in finite dimensional Hilbert spaces, but we can prove weak and strong convergence theorems in infinite dimensional Hilbert spaces.

In [2], Byrne presented a new method $\{x_n\}$, which is called the CQ-algorithm for solving the problem (SFP) that does not involve matrix inverses, defined as follows:

For any $x_0\in C$ and $n\ge 1,$

$$x_{n+1}=P_C(x_n+\gamma A^T(P_Q-I)x_n),$$

(2)

where $P_C$ and $P_Q$ is the orthogonal projections onto C and $Q,$ respectively, $\gamma \in (0,\frac{2}{L}),$ L is the largest eigenvalue of the matrix $A^{T}A$ and I is the identity matrix.

After that many authors [3,4,5,6,7] study extend some iterative algorithms from Hilbert spaces to Banach spaces by using Bregman’s technic as follows:

In solving the problem (SFP) in p-uniformly convex real Banach spaces which are also uniformly smooth, Schopfer et al. [8] proposed the following algorithm $\{x_n\}$ defined as follows:

For any $x_1\in E_1$ and $n\ge 1,$

$$x_{n+1}={\Pi }_C{J}_{E_1}^{*}(J_{E_1}(x_n)-s_n{A}^{*}{J}_{E_2}(A{x}_n-P_Q(A{x}_n))),$$

(3)

where ${\Pi }_C$ denotes the Bregman projection and J the duality mapping.

Clearly, the algorithm (3) covers Byrne’s CQ algorithm (2), which is a gradient-projection method (GPM) in convex minimization as a special case. The duality mapping of $E_1$ is sequentially weak-to-weak-continuous (see [8]) in Banach spaces such as the classical $L_p(2<p<\infty )$ spaces.

In [9], Wang modified the algorithm (3) and proved strong convergence theorems for the following multiple-sets split feasibility problem (MSSFP):

$$\text{Find}x\in {\displaystyle \bigcap _{i=1}^r}{C}_i\text{such}\text{that}Ax\in {\displaystyle \bigcap _{j=1+r}^{r+s}}{Q}_j,$$

(4)

where $r,s$ are two given integers, $C_i,i=1,2,3,\cdots ,r$, is a closed convex subset in $E_1$ and $Q_j,j=r+1,\cdots ,r+s,$ is a closed convex subset in $E_2.$ He defined the following: for each $n\in \mathbb{N},$

$$T_n(x)=\left\{\begin{array}{cc}{\Pi }_{C_i(n)}(x),\hfill & 1\le i(n)\le r,\hfill \\ J_{E_1}^{*}[J_{E_1}(x)-s_n{A}^{*}{J}_{E_2}(Ax-P_{Q_{j(n)}}(Ax))],\hfill & r+1\le i(n)\le r+s,\hfill \end{array}\right.$$

(5)

where $i:\mathbb{N}\to \mathcal{I}$ is the cyclic control mapping $i(n)=n\mathrm{mod}(r+s)+1$ and $t_n$ satisfies

$$0<s\le s_n\le {\displaystyle \frac{q}{C_q{\parallel A\parallel }^q}}{)}^{\frac{1}{q-1}}$$

(6)

with a constant $C_q$ and proposed the following algorithm $\{x_n\}$ defined as follows: For any $x_1=\overline{x}$ and $n\ge 1$,

$$\left\{\begin{array}{c}{y}_n=T_n{x}_n,\hfill \\ D_n=\{w\in E_1:d_p(y_n,w)\le d_p(x_n,w)\},\hfill \\ E_n=\{w\in E_1:⟨x_n-w,J_p(\overline{x})-J_p(x_n)\ge 0\},\hfill \\ x_{n+1}={\Pi }_{D_n\cap E_n}(\overline{x}).\hfill \end{array}\right.$$

(7)

Recently, Zegeye and Shahzad [10] proved a strong convergence theorem for a common fixed point of a finite family of right Bregman strongly nonexpansive mappings in the framework of real reflexive Banach spaces. Furthermore, they applied their method to approximate a common zero of a finite family of maximal monotone operators and a solution of a finite family of convex feasibility problems in reflexive real Banach spaces.

Let $f:E\to \mathbb{R}$ be a cofinite function which is bounded, uniformly Fŕechet differentiable and totally convex on bounded subsets of $E.$ Let C be a nonempty closed convex subset of int(dom f) and let $T_i:C\to C,$ for $i=1,2,\cdots ,N,$ be a finite family of right Bregman strongly nonexpansive mappings such that $F(T_i)=\widehat{F}(T_i)$ for each $i\in \{1,2,\cdots ,N\}.$ Assume that $F:=\widehat{F}(T_i)$ is nonempty. For any $u,x_1\in C,$ let $\{x_n\}$ be a sequence generated by

$$x_{n+1}={\alpha }_{n}u+(1-{\alpha }_n)T{x}_n$$

for each $n\ge 1$, where $T=T_N\circ T_{N-1}\circ \cdots \circ T_1$ and $\{{\alpha }_n\}\subset (0,1)$ satisfy the following conditions:

(i)

$\underset{n\to \infty }{lim}{\alpha }_n=0;$

(ii)

${\displaystyle \sum _{n=1}^{\infty }}{\alpha }_n=\infty .$

Then $\{x_n\}$ converges strongly to a point $\widehat{x}.$

In this paper, we modify the Halpern-Mann iterative method for split feasibility problems and fixed point problems concerning right Bregman strongly quasi-nonexpansive mappings in p-uniformly convex and uniformly smooth Banach spaces. We prove strong convergence theorem of the sequences generated by our scheme under some appropriate conditions in real p-uniformly convex and uniformly smooth Banach spaces. Also, we give numerical examples of our result to study its efficiency and implementation. Our results extend and improve the recent ones of some others in the literature.

2. Preliminaries

Let $E_1$, $E_2$ be real Banach spaces and A: $E_1\to E_2$ be a bounded linear operator. The dual (adjoint) operator of A, denoted by $A^{*}$, is a bounded linear operator defined by $A^{*}$: $E_2^{*}\to E_1^{*}$

$$⟨A^{*}\overline{y},x⟩:=⟨\overline{y},Ax⟩$$

(8)

for all $x\in E_1$ and $\overline{y}\in E_2^{*}$ and the equalities $\parallel A^{*}\parallel =\parallel A\parallel$, $\mathcal{N}(A^{*})=\mathcal{R}{(A)}^{\perp }$ are valid, where

$$\mathcal{R}{(A)}^{\perp }:=\{x^{*}\in E_2^{*}:⟨x^{*},u⟩=0,\forall u\in \mathcal{R}(A)\}.$$

For more details on bounded linear operators and their duals, see [11,12].

Definition 1.

(1) The duality mapping $J_E^p:E\to E^{*}$ is defined by

$$J_E^p(x)=\{x^{*}\in E^{*}:⟨x,x^{*}⟩={\parallel x\parallel }^p,\parallel x^{*}\parallel ={\parallel x\parallel }^{p-1}\}.$$

(2) The duality mapping $J_E^p$ is said to be weak-to-weak continuous if

$$x_n\rightharpoonup x⟹⟨J_E^p{x}_n,y⟩\to ⟨J_E^{p}x,y⟩$$

holds true for any $y\in E.$

We note here that $l_p(p>1)$ spaces has such a property, but the $L_p(p>2)$ space does not share this property. The domain of a convex function $f:E\to \mathbb{R}$ is defined by dom$f:=\{x\in E:f(x)<+\infty \}.$ When dom$f\ne \varnothing ,$ then we say that f is proper.

In the sequel, we adopt the following notations in this paper: $x_n\to x$ means that $x_n\to x$ strongly and $x_n\rightharpoonup x$ meansthat $x_n\to x$ weakly.

Definition 2 

([13]).Let f: $E\to \mathbb{R}$ be a convex and Gâteaux differentiable function. The Bregman distance with respect to f is defined by

$$d_f(x,y):=f(y)-f(x)-⟨f^{\prime }(x),y-x⟩$$

for all $x,y\in E$.

The duality mapping $J_E^p$ is actually the derivative of the function $f_p(x)=\frac{1}{p}{\parallel x\parallel }^p.$ If $f=f_p$, then the Bregman distance with respect to $f_p$ now becomes

$$\begin{array}{cc}\hfill d_p(x,y)& =\frac{1}{q}{\parallel x\parallel }^p-⟨J_E^{p}x,y⟩+\frac{1}{p}{\parallel y\parallel }^p\hfill \\ & =\frac{1}{p}{(\parallel y\parallel }^p-{\parallel x\parallel }^p)+⟨J_E^{p}x,x-y⟩\hfill \\ & =\frac{1}{q}{(\parallel x\parallel }^p-{\parallel y\parallel }^p)-⟨J_E^{p}x-J_E^{p}y,y⟩.\hfill \end{array}$$

(9)

The Bregman distance is not symmetric and so it is not a metric, but it posses the following important properties: for all $w,x,y\in E$,

$$d_p(x,y)=d_p(x,w)+d_p(w,y)+⟨w-y,J_E^{p}x-J_E^{p}y⟩$$

(10)

and

$$d_p(x,y)+d_p(y,x)=⟨x-y,J_E^{p}x-J_E^{p}y⟩.$$

(11)

Let $1<q\le 2\le p$ with $\frac{1}{p}+\frac{1}{q}=1.$ The modulus of smoothness of E is the function ${\rho }_E:[0,\infty )\to [0,\infty )$ defined by

$${\rho }_E(t):=sup\left\{{\displaystyle \frac{1}{2}}(\parallel x+y\parallel +\parallel x-y\parallel )-1:\parallel x\parallel \le 1,\parallel y\parallel \le t\right\}.$$

A Banach space E is said to be uniformly smooth if

$$\underset{t\to 0}{lim}{\displaystyle \frac{{\rho }_E(t)}{t}}=0$$

and, for any $q>1$, a Banach space E is said to be q-uniformly smooth if there exists $C_q>0$ such that ${\rho }_E(t)\le C_q{t}^q$ for any $t>0.$

Let $x,y\in E$ and $q>1$. If a Banach space E is q-uniformly smooth, then there exists $C_q>0$ such that

$${\parallel x-y\parallel }^q\le {\parallel x\parallel }^q-q⟨J_E^p(x),y⟩+C_q{\parallel y\parallel }^q.$$

(12)

Let $\text{dim}(E)\ge 2.$ The modulus of convexity of E is the function ${\delta }_E(ϵ)$: $(0,2]\to [0,1]$ defined by

$${\delta }_E(ϵ):=inf\left\{1-\parallel {\displaystyle \frac{x+y}{2}}\parallel :\parallel x\parallel =\parallel y\parallel =1,ϵ=\parallel x-y\parallel \right\}.$$

A Banach space E is said to be uniformly convex if ${\delta }_E(ϵ)>0$ for all $ϵ\in (0,2]$ and, for any $p>1$, a Banach space E is said to be p-uniformly convex if there is $C_p>0$ such that ${\delta }_E(ϵ)\ge C_p{ϵ}^p$ for any $ϵ\in (0,2].$ More information concerning uniformly convex spaces can be found, for example, in the book by Goebel and Reich [14].

It is known that a Banach space E is p-uniformly convex and uniformly smooth if and only if its dual $E^{*}$ is q-uniformly smooth and uniformly convex. It is also well known that the duality $J_E^p$ is one-to-one, single valued and satisfies $J_E^p={(J_{E^{*}}^q)}^{-1},$ where $J_{E^{*}}^q$ is the duality mapping of $E^{*}.$

For any p-uniformly convex Banach space E, the metric and the Bregman distance have the following relation:

$${\tau \parallel x-y\parallel }^p\le d_p(x,y)\le ⟨x-y,J_E^{p}x-J_E^{p}y⟩,$$

(13)

where $\tau >0$ is a fixed number.

Let C be a nonempty closed convex subset of $E.$ The metric projection

$$P_{C}x:=\text{arg}\underset{y\in C}{min}\parallel x-y\parallel$$

for all $x\in E$ is the unique minimizer of the norm distance, which can be characterized by a variational inequality

$$⟨J_E^p(x-P_{C}x),z-P_{C}x⟩\le 0$$

(14)

for all $z\in C$.

Similarly, the Bregman projection is defined as follows:

$${\Pi }_{C}x=\text{arg}\underset{y\in C}{min}{d}_p(x,y)$$

for all $x\in E$, which is the unique minimizer of the Bregman distance. In addition, the Bregman projection can also be characterized by a variational inequality

$$⟨J_E^p(x)-J_E^p({\Pi }_{C}x),z-{\Pi }_{C}x⟩\le 0$$

(15)

for all $z\in C$, from which one has

$$d_p({\Pi }_{C}x,z)\le d_p(x,z)-d_p(x,{\Pi }_{C}x)$$

(16)

for all $z\in C$.

Following [15,16], we will make use of the function $V_p$: $E^{*}\times E\to [0,+\infty )$ associated with $f_p,$ which is defined by

$$V_p(\overline{x},x)=\frac{1}{q}{\parallel \overline{x}\parallel }^q-⟨\overline{x},x⟩+\frac{1}{p}{\parallel x\parallel }^p$$

for all $x\in E$ and $\overline{x}\in E^{*}$. Then $V_p$ is nonnegative and

$$V_p(\overline{x},x)=d_p(J_E^{*}(\overline{x}),x)=d_p(J_E^q(\overline{x}),x)$$

(17)

for all $x\in E$ and $\overline{x}\in E^{*}.$ Moreover, by the subdifferential inequality, we have

$$V_p(\overline{x},x)+⟨\overline{y},J_E^{*}(\overline{x})-x⟩\le V_p(\overline{x}+\overline{y},x)$$

(18)

for all $x\in E$ and $\overline{x},\overline{y}\in E^{*}$ (see also [17,18]). In addition, $V_p$ is convex in the first variable. Thus, for all $z\in E,$

$$d_p\left(J_E^q\left({\displaystyle \sum _{i=1}^N}{t}_i{J}_E^p(x_i)\right),w\right)=d_p\left(J_E^{*}\left({\displaystyle \sum _{i=1}^N}{t}_i{J}_E^p(x_i)\right),w\right)\le {\displaystyle \sum _{i=1}^N}{t}_i{d}_p(x_i,w),$$

(19)

where $\{x_i\}\subset E$ and $\{t_i\}\subset (0,1)$ with ${\displaystyle \sum _{i=1}^N}=1.$ For more details, see [19,20].

Let C be a nonempty, closed and convex subset of E. A mapping T: $C\to C$ is said to be nonexpansive if

$$\parallel Tx-Ty\parallel \le \parallel x-y\parallel$$

for all $x,y\in C$. We denote by $F(T)$ the set of fixed points of $T,$ that is, $F(T)=\{x\in C:Tx=x\}.$

Let C be a convex subset of int (dom $f_p$), where $f_p(x)=(\frac{1}{p}){\parallel x\parallel }^p,2\le p<\infty$, and T be a self-mapping of $C.$ A point $\widehat{x}\in C$ is called an asymptotic fixed point of T if C contains a sequence $\{x_n\}$ which converges weakly to $\widehat{x}$ and $\underset{n\to \infty }{lim}\parallel x_n-T{x}_n\parallel =0.$ The set of asymptotic fixed point of T is denoted by $\widehat{F}(T)$ (see [21]).

In general, the Bregman distance is not a metric due to the absence of symmetry, but it has some distance-like properties.

Definition 3.

A nonlinear mapping T with a nonempty asymptotic fixed point set is said to be:

(1) 

T is called right Bregman quasi-nonexpansive (shortly, R-BQNE) (see [22]) if $F(T)\ne \varnothing$ and

$$d_p(Tx,\overline{x})\le d_p(x,\overline{x})$$

for all $x\in C$ and $\overline{x}\in F(T)$.

(2) 

T is called right Bregman strongly quasi-nonexpansive (shortly, R-BSQNE) (see [23,24]) with respect to a nonempty $\widehat{F}(T)$ if

$$d_p(Tx,\widehat{x})\le d_p(x,\widehat{x})$$

for all $\widehat{x}\in \widehat{F}(T),$ $x\in C$, and if whenever $\{x_n\}\subset C$ is bounded, $\widehat{x}\in \widehat{F}(T)$ and $\underset{n\to +\infty }{lim}(d_p(x_n,\widehat{x})-d_p(T{x}_n,\widehat{x}))=0,$ then it follows that $\underset{n\to +\infty }{lim}{d}_p(x_n,T{x}_n)=0.$

(3) 

T is called right Bregman firmly nonexpansive (shortly, R-BFNE) if

$$⟨\nabla f(Tx)-\nabla f(Ty),Tx-Ty⟩\le ⟨\nabla f(x)-\nabla f(y),Tx-Ty⟩$$

for all $x,y\in C$ or, equivalently,

$$d_p(Tx,Ty)+d_p(Ty,Tx)+d_p(x,Tx)+d_p(y,Ty)\le d_p(x,Ty)+d_p(y,Tx)$$

for all $x,y\in C$.

Lemma 1 

([25]). Let $\{a_n\}$ be a sequence of real numbers such that there exists a nondecreasing subsequence $\{n_i\}$ of $\{n\},$ that is, $a_{n_i}\le a_{n_i+1}$ for all $i\in \mathbb{N}.$ Then there exists a nondecreasing subsequence $\{m_k\}\subset \mathbb{N}$ such that $m_k\to \infty$ and the following properties are satisfied for all (sufficiently large number $k\in \mathbb{N}$)$:a_{m_k}\le a_{m_k+1}$ and $a_k\le a_{m_k+1}.$ In fact, $m_k=max\{j\le k:a_j\le a_{j+1}\}.$

Lemma 2 

([26]). Let $\{a_n\}$ be a sequence of nonnegative real numbers satisfying the following relation:

$$a_{n+1}\le (1-{\alpha }_n)a_n+{\alpha }_n{\sigma }_n+{\gamma }_n$$

for each $n\ge 0$, where

(i) 

$\{{\alpha }_n\}\subset [0,1]$ and ${\displaystyle \sum _{n=1}^{\infty }}=\infty$;

(ii) 

$\underset{n\to \infty }{lim\; sup}{\sigma }_n\le 0;$

(iii) 

${\gamma }_n\ge 0$ and ${\displaystyle \sum _{n=1}^{\infty }}{\gamma }_n<\infty .$

Then $\underset{n\to \infty }{lim}{a}_n=0.$

3. Results

Now, we give our main results in this paper.

Theorem 1.

Let $E_1$, $E_2$ be p-uniformly convex real Banach spaces which are also uniformly smooth and C, Q be nonempty closed convex subsets of $E_1$, $E_2,$ respectively. Let A: $E_1\to E_2$ be a bounded linear operator and $A^{*}$: $E_2^{*}\to E_1^{*}$ be the adjoint of $A.$ Suppose that the problem (SFP) has a nonempty solution set $\mathcal{F}$. Let $T:C\to C$ be a right Bregman strongly quasi-nonexpansive mapping such that $F(T)=\widehat{F}(T)\ne \varnothing$ and $F(T)\cap \mathcal{F}\ne \varnothing .$ Suppose that $\{{\alpha }_n\}$, $\{{\beta }_n\}$, $\{{\gamma }_n\}$ and $\{{\delta }_n\}$ are the sequences in $(0,1)$ such that ${\alpha }_n+{\beta }_n+{\gamma }_n+{\delta }_n=1$, ${\alpha }_n\le b<1,(1-{\alpha }_n)a<{\gamma }_n<{\delta }_n,a\in (0,\frac{1}{2}).$ For any fixed $u\in C,$ let the sequences $\{x_n\}$ and $\{u_n\}$ be iteratively generated by $u_0\in E_1$ and

$$\left\{\begin{array}{l}{x}_n={\Pi }_C{J}_{E_1^{*}}^q(J_{E_1}^p(u_n)-s_n{A}^{*}{J}_{E_2}^p(I-P_Q)A{u}_n),\\ u_{n+1}={\Pi }_C{J}_{E_1^{*}}^q({\alpha }_n{J}_{E_1}^p(u)+(1-{\alpha }_n)({\beta }_n{J}_{E_1}^p(u)+{\gamma }_n{J}_{E_1}^p(x_n)+{\delta }_n{J}_{E_1}^p(T{x}_n)))\end{array}\right.$$

(20)

for each $n\ge 1$. Suppose the following conditions are satisfied:

(a) 

$\underset{n\to \infty }{lim}{\alpha }_n=0;$

(b) 

${\displaystyle \sum _{n=1}^{\infty }}{\alpha }_n=\infty ;$

(c) 

$0<s\le s_n\le k<{\left({\displaystyle \frac{q}{C_q{\parallel A\parallel }^q}}\right)}^{\frac{1}{q-1}}.$

Then the sequence $\{x_n\}$ and $\{u_n\}$ converge strongly to a point ${\Pi }_{F(T)\cap \mathcal{F}}u.$

Proof. 

Firstly, we prove that the sequences $\{x_n\}$ and $\{u_n\}$ are bounded. Setting $z_n:=A{u}_n-P_Q(A{u}_n)$ for each $n\ge 1.$ From (14), it follows that, for any $w\in F(T)\cap \mathcal{F}$,

$$\begin{array}{cc}\hfill ⟨J_{E_2}^p(z_n),A{u}_n-Aw⟩& ={\parallel A{u}_n-P_Q(A{u}_n)\parallel }^p+⟨J_{E_2}^p(z_n),P_Q(A{u}_n)-Aw⟩\hfill \\ & \ge {\parallel A{u}_n-P_Q(A{u}_n)\parallel }^p\hfill \\ & ={\parallel z_n\parallel }^p.\hfill \end{array}$$

(21)

So, from (21) and (12), it follows that

$$\begin{array}{l}{d}_p(x_n,w)\\ \le d_p(J_{E_1^{*}}^q[J_{E_1}^p(u_n)-s_n{A}^{*}{J}_{E_2}^p(I-P_Q)A{u}_n],w)\\ ={\displaystyle \frac{1}{q}}{\parallel J_{E_1}^p(u_n)-s_n{A}^{*}{J}_{E_2}^p(z_n)\parallel }^q-⟨J_{E_1}^p(u_n),w⟩+s_n⟨J_{E_2}^p(z_n),Aw⟩+{\displaystyle \frac{1}{p}}{\parallel w\parallel }^p\\ \le \parallel J_{E_1}^p(u_n)\parallel -s_n⟨A{u}_n,J_{E_2}^p(z_n)⟩+{\displaystyle \frac{C_q(s_n{\parallel A\parallel )}^q}{q}}{\parallel J_{E_2}^p(z_n)\parallel }^p\\ -⟨J_{E_1}^p(u_n),w⟩+{\displaystyle \frac{1}{p}}{\parallel w\parallel }^p+s_n⟨Aw,J_{E_2}^p(z_n)⟩\\ ={\displaystyle \frac{1}{q}}{\parallel u_n\parallel }^p-⟨J_{E_1}^p(u_n),w⟩+{\displaystyle \frac{1}{q}}{\parallel w\parallel }^p+s_n⟨J_{E_2}^p(z_n),Aw-A{u}_n⟩\\ +{\displaystyle \frac{C_q(s_n{\parallel A\parallel )}^q}{q}}{\parallel z_n\parallel }^p\\ =d_p(u_n,w)+s_n⟨J_{E_2}^p(z_n),Aw-A{u}_n⟩+{\displaystyle \frac{C_q(s_n{\parallel A\parallel )}^q}{q}}{\parallel z_n\parallel }^p\\ \le d_p(u_n,w)-(s_n-{\displaystyle \frac{C_q(s_n{\parallel A\parallel )}^q}{q}}){\parallel z_n\parallel }^p.\end{array}$$

(22)

By using $(c),$ we obtain

$$d_p(x_n,w)\le d_p(u_n,w).$$

From (20), we have

$$\begin{array}{l}{d}_p(u_{n+1},w)\\ \le d_p(J_{E_1^{*}}^q[{\alpha }_n{J}_{E_1}^p(u)+(1-{\alpha }_n)({\beta }_n{J}_{E_1}^p(u)+{\gamma }_n{J}_{E_1}^p(x_n)+{\delta }_n{J}_{E_1}^p(T{x}_n))],w)\\ =d_p(J_{E_1^{*}}^q[{\alpha }_n{J}_{E_1}^p(u)\\ +(1-{\alpha }_n){\beta }_n{J}_{E_1}^p(u)+(1-{\alpha }_n){\gamma }_n{J}_{E_1}^p(x_n)+(1-{\alpha }_n){\delta }_n{J}_{E_1}^p(T{x}_n)],w)\\ \le {\alpha }_n{d}_p(u,w)+(1-{\alpha }_n){\beta }_n{d}_p(u,w)\\ +(1-{\alpha }_n){\gamma }_n{d}_p(x_n,w)+(1-{\alpha }_n){\delta }_n{d}_p(T{x}_n,w)\\ \le {\alpha }_n{d}_p(u,w)+(1-{\alpha }_n){\beta }_n{d}_p(u,w)\\ +(1-{\alpha }_n){\gamma }_n{d}_p(x_n,w)+(1-{\alpha }_n){\delta }_n{d}_p(x_n,w)\\ =({\alpha }_n+(1-{\alpha }_n){\beta }_n)d_p(u,w)+(1-{\alpha }_n)({\gamma }_n+{\delta }_n)d_p(x_n,w)\\ \le ({\alpha }_n+(1-{\alpha }_n){\beta }_n)d_p(u,w)+(1-{\alpha }_n)({\gamma }_n+{\delta }_n)d_p(u_n,w)\\ \le max\{d_p(u,w),d_p(u_n,w)\}\\ \cdots \\ \le max\{d_p(u,w),d_p(u_1,w)\}.\end{array}$$

(23)

Thus $\{d_p(u_n,w)\}$ is bounded and, consequently, we have that $\{d_p(x_n,w)\}$ is bounded. Hence the sequence $\{x_n\}$ and $\{u_n\}$ are bounded. Setting

$$y_n=J_{E_1^{*}}^q[{\alpha }_n{J}_{E_1}^p(u)+(1-\alpha )({\beta }_n{J}_{E_1}^p(u)+{\gamma }_n{J}_{E_1}^p(x_n)+{\delta }_n{J}_{E_1}^p(T{x}_n))]$$

for each $n\ge 1$. Then we have

$$\begin{array}{l}{d}_p(x_{n+1},w)\\ \le d_p(u_{n+1},w)\\ \le d_p(J_{E_1^{*}}^q[{\alpha }_n{J}_{E_1}^p(u)+(1-{\alpha }_n)({\beta }_n{J}_{E_1}^p(u)+{\gamma }_n{J}_{E_1}^p(x_n)+{\delta }_n{J}_{E_1}^p(T{x}_n))],w)\\ =V_f({\alpha }_n{J}_{E_1}^p(u)+(1-{\alpha }_n)({\beta }_n{J}_{E_1}^p(u)+{\gamma }_n{J}_{E_1}^p(x_n)+{\delta }_n{J}_{E_1}^p(T{x}_n)),w)\\ \le V_f({\alpha }_n{J}_{E_1}^p(u)+(1-{\alpha }_n)({\beta }_n{J}_{E_1}^p(u)+{\gamma }_n{J}_{E_1}^p(x_n)+{\delta }_n{J}_{E_1}^p(T{x}_n))\\ -{\alpha }_n(J_{E_1}^p(u)-J_{E_1}^p(w)),w)-⟨-{\alpha }_n(J_{E_1}^p(u)-J_{E_1}^p(w)),\\ J_{E_1^{*}}^q[{\alpha }_n{J}_{E_1}^p(u)+(1-{\alpha }_n)({\beta }_n{J}_{E_1}^p(u)+{\gamma }_n{J}_{E_1}^p(x_n)+{\delta }_n{J}_{E_1}^p(T{x}_n))]-w⟩\\ =V_f({\alpha }_n{J}_{E_1}^p(u)+(1-{\alpha }_n)({\beta }_n{J}_{E_1}^p(u)+{\gamma }_n{J}_{E_1}^p(x_n)+{\delta }_n{J}_{E_1}^p(T{x}_n)),w)\\ +{\alpha }_n⟨J_{E_1}^p(u)-J_{E_1}^p(w),y_n-w⟩\\ =V_f({\alpha }_n{J}_{E_1}^p(w)+(1-{\alpha }_n)({\beta }_n{J}_{E_1}^p(u)+{\gamma }_n{J}_{E_1}^p(x_n)+{\delta }_n{J}_{E_1}^p(T{x}_n)),w)\\ +{\alpha }_n⟨J_{E_1}^p(u)-J_{E_1}^p(w),y_n-w⟩\\ =d_p(J_{E_1^{*}}^q[{\alpha }_n{J}_{E_1}^p(w)+(1-{\alpha }_n)({\beta }_n{J}_{E_1}^p(u)+{\gamma }_n{J}_{E_1}^p(x_n)+{\delta }_n{J}_{E_1}^p(T{x}_n))],w)\\ +{\alpha }_n{⟨}_n{J}_{E_1}^p(u)-J_{E_1}^p(w),y_n-w⟩\\ \le {\alpha }_n{d}_p(w,w)+(1-{\alpha }_n){\beta }_n{d}_p(w,w)+(1-{\alpha }_n){\gamma }_n{d}_p(x_n,w)\\ +(1-{\alpha }_n){\delta }_n{d}_p(T{x}_n,w)\end{array}$$

$$\begin{array}{l}\le (1-{\alpha }_n){\gamma }_n{d}_p(x_n,w)+(1-{\alpha }_n){\delta }_n{d}_p(x_n,w)\\ +{\alpha }_n⟨J_{E_1}^p(u)-J_{E_1}^p(w),y_n-w⟩\\ =(1-{\alpha }_n)({\gamma }_n+{\delta }_n)d_p(u_n,w)+{\alpha }_n⟨J_{E_1}^p(u)-J_{E_1}^p(w),y_n-w⟩\\ \le (1-{\alpha }_n)d_p(u_n,w)+{\alpha }_n⟨J_{E_1}^p(u)-J_{E_1}^p(w),y_n-w⟩.\end{array}$$

(24)

Now, we prove the strong convergence theorem by the two cases:

Case I.

Suppose that there exists $n_0\in \mathbb{N}$ such that $\{d_p(x_n,w)\}$ is monotonically non-increasing for all $n\ge n_0$. Then $\{d_p(x_n,w)\}$ converges and, as $n\to \infty$,

$$d_p(x_{n+1},w)-d_p(x_n,w)\to 0.$$

(25)

Setting $t_n=J_{E_1^{*}}^q(\frac{{\beta }_n}{1-{\alpha }_n}{J}_{E_1}^p(x_n)+\frac{{\gamma }_n}{1-{\alpha }_n}{J}_{E_1}^p(x_n)+\frac{{\delta }_n}{1-{\alpha }_n}{J}_{E_1}^p(T{x}_n)).$ Then we have

$$\begin{array}{cc}\hfill d_p(t_n,w)& =d_p\left(J_{E_1^{*}}^q\left(\frac{{\gamma }_n}{1-{\alpha }_n}{J}_{E_1}^p(x_n)+\frac{{\delta }_n}{1-{\alpha }_n}{J}_{E_1}^p(T{x}_n)\right),w\right)\hfill \\ & \le \frac{{\gamma }_n}{1-{\alpha }_n}{d}_p(x_n,w)+\frac{{\delta }_n}{1-{\alpha }_n}{d}_p(T{x}_n,w)\hfill \\ & \le \frac{{\gamma }_n+{\delta }_n}{1-{\alpha }_n}{d}_p(x_n,w)\hfill \\ & \le d_p(x_n,w).\hfill \end{array}$$

(26)

Therefore, we have

$$\begin{array}{cc}\hfill 0& \le d_p(x_n,w)-d_p(t_n,w)\hfill \\ & =d_p(x_n,w)-d_p(x_{n+1},w)+d_p(x_{n+1},w)-d_p(t_n,w)\hfill \\ & \le d_p(x_n,w)-d_p(x_{n+1},w)+d_p(u_{n+1},w)-d_p(t_n,w)\hfill \\ & \le d_p(x_n,w)-d_p(x_{n+1},w)+{\alpha }_n{d}_p(u,w)+(1-{\alpha }_n)d_p(t_n,w)-d_p(t_n,w)\hfill \\ & =d_p(x_n,w)-d_p(x_{n+1},w)+{\alpha }_n{d}_p(u,w)-{\alpha }_n{d}_p(t_n,w)\to 0\hfill \end{array}$$

(27)

as $n\to \infty$. Again, we obtain

$$\begin{array}{cc}\hfill d_p(t_n,w)& \le \frac{{\gamma }_n}{1-{\alpha }_n}{d}_p(x_n,w)+\frac{{\delta }_n}{1-{\alpha }_n}{d}_p(T{x}_n,w)\hfill \\ & =\left(1-\frac{{\beta }_n+{\delta }_n}{1-{\alpha }_n}\right)d_p(x_n,w)+\frac{{\delta }_n}{1-{\alpha }_n}{d}_p(T{x}_n,w)\hfill \\ & =d_p(x_n,w)-\frac{{\beta }_n}{1-{\alpha }_n}{d}_p(x_n,w)+\frac{{\delta }_n}{1-{\alpha }_n}(d_p(T{x}_n,w)-d_p(x_n,w))\hfill \\ & \le d_p(x_n,w)+\frac{{\delta }_n}{1-{\alpha }_n}(d_p(T{x}_n,w)-d_p(x_n,w)).\hfill \end{array}$$

(28)

Since ${\alpha }_n+{\delta }_n\le 1$ and ${\alpha }_n\le b<1,$ we have

$$\begin{array}{cc}\hfill a(d_p(x_n,w)-d_p(T{x}_n,w))& <\frac{{\delta }_n}{1-{\alpha }_n}(d_p(x_n,w)-d_p(T{x}_n,w))\hfill \\ & \le d_p(x_n,w)-d_p(t_n,w)\to 0\hfill \end{array}$$

(29)

as $n\to \infty$. By using $(c)$, we have

$$d_p(x_n,w)-d_p(T{x}_n,w)\to 0$$

as $n\to \infty$. Since T is right Bregman strongly quasi-nonexpansive, we obtain

$$\underset{n\to \infty }{lim}{d}_p(T{x}_n,x_n)=0,$$

which implies that

$$\underset{n\to \infty }{lim}\parallel T{x}_n-x_n\parallel =0.$$

(30)

Since $\{x_n\}$ is bounded and E is reflexive, there exists a subsequence $\{x_{n_i}\}$ of $\{x_n\}$ which converges weakly to $\overline{x}\in C.$ From (30), it follows that $\overline{x}\in F(T)$ since $F(T)=\widehat{F}(T).$

Next, we prove that $A\overline{x}\in Q,$ that is, $\overline{x}\in \mathcal{F}.$ Setting

$$v_n=J_{E_1^{*}}^q[J_{E_1}^p(u_n)-s_n{A}^{*}{J}_{E_2}^p(I-P_Q)A{u}_n].$$

From (16), (22) and (24), it follows that

$$\begin{array}{cc}\hfill d_p(v_n,x_n)& =d_p(v_n,{\Pi }_c{v}_n)\hfill \\ & \le d_p(v_n,w)-d_p(x_n,w)\hfill \\ & \le d_{(}{u}_n,w)-d_p(x_n,w)\hfill \\ & \le {\alpha }_n\mathcal{M}+d_p(x_{n-1},w)-d_p(x_n,w)\to 0\hfill \end{array}$$

(31)

as $n\to \infty$, where $\mathcal{M}>0$ and $d_p(x_{n-1},w)+⟨J_{E_1}^p(u)-J_{E_1}^p(w),y_{n-1}-w⟩\le \mathcal{M}.$ Hence we have

$$\underset{n\to \infty }{lim}\parallel x_n-v_n\parallel =0.$$

(32)

From (22), it follows that, as $n\to \infty$,

$$\begin{array}{cc}\hfill \left(s_n-{\displaystyle \frac{C_q(s_n{\parallel A\parallel )}^q}{q}}\right){\parallel z_n\parallel }^p& \le d(u_n,w)-d_p(x_n,w)\hfill \\ & \le {\alpha }_n\mathcal{M}+d_p(x_{n-1},w)-d_p(x_n,w)\to 0.\hfill \end{array}$$

(33)

Since

$$s\left(1-{\displaystyle \frac{C_q{k}^{q-1}{(\parallel A\parallel )}^q}{q}}\right)\le \left(s_n-{\displaystyle \frac{C_q(s_n{\parallel A\parallel )}^q}{q}}\right),$$

(34)

it follows that $\parallel z_n{\parallel }^p\to 0\text{as}n\to \infty ,$ which implies that $\parallel A{u}_n-P_Q(u_n)\parallel \to 0\text{as}n\to \infty .$ By the definition of $v_n,$ we have

$$\begin{array}{cc}\hfill 0& \le \parallel J_{E_1}^p(v_n)-J_{E_1}^p(u_n)\hfill \\ & \le s_n\parallel A^{*}\parallel \parallel J_{E_2}^p(A{u}_n-P_Q(A{u}_n))\parallel \hfill \\ & \le {\left({\displaystyle \frac{q}{C_q{\parallel A\parallel }^q}}\right)}^{\frac{1}{q-1}}\parallel A^{*}\parallel \parallel A{u}_n-P_Q(A{u}_n)\parallel \to 0\hfill \end{array}$$

(35)

as $n\to \infty$. Since $J_{E_1^{*}}^q$ is norm to norm uniformly continuous on bounded subsets of $E_1^{*},$ we obtain

$$\underset{n\to \infty }{lim}\parallel v_n-u_n\parallel =\underset{n\to \infty }{lim}\parallel J_{E_1^{*}}^q(J_{E_1}^p(v_n))-J_{E_1^{*}}^q(J_{E_1}^p(u_n))\parallel \to 0$$

(36)

as $n\to \infty$. From (3) and (36), we obtain

$$\parallel x_n-u_n\parallel \le \parallel x_n-y_n\parallel +\parallel y_n-u_n\parallel \to 0.$$

(37)

as $n\to \infty$. From (14), it follows that

$$\begin{array}{l}{\parallel (I-P_Q)A\overline{x}\parallel }^p\\ =⟨J_{E_2}^p(A\overline{x}-P_{Q}A\overline{x}),A\overline{x}-P_{Q}A\overline{x}⟩\\ =⟨J_{E_2}^p(A\overline{x}-P_{Q}A\overline{x}),A\overline{x}-A{u}_{n_i}⟩+⟨J_{E_2}^p(A\overline{x}-P_{Q}A\overline{x}),A{u}_{n_i}-P_{Q}A{u}_{n_i}⟩\\ +⟨J_{E_2}^p(A\overline{x}-P_{Q}A\overline{x}),P_{Q}A{u}_{n_i}-P_{Q}A\overline{x}⟩\\ \le ⟨J_{E_2}^p(A\overline{x}-P_{Q}A\overline{x}),A\overline{x}-A{u}_{n_i}⟩+⟨J_{E_2}^p(A\overline{x}-P_{Q}A\overline{x}),A{u}_{n_i}-P_{Q}A{u}_{n_i}⟩.\end{array}$$

(38)

By the continuity of A and $\parallel x_n-u_n\parallel \to 0\text{as}n\to \infty ,$ we have $A{u}_{n_i}\rightharpoonup A\overline{x}$ as $n\to \infty .$ Thus, letting $i\to \infty ,$ we have

$$\parallel A\overline{x}-P_{Q}A\overline{x}\parallel =0.$$

Hence $A\overline{x}=P_{Q}A\overline{x},$ that is, $A\overline{x}\in Q.$ Therefore, we have that $\overline{x}\in F(T)\cap \mathcal{F}.$

Next, we prove that $\{x_n\}$ converges strongly to ${\Pi }_{P(T)\cap \mathcal{F}}u.$ Now, we have

$$\begin{array}{l}{d}_p(y_n,x_n)\\ =d_p(J_{E_1^{*}}^q[{\alpha }_n{J}_{E_1}^p(u)+(1-{\alpha }_n)({\beta }_n{J}_{E_1}^p(u)+{\gamma }_n{J}_{E_1}^p(x_n)+{\delta }_n{J}_{E_1}^p(T{x}_n))],x_n)\\ \le {\alpha }_n{d}_p(u,x_n)+(1-{\alpha }_n){\beta }_n{d}_p(u,x_n)\\ +(1-{\alpha }_n){\gamma }_n{d}_p(x_n,x_n)+(1-\alpha ){\delta }_n{d}_p(T{x}_n,x_n)\\ \to 0\end{array}$$

as $n\to \infty$. Thus we have

$$\parallel y_n-x_n\parallel \to 0$$

as $n\to \infty$. Let $\widehat{x}={\Pi }_{P(T)\cap \mathcal{F}}u.$ From (24), we have

$$d_p(x_{n+1},\widehat{x})\le (1-{\alpha }_n)d_p(x_n,\widehat{x})+{\alpha }_n⟨J_{E_1}^p(u)-J_{E_1}^p(\widehat{x}),y_n-\widehat{x}⟩.$$

Then there exists a subsequence $\{x_{n_j}\}$ of $\{x_n\}$ such that

$$\underset{n\to \infty }{lim\; sup}⟨J_{E_1}^p(u)-J_{E_1}^p(\widehat{x}),x_n-\widehat{x}⟩=\underset{j\to \infty }{lim}⟨J_{E_1}^p(u)-J_{E_1}^p(\widehat{x}),x_{n_j}-\widehat{x}⟩$$

and $x_{n_j}\to \overline{x}.$ Thus, from (15), it follows that

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim\; sup}⟨J_{E_1}^p(u)-J_{E_1}^p(\widehat{x}),x_n-\widehat{x}⟩& =\underset{j\to \infty }{lim}⟨J_{E_1}^p(u)-J_{E_1}^p(\widehat{x}),x_{n_j}-\widehat{x}⟩\hfill \\ & =⟨J_{E_1}^p(u)-J_{E_1}^p(\widehat{x}),\overline{x}-\widehat{x}⟩\hfill \\ & \le 0.\hfill \end{array}$$

Since $\parallel x_n-y_n\parallel \to 0\text{as}n\to \infty ,$ we have

$$\underset{n\to \infty }{lim\; sup}⟨J_{E_1}^p(u)-J_{E_1}^p(\widehat{x}),y_n-\widehat{x}⟩\le 0.$$

Hence, by Lemma 2, we conclude that $d_p(x_n,\widehat{x})\to 0$ as $n\to \infty .$ Therefore, $x_n\to \widehat{x}$ as $n\to \infty$ and, since $\parallel x_n-u_n\parallel \to 0$ as $n\to \infty$, we have $u_n\to \widehat{x}$ as $n\to \infty .$

Case II.

Suppose that there exists a subsequence $\{n_j\}$ of $\{n\}$ such that

$$d_p(x_{n_i},\widehat{x})<d_p(x_{n_i+1},\widehat{x})$$

for all $j\in \mathbb{N}.$ Then, by Lemma 1, there exists a nondecreasing sequence $\{m_k\}\subset \mathbb{N}$ with $m_k\to \infty$ as $n\to \infty$ such that

$$d_p(x_{m_k},\widehat{x})\le d_p(x_{m_k+1},\widehat{x}),d_p(x_k,\widehat{x})\le d_p(x_{m_k+1},\widehat{x})$$

for all $k\in \mathbb{N}.$ Thus it follows from (27) and the same methods in the proof of Case I that

$$\parallel x_{m_k+1}-x_{m_k}\parallel \to 0,\parallel T{x}_{m_k}-x_{m_k}\parallel \to 0$$

as $k\to \infty .$ Therefore, we have

$$\underset{k\to \infty }{lim\; sup}⟨J_{E_1}^p(u)-J_{E_1}^p(\widehat{x}),y_{m_k+1}-\widehat{x}⟩=\underset{k\to \infty }{lim\; sup}⟨J_{E_1}^p(u)-J_{E_1}^p(\widehat{x}),y_{m_k}-\widehat{x}⟩\le 0.$$

(39)

From (24), also, we have

$$d_p(x_{m_k+1},\widehat{x})\le (1-{\alpha }_{m_k})d_p(x_{m_k},\widehat{x})+{\alpha }_{m_k}⟨J_{E_1}^p(u)-J_{E_1}^p(\widehat{x}),y_{m_k}-\widehat{x}⟩.$$

(40)

Since $d_p(x_{m_k},\widehat{x})\le d_p(x_{m_k+1},\widehat{x}),$ it follows from (40) that

$$\begin{array}{cc}\hfill {\alpha }_{m_k}{d}_p(x_{m_k},\widehat{x})& \le d_p(x_{m_k},\widehat{x})-d_p(x_{m_k+1},\widehat{x})+{\alpha }_{m_k}⟨J_{E_1}^p(u)-J_{E_1}^p(\widehat{x}),y_{m_k}-\widehat{x}⟩\hfill \\ & \le {\alpha }_{m_k}⟨J_{E_1}^p(u)-J_{E_1}^p(\widehat{x}),y_{m_k}-\widehat{x}⟩\hfill \end{array}$$

(41)

Since ${\alpha }_{m_k}>0,$ we obtain

$$d_p(x_{m_k},\widehat{x})\le ⟨J_{E_1}^p(u)-J_{E_1}^p(\widehat{x}),y_{m_k}-\widehat{x}⟩.$$

(42)

Then, from (39), it follows that $d_p(x_{m_k},\widehat{x})\to 0$ as $k\to \infty .$ This together with (40), we obtain $d_p(x_{m_k+1},\widehat{x})\to 0$ as $k\to \infty .$ Since $d_p(x_k,\widehat{x})\le (x_{m_k+1},\widehat{x})$ for all $k\in \mathbb{N},$ we have $x_k\to \widehat{x}$ as $k\to \infty ,$ which implies that $x_n\to \widehat{x}$ as $k\to \infty .$

Therefore, from the above two cases, we conclude that $\{x_n\}$ converges strongly to $\widehat{x}={\Pi }_{P(T)\cap \mathcal{F}}u.$ This completes the proof. ☐

Corollary 1 

([19]). Let $E_1$, $E_2$ be two p-uniformly convex real Banach spaces which are also uniformly smooth and C, Q be nonempty closed convex subsets of $E_1$, $E_2,$ respectively. Let $A:E_1\to E_2$ be a bounded linear operator and $A^{*}:E_2^{*}\to E_1^{*}$ be the adjoint of $A.$ Suppose that the problem (SFP) has a nonempty solution set $\mathcal{F}$. Let $T:C\to C$ be a right Bregman strongly quasi-nonexpansive mapping such that $F(T)=\widehat{F}(T)\ne \varnothing$ and $F(T)\cap \mathcal{F}\ne \varnothing .$ Suppose that $\{{\beta }_n\},\{{\gamma }_n\}$ and $\{{\delta }_n\}$ are the sequences in $(0,1)$ such that ${\beta }_n+{\gamma }_n+{\delta }_n=1$, ${\beta }_n\le b<1,(1-{\beta }_n)a<{\gamma }_n<{\delta }_n,a\in (0,\frac{1}{2}).$ For any fixed $u\in C,$ let the sequences $\{x_n\}$ and $\{u_n\}$ be iteratively generated by $u_0\in E_1$ and

$$\left\{\begin{array}{c}{x}_n={\Pi }_C{J}_{E_1^{*}}^q(J_{E_1}^p(u_n)-s_n{A}^{*}{J}_{E_2}^p(I-P_Q)A{u}_n),\hfill \\ u_{n+1}={\Pi }_C{J}_{E_1^{*}}^q({\beta }_n{J}_{E_1}^p(u)+{\gamma }_n{J}_{E_1}^p(x_n)+{\delta }_n{J}_{E_1}^p(T{x}_n))\hfill \end{array}\right.$$

(43)

for each $n\ge 1$. Suppose the following condition is satisfied:

(a) 

$\underset{n\to \infty }{lim}{\beta }_n=0;$

(b) 

${\displaystyle \sum _{n=1}^{\infty }}{\beta }_n=\infty ;$

(c) 

$0<s\le s_n\le k<{\left({\displaystyle \frac{q}{C_q{\parallel A\parallel }^q}}\right)}^{\frac{1}{q-1}}.$

Then the sequence $\{x_n\}$ and $\{u_n\}$ converges strongly to a point ${\Pi }_{F(T)\cap \mathcal{F}}u.$

Proof. 

If ${\alpha }_n=0$ for all $n\ge 1$ in Theorem 1, then we obtain the desired conclusion.  ☐

Corollary 2.

Let $E_1$, $E_2$ be two p-uniformly convex real Banach spaces which are also uniformly smooth and C, Q be nonempty closed convex subsets of $E_1$, $E_2,$ respectively. Let $A:E_1\to E_2$ be a bounded linear operator and $A^{*}:E_2^{*}\to E_1^{*}$ be the adjoint of $A.$ Suppose that the problem (SFP) has a nonempty solution set $\mathcal{F}$. Let $T:C\to C$ be a right Bregman strongly quasi-nonexpansive mapping such that $F(T)=\widehat{F}(T)\ne \varnothing$ and $F(T)\cap \mathcal{F}\ne \varnothing .$ Suppose that $\{{\alpha }_n\}$ is a sequences in $(0,1)$ such that ${\alpha }_n\le b<1,a\in (0,\frac{1}{2}).$ For any fixed $u\in C,$ let the sequences $\{x_n\}$ and $\{u_n\}$ be iteratively generated by $u_0\in E_1$ and

$$\left\{\begin{array}{c}{x}_n={\Pi }_C{J}_{E_1^{*}}^q(J_{E_1}^p(u_n)-s_n{A}^{*}{J}_{E_2}^p(I-P_Q)A{u}_n),\hfill \\ u_{n+1}={\Pi }_C{J}_{E_1^{*}}^q({\alpha }_n{J}_{E_1}^p(u)+(1-{\alpha }_n)J_{E_1}^p(T{x}_n))\hfill \end{array}\right.$$

(44)

for each $n\ge 1$. Suppose the following conditions are satisfied:

(a) 

$\underset{n\to \infty }{lim}{\alpha }_n=0;$

(b) 

${\displaystyle \sum _{n=1}^{\infty }}{\alpha }_n=\infty ;$

(c) 

$0<s\le s_n\le k<{\left({\displaystyle \frac{q}{C_q{\parallel A\parallel }^q}}\right)}^{\frac{1}{q-1}}.$

Then the sequence $\{x_n\}$ and $\{u_n\}$ converges strongly to a point ${\Pi }_{F(T)\cap \mathcal{F}}u.$

Proof. 

If ${\beta }_n={\gamma }_n={\delta }_n=0$ for all $n\ge 1$ in Theorem 1, then we obtain the desired conclusion.  ☐

Next, we consider the mapping $T:C\to C$ defined by $T=T_N\circ T_{N-1}\circ \cdots \circ T_1,$ where $T_i$ for each $i=1,2,\cdots ,N$ is a right Bregman strongly quasi-nonexpansive mapping on $E.$ Using the results in [10], we have the following:

Corollary 3.

Let $E_1$, $E_2$ be two p-uniformly convex real Banach spaces which are also uniformly smooth and C, Q be nonempty closed convex subsets of $E_1$, $E_2,$ respectively. Let $A:E_1\to E_2$ be a bounded linear operator and $A^{*}:E_2^{*}\to E_1^{*}$ be the adjoint of $A.$ Suppose that the problem (SFP) has a nonempty solution set $\mathcal{F}$. Let $T=T_N\circ T_{N-1}\circ \cdots \circ T_1,$ where $T_i:C\to C$ for each $i=1,2,\cdots N$ be a finite family of right Bregman strongly quasi-nonexpansive mappings such that $F(T_i)=\widehat{F}(T_i)\ne \varnothing$ and $({\displaystyle \bigcap _{i=1}^N}F(T_i))\cap \mathcal{F}\ne \varnothing .$ Suppose that $\{{\alpha }_n\},\{{\beta }_n\},\{{\gamma }_n\}$ and $\{{\delta }_n\}$ are the sequences in $[0,1)$ such that ${\alpha }_n+{\beta }_n+{\gamma }_n+{\delta }_n=1,{\alpha }_n\le b<1$, $(1-{\alpha }_n)a<{\gamma }_n<{\delta }_n,a\in (0,\frac{1}{2}).$ For any fixed $u\in C,$ let the sequences $\{x_n\}$ and $\{u_n\}$ be iteratively generated by $u_0\in E_1$ and

$$\left\{\begin{array}{c}{x}_n={\Pi }_C{J}_{E_1^{*}}^q(J_{E_1}^p(u_n)-s_n{A}^{*}{J}_{E_2}^p(I-P_Q)A{u}_n),\hfill \\ u_{n+1}={\Pi }_C{J}_{E_1^{*}}^q({\alpha }_n{J}_{E_1}^p(u)+(1-{\alpha }_n)({\beta }_n{J}_{E_1}^p(u)+{\gamma }_n{J}_{E_1}^p(x_n)+{\delta }_n{J}_{E_1}^p(T{x}_n)))\hfill \end{array}\right.$$

(45)

for each $n\ge 1$. Suppose the following conditions are satisfied:

(a) 

$\underset{n\to \infty }{lim}{\alpha }_n=0;$

(b) 

${\displaystyle \sum _{n=1}^{\infty }}{\alpha }_n=\infty ;$

(c) 

$0<s\le s_n\le k<{\left({\displaystyle \frac{q}{C_q{\parallel A\parallel }^q}}\right)}^{\frac{1}{q-1}}.$

Then the sequence $\{x_n\}$ and $\{u_n\}$ converges strongly to a point ${\Pi }_{F(T)\cap \mathcal{F}}u.$

Proof. 

If $T=T_N\circ T_{N-1}\circ \cdots \circ T_1$ in Theorem 1, then we obtain the desired conclusion.  ☐

Corollary 4.

Let $H_1$, $H_2$ be two real Hilbert spaces and C, Q be nonempty closed convex subsets of $H_1$, $H_2,$ respectively. Let $A:H_1\to H_2$ be a bounded linear operator and $A^{*}:H_2\to H_1$ be the adjoint of $A.$ Suppose that the problem (SFP) has a nonempty solution set $\mathcal{F}$. Let $T:C\to C$ be a right Bregman strongly quasi-nonexpansive mapping such that $F(T)=\widehat{F}(T)\ne \varnothing ,I-T$ is demiclosed at zero and $F(T)\cap \mathcal{F}\ne \varnothing .$ Suppose that $\{{\alpha }_n\},\{{\beta }_n\},\{{\gamma }_n\}$ and $\{{\delta }_n\}$ are the sequences in $[0,1)$ such that ${\alpha }_n+{\beta }_n+{\gamma }_n+{\delta }_n=1$, ${\alpha }_n\le b<1,(1-{\alpha }_n)a<{\gamma }_n<{\delta }_n,a\in (0,\frac{1}{2}).$ For any fixed $u\in C,$ let the sequences $\{x_n\}$ and $\{u_n\}$ be iteratively generated by $u_0\in E_1$ and

$$\left\{\begin{array}{c}{x}_n=P_C\left(u_n-s_n{A}^{*}(I-P_Q)A{u}_n\right),\hfill \\ u_{n+1}=P_C\left({\alpha }_{n}u+(1-{\alpha }_n)({\beta }_{n}u+{\gamma }_n{x}_n+{\delta }_{n}T{x}_n)\right)\hfill \end{array}\right.$$

(46)

for each $n\ge 1$. Suppose the following conditions are satisfied:

(a) 

$\underset{n\to \infty }{lim}{\alpha }_n=0;$

(b) 

${\displaystyle \sum _{n=1}^{\infty }}{\alpha }_n=\infty ;$

(c) 

$0<s\le s_n\le k<{\displaystyle \frac{2}{{\parallel A\parallel }^2}}.$

Then the sequence $\{x_n\}$ and $\{u_n\}$ converges strongly to a point ${\Pi }_{F(T)\cap \mathcal{F}}u.$

Proof. 

Let $E=H$ in Theorem 1. Since the duality mappings $J_{E_1^{*}}^q,J_{E_1}^p$ and $J_{E_2}^p$ are the identity mapping in a Hilbert space H, from Theorem 1, we obtain the desired conclusion.  ☐

Corollary 5.

Let $H_1$, $H_2$ be two real Hilbert spaces and C, Q be nonempty closed convex subsets of $H_1$, $H_2,$ respectively. Let $A:H_1\to H_2$ be a bounded linear operator and $A^{*}:H_2\to H_1$ be the adjoint of $A.$ Suppose that the problem (SFP) has a nonempty solution set $\mathcal{F}$. Let $T:C\to C$ be a right Bregman strongly quasi-nonexpansive mapping such that $F(T)=\widehat{F}(T)\ne \varnothing ,I-T$ is demiclosed at zero and $F(T)\cap \mathcal{F}\ne \varnothing .$ Suppose that $\{{\beta }_n\},\{{\gamma }_n\}$ and $\{{\delta }_n\}$ are sequences in $[0,1)$ such that ${\beta }_n+{\gamma }_n+{\delta }_n=1,{\beta }_n\le b<1$, $(1-{\beta }_n)a<{\gamma }_n<{\delta }_n,a\in (0,\frac{1}{2}).$ For any fixed $u\in C,$ let the sequences $\{x_n\}$ and $\{u_n\}$ be iteratively generated by $u_0\in E_1$ and

$$\left\{\begin{array}{c}{x}_n=P_C\left(u_n-s_n{A}^{*}(I-P_Q)A{u}_n\right),\hfill \\ u_{n+1}=P_C\left({\beta }_{n}u+{\gamma }_n{x}_n+{\delta }_{n}T{x}_n\right)\hfill \end{array}\right.$$

(47)

for each $n\ge 1$. Suppose the following conditions are satisfied:

(a) 

$\underset{n\to \infty }{lim}{\beta }_n=0;$

(b) 

${\displaystyle \sum _{n=1}^{\infty }}{\beta }_n=\infty ;$

(c) 

$0<s\le s_n\le k<{\displaystyle \frac{2}{{\parallel A\parallel }^2}}.$

Then the sequence $\{x_n\}$ and $\{u_n\}$ converges strongly to a point ${\Pi }_{F(T)\cap \mathcal{F}}u.$

Proof. 

Let $E=H$ and ${\alpha }_n=0$ for each $n\ge 1$. Since the duality mappings $J_{E_1^{*}}^q,J_{E_1}^p$ and $J_{E_2}^p$ are the identity mapping in a Hilbert space H, from Theorem 1, we obtain the desired conclusion.  ☐

Remark 1.

A prototype for the sequences $\{{\alpha }_n\},\{{\beta }_n\},\{{\gamma }_n\},\{{\delta }_n\}$ and $\{s_n\}$ in Theorem 1 are as follows:

$${\alpha }_n={\displaystyle \frac{1}{n+1}},{\beta }_n=1-{\displaystyle \frac{2an+1}{n+1}},{\gamma }_n={\displaystyle \frac{{\displaystyle \frac{1}{2}}an}{n+1}},{\delta }_n={\displaystyle \frac{{\displaystyle \frac{3}{2}}an}{n+1}},a\in \left(0,{\displaystyle \frac{1}{2}}\right)$$

and

$$s_n=\left({\displaystyle \frac{n}{n+1}}\right){\left({\displaystyle \frac{q}{C_q{\parallel A\parallel }^q}}\right)}^{\frac{1}{q-1}}$$

for each $n\ge 0$.

4. Some Numerical Examples

In this section, we present some preliminary numerical results to illustrate the main result, Theorem 1. All codes were written in Matlab 2013b and run on Sumsung i-3 Core laptop.

Example 1.

We find a numerical example in $({\mathbb{R}}^3,\parallel ·{\parallel }_2)$ of the problem considered in Theorem 1 of the previous section. Now, take

$$C:=\{x=(x_1,x_2,x_3)\in {\mathbb{R}}^3:⟨a,x⟩\ge b\},$$

where $a=(2,-6,1)$ and $b=-4.$ Then we have

$$P_C(x)={\displaystyle \frac{b-⟨a,x⟩}{{\parallel a\parallel }_2^2}}a+x.$$

Let $Q:=\{x=(x_1,x_2,x_3)\in {\mathbb{R}}^3:⟨c,x⟩=d\}$, where $c=(3,5,7)$ and $d=2.$ Then we have

$${\Pi }_Q(x)=P_Q(x)=max\left\{0,{\displaystyle \frac{d-⟨c,x⟩}{{\parallel c\parallel }_2^2}}\right\}c+x.$$

Suppose that the mapping T in Theorem 1 is defined as $T:=P_C,$ the metric projection on $C.$ Then the problem considered in Theorem 1 reduces to the problem:

$$\text{Find}x\in F(T)\cap C(=C)\text{such}\text{that}Ax\in Q.$$

(48)

Let $\mathcal{F}$ denote the set of solutions of the problem (48) with $\mathcal{F}\ne \varnothing .$ Furthermore, let

$${\alpha }_n={\displaystyle \frac{1}{n+1}},{\beta }_n={\displaystyle \frac{n}{8(n+1)}},{\gamma }_n={\displaystyle \frac{n}{8(n+1)}},{\delta }_n={\displaystyle \frac{3n}{8(n+1)}},A=\left(\begin{array}{ccc}4& -6& -8\\ -5& 1& -5\\ -8& -5& 4\end{array}\right).$$

Then our iterative processes (20) becomes

$$\left\{\begin{array}{c}{x}_n=P_C\left(u_n-s_n{A}^T(I-P_Q)A{u}_n\right),\hfill \\ u_{n+1}=P_C\left[{\displaystyle \frac{u}{n+1}}+\left(1-{\displaystyle \frac{1}{n+1}}\right)\left({\displaystyle \frac{n}{2(n+1)}}u+{\displaystyle \frac{n}{8(n+1)}}{x}_n+{\displaystyle \frac{3n}{8(n+1)}}{P}_C{x}_n\right)\right]\hfill \end{array}\right.$$

(49)

for each $n\ge 1$. Now, we make different choices of $u,u_1,s_n$ and take ${\displaystyle \frac{\parallel x_{n+1}-x_n\parallel }{\parallel x_2-x_1\parallel }}<{10}^{-2}$ as our stopping criterion.

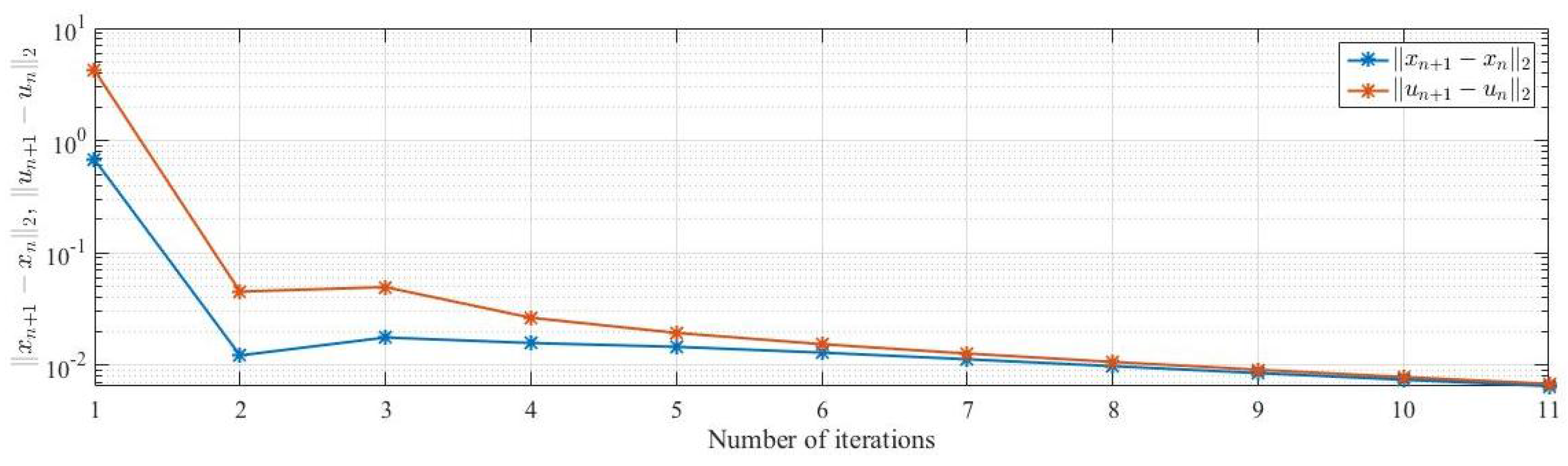
Case I.

Take $u=(1,1,1),u_1=(3,0,4)$ and $s_n=0.0137.$ Then we have the numerical analysis tabulated in Table 1 and show in Figure 1.

Table 1. Example 1, case I.

${\mathit{s}}_{\mathit{n}}$	Time Taken	Number of Iterations	${\mathbf{\parallel }{\mathit{x}}_{\mathit{n}\mathbf{+}\mathbf{1}}\mathbf{-}{\mathit{x}}_{\mathit{n}}\mathbf{\parallel }}_{\mathbf{2}}$	${\mathbf{\parallel }{\mathit{u}}_{\mathit{n}\mathbf{+}\mathbf{1}}\mathbf{-}{\mathit{u}}_{\mathit{n}}\mathbf{\parallel }}_{\mathbf{2}}$
0.0137	0.0400	2	0.6758	4.2169
		3	0.0122	0.0453
		4	0.0177	0.0497
		5	0.0158	0.0265
		6	0.0146	0.0194
		7	0.0130	0.0154
		8	0.0113	0.0127
		9	0.0098	0.0107
		10	0.0085	0.0091
		11	0.0074	0.0079

Figure 1. Example 1, case I.

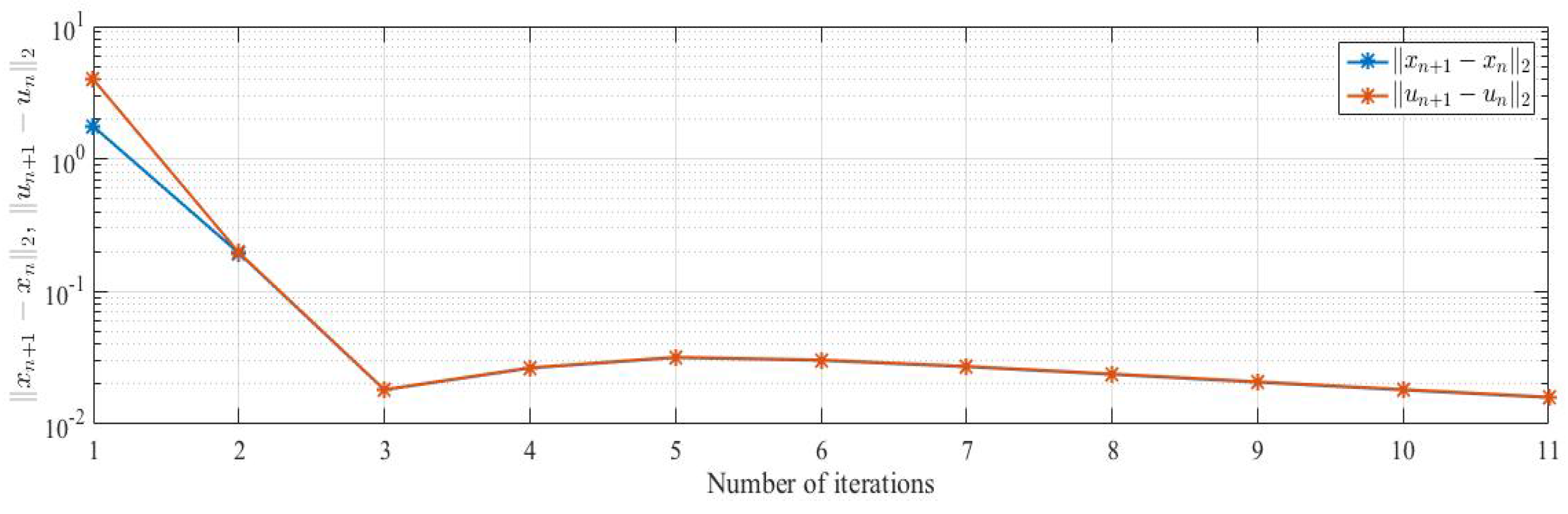
Case II.

Take $u=(1,1,1),u_1=(3,0,4)$ and $s_n=0.0001.$ Then we have the numerical analysis tabulated in Table 2 and show in Figure 2.

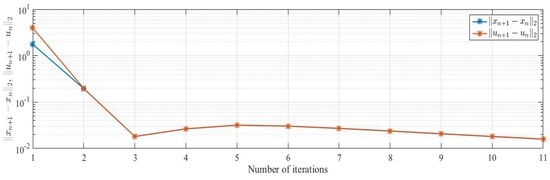
Table 2. Example 1, case II.

${\mathit{s}}_{\mathit{n}}$	Time Taken	Number of Iterations	${\mathbf{\parallel }{\mathit{x}}_{\mathit{n}\mathbf{+}\mathbf{1}}\mathbf{-}{\mathit{x}}_{\mathit{n}}\mathbf{\parallel }}_{\mathbf{2}}$	${\mathbf{\parallel }{\mathit{u}}_{\mathit{n}\mathbf{+}\mathbf{1}}\mathbf{-}{\mathit{u}}_{\mathit{n}}\mathbf{\parallel }}_{\mathbf{2}}$
0.0001	0.0400	2	1.7588	3.9690
		3	0.1950	0.1968
		4	0.0181	0.0182
		5	0.0265	0.0266
		6	0.0318	0.0320
		7	0.0303	0.0305
		8	0.0271	0.0273
		9	0.0237	0.0239
		10	0.0207	0.0209
		11	0.0181	0.0182

Figure 2. Example 1, case II.

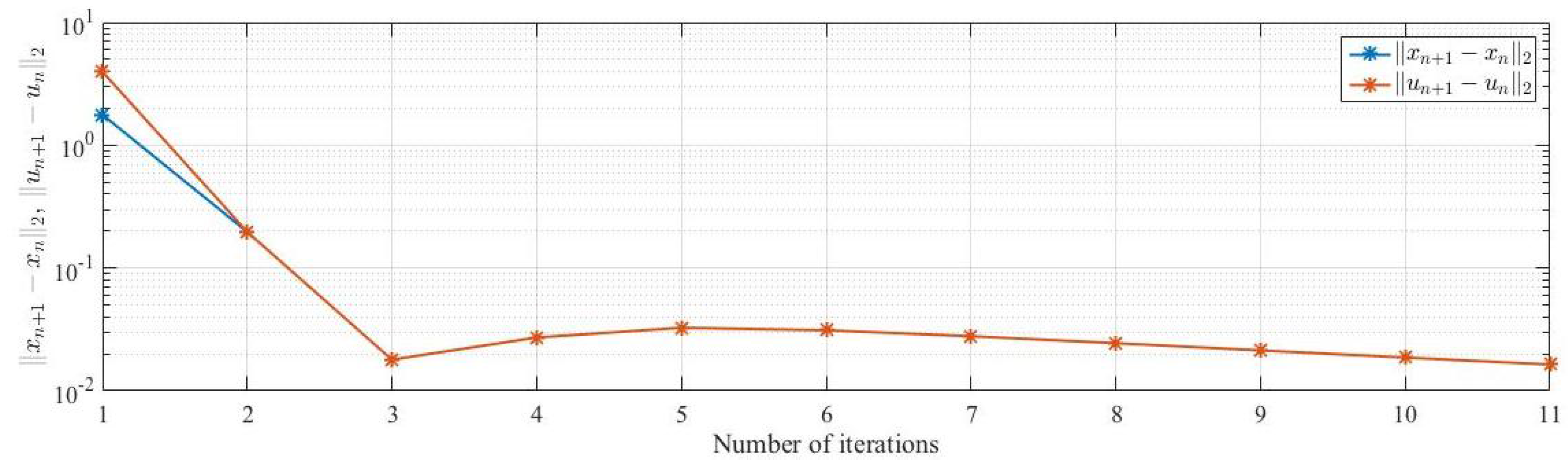
Case III.

Take $u=(1,1,1),u_1=(3,0,4)$ and $s_n=0.0000001.$ Then we have the numerical analysis tabulated in Table 3 and show in Figure 3.

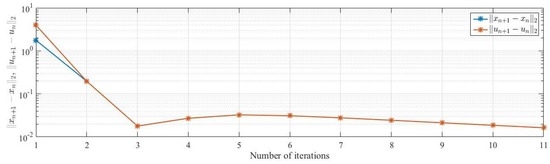
Table 3. Example 1, case III.

${\mathit{s}}_{\mathit{n}}$	Time Taken	Number of Iterations	${\mathbf{\parallel }{\mathit{x}}_{\mathit{n}\mathbf{+}\mathbf{1}}\mathbf{-}{\mathit{x}}_{\mathit{n}}\mathbf{\parallel }}_{\mathbf{2}}$	${\mathbf{\parallel }{\mathit{u}}_{\mathit{n}\mathbf{+}\mathbf{1}}\mathbf{-}{\mathit{u}}_{\mathit{n}}\mathbf{\parallel }}_{\mathbf{2}}$
0.0000001	0.0400	2	1.7720	3.9674
		3	0.1969	0.1969
		4	0.0179	0.0179
		5	0.0272	0.0272
		6	0.0326	0.0326
		7	0.0311	0.0311
		8	0.0278	0.0278
		9	0.0244	0.0244
		10	0.0213	0.0213
		11	0.0186	0.0186

Figure 3. Example 1, case III.

Remark 2.

We make the following comments from Example 1. We observe that different choices of $s_n$ has no effect in terms of number of iterations obtained and the time taken for the convergence of our algorithm.

5. Conclusions

Our iterative processes can be used for finding a common element of the solution set $\mathcal{F}$ of the split feasibility problem and the fixed point set $F(T)$ of a right Bregman strongly quasi-nonexpansive mapping T in p-uniformly convex Banach spaces, which are also uniformly smooth.