1. Introduction
The page migration problem is a classical formulation of efficient memory management in a shared memory multiprocessor system comprising a network of processors having their own local memories. In this problem, we are given a sequence of requests issued by processors to access a single shared data object, called a page. Each request must be served via communication between the processor issuing the request and the processor holding the page at the time of the request. The service for the request costs the distance of the communication. After each service, the page is allowed to migrate from the current processor to a new processor before the next request is issued. The migration of the page costs the distance of the migration multiplied by the page size. The objective of the page migration problem is to minimize the total costs of services and migrations (see
Section 2 for a formal definition of this problem). This problem can also be viewed as a formulation of general situations for managing shared information in a distributed network, such as the efficient allocation of each shared data object to be accessed by a distributed program running on the network [
1].
Black and Sleator [
2] first studied online algorithms for the page migration problem via competitive analysis. Some basic notions of competitive analysis are given in
Section 2. Chrobak, Larmore, Reingold, and Westbrook [
3] studied this problem on continuous metric spaces as well as networks. They proposed a
-competitive randomized algorithm on trees against oblivious adversaries, together with the same lower bound as this competitiveness even at two points, where
is a positive integer representing the page size. They also proved that any randomized page migration algorithm on
can be derandomized while preserving its competitiveness. As any page migration algorithm on a space can be generalized on Cartesian products of the space [
2], a
-competitive deterministic algorithm on
under
norm can be obtained through generalizing the algorithm on trees in
[
3]. For general metric spaces, Westbrook [
4] proposed a
-competitive randomized algorithm against oblivious adversaries, where
is a function defined in [
4] that tends toward
as
grows large. Derandomizing this algorithm on
, we have a
-competitive deterministic algorithm on
under any norm [
3].
Moreover,
is a lower bound for any randomized or deterministic algorithm in the interval
[
3]. This lower bound is also admitted on
under
norm. This is because, for the interval
on a dimension
in
, any online algorithm
A locating its server in
for requests only in
has a cost of at least that of a certain algorithm locating its server only in
, i.e., projection on the
kth coordinate of
A’s server location if the projection is in
, and the closer endpoint of
otherwise. It is a longstanding open question whether we can close the gap of
and
under
norm even with any
.
In this paper, we partially answer this question by proposing a
-competitive deterministic algorithm on
under
norm for the case
. We note that the competitiveness improves
, which is equal to
as mentioned in [
4]. We also provide a lower bound of
for our algorithm. Our algorithm is extremely simple: it maintains the page at the center of two special points, both initially located at the initial location of the server. Upon each request, the algorithm chooses one of the points farther from the requested location and moves the point to the requested location; the other point does not move. This algorithm can be viewed as a natural extension of the
-competitive algorithm under
norm of [
3]. We note that if there exists a
-competitive algorithm under
norm, then it would have to behave on any line in the same way as the
-competitive algorithm of [
3]. The setting of the unit page size, i.e.,
is called the uniform model in the context of data management problems including the page migration problem [
1,
5,
6,
7].
Other previous results for the page migration problem are as follows. Bartal, Charikar, and Indyk [
8] proposed a
-competitive deterministic algorithm for general networks. For trees and uniform networks, Black and Sleator [
2] presented 3-competitive deterministic algorithms, together with the lower bound of 3 even at two points. The first deterministic lower bound larger than 3 for general networks was
[
3], which was improved to
by Matsubayashi [
5]. Although these lower bounds, larger than
, were proved only for
, the first lower bound of
was recently proved [
9], where
notation is with respect to
. For three points,
-competitive deterministic algorithms with
[
3,
10] and a
-competitive deterministic algorithm with
[
10] were proposed. The latter algorithm asymptotically matches the lower bound of
on three points for every
[
10]. As for randomized algorithms against adaptive online adversaries, a
-competitive algorithm for general metric spaces was proposed in [
4] and the upper bound of
is also a lower bound on two points [
11]. As for a randomized algorithm against oblivious adversaries, Lund, Reingold, Westbrook, and Yan [
12] proved that the optimal competitiveness of
can be achieved even on uniform networks.
The rest of this paper is organized as follows. Some preliminaries are given in
Section 2. We define our algorithm on
under
norm and prove its
competitiveness in
Section 3. In
Section 4, we prove a lower bound of
for our algorithm. We conclude the paper with remarks and future works in
Section 5.
2. Preliminaries
Let be a metric space with a distance function . For a given initial page location , a sequence of requests , and a page size , the page migration problem is to compute page locations such that the cost function is minimized. We call a server.
An online algorithm must compute without any information regarding , whereas an offline algorithm may compute using the entire sequence of requests . An adversary against an online algorithm A generates a sequence of requests given to A and computes an output sequence for the generated requests. If A is deterministic, then the adversary generates requests using the definition of A, or equivalently, the information of the actual behavior of A, and computes its own output according to an optimal offline algorithm OPT. The deterministic algorithm A is -competitive if for the initial server and any sequence of requests, where and are costs of A and OPT, respectively, and is a constant. For randomized online algorithms, there are two types of adversaries. An adversary is said to be oblivious if it generates requests in advance only using the definition of A, i.e., without any information about the random behavior of A and computes its own output according to OPT. In contrast, an adaptive online adversary generates requests using information of the random behavior of A and computes its own output in an online fashion. The competitiveness of a randomized online algorithm against oblivious or adaptive online adversaries is defined in a similar way to that of a deterministic online algorithm, except that expected values are used for randomized costs.
One commonly used technique for proving the competitiveness of an online algorithm A is to utilize a potential function , which typically maps the situation at a point of time, such as the page locations of A and OPT, to a real value. More specifically, we suitably divide the sequence of the online processes of A and OPT into certain events. Our goal is to define the value of in such a way that the initial value of is at most some constant , is always at least some constant and that for any event, where denotes the change of values by the event. Summing the inequality over all events for an initial server and a request sequence , we have , which means that A is -competitive.
3. Algorithm and Its Upper Bound Analysis
We focus on the page size
and the metric space
under
norm
for
. We state our deterministic algorithm, called PQ, in the following paragraph. Intuitively, the algorithm determines the location of the page using two locations from previous requests. We prove the competitiveness of
, claimed in Theorem 1, using a potential function
. As mentioned in
Section 2, defining suitable events and showing that
for any defined event is sufficient. For the proof of the theorem, we need to show an inequality different from a triangle inequality. We separately provide a technical part for that inequality as Lemma 1. The lemma is about points computed by the algorithm.
Algorithm PQ.
This algorithm maintains the server at the center of two points and , both of which are initially located at the initial server location. Upon each request at location , if , then moves to ; otherwise, moves to . The algorithm migrates its server to after or moves.
Lemma 1. For any and such that , , and is the center of and , is maximized if , or , or .
Proof. We may assume without loss of generality that and with . Moreover, we fix and regard as a function of . The aim is to prove that is maximized at or .
Therefore, we have
monotonically increases from
to 1 as
changes from
to
. If
, then
for any
. Therefore,
is maximized at
. Otherwise, since
, there exists
such that
. Since
for
and
for
,
is maximized at
or
. ☐
Theorem 1. PQ is -competitive for and the page size .
Proof. We use the following potential function for OPT’s server location
, PQ’s server
, and point locations
and
:
We separate the online events into two parts. The first is to consider only the migration costs incurred by OPT’s server, and the second is to consider the service costs incurred by OPT together with the migration and service costs incurred by PQ. It is sufficient to show that the inequality follows in both parts, upon each request located at .
Part 1. The migration of OPT’s server from
to
induces a change of
to the total cost of the optimal algorithm OPT but no change to the cost incurred by PQ. The total change of
is then
. Therefore, it is sufficient to show the following inequality:
This follows by the symmetry of the distance function () and the triangle inequalities and .
Part 2. We may assume, without loss of generality, that
. By this assumption, PQ moves
to
. Since PQ maintains its server at the center of
and
, the migration cost incurred by PQ is then
. For this part, we have the following equalities:
Therefore, we shall show the following inequality:
Since
, it is sufficient to show:
This follows for the cases and , because and , respectively. We assume and . It is sufficient to show that the maximum value of the left-hand side of Equation (1) is less than or equal to zero. If we regard , , , and as vectors in , then at most three vectors of them, say , , and , are independent. Therefore, the points , , , and are on a plane in . Applying Lemma 1 on this plane, the left-hand side of Equation (1) is maximized in one of three situations. Situation 1: , Situation 2: , or Situation 3: . We proceed to show inequality (1) for each of these three situations.
Situation 1: Substitution of
by
in Equation (1) reveals the following inequality.
By applying
and dividing both sides by
, it is sufficient to show
Since
, Equation (2) can be written as:
By taking the derivative with respect to on the plane containing , , and , the left-hand side of Equation (2) is maximized at and . Therefore, Equation (2) follows.
Situation 2: The inequality in Equation (1) can be rewritten as:
In this situation, we recall that and are all located on the same line segment. Since , and is located at the center of and , it follows that . Since , the inequality in Equation (3) follows.
Situation 3: Since
, we rewrite Equation (1) as:
The points and are also located on the same line segment in this situation. By , we have . By we have . In addition, by we have .
Therefore, the proof completes. ☐
4. A Lower Bound for PQ
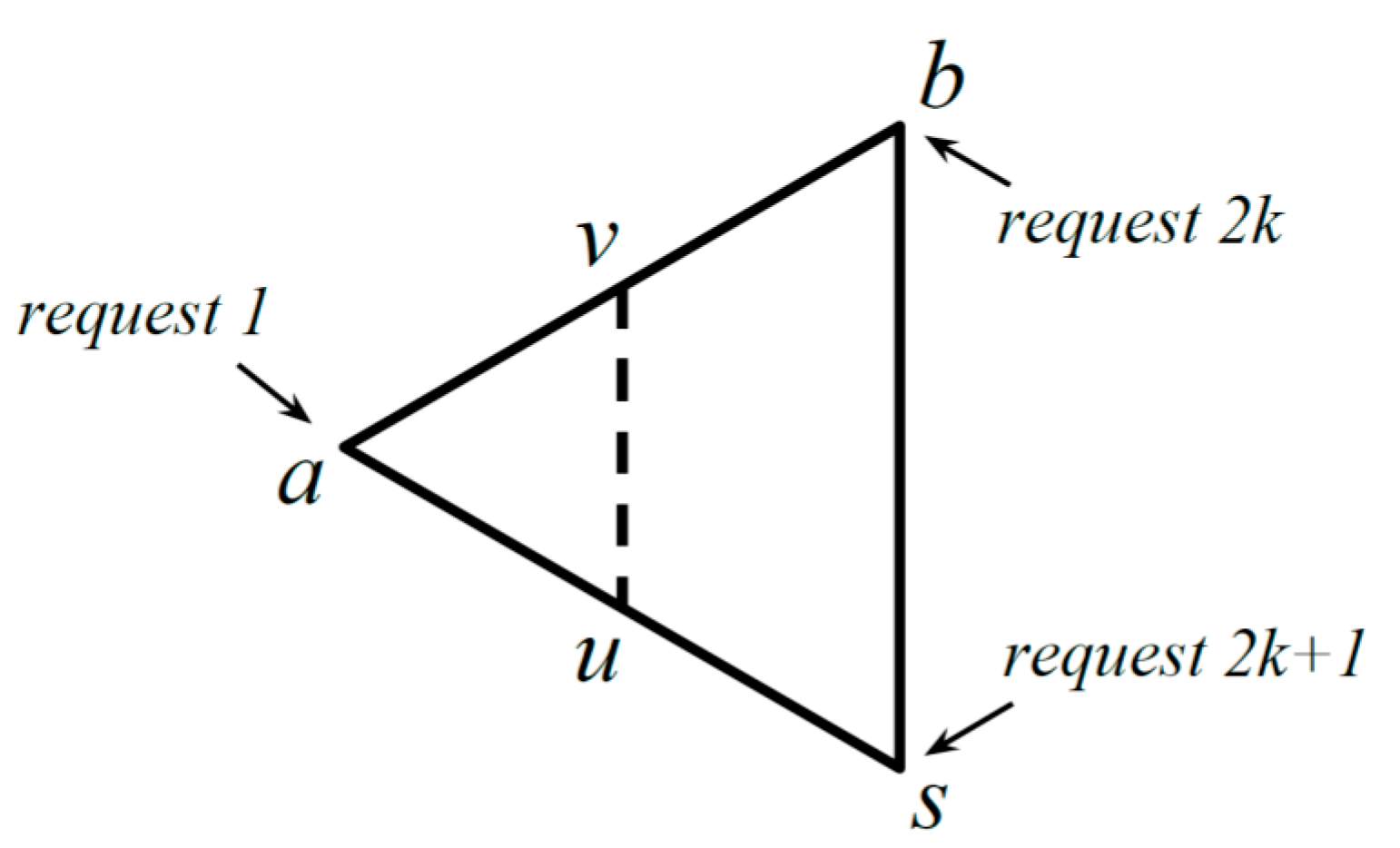
In this section, we show that the exact competitiveness of the algorithm is greater than . We introduce an adversary through Theorem 2 and prove the existence of such a lower bound. The adversary makes a special sequence of requests on against the proposed algorithm. The requests are given at vertices of a triangle that tends to be equilateral. After the second request, the server repeatedly migrates between the center points of two sides of the triangle.
Theorem 2. For a sufficiently large integer , there exist a request sequence , three request locations and on a plane, and the initial server location , such that for .
Proof. We describe our approach before more technical discussion in the subsequent paragraphs. In
Figure 1, we illustrate the behavior of PQ against requests by our adversary. We assume that
is slightly larger than
. Points
and
are the centers of
and
, and
and
, respectively. For requests
, PQ migrates its server along the dashed line, because
does not move from
. A request occurs at
when the server is at
, and a request occurs at
when the server is at
. Note that
,
, and
tend to be the vertices of an equilateral triangle as
approaches
.
For , , and , where and , , and are the vertices of an equilateral triangle with a unit side length, the cost of the optimal algorithm is at most by keeping the server at the initial location .
The adversary infinitesimally perturbs the distances by slightly increasing the distance between and . Upon the first request at , PQ serves the request by the cost of and migrates the server to , which is the center of and , by the cost of . This is because point at moves to . The th request at is served with the cost of , causing point at to move to , and the server migrates to , which is at the center of and , with the cost of . The st request at is served with the cost of . The point at moves to ; hence, the server migrates to with the cost of .
We compute the total cost of PQ by using the distances of the unperturbed triangle, since the actual distances (and hence the actual costs of PQ and OPT) may differ by an infinitesimally small amount from these computations. Therefore, we have
Since
then
is at least
. This completes the proof. ☐