Abstract
Due to the traditional state recognition approaches for complex electromechanical equipment having had the disadvantages of excessive reliance on complete expert knowledge and insufficient training sets, real-time state identification system was always difficult to be established. The running efficiency cannot be guaranteed and the fault rate cannot be reduced fundamentally especially in some extreme working conditions. To solve these problems, an online state recognition method for complex equipment based on a fuzzy probabilistic neural network (FPNN) was proposed in this paper. The fuzzy rule base for complex equipment was established and a multi-level state space model was constructed. Moreover, a probabilistic neural network (PNN) was applied in state recognition, and the fuzzy functions and quantification matrix were presented. The flowchart of proposed approach was designed. Finally, a simulation example of shearer state recognition and the industrial application with an accuracy of 90.91% were provided and the proposed approach was feasible and efficient.
1. Introduction
With the rapid development of modern industry, electromechanical devices are developing towards the direction of large scale and complex structures. Large field investigation and theoretical studies show it is of great significance to recognize the state of complex equipment [1,2,3]. State recognition is the process of identification and classification of the equipment working condition. In this process, appropriate features are extracted to describe each part of the object, and then it is divided into different states according to the characteristics [4]. Thus, the state can be distinguished from others according to the extracted features [5].
As for the low reliability and accuracy, a multiple sensor information fusion system was gradually applied to substitute a single sensor system since the 1980s. Nowadays, multiple sensors are installed on complex equipment to record information of different scales and levels [6]. Traditional state recognition methods mainly combine the field sensor information according to the existing knowledge and experience [7]. However, if the information gathered by sensors is handled without deep fusion, the internal relationship between the information would often be cut off, and the surrounding characteristics indicated by the rational combination of information may be lost [8,9,10]. To realize state recognition accurately, a deep sensor data fusion method should be used, and redundancy and contradiction among the sensors need to be eliminated [11,12]. Thus, state recognition of complex equipment is in fact the process of selecting appropriate field sensors and fusing the information effectively [13,14].
Bearing the above observation in mind, we apply a fuzzy probabilistic neural network (FPNN) to solve the problem of state recognition for complex equipment, and the rest of this paper is organized as follows. In Section 2, some related work is outlined based on the literature. In Section 3, the key technologies of proposed methods such as construction of a multi-level state space, probabilistic neural networks, fuzzy functions and quantification matrix are described in detail, and the flowchart of proposed method is designed. In Section 4, a simulation example is put forward to verify the feasibility and efficiency of the proposed method. An industrial application of mining automation production based on the proposed system is provided in Section 5. Our conclusions and future work are summarized in Section 6.
2. Literature Review
In this section, we try to summarize the relevant literature to this paper. Recent publications related to this paper are about two research streams: state recognition and fuzzy probabilistic neural networks.
2.1. State Recognition
In recent years, many qualitative and quantitative state recognition methods have quickly developed both at home and abroad, promoted development of science and technology, and have been widely applied in the engineering field.
In order to accurately discriminate the real-time operating status of crude oil tanks, ref. [15] proposed a new method based on an expert system and associated cluster analysis. In [16], a method of equipment degradation state recognition based on wavelet correlation feature scale entropy and hidden semi-Markov models was proposed to prevent the equipment from further degradation and failure. The authors take a roller bearing as an example, and the experiment results showed that the proposed method was effective. In [17], a new state recognition method based on a hierarchical hidden Markov model was presented. Based on the method, the computational complexity and the inference time were decreased, and state of gearbox could be recognized accurately. In [18], a high-speed train running state monitoring technique was presented based on a fuzzy grey correlation degree. In [19], a novel approach for screw compressor state recognition and fault diagnosis based on wavelet theory was proposed. According to tested rotor and valve vibration signal energy changing characteristics under different working conditions of the compressor, the working state could be obtained clearly, and an experiment validated the accuracy of the proposed method. In [20], to recognize the state of viscoelastic sandwich structure, an approach based on the adaptive redundant second-generation wavelet packet transform, permutation entropy and the wavelet support vector machine (SVM) was proposed. In [21], a novel state recognition method combining kernel principal component analysis and support vector machine was proposed, and experimental results demonstrated the effectiveness of the proposed algorithm. In [22,23], an artificial neural network was applied to wear state recognition. In [24], aiming at the non-stationary and time-variation characteristics of the gear-box signal, a new method that combined wavelet analysis and a neural network was proposed to recognize the state. To verify the proposed approach, three conditions of a gear-box were simulated by experiments, and the result indicated that the method could recognize the three conditions effectively. In [25], a multi-fractal analysis was applied in state recognition by extract nonlinear features from complex systems.
2.2. Fuzzy Probabilistic Neural Network
A fuzzy set and system was introduced by Zadeh about five decades ago [26]. As the fuzzy theory has advantages in dealing with indeterminate and nonlinear problems, it was widely used in control engineering, state recognition, information processing, decision making, and so on [27]. With the rapid development of electronic techniques in recent decades, Artificial Neural Network (ANN) has developed as an important tool in many fields [28,29]. PNN was proposed by Specht in 1989 [30], which was a significant part of ANN. PNN has a better ability for self-adaption, self-organization and self-learning compared with a SVM and K-nearest neighbor (KNN), and it was mainly applied in classification [31].
A Fuzzy Probabilistic Neural Network (FPNN) combines the existing expert knowledge, fuzzy control theory and probabilistic neural network organically, and it is widely used in prediction, classification and fault diagnosis. In [32], to identify partial discharge location in a power cable, the fuzzy inference system and probabilistic neural network was proposed, the peak absolute value and average power of partial discharge signals were set as input variables, and the experimental results validated the proposed approach. In [33], a novel approach based on fuzzy logic control and PNN was presented to realize direct torque control in permanent magnet synchronous motor drives. In [34], a credit risk assessment model of commercial banks through a fuzzy probabilistic neural network model was proposed, which combined the relative membership degree in fuzzy mathematics with probabilistic neural network. Ref. [35] put forward a fuzzy system to improve the performance of a probabilistic neural network for detecting MEMS analog faults, which was actually a pattern recognition task.
2.3. Discussion
Although many approaches were proposed for state recognition of complex equipment in the above literature, they had some common disadvantages as follows. Firstly, the proposed methods need a large number of simulation data to train the algorithms, while it is difficult to gain real-time and accurate data due to the complicated working conditions. Secondly, in several approaches, an expert knowledge base is needed. However, the existing knowledge base is usually incomplete and could only describe part of the working conditions for the complex equipment. Finally, different judgments may be available for a certain working conditions and have limitations in some working conditions.
In order to tackle the above problems, this paper proposes a novel multi-sensor information fusion method for state recognition through integration of fuzzy logic theory and a probabilistic neural network. The simulation example and industry application are provided and the proposed approach is proven feasible.
3. The Proposed Approach
3.1. Construction of the Multi-Level State Space
To train the initial PNN, a fuzzy rule base founded on the existing expert knowledge system is utilized. Based on deep analysis of the complex equipment, a multi-level segmentation is operated to obtain the state space for the complex equipment.
Generally, a complex equipment is composed of several units: U1, U2, U3,..., Un, and each unit can be described by a number of sub-units, which can be depicted through a series of state variables. Moreover, several features might be extracted from each variable. The multi-level description for complex equipment can be shown in Figure 1.
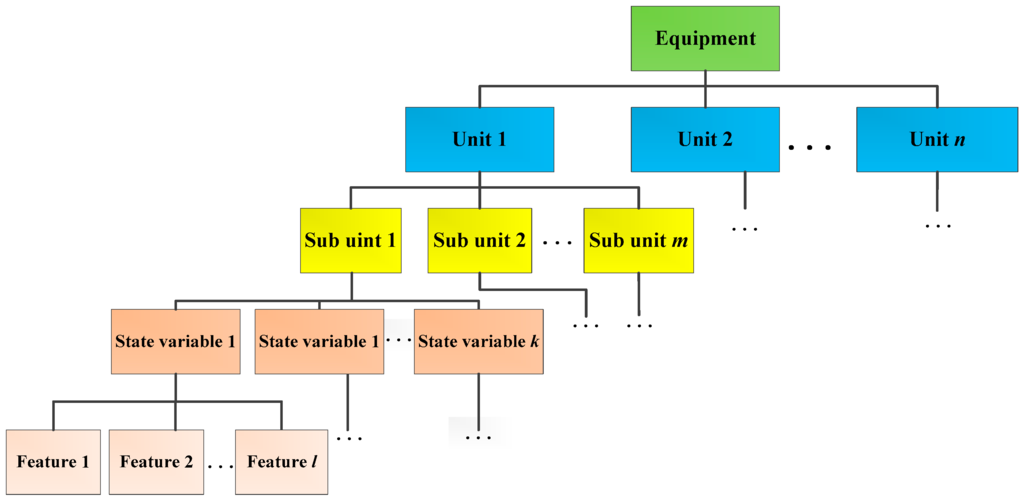
Figure 1.
Multi-level state space for the complex equipment.
For an arbitrary state variable i, descripted by P, it can be described by feature 1 (f_1 for short), feature 2 (f_2),..., feature l (f_l), and can be expressed as follows:
- Rule 1: IF f_1 is NB, and f_2 is NB,..., and f_l is NB, THEN P is p_1,
- Rule 2: IF f_1 is NB, and f_2 is NB,..., and f_l is NM, THEN P is p_2,
- Rule 3: IF f_1 is NB, and f_2 is NB,..., and f_l is NS, THEN P is p_3,
- ......
For state variable i, feature matrix Xi is generalized by summarizing the state of each feature and can be expressed as follows:
where i = 1, 2, 3,…k, vector βi representing the state of state variable i.
3.2. Probabilistic Neural Network
Typical probabilistic neural network contains an input layer, hidden layer, summation layer and output layer. The structure of a typical PNN can be seen in Figure 2.
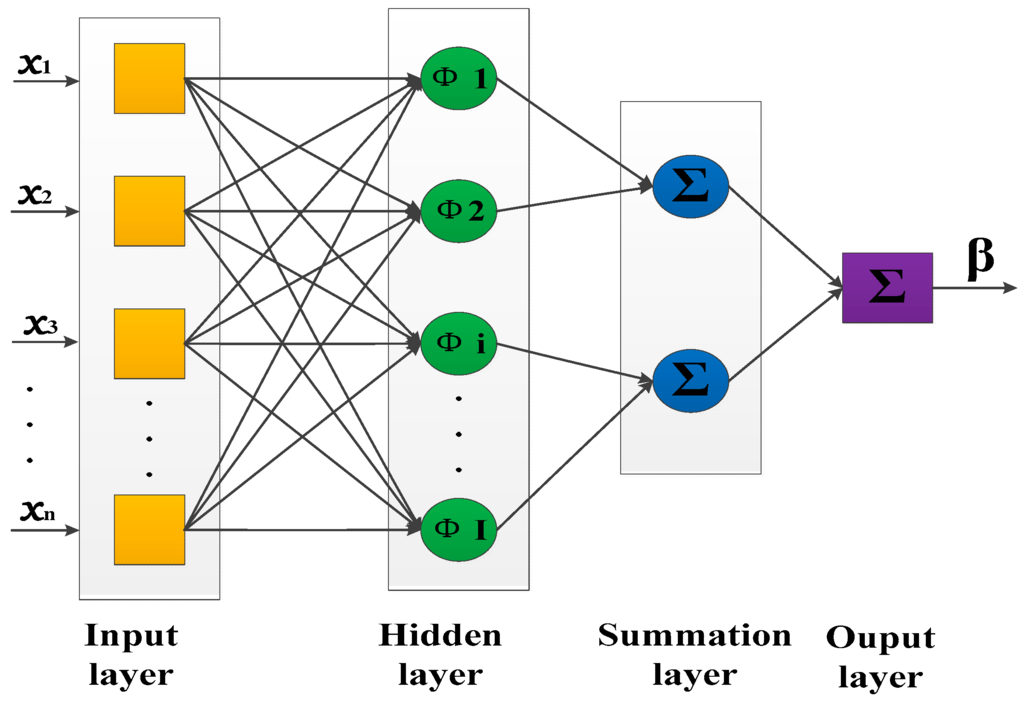
Figure 2.
Structure of typical PNN.
As shown, the input layer receives external data at first, and then data is transported to the hidden layer. The hidden layer is a radial base layer, in which each neuron has its own center. The hidden layer accepts information from the input layer, then distance between input data and computing center is calculated. Input layer nodes and hidden layer nodes run the length of input eigenvectors. Relations of neural node between type i and type j in the hidden layer can be expressed as follows:
where i = 1, 2, 3,…M, M is the total number of classes in the training sample, d is dimension of the training sample, xij is j-th center of the x-th sample, and σ is smoothing factor.
In the summation layer, the output is the weighted average of the same type of neuron nodes from the hidden layer. The weighted average can be calculated as follows:
where νi is output of i-th type, L stands for the number of i-th type neuron node, and the amount of summation layer neuron is equal to M. After calculating each neuron node in the summation layer, we select the maximum probability as the result node and transport it into the output layer. The result can be expressed as follows:
In competitive neurons constituting the output layer, the number of neuron nodes is equal to that in the summation layer. Threshold detection is operated at last, resulting in the output layer with maximum a posteriori estimation of 1, and the others are 0.
For the PNN training process, the inputs and outputs of state variables could be expressed by matrix Xi and vector βi based on the fuzzy rule base.
3.3. Fuzzy Functions and Quantification Matrix
Field sensor data are continuously changing, and quantification is necessary before the fuzzy processing. Generally, the state of a parameter can be described in set: {NB, NM, NS, ZO, PS, PM, PB}, and all elements or several elements may be selected in a practical application. An elementary assumption can be made that the initial value range of the parameter was [−re, re], and the quantification value range can be described as follows:
Usually, re ≠ d, quantifying factor K is introduced as follows:
Thus, an arbitrary input parameter q can be dispersed into the corresponding value in Q, which can be described as below:
According to the field sensor data, the actual value range of the parameter q is [a,b], and d = 6 is selected, so the quantification formula can be expressed as follows:
Similarly, the features of each state variable can be quantified following the scheme provided above, and the quantification matrix for the corresponding variable can be calculated as follows:
3.4. The State Recognition Flow
According to the above description on the comprehensive method based on fuzzy control logic and a probabilistic neural network, the proposed approach can be coded easily on the computer and the flowchart can be summarized as in Figure 3, and the main control processes can be presented as follows:
- (a)
- According to the structural characteristics of the equipment, a multi-level description for the equipment is constructed, and a bottom-up rule base is established based on preliminary statistic data and expert experience.
- (b)
- A feature matrix is set up for each state variable on the basis of the established rule base. Each matrix is the state set of the corresponding variable and can be divided into training rows and testing rows.
- (c)
- The desired recognition accuracy is set up before the training. Then, the initial smoothing factor and iteration number are designated, and the two parameters are adjusted according to the training processing. Initial PNN is trained by the training rows and the training effect is justified by the testing rows.
- (d)
- For an arbitrary group of field data, quantification is conducted by the fuzzy functions, so the data can be extracted as a feature vector. The vector is the input of the trained PNN, and the state of each variable can be obtained according to the trained PNN.
- (e)
- The state of each sub-unit, unit and the whole equipment are acquired by the established bottom-up rule base.
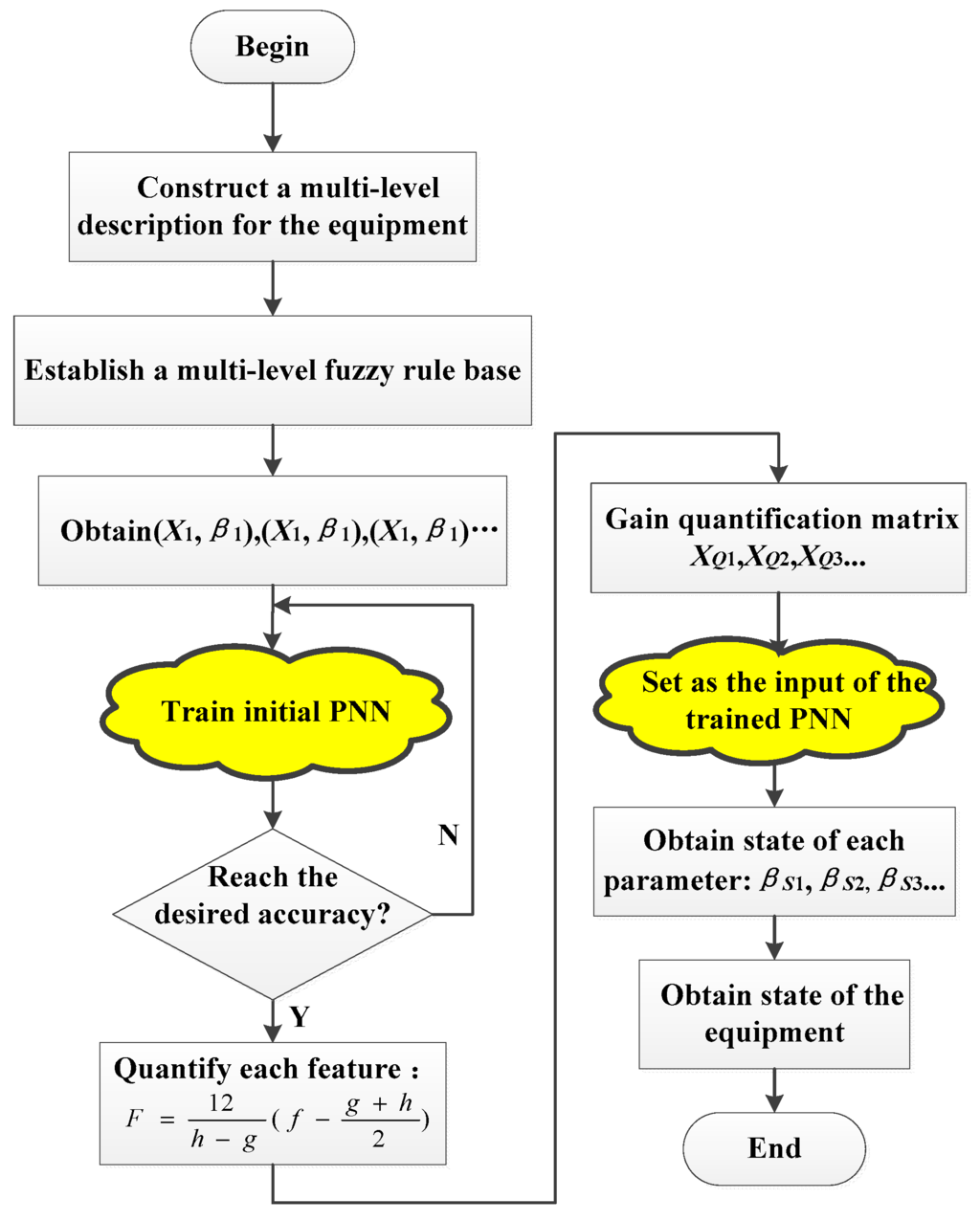
Figure 3.
Flowchart of the proposed method.
4. Simulation Example
The shearer in a fully mechanized coal mining working face is a typical kind of complex device that synthesizes mechanism, electronic and hydraulic-drive technologies. The state identification for the shearer is crucial in coal production. The running efficiency has a direct effect on the coal output. In addition, it is of great significance to guarantee its safe and steady operation. Thus, the state recognition of the shearer was taken as an example to validate the proposed method.
4.1. Constructing the Multi-Level State Space and Training PNN
The model of a shearer was shown in Figure 4, and three units can be separated according to the structural characteristics of the shearer. The cutting and haulage unit can be divided into the left and right sub-unit separately. The states of each sub-unit and transformer are described by the current and temperature, and each state variable consists of four features. The multi-level state space for the shearer was constructed as shown in Figure 5.
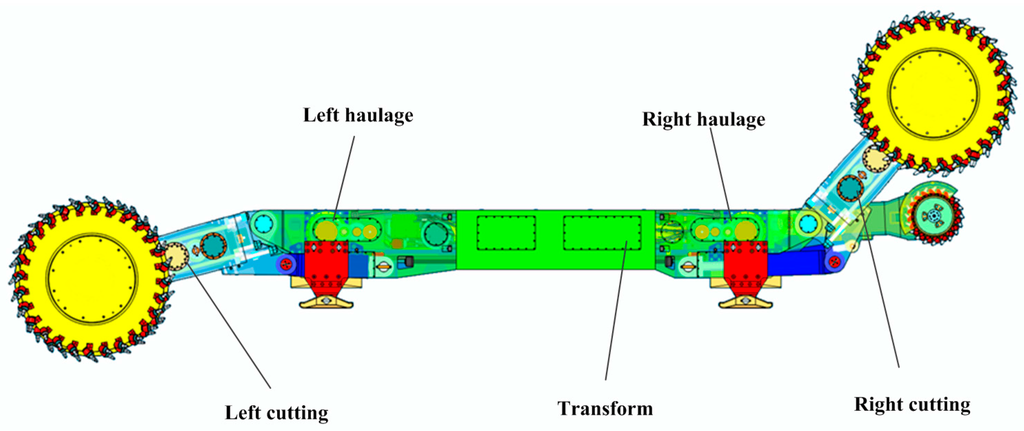
Figure 4.
Structure of the shearer.
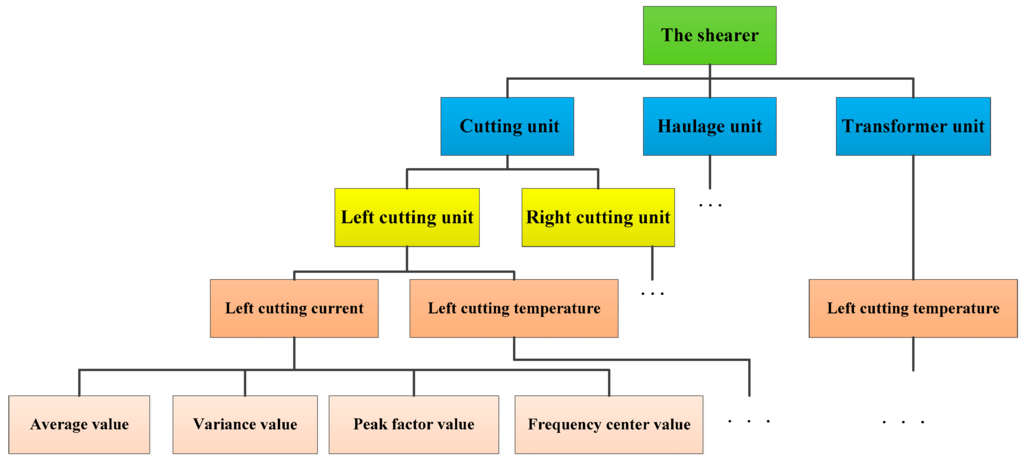
Figure 5.
A multi-level state space for the shearer.
After preliminary analysis on the current and temperature of the shearer, the average, variance, peak factor, and frequency center are selected as the features. According to the combination of vast statistic data, expert knowledge and experience, the state set of the average value of the left cutting current was {RS, NM, RB, B}, the state set of stand deviation was {NM, RB}, the state set of peak factor was {RS, NM, RB}, and the state set of the frequency center was {NM, AN}. Then, the fuzzy rule base on each feature of the left cutting current could be shown as below:
- Rule 1: If A is LC_A_RS, S is LC_S_NM, P is LC_P_RS and F is LC_F_NM, Then LC is LC_RST,
- Rule 2: If A is LC_A_RS, S is LC_S_NM, P is LC_P_RS and F is LC_F_AN, Then LC is LC_FT,
- Rule 3: If A is LC_A_RS, S is LC_S_NM, P is LC_P_NM and F is LC_F_NM, Then LC is LC_VST,
- Rule 4: If A is LC_A_RS, S is LC_S_NM, P is LC_P_NM and F is LC_F_AN, Then LC is LC_RST,
- ......
- Rule 46: If A is LC_A_B, S is LC_S_RB, P is LC_P_NM and F is LC_F_AN, Then LC is LC_AN,
- Rule 47: If A is LC_A_B, S is LC_S_RB, P is LC_P_RB and F is LC_F_NM, Then LC is LC_AN,
- Rule 48: If A is LC_A_B, S is LC_S_RB, P is LC_P_RB and F is LC_F_AN, Then LC is LC_AN.
| Symbol | Meaning | Symbol | Meaning |
| LC_A_RS | The average value is relative small(RS) | LC_P_RB | The peak factor is relative big(RB) |
| LC_A_NM | The average value is normal(NM) | LC_F_NM | The frequency center is normal(NM) |
| LC_A_RB | The average value is relative big(RB) | LC_F_AN | The frequency center is abnormal(AN) |
| LC_A_B | The average value is big | LC_VST | The left cutting current is very stable(VST) |
| LC_S_NM | The stand deviation is normal(NM) | LC_ST | The left cutting current is stable(ST) |
| LC_S_RB | The stand deviation is relative big(RB) | LC_RST | The left cutting current is relative stable(RST) |
| LC_P_RS | The peak factor is relative small(RS) | LC_FT | The left cutting current is fluctuant(FT) |
| LC_P_NM | The peak factor is normal(NM) | LC_AN | The left cutting current is abnormal(AN) |
In the same way, the fuzzy rule base of other parameters, sub-units, units, and the whole shearer were established successively.
Then, the feature matrix of the left cutting current could be summarized as shown:
Likewise, the feature matrix of the left cutting temperature and other parameters could be obtained. At this point, all fuzzy rule bases and feature matrices of features could be established.
In the process of sample training for initial PNN, the inputs were XLC, XLT, XRC, XRT, XLHC, XLHT, XLHT, XRHC, XRHT, XTT, and the outputs were βLC, βLT, βRC, βRT, βLHC, βLHT, βRHC, βRHT, βTT. In the input layer of PNN, the row vector of feature matrix was transported. The probability of LC_VST, LC_ST, LC_RST, LC_FT and LC_AN was calculated individually in the summation layer in the training process of the left cutting current. Finally, results with the biggest posteriori probability were the outputs of the row vectors. The same operation could be done for other feature matrixes.
The predetermined accuracy was set at 95%, the smooth factor σ in PNN was 0.1, and the iteration number was 500. To verify the effect of the training process, the front 40 rows in each feature matrix were selected as the training samples, the last eight rows were extracted as the test sample. Thus, there were 360 training samples and 72 test samples in total. For the left cutting current, the input of the training sample was actually XLC40 × 4, the output was βLC40 × 1, and it was the same as the other state variables. After training the initial PNN, 72 row vectors were input into the trained PNN, and the results showed 69 outputs were in accordance with the actual conditions of each parameter, and the accuracy was 95.83%. Thus, the training effect satisfies the demand.
4.2. Recognizing State of the Shearer
Eight groups of sensor information were extracted in Table 1, and each group was composed of 128 sample points, which contained the left cutting current, left cutting temperature, right cutting current, right cutting temperature, left haulage current, left haulage temperature, right haulage current, right haulage temperature and transformer temperature. In order to extract key features from field sensors, four typical characteristics in the time-frequency domain, such as the average value, standard deviation, peak factor, and frequency center of the data were selected. Then, the fuzzy rule base and feature matrix were established. The features of the left cutting current could be shown in Figure 6.

Table 1.
Field sensor data.
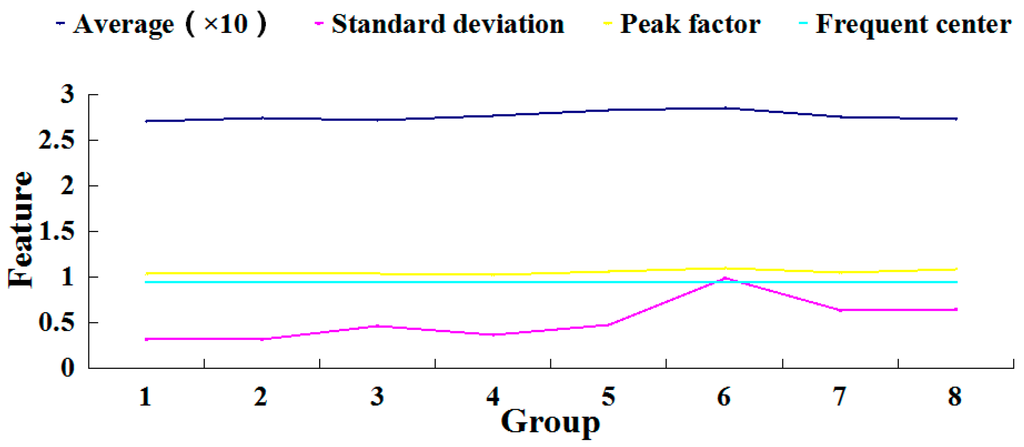
Figure 6.
Feature curve of the left cutting current.
Fuzzy membership functions and quantification matrices were calculated to quantify sensor data gathered from field sensors. For the left cutting current, fuzzy functions for each feature can be determined according to feature curves of the left cutting current and the existing experience.
μcj was the membership function of the average value and could be shown as below:
μcb was the membership function of the standard deviation and could be shown as below:
μcf was the membership function of the peak factor and could be shown as below:
Moreover, μpf was the membership function of the frequency center and could be shown as below:
Then, a quantification matrix of left cutting current was obtained as below:
Working condition of the shearer was recognized by the trained PNN and the multi-level fuzzy rule base. The state of each left cutting current was obtained by inputting a four-dimensional row vector into the trained PNN. Row vector xq1 × 4 = (1.0599 0.1067 1.0208 1.0000) was inputted into PNN to gain the left cutting current of group 1. In the same way, parameter states of other groups were obtained by the trained PNN as shown below:
| Parameters | State Set |
| Left cutting current | LCC_RST, LCC_RST, LCC_RST, LCC_RST, LCC_RST, LCC_RST, LCC_RST, LCC_RST |
| Left cutting temperature | LCT_N, LCT_N, LCT_N, LCT_N, LCT_N, LCT_N, LCT_N, LCT_N |
| Right cutting current | RCC_RST, RCC_RST, RCC_RST, RCC_RST, RCC_RST, RCC_RST, RCC_RST, RCC_RST |
| Right cutting temperature | RCT_N,RCT_N, RCT_N, RCT_N, RCT_N, RCT_N, RCT_N, RCT_N |
| Left haulage current | LHC_RST, LHC_RST, LHC_RST, LHC_FT, LHC_FT, LHC_RST, LHC_FT, LHC_FT |
| Left haulage temperature | LHT_N, LHT_N, LHT_N, LHT_N, LHT_N, LHT_N, LHT_N, LHT_N |
| Right haulage current | LHC_RST, LHC_RST, LHC_RST, LHC_RST, LHC_FT, LHC_RST, LHC_RST, LHC_RST |
| Right haulage temperature | RHT_N, RHT_N, RHT_N, RHT_N, RHT_N, RHT_N, RHT_N, RHT_N |
| Transport temperature | TT_N, TT_N, TT_N, TT_N, TT_N, TT_N, TT_N, TT_N |
After calculating the fuzzy state set of each parameter by the trained PNN, working conditions of each sub-unit, unit, and the shearer could be gained on the established multi-level fuzzy rule base. The working condition of the shearer could be shown as below:
where:
in which, working state of group 1, group 2, group 3, and group 6 was Normal, and group 4, group 5, group 7, and group 8 was Alarm.
{SH_N, SH_N, SH_N, SH_AL, SH_AL, SH_N, SH_AL, SH_AL},
| Symbol | Meaning |
| SH_N | State of the shearer is normal |
| SH_AL | State of the shearer is alarm |
| SH_F | State of the shearer is fault |
5. Industrial Application
In this section, a state recognition system based on the proposed approach was developed and applied in the field of mining automation production as shown in Figure 7. The information database was acquired from the 71506 coal mining face in the NO. 13 Mine of Yangquan Coal Industry Group Corporation.
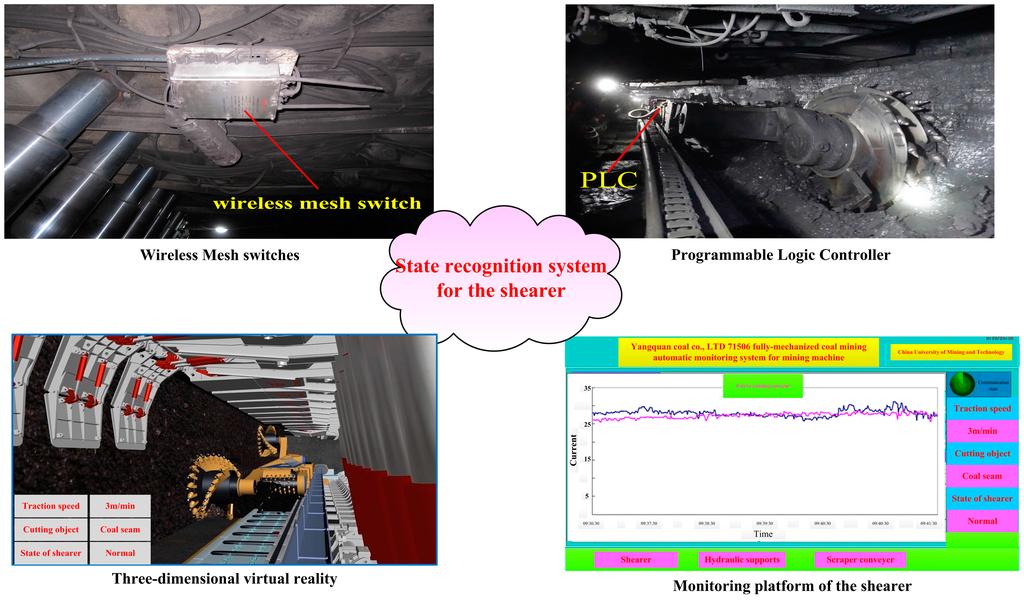
Figure 7.
State recognition system for the shearer.
In order to illustrate the application effect of the proposed system, running parameters of the shearer were collected from the programmable logic controller (PLC) and transported by wireless mesh switches and fiber channel switches. The three-dimensional virtual reality system and the monitoring platform were established to show real-time working state of the shearer. An industrial test lasting for an hour was conducted, and the state of shearer was updated every 10 s. The current and temperature data of the coal mining shearer were collected in each time interval. Then, a comprehensive running state was obtained and recorded automatically. The running log of the shearer was shown in Table 2, where Alarm was recognized 21 times by the proposed system, and one of them was a false Alarm. Moreover, an Alarm event was missing. Thus, the accuracy of the industrial was 90.91%. The average computing time of the recognition process was 0.8632 s, which could basically meet the practical production.

Table 2.
The shearer running log.
The shearer operator adjusted the shearer according to the real-time state recognition system, and the running parameters trended towards stable, where the cutting current was shown in Figure 8. It could be calculated from the figure that the average value of the left and right currents were 27.9578A and 27.2498, respectively, and the maximal values were about 10.95% and 4.77% larger than the average. In addition, the standard deviations of the two curves were 0.9601 and 0.6794. As the geological condition of the working area was complicated and changeable, the slight fluctuation was caused by the changing hardness and the variable thickness of the coal seam.
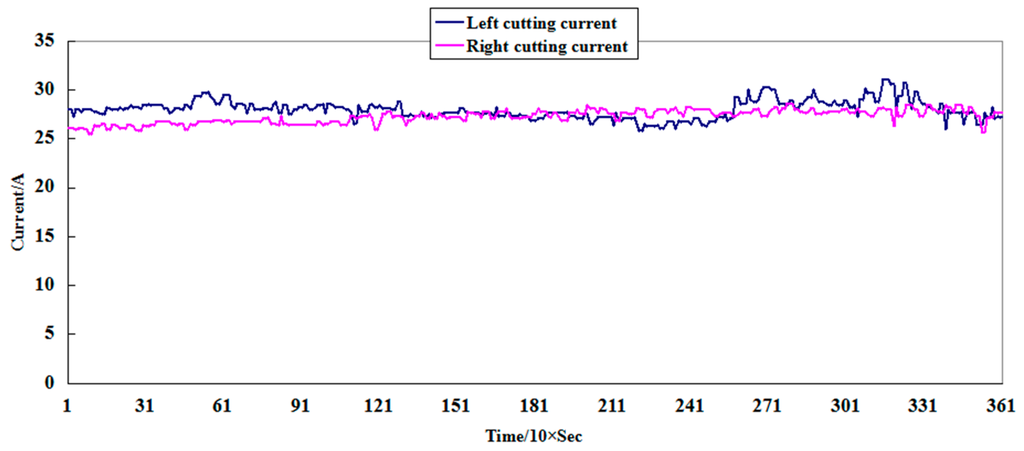
Figure 8.
Cutting current curve.
6. Conclusions
A state recognition approach through integration of fuzzy logic theory and a probabilistic neural network was proposed to improve running efficiency and reduce fault occurrence of complex equipment. The key techniques of the proposed method such as construction of a multi-level state space, a probabilistic neural network, fuzzy functions and quantification matrices were described in detail, and the flowchart of proposed method was designed. Finally, a simulation example and the industrial application were provided. Experiment results showed that the proposed approach was feasible and efficient.
However, there are also some limitations and trouble in this paper listed as follows: (1) the initial training rules for PNN were obtained from expert experience and the level of intelligence was not high enough; (2) parameter selection during the training process for a cognitive PNN relied on extensive simulations; and (3) the online system still has a problem of response delay in the present model. In future studies, the authors plan to investigate some improvements for the proposed approach. Possible improvements may include the adaptive algorithm to establish the rule base and select appropriate parameters, higher execution efficiency of the algorithm code, and applications of the proposed approach in other fields.
Acknowledgments
The support of the Joint Funds of the National Natural Science Foundation of China (No. U1510117), the National Key Basic Research Program of China (No. 2014CB046301), the Innovation Funds of Production and Research Cooperation Project in Jiangsu Province (BY2014107) and the Priority Academic Program Development (PAPD) of Jiangsu Higher Education Institutions in carrying out this research are gratefully acknowledged.
Author Contributions
Zhongbin Wang and Jing Xu contributed the new processing method; Chao Tan designed the simulations and experiments; Xinhua Liu performed the experiments; Jing Xu wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, N.; Sun, S.D.; Li, S.M.; Cai, Z.Q. Equipment state recognition and fault prognostics method based on DD-HSMM model. Comput. Integr. Manuf. Syst. 2012, 18, 1861–1868. [Google Scholar]
- Zeng, Q.H.; Qiu, J.; Liu, G.Q. Equipment degradation state recognition and fault prognosis method based on wavelet correlation feature scale entropy and HSMM. Chin. J. Sci. Instrum. 2008, 29, 2559–2564. [Google Scholar]
- Gu, L.C.; Liu, P.J.; Chen, J.C. State recognition technique of hydraulic system based on electrical parameters information fusion. Jixie Gongcheng Xuebao 2011, 47, 141–150. [Google Scholar] [CrossRef]
- Wang, W.C.; Chau, K.W.; Xu, D.M.; Chen, X.Y. Improving Forecasting Accuracy of Annual Runoff Time Series Using ARIMA Based on EEMD Decomposition. Water Resour. Manag. 2015, 29, 2655–2675. [Google Scholar] [CrossRef]
- Huang, Q.; Ouyang, X.Z.; Huang, Q.P. The state recognition for rotary machines based on fractal theory and neural network. Appl. Mech. Mater. 2013, 404, 485–489. [Google Scholar] [CrossRef]
- Zhang, J.; Chau, K.W. Multilayer Ensemble Pruning via Novel Multi-Sub-Swarm Particle Swarm Optimization. J. Univ. Comput. Sci. 2009, 15, 840–858. [Google Scholar]
- Yang, J.X.; Zhou, J.T.; Chen, Y. Study on state recognition of ASCE benchmark based on lyapunov exponent spectrum entropy. Adv. Mater. Res. 2011, 243, 5435–5439. [Google Scholar] [CrossRef]
- Ding, Q.; Peng, Z.H.; Liu, T.Z.; Tong, Q.H. Multi-sensor building fire alarm system with information fusion technology based on D-S evidence theory. Algorithms 2014, 7, 523–537. [Google Scholar] [CrossRef]
- Luo, R.C.; Chang, C.C.; Lai, C.C. Multisensor fusion and integration: Theories, applications, and its perspectives. IEEE Sens. J. 2011, 11, 3122–3138. [Google Scholar] [CrossRef]
- Wang, G.H.; Liu, Y.; Xiong, C.Q. An optimization clustering algorithm based on texture feature fusion for color image segmentation. Algorithms 2015, 8, 234–247. [Google Scholar] [CrossRef]
- Francois, Y.; Grandvalet, T.; Deneux, C.; Roger, J.M. Resample and combine: An approach to improving uncertainty representation in evidential pattern classification. Inform. Fusion 2003, 4, 75–85. [Google Scholar] [CrossRef]
- Zhang, S.W.; Chau, K.W. Dimension Reduction Using Semi-Supervised Locally Linear Embedding for Plant Leaf Classification. Lect. Notes Comput. Sci. 2009, 5754, 948–955. [Google Scholar]
- Mohamed, E.A.; Abdelaziz, A.; Mostafa, A.S. A neural network-based scheme for fault diagnosis of power transformers. Electr. Power Syst. Res. 2005, 75, 29–39. [Google Scholar] [CrossRef]
- Taormina, R.; Chau, K.W. Data-driven input variable selection for rainfall-runoff modeling using binary-coded particle swarm optimization and Extreme Learning Machines. J. Hydrol. 2015, 529, 1617–1632. [Google Scholar] [CrossRef]
- Liu, C.T.; Chen, X.G. Study on operating status recognition and fault diagnosis for net crude-oil tank. Chin. J. Sci. Instrum. 2007, 28, 703–707. [Google Scholar]
- Zeng, Q.H.; Qiu, J.; Liu, G.J. Application of hidden semi-markov models based on wavelet correlation feature scale entropy in equipment degradation state recognition. In Proceedings of the 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008.
- Teng, H.Z.; Jia, X.S.; Zhao, J.M.; Zhang, X.H.; Wang, Z.G.; Ge, J.Y. Research on gearbox state recognition based on hierarchical hidden Markov model. China Mech. Eng. 2011, 22, 2175–2181. [Google Scholar]
- Li, J.H.; Jin, W.D.; Xiong, L.Y. Running state recognition of high-speed train based on fuzzy grey correlation analysis. J. Vib. Shock 2014, 33, 188–193. [Google Scholar]
- Niu, Q.F.; Wang, L. Working condition recognition of screw compressor using wavelets theory. In Proceedings of the 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008.
- Qu, J.X.; Zhang, Z.S.; Wen, J.P. State recognition of the viscoelastic sandwich structure based on the adaptive redundant second generation wavelet packet transform, permutation entropy and the wavelet support vector machine. Smart Mate. Struct. 2014, 23, 650–661. [Google Scholar] [CrossRef]
- Niu, Q.; Xia, S.X.; Zhou, Y.; Zhang, L. Fault condition recognition of mine hoist combining kernel PCA and SVM. In Proceedings of the IEEE International Conference on Integration Technology, Shenzhen, China, 20–24 March 2007.
- Nie, P.; Chen, X.; Xu, T.; Sun, B.L. State recognition of tool wear based on wavelet neural network. J. Beijing Univ. Aeronaut. Astronaut. 2011, 37, 106–109. [Google Scholar]
- Xu, Y. Wear state recognition of drills based on K-means cluster and radial basis function neural network. Int. J. Autom. Comput. 2010, 7, 271–276. [Google Scholar]
- Hu, Y.P.; An, G.; Niu, Y.T.; Liu, G.Y. Condition recognition of gear-box with combination of wavelet analysis and neural network. J. Acad. Armored Force Eng. 2009, 23, 36–39. [Google Scholar]
- Lui, Y.Q.; Gao, J.M.; Jiang, H.Q.; Chen, K. Condition recognition of complex systems based on multi-fractal analysis. In Proceedings of the Annual Reliability and Maintainability Symposium, Lake Buena Vista, FL, USA, 24–27 January 2011.
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Feng, G. A survey on analysis and design of model-based fuzzy control systems. IEEE Trans. Fuzzy Syst. 2006, 14, 676–697. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W.; Li, Y.S. Methods to improve neural network performance in daily flows prediction. J. Hydrol. 2009, 372, 80–93. [Google Scholar] [CrossRef]
- Chau, K.W.; Wu, C.L. A hybrid model coupled with singular spectrum analysis for daily rainfall prediction. J. Hydroinform. 2010, 12, 458–473. [Google Scholar] [CrossRef]
- Specht, D.F. Probabilistic neural networks and the polynomial Adaline as complementary techniques for classification. IEEE Trans. Neural Netw. 1990, 1, 111–121. [Google Scholar] [CrossRef] [PubMed]
- Lotfi, A.; Benyettou, A. A reduced probabilistic neural network for the classification of large database. Turk. J. Electr. Eng. Comput. Sci. 2014, 22, 979–989. [Google Scholar] [CrossRef]
- Su, M.S.; Chen, J.F.; Lin, Y.H. Identification of partial discharge location in a power cable using fuzzy inference system and probabilistic neural networks. Electr. Power Compon. Syst. 2012, 40, 613–627. [Google Scholar] [CrossRef]
- Lin, H.; Yan, W.S.; Li, H. Fuzzy and PNN-based Direct Torque Control for Permanent Magnet Synchronous Motor. In Proceedings of the 4th IEEE Conference on Industrial Electronics and Applications, Xi’an, China, 25–27 May 2009.
- Huang, Y.S.; Tian, C.F. Research on credit risk assessment model of commercial banks based fuzzy probabilistic neural network. In Proceedings of the 2nd International Conference on Risk Management and Engineering Management, Beijing, China, 4–6 November 2008.
- Asgary, R.; Mohammadi, K. Using fuzzy probabilistic neural network for fault detection in MEMS. In Proceedings of the 5th International Conference on Intelligent Systems Design and Applications, Wroclaw, Poland, 8–10 September 2005.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).