Abstract
Parsing for mildly context-sensitive language formalisms is an important area within natural language processing. While the complexity of the parsing problem for some such formalisms is known to be polynomial, this is not the case for all of them. This article presents a series of results regarding the complexity of parsing for linear context-free rewriting systems and deterministic tree-walking transducers. We discuss the difference between uniform and nonuniform complexity measures and how parameterized complexity theory can be used to investigate how different aspects of the formalisms influence how hard the parsing problem is. The main results we survey are all hardness results and indicate that parsing is hard even for relatively small values of parameters such as rank and fan-out in a rewriting system.
1. Introduction
Context-free and context-sensitive grammars were introduced in the 1950s by Noam Chomsky, as possible formalisms for describing the structure of natural languages; see, e.g., [1]. Context-free grammars (CFG for short), in particular, have been very successful, both when it comes to natural language modelling and, perhaps to an even larger degree, the description of the syntax of programming languages.
During the sixty years since their introduction, it has become clear that context-free grammars, though immensely useful in many applications, also have certain limitations in their ability to formalize natural language grammar. As an example, they are unable to model the cross-serial dependencies that appear in some languages and that are archetypically captured by the copy language over an alphabet Σ defined by
An example of this phenomenon in English is the construction used together with “respectively”:
Cats, rabbits, dogs, and monkeys like fish, carrots, bones, and bananas, respectively.
Context-sensitive grammars, on the other hand, are able to model these and many other natural language constructions that go beyond the context-free languages. The drawback of using them for natural language processing is the computational complexity of their associated decision problems. It is well known that the membership problems (and thus parsing) for context-sensitive languages are equivalent to the acceptance problems for linear-bounded nondeterministic Turing machines. The emptiness problem for context-sensitive grammars is undecidable; see, e.g., [2].
For these reasons, Aravind Joshi suggested the concept of mildly context-sensitive languages in 1985. The idea was to capture the full richness of natural language syntax and still have a computationally tractable formalism. Mildly context-sensitive formalisms should extend the context-free languages to include relevant natural language features, while preserving constant growth and polynomial time parsing. Joshi himself suggested tree-adjoining grammars (TAGs) as a suitable formalism [3]. Other suggested formalisms, such as Linear Indexed Grammars (LIG), Combinatory Categorial Grammars (CCG), and Head Grammars (HG) have been shown to be expressively equivalent to TAGs [4]. (The equivalence holds for the CCG version used in [4], but not for all CCG definitions that are currently used; see, e.g., [5].)
There were, however, still some linguistic constructions that TAGs could not fully model. (This has to do with the locality of dependencies in TAGSs; for details, see, e.g., [6].) This led to other formalisms being suggested during the late 1980s, notably multi-component TAGs [7], linear context-free rewriting systems (LCFRSs) [8], and the very similar multiple context-free grammars [9].
Already in 1971, Aho and Ullman had introduced deterministic tree-walking transducers (DTWTs). Their goal was to characterize transformations over context-free grammars [10]. It was later shown that these transducers produce the same class of output languages as a kind of context-free hypergraph grammar [11,12]. In 1992, rather surprisingly, Weir showed that they also produce the same class of languages as LCFRSs [13]. That put DTWTs in the running as a candidate formalism for representing mildly context-sensitive languages.
2. Uniform and Nonuniform Membership Complexity
In formal language theory, three of the fundamental concepts are languages, language formalisms, and language classes. By a language formalism we mean a class of language representations. Examples of language formalisms are deterministic finite automata, regular expressions, CFGs, LCFRSs, etc. Each formalism also gives rise to a language class, i.e., the class of all languages that can be represented by the formalism. For both deterministic finite automata and regular expressions this class is the regular languages. For CFGs, it is the context-free languages.
The difference between the uniform and the nonuniform complexity of a formal language membership problem for a certain formalism is whether we consider the language description as part of the input or not. In the uniform case we do, but in the nonuniform case we do not.
Definition 1.
Let be a formal language over alphabet Σ. The membership problem for is the following:
- Input: A string .
- Question: Does w belong to ?
The above definition coincides with the complexity-theoretical concept of a decision problem. When we talk about the nonuniform complexity for a formalism, we are actually referring to a whole class of decision problems—one for each language in the corresponding language class.
In the uniform case, however, we consider the actual language representation as a part of the input. This means that when we talk about the uniform complexity for a formalism, we are only referring to a single decision problem:
Definition 2.
Let be a language formalism. The uniform membership problem for is the following:
- Input: A language representation and a string w.
- Question: Does w belong to ?
It may seem strange to talk about the nonuniform complexity, but there are actually a number of fields in computer science where we come across similar notions. In database theory, we often use the notions of query complexity, data complexity and combined complexity. Here, the query complexity and the data complexity describe how the difficulty of evaluating a query over a database grows with the size of the query and the database, respectively. They are both nonuniform complexity measures. The combined complexity, that takes both the query and the database into account, is a uniform measure. Similarly, in model checking, we can talk about the formula complexity, the model complexity and the combined complexity. We know that model checking for linear temporal logic (LTL) over Kripke structures is linear in the size of the model, but exponential in the size of the formula. For a formula ϕ and a model M, the complexity of the best known algorithms is .
In formal languages, we often say things like “the membership problem for nondeterministic finite automata is linear”. In the terminology presented above, this is not entirely correct. It would be more appropriate to say that the nonuniform membership problem for regular languages is linear or that the uniform membership problem for nondeterministic finite automata is linear in the size of the input string.
It is crucially important for what follows that when we say that the nonuniform membership problem for a formalism is solvable in polynomial time, this only means that for each language that can be represented by the formalism, the corresponding membership problem is polynomial. It does not mean that there is one single polynomial that bounds the amount of time it takes to solve the membership problems for all the languages the formalism can represent.
3. Linear Context-Free Rewriting Systems
Linear context-free rewriting systems, just like CFGs, have nonterminals, including a special starting nonterminal, terminals, and context-free rules. The difference is that the languages produced by the nonterminals are languages of tuples of strings, rather than just strings. Each nonterminal is assigned a fan-out that determines the arity of the tuples it produces. For instance, a nonterminal with fan-out 1 produces strings, one with fan-out two produces 2-tuples of strings, one with fan-out three produces 3-tuples of strings, etc. The rules are equipped with linear regular functions that govern how the tuples produced by the nonterminals on the right hand side can be combined. Such a function takes a number of tuples of strings as input and rearranges the components of the tuples into one tuple of strings. (Actually, the functions of the rules can also add terminal strings to the tuples produced by the nonterminals on the right hand side.)
As an example, consider a rule
where A and C have fan-out two, B has fan-out 3, and φ is the linear regular function of the rule. Then φ rearranges the three elements of the tuple produced by B and the two elements of the tuple produced by C into a 2-tuple produced by A. For concreteness, assume that φ is defined by
If the tuple can be derived from B and can be derived from C, this means that the tuple can be derived from A. A derivation of this kind is illustrated in Figure 1.
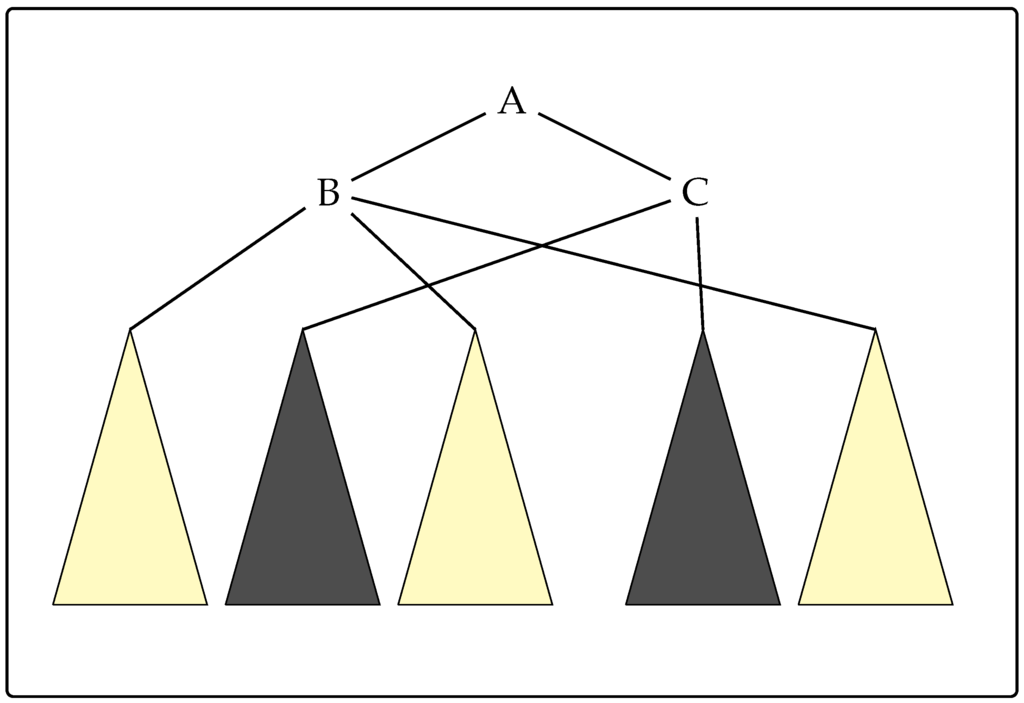
Figure 1.
An illustration of a LCFRS derivation. The rule has rank two. Nonterminal B has fan-out 3, while C has fan-out 2.
The fan-out of an LCFRS is the maximal fan-out of any nonterminal in the system. An LCFRS with fan-out one is equivalent to a CFG. Since every nonterminal produces strings (rather than tuples of strings), the linear regular functions can only rearrange the strings produced by the nonterminals on the right-hand side. Such rearrangements can be simulated in a CFG by ordering the nonterminals on the right-hand sides of rules appropriately.
The rank of a rule is the number of nonterminals on the right hand side. The rank of an LCFRS is the maximal rank of any rule in the system. In the terminology of Satta [14], the fan-out is a measure of the synchronized parallelism in an LCFRS, while the rank is a measure of the independent parallelism. This is because the elements of a tuple derived from a nonterminal are not independent of each other, while the tuples derived from two different nonterminals on the right hand side of a rule are.
For , we write i-LCFRS for the class of all LCFRSs of rank at most i and LCFRS for the class of all LCFRSs of fan-out at most i. We also write i-LCFRS for i-LCFRS∩LCFRS.
4. Previous Results
We are now equipped to take a closer look at the complexity of parsing for mildly context-sensitive languages. While the formalisms described above differ in how much they can express, the classes of languages they define all fulfill the following criteria for mild context-sensitivity, suggested by Joshi.
- They extend the context-free languages.
- They have the constant growth property, i.e., the difference in length between a word and the next shorter word is bounded by a constant. (Formally, a language has the constant growth property if there is a constant c such that for every string , if the length of u is larger than c, then there is a string such that and .)
- They can be parsed in polynomial time.
Here, it is the polynomial time parsing that interests us in particular. The fact is that while the nonuniform membership problem associated with any of the formalisms is solvable in polynomial time, the uniform membership problem is only known to be polynomial for some of the formalisms.
For TAGs and similar formalisms, the uniform membership problem is solvable in polynomial time. Concretely, there are algorithms that run in time , where n is the size of the input string, p is a polynomial and is the size of the grammar. For LCFRSs, the situation is different. The best known algorithms for their uniform membership problem have a running time of , where G is the grammar, n again the length of the string, and f and r are the fan-out and rank of the grammar, respectively [9,15,16]. For an excellent overview of the available algorithms for parsing mildly context-sensitive languages, see the book by Kallmeyer [17].
In fact, the uniform membership problem for LCFRSs is PSPACE-complete even if the rank is fixed to 1 (1-LCFRS) [18] and NP-hard even if the fan-out is fixed to 2 (LCFRS) [19]. This shows that parsing for such grammars is a far from trivial problem.
Since the languages generated by DTWTs are the same as those generated by LCFRSs, we know that each such language has a polynomial time nonuniform membership problem. Not much has been written, however, about the uniform membership problem for DTWTs. It is rather easy to show that it is in fact EXPTIME-complete. Membership follows by standard automata-theoretic techniques. For the hardness result, it is already known that the emptiness problem for deterministic tree-walking automata is EXPTIME-hard; see, e.g., [20]. The only remaining step is to argue that a small technical difference in the definition of the transducer part of DTWTs and tree-walking automata can be overcome by an encoding trick.
5. Parameterized Complexity
We begin this section by recalling the most fundamental notions of parameterized complexity theory. A complete treatment can be found in the monographs by Downey and Fellows [21] or Flum and Grohe [22].
A parameterized problem over alphabet Σ is a language . Given an instance , we say that k is the parameter and is the instance size. Let A be an algorithm for the parameterized problem . We say that A is fixed-parameter tractable if the follwing conditions hold. There is a computable function f and a polynomial p such that A, given an instance , halts in time and decides whether . We say that the problem is fixed-parameter tractable if there is a fixed-parameter tractable algorithm for . The class FTP consists of all parameterized problems that are fixed-parameter tractable.
A parameterized reduction is, intuitively, a reduction from one parameterized problem to another that runs in fixed-parameter tractable time and such that the parameter in the output only depends on the parameter in the input. Formally is fpt-reducible to if there is a function such that
- for , we have if and only if ,
- can be computed in time , where f is computable and p is a polynomial, and
- there is a computable function g such that for with , we have .
We will sometimes consider more than one parameter. In this case, we actually use the sum of their values as a single parameter.
The most well known hierarchy in parameterized complexity is the following.
The only one of these inclusions that is known to be strict is [21]. XP is the class of all parameterized problems that are “slicewise polynomial”, i.e., those that can be decided in time , for some computable function f.
6. The Parameterized Complexity of LCFRS Membership
We now summarize the results we have obtained concerning the parameterized complexity of the uniform membership problem for LCFRS and related formalisms.
Recall that the complexity of the best known algorithms for LCFRS parsing is where f is the fan-out and r the rank. The main idea of our investigation was to find out whether the fan-out and rank have to end up in the exponent of n (the length of the input string). Imagine, for example, that we could achieve a complexity like , for some constant c. If f and r were considered parameters, this would be fixed-parameter tractable. The complexity would still be exponential in f and r, but consider what happens to the polynomial that describes the dependency on n. Instead of f and r determining the rank of this polynomial, they would only determine the coefficient. This would be a substantial improvement. We therefore set out to investigate what happens if we treat the fan-out, the rank, or both as parameters. In particular, we wanted to know if it was possible to achieve fixed-parameter tractability. The fan-out and rank are also a natural choice for parameters from a linguistic point of view, since they can be kept small in most linguistic applications; see, e.g., [23].
Unfortunately, the answers we got were negative. We proved hardness for presumably intractable complexity classes, showing that the rank and fan-out probably do have to go into the exponent of n.
For our first result, we fixed the rank to 1 and treated the fan-out as a parameter.
Theorem 1
([24]). The uniform membership problem for 1-LCFRS, where the fan-out is the parameter, is W[SAT]-hard.
We proved this result by reduction from the Weighted Monotone Satisfiability problem, which is known to be W[SAT]-complete [21,25,26]. A monotone Boolean formula is a formula built up from only variables, conjunctions, and disjunctions. In particular, there are no negations. In the Weighted Monotone Satisfiability problem, we are given a pair , where φ is a monotone Boolean formula and k is an integer. The question is whether φ has a satisfying assignment with weight exactly k, i.e., one that sets exactly k variables to true. In the parameterized version, the parameter is k.
In the reduction, the input string represents an encoding of the variables of the formula we reduce from. The structure of the formula is encoded into the rules. The grammar then “guesses” k variables to be set to true by partitioning the input string into sections. It can use its encoded knowledge of the formula to verify that the guessed assignment indeed satisfies the formula. This shows off the general ability of an LCFRS with fan-out k to guess k items by partitioning the input string, allowing for many reductions from problems of the kind “is there a subset of size k with a certain property”.
Interestingly, though, we were not able to find a reduction from any W[P]-hard problem of this kind. Here, we did not manage to find a way of encoding the verification step into an LCFRS. As an example, we can mention the Minimum Axiom Set problem. Here, we are given a set S, a relation R of pairs , where and , and an integer k. The question is whether there is a subset of size k from which we can “generate” all of S using R. This problem is W[P]-complete [25]. Here, as above, it is not too difficult to simulate the “guessing” of the subset C. The problem is how to simulate the verification step, i.e., checking whether C generates all of S, in an LCFRS membership problem where the fan-out only depends on k. Since the generation chains can be linear in the size of S, it seems that the simulation needs a way of “remembering” what subset of S has been generated so far. We were unable to construct a solution for this. This does, of course, not mean that it is impossible to do so.
We have not been able to provide any parameterized upper bound for the problem, besides the trivial XP membership. This difficulty may be explained by a conjecture of Pietrzak [27], stating that if a problem has a certain property, that Pietrzak calls additive, then it is either fixed-parameter tractable or does not belong to W[P]. Simply put, a parameterized problem is additive if, whenever we have a number of instances , all with the same parameter value k, we can in polynomial time compute an instance I, also with parameter value k, such that I is a yes-instance if and only if are all yes-instances. We do not know if 1-LCFRS membership, parameterized by the fan-out, is additive. We can, however, prove that 2-LCFRS membership, parameterized by the fan-out, is. This means that if Pietrzak’s conjecture holds and the W-hierarchy does not collapse, then 2-LCFRS membership, parameterized by the fan-out, cannot belong to W[P].
For our second result, we fixed the fan-out to 2 (remember that an LCFRS with fan-out 1 is a CFG) and treated the rank as parameter.
Theorem 2
([24]). The uniform membership problem for LCFRS(2), where the rank is the parameter, is W[1]-hard.
The reduction is from k-Clique and illustrates the ability of LCFRS to transfer and compare information from different parts of the input string. Concretely, the grammar encodes the structure of the graph. Unlike the reduction for Theorem 1 above, where k items are guessed by having one nonterminal with large fan-out selecting parts of the input string, we now use k nonterminals, each with fan-out 2, to each select, as the first component of their tuples, one of the k vertices to be included in the clique. The second component is used for bookkeeping and verification, using a scheme that is similar to the one utilized by Satta in his proof that the membership problem for LCFRS(2) is NP-hard [19].
Given the negative results reported above, we tried yet another parameterization, hoping to achieve fixed-parameter tractability. In a “short derivation” membership problem for a grammar, we are given an integer k as additional input. The question is whether the grammar can generate the input string by a derivation that has length at most k. The length of a derivation is the number of rule applications it uses. This time we used rank, fan-out, and derivation length as parameters. Unfortunately, the problem remains W[1]-hard:
Theorem 3
([24]). The uniform short derivation membership problem, where rank, fan-out, and derivation length are parameters, is W[1]-hard.
By polynomial time reductions, all the results above immediately transfer to multiple context-free grammars, multi-component TAGs, and string-producing hyperedge replacement grammars. We discovered, however, that the situation for DTWTs is a little bit different.
A DTWT is a regular tree-grammar G together with a deterministic tree-walking transducer T. The system is said to produce a string s if there is a tree t produced by G such that when running T on t, it accepts and outputs s. As mentioned above the emptiness problem for DTWTs is hard (EXPTIME-complete). Since the emptiness problem for LCFRSs is polynomial and P ≠ EXPTIME, this allows us to conclude that there is no polynomial time procedure for transforming DTWTs into language equivalent LCFRSs. It also turned out to allow us to show a stronger parameterized complexity result for this formalism.
Theorem 4
([28]). Deciding whether a DTWT accepts the empty string, parameterized by the crossing number, is XP-hard.
The crossing number of a DTWT is the maximal number of times the tree-transducer enters any subtree of a tree produced by the regular tree grammar. It corresponds to the fan-out of an LCFRS.
It is interesting that the result holds already for the empty string. This shows that for DTWTs, membership is as hard as emptiness. On the positive side, using an algorithm by Weir for converting a DTWT into a language-equivalent LCFRS [13], we could show the following tractability result, using a parameter that is very easy to compute.
Theorem 5
([28]). The emptiness problem for DTWT, parameterized by the number of states of the transducer, is fixed-parameter tractable.
7. Future work
There are still a number of questions that remain unanswered. In particular, we have not yet achieved any completeness results for the uniform LCFRS membership problem, whether we parameterize by rank, fan-out, or both. The only known upper bound is the trivial XP membership.
Another interesting question is, of course, if there is some completely different parameterization that makes sense and gives a more uplifting complexity analysis.
Acknowledgments
We thank Frank Drewes for his part in obtaining the results summarized here and for many useful discussions. We also thank the anonymous reviewers for many helpful suggestions. We also gratefully acknowledge the financial support from the Swedish Research Council grant 621-2011-6080.
Author Contributions
Henrik Björklund and Martin Berglund did most of the work on the results concerning LCFRSs. Henrik Björklund and Petter Ericson did the work on the results concerning DTWTs. Henrik Björklund wrote the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chomsky, N. Three models for the description of language. IRE Trans. Inf. Theory 1956, 2, 113–124. [Google Scholar] [CrossRef]
- Hopcroft, J.E.; Ullman, J.D. Introduction to Automata Theory, Languages, and Computation; Addison-Wesley: Reading, MA, USA, 1979. [Google Scholar]
- Joshi, A.K. Tree adjoining grammars: How much context-sensitivity is required to provide reasonable structural descriptions. In Natural Language Parsing; Cambridge University Press: Cambridge, UK, 1985; pp. 206–250. [Google Scholar]
- Vijay-Shanker, K.; Weir, D.J. The equivalence of four extensions of context-free grammars. Math. Syst. Theory 1994, 27, 511–546. [Google Scholar] [CrossRef]
- Kuhlmann, M.; Koller, A.; Satta, G. Lexicalization and generative power in CCG. Comput. Linguist. 2015, 41, 187–219. [Google Scholar] [CrossRef]
- Weir, D.J. Characterizing Mildly Context-Sensitive Grammar Formalisms. Ph.D. Thesis, University of Pennsylvania, Philadelphia, PA, USA, 1 January 1988. [Google Scholar]
- Joshi, A.K. An Introduction to Tree Adjoining Grammars. In Mathematics of Language; John Benjamins Publishing Company: Amsterdam, NY, USA, 1987; pp. 87–114. [Google Scholar]
- Vijay-Shanker, K.; Weir, D.J.; Joshi, A.K. Characterizing structural descriptions produced by various grammatical formalisms. In Proceedings of the 25th Meeting of the Association for Computational Linguists (ACL’87), Stanford, CA, USA, 6–9 July 1987; pp. 104–111.
- Seki, H.; Matsumura, T.; Fujii, M.; Kasami, T. On multiple contex-free grammars. Theor. Comput. Sci. 1991, 88, 191–229. [Google Scholar] [CrossRef]
- Aho, A.V.; Ullman, J.D. Translations on a context-free grammar. Inf. Control 1971, 19, 439–475. [Google Scholar] [CrossRef]
- Engelfriet, J.; Heyker, L. The string generating power of context-free hypergraph grammars. J. Comput. Syst. Sci. 1991, 43, 328–360. [Google Scholar] [CrossRef]
- Engelfriet, J.; Rozenberg, G.; Slutzki, G. Tree transducers, L systems, and two-way machines. J. Comput. Syst. Sci. 1980, 20, 150–202. [Google Scholar] [CrossRef]
- Weir, D.J. Linear contex-free rewriting systems and deterministic tree-walking transducers. In Proceedings of the 30th Meeting of the Association for Computational Linguists (ACL’92), Newark, DE, USA, 2–7 August 1992; pp. 136–143.
- Satta, G. Trading independent for synchronized parallelism in finite copying parallel rewriting systems. J. Comput. Syst. Sci. 1998, 56, 27–45. [Google Scholar] [CrossRef]
- Burden, H.; Ljunglöf, P. Parsing linear context-free rewriting systems. In Proceedings of the 9th International Workshop on Parsing Technologies, Vancouver, BC, Canada, 9–10 October 2005.
- Boullier, P. Range concatenation grammars. In New Developments in Parsing Technology; Kluwer Academic Publishers: Dodrecht, The Netherlands, 2004; pp. 269–289. [Google Scholar]
- Kallmeyer, L. Parsing Beyond Context-Free Grammars; Springer: New York, NY, USA, 2010. [Google Scholar]
- Kaji, Y.; Nakanisi, R.; Seki, H.; Kasami, T. The universal recognition problem for multiple context-free grammars and for Linear context-free rewriting systems. IEICE Trans. Inf. Syst. 1992, 75, 78–88. [Google Scholar]
- Satta, G. Recognition of linear context-free rewriting systems. In Proceedings of the 30th Annual Meeting of the Association for Computational Linguistics (ACL’92), Newark, DE, USA, 2–7 August 1992; pp. 89–95.
- Bojańczyk, M. Tree-walking automata. In Proceedings of the Second International Conference on Language and Automata Theory and Applications (LATA’08), Tarragona, Spain, 13–19 March 2008; pp. 1–2.
- Downey, R.G.; Fellows, M.R. Parameterized Complexity; Springer-Verlag: Heidelberg, Germany, 1999. [Google Scholar]
- Flum, J.; Grohe, M. Parameterized Complexity Theory; Springer-Verlag: Heidelberg, Germany, 2006. [Google Scholar]
- Kuhlmann, M. Dependency Structures and Lexicalized Grammars: An Algebraic Approach; Lecture Notes in Computer Science; Springer: New York, NY, USA, 2010; Volume 6270. [Google Scholar]
- Berglund, M.; Björklund, H.; Drewes, F. On the parameterized complexity of linear context-free rewriting systems. In Proceedings of the Mathematics of Language (MOL’13), Sofia, Bulgaria, 9 August 2013; pp. 21–29.
- Abrahamson, K.A.; Downey, R.G.; Fellows, M.R. Fixed-parameter tractability and completeness IV: On completeness for W[P] and PSPACE-analogues. Ann. Pure Appl. Logic 1995, 73, 235–276. [Google Scholar] [CrossRef]
- Abrahamson, K.A.; Downey, R.G.; Fellows, M.R. Fixed-parameter intractability II (Extended abstract). In Proceedings of the 10th Annual Symposium on Theoretical Aspects of Computer Science (STACS’93), Würzburg, Germany, 25–27 February 1993; pp. 374–385.
- Pietrzak, K. A conjecture on the parameterized hierarchy. Notes on a talk given at Dagstuhl Seminar 03311. Unpublished work. 2003. [Google Scholar]
- Björklund, H.; Ericson, P. A note on the complexity of deterministic tree-walking transducers. In Proceedings of the Non-Classical Models of Automata and Applications (NCMA’13), Umea, Sweden, 13–14 August 2013; pp. 69–83.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).