Multivariate Algorithmics for Finding Cohesive Subnetworks

Abstract

Community detection is an important task in the analysis of biological, social or technical networks. We survey different models of cohesive graphs, commonly referred to as clique relaxations, that are used in the detection of network communities. For each clique relaxation, we give an overview of basic model properties and of the complexity of the problem of finding large cohesive subgraphs under this model. Since this problem is usually NP-hard, we focus on combinatorial fixed-parameter algorithms exploiting typical structural properties of input networks.

1. Introduction

Networks, or in mathematical terms, graphs, are the standard tool to model interactions between entities. These entities may stem from virtually every application domain. They may be, for example, proteins that interact physically within a cell [1], people in social networks [2] or websites that are connected via hyperlinks [3]. A standard task in the analysis of these networks is to identify subnetworks that correspond to a cohesive group of entities, also called a community, in the scenario modeled by the network.

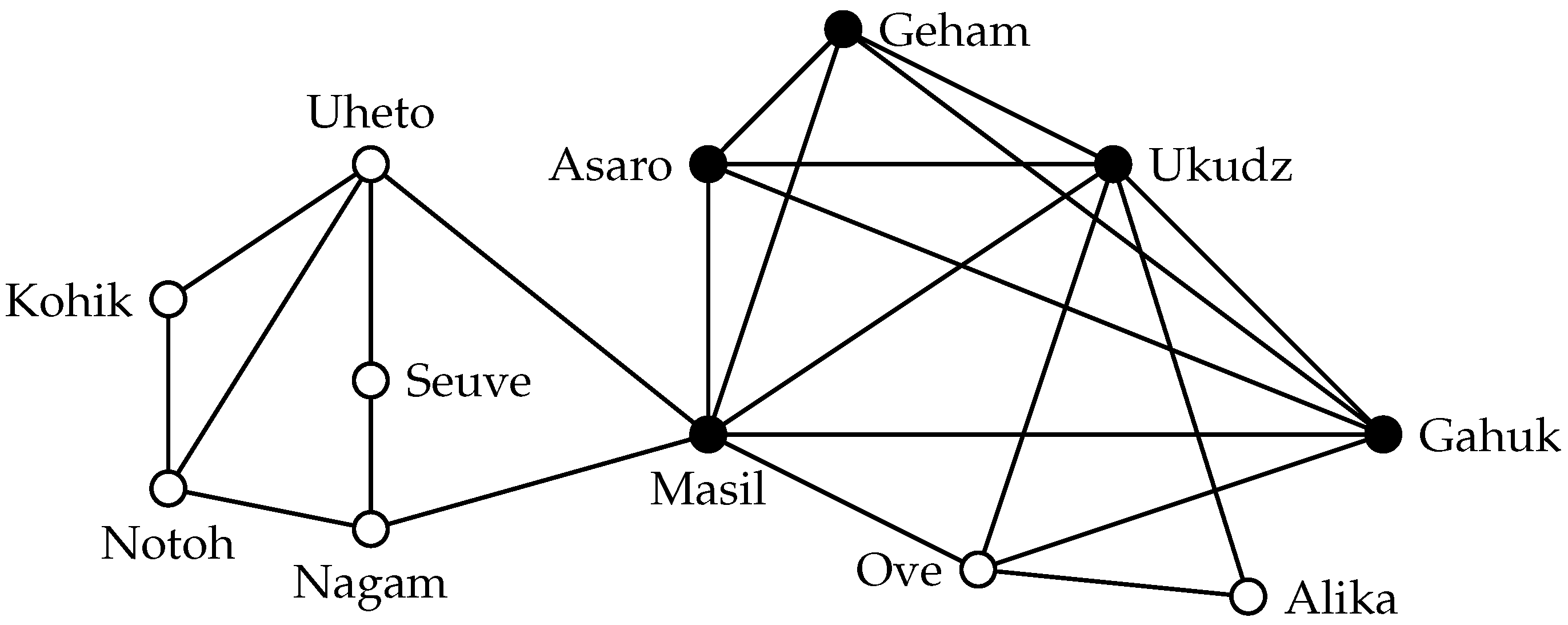
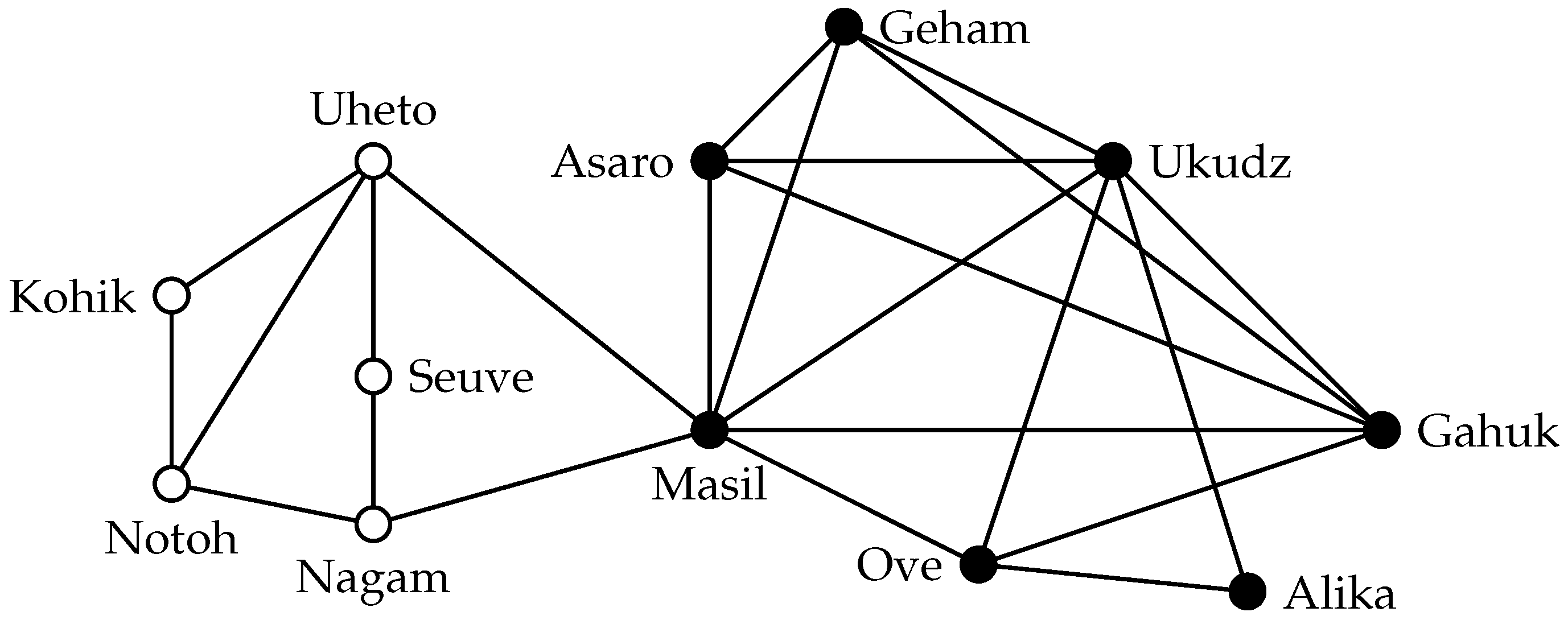
Consider, for example, a group of tribes in the highlands of New Guinea that was studied by Read [4]. To gain an overview of the relationships between these tribes, Read [4] determined in a field study for pairs of tribes whether they have a friendly or hostile relationship and summarized these data in a social network. Figure 1 shows a part of this network where edges signify a friendly relationship between two tribes (we omit the hostile relationships). To better understand the society of the highland tribes, one might be interested in determining whether there are any communities of friendly tribes in this network. The most obvious approach to model such a community is to demand that all members of the community have a friendly relationship. In graph-theoretic terminology, such communities are called cliques.

Definition 1. A set S in a graph $G=(V,E)$ is a clique if each pair of vertices $u,v\in S$ is adjacent.

Assuming that cliques are an appropriate model for communities, by searching for a clique in the network, one may identify a community. Of course, we are not so much interested in cliques that are subsets of other cliques, as the larger clique is more likely to represent a community. Thus, in the community identification scenario, one could aim to find maximal cliques. It is not sufficient to ask for a maximal clique, however. Consider for example the maximal clique formed by “Seuve” and “Nagam”. This clique has only size two, and therefore, it is not a convincing candidate for a community. In contrast, the maximum clique in this graph, which has size five, gives more evidence for the presence of a community of mutually friendly tribes. Thus, to find a good candidate for a community in a given network, one will search for large cliques, which leads to the following computational problem. (For the sake of mathematical precision, we state all problems as decision problems; the positive algorithmic results mentioned in this work usually hold also for the optimization version where the task is to report the largest solution.)

Clique

Input: An undirected graph $G=(V,E)$ and an integer k.

Question: Does G contain a clique of size k?

The maximum clique of the example social network is also shown in Figure 1. Using the clique definition as the community model, this set of vertices would be a predicted community. In most applications, however, using cliques as a community model is inappropriate.

The Clique Model is Usually Too Strict

There are two reasons why this is the case. First, the data collection is usually subject to noise. In the example, this could be the case if the researcher misinterpreted the relationships between some tribes. Thus, even if cliques are the correct model for communities, the real communities will not appear as cliques in the network, because some edges are missing due to noise. The second issue, which cannot be avoided by being more careful in the data collection, is that in many scenarios, it may be allowed that not all members of a community have to interact with each other. In the example network, the “Ove” and “Geham” tribes have no friendly relationship with each other. This is not necessarily a sign of a hostile relationship, but, as a geographic overview over the areas settled by the tribes suggests [4], is simply due to the fact that these two tribes are not geographic neighbors. Nevertheless, these two tribes may belong to the same community, for example because they have friendly relations with all common neighbors. Thus, a community may not necessarily appear as a clique in the network, but it may fulfill certain less strict cohesiveness properties.

Clique Relaxations

To overcome the modeling drawbacks of cliques, one can replace the clique model with a clique relaxation. As the name suggests, this is a model that relaxes one or more clique-defining properties [5]. These are properties that are only fulfilled by cliques. In particular, we consider models relaxing the following clique-defining properties:

Clique definition via vertex degrees: A size-k set S in a graph G is a clique if and only if every vertex $v\in S$ has degree $k-1$ in $G\left[S\right]$, the subgraph induced by S.

Clique definition via diameter: A size-k set S in a graph G is a clique if and only if $G\left[S\right]$ has diameter one, that is, there is a path consisting of one edge between every pair of vertices in S.

Clique definition via density: A size-k set S in a graph G is a clique if and only if $G\left[S\right]$ has $\left(\genfrac{}{}{0pt}{}{k}{2}\right)$ edges.

Clique definition via connectivity: A size-k set S in a graph G is a clique if and only if $G\left[S\right]$ is $(k-1)$-vertex-connected ($(k-1)$-edge-connected), that is, at least $k-1$ vertex deletions (edge deletions) are necessary to transform $G\left[S\right]$ into a disconnected graph or into a graph consisting of only one vertex.

For example, a set S in a graph G is an s-club if $G\left[S\right]$ has diameter s, that is, for every pair $u,v$ of vertices in S, there is a path from u to v in $G\left[S\right]$ that consists of at most s edges. Hence, s-clubs are a clique relaxation that relaxes the clique-defining property of having diameter one.

In this work, we survey different types of clique relaxations; each of the above-mentioned four clique-defining properties will be the focus of one of the four main sections of this work. In particular, we are interested in the computational problems that have to be solved when applying clique relaxations based on these four properties.

Finding Large Cliques is Hard

Apart from the modeling disadvantages, there is a second independent issue that has to be overcome when applying cliques as a community model: Clique is NP-hard [6]. Thus, we expect that every algorithm that solves Clique has superpolynomial running time. Such algorithms can quickly solve small instances, such as the example in Figure 1. In contrast, large instances, such as online social networks or biological networks obtained from high-throughput experiments, cannot be solved within an acceptable amount of time by an algorithm running, for example, in $\Theta \left(2^n\right)$ time (where n denotes the number of vertices in the network). As we will discuss, the issue of computational hardness is not remedied by using clique relaxations instead of cliques: in most cases, the problems that have to be solved when applying clique relaxations are more difficult than Clique. Hence, the modeling advantages of clique relaxations usually come along with additional computational overhead.

The Multivariate Algorithmic Approach to Hard Problems

To cope with large instances of hard problems, different algorithmic paradigms may be followed. For example, one may use approximation or heuristic algorithms, or one may reduce the problem to generic problems, such as ILP (integer linear programming) or SAT, which can be solved using sophisticated ILP or SAT solvers. In this survey, we focus on the approach of multivariate, or parameterized, algorithmics. Here, the idea is to insist on optimal solutions, but to accept exponential running time. The exponential running time may not depend on the overall input size, but only on one or several parameters describing the structural properties of the instance. If these parameters are small in an instance, then the instance can be solved quickly, even if it is large.

We consider the following parameters in this survey.

• The solution size k. We formulate all problems such that solutions are vertex sets, and the task is to determine whether there is a solution of size at least k. In most applications, the solution size is substantially smaller than the number n of vertices in the input graph.
• The “dual” parameter $\ell :=n-k$. This parameter measures the number of vertices to delete so that only the subgraph induced by the solution remains. The value of ℓ is expected to be large compared to k. In some situations, however, the value of ℓ is not much larger or even smaller than k, for example when data reduction has been applied.
• The maximum degree Δ of G. While many real-world networks, for example social networks, have a large maximum degree Δ, the value of Δ is still much smaller than n in most cases.
• The degeneracy d of G. The degeneracy of a graph G is the smallest integer d such that every subgraph of G has at least one vertex whose degree is at most d. This number is upper-bounded by the maximum degree, and in most real-world networks, it is much smaller than Δ.
• The h-index of G [7]. The h-index of a graph G is the maximum number h such that G has at least h vertices with degree at least h. The value of the h-index is sandwiched between the degeneracy and the maximum degree of a graph.

The theme of this survey will be to inspect the computational problems involved in applying different types of clique relaxations from the viewpoint of multivariate algorithmics. For each problem, we survey the known tractability and intractability results with respect to the above-mentioned parameters. To give a comprehensive picture of the current knowledge, we also state new tractability and intractability results whenever they follow from simple observations. Maybe most importantly, we then identify concrete open questions and open topics for future research. In the conclusion, we give a condensed overview of the considered clique relaxations and the corresponding complexity results.

1.1. Related Work

The computational problems related to clique relaxations have attracted a considerable amount of interest over the last few years. Consequently, there is a large number of works dealing with different aspects of these problems. It is beyond the scope of this work to survey all results for clique relaxations. Fortunately, a number of surveys already provides a comprehensive overview, for example of classic complexity results and approximation algorithms.

Kosub [8] reviews different models of locally dense groups in networks and describes some model properties and different algorithmic approaches to find occurrences of these models in networks.

A survey by Balasundaram and Pajouh [9] gives an overview of NP-hardness results and approximation hardness results for different clique relaxations. Moreover, for some clique relaxations, integer programming formulations of the corresponding computational problems are given. In this context, useful properties of the incidence polytopes of several clique relaxations are also described.

A historical account of the development of the area of clique relaxations, describing for example the order in which the single concepts were proposed, is given by Pattillo et al. [5]. This survey also proposes a taxonomy of clique relaxations that may be used, for example to systematically derive new potentially interesting clique relaxations. We follow the systematic distinction between relative and absolute relaxation proposed by Pattillo et al. [5]. In this distinction, relative relaxations feature a parameter $\gamma \in [0,1]$; absolute relaxations feature a parameter $s\in \mathbb{N}$; and setting $\gamma =1$ or $s=1$ gives the clique definition.

It should be noted that there are some models of dense or cohesive graphs where the problem of finding a largest subgraph fulfilling the model requirements is solvable in polynomial time. Examples are s-cores [10] (subgraphs that have minimum degree s), s-trusses [11] (subgraphs in which every edge is contained in at least s triangles) and densest subgraphs [12] (subgraphs of maximum average degree). For these models, the quantity described by the cohesiveness requirement is usually size independent. As a consequence, the larger the respective subgraph, the less cohesive it may be. For example, any cycle is a 2-core, and the larger the cycle, the less cohesive it is.

1.2. Preliminaries

In this section, we first describe the notation and present some basic graph-theoretic definitions used throughout this work. Then, we give a very brief introduction to multivariate algorithmics, in particular to the complexity-theoretic framework used to show intractability. Finally, we discuss the multivariate complexity of Clique with respect to the parameters under consideration in this survey.

Notation, Basic Definitions and Basic Results

We consider undirected graphs $G=(V,E)$ where V is the vertex set and $E\subseteq \left\{\right\{u,v\}\mid u,v\in V\}$ is the edge set of the graph. We let $n:=\left|V\right|$ and $m:=\left|E\right|$ denote the number of vertices and edges in the graph G, respectively. The (open) neighborhood of a vertex v is denoted by $N\left(v\right):=\{u\mid \{u,v\}\in E\}$ and the closed neighborhood by $N\left[v\right]:=N\left(v\right)\cup \left\{v\right\}$. For a vertex set $S\subseteq V$; let $G\left[S\right]:=(S,\{\{u,v\}\in E\mid u,v\in S\left\}\right)$ denote the subgraph of G induced by S. For a vertex set $S\subseteq V$, let $G-S:=G[V\setminus S]$ denote the induced subgraph of G obtained by deleting the vertices of S and their incident edges. Similarly, for a vertex $v\in V$, let $G-v:=G-\left\{v\right\}$ denote the graph obtained by deleting this vertex and all its incident edges.

A vertex set $D\subseteq V$ in a graph $G=(V,E)$ is dominating if every vertex of G is either contained in D or has a neighbor in D. The complement graph $\overline{G}$ of a graph $G=(V,E)$ is $(V,\{\{u,v\}\mid u,v\in V\wedge u\ne v\wedge \{u,v\}\notin E\left\}\right)$. For two vertices u and v in a graph G, let ${dist}_G(u,v)$ denote the length (that is, the number of edges) of a shortest path between u and v in G. The diameter of a graph is the maximum value of ${dist}_G(u,v)$ over all $u,v\in V$. The k-th power of a graph $G=(V,E)$ is the graph $G^k:=(V,\{\{u,v\}\mid u\ne v\wedge {dist}_G(u,v)\le k\})$. The closed k-neighborhood of a vertex v in a graph G is the set $N_k\left[v\right]:=\{u\in V\mid {dist}_G(u,v)\le k\}$.

Formally, clique relaxations are vertex sets fulfilling certain properties in a graph, and thus, they are closely related to graph properties. (Most clique relaxations can be defined either as graphs or as vertex sets within some graph. One exception are s-cliques discussed in Section 3. To make the definitions coherent, we use definitions based on vertex sets.) An important feature of a graph property is whether or not it is closed under vertex deletion.

Definition 2. A graph property Π is hereditary if for every graph $G=(V,E)$ fulfilling Π and every vertex $v\in V$, the graph $G-v$ also fulfills Π.

We extend this definition to vertex sets S in the natural way, that is, a property on vertex sets is hereditary if the following holds: if a set $S\subseteq V$ fulfills the property, then so does every $S^{\prime }\subseteq S$. Many graph properties tied to clique relaxations are hereditary. Thus, from the following classic result on vertex deletion problems, we can directly infer the NP-hardness of many problems related to clique relaxations.

Theorem 1 

([13]). For every nontrivial hereditary graph property Π, the problem of deciding whether at most ℓ vertices can be deleted from a graph G to obtain a graph $G^{\prime }$ that fulfills Π is NP-hard.

Hereditary graph properties allow for the deletion of any vertex. A weaker, but still useful feature of graph properties is being quasi-hereditary, also called nested [8].

Definition 3. A graph property Π is quasi-hereditary if for every graph $G=(V,E)$ fulfilling Π, there is a vertex $v\in V$, such that the graph $G-v$ also fulfills Π.

The following is based on an algorithm that enumerates all connected subgraphs of order k in degree-bounded graphs [14]. For the sake of completeness, we give a short proof.

Proposition 1. 

Let Π be a graph property such that:

• all graphs in Π are connected,
• containment in Π can be tested in polynomial time and
• all graphs $H=(W,F)$ with maximum degree Δ and property Π fulfill $\left|W\right|\le c·\Delta$ for some constant c depending only on Π.

Then, in ${\Delta }^{O(\Delta )}·n^{O\left(1\right)}$ time, we can determine whether a graph G with maximum degree Δ contains a subgraph from Π of order at least k.

Proof. 

Use the following algorithm. If $k>c·\Delta$, then output “no”. Otherwise, for each value of $k^{\prime }$ such that $k\le k^{\prime }\le c·\Delta$, enumerate all connected induced subgraphs of G in ${\Delta }^{O\left(k^{\prime }\right)}·n$ time [14]. For each enumerated subgraph, check whether it fulfills Π. If this is the case, then output “yes”. If none of the enumerated connected subgraphs fulfill Π, then output “no”. The running time bound follows from $k^{\prime }\le c·\Delta$, the time bound for enumerating all connected subgraphs and from the fact that property Π can be checked in polynomial time.   □

Multivariate Algorithmics

Parameterized and multivariate algorithmics aim at a refined complexity analysis of hard computational problems [15,16]. To this end, each input I is equipped with an additional parameter p, usually a nonnegative integer. The central idea is to exploit situations in which the value of the parameter p is small. This is captured by the central definition in parameterized algorithmics.

Definition 4. A parameterized problem L is fixed-parameter tractable if every instance $(I,p)$ of L can be solved in $f\left(p\right)·{\left|I\right|}^{O\left(1\right)}$ time, where f is a computable function depending only on p.

Algorithms that achieve such a running time are called fixed-parameter algorithms. The idea behind the definition is that for small values of p, the problem can be solved efficiently as the exponential part of the running time depends only on k. In the context of parameterized algorithmics, the term multivariate refers to the fact that there is not only one interesting parameter, but that several different parameters and combinations of parameters may be potentially interesting [17,18].

Of course, not all parameterized problems are fixed-parameter tractable. This is obvious for problems that are NP-hard for constant parameter values, such as SAT with the parameter clause size. There are, however, also problems that can be solved in polynomial time for every constant parameter value (that is, in ${\left|I\right|}^{f\left(k\right)}$ time for some computable f), but that resist any attempts to devise fixed-parameter algorithms. There are two complexity-theoretic assumptions that are used to show that fixed-parameter algorithms are unlikely for such problems.

Downey and Fellows [15] developed a theory of parameterized intractability by defining the so-called W-hierarchy of problems that are unlikely to be fixed-parameter tractable. The basic class of intractability is W[1], that is, the central conjecture is $\mathrm{W}\left[1\right]\ne \mathrm{FPT}$ where $\mathrm{FPT}$ is the class of fixed-parameter tractable problems. Thus, if a problem is $\mathrm{W}\left[1\right]$-hard, it is unlikely to be fixed-parameter tractable; $\mathrm{W}\left[1\right]$-hardness of a parameterized problem L can be shown via a parameterized reduction from a $\mathrm{W}\left[1\right]$-hard problem $L^{\prime }$; for a definition of parameterized reduction, refer to [15,16].

For the problem of finding large subgraphs fulfilling a hereditary graph property Π, there exists the following general $\mathrm{W}\left[1\right]$-hardness result.

Theorem 2 

([19]). Let Π be a hereditary graph property that does not contain all independent sets. Then, given an undirected graph $G=(V,E)$ and integer k, deciding whether there is a size-k set $S\subseteq V$ such that $G\left[S\right]\in \Pi$ is W[1]-hard with respect to k.

Since any sensible clique relaxation has to exclude independent sets that are too large, Theorem 2 applies if the property of the clique relaxation is hereditary.

More fine-grained running time lower bounds can be achieved via assuming the so-called exponential-time hypothesis (ETH) [20]. The ETH states that 3-SAT cannot be solved in $2^{o\left(n\right)}$ time, where n is the number of variables in the input formula. The ETH implies $\mathrm{W}\left[1\right]\ne \mathrm{FPT}$, but the converse is not known to be true. Consequently, the ETH can be regarded as a stronger assumption. An even stronger assumption that yields even more refined running time bounds is the strong exponential-time hypothesis (SETH), which essentially states that CNF-SAT cannot be solved in ${(2-ϵ)}^n·{\left|I\right|}^{O\left(1\right)}$ time for any $ϵ>0$ [20].

The Clique Problem from the Viewpoint of Multivariate Algorithmics

Let us quickly review the complexity of Clique with respect to the parameters defined above: the clique size k, the dual parameter $\ell :=n-k$, and the maximum degree Δ, degeneracy d and h-index of G. The natural parameter for Clique is the size k of the clique. For this parameter, Clique is W[1]-hard [15]; in fact, Clique is the most prominent $\mathrm{W}\left[1\right]$-hard problem. Thus, it is unlikely that Clique can be solved in $f\left(k\right)·n^{O\left(1\right)}$ time. Moreover, assuming the ETH, even an $n^{o\left(k\right)}$-time algorithm for Clique is impossible [21].

For the dual parameter $\ell :=n-k$, the situation is better. In terms of the dual parameter, the Clique problem is to find a set C of at most ℓ vertices of V such that for every nonadjacent pair $\{u,v\}$ of vertices in V, at least one of u and v is in C. This is exactly the Vertex Cover problem in the complement graph $\overline{G}$ of G, parameterized by the size ℓ of the vertex cover. Therefore, Clique parameterized by ℓ can be solved in $O(1.{28}^k+n^2)$ time by constructing the complement graph and then using the currently best fixed-parameter algorithm for Vertex Cover [22]. This approach, when combined with other techniques, such as the degeneracy-ordering described below, efficiently solves Clique in biological, financial and social networks [23,24].

For degree-based parameterizations, the complexity picture of Clique is also quite positive: Clique is fixed-parameter tractable with respect to the degeneracy d of G. This result is easily obtained by the fact that every clique is completely contained in the closed neighborhood of any of its vertices. Thus, a simple fixed-parameter algorithm for Clique and the degeneracy parameter d is the following. While G is not empty, pick a vertex v of minimum degree in G. By the definition of degeneracy, we have $deg\left(v\right)\le d$. Now, check for each $S\subseteq N\left(v\right)$ whether $S\cup \left\{v\right\}$ is a clique of size at least k. If this is the case, then output $S\cup \left\{v\right\}$. Otherwise, continue with $G-v$, that is, delete v from the input graph. The overall number of subsets to investigate is at most $2^d·n$. Since d is often very small, this simple algorithm can serve as a basis for efficient Clique algorithms. The approach based on degeneracy can also be used to enumerate all maximal cliques in $O(3^{d/3}·n)$ time [25].

2. Degree-Based Clique Relaxations

In a clique S, every vertex v of S is adjacent to all other vertices of S, that is, it has degree $\left|S\right|-1$ in $G\left[S\right]$. This is the strongest possible requirement on the degrees of the vertices in $G\left[S\right]$. In degree-based clique relaxations, one still requires that the vertices have a certain minimum degree, but the requirement is less strict.

2.1. Absolute Relaxation of the Maximum Degree: s-Plexes

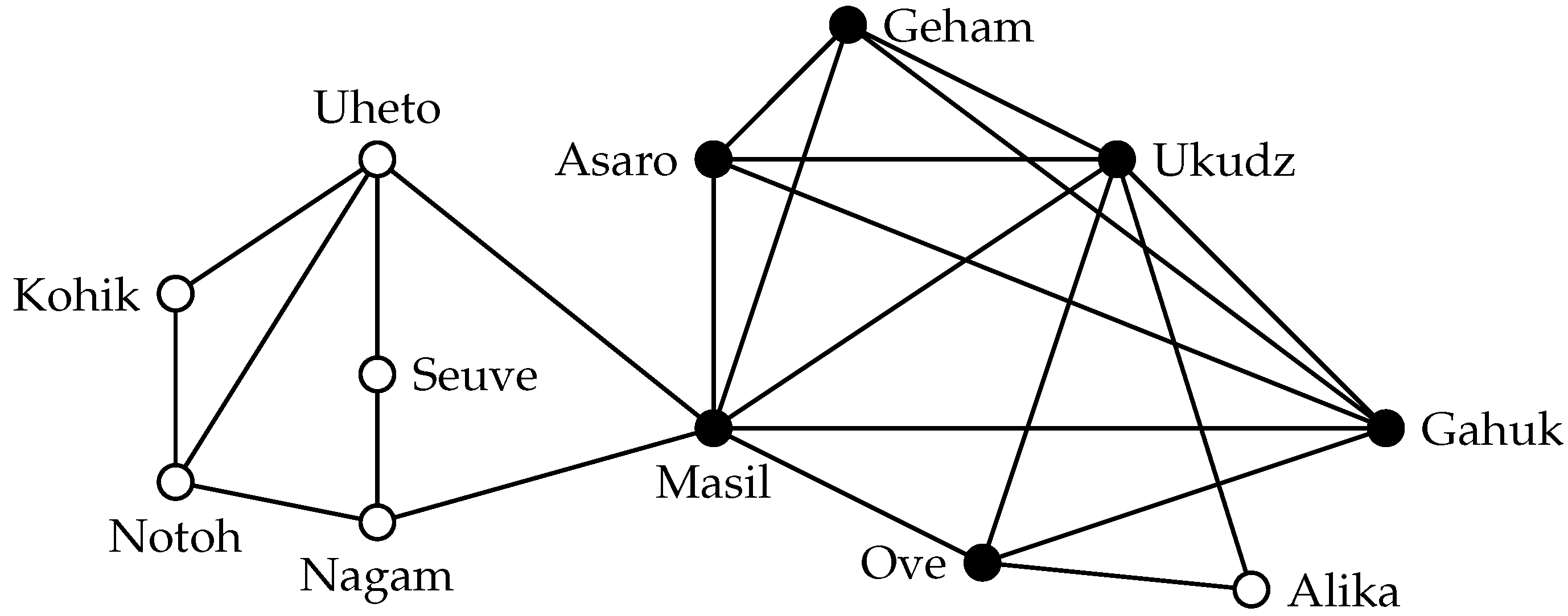
A natural idea is to relax the clique definition by allowing for each vertex of S a fixed number of non-neighbors in S.

Definition 5. A set $S\subseteq V$ is an s-plex in a graph $G=(V,E)$ if every vertex in $G\left[S\right]$ has degree at least $\left|S\right|-s$.

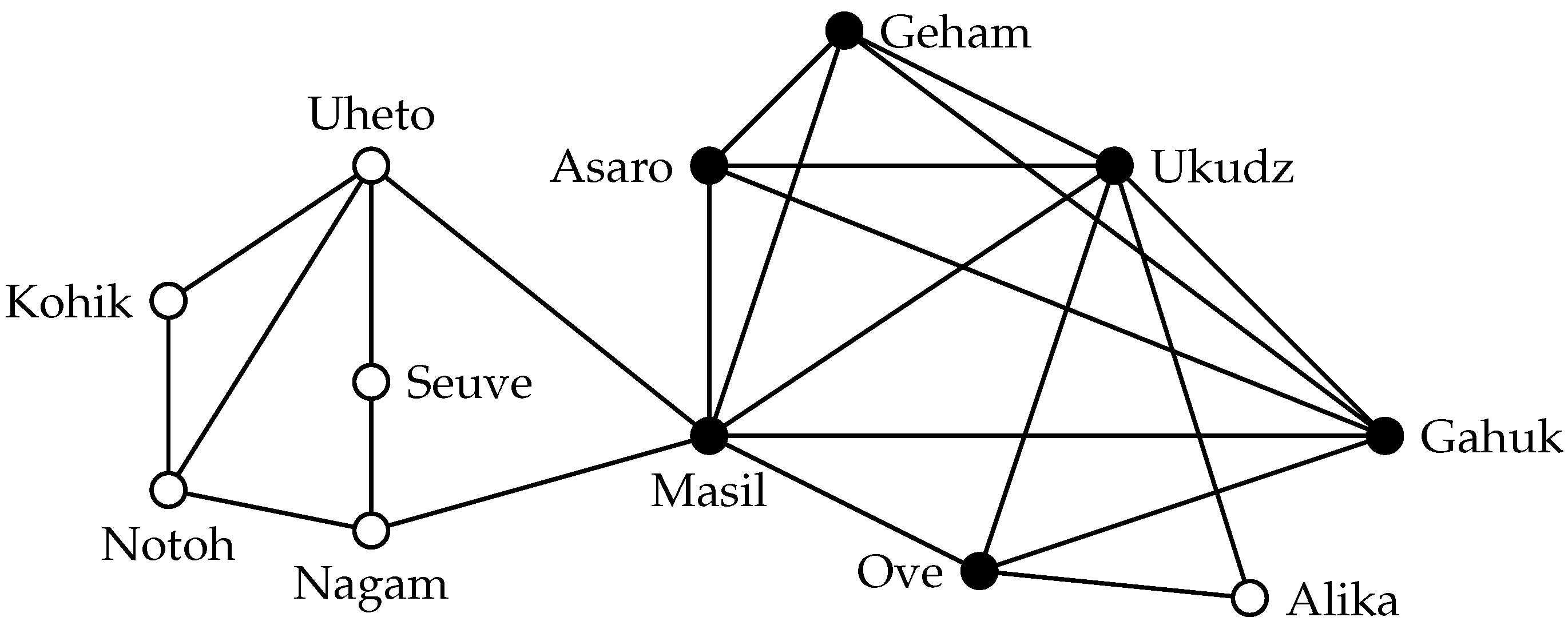
This clique relaxation was introduced by Seidman and Foster [26]. An equivalent definition is that a set S is an s-plex if and only if every set of s vertices of S is a dominating set in $G\left[S\right]$ [26]. Figure 2 shows the maximum-cardinality 3-plex in the highland tribes example. This 3-plex is a proper superset of the maximum clique, and thus, it represents a cohesive group with additional members (that would be missing from an analysis solely based on the clique definition). The property of being an s-plex is hereditary: deleting a vertex v from an s-plex may reduce the degree of every other vertex by at most one; at the same time, it decreases the number of vertices by one. The structural properties of s-plexes are influenced by the relation between the size k of an s-plex and s. For example, every graph of order at most $s+1$ is an s-plex. In contrast, if $s<k/2+1$, then $G\left[S\right]$ has diameter two [26]. This is of course a desirable property for cohesive groups.

As for Clique, we are interested in the problem of finding large s-plexes.

$\mathit{s}$-Plex

Input: An undirected graph G and an integer k.

Question: Does G contain an s-plex S of size at least k?

Since the s-plex property is hereditary, Theorem 1 implies that s-Plex is NP-hard. Let us thus inspect the multivariate complexity picture for s-Plex. The first, obvious, parameter to consider is the solution size k. Here, fixed-parameter algorithms are unlikely: for every fixed s, s-Plex is W[1]-hard for the parameter k. This follows from Theorem 2 and from a simple parameterized reduction from Clique [27]. This reduction reduces Clique instances in which we search for a clique of size at least k to s-Plex instances in which we search for an s-plex of size at least $s·k$. Thus, for every constant s, an $n^{o\left(k\right)}$-time algorithm for s-Plex implies an $n^{o\left(k\right)}$-time algorithm for Clique, which violates the ETH. Summarizing, as for Clique, we cannot really exploit the solution size parameter, and one should search for different parameters or parameter combinations.

Fortunately, positive results can be obtained for the dual parameter $\ell :=n-k$ by generalizing the reduction of Clique to Vertex Cover described in Section 1.2. For Clique, the observation is that every clique is an independent set in the complement graph. Similarly, an s-plex has bounded degree in the complement graph: a vertex set S is an s-plex in G if and only if $\overline{G}\left[S\right]$ has maximum degree at most $s-1$. Thus, after transforming the input graph G to its complement graph $\overline{G}$, we have to determine whether we can delete at most ℓ vertices in $\overline{G}$ to obtain a graph with maximum degree at most $s-1$. This can be easily determined in ${(s+1)}^{\ell }·n^{O\left(1\right)}$ time by a search tree algorithm that explores all possibilities to destroy subgraphs containing a vertex of degree at least s [27]. This algorithm is a fixed-parameter algorithm for the combined parameter $(s,\ell )$. Improving this to an $f\left(\ell \right)·n^{O\left(1\right)}$-time algorithm, that is, to a fixed-parameter algorithm only for the parameter ℓ, is unlikely: s-Plex is W[2]-hard for the parameter ℓ if s is part of the input [28].

The usefulness of the fixed-parameter algorithms based on the combined parameter $(s,\ell )$ was also confirmed experimentally for $s=2$ and $s=3$ [29]. Other approaches based on branch and cut [30] and on combinatorial algorithms [31] have roughly comparable performance. The current-best algorithm for s-Plex is also based on a combinatorial search tree algorithm, which exploits that the s-plex property is hereditary [32].

Degree-based parameterizations of s-Plex have not been considered so far. For the parameter maximum degree Δ of G, a fixed-parameter algorithm can be easily obtained when s is also part of the parameter. First, the range of interesting values of k is bounded in $\Delta +s$.

Observation 1. Any s-plex in a graph with maximum degree Δ has size at most $\Delta +s$.

Consequently, instances where $k>\Delta +s$ can be rejected immediately. Afterwards, any algorithm running in $f(\Delta ,k)·n^{O\left(1\right)}$ time is also a fixed-parameter algorithm for the parameter $(\Delta ,s)$. If we are interested only in connected s-plexes, then Proposition 1 can be directly applied. Otherwise, the algorithm is more complicated, but by applying a generic algorithm [14] (Theorem 4), one obtains a ${\Delta }^{O(\Delta +s)}·n$-time algorithm for s-Plex. (To check that [14] (Theorem 4) applies to s-Plex, it is sufficient to formulate s-Plex as an optimization problem satisfying certain criteria. We omit the straightforward proof.)

Proposition 2. 

s-Plex is fixed-parameter tractable with respect to the parameter $(\Delta ,s)$.

There are two ways of improving this observation. Obviously, one should try to improve the running time. For example, is a running time of $2^{O(\Delta +s)}·n^{O\left(1\right)}$ possible? Maybe it would be more relevant in applications to improve the parameterization, that is, to obtain fixed-parameter algorithms for the smaller parameters h-index of G or degeneracy of G. Given the small value of the degeneracy d in practice, parameterization by d seems particularly promising. The following tractability result can be easily obtained.

Proposition 3. 

s-Plex can be solved in $2^d·n^{O\left(s\right)}$ time.

Proof. 

Use the following algorithm. Pick a vertex v of G that has degree at most d. Determine whether there is an s-plex S of order at least k containing v by trying all possibilities for $S\cap N\left(v\right)$ (there are $O\left(2^d\right)$ many) and all possibilities for $S\setminus N\left[v\right]$ (there are $O\left(n^{s-1}\right)$ many). For each combination, check in polynomial time whether it is an s-plex. If no s-plex has been found, then continue with $G-v$.   □

Thus, for constant s, we achieve a fixed-parameter algorithm for the degeneracy parameter d. Since n is very large in many applications, the $n^{O\left(s\right)}$ term is, however, prohibitive in many practical settings already for $s=3$. A more efficient algorithm running in $f(d,s)·n^{O\left(1\right)}$ time is thus highly desirable.

Open Question 1. Is s-Plex fixed-parameter tractable with respect to the parameter $(d,s)$ where d is the degeneracy of the input graph G?

A positive answer to this question could provide a sizable step towards efficient fixed-parameter algorithms for many real-world instances of s-Plex.

2.2. Relative Relaxation of the Maximum Degree: γ-Complete Graphs

In s-plexes, we relax the degree condition of cliques by an absolute amount of $s-1$. It is just as natural to specify the amount of relaxation in a relative way, that is, to demand that each vertex of the set is adjacent to a large fraction of the set.

Definition 6. A vertex set S is γ-complete, $0\le \gamma \le 1$, if every vertex in $G\left[S\right]$ has degree at least $\gamma ·\left(\right|S|-1)$. The graph $G\left[S\right]$ is called a γ-complete graph.

The model of γ-complete graphs was introduced several times [33,34]. Sometimes, γ-complete graphs are also referred to as γ-quasi-cliques [35], but the term quasi-clique is more common in density-based clique relaxations (see Section 4). The 3-plex shown in Figure 2 is also a maximum $0.6$-complete set in this network. In contrast to s-plexes, the property of being γ-complete is not hereditary. Removing for example “Gahuk” from the group gives a $0.5$-complete set that is not $0.6$-complete. Moreover, the γ-completeness property is not even quasi-hereditary: Consider a cycle on five vertices. This graph is $0.5$-complete. Deleting any vertex in this graph gives a path on four vertices. This graph is not $0.5$-complete, as its degree-one vertices have too low a degree. If we consider only sets of a fixed size k, then there is a direct correspondence between γ-complete sets and s-plexes: setting s to the largest integer such that $k-s\ge \gamma (k-1)$, makes the definitions equivalent.

When applying γ-complete sets in community detection, we have to solve the following problem.

$\mathbf{\gamma }$-Complete Graph

Input: An undirected graph G and an integer k.

Question: Does G contain a γ-complete set S of size at least k?

Quite surprisingly, γ-Complete Graph has received much less attention than s-Plex. Since γ-completeness is not hereditary, Theorem 1 does not apply. From a complexity-theoretic perspective, it is known that γ-Complete Graph is NP-hard for $\gamma =0.5$ [33]. A study of the complexity of γ-Complete Graph for all possible values of γ is clearly desirable. Moreover, a multivariate complexity analysis is also lacking. This leads us to the first open topic.

Open Topic 1. Perform a multivariate complexity analysis for γ-Complete Graph for all values of γ.

Similar to the case of s-Plex, the first tractability result for the parameter maximum degree Δ can be obtained by observing that for fixed γ, γ-complete sets cannot be too large compared to Δ.

Observation 2. Any γ-complete set in a graph with maximum degree Δ has size at most $\Delta /\gamma +1$.

Thus, one may again reject instances where k is too big. Afterwards, for each $k^{\prime }\in [k,\Delta /\gamma +1]$, we may solve γ-Complete Graph by solving s-Plex with the appropriate s, as described above. Since $s<k^{\prime }\le \Delta /\gamma +1$, we immediately obtain the following.

Proposition 4. 

γ-Complete Graph is fixed-parameter tractable with respect to the parameter $(\Delta ,\gamma )$.

This just indicates that interesting tractability results are possible for γ-Complete Graph. Obtaining them for smaller parameters, such as the degeneracy of G, would be clearly desirable. We mention in passing that for $\gamma \ge 0.5$, there are close connections to connectivity-based clique relaxations, which we discuss in Section 5.

3. Distance-Based Clique Relaxations

In a clique S, every pair of vertices has distance one in G or, equivalently, the graph $G\left[S\right]$ has diameter one. This requirement can be relaxed by allowing that members of a group are connected via short paths of length two or more. For these paths, one may in addition distinguish whether or not they may contain vertices that are not part of the group.

3.1. Induced Subgraphs with a Small Diameter: s-Clubs

Demanding that all vertices of the group are connected by short paths within the group is equivalent to demanding that the graph induced by the group has a low diameter.

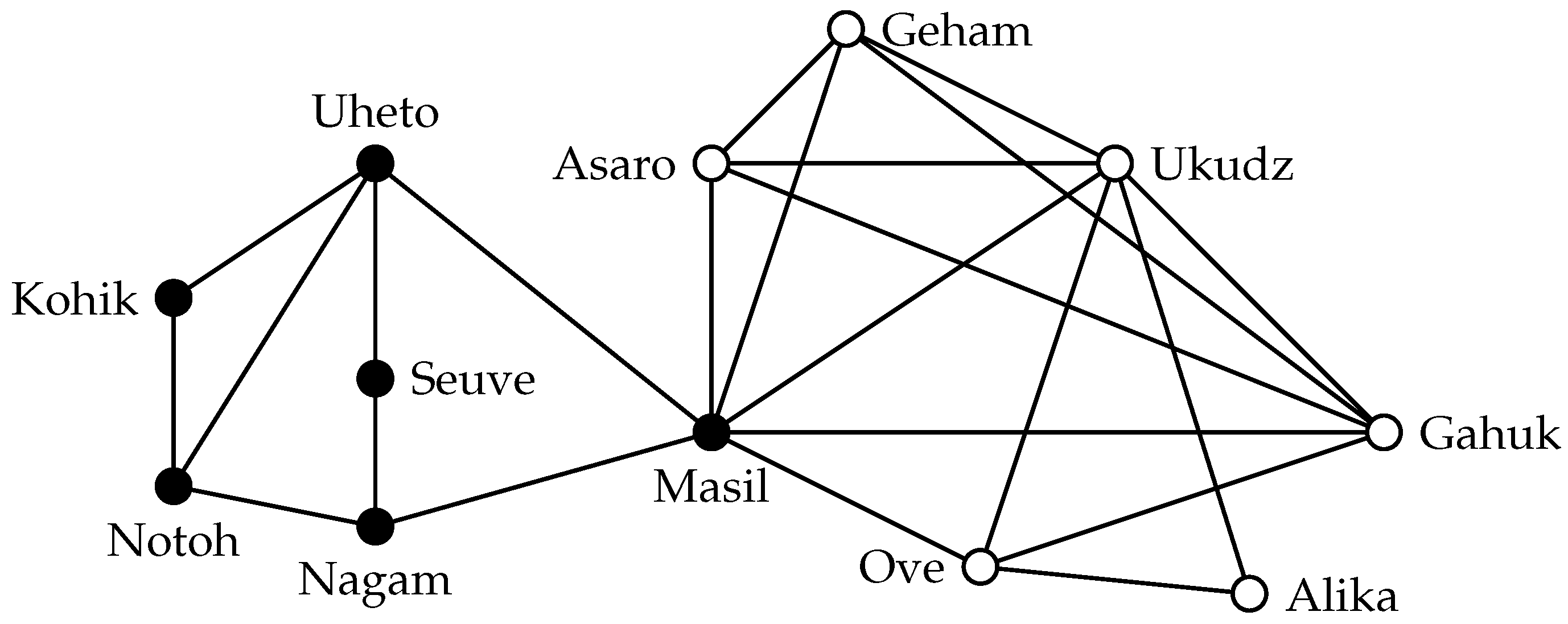
Definition 7. A set $S\subseteq V$ is an s-club in a graph $G=(V,E)$ if $G\left[S\right]$ has diameter at most s.

The first definition of a clique relaxation that demands short paths in the induced subgraph was given by Alba [36], who introduced the concept of sociometric clique. The notion of s-club as it is stated here was introduced by Mokken [37]. An example of a maximal 2-club is shown in Figure 3. The s-club property is not hereditary: removing “Uheto” in the illustrated 2-club results in a set whose induced subgraph has diameter three. Further examples for the nonhereditary nature of s-clubs are trees of diameter s: here, a vertex deletion may even destroy connectivity. Moreover, s-club is not even quasi-hereditary. Consider for example a $C_5$, a cycle on five vertices. Deleting any vertex in this graph results in a path on four vertices, which has diameter three. Finally, the example of star graphs shows that there are very sparse 2-clubs. Hence, one may not expect that there are many connections within an s-club. We are interested in the problem of finding large s-clubs in a graph.

$\mathit{s}$-Club

Input: An undirected graph G and an integer k.

Question: Does G contain an s-club of size at least k?

The fact that the s-club property is not quasi-hereditary implies that asking for an s-club of size exactly k is not equivalent: a graph may contain no s-club of size exactly k even if it contains an s-club of size $k+1$.

For every $s>1$, s-Club is NP-hard [38], even when the input graph has diameter $s+1$ [39]. For $s=1$, s-Club is equivalent to Clique and, thus, W[1]-hard with respect to the solution size k. In contrast, s-Club is fixed-parameter tractable with respect to k for all $s>1$ [40,41,42]. There are two possible routes to obtain a fixed-parameter algorithm. Both rely on the following observation, where $N_{\delta }\left[v\right]$ denotes the set of vertices that have distance at most δ to v.

Observation 3. For every vertex v, the set $N_{\lfloor s/2\rfloor }\left[v\right]$ is an s-club.

Hence, if $|N_{\lfloor s/2\rfloor }\left[v\right]|\ge k$ for some vertex v, then $N_{\lfloor s/2\rfloor }\left[v\right]$ is a valid solution of the problem. Otherwise, one may search for a maximum-cardinality s-club by inspecting for each vertex v the graph $G\left[N_s\left[v\right]\right]$: if v is contained in the maximum s-club S, then $S\subseteq N_s\left[v\right]$. Now, since $|N_{\lfloor s/2\rfloor }\left[v\right]|\le k$, the size of $N_s\left[v\right]$ is $O\left(k^2\right)$ for even s and $O\left(k^3\right)$ for odd s [40,41,42]. Thus, finding the maximum-cardinality s-clubs in these n many sets, for example by a brute-force algorithm, gives a fixed-parameter algorithm for s-Club and the parameter k.

The second approach works for the variant of s-Club, where we ask to find an s-club of size exactly k, and is based on a special case of Observation 3. More precisely, it exploits the fact that for every vertex v, $N\left[v\right]$ is a 2-club. Hence, any graph with maximum degree Δ has an s-club of size $\Delta +1$. As a consequence, s-Club is nontrivially posed only if $k>\Delta +1$. In this case, enumerating all connected induced subgraphs on at most k vertices, which can be done in ${(e·(\Delta -1))}^k·n^{O\left(1\right)}$ time [14], is possible in ${\left(ek\right)}^k·n^{O\left(1\right)}$ time. Since s-clubs are connected, all that remains to be done is to check the s-club property for each enumerated induced subgraph in polynomial time. It is open to improve the worst-case running time substantially or to show a running time lower bound.

Open Question 2. Is it possible to determine in $2^{O\left(k\right)}·n^{O\left(1\right)}$ time whether a graph G has an s-club of size exactly k?

This question is open already for $s=2$. Clearly, it would also be desirable to obtain good running time bounds for the definition of s-Club as stated above, where we aim to find an s-club of size at least k.

For the dual parameter $\ell :=n-k$, an efficient fixed-parameter algorithm for s-Club is achievable [41]. This algorithm is based on the fact that if V is not an s-club, then there are two vertices u and v in G that have distance at least $s+1$. One of these two vertices cannot belong to S. Thus, one may search recursively for an s-club of size at least k in $G-v$ and in $G-u$. In both recursive calls, n decreases by one, and since k remains the same, ℓ decreases by one, as well. Since recursion can be stopped if $n<k$, the search tree created by this branching procedure has size $O\left(2^{\ell }\right)$ leading to an overall running time of $O(2^{\ell }·nm)$ [41]. An obvious goal would be to improve this algorithm, but assuming the SETH, a running time of ${(2-ϵ)}^{\ell }·n^{O\left(1\right)}$ is impossible [43]. Despite this running time lower bound, the search tree algorithm based on the parameter ℓ yields the current-best solver for the 2-Club problem [43]. For $s>3$, a systematic experimental study of this parameterization is lacking.

Open Topic 2. Perform an experimental study of the $2^{\ell }$-search tree algorithm for $s>3$.

It is easy to observe fixed-parameter tractability for the combined parameter $(\Delta ,s)$: As mentioned above, we may find a maximum s-club by inspecting for each vertex $v\in V$ the graph $G\left[N_s\left[v\right]\right]$. As witnessed by a breadth-first search tree algorithm that constructs $N_s\left[v\right]$, we have $|N_s\left[v\right]|=O\left({\Delta }^s\right)$, and thus, a brute-force algorithm solving each inspected graph gives a running time of $2^{O\left({\Delta }^s\right)}·n^{O\left(1\right)}$. This running time guarantee is not useful in practice, and it would be much more desirable to obtain an algorithm that makes better use of the fact that the maximum degree is bounded.

Open Question 3. Can s-Club be solved in $2^{{\Delta }^{o\left(s\right)}}·n^{O\left(1\right)}$ time? Is s-Club fixed-parameter tractable with respect to Δ for unbounded s?

Another possible improvement would be to consider the smaller degree-related parameters h-index and degeneracy. For these parameters, however, tractability results are unlikely: The 2-Club problem is W[1]-hard with respect to the h-index of G and NP-hard even if G has degeneracy six [44]. We would expect that s-Club with $s>2$ is at least as hard as 2-Club with respect to these parameters.

3.2. Sets of Vertices Connected by Short Paths: s-Cliques

In a related clique relaxation, it is allowed that the short paths between group members use vertices that are not part of the group.

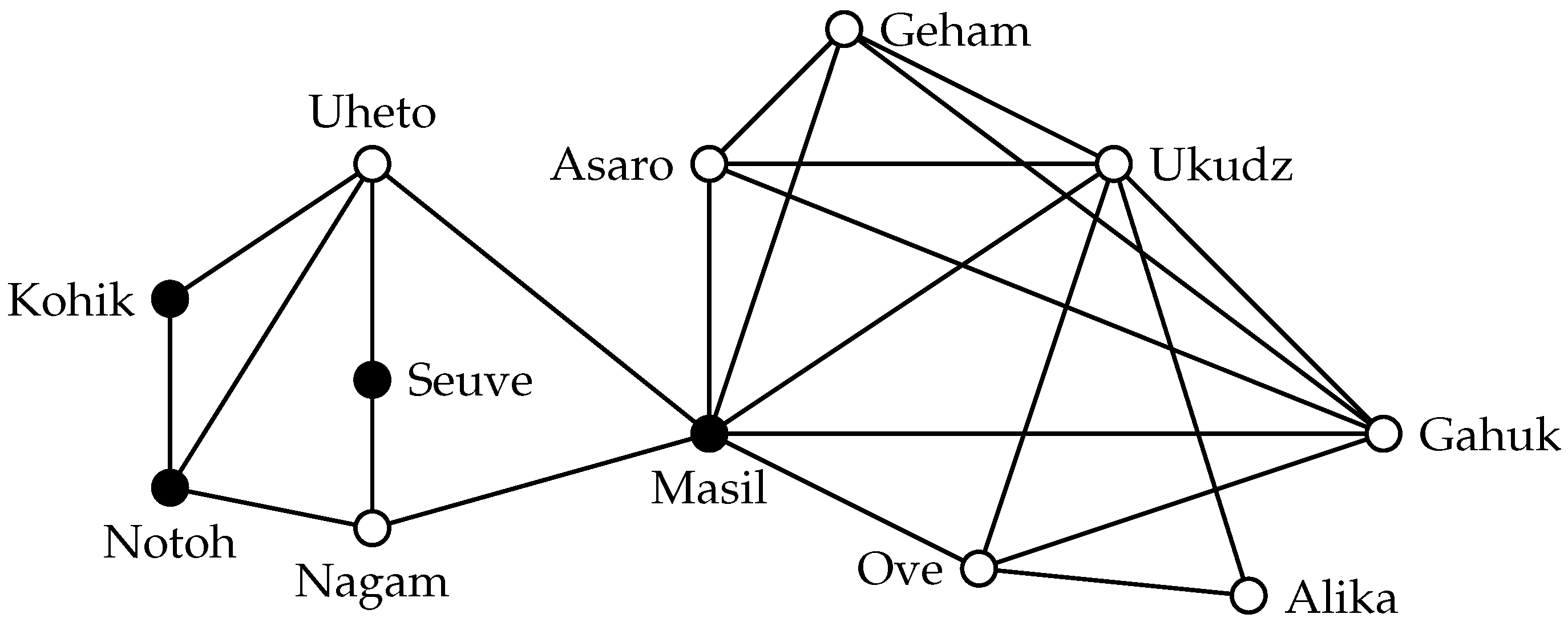
Definition 8. A set $S\subseteq V$ is an s-clique in a graph $G=(V,E)$ if every $u\in S$ and every $v\in S$ have distance at most s in G.

The s-clique model, introduced by Luce [45], is a precursor of s-clubs. Figure 4 shows a 2-clique in the highland tribes network that does not induce a connected graph. In applications, cohesive groups are usually expected to be connected. Thus, this property of s-cliques is undesirable and led to the consideration of distances in the induced subgraph [36,37]. In the example, the shown disconnected 2-clique is a subset of a maximally-connected 2-clique. In general, however, there may be maximal 2-cliques that do not induce connected subgraphs: a cycle on six vertices, for example, has a maximum independent set of size three, which is also a maximal 2-clique. Despite these drawbacks from the application point of view, we may still be interested in the problem of finding large s-cliques from an algorithmic point of view.

$\mathit{s}$-Clique

Input: An undirected graph G and an integer k.

Question: Does G contain an s-clique of size at least k?

For example, a known heuristic for s-Club is to first compute a maximum s-clique and then to find a maximum s-club $S^{\prime }\subseteq S$ [46]. Hence, algorithmic improvements for s-Clique may yield improved algorithms for s-Club. In this context, it is of interest that being an s-clique is hereditary: to determine whether a set S is an s-clique, one considers simply each pair u and v of vertices and evaluates a predicate that depends only on G, u and v and not on other vertices in S. Hence, removing any vertex from an s-clique S yields another s-clique. Thus, one may, for example, solve s-Clique by deciding whether or not G contains an s-clique of size exactly k.

Most tractability results that have been achieved for s-Club transfer easily to s-Clique. For example, Observation 3 is also valid if we replace s-club by s-clique. It also holds trivially that every s-clique of a graph G is a subset of $N_s\left[v\right]$ for some vertex v. These two facts give immediately the following tractability results.

Proposition 5. 

For $s>1$, s-Clique is fixed-parameter tractable with respect to k and also with respect to $(\Delta ,s)$.

Concerning the dual parameter $\ell :=n-k$, one can exploit once more the close connection to Vertex Cover to obtain fixed-parameter tractability.

Proposition 6. 

For all s,s-Clique can be solved in $O(1.{28}^{\ell }+\ell n+nm)$ time.

Proof. 

First, compute in $O\left(nm\right)$ time the s-th power $G^s$ of the input graph G. Then, use the fact that a set S is an s-clique in G if and only if it is a clique in $G^s$. To this end, compute whether $G^s$ has a clique of size at least k by finding a vertex cover of size at most ℓ in $\overline{G^s}$, the complement graph of $G^s$. The running time bound follows from the running time of the current-best Vertex Cover algorithm for the parameter solution size [22].   □

Proposition 6 shows that a SETH-based lower bound as it is known for s-Club parameterized by ℓ is unlikely for s-Clique. Of course, it would be interesting to obtain faster algorithms by exploiting that the input graphs for the Vertex Cover instance are not arbitrary graphs, but powers of other graphs. Maybe it could be more interesting to find situations where the complexity of s-Clique and s-Club are really different. For example, the complexity of s-Clique for the two remaining parameters is open.

Open Question 4. Is s-Clique fixed-parameter tractable with respect to the h-index or the degeneracy of the input graph?

4. Density-Based Clique Relaxations

In a clique, all possible edges are present. A different view on clique relaxations is, thus, obtained by assuming that the number of edges in cohesive subgraphs is large.

4.1. Relative Relaxation of the Density: γ-Quasi-Cliques

A natural way of using the number of edges in a graph to measure cohesiveness is to divide this number by the number of edges in a clique of the same order.

Definition 9. The density of a graph $G=(V,E)$ is $2m/\left(n\right(n-1\left)\right)$. A set S is a γ-quasi-clique if $G\left[S\right]$ has density at least γ.

This notion was proposed, among others, by Abello et al. [47]; γ-quasi-cliques are also referred to as μ-dense graphs [8] or μ-cliques [14]. The combination of γ-quasi-cliques and γ-complete graphs has also received interest [48].

An example of a 0.7-clique is shown in Figure 5. The γ-quasi-clique property is not hereditary: deleting, for example, “Masil” from the illustrated 0.7-quasi-clique results in a set whose induced subgraph has 10 out of 15 possible edges and, thus, density $2/3<0.7$. In fact, the property is hereditary only for the two extreme cases $\gamma =1$ (when only cliques fulfill the property) and $\gamma =0$ (when every vertex set fulfills the property). The property is, however, quasi-hereditary for every $\gamma \in [0,1]$: removing a vertex of minimum degree from a γ-quasi-clique results in another γ-quasi-clique [8,49]. As for the other clique relaxations, we are interested in finding large γ-quasi-cliques.

$\mathbf{\gamma }$-Quasi-Clique

Input: An undirected graph G and an integer k.

Question: Does G contain a γ-quasi-clique S of size at least k?

The γ-Quasi-Clique problem is NP-hard for all $\gamma \in (0,1]$ [49]. Since the γ-quasi-clique property is quasi-hereditary, one may solve γ-Quasi-Clique by deciding whether G has a γ-quasi-clique of size exactly k. Consequently, γ-Quasi-Clique can be directly reduced to Dense-k-Subgraph, where we aim to find a size-k set $S\subseteq V$ such that $G\left[S\right]$ has a maximum number of edges [50].

When considering the parameterized complexity of γ-Quasi-Clique, we face hardness for both solution size-related parameters. More precisely, for every $\gamma \in (0,1]$, γ-Quasi-Clique is W[1]-hard with respect to k and W[1]-hard with respect to ℓ [14]. Moreover, for every $\gamma \in (0,1]$, γ-Quasi-Clique is W[1]-hard even for the combined parameter $(k,d)$ where d is the degeneracy of the input graph [14].

In contrast, fixed-parameter tractability can be obtained for the parameter maximum degree and also for the smaller parameter h-index. The fixed-parameter algorithms for both parameters are based on the following fact, which we state for the smallest of the three degree-based parameters under consideration.

Observation 4 ([14] (Lemma 4)). If G has degeneracy d, then for every fixed $\gamma \in (0,1]$, every γ-quasi-clique in G has $O\left(d\right)$ vertices.

Clearly, the same statement holds for the maximum degree and the h-index of G. Thus, the relevant values of k are bounded in the maximum degree Δ, in the h-index h and in the degeneracy d of the input graph G. The constants hidden in the O-notation depend on γ and are different for each parameter. Observation 4 implies a polynomial-time algorithm for constant values of d, but a fixed-parameter algorithm for d is unlikely (recall that γ-Quasi-Clique is $\mathrm{W}\left[1\right]$-hard with respect to $(d,k)$). For the parameters Δ and h, one can solve γ-Quasi-Clique in ${\Delta }^{O(\Delta )}·n^{O\left(1\right)}$ or in $h^{O\left(h\right)}·n^{O\left(1\right)}$ time [14].

An experimental evaluation and heuristic improvement of the corresponding fixed-parameter algorithm turned out to be competitive with a state-of-the art solver [51] when $\gamma >0.5$, and the aim is to find connected γ-quasi-cliques [52]. Roughly speaking, for this task, the fixed-parameter algorithms for the parameter Δ can find maximum γ-quasi-cliques of size $k\approx 15$. The known fixed-parameter algorithms are based on enumeration of connected subgraphs; to obtain substantially better algorithms both in theory and in practice, a different approach seems to be necessary. This leads us to an open question for γ-Quasi-Clique.

Open Question 5. Can γ-Quasi-Clique be solved in $2^{O(\Delta )}·n^{O\left(1\right)}$ time?

4.2. Absolute Relaxation of the Average Degree: Average s-Plexes

Density conditions may also be expressed in terms of the average degree of a graph.

Definition 10. The average degree of a graph $G=(V,E)$ is $2m/n$. A set S is an average s-plex if $G\left[S\right]$ has average degree at least $\left|S\right|-s$.

This clique relaxation was studied in the context of graph clustering problems [53]. If we consider only sets of a fixed size k, then there is a direct correspondence between average s-plexes and γ-quasi-cliques.

Observation 5. Let S be a vertex set of size k in a graph $G=(V,E)$, and let $\gamma \in (0,1]$. Then, for $s=k-\gamma ·k+\gamma$, S is a γ-quasi-clique if and only if S is an average s-plex.

Proof. 

Let $m_S$ denote the number of edges in $G\left[S\right]$. A size-k vertex set S is a γ-quasi-clique if and only if $2·m_S/\left(k(k-1)\right)\ge \gamma$ or, equivalently, if $2m_S/k\ge \gamma (k-1)$. In other words, a set S is a γ-quasi-clique if the average degree is at least $\gamma ·(k-1)$. Setting $s=k-\gamma ·k+\gamma$ yields $k-s=\gamma (k-1)$, and thus, the two average degree conditions are equivalent.   □

Moreover, as for γ-quasi-cliques, we can observe the following useful feature of average s-plexes.

Proposition 7. 

The average s-plex property is quasi-hereditary.

Proof. 

Let S be an average s-plex of size k in a graph G. Then, there is some $\gamma \le 1$ such that $G\left[S\right]$ is a γ-quasi-clique and $\gamma ·(k-1)\ge k-s$. Now, since the γ-quasi-clique property is quasi-hereditary [8,49], there is a vertex $v\in S$ such that $S\setminus \left\{v\right\}$ a γ-quasi-clique. That is, $G[S\setminus \{v\left\}\right]$ has average degree at least $\gamma ·(k-2)$. This means that $G[S\setminus \{v\left\}\right]$ is an average s-plex: since $\gamma \le 1$ and $\gamma ·(k-1)\ge k-s$, we have $\gamma ·(k-2)\ge k-s-1$.   □

Once again, we are concerned with the problem of finding large average s-plexes.

Average $\mathit{s}$-Plex

Input: An undirected graph G and an integer k.

Question: Does G contain an average s-plex S of size at least k?

Since being an average s-plex is quasi-hereditary, it is sufficient to search for an average s-plex of size exactly k. Hence, for every fixed k, the problem is equivalent to γ-Quasi-Clique and, therefore, NP-hard; the only difference is that s and γ assume different values and, thus, present different possibilities for parameterization.

An integer programming formulation for Average s-Plex was presented by Veremyev et al. [54], but the multivariate complexity of Average s-Plex has not been studied so far.

Open Topic 3. Perform a multivariate complexity analysis of Average s-Plex.

A first hardness result is easily obtained by exploiting the connection between average s-plexes and γ-quasi-cliques.

Proposition 8. 

Average s-Plex is W[1]-hard with respect to the combined parameter $(d,k,s)$.

Proof. 

We present a simple parameterized reduction from γ-Quasi-Clique. Let $(G,k)$ be an instance of γ-Quasi-Clique. Due to the quasi-hereditarity, this instance is a yes-instance if and only if G contains a γ-quasi-clique of order exactly k. By Observation 5, this is the case if and only if G contains an average s-plex of size k where $s=k-\gamma ·k+\gamma \le k$. Thus, setting s to this value and leaving G and k unchanged gives a parameterized reduction from γ-Quasi-Clique parameterized by $(d,k)$ to average s-plex parameterized by $(d,k,s)$.   □

As in the case of s-Plex, a fixed-parameter algorithm for Average s-Plex can be easily obtained for the parameter $(\Delta ,s)$. First, we observe that the size of average s-plexes is bounded in $\Delta +s$.

Observation 6. Any average s-plex in a graph with maximum degree Δ has size at most $\Delta +s$.

Thus, after rejecting instances where k is too big, any algorithm running in $f(\Delta ,k)·n^{O\left(1\right)}$ time is also a fixed-parameter algorithm for the parameter $(\Delta ,s)$. Such an algorithm can be obtained by a reduction to γ-Quasi-Clique that consists only of setting γ appropriately (observe that γ depends only on Δ and s).

Proposition 9. 

Average s-Plex is fixed-parameter tractable with respect to $(\Delta ,s)$.

For all of the parameters under consideration so far, the complexity of γ-Quasi-Clique and Average s-Plex are the same. Therefore, it is not clear whether or not the parameter s can be exploited by fixed-parameter algorithms at all. One candidate for positive results is to combine s with the dual parameter ℓ. Here, it is less obvious whether previous hardness results for γ-Quasi-Clique transfer.

Open Question 6. Is Average s-Plex fixed-parameter tractable with respect to $(\ell ,s)$?

This question is particularly interesting, because for the related s-Plex problem, parameterization by $(\ell ,s)$ leads to practical fixed-parameter algorithms [29].

5. Connectivity-Based Clique Relaxations

Cliques achieve maximum values of vertex- and edge-connectivity. More precisely, a clique of size k is $(k-1)$-vertex-connected and $(k-1)$-edge-connected. That is, one needs at least $k-1$ vertex or edge deletions to transform a clique into a set that is disconnected or has only one vertex. Moreover, cliques are the only sets of size k assuming these connectivity values. Hence, vertex-connectivity and edge-connectivity can be used as clique-defining properties when related to the total number of vertices. Thus, clique relaxations can be obtained by relaxing them. In the following, let $\kappa \left(G\right)$ denote the vertex-connectivity of a graph G, and let $\lambda \left(G\right)$ denote its edge-connectivity. Observe that $\kappa \left(G\right)\le \lambda \left(G\right)\le \delta \left(G\right)$ where $\delta \left(G\right)$ denotes the minimum degree in G.

5.1. Relative Relaxation of Vertex-Connectivity

A natural way to relax the connectivity is to introduce a relative slack parameter $\gamma \in (0,1]$ that can be set to vary between perfect vertex-connectivity and “mere” connectivity.

Definition 11. A set $S\subseteq V$ in a graph $G=(V,E)$ is γ-relative-vertex-connected if $\kappa \left(G\right[S\left]\right)\ge \gamma ·\left(\right|S|-1)$.

This clique relaxation was proposed quite recently [55]; Figure 6 shows a 0.5-relative-vertex-connected set. There is the following relation between γ-relative-vertex-connected sets and γ-complete sets: if a set is γ-relative-vertex-connected, then it is also γ-complete (and consequently, also a γ-quasi-clique). This relation follows from the fact that it is possible to isolate a vertex by deleting all of its neighbors. Moreover, being γ-relative-vertex-connected is not hereditary and not even quasi-hereditary: consider a cycle on five vertices. This graph is 2-vertex-connected and, thus, $0.5$-relative-vertex-connected. Deleting one vertex results in a path on four vertices. This graph is only one-vertex-connected and, thus, not $0.5$-relative-vertex-connected.

The computational problem of finding large γ-relative-vertex-connected sets is formulated as follows.

$\mathbf{\gamma }$-Relative-Vertex-Connected Subgraph

Input: An undirected graph $G=(V,E)$ and an integer k.

Question: Does G contain a γ-relative-vertex-connected set of size at least k?

Unsurprisingly, γ-Relative-Vertex-Connected Subgraph is NP-hard for all fixed rational values $\gamma \in (0,1]$ [55]. To our knowledge, this is the only known complexity result for γ-Relative-Vertex-Connected Subgraph.

Open Topic 4. Perform a multivariate complexity analysis for γ-Relative-Vertex-Connected Subgraph.

Observe that since γ-relative-vertex-connected sets are also γ-quasi-cliques, Observation 4 applies also to γ-relative-vertex-connected sets. Hence, $k\in O(\Delta )$ for fixed γ. Thus, by Proposition 1, γ-Relative-Vertex-Connected Subgraph can be solved in ${\Delta }^{O(\Delta )}·n^{O\left(1\right)}$ time; for all other parameters, the parameterized complexity is open.

5.2. Relative Relaxation of Edge-Connectivity

Instead of relaxing vertex-connectivity, one may also relax edge-connectivity in a relative way.

Definition 12. A set $S\subseteq V$ in a graph $G=(V,E)$ is γ-relative-edge-connected if $\lambda \left(G\right[S\left]\right)\ge \gamma ·\left(\right|S|-1)$.

As for γ-relative-vertex-connected sets, there is a relation to γ-complete sets and γ-quasi-cliques: any γ-relative-edge-connected set is γ-complete. For large values of γ, there is an even stronger connection between edge-connectivity and γ-complete graphs.

Theorem 3 ([56]). 

Let G be a graph on n vertices and let $\gamma \ge n/(2n-2)$. Then, a graph G has edge-connectivity $\gamma ·(n-1)$ if and only if it is γ-complete.

Hence, γ-relative-edge-connectedness and γ-completeness are essentially the same for all constant $\gamma >1/2$.

$\mathbf{\gamma }$-Relative-Edge-Connected Subgraph

Input: An undirected graph $G=(V,E)$ and an integer k.

Question: Does G contain a γ-relative-edge-connected set of size at least k?

To our knowledge, γ-Relative-Edge-Connected Subgraph has not been studied so far, and the only computational problem in this context that has received attention deals with the following graph property.

Definition 13. A graph $G=(V,E)$ on n vertices is highly connected if $\lambda \left(G\right)>n/2$.

The notion of highly connected subgraphs was introduced in the context of graph clustering [57].

Highly Connected Subgraph

Input: An undirected graph $G=(V,E)$ and an integer k.

Question: Does G contain a highly connected subgraph of order k?

Highly Connected Subgraph turns out to be quite hard from a computational point of view. Highly Connected Subgraph is NP-hard and $\mathrm{W}\left[1\right]$-hard for the parameter $(d,k)$ and $\mathrm{W}\left[1\right]$-hard for the parameter ℓ [58]. The parameter Δ has not been considered so far, but the fact that every highly connected graph on k vertices has minimum degree $k/2$ or more implies that the problem is nontrivial only if $k\le 2\Delta$. Hence, once again, we may apply Proposition 1 to obtain a fixed-parameter algorithm with running time ${\Delta }^{O(\Delta )}·n^{O\left(1\right)}$ for Δ. The complexity with respect to the h-index of G is open.

Theorem 3 shows that the most interesting set of problems to study here are those where the edge-connectivity is below $n/2$. It would be particularly interesting to highlight situations in which the complexities of γ-Relative-Edge-Connected Subgraph with $\gamma <1/2$ and those of Highly Connected Subgraph and γ-Complete Graph differ.

Open Topic 5. Perform a multivariate complexity analysis for γ-Relative-Edge-Connected Subgraph.

By the same reasoning as for γ-relative-vertex-connected sets, we have that γ-relative-edge-connected sets have size $O(\Delta )$ for fixed values of γ. Thus, by Proposition 1, there is an algorithm that solves γ-Relative-Edge-Connected Subgraph in ${\Delta }^{O(\Delta )}·n^{O\left(1\right)}$ time. For the other parameters, the complexity is open.

5.3. Absolute Relaxation of Vertex-Connectivity

A further connectivity-based clique relaxation is to relax the connectivity demand by an absolute amount $s>1$. That is, instead of demanding vertex-connectivity $k-1$ for k-vertex graphs, we demand vertex-connectivity $k-s$.

Definition 14 ([5]). A set S in a graph $G=(V,E)$ is an s-bundle if $G\left[S\right]$ is $\left(\right|S|-s)$-vertex-connected.

As for degree-based and density-based clique relaxations, there are relations between s-bundles and their relative counterpart, the γ-relative-vertex-connected sets. In addition, every s-bundles is also an s-plex, since $\kappa \left(G\right)$ is upper-bounded by the minimum degree of G. Hence, the s-bundle property is more restrictive than the s-plex property. For $s=2$, the two properties coincide, that is, every 2-bundle is also a 2-plex. For $s=3$, the properties are different. Consider, for example, a graph consisting of two isolated edges. This graph is a 3-plex (the minimum degree is $1=4-3$), but not a 3-bundle (it is not connected, but a 3-bundle on four vertices needs to be connected).

It is evident from the definition of vertex-connectivity that being an s-bundle is hereditary. Thus, the problem of finding large s-bundles, defined below, is NP-hard by Theorem 1.

$\mathit{s}$-Bundle

Input: An undirected graph G and an integer k.

Question: Does G contain an s-bundle S of size at least k?

As this problem has not received any attention so far, it is open to study its complexity, in particular its multivariate complexity, in more detail.

Open Topic 6. Perform a multivariate complexity analysis for s-Bundle.

Since being an s-bundle is hereditary, Theorem 2 shows that s-Bundle is W[1]-hard with respect to k for every constant s. Identifying differences between s-Bundle and s-Plex for other parameters could be one interesting aim of a multivariate complexity analysis. Furthermore, given that s-Plex can be solved quite efficiently in practice [29,30,31,32], an implementation of efficient fixed-parameter algorithms for s-Bundle seems clearly within reach.

6. Conclusions

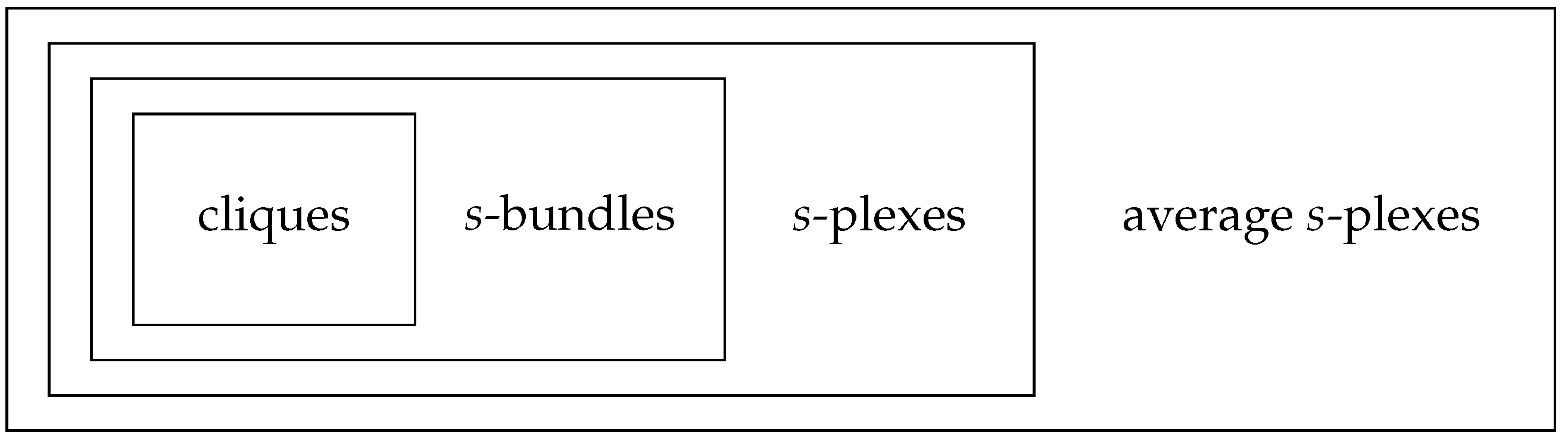
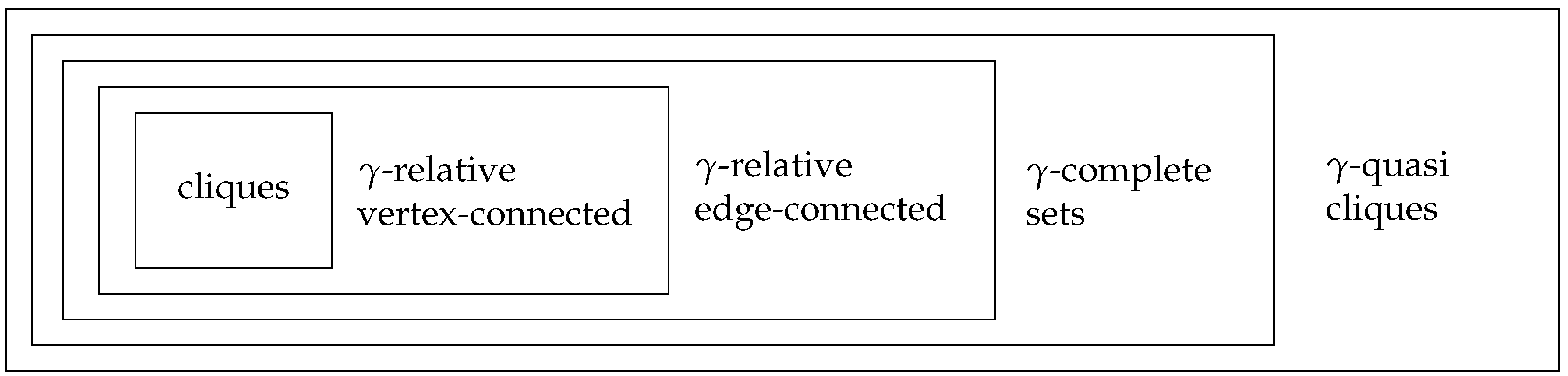
We have surveyed the complexity status of several problems that are related to finding large cohesive subgraphs of a graph. An overview of the complexity for clique relaxations with absolute and relative relaxation parameter is given in

Table 1. An overview of the complexity of the subgraph problems for clique relaxations with absolute relaxation parameter $s>1$. In all complexity results, s is allowed to be a parameter of the algorithm; a question mark denotes that the complexity is open for this parameter.

Problem Name	k	ℓ	Δ	h	d
Clique	W[1]-h [15]	FPT	FPT	FPT	FPT
s-Plex	W[1]-h [19,27]	FPT [27]	FPT (Prop. 2)	?	?
A. s-Plex	W[1]-h (Prop. 8)	?	FPT (Prop. 9)	?	W[1]-h (Prop. 8)
s-Bundle	W[1]-h [19]	?	?	?	?
s-Club	FPT [41]	FPT [41]	FPT	W[1]-hard [43]	NP-h for $d=2$
s-Clique	FPT (Prop. 5)	FPT (Prop. 6)	FPT (Prop. 5)	?	?

and

Table 2. An overview of the complexity of the subgraph problems for clique relaxations with relative relaxation parameter $\gamma \in (0,1]$. In all complexity results, γ is allowed to be a parameter of the algorithm; a question mark denotes that the complexity is open for this parameter. The abbreviations γ-RVCS and γ-RECS stand for γ-Relative-Vertex-Connected Subgraph and γ-Relative-Edge-Connected Subgraph, respectively.

Problem Name	k	ℓ	Δ	h	d
Clique	W[1]-h [15]	FPT	FPT	FPT	FPT
γ-Complete Graph	?	?	FPT (Prop. 4)	?	?
γ-Quasi-Clique	W[1]-h [14]	W[1]-h [14]	FPT [14]	FPT [14]	W[1]-h [14]
γ-RVCS	?	?	FPT (Prop. 1)	?	?
γ-RECS	?	?	FPT (Prop. 1)	?	?

. Moreover, Figure 7 and Figure 8 display the relation between the different clique relaxations for absolute and relative relaxation parameters. Since distance-based clique relaxations behave in a somewhat orthogonal way to the other clique relaxations, they are omitted from the diagrams.

In the following, we highlight some possible avenues for research that may be particularly interesting beyond the open questions and topics mentioned above.

For most clique relaxations, it is easy to obtain fixed-parameter tractability for the parameter Δ, the maximum degree of the input graph. In most cases, these fixed-parameter algorithms have running time ${\Delta }^{\Theta (\Delta )}·n^{O\left(1\right)}$, which limits their usefulness in practice. Here, it would be interesting to find either algorithms running in $2^{O(\Delta )}·n^{O\left(1\right)}$ time or to show that such algorithms cannot be achieved (assuming, for example, the ETH).

A further natural approach to obtain practical algorithms and stronger theoretical results is to consider smaller degree-related parameters, such as the h-index and the degeneracy of G. In particular, for most of the presented clique relaxations, the complexity with respect to the h-index of G is open. Thus, one line of research could focus on fixed-parameter algorithms for the parameter h-index. Note that in many cases, it is known that the problems become hard when the degeneracy of the input graph is a parameter. The degeneracy of a real-world network is often substantially smaller than its h-index. It would thus be very interesting to find a further parameter that is now sandwiched between h-index and degeneracy and to obtain positive algorithmic results for this parameter.

Most implementations of efficient algorithms that find cohesive subgraphs based on clique relaxations are developed purely for experimental purposes and often based on mathematical programming approaches. This may limit their appeal to users that expect a flexible tool providing good algorithms for a large collection of models of cohesive subgraphs. Developing such a tool is a challenging task.

Connectivity-based clique relaxations have received the least interest so far, both from a theoretical and a practical point of view. Hence, this class of clique relaxation yields the most open field for future research. As the minimum connectivity of a graph is a structurally more restrictive (or “deep”) property than, for example, its minimum degree, efficient fixed-parameter algorithms are likely to rely on new techniques.

This survey and most parts of the literature study clique relaxations only in undirected graphs. Applications of clique relaxations in directed graphs or graphs with different types of edges (such as the original highland tribes network [4] and many other social networks) should give rise to many further interesting computational problems.

In addition to the subgraph problems considered in this work, clique relaxations also find application in graph clustering and graph partitioning problems [53,57,59,60,61,62,63]. In the corresponding computational problems, one searches for a partition of the vertex set of the input graph such that each part of the partition represents a cohesive group. As for subgraph problems, depending on the application, it may be appropriate to use different clique relaxations as models for cohesive groups. A typical optimization goal would be to maximize the overall number of edges of the input graph that have both endpoints within the same part (this is often called edge coverage). A systematic study of the relation between the complexity of such clustering problems and the used clique relaxations is still lacking.

Finally, a further related avenue yielding many interesting computational problems is to consider concepts and parameterizations that take the edges between S and $V\setminus S$ into account. One example of such concepts are alliances [64,65], which are, roughly speaking, vertex sets S such that every vertex of S has more neighbors in S than outside of S. Finding various types of alliances of size k is fixed-parameter tractable with respect to k [66,67]. A multivariate complexity study, however, is lacking. Moreover, the known fixed-parameter algorithms for these problems have running time $k^{\Theta \left(k\right)}·n^{O\left(1\right)}$. Therefore, running time improvements or tight running time lower bounds are desirable. One idea here could be to mix clique relaxations and alliances, that is, to consider types of alliances that fulfill cohesiveness demands. This might yield efficient algorithms to identify certain types of alliances. A related field would be to systematically investigate the combination of clique relaxations and isolation concepts [24,27,58,68], where the number of outgoing edges from a set S is restricted.

To summarize, studies for degree-based [27,29], distance-based [43,44] and density-based [14,52] clique relaxations show that clique relaxations are a rewarding working area for multivariate algorithmics: problems related to clique relaxations may admit fixed-parameter algorithms that can be tuned to yield competitive algorithms in practice. Consequently, we feel that the combination of multivariate algorithmics and clique relaxations will remain a relevant and challenging field of study in the near future. The abundance of freely available data makes this area particularly suitable to the implementation of fixed-parameter algorithms and their experimental analysis.