Abstract
Subnetwork mining is an essential issue in the analysis of biological, social and communication networks. Recent applications require the simultaneous mining of several networks on the same or a similar vertex set. That is, one searches for subnetworks fulfilling different properties in each input network. We study the case that the input consists of a directed graph D and an undirected graph G on the same vertex set, and the sought pattern is a path P in D whose vertex set induces a connected subgraph of G. In this context, three concrete problems arise, depending on whether the existence of P is questioned or whether the length of P is to be optimized: in that case, one can search for a longest path or (maybe less intuitively) a shortest one. These problems have immediate applications in biological networks and predictable applications in social, information and communication networks. We study the classic and parameterized complexity of the problem, thus identifying polynomial and NP-complete cases, as well as fixed-parameter tractable and W[1]-hard cases. We also propose two enumeration algorithms that we evaluate on synthetic and biological data.
1. Introduction
The use of social and telecommunication networks has dramatically increased recently, resulting in new prominent applications of network analysis. In addition to these real-world applications, network representations of new types of data, in particular biological data, highlight the drastic need for a new, multi-dimensional, type of (sub)network mining in which several networks, representing several relations between the same objects, are simultaneously investigated for the extraction of a multi-dimensional pattern [1,2,3].
The study of multi-dimensional mining started several years ago, but it mainly concerns homogeneous representations of data: directed graph alignment [4], undirected graph alignment [5], relational data mining [6] and social networks mining [2] are several examples. Recently, such approaches found applications in computational biology [7,8,9], but also showed their limits, due to the multiple types of biological networks that are used to describe different views of the same biological process. In such applications, a process is often represented as a path in a directed network, for example a metabolic network [9,10,11] or a signaling network [12,13], and as a connected graph in an undirected network, for example a protein-protein interaction network [14]; the two networks are linked by the components involved in the process, which are represented as vertices in each network. Identifying a particular biological process then requires identifying parts of the two networks (directed and undirected) that have the desired topological patterns and the same vertex set. This multi-dimensional mining approach has led to the discovery of novel biological insights [3,15,16,17].
In this paper, we consider a network mining across two heterogeneous networks, driven by the previously-cited applications in biological networks. Following the situation described above, we consider the case in which we are given a directed graph D and an undirected graph G and want to find a path P in D (that is, a graph with vertex set , , and arc set ), whose vertices induce a connected subgraph in G. In the application context when D is a metabolic network and G is a protein interaction network, such a problem corresponds to searching for a chain of reactions (a path in D) involving proteins that form a complex (that is connected in G).
Definition 1. Let be a directed graph and be an undirected graph on the same vertex set. A -supported path is a simple (directed) path P of length at least one in D, such that the subgraph of G induced by , denoted , is connected.
The length restriction in the definition simply allows us to disregard trivial -supported paths consisting of only one vertex. We consider several natural variants of finding -supported paths. The most basic problem simply asks for the existence of such a path.
- Supported Path (SP)
- Instance: A directed graph and an undirected graph .
- Question: Is there a -supported path?
In applications, one might additionally try to optimize certain criteria of such a path. We study here the fundamental problems of maximizing or minimizing path length:
- Longest Supported Path (LSP)
- Instance: A directed graph and an undirected graph .
- Task: Find the longest -supported path.
- Shortest Supported Path (SSP)
- Instance: A directed graph and an undirected graph .
- Task: Find the shortest -supported path.
In this work, we study the complexity landscape of these computational problems by identifying polynomial-time solvable, as well as NP-hard cases of the problem. Clearly, more general variants of the problem, for example when D and G have different, but related vertex sets, may be also useful in practice, but their study is beyond the scope of this work.
Before presenting our main results, we make some basic observations on the complexity of the problems. First, with respect to polynomial-time solvability, SP is clearly not harder than SSP and LSP. Moreover, consider the special case in which G is a clique. This simply means that the graph G does not put any additional constraints on the desired paths. In this case, SP and SSP reduce to the polynomial-time problem of deciding whether D has at least one arc, but LSP is the NP-hard Longest Path path problem. Therefore, intuitively, LSP is the hardest of the three problems. Note that for LSP, the special case in which the directed graph D is a DAG and in which G is a clique is polynomial-time solvable, since it reduces to finding the longest path in a DAG.
Preliminaries. Throughout the paper, D will denote a directed graph and G an undirected graph, built on the same vertex set V. We use to denote the number of vertices in D (or equivalently, in G). Given a graph H and a set , let denote the subgraph of H induced by S, that is the graph with vertex set S and all edges (arcs) of H that have both endpoints in S. We use to denote the neighborhood of a vertex v in a graph H and to denote the closed neighborhood of v in H. A path P is called simple if it contains every vertex of exactly once.
A star is a tree with one non-leaf, a bi-star is a tree with two non-leafs. The diameter of a graph is the maximum length of a shortest path between any two of its vertices. An outerplanar graph is a graph admitting a planar embedding with all vertices on a circle, all edges inside the circle and such that edges do not cross each other.
A problem with input size n is called fixed-parameter tractable with respect to a parameter k if it can be solved in time, where f is a computable function only depending on k. A fundamental class of presumed parameterized intractability is called W[1]. Hardness for W[1] can be shown by a parameterized reduction from a problem that is known to be W[1]-hard. A parameterized reduction transforms an instance of a parameterized problem L in time into an equivalent instance of a parameterized problem . We refer to [18,19,20] for further details concerning parameterized complexity.
Our Results. Our findings for the three problems can be summarized as follows (see Table 1 for an overview, where h is the number of vertices of degree two or more). Here, for any directed graph H, the underlying undirected graph of H, denoted , is the graph that is obtained from H simply by removing arc directions.

Table 1.
Complexity of the variants of Supported Path. Herein, is the underlying undirected graph of D. If no problem names are specified, then the results hold for SP, Longest Supported Path (LSP)and Shortest Supported Path (SSP); arrows indicate that a result is implied by another result in the table.
| G | Acyclic D | General D | ||
|---|---|---|---|---|
| Tree | Outerplanar | Treewidth 3 | ||
| path or cycle | P (Proposition 2) | NPC [21] | ||
| h vertices of degree ≥ 2 | P ↓ | (Proposition 2) | LSP, : NPC (Theorem 2) | |
| SSP, : P (Proposition 1) | ||||
| SSP, SP, and G is a tree: | ||||
| NPC (Theorem 1) | ||||
| tree with diameter 4 | P ↓ | LSP: NPC (Theorem 3) | NPC (Theorem 4) | NPC ↑ |
| general graph | P (Proposition 2) | LSP: NPC ↑ | NPC ↑ | NPC ↑ |
If the underlying undirected graph of D is a tree, then all three problems can be solved in polynomial time. If is outerplanar, then LSP is already NP-hard. If has treewidth three, then even SP is NP-complete. These hardness results hold even if D is acyclic and G is a tree with diameter four. For general digraphs, all problems become hard even if G is a tree with a constant number, at least three, of non-leaf vertices. In contrast, if D is acyclic, then all three problems become fixed-parameter tractable with respect to the number of vertices with degree at least two in G. These general complexity results are presented in Section 2 (which considers general digraphs) and Section 3 (which considers the special case where D is acyclic).
In Section 4, we then study the parameterized complexity of the problems, showing that deciding whether G contains a -supported path of length exactly k is W[1]-hard, that is a fixed-parameter algorithm for this parameter is unlikely. Thus, a running time of seems to be more or less unavoidable for finding -supported paths of length k. This holds even if G is a tree and D is acyclic.
In Section 5, we propose two enumeration-based algorithms for solving the problem of finding -supported paths of length exactly k. One algorithm is a fixed-parameter algorithm for the combined parameter , where is the minimum of the maximum outdegree and maximum indegree in D. The other algorithm is a fixed-parameter algorithm for the combined parameter , where Δ is the maximum degree in G. Furthermore, we describe in Section 6 several data reduction rules that are used in the implementation of our algorithms.
In Section 7, we evaluate our two enumeration-based algorithms on synthetic and biological data. Our main observations are that finding -supported paths with at most eight vertices is tractable in the considered biological network and that the case in which G is very sparse compared to D is hard to handle for our algorithm. This is in line with our theoretical findings that show that all three problem variants remain hard if G is a tree. In Section 8, we conclude with a summary of our results and directions for future research.
2. Complexity Classification for General Digraphs
In this section, we study the complexity of SP, LSP and SSP considering the most general case for the directed graph while putting very strong restrictions on the undirected graph G. Our main result here is the following hardness result.
Theorem 1. Supported Path is NP-hard even if G is a tree with two vertices that have degree at least three and one degree-two vertex.
Proof. We describe a reduction from the following NP-hard problem (see also Figure 1 for an illustration).
- Directed Disjoint Paths
- Instance: A directed graph , and k vertex pairs , .
- Question: Is there a set of vertex-disjoint paths , each going from to ?
Directed Disjoint Paths are NP-hard even if [22]. Let be an instance of Directed Disjoint Paths. Assume, without loss of generality, that and have only outgoing incident arcs and and have only incoming incident arcs. Furthermore, assume that is not a neighbor of (and note that it cannot be a neighbor of by the assumption above). Furthermore, assume that and are disjoint. This can be easily achieved for example by subdividing the arcs incident with . Construct an instance of Supported Path as follows. First, initialize the directed graph as and add the arc to D. Note that is the only outneighbor of and is the only inneighbor of . Then, let G be the tree on W with the following properties:
- is a neighbor of and ,
- all neighbors of in D are leaf neighbors of and
- and all other vertices of D are leaf neighbors of .
Note that, by definition, in G, all vertices are leaves, except , which has degree two, and and , which have an arbitrarily large degree. We now show the equivalence of the instances, that is H has two vertex-disjoint paths from to and from to if and only if there exists a -supported path.
⇒: Let and be two vertex-disjoint paths in H from to and from to , respectively. Then, the concatenation of and is a simple directed path in D, since D additionally contains the arc . Further, is connected, since all vertices that are in have degree one in G, and thus, their deletion from G cannot make G disconnected.

Figure 1.
Illustration of the reduction in the proof in the proof of Theorem 1. The arcs/edges of and G are drawn with plain lines. The dotted lines represent, respectively: in H, the paths joining to and to ; in D, the corresponding -supported path; in G, the connected subgraph given by the vertices of the -supported path.
⇐: Let P be a -supported path. Every edge in G has one of its endpoints in . Hence, P contains either or . Since P contains at least two nodes, then it contains, in D, a neighbor of or a neighbor of . All neighbors of in D are leaf neighbors of in G, and all neighbors of in D are leaf neighbors of in G (recall that we assume to be disjoint from ). Consequently, P contains and and, thus, also . Since has no incoming arcs, P starts in , and since has no outgoing arcs, P ends in . Consequently, P contains an outneighbor of , which by construction is . Hence, P is a simple path in D from to to to . Hence, there are two vertex-disjoint paths and from to and from to in H. ☐
Hence, to obtain tractable cases for general D, one would need to constrain G even further. If G is a bi-star, Shortest Supported Path and, thus, also Supported Path, are easily solvable in polynomial time.
Proposition 1. Shortest Supported Path can be solved in polynomial time if G is a bi-star.
Proof. Let G be a bi-star with non-leaf vertices u and v. Every -supported path P thus contains either u or v. In the case where contains an arc incident with u, then there is a -supported path of length one containing u, and we are done. Similarly, in the case where contains an arc incident with v, then there is a -supported path of length one containing v.
Let us now consider the case where does not contain an arc incident with u, and contain no arc incident with v. Let P be a -supported path (if any). Thus, (the underlying undirected path of P) contains no edge, which is also present in G. Consequently, P links a neighbor of v to u, or a neighbor of u to v, or a neighbor of v to a neighbor of u, or a neighbor of u to a neighbor of v. If u or v does not belong to P, then cannot be connected. Thus, P contains u and v. Further, since G is a bi-star with non-leaf vertices u and v, every path in D containing u and v is supported. Hence, the problem can be solved by computing the shortest path between u and v in this case (considering both possible directions of the path). If such a path does not exist, then there is no -supported path. ☐
The Longest Supported Path problem is more difficult, since it remains NP-hard even if G is a star: a simple reduction from the NP-hard Hamiltonian Path problem, which asks for a simple path on all vertices of a directed graph D, can be achieved by making G an arbitrary star on the same vertex set as the input graph D of the Hamiltonian Path instance. Then, by finding the longest -supported path, one can clearly solve the Hamiltonian Path.
Theorem 2. The decision version of Longest Supported Path is NP-hard, even if G is a star.
A similar hardness result for Longest Supported Path can be easily obtained if G is a path and apparently even Supported Path is NP-hard in this case [21].
3. Complexity Classification for Acyclic Digraphs
In this section, we continue our complexity analysis for the special case where D is acyclic. First, we identify some special cases in which all three problems can be solved in polynomial time.
Proposition 2. If D is acyclic, then Longest Supported Path and Shortest Supported Path can be:
- (a)
- solved in polynomial time if is a tree,
- (b)
- solved in polynomial time if G is a chordless path or cycle or
- (c)
- solved in time if G has at most k vertices with degree two or more.
Proof. Before studying each case, we note that, in a DAG, the longest path, as well as the longest path between two given vertices can be computed in linear time, using dynamic programming.
- (a)
- Since is a tree, the set of (directed) paths in D can be computed in polynomial time: there is at most one path between every pair of vertices in D, and if it exists, it can be found in linear time for each pair of endpoints. Hence, the longest and the shortest -supported path can be found as follows. Check for each pair of endpoints u and v whether there is a path P between u and v in D. If this is the case, check whether is connected. If this is the case, keep P if it is longer or shorter than the currently stored shortest or longest paths.
- (b)
- Since G is a path or a cycle, the number of connected subgraphs of G is , and they may be computed in polynomial time. Further, for each connected subgraph of them, one can compute in linear time whether has a Hamiltonian path, because D is acyclic. The longest (resp. shortest) -supported path is the maximum-order (resp. minimum-order) subgraph of G for which this is the case.
- (c)
- Let X denote the set of k vertices with degree two or more in G. For each , we solve the problem of finding a -supported path that contains as follows. Clearly, we only need to consider , such that is connected. Further, we can remove from G all degree-one vertices that have no neighbor in . Let Y denote the set of remaining degree-one vertices, and note that is connected for all . Hence, it is sufficient to compute the longest (resp. shortest) path in that contains all vertices of . Fix an arbitrary topological ordering of . Then, the order of the vertices of in this topological ordering determines the order of the vertices of in any path that contains : by definition of topological orderings, there is no directed path from to , so must be after in such a path. By the same argument, for each , , any path between and contains only vertices that are put between and by this topological ordering. Hence, the longest (resp. shortest) path that contains in this graph can be computed by concatenating the longest (resp. shortest) paths between and for all i, . As discussed above, each such path can be computed in polynomial time. Hence, the overall running time is .
Note that Case (c) includes the cases in which G is a star or a bi-star, that is, all trees with diameter at most three. To extend these tractability results, one might try, for example, to achieve polynomial-time algorithms for the case that and G have bounded treewidth or for the case that G has diameter four. The theorem below, however, shows that Longest Supported Path becomes NP-hard in these cases.
Theorem 3. The decision version of Longest Supported Path is NP-complete, even when D is acyclic, is an outerplanar graph and G is a tree with diameter four.
Proof. The problem is clearly in NP. To show NP-hardness, we describe a reduction from MAX 2-Sat [23] (see also Figure 2 for an illustration of the reduction). Let be an instance of MAX 2-Sat, built from a collection of p clauses with two literals each, over the variable set . Let D be built on levels, called optional (marked with a star) or compulsory (not marked):
- Level 0: a vertex s;
- , : two vertices and corresponding to the literals of clause ;
- level , : a vertex corresponding to clause ;
- level : two vertices and corresponding, respectively, to literals and ;
- level : a vertex ;
- level , : two vertices and ;
- level , : a vertex .
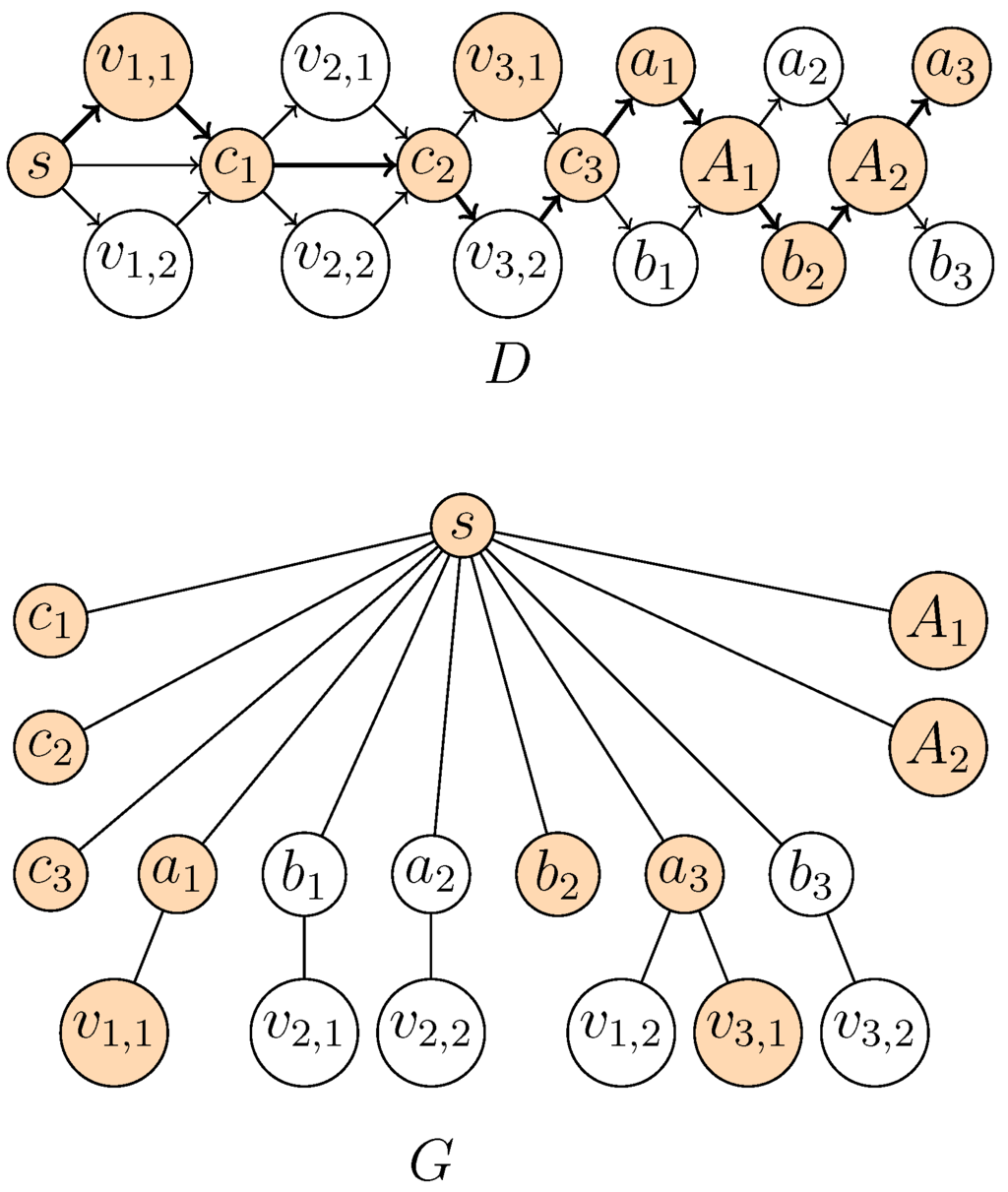
Figure 2.
Construction of D and G from the following instance of MAX 2-Sat with and : . Levels in D are represented from left to right. The orange vertices form the -supported path corresponding to the assignment .
Then, add (a) all possible arcs between any two consecutive levels, (b) the arc and (c) the arcs . It is clear that D is a DAG. To see that is an outerplanar graph, it is sufficient to draw the vertices on a circle according to the order , , , , .
Graph G is a tree with root s. There is an edge between s and each vertex in . There is an edge between each vertex (resp. ) and any vertex with , such that corresponds to the literal (resp. ). Figure 2 is an illustration of the reduction described above, with . Notice that G is of diameter four, where s plays a central role. We now claim that there is an assignment for the variables in that satisfies at least k clauses if and only if there is a -supported path of length at least .
⇒: Let be an assignment of the variable set that satisfies clauses of , where . Assume without loss of generality that vertices , correspond to true literals. Let if is true, and otherwise. Then, the path P with vertices , is -supported and has length . Indeed, in G, the vertices are connected to s using the corresponding vertex (where is or ), and , respectively. All of the other vertices are adjacent to s.
⇐: Let P be a -supported path P of length at least , i.e., with at least vertices. Now, there are at most compulsory levels implying that P contains at least k vertices from optional levels. As P cannot contain two vertices associated with literals for some i (because at most one of the vertices and , needed for the connection in G, belong to P), we may safely assign the value to the literals associated with the vertices in P on optional levels. These literals yield a correct assignment that satisfies k clauses. ☐
The above reduction shows hardness for Longest Supported Path. By slightly extending the class of graphs for , we can also show hardness for Supported Path and, thus, also for Shortest Supported Path, even if D is acyclic. This reduction also implies that Longest Supported Path is not f-approximable, for any function f, even if D is acyclic.
Theorem 4. Supported Path is NP-complete even when G is a tree of diameter four, and the underlying undirected graph of D has treewidth three.
Proof. The proof is by a reduction from 3-SAT. Let ϕ be a Boolean formula with clauses , over the set of variables . Assume that (this can be achieved by adding one variable and one clause to the input formula ϕ). We now describe how to build D and G from ϕ. The directed acyclic graph D is built on levels, numbered from zero to . Each level contains between one and three vertices:
- Level 0: one vertex s,
- level i, : three vertices that correspond to the variables occurring in clause ,
- level , : two vertices and .
We complete the construction of D by adding all arcs from any vertex on level i to any vertex on level , for all . The undirected graph G has the same vertex set as D. We define (resp. ) to be the set of vertices in such that the literal corresponding to this vertex is (resp. ), for all . The edges of G are obtained as follows:
- put an edge between each vertex in and vertex
- put an edge between each vertex in and vertex
- put an edge for each and an edge for each
Figure 3 gives an illustration of the above reduction. Notice that G is a tree of diameter four, in which s plays a central role. Note also that has treewidth three, since each level consists of three vertices, and all arcs are between consecutive levels. It remains to show the equivalence of the instances, which is formalized as follows: ϕ is satisfiable if and only if there is a -supported path of length at least one.
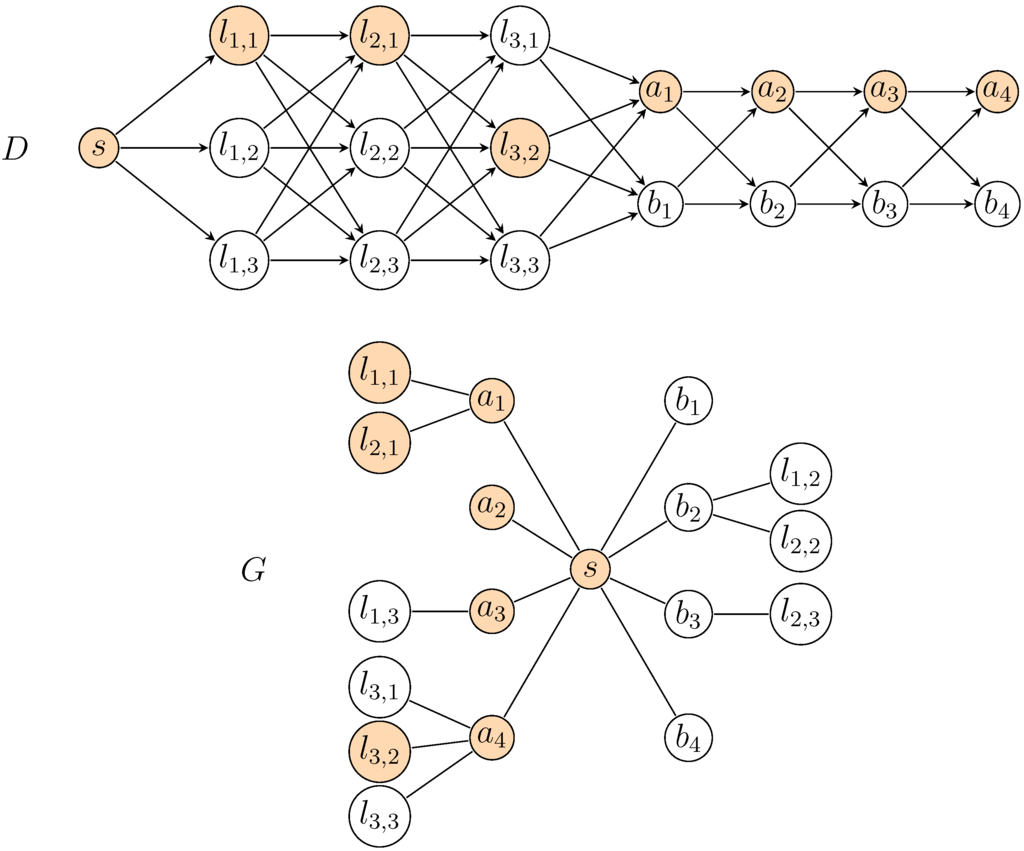
Figure 3.
Illustration of the reduction in the proof of Theorem 4. Here, , and the levels are drawn from left to right. The -supported path marked in orange corresponds to the assignment .
⇒: Let be an assignment of the variables that satisfy ϕ. Consider a path P in D that contains s and for each level i, , one (arbitrary) vertex that corresponds to a literal that is set to true by , and for each level i, , the vertex if assigns true to and the vertex , otherwise. We now show that is connected, which implies that P is a -supported path of length at least one.
First, each vertex or is adjacent to s, so the subgraph of induced by s plus the vertices from levels is connected. Every other vertex is adjacent to one vertex in this subgraph: Since satisfies , assignment sets the corresponding literal to true. By construction, this means that if corresponds to a non-negated variable , then and and are adjacent in G; otherwise, and and are adjacent in G.
⇐: We first show that any -supported path P of length at least one contains a vertex from each level of D. Every edge in G has one endpoint in a vertex that is in level in D. Now, the other endpoint of this edge is in some level in D. Consequently, P contains one of the vertices from layer p in D. These vertices all correspond to the literal , and thus, P contains , since is the only neighbor of these vertices in G. Now, this means that P contains one vertex from all levels . Since is connected, P contains s. Consequently, P contains a vertex from the first and the last level of D, and thus, it contains a vertex from each level of D.
By construction, P contains at most one vertex from each level, and thus, the selected vertices from levels directly define an assignment of the variables of ϕ: set variable to true if and to false if . Moreover, this assignment satisfies ϕ: Each vertex v in layer i, , corresponds to a literal of C. Since is connected, this vertex v has a neighbor in . If the literal corresponds to a non-negated variable , then this neighbor is ; otherwise, this neighbor is . Hence, assignment makes this literal true, and thus, satisfies each clause of ϕ. ☐
4. Parameterized Hardness
The hardness results presented so far do not exclude efficient algorithms for the case in which one is satisfied with finding a -supported path of length exactly k for some given constant k. Such an algorithm might be interesting for example in case the longest path in D has bounded length. In fact, an -time algorithm for this problem is easily achievable by guessing the vertices of the path in the correct order and then checking in polynomial time whether the subgraph of G is connected. As we show in the following, it is unlikely that this can be improved to a running time of .
Theorem 5. The problem of deciding whether there is a -supported path of length exactly k is W[1]-hard even if D is acyclic and G is a tree of diameter four.
Proof. We describe a parameterized reduction from the W[1]-hard Multicolored Clique problem [24]:
- Instance: An undirected graph with a proper vertex coloring .
- Question: Is there a clique S of order k in H such that S contains one vertex from each color?
Given an instance of Multicolored Clique, the instance of Supported Path is constructed as follows. The vertex set is , that is we create one vertex for each vertex of H, two vertices for each edge of H and one additional vertex . We call the two vertices that correspond to the same edge in H siblings. In the construction, assume that an arbitrary, but fixed ordering of unordered color pairs is given.
The directed graph has the following levels:
- Level 0 contains s,
- level i, , contains all vertices of W that have color i,
- level , , contains all vertices where is the i-th color pair and and
- level , , contains all vertices where is the i-th color pair and .
Now, add arcs in D as follows:
- for level , add an arc from each vertex in level i to each vertex in level ,
- for level , , add an arc from each vertex in level to its sibling in level and
- for level , , add an arc from each vertex in level to each vertex in level .
This completes the construction of D. The undirected graph G is now constructed by adding the following edges:
- for each , add and
- for each , add .
Informally, the idea of the construction is to force with D that each supported path of the correct length selects exactly one vertex of each color and two vertices for each color pair. With the arcs in D between levels and , we force that two vertices of the same color pair that are selected correspond to an edge in H. Finally, with the construction of G, we force that a vertex of a color pair can only be selected if its endpoint i is selected. To complete the formal correctness proof of our parameterized reduction, we show the equivalence of the instances.
- is a yes instance if and only if there is a -supported path of length exactly .
⇒: Let S be a clique of order k in H. Since c is a proper vertex coloring, S contains exactly one vertex of each color. Now, consider the vertex set that contains , S, and all vertices corresponding to an edge of . First, note that . Second, is connected, since is a star, and every vertex in is in G a neighbor of one of its endpoints in . Finally, is an induced path of length , which can be seen as follows. All vertices are on different levels of D. For each , the vertex of on level i has an arc to the vertex of on level . Similarly, for each i, , the vertex of on level has an arc to the vertex of on level . We now show that the remaining vertices of also have arcs to the vertices of on the next level. Observe that these vertices and the vertices on the next level correspond to edges of H whose endpoints have the same unordered color pair. Hence, consider two vertices in corresponding to two edges of H with the same unordered color pair . Since S is a clique, these two vertices in are siblings, that is they correspond to the same undirected edge. Hence, there is in D an arc between the two vertices. Hence, is a connected graph containing one vertex from each level, and thus, it is a path of length .
⇐:Let P be a -supported path of length . Clearly, P contains exactly one vertex from each of the levels of D. Let . First, since P contains exactly one vertex from each level, S contains one vertex from each color class of H. It remains to show that every pair of vertices is adjacent in H. Again, since P contains exactly one vertex from each level, it contains two vertices corresponding to the unordered color pair . Since there is an arc between these vertices, they are siblings, so we can call them and , and we have . The only neighbors of these vertices in G are i and j, respectively. Since is connected, we thus have . Furthermore, , and thus, we can assume that and . Since u is the only vertex in P with color , we have . Similarly, . Hence, u and v are adjacent in H. ☐
Note that we can adapt the construction slightly in order to show W[1]-hardness for the problem of finding a -supported path of length at most k. To achieve this, add two additional vertices t and w to the construction. Then, make t in D an outneighbor of all vertices in level k and an inneighbor of all vertices in level . Moreover, remove all arcs between level k and . Make vertex w an outneighbor of all vertices in the last level of D. Now, modify G as follows: instead of making s adjacent to all vertices of the Levels 1 through k, make w adjacent to these vertices. Then, make t adjacent to s and s adjacent to w.
With this construction, one can ensure that every -supported path takes one vertex from each layer plus t and w. This can be seen as follows (recall that any -supported path must contain at least two vertices). If the path P contains vertex t, then it must contain s and, therefore, also w, since only w is in G adjacent to any further vertices. Similarly, if the path contains s, then it must contain w. If the path contains more than one vertex from Layer 1 through k, then it must contain w and, thus, also t and s. If the path contains any vertex from any other layer, then it must contain at least one vertex from Layers 1 through k, which implies that it contains t. Thus, in all cases, the path contains s and w, which means that any -supported path, if it exists, has length . All other arguments remain the same.
Corollary 1. The problem of deciding whether there is a -supported path of length at most k is W[1]-hard, even if D is acyclic and G is a tree of diameter four.
5. Enumeration-Based Algorithms
We now describe two algorithms for deciding whether there is a -supported path of length exactly k that begins in a vertex u and ends in a vertex v. Both algorithms work for general graphs G and D. The first algorithm enumerates the paths of length k starting in u.
Theorem 6. Let denote the minimum of the maximum outdegree and the maximum indegree of G. Given two vertices , one can determine in time, by an algorithm that we call SPSearch(), whether there is a -supported path of length k from u to v.
Proof. We describe the algorithm for the case that is the maximum outdegree of D. The running time bound for the case that is the maximum indegree of D can be obtained by using the same algorithm on the instance that is obtained by reversing all arcs of D and searching for a -supported path from v to u.
The algorithm SPSearch() is a search tree algorithm. At the root, set , that is P is the trivial path of length zero that contains only u. At each search tree node, we check whether there is a -supported path that has P as the prefix. If P has length k, P is a path from u to v and is connected, then return P. Otherwise, abort the branch. If the length of P is at most , then find a solution recursively by extending P. That is, for each arc in D, where , search recursively for a solution whose prefix is (the condition is due to the fact that the solution has to be a simple path).
This approach clearly finds a -supported path from u to v if it exists. The search tree has depth k, and in each search tree node, the number of new branches is at most . Moreover, in each search tree node, we can check in time whether is connected. ☐
The second algorithm relies on an enumeration algorithm for connected subgraphs of order k in undirected graphs [25]. In the running time bound, e denotes Euler’s number.
Theorem 7. Let Δ be the maximum degree of G and be the minimum of the maximum outdegree and maximum indegree of D. Given two vertices , one can determine in time whether there is a -supported path of length k from u to v.
Proof. Assume first that a vertex set S of size k is given and that we need to determine whether has a -supported path from u to v of length . That is, we check whether has a Hamiltonian path that starts in u and ends in v. Since , this can be done in time by first building in time and then applying the standard dynamic programming algorithm for the Traveling Salesman [26,27].
Now, to obtain S or to determine that no suitable S exists, we can use the fact that all connected subgraphs of G that contain u and have k vertices can be enumerated in time [25]. The overall running time bound follows by multiplying the number of enumerated subgraphs by the time needed to verify the existence of a Hamiltonian path in each . ☐
6. Reduction Rules
We now present some data reduction rules that are used in our implementation. The first two reduction rules are obvious and can be applied in the general case when we do not search for a -supported path between u and v, but for any shortest or longest -supported path.
Rule 1. If D contains an arc , such that a and b are in different connected components of G, then remove from D.
This rule is correct since the arc cannot be part of any -supported path.
Rule 2. If G contains an edge , such that there is no path from a to b and no path from b to a in D, then remove from G.
This rule is correct, since a and b cannot be part of any -supported path. The next rule is trivial; we mention it since it is part of our implementation.
Rule 3. Remove all vertices that are isolated in either G or D.
The next two rules apply to the problem when we search a -supported path of length at most k from u to v. Their correctness is obvious as they delete vertices that cannot be in any -supported path of length at most k from u to v.
Rule 4. If V contains a vertex w, such that the sum of the length of the shortest path from u to w in D and the length of the shortest path w to v is more than k, then remove w from D and G.
Rule 5. If V contains a vertex w that is in G in a different component than u or v, then remove w from D and G. If or , then return “no”.
Our final rule removes vertices that can be reached from u and that can reach v, but that need to visit the same vertex on both paths.
Rule 6. If V contains a vertex w and a vertex x such that, in , there is no path from u to x and no path from x to v, then remove x from D and G.
The correctness of the rule follows from the fact that every path from u to x contains w, and every path from x to v also contains w. Hence, every path from u to v that visits x is not simple. As we will discuss in Section 7, these reduction rules considerably reduce the size and the maximum degrees of the biological instances.
7. Experiments
To assess the range of instances that can be solved by enumeration-based algorithms, we performed experiments on biological and synthetic data. We implemented and evaluated both algorithms.
Experimental Setup and Implementation Details. Our algorithms were implemented in Python, Version 2.7.3; source code and data are publicly available [28]. We used the NetworkX package for the graph data structures and basic graph algorithms, such as computing the shortest path. The test machine is a 4-core 3.6-GHz Intel Xeon E5-1620 (Sandy Bridge-E) with 10 MB L3 cache and 64 GB main memory, running under Debian GNU/Linux 7.0. We report wall-clock times. In all experiments, a timeout threshold of 30 seconds was used. The reported running times do not include the time for the first pass of Rules 1 to 3 (as it was performed only once in advance for the biological instance), but they include the time needed for the exhaustive application of all other data reduction rules. The first pass of Rules 1 to 3 takes less than s in all instances and is thus negligible.
The algorithm that enumerates paths, which we will call the path enumeration algorithm, is implemented as follows. Given a pair of vertices u and v, it tries to determine whether there is a -supported path from u to v as follows. First, perform the data reduction rules exhaustively. Then, determine for increasing values of k whether there is a -supported path of length at most k from u to v. This is done by invoking the enumeration algorithm SPSearch() in Theorem 6. The initial k is the maximum of the length of a shortest path from u to v in D and in G.
Moreover, when branching into the cases to extend a path by a vertex x, we perform a check based on the following observation.
Observation 1. If is a path of length ℓ and the shortest path from x to v has length at least , then there is no -supported path of length at most k with prefix .
That is, we check for each arc whether taking the shortest path from x to v gives a path of length at most k. If this is not the case, then x is discarded.
In preliminary experiments, we also tested whether reversing D and starting the search from v instead of u has an impact on the running time. Unfortunately, even if one runs both (direct and reverse) algorithms in parallel (that is, one only retains the minimum of the running times of the two algorithms), this approach does not yield a substantial speedup.
For the algorithm that enumerates connected subgraphs of G, that we call the tree enumeration algorithm (since it essentially enumerates spanning trees of subgraphs of G), we used a simple procedure for the subgraph enumeration that maintains a set S, such that and is connected. If and , then the algorithm checks whether has a Hamiltonian path from u to v. Otherwise, it recursively extends S by considering each neighbor of a vertex in S. In this procedure, we use the two following observations for early termination of the subgraph enumeration. The first observation identifies sets that are too far from v.
Observation 2. If and all vertices in S have distance at least to v, then there is no order- set such that , and is connected.
The second observation identifies sets S such that the number of arcs in is too low to obtain a directed path from u to v.
Observation 3. If has less than arcs, then there is no order- set such that , has a Hamiltonian path.
The correctness stems from the fact that the desired path has k arcs and that every deletion of a vertex can remove at most two path arcs from the graph. Unfortunately, the second observation yields a reduction only if . Nevertheless, it proved to be crucial for this algorithm, as without the corresponding early termination rule, the number of enumerated subgraphs is too large.
Biological Data. We downloaded the biochemical pathways information from the Saccharomyces Genome Database (SGD) [29], which contains for each enzyme of S. cerevisiae a mapping from its EC (enzyme catalog) number to its gene identifier. Then, also from SGD, we obtained the protein interactions for the proteins encoded by these genes. To obtain the reactions from the EC numbers, we used the Explore Enz database [30]: For each pair of EC numbers x and y, we checked whether there is at least one product of x that is a substrate of y. If this were the case, then the arc was added to D, where and are the gene identifiers associated with the EC numbers x and y, respectively. To restrict the product/substrate relationships in the directed graph to meaningful ones, we excluded five frequent metabolites (“ATP”, “ADP”, “AMP”, “H2O” and “H+”) that have high abundance in the cell. For the resulting pair of directed graph D and undirected graph G, we randomly sampled 500 vertex pairs and tried to determine for each pair whether there is a -supported path from u to v.
Synthetic Data. We performed experiments on random graphs with and vertices. The undirected graphs are created using the -model due to Erdős, Rényi and Gilbert, where each edge is present with a fixed probability p. Similarly, in the directed graph, each arc is present with a fixed probability p, that is for each pair of vertices u and v, the arc is present with probability p and the arc is also present with probability p. We use to denote the probability used for generating G and to denote the one for generating D.
For each value of n, we created two classes of instances: (i) sparse instances for which either and or and ; and (ii) dense instances for which either and or and . For each triple of values of n, and , we created 500 instances and randomly picked a pair of vertices u and v such that we aim to find a -supported path from u to v (we chose a higher number of pairs for the real-world instance to compensate for the fact that we considered only one biological instance).
Experimental Results. We first describe the experiments on the biological data. Some properties of the two networks and the effect of the data reduction rules are shown in Table 2. It can be seen that the data reduction substantially reduces the size of the remaining instances. In addition, for 358 of 500 random endpoint pairs, the data reduction solved the instance directly (by removing either v or u). Our running time results for both algorithms are shown in Figure 4. As expected, searching only for short paths is much easier than considering all solutions. In particular, we conclude that -supported paths of length at most eight can be found quickly with both algorithms. Path enumeration is consistently faster, but the difference is slightly less pronounced for .

Table 2.
Instance properties and effect of data reduction. Here, n denotes the number of vertices, and denote the number of edges in D and G, denotes the maximum outdegree in D, denotes the maximum outdegree in D, Δ denotes the maximum degree in G and and denote the number of connected components in D and G. The values in the second line are arithmetic means over those instances that where not solved by the data reduction; Rule 4 is excluded since it depends on k.
| n | Δ | |||||||
|---|---|---|---|---|---|---|---|---|
| input | 301 | 1221 | 35 | 49 | 6 | 1402 | 59 | 2 |
| after Rules 1–3, 5, 6 | 104.6 | 526.9 | 25.8 | 24.4 | 1 | 270.4 | 22.2 | 1 |
Our results for the experiments with synthetic data are shown in Figure 5 and Figure 6. Our main observations here are that sparser instances are harder than dense instances. For the path enumeration algorithm, the case when G is sparse compared to D is difficult. Here, the tree enumeration algorithm performs better both in sparse and in dense instances. The reason is most likely that in this case, short paths in D are unlikely to induce connected graphs in G. Conversely, the case in which G is dense compared to D appears to be easily solvable by the path enumeration algorithm on graphs with up to 100 vertices. Our experiments furthermore suggest that running times depend less on the vertex number than on the density of the respective graphs. Data reduction is much less effective on synthetic data: it very rarely reduces the number of edges or vertices at all. This suggests that the data reduction rules efficiently exploit the structure of real-world instances. Altogether, the experiments show that it may make sense to first compute the density of the two input graphs and then to choose the correct algorithm.
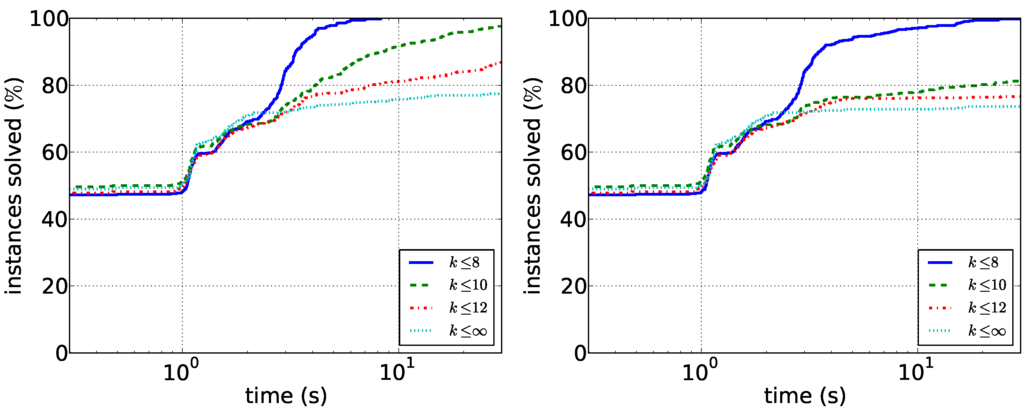
Figure 4.
Running times for the biological data. (Left) The running times of the path enumeration algorithm with restricted and unrestricted path length; (right) the running times of the tree enumeration algorithm.
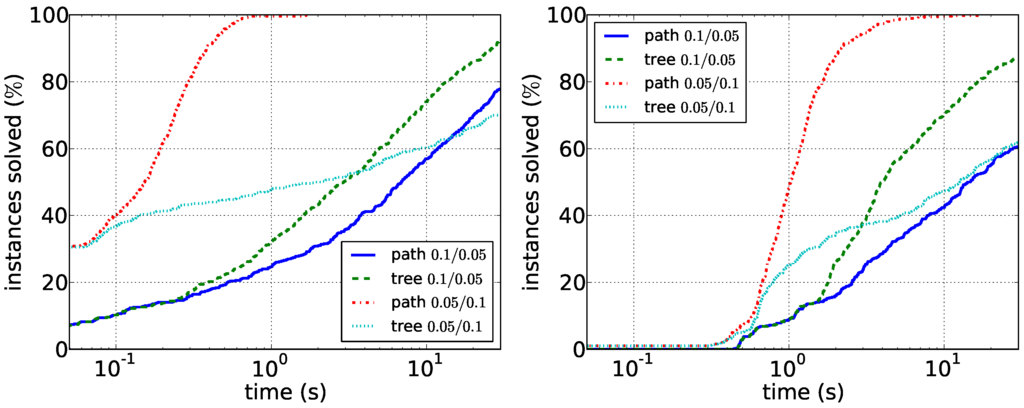
Figure 5.
Comparison of the path enumeration algorithm and the tree enumeration algorithm in sparse synthetic data. In the legend, the first number is and the second number is . (Left) ; (right) .
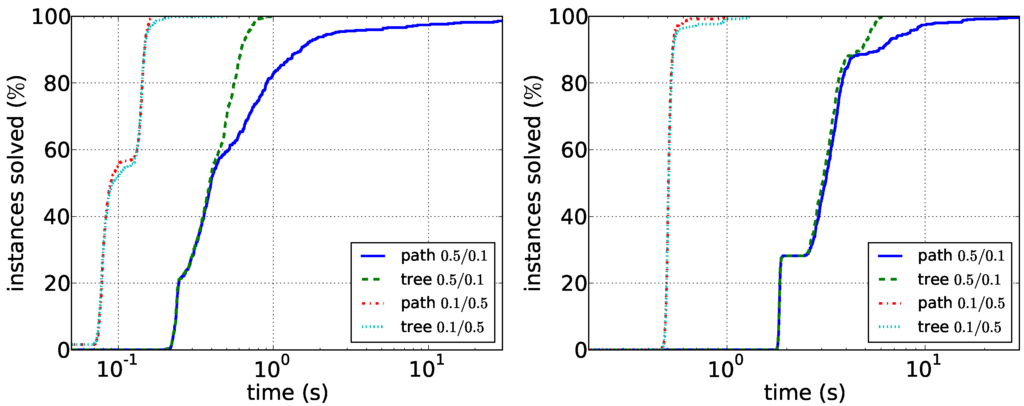
Figure 6.
Comparison of the path enumeration algorithm and the tree enumeration algorithm in dense synthetic data. In the legend, the first number is and the second number is . (Left) ; (right) .
As a final remark on random graphs, the fact that dense graphs are easily solvable is not surprising: for a fixed vertex w, the probability that there is a path in D is . The probability that is connected is: . Thus, for constant values of and , the probability that a vertex pair has a -supported path in n-vertex graph is one in the limit.
Biological Examples. A short -supported path that was found in the biological dataset is ENO2 → ARO1 → BNA4 → ALD6. Interestingly, ENO2 and ALD6 encode enzymes of the glucose fermentation pathway, whereas the enzymes encoded by ARO1 and BNA4 are not annotated as parts of this pathway. Ideally, the existence of an alternative short -supported path between ENO2 and ALD6 could either point to alternative (sub)pathways for glucose fermentation or to missing data in the yeast protein interaction network.
The longest -supported path that was found is the length 13 path HOM6 → HOM2 → BNA4 → ARO1 → ARO2 → TRP3 → GDH3 → AAT2 → GDH2 → SER1 → ALT1 → ARO9 → AGX1 → GCV2. Statistical analysis using YeastMine [31] (where the test calculates hypergeometric enrichment p-values, the significance level was set to and the p-values were corrected with the Holm–Bonferroni method) shows significant enrichment of annotation in more than 20 different GO (gene ontology) terms; all genes are annotated as parts of the “cellular amino acid metabolic process”. There is only one pathway annotation with significant enrichment: the “superpathway of phenylalanine, tyrosine and tryptophan biosynthesis”; only four genes are annotated as parts of this pathway. This discrepancy might point to missing pathway annotations.
For such direct biological conclusions, however, a more extensive analysis is necessary. In particular, a more careful construction of the metabolic network might be needed. In addition, adding further side constraints may help in finding better biological solutions. Nevertheless, the general approach of including data from two networks may prove useful, for example in the discovery of new pathways.
8. Conclusions
Supported Path belongs to a new type of subnetwork mining problems, arising from recent applications of biological, social or information networks: several graphs, of various types, represent different relations between objects, and a subset of objects is sought, with particular properties in each network. Our study of Supported Path shows that these new problems can be very hard, even if one of the input networks has a very restricted structure. For the particular case of Supported Path and its variants, we showed, for example, that the problem remains hard even if D is acyclic and G is a tree. We also provided several initial positive results, for example two algorithms for finding -supported paths, that we tested on both biological and synthetic data. In particular, this allowed us to show that short -supported paths can be found efficiently on realistic data.
Only two cases are left open by our complexity analysis: D is acyclic; is outerplanar; and G is either a tree or a general graph. For these two input restrictions, the complexities of Supported Path and of Shortest Supported Path are open. It would be interesting to determine if these problems are polynomial or NP-complete.
Further studies could either investigate the complexity of Supported Path in terms of approximability (on specific graph classes) or inexact variants of the problem obtained, for instance, by allowing small differences between the vertex set of the path in D and the connected set in G. It is also an open problem to find efficient exact exponential-time algorithms with a running time of for some small c. As Longest Supported Path is already a generalization of a Directed Hamiltonian Path, it might be interesting to focus either on Supported Path and Shortest Supported Path or on special cases of the problem, for example the case that D is acyclic. Furthermore, it is open to identify cases in which Supported Path is polynomial-time solvable, but Shortest Supported Path is NP-hard. Finally, our results show that finding supported paths remains hard if both and G have constant treewidth. The graph where is the union of the edges of and G, however, might have unbounded treewidth. Hence, the complexity of all three problems remains open for the case that has bounded treewidth.
Concerning the implementation, we showed that a simple approach can find -supported paths of length at most eight. With a more efficient implementation of the graph data structures and shortest path algorithms, it should be possible to increase the “maximum tractable” path length by one or two. To find even longer paths, either further data reduction rules or more efficient early termination rules could be promising approaches. Finally, it could be interesting to study heuristic approaches that reduce the general problems that are very hard to restricted variants; for example, to the variant in which D is acyclic [32].
Acknowledgments
The authors would like to thank the referees for their detailed and constructive remarks that substantially helped to improve the paper.
Christian Komusiewicz was partially supported by a post-doctoral grant funded by the Région Pays de la Loire and by the DAAD Procope program (Project 55934856).
Author Contributions
The problem definition, theoretical analysis, and algorithm design were performed jointly by all authors; C.K. implemented the algorithms and performed the experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cai, D.; Shao, Z.; He, X.; Yan, X.; Han, J. Mining Hidden Community in Heterogeneous Social Networks. In Proceedings of the ACM-SIGKDD Workshop on Link Discovery: Issues, Approaches and Applications (LinkKDD 2005), Chicago, IL, USA, 21–25 August 2005; pp. 58–65.
- Matsuo, Y.; Hamasaki, M.; Takeda, H.; Mori, J.; Bollegara, D.; Nakamura, Y.; Nishimura, T.; Hasida, K.; Ishizuka, M. Spinning Multiple Social Networks for Semantic Web. In Proceedings of the Association for the Advancement of Artificial Intelligence (AAAI 2006), Boston, MA, USA, 16–20 July 2006; pp. 1381–1387.
- Vicentini, R.; Menossi, M. Data Mining and Knowledge Discovery in Real Life Applications; Ponce, J., Karahoca, A., Eds.; In-Tech: Croatia, Rijeka, 2009. [Google Scholar]
- Bunke, H. Graph matching: Theoretical foundations, algorithms and applications. In Proceedings of the International Conference on Vision Interface (VI 2000), Montréal, QC, Canada, 14–17 May 2000; pp. 82–88.
- Conte, D.; Foggia, P.; Sansone, C.; Vento, M. Thirty years of graph matching in pattern recognition. Int. J. Pattern Recogn. Artif. Intell. 2004, 18, 265–298. [Google Scholar] [CrossRef]
- Džeroski, S. Relational Data Mining; Springer: Berlin, Germany, 2010. [Google Scholar]
- Kelley, B.P.; Yuan, B.; Lewitter, F.; Sharan, R.; Stockwell, B.R.; Ideker, T. PathBLAST: A tool for alignment of protein interaction networks. Nucleic Acids Res. 2004, 32. [Google Scholar] [CrossRef] [PubMed]
- Sharan, R.; Suthram, S.; Kelley, R.M.; Kuhn, T.; Mccuine, S.; Uetz, P.; Sittler, T.; Karp, R.M.; Ideker, T. Conserved patterns of protein interaction in multiple species. Proc. Natl. Acad. Sci. USA 2005, 102, 1974–1979. [Google Scholar] [CrossRef] [PubMed]
- Wernicke, S.; Rasche, F. Simple and Fast Alignment of Metabolic Pathways by Exploiting Local Diversity. Bioinformatics 2007, 23, 1978–1985. [Google Scholar] [CrossRef] [PubMed]
- Pinter, R.Y.; Rokhlenko, O.; Yeger-Lotem, E.; Ziv-Ukelson, M. Alignment of metabolic pathways. Bioinformatics 2005, 21, 3401–3408. [Google Scholar] [CrossRef] [PubMed]
- Bourqui, R.; Lacroix, V.; Cottret, L.; Auber, D.; Mary, P.; Sagot, M.F.; Jourdan, F. Metabolic network visualization eliminating node redundance and preserving metabolic pathways. BMC Syst. Biol. 2007, 1. [Google Scholar] [CrossRef] [PubMed]
- Planes, F.; Beasley, J. A critical examination of stoichiometric and path-finding approaches to metabolic pathways. Brief. Bioinform. 2008, 9, 422–436. [Google Scholar] [CrossRef] [PubMed]
- Zubarev, R.; Nielsen, M.; Fung, E.; Savitski, M.; Kel-Margoulis, O.; Wingender, E.; Kel, A. Identification of dominant signaling pathways from proteomics expression data. J. Proteom. 2008, 71, 89–96. [Google Scholar] [CrossRef] [PubMed]
- Bruckner, S.; Hüffner, F.; Karp, R.M.; Shamir, R.; Sharan, R. Topology-Free Querying of Protein Interaction Networks. J. Comput. Biol. 2010, 17, 237–252. [Google Scholar] [CrossRef] [PubMed]
- Boyer, F.; Morgat, A.; Labarre, L.; Pothier, J.; Viari, A. Syntons, metabolons and interactons: An exact graph-theoretical approach for exploring neighbourhood between genomic and functional data. Bioinformatics 2005, 21, 4209–4215. [Google Scholar] [CrossRef] [PubMed]
- Durek, P.; Walther, D. The integrated analysis of metabolic and protein interaction networks reveals novel molecular organizing principles. BMC Syst. Biol. 2008, 2. [Google Scholar] [CrossRef] [PubMed]
- Williams, E.; Bowles, D.J. Coexpression of neighboring genes in the genome of Arabidopsis thaliana. Genome Res. 2004, 14, 1060–1067. [Google Scholar] [CrossRef] [PubMed]
- Downey, R.G.; Fellows, M.R. Parameterized Complexity; Springer: Berlin, Germany, 1999. [Google Scholar]
- Flum, J.; Grohe, M. Parameterized Complexity Theory; Springer: Berlin, Germany, 2006. [Google Scholar]
- Niedermeier, R. Invitation to Fixed-Parameter Algorithms; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Hartung, S.; Nichterlein, A.; Technische Universität Berlin. Personal communication, 2013.
- Fortune, S.; Hopcroft, J.; Wyllie, J. The directed subgraph homeomorphism problem. Theor. Comput. Sci. 1980, 10, 111–121. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness (Series of Books in the Mathematical Sciences); W. H. Freeman and Company: San Francisco, CA, USA, 1979. [Google Scholar]
- Fellows, M.R.; Hermelin, D.; Rosamond, F.A.; Vialette, S. On the parameterized complexity of multiple-interval graph problems. Theor. Comput. Sci. 2009, 410, 53–61. [Google Scholar] [CrossRef]
- Komusiewicz, C.; Sorge, M. An Algorithmic Framework for Fixed-Cardinality Optimization in Sparse Graphs Applied to Dense Subgraph Problems. Discret. Appl. Math. 2015, in press. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming Treatment of the Traveling Salesman Problem. J. ACM 1962, 9, 61–63. [Google Scholar] [CrossRef]
- Held, M.; Karp, R.M. A dynamic programming approach to sequencing problems. J. Soc. Ind. Appl. Math. 1962, 10, 196–210. [Google Scholar] [CrossRef]
- Supported Path Software. Available online: http://fpt.akt.tu-berlin.de/supported-path (accessed on 8 October 2015).
- Cherry, J.M.; Hong, E.L.; Amundsen, C.; Balakrishnan, R.; Binkley, G.; Chan, E.T.; Christie, K.R.; Costanzo, M.C.; Dwight, S.S.; Engel, S.R.; et al. Saccharomyces Genome Database: The genomics resource of budding yeast. Nucleic Acids Res. 2012, 40. [Google Scholar] [CrossRef] [PubMed]
- McDonald, A.; Boyce, S.; Moss, G.; Dixon, H.; Tipton, K. ExplorEnz: A MySQL database of the IUBMB enzyme nomenclature. BMC Biochem. 2007, 8. [Google Scholar] [CrossRef] [PubMed]
- Balakrishnan, R.; Park, J.; Karra, K.; Hitz, B.C.; Binkley, G.; Hong, E.L.; Sullivan, J.; Micklem, G.; Cherry, J.M. YeastMine—An integrated data warehouse for Saccharomyces cerevisiae data as a multipurpose tool-kit. Database 2012. [Google Scholar] [CrossRef] [PubMed]
- Blin, G.; Fertin, G.; Mohamed-Babou, H.; Rusu, I.; Sikora, F.; Vialette, S. Algorithmic Aspects of Heterogeneous Biological Networks Comparison. In Proceedings of the 5th International Conference on Combinatorial Optimization and Applications (COCOA 2011), Zhangjiajie, China, 4–6 August 2011; pp. 272–286.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).