Abstract
DNA fragment assembly represents an important challenge to the development of efficient and practical algorithms due to the large number of elements to be assembled. In this study, we present some graph theoretical linear time algorithms to solve the problem. To achieve linear time complexity, a heap with constant time operations was developed, for the special case where the edge weights are integers and do not depend on the problem size. The experiments presented show that modified classical graph theoretical algorithms can solve the DNA fragment assembly problem efficiently.
1. Introduction
Since its discovery by Watson and Crick [1], the importance of DNA to biology, medicine and human kind has been evident. However, we had to wait some time until it was possible to sequence the DNA bases, which was accomplished by Sanger in the mid-1970s [2], by detecting small dark bands on a thin gel layer. This method severely constrains the length of the DNA to be sequenced due to the limited resolution of the dark bands. In order to solve this problem, the DNA is first cut in known places by using restriction enzymes, which will divide the DNA at the point where a specific base sequence is found. The resulting sub-sequences, are divided again, this time using a different restriction enzyme, and this process is repeated until the resulting fragments can be divided in random places yielding sub-fragments that are small enough as to provide the complete sequence of bases using Sanger’s method. This process was slow and expensive because every time that a sequence was divided, each resulting subsequence had to be cloned in order to have enough material for the next division. This problem prompted scientists to start dividing sequences in random positions from the beginning, instead of doing it after several divisions, saving time and money [3]. This method, in turn, created a severe computational problem since there is no information about the order of the fragments. If one starts with many copies of the original problem and the derived fragments are sequenced, then each base of the original problem could appear in several fragments. The sum of the lengths of the fragments divided by the length of the original problem is known as its coverage. We hope that if we have a large enough coverage, the fragments will overlap in such a way that the sequence at the end of a fragment overlaps with the sequence at the beginning of another one. Hence, in theory, we should be able to use this information to sort the fragments and reconstruct the original DNA sequence.
What really happens is not very simple since, by chance, there are a huge number of false overlaps amongst the fragments. There is also the problem that fragment sequencing is not perfect. Two percent error is common, as well as having fragments that do not belong to the original problem, some due to contamination with DNA foreign to the problem, and others because of the appearance of chimeras from the process of DNA cloning, in which bacteria DNA is used, so that we could get fragments with portions of bacteria DNA. On top of what was said, we have repeats, which are DNA sections that appear tens or hundreds of times one after another (tandem repeats) or in far away parts of the original DNA (interspersed repeats) [4].
As far as we know, at this point there is no good probabilistic model of DNA. Simple, or relatively simple ones do not explain the repeats. For instance, in the real life problem that we will present later in this paper, there are sequences of A bases that are extremely long. Figure 1 show some examples of fragments that come from the sample problem that we will use in Section 4 of this paper and Table 1 shows the probability that it happens considering that among the total number of fragments, the A bases occurs with probability 0.3249. As can be seen from the figure, the number of times that the A chain occurs in the real data is much larger than the expected value according to a simple probabilistic model. Despite these anomalies and some others, some of the parameters that are used in the assembly of fragments, such as the minimum number of bases that an overlap must have to be considered important, have an empirical basis [5].
There is also the problem that in real situations, sections of the original DNA problem have no coverage since fragments are obtained by a random process and it is not possible guarantee that there are fragments from every part of the genome under study. This is the reason why the resulting assembly of all fragments is a set of contigs or subsequences and almost never the entire sequence of the problem. It is the job of specialized biologists to fill in the gaps and correct assembly errors made during the automated process.

Figure 1.
Some fragments from the S. aureus strain MW2 problem.

Table 1.
Observed frequency on n bases A vs. expected value for p = 0.3249 and 5,324,340 fragments.
| n | Observed | Probability | Expected Value |
|---|---|---|---|
| 15 | 101 | 0.000000475 | 2.528889873 |
| 16 | 74 | 0.000000147 | 0.784225487 |
| 17 | 65 | 0.000000046 | 0.242640081 |
| 18 | 51 | 0.000000014 | 0.074884674 |
| 19 | 40 | 4.32861E−09 | 0.023046972 |
| 20 | 39 | 1.32807E−09 | 0.007071095 |
| 21 | 18 | 4.06052E−10 | 0.002161959 |
| 22 | 28 | 1.23662E−10 | 0.000658416 |
| 23 | 14 | 3.74924E−11 | 0.000199622 |
| 24 | 15 | 1.13089E−11 | 0.000060212 |
| 25 | 22 | 3.3908E−12 | 0.000018054 |
| 26 | 15 | 1.00958E−12 | 0.000005375 |
| 27 | 22 | 2.9809E−13 | 0.000001587 |
| 28 | 11 | 8.71281E−14 | 0.000000464 |
| 29 | 15 | 2.51495E−14 | 0.000000134 |
| 30 | 10 | 7.14487E−15 | 3.80417E−08 |
| 31 | 9 | 1.98796E−15 | 1.05846E−08 |
| 32 | 6 | 5.37563E−16 | 2.86217E−09 |
| 33 | 4 | 1.3946E−16 | 7.42531E−10 |
| 34 | 4 | 3.38757E−17 | 1.80366E−10 |
| 35 | 1 | 7.29107E−18 | 3.88201E−11 |
DNA fragment sequencing technology has continued to advance while costs continue to go down. The original shotgun technology has been called “long reads” because the fragments would normally have more than 500 bases. Using new technologies, commonly known as Next Generation Sequencing, the cost to sequence a million bases is about $1 [6]. Unfortunately, the length of the fragments is shorter using this newer technology. Today, 150 bases reads are common with the Illumina sequencers. To compensate for the problems derived from the short size of each fragment, coverage of about 40 is needed instead of a coverage of about 10 in the case of long reads. If we consider the number of fragments to be sequenced with newer technologies, we need to assemble three to four million fragments to sequence a bacterium, while using long reads, only 50,000 fragments were enough. These are really bad news due to the combinatorial nature of the solutions to the problem.
Since the very beginning of DNA fragment sequencing, greedy algorithms have been used; for instance, we pick a random fragment and connect to it the one that has the longest overlap. This process is repeated until no overlapping fragments are available. Nowadays, this technique would be difficult to use, since fragments are too short, which often produces several different fragments with the same overlap size. Another popular technique is the use of De Bruijn graphs [7]. In order to build these graphs, all possible k-mers (subsequence of k consecutive bases) of each fragment are used to find all possible overlaps among them. Using these graphs, several problems can be solved by using heuristics; for instance, given a k-mer, there might be two parallel paths to other k-mer, creating what is called a bubble. The bubble is then popped by removing the shortest side or projecting one side onto the other when they have the same length. Short sequences that originate from long ones are eliminated. It is common to use a value of k close to 20 in order to obtain the k-mers.
An approach based on genetic algorithm optimization was suggested by Parsons in 1993 [8]. Later, other scientists applied similar metaheuristics [9,10,11,12], but their results were based on very small benchmarks, the largest had about 1000 fragments, and even though results were improving slowly, they were still far from real problems, including the long reading ones, with tens of thousands of fragments. In 2013, a reduction from fragment DNA sequencing to the Traveling Salesman Problem (TSP) was used [13]. Taking advantage of formal heuristics and algorithms for the TSP, optimal values were found for the most commonly used benchmarks, and, for the first time, a real life problem was solved using optimization.
The remainder of this paper is organized as follows: Section 2 provides the basic ideas on the use of graph theory for the solution of DNA sequencing problems; Section 3 explains those algorithms that are necessary to tackle the problem; Section 4 illustrates the use of our algorithms on real life problem benchmarks; and, in Section 5, we give our conclusions and future work.
2. Use of Graph Theory
2.1. Generalities
In reference [13], a graph theory approach was used by means of the TSP, where the solution obtained from the assembly of fragments is a series of contigs rather than a Hamiltonian Path. In TSP, all possible edges of the graph are considered, but when there is no possible connection between two nodes, it is usually represented using a very large weight to prevent it from showing up in the final solution. Applying TSP to DNA fragment assembly might be considered excessive, even though the expected results are obtained, since the fraction of real connections is very small. A graph theoretical approach using other algorithms might give better results.
The size of real life DNA fragment assembly problems is huge, with 35 base fragments and a coverage of 40, we get about 700 million fragments for human chromosome number 1, which has 245 million base pairs. It is known that the DNA fragment assembly problem is NP-hard (Non-deterministic Polynomial time hard), since it can be reduced from the shortest common superstring problem [14]; in practice, we must only use linear time algorithms, even if by doing so we sacrifice correctness and obtain only an approximate solution.
2.2. DNA Fragment Assembly as a Graph
The DNA fragment assembly problem can be transformed into a directed graph: we need to find a sequence of fragments where each one is always the prefix of the next one. We know that DNA comes in pairs of strands (double helix) that run in opposite directions, where in front of each base of one strand, there is a base of the reverse-complement on the other; for instance, an A in front of a T and a C in front of a G, which clearly means that the information contained in each one of the strands is the same. When DNA fragment overlaps are obtained, it is not known what strand they come from, i.e., every time that an overlap is computed, the strand and its reverse-complement must be considered. This means that a prefix of a normal overlap becomes a suffix of the reverse-complement. At first, it might seem that this case could be represented by a simple non-directed edge between the two fragments. However, this is not so if we consider that each node or fragment that is a reverse-complement must also be a reverse-complement for every edge that connects to it.
As a small example, we present a set of 13 fragments, Table 2, the associated overlap matrix, Table 3 and the resulting graph, Figure 2.

Table 2.
Graph example: fragments.
| Fragment number | Sequence |
|---|---|
| 1 | GTGTACCACGTACTGATGTACTATTTGAAGCTTAT |
| 2 | CCCAATTCCTAATGTACTATTTGAAGCTTATTCGG |
| 3 | CATAAGCTTCATGATGAAGCTTATTCGGCCAATCG |
| 4 | TTTGATTCCTGCTGATGTACTATTTGATGAAGCTT |
| 5 | ATGTACTATTTGAAGCTTATTCGGCCAATCGTACT |
| 6 | GAAGCTTATTCGGCCAATCGTACTGATGTACTATT |
| 7 | CTTATTCGGCCAATCGTACTATTTACTGATGTACA |
| 8 | TGATGAAGCTTATTCGGCCAATCGTACTGATGTAC |
| 9 | GGCCAATCGTACTGATGTACTATTTGATGAAGCTT |
| 10 | CTGATGTACTATTTGATGAAGCTTATTCGGCCAAT |
| 11 | TGTACTATTTGATGAAGCTTATCAGTACGTGGAAC |
| 12 | AATCGTACTGATGTACTATTTACTGATGTACAATA |
| 13 | CTATTTACTGATGTACAATAGTACATCAGTAAAAA |

Table 3.
Graph example: overlaps matrix.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 20 | ||||||||||||
| 2 | 24 | ||||||||||||
| 3 | 20 | 24 | |||||||||||
| 4 | 24 | ||||||||||||
| 5 | 20 | 20 | |||||||||||
| 6 | 24 | 20 | |||||||||||
| 7 | 17 | ||||||||||||
| 8 | 20 | ||||||||||||
| 9 | 24 | 20 | |||||||||||
| 10 | 22 | ||||||||||||
| 11 | |||||||||||||
| 12 | 20 | ||||||||||||
| 13 |
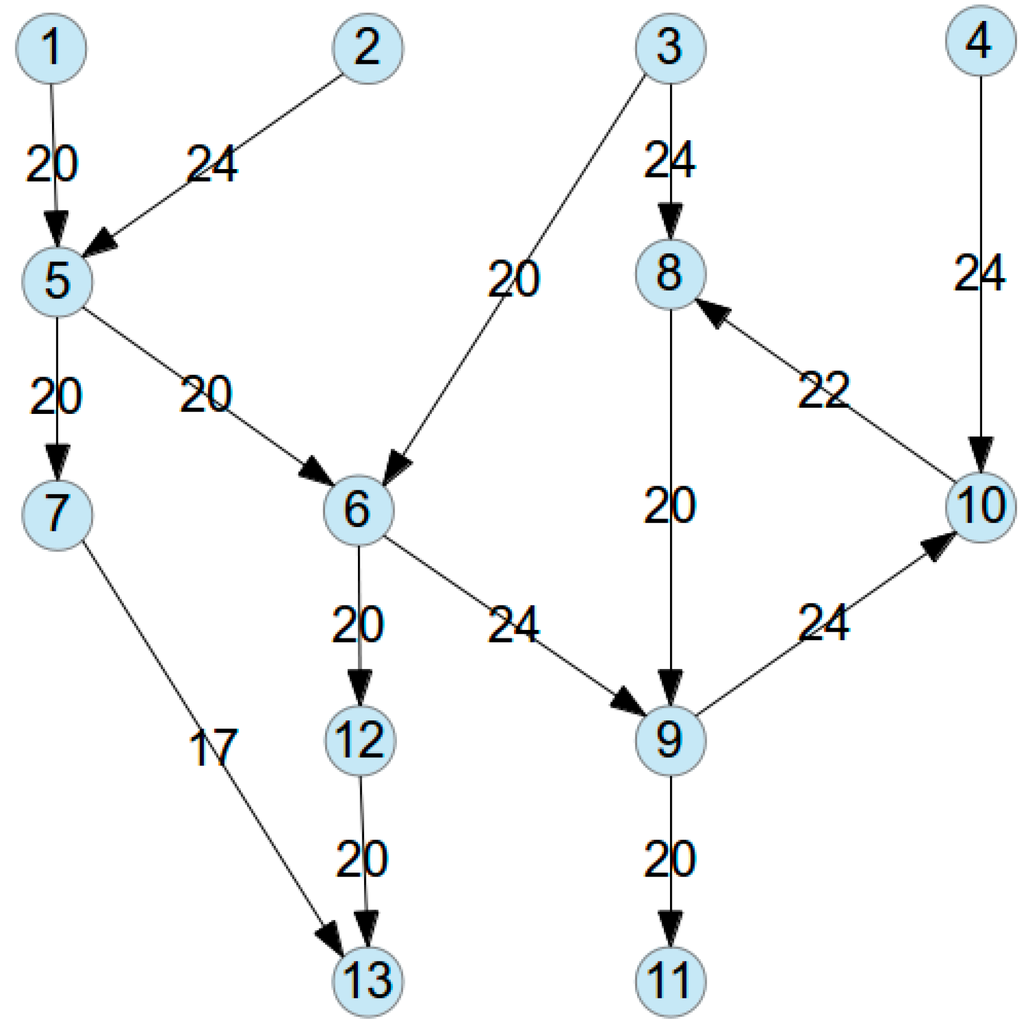
Figure 2.
Graph example: graph.
2.3. Objective Function
In the literature, using nature inspired algorithms to solve the DNA fragment assembly problem published after Parsons [8], the associated graph has been considered to be an undirected graph. Other literature considered bi-directed graphs, especially when De Bruijn graphs were proposed. It is common to use a Hamiltonian path, even though sometimes Eulerian paths have been used too [7]. In any case, it is not entirely clear how many times each one of the fragments should be used, since, from the physical point of view, it is feasible for a sequence to repeat in different sections of the DNA, and for identical fragments to come from different places. Thinking that a fragment and it reverse-complement are the same, creates too much complexity from the algorithmic point of view as well as from the programming one, and would only be justified as long as it was strictly required to consider Hamiltonian paths. Hence, we consider each reverse-complement fragment as an independent fragment. Another possibility might be to trust the huge cover that is customary in Next Generation Sequencing (NGS) and not use reverse-complements.
With respect to the objective function for the optimization, in many papers, the sum of the overlaps of each fragment with the next one is used, which has probably been inherited from the use of some greedy algorithms. In addition to this objective function, we propose to maximize the sum of the lengths of the contigs. This can be achieved by considering that each time that a new fragment is added at the end of a contig, its length is incremented by an amount equal to the length of the fragment minus the overlap length. So we would have the following objective functions:
where w(i, i + 1) is the number of overlapped bases between fragment i and the next one in the sequence, n is the number of fragments, and L is the length of the fragment. Notice that Equation (2) can easily be transformed into a minimization:
Because
The boundary between contigs appears because there are values of w(i, i + 1) that are equal to 0. Since there is usually some contamination with foreign DNA and there might be chimeras, some of the obtained contigs do not belong to the original DNA, and, at some point, which is not within the scope of this paper, useful contigs must be separated from the useless ones.
In order to obtain each contig, an agreement must be reached (computed) for each base, i.e., since we know that there might be redundancy for each base (due to the original cover) and that there might be sequencing errors in the fragments, it is possible for each base in each contig to have several versions, from which the most frequent value must be accepted, even if it is the minimum acceptable value. Since most of the errors in the contigs are at the ends, due to chemical problems in the sequencing equipment or because of the lack of enough redundancy, it might be necessary to cut them off.
3. Algorithms
3.1. Basic Algorithm for F1 and F2
For the objective function F1, we propose an algorithm similar to topological sorting. Let G = (V, E) be a directed acyclic graph (DAG) where V is the set of vertices, E is the set of edges and w(u, v) is the weight of edge u→v. In this graph, the longest path will go from a node that has no edge going in (initial vertex) and those nodes that are connected to it. Notice that there might be several “initial vertices”, and that there is no single privileged node. Let be the set of vertices with in-degree din(v) = 0 and let Q be a stack. The algorithm to determine the longest distance from a given vertex to each of the other vertices is the following (Algorithm 1):
| Algorithm 1. Longest distance from initial vertices |
| 1. For each vertex with din(v) = 0 |
| 1.1. push(Q,v) |
| 1.2. d(v):=0 |
| 1.3. origin(v):=v |
| 2. While Q is not empty |
| 2.1. u:=pop(Q) |
| 2.2. for each vertex v |
| 2.2.1. din(v):=din(v)−1 |
| 2.2.2. if din(v)=0 |
| 2.2.2.1. push(Q,v) |
| 2.2.2.2. |
| 2.2.2.3. father(v):=x |
This algorithm only works if the graph is acyclic. In real life DNA fragment assembly problems, there are cycles. When this algorithm is applied to a graph with cycles, neither the cycles nor the nodes that are further from the cycles are detected. Later we will discuss how to take care of cycles.
3.2. Constant Time Heap
Aside from a modified version of the algorithm of Section 3.1, there are other ways to tackle the cycle problem. One way, not necessarily the best way, would be to build a minimum spanning tree, even if it ignores the direction of the edges. It is clear that if there are no undirected cycles in the equivalent undirected graph, there should be no directed cycles in its directed version. So we could use one of several algorithms like Prim [15] and Kruskal [16], both with time complexity in O(|E| log|V|) when using a Fibonacci Heap.
In order to achieve the linear time complexity that we require, we notice that in the case of the DNA fragment sequencing problem, we should use a heap that can insert and extract-min in constant time, thus improving the time complexity of other data structures where the extract-min operation is in O(log n).
Our heap requires that the ordering values are integers independent from the number of nodes in the graph. In the DNA fragment sequencing problem, the edges of the graph are the fragment overlaps, hence it is an integer value representing the number of bases, and its value is also bounded by 0 < w(u, v) < L, where L does not depend of the number of fragments, and has a value of at most a few hundred bases. The heap that we propose is based on a Stack Pi for each possible value to be introduced. The heap operations are:
| Algorithm 2. Stack heap insert and extract min |
| insert x |
| 1. push(Px,x) |
| 2. if x<xmin |
| 2.1. xmin:=x |
| 3. if x > xmax |
| 3.1. xmax:=x |
| extract-min |
| 1. x:=pop(Pxmin) |
| 2. While the stack Pxmin is empty and xmin ≤ xmax |
| 2.1. xmin: = xmin + 1 |
In the extract-min operations shown, the value that is in the stack corresponding to xmin is extracted. If the stack is empty, the next non-empty stack smaller than the maximum value is used. When the number of stacks is large enough, it is useful to use some other kind of heap, such as a binary or a Fibonacci heap instead of sequential search. In the example that we provide in Section 4, we use no more than 34 stacks (0 ≤ x ≤ 34), hence sequential search turns out to be faster. The time complexity of the insert operation is constant because Steps 1 through 3.1 always require the same amount of time. In the extract-min operation, Step 1 is of constant time and Step 2, which is only executed when the stack with the minimum values is empty, in the worst case depends on the value xmax, and could be linear, in the case of sequential search, or logarithmic if a heap is used. In the case of DNA fragment assembly, millions of edges or nodes will be inserted into the heap, hence the value of xmax should be close to a few hundred, which makes the probability of Step 2 executing more than once negligible. In any case, since the time complexity of our heap is independent from the number of nodes or vertices inserted into it, then Prim’s algorithm [15] as well as Kruskal’s [16] algorithm become linear. Even though our technique is designed to work in the particular case of DNA fragment assembly, it is possible that it could also be used in other problems.
3.3. MST in Linear Time
As mentioned before, when using our heap, Algorithm 2, Prim’s algorithm as well as Kruskal’s algorithm become linear, and even though it is possible to implement operations such as delete-key and decrease-key in our heap, it is more convenient to allow the edge values to create a cycle and discard them when leaving the heap, since this is more efficient and is also of constant time. Let M(F, V) be the MST of graph G(E, V) and let S be the set of vertices that have been added to the MST at some point during the execution of Prim’s algorithm. Here is our version of Prim’s algorithm:
| Algorithm 3. Prim’s algorithm |
| 1. For some vertex u |
| 1.1. Put u in S |
| 1.2. For each |
| 1.2.1. insert w(u,v) in the heap |
| 2. While the heap is not empty |
| 2.1. Extract the edge (u, v) from the heap |
| 2.1.1. if |
| 2.1.1.1. Put u in S and (u,v) in F |
| 2.1.1.1.1. For each insert w(u,x) in the heap |
| 2.1.2. if |
| 2.1.2.1. Put v in S and (v,u) in F |
| 2.1.2.1.1. For each insert w(v,x) in the heap |
Since at most |E| edges will be inserted and extracted in constant time, Algorithm 3 will have a time complexity in O(|E|).
Now, our version of Kruskal’s algorithm (Algorithm 4):
| Algorithm 4. Kruskal’s algorithm |
| 1. Insert E in a heap in increasing order of w(u,v) |
| 2. Create a forest F where each vertex is an independent tree |
| 3. While the heap is not empty |
| 3.1. Extract (u,v) from heap |
| 3.1.1. If u and v belong to different trees, merge both trees |
In order to merge the trees, we use union by rank with path compression [17]. The time complexity of Step 1 is O(|E|), Step 2 is O(|V|). Step 3 is repeated |E| times and every time the following operations are performed: extraction of the minimum value from the heap, a find of two nodes, and in the worst case, the union of two trees. Find is in O(1) and the union is O(log*|E|) [17], which for problems with 65,535 edges up to the maximum physical size of DNA fragment assembly problems is 5; therefore, in practice the algorithm is in O(1). The total running time of Kruskal’s algorithm using our heap, Algorithm 2, with union by rank and path compression, applied to the DNA fragment assembly problem is in O(|E| + |V|). Once the MST has been computed, its maximum distances are computed using Algorithm 1. In this case, there are no cycles (directed or undirected), so Algorithm 1 works correctly.
3.4. Modification of the Basic Algorithm
There are two kinds of cycles that cause trouble: cycles that are connected to a start node, and disconnected cycles. In both cases, there might be sets of nodes that are created like attachments to nodes of the cycle, but do not belong to them, and are not detected by Algorithm 1. In the case of disconnected cycles, we would need to take any node as a start node, which can require some trial and error since a randomly selected node could be attached to the cycle but not necessarily in the cycle itself. However, disconnected cycles in real life DNA fragment sequencing problems are rare, and when they appear, they are usually very small, two or three nodes, that lead to contigs that are too small and that would have been discarded anyway.
A cycle connected to a start node of the graph appears when there are nodes for which, even when paths that go from a start node to another node u in the cycle, the value of din(u) never goes to zero because at least one edge comes from the cycle. When Algorithm 1 is done, we can take one of the nodes that went through Step 2.2.1, but that remained with a final value of din(u) > 0, and insert it into the stack to continue with Step 2 of the algorithm. It is necessary, however, to mark those nodes so that they will not be considered again and to avoid the cycle being traversed more than once. The total distance from a start node to the last processed node in the cycle is the sum of the distance from a start point to the cycle entry point plus the length of the cycle, minus the edge that would close the cycle on the start node in the cycle. So we have that if the selected node is s, the previous node in the cycle is t, and the total length of the cycle is C then:
Among the distinct entry nodes to the cycle, we could select one with the longest distance to a start node. However, it does not guarantee that we will always find the longest distance to node t since the value of w(t, s) changes with the selection of s and there could be another cycle entry node with a smaller value of d(s) but with a small enough value of w(t, s) to give a longest distance. In the case of the DNA fragment assembly problem the values of w( ) are in a very narrow range, most of the distances to the start node are big and it is uncommon for them to be similar, so that if our heuristic consists of selecting an s with the longest distance to the start point, we will have a high probability of finding the maximum distance. The modified algorithm (Algorithm 5) is as follows:
| Algorithm 5. Modified maximum distance algorithm |
| 1. For each vertex with din(v) = 0 |
| 1.1. push(Q,v) |
| 1.2. d(v):=0 |
| 1.3. origin(v):=v |
| 2. While there are vertices v with din(v) > 0 |
| 2.1. While Q is not empty |
| 2.1.1. u:=pop(Q) |
| 2.1.2. For every vertex v where and v is not marked |
| 2.1.2.1. din(v):=din(v)-1 |
| 2.1.2.2. If din(v)=0 |
| 2.1.2.2.1. push(Q,v) |
| 2.1.2.2.2. |
| 2.1.2.2.3. insert d(v) in a heap |
| 2.1.2.2.4. father(v):=x |
| 2.1.2.2.5. origin(v):=origin(x) |
| 2.2. If the heap is not empty |
| 2.2.1. extract the node v from heap |
| 2.2.1.1. If din(v)>0 |
| 2.2.1.1.1. Make din(v)=0 |
| 2.2.1.1.2. Insert v in the stack |
| 2.2.1.1.3. Mark the node v |
| 2.2.1.1.4. Go to step 2.1 |
Notice that Step 2.2.1.1 is required since node v could have gone through Step 2.1.1 and already be in a path. In this case, we can use the heap to keep the time complexity of the algorithm linear.
3.5. Assembly Algorithm
The output from Algorithms 1 and 4 is a sequence of directed edges and nodes that allow us to directly build the contigs. Considering reverse-complement fragments as independent of the original ones makes the job easier. The reconstruction of the sequence of DNA in the contig consists of placing the first fragment, and then adding the overlap-free portion of the next fragment. In our method, we do not need to reach a computed agreement as in other methods [18] since we do not differentiate among overlapped bases from one or other fragment. However, the ends of the contig might have sequencing errors and there is nothing to verify that there are no such errors. The solution is to cut off the ends in such a way that a minimum agreement is reached, i.e., that the bases must appear in at least a given number of fragments.
4. Experiments
In order to test our algorithms, we used several benchmarks that are available for use by researchers [19]. We selected the benchmarks of S. aureus MW2 with short reads. The benchmarks that we used have the following number of fragments: 2,278,504, 730,201, 298,194, 89,718 and 22,447. From now on, we will refer to each one of these problems by its number of fragments. In order to have something to compare our results to, we ran the Edena assembler using the same data, Table 4. This comparison has some limitations due to the fact that Edena uses a series of heuristics in order to refine its solution, by eliminating contigs that have no real meaning, while our results are those directly generated by our algorithms with no refinement. Refining the raw results from our algorithms might be part of our future research.

Table 4.
Edena benchmark results.
| Problem | ||||||
|---|---|---|---|---|---|---|
| Fragments | 22,448 | 89,718 | 298,194 | 730,201 | 2,278,504 | |
| Contigs Obtained | 186 | 258 | 575 | 837 | 2046 | |
| Total Number of Bases | 26,284 | 102,684 | 314,120 | 788,198 | 2,526,278 | |
| Contigs Found | Contigs Found | 184 | 256 | 565 | 823 | 1920 |
| % | 98.9 | 99.2 | 98.3 | 98.3 | 93.8 | |
| Bases Found | 26,024 | 102,249 | 310,965 | 777,583 | 2,463,563 | |
| % | 99 | 99.6 | 99 | 98.7 | 97.5 | |
| N50 | 188 | 1247 | 2911 | 4132 | 5250 | |
| Average Length | 141.4 | 399.4 | 550.4 | 944.8 | 1283.10 | |
| Minimum Length | 52 | 52 | 52 | 52 | 52 | |
| Maximum Length | 880 | 7295 | 10,985 | 20,521 | 20,579 | |
| Contigs not Found | Contigs not Found | 2 | 2 | 10 | 14 | 126 |
| % | 1.1 | 0.8 | 1.7 | 1.7 | 6.2 | |
| Bases not Found | 260 | 435 | 3155 | 10,615 | 62,715 | |
| % | 1 | 0.4 | 1 | 1.3 | 2.5 | |
| N50 | NA | NA | NA | NA | 5599 | |
| Average Length | 130 | 217.5 | 315.5 | 758.2 | 497.7 | |
| Minimum Length | 99 | 99 | 56 | 56 | 52 | |
| Maximum Length | 161 | 336 | 2521 | 5941 | 18,158 | |
From each benchmark, we took only the fragment file in FASTA format, and from it we computed the overlaps among all fragments considering that reverse-complement fragments are also independent fragments (In the original benchmarks, there is a file of overlaps where reverse-complements are not considered as independent fragments). To compute overlaps, we used a trie (prefix tree). The computed overlaps are all larger than 20 bases. From these overlaps other sets of test data were obtained: one discarding redundant overlaps because of transitivity, and the other one, computing the MST. In all of the cases, the minimum agreement in Algorithm 5 was 4. The contigs obtained in each experiment were searched in the complete genome [20].
In Experiment 1, we used all of the overlaps larger than 20 bases and executed Algorithm 1 for the two objective functions. The results are presented in Table 5, Table 6 and Table 7.

Table 5.
Experiments summary.
| Problem | |||||||
|---|---|---|---|---|---|---|---|
| Algorithm | Fragments | 22,448 | 89,718 | 298,194 | 730,201 | 2,278,504 | |
| Edena | Edena | Contigs Found | 184 | 256 | 565 | 823 | 1920 |
| % | 98.9 | 99.2 | 98.3 | 98.3 | 93.8 | ||
| Bases Found | 26,024 | 102,249 | 310,965 | 777,583 | 2,463,563 | ||
| % | 99 | 99.6 | 99 | 98.7 | 97.5 | ||
| Algorithm 1 | F1 Objective Function, all Overlaps. | Contigs Found | 74 | 101 | 149 | 204 | 480 |
| % | 90.2 | 88.6 | 91.4 | 91.1 | 94.1 | ||
| Bases Found | 15,822 | 70,250 | 206,826 | 463,582 | 1,102,152 | ||
| % | 81.8 | 83 | 86.1 | 83.9 | 83.4 | ||
| Algorithm 1 | F2 Objective Function, all Overlaps | Contigs found | 74 | 102 | 146 | 189 | 450 |
| % | 90.2 | 89.5 | 89.6 | 84.4 | 88.2 | ||
| Bases found | 15,515 | 70,843 | 189,927 | 369,001 | 931,343 | ||
| % | 81.5 | 83.8 | 79 | 66.8 | 69.9 | ||
| Algorithm 1 | F1 Objective Function, no Transitive overlaps | Contigs found | 74 | 102 | 149 | 204 | 481 |
| % | 90.2 | 89.5 | 91.4 | 91.1 | 93.9 | ||
| Bases found | 15,806 | 71,652 | 206,826 | 462,774 | 1,103,587 | ||
| % | 83.7 | 84.6 | 86.1 | 83.9 | 82.7 | ||
| Algorithm 1 | F2 Objective Function, no Transitive Overlaps | Contigs found | 75 | 103 | 142 | 181 | 417 |
| % | 91.5 | 90.4 | 87.1 | 80.8 | 81.4 | ||
| Bases found | 15,599 | 72,245 | 174,244 | 320,502 | 791,376 | ||
| % | 84 | 85.4 | 72.5 | 58.1 | 58.9 | ||
| Algorithm 1 | F1 Objective Function, MST | Contigs found | 304 | 1827 | 5980 | 15,443 | 46,187 |
| % | 91 | 97 | 98.4 | 98.9 | 95.7 | ||
| Bases found | 35,980 | 256,641 | 815,994 | 2,081,306 | 6,208,258 | ||
| % | 89.8 | 96.6 | 98.1 | 98.7 | 93.9 | ||
| Algorithm 5 | F1 Objective function, no Transitive Edges | Contigs found | 74 | 102 | 150 | 205 | 480 |
| % | 90.2 | 88.7 | 91.5 | 91.1 | 94.1 | ||
| Bases found | 15,822 | 70,318 | 206,927 | 463,684 | 1,102,152 | ||
| % | 81.8 | 83 | 86.1 | 83.9 | 83.4 | ||

Table 6.
Algorithm 1, F1 objective function, all overlaps.
| Problem | ||||||
|---|---|---|---|---|---|---|
| Fragments | 22,448 | 89,718 | 298,194 | 730,201 | 2,278,504 | |
| Contigs Obtained | 82 | 114 | 163 | 224 | 510 | |
| Total Number of Bases | 19,343 | 84,659 | 240,314 | 552,408 | 1,321,969 | |
| Contigs Found | Contigs Found | 74 | 101 | 149 | 204 | 480 |
| % | 90.2 | 88.6 | 91.4 | 91.1 | 94.1 | |
| Bases Found | 15,822 | 70,250 | 206,826 | 463,582 | 1,102,152 | |
| % | 81.8 | 83 | 86.1 | 83.9 | 83.4 | |
| N50 | 360 | 1614 | 3326 | 4937 | 4499 | |
| Average Length | 213.8 | 695.5 | 1388.10 | 2272.50 | 2296.20 | |
| Minimum Length | 54 | 58 | 54 | 62 | 53 | |
| Maximum Length | 882 | 7261 | 10,943 | 22,745 | 24,396 | |
| Contigs not Found | Contigs not Found | 8 | 13 | 14 | 20 | 30 |
| % | 9.8 | 11.4 | 8.6 | 8.9 | 5.9 | |
| Bases not Found | 3521 | 14,409 | 33,488 | 88,826 | 219,817 | |
| % | 18.2 | 17 | 13.9 | 16.1 | 16.6 | |
| N50 | 758 | 2308 | 3954 | 7258 | 11,798 | |
| Average Length | 440.1 | 1108.40 | 2392.00 | 4441.30 | 7327.20 | |
| Minimum Length | 95 | 95 | 95 | 181 | 255 | |
| Maximum Length | 826 | 3703 | 6809 | 9542 | 23,614 | |

Table 7.
Algorithm 1, F2 objective function, all overlaps.
| Problem | ||||||
|---|---|---|---|---|---|---|
| Fragments | 22,448 | 89,718 | 298,194 | 730,201 | 2,278,504 | |
| Contigs Obtained | 82 | 114 | 163 | 224 | 510 | |
| Total Number of Bases | 19,028 | 84,584 | 240,280 | 552,509 | 1,331,757 | |
| Contigs Found | Contigs Found | 74 | 102 | 146 | 189 | 450 |
| % | 90.2 | 89.5 | 89.6 | 84.4 | 88.2 | |
| Bases Found | 15,515 | 70,843 | 189,927 | 369,001 | 931,343 | |
| % | 81.5 | 83.8 | 79 | 66.8 | 69.9 | |
| N50 | 356 | 1527 | 3184 | 4298 | 4201 | |
| Average Length | 209.7 | 694.5 | 1300.90 | 1952.40 | 2069.70 | |
| Minimum Length | 54 | 58 | 54 | 59 | 53 | |
| Maximum Length | 882 | 7261 | 10,943 | 21,185 | 16,135 | |
| Contigs not Found | Contigs not Found | 8 | 12 | 17 | 35 | 60 |
| % | 9.8 | 10.5 | 10.4 | 15.6 | 11.8 | |
| Bases not Found | 3513 | 13,741 | 50,353 | 183,508 | 400,414 | |
| % | 18.5 | 16.2 | 21 | 33.2 | 30.1 | |
| N50 | 758 | 2308 | 6336 | 7620 | 9472 | |
| Average Length | 439.1 | 1145.10 | 2961.90 | 5243.10 | 6673.60 | |
| Minimum Length | 95 | 96 | 103 | 181 | 251 | |
| Maximum Length | 826 | 3703 | 7626 | 22,745 | 24,396 | |
From the DNA fragment assembly point of view, we are interested in large contigs with no errors. The most important elements to be computed are the number of bases and the contigs that were found in the complete genome, as well as the mean length of each contig. When we compare the results obtained by Algorithm 1 for F1 and F2 using all overlaps, we find that F1 is a little bit better than F2, except in the number of bases found for problem 89,718. In terms of multi objective function optimization, the solution obtained for F1 is not enough to dominate the solution obtained by F2, but since it is better in most of the test, we can say that it is almost dominant. In the other experiments, we find a similar situation, where F1 is almost dominant with respect to F2.
For Experiment 2, we excluded transitive overlaps and used Algorithm 1 for F1 and F2. The results are given in Table 5, Table 8 and Table 9.

Table 8.
Algorithm 1, F1 objective function, no transitive overlaps.
| Problem | ||||||
|---|---|---|---|---|---|---|
| Fragments | 22,448 | 89,718 | 298,194 | 730,201 | 2,278,504 | |
| Contigs Obtained | 82 | 114 | 163 | 224 | 512 | |
| Total Number of Bases | 18,879 | 84,646 | 240,314 | 551,600 | 1,333,881 | |
| Contigs Found | Contigs Found | 74 | 102 | 149 | 204 | 481 |
| % | 90.2 | 89.5 | 91.4 | 91.1 | 93.9 | |
| Bases Found | 15,806 | 71,652 | 206,826 | 462,774 | 1,103,587 | |
| % | 83.7 | 84.6 | 86.1 | 83.9 | 82.7 | |
| N50 | 360 | 1527 | 3326 | 4937 | 4499 | |
| Average Length | 213.6 | 702.5 | 1388.10 | 2268.50 | 2294.40 | |
| Minimum Length | 54 | 58 | 54 | 62 | 53 | |
| Maximum Length | 882 | 7261 | 10,943 | 22,745 | 24,396 | |
| Contigs not Found | Contigs not Found | 8 | 12 | 14 | 20 | 31 |
| % | 9.8 | 10.5 | 8.6 | 8.9 | 6.1 | |
| Bases not Found | 3073 | 12,994 | 33,488 | 88,826 | 230,294 | |
| % | 16.3 | 15.4 | 13.9 | 16.1 | 17.3 | |
| N50 | 539 | 2308 | 3954 | 7258 | 11,657 | |
| Average Length | 384.1 | 1082.80 | 2392.00 | 4441.30 | 7428.80 | |
| Minimum Length | 95 | 95 | 95 | 181 | 255 | |
| Maximum Length | 826 | 3703 | 6809 | 9542 | 23,614 | |
In general, we found that F1 is better than F2 without dominating it. Comparing the results where transitive overlaps are excluded (Table 8 and Table 9 or Table 5) to those where they are not (Table 6 and Table 7 or Table 5), we can see that the results are similar for F1, hence it is not clear whether it is better to exclude or not to exclude transitive overlaps. There is, however, an obvious advantage of excluding transitive overlaps, which is that the problem size is reduced and requires less computational resources. So, our recommendation is to exclude transitive overlaps.
Comparing our results so far to Edena, we find out that we obtained fewer correct bases and more contigs that are not in the genome, but the length of our contigs is better.

Table 9.
Algorithm 1, F2 objective function, no transitive overlaps.
| Problem | ||||||
|---|---|---|---|---|---|---|
| Fragments | 22,448 | 89,718 | 298,194 | 730,201 | 2,278,504 | |
| Contigs Obtained | 82 | 114 | 163 | 224 | 512 | |
| Total Number of Bases | 18,579 | 84,571 | 240,265 | 551,701 | 1,343,637 | |
| Contigs Found | Contigs Found | 75 | 103 | 142 | 181 | 417 |
| % | 91.5 | 90.4 | 87.1 | 80.8 | 81.4 | |
| Bases Found | 15,599 | 72,245 | 174,244 | 320,502 | 791,376 | |
| % | 84 | 85.4 | 72.5 | 58.1 | 58.9 | |
| N50 | 356 | 1527 | 2984 | 3910 | 4135 | |
| Average Length | 208 | 701.4 | 1227.10 | 1770.70 | 1897.80 | |
| Minimum Length | 54 | 58 | 54 | 59 | 53 | |
| Maximum Length | 882 | 7,261 | 10,943 | 10,648 | 16,135 | |
| Contigs not Found | Contigs not Found | 7 | 11 | 21 | 43 | 95 |
| % | 8.5 | 9.6 | 12.9 | 19.2 | 18.6 | |
| Bases not Found | 2980 | 12,326 | 66,021 | 231,199 | 552,261 | |
| % | 16 | 14.6 | 27.5 | 41.9 | 41.1 | |
| N50 | 539 | 2308 | 6336 | 8135 | 7554 | |
| Average Length | 425.7 | 1120.50 | 3143.90 | 5376.70 | 5813.30 | |
| Minimum Length | 95 | 96 | 103 | 181 | 251 | |
| Maximum Length | 826 | 3703 | 10,648 | 22,745 | 24,396 | |

Table 10.
Algorithm 1, F1 objective function, Minimum Spanning Tree (MST).
| Problem | ||||||
|---|---|---|---|---|---|---|
| Fragments | 22,448 | 89,718 | 298,194 | 730,201 | 2,278,504 | |
| Contigs Obtained | 334 | 1883 | 6080 | 15,618 | 48,263 | |
| Total Number of Bases | 40,076 | 265,584 | 831,449 | 2,109,070 | 6,613,747 | |
| Contigs Found | Contigs Found | 304 | 1827 | 5980 | 15,443 | 46,187 |
| % | 91 | 97 | 98.4 | 98.9 | 95.7 | |
| Bases Found | 35,980 | 256,641 | 815,994 | 2,081,306 | 6,208,258 | |
| % | 89.8 | 96.6 | 98.1 | 98.7 | 93.9 | |
| N50 | 135 | 165 | 154 | 153 | 153 | |
| Average Length | 118.4 | 140.5 | 136.5 | 134.8 | 134.4 | |
| Minimum Length | 62 | 62 | 61 | 57 | 57 | |
| Maximum Length | 446 | 660 | 747 | 894 | 1152 | |
| Contigs not Fund | Contigs not Found | 30 | 56 | 100 | 175 | 2076 |
| % | 9 | 3 | 1.6 | 1.1 | 4.3 | |
| Bases not Found | 4096 | 8943 | 15,455 | 27,764 | 405,489 | |
| % | 10.2 | 3.4 | 1.9 | 1.3 | 6.1 | |
| N50 | 154 | 199 | 198 | 194 | 245 | |
| Average Length | 136.5 | 159.7 | 154.6 | 158.7 | 195.3 | |
| Minimum Length | 64 | 65 | 65 | 64 | 63 | |
| Maximum Length | 362 | 481 | 481 | 493 | 1130 | |
In Experiment 3, we obtained the Minimum Spanning Tree (MST) from all overlaps using our version of Kruskal’s algorithm. We only show the results for F1 (Table 5 and Table 10). In this case, we were able to find much more bases in the genome than in previous experiments, including Edena, but the size of our contigs is small. There appears to be a tradeoff between the number of bases that can be found and contig length.
In other experiments, we used Algorithm 4 without transitive overlaps, obtaining similar results to those of Algorithm 1 for F1 (F1 was again better than F2). Analyzing the contigs obtained by the algorithm, we found that if the contig is split at the edge that joins the cycle with the path, we have a better chance of finding both contigs. Therefore, we modified Algorithm 4 making d(v) = 0 in Step 2.2.1.1 and repeated Experiment 4 without transitive overlaps. In this case, the objective function F1 was better than F2 without being dominant. These results are given in Table 5 and Table 11.

Table 11.
Algorithm 5, F1 objective function, no transitive edges.
| Problem | ||||||
|---|---|---|---|---|---|---|
| Fragments | 22,448 | 89,718 | 298,194 | 730,201 | 2,278,504 | |
| Contigs Obtained | 82 | 115 | 164 | 225 | 510 | |
| Total Number of Bases | 19,343 | 84,727 | 240,415 | 552,510 | 1,321,969 | |
| Contigs Found | Contigs Found | 74 | 102 | 150 | 205 | 480 |
| % | 90.2 | 88.7 | 91.5 | 91.1 | 94.1 | |
| Bases Found | 15,822 | 70,318 | 206,927 | 463,684 | 1,102,152 | |
| % | 81.8 | 83 | 86.1 | 83.9 | 83.4 | |
| N50 | 360 | 1614 | 3326 | 4937 | 4499 | |
| Average Length | 213.8 | 689.4 | 1379.50 | 2261.90 | 2296.20 | |
| Minimum Length | 54 | 58 | 54 | 62 | 53 | |
| Maximum Length | 882 | 7261 | 10,943 | 22,745 | 24,369 | |
| Contigs not Found | Contigs not Fund | 8 | 13 | 14 | 20 | 30 |
| % | 9.8 | 11.3 | 8.5 | 8.9 | 5.9 | |
| Bases not Found | 3521 | 14,409 | 33,488 | 88,826 | 219,817 | |
| % | 18.2 | 17 | 13.9 | 16.1 | ||
| N50 | 758 | 2308 | 3954 | 7258 | 11,798 | |
| Average Length | 440.1 | 1108.40 | 2392.00 | 4441.30 | 7327.20 | |
| Minimum Length | 95 | 95 | 95 | 181 | 255 | |
| Maximum Length | 826 | 3703 | 6809 | 9542 | 23,614 | |
In an analysis of those contigs that were not found in the genome, we considered the possibility of splitting them in two or more pieces hoping that all of them could be found. There are few cases in which contigs should be divided; in problem 730,201, using the modified Algorithm 4 with F1, there were 513 contigs from which 414 were found directly, 76 were split in two to be found, 14 in three, 10 in four or more pieces, and two produced pieces that were too small to be considered. With appropriate rules, it should be possible to find the correct split points in most of the cases, as other assemblers do. We also analyzed residual paths, after removing paths of maximum length, from which we considered the possibility of recovering several long contings, which we will do in the future.
5. Conclusions and Future Work
In order to assemble DNA, it is possible to use traditional graph theory concepts being careful to use only linear algorithms due to the large amount of data that is handled. With this idea, we developed a constant time heap, appropriate for this particular case (and maybe to other cases as well), which allowed us to reduce the time complexity of other algorithms, such as Prim’s and Kruskal’s, making them linear.
If we compare the results of the objective functions F1 and F2, even though one does not dominate over the other, better results are obtained using F1, hence we recommend its use. We also recommend the removal of transitive overlaps because of resource reduction considerations, even though the results of the assembly are almost the same for function F1. The use of the MST considerably improves the number of correct bases, but the contigs obtained in this way are too small. It can be seen from the experiments that there is a tradeoff between contig length and the number of bases detected. Comparing our results to those of Edena is not completely objective since we do not apply heuristics after the algorithms are executed in order to refine the solutions, but Edena (as well as the Velvet assembler) do so intensively. In any case, compared to Edena, our method produced, in some cases, less bases but longer contigs, while, in other cases, we found more bases, but shorter contigs, especially when using MST. Therefore, the problem must be considered as a multi objective optimization, with an objective function that is able to maximize the number of mean contig length, giving the user a Pareto Front from which he can obtain the most convenient solution according to his particular criteria.
Our future work includes:
- Developing rules to split contigs in such a way that most of the pieces can be found.
- Attempting to recover other contigs after extracting the longest ones.
- Implementing a solution to DNA fragment assembly as a multi objective optimization problem.
Acknowledgments
This work has been developed with the support of Universidad Iberoamericana.
Author Contributions
Guillermo Mallén-Fullerton started the idea and developed the algorithms. Emilio Quiroz-Ibarra developed test programs and provided helpful observations about the implementation problems associated with some of the algorithms. Antonio Miranda and Guillermo Fernández-Anaya provided algorithms complexity analysis and observations to improve it. Guillermo Fernández-Anaya collaborated in the experiments design and interpretation and Antonio Miranda wrote the English version of the article. All authors approved the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Watson, J.D.; Crick, F.H. Molecular structure of nucleic acids. Nature 1953, 171, 737–738. [Google Scholar] [CrossRef] [PubMed]
- Sanger, F.; Nicklen, S.; Coulson, A.R. DNA sequencing with chain-terminating inhibitors. Proc. Natl. Acad. Sci. 1977, 74, 5463–5467. [Google Scholar] [CrossRef] [PubMed]
- Staden, R. A strategy of DNA sequencing employing computer programs. Nucl. Acid. Res. 1979, 6, 2601–2610. [Google Scholar] [CrossRef]
- Van Belkum, A.; Scherer, S.; van Alphen, L.; Verbrugh, H. Short-sequence DNA repeats in prokaryotic genomes. Microbiol. Mol. Biol. Rev. 1998, 62, 275–293. [Google Scholar]
- Salzberg, S.L.; Phillippy, A.M.; Zimin, A.; Puiu, D.; Magoc, T.; Koren, S.; Yorke, J.A. GAGE: A critical evaluation of genome assemblies and assembly algorithms. Gen. Res. 2012, 22, 557–567. [Google Scholar] [CrossRef] [PubMed]
- Shendure, J.; Ji, H. Next-generation DNA sequencing. Nat. Biotechnol. 2008, 26, 1135–1145. [Google Scholar] [CrossRef] [PubMed]
- Pevzner, P.A.; Tang, H.; Waterman, M.S. An Eulerian path approach to DNA fragment assembly. Proc. Natl. Acad. Sci. 2001, 98, 9748–9753. [Google Scholar] [CrossRef] [PubMed]
- Parsons, R.J.; Forrest, S.; Burks, C. Genetic algorithms for DNA sequence assembly. In Proceedings of the First International Conference on Intelligent Systems for Molecular Biology (ISMB), Bethesda, MD, USA, 6–9 July 1993; pp. 310–318.
- Krause, J.; Cordeiro, J.; Parpinelli, R.S.; Lopes, H.S. A Survey of Swarm Algorithms Applied to Discrete Optimization Problems. In Swarm Intelligence and Bio-inspired Computation: Theory and Applications; Elsevier Science Publishers: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Alba, E.; Luque, G. A new local search algorithm for the DNA fragment assembly problem. In Evolutionary Computation in Combinatorial Optimization; Springer: Berlin/Heidelberg, Germany, 2007; pp. 1–12. [Google Scholar]
- Luque, G.; Alba, E. Metaheuristics for the DNA fragment assembly problem. Int. J. Comput. Intel. Res. 2005, 1, 98–108. [Google Scholar] [CrossRef]
- Firoz, J.S.; Rahman, M.S.; Saha, T.K. Bee algorithms for solving DNA fragment assembly problem with noisy and noiseless data. In Proceedings of the 14th ACM Annual Conference on Genetic and Evolutionary Computation, Philadelphia, PA, USA, 7–11 July 2012; pp. 201–208.
- Mallen-Fullerton, G.M.; Fernandez-Anaya, G. DNA fragment assembly using optimization. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation (CEC), Cancun, Mexico, 20–23 June 2013; pp. 1570–1577.
- Gallant, J.; Maier, D.; Astorer, J. On finding minimal length superstrings. J. Comput. Syst. Sci. 1980, 20, 50–58. [Google Scholar] [CrossRef]
- Prim, R.C. Shortest connection networks and some generalizations. Bell Syst. Tech. J. 1957, 36, 1389–1401. [Google Scholar] [CrossRef]
- Kruskal, J.B. On the shortest spanning subtree of a graph and the traveling salesman problem. Proc. Am. Math. Soc. 1956, 7, 48–50. [Google Scholar] [CrossRef]
- Hopcroft, J.E.; Ullman, J.D. Set merging algorithms. SIAM J. Comput. 1973, 2, 294–303. [Google Scholar] [CrossRef]
- Bonfield, J.K.; Smith, K.; Staden, R. A new DNA sequence assembly program. Nucl. Acid. Res. 1995, 23, 4992–4999. [Google Scholar] [CrossRef]
- Mallén-Fullerton, G.M.; Hughes, J.A.; Houghten, S.; Fernández-Anaya, G. Benchmark datasets for the DNA fragment assembly problem. Int. J. Bio-Inspir. Comput. 2013, 5, 384–394. [Google Scholar] [CrossRef]
- Staphylococcus aureus subsp. aureus MW2 DNA, complete genome, GenBank: BA000033.2. Available online: http://www.ncbi.nlm.nih.gov/nuccore/47118312?report=fasta (accessed on 3 June 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).